Introduction

The interplay between quantum physics and machine learning gives rise to an emergent research frontier of quantum machine learning that has attracted tremendous attention recently1,2,3,4. In particular, certain carefully designed quantum algorithms for machine learning, or more broadly artificial intelligence, may exhibit exponential advantages compared to their best possible classical counterparts2,3,4,5,6,7,8. An intriguing example concerns quantum generative adversarial networks (QGANs)7, where near-term quantum devices have the potential to showcase quantum supremacy9 with real-life practical applications. Indeed, applications of QGANs with potential quantum advantages in generating high-resolution images10,11, loading classical data12, and discovering small molecular drugs13 have been investigated actively at the current stage.

The general framework of QGANs consists of a generator learning to generate statistics for data mimicking those of a true data set, and a discriminator trying to discriminate generated data from true data7,12,14,15,16,17,18. The generator and discriminator follow an adversarial learning procedure to optimize their strategies alternatively and arrive at a Nash equilibrium point, where the generator learns the underlying statistics of the true data and the discriminator can no longer distinguish the difference between the true and generated data. In a previous QGAN experiment16, the generator is trained via the adversarial learning process to replicate the statistics of the single-qubit quantum data output from a quantum channel simulator. However, the implementation of quantum gradient, which is crucial for training QGANs6, is still absent. In addition, the involvement of entanglement in QGANs, which is a characterizing feature of quantumness and a vital resource for quantum supremacy, has not yet been achieved during the learning process3.

In this article, we add these two crucial yet missing blocks by reporting an experiment realization of a QGAN based on a programmable superconducting processor with multiple qubits and all-to-all qubit connectivity previously reported in ref. 19. Superconducting qubits are a promising platform for realizing QGANs, owing to their flexible design, excellent scalability, and remarkable controllability. In our implementation, both the generator and discriminator are composed of multiqubit parameterized quantum circuits, also referred to as quantum neural networks in some contexts20,21,22,23. Here, we benchmark the functionality of the quantum gradient method by learning an arbitrary mixed state, where the state is replicated with a fidelity up to 0.999. We further utilize our QGAN to learn an classical XOR gate, and the generator is successfully trained to exhibit a truth table close to that of the XOR gate.

Results

Framework of QGAN algorithm

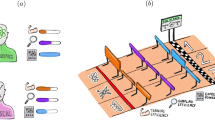
We first introduce a general recipe for our QGAN and then apply it to two typical scenarios: learning quantum states and the classical XOR gate. The overall structure of the QGAN is outlined in Fig. 1a, which includes an input label, a real source (R), a generator (G), a discriminator (D), and a quantum gradient subroutine. The input label sorts the training data stored in R, and also instructs G to generate data samples mimicking R. D receives the label and corresponding data samples from either G or R, and then evaluates with appropriate scores, based on which a loss function V is constructed to differentiate between R and G. The adversarial training procedure is repeated in conjugation with the quantum gradient subroutine, which yields the partial derivatives of V with respect to the parameters constructing D or G, so as to maximize V for the optimal configuration of D and to minimize V for the optimal G in terms of the chosen values of the constructing parameters.

Fig. 1: QGAN algorithm and its implementation.
figure 1

a Overview of the QGAN logic. b Sketch of the superconducting processor used to implement the QGAN algorithm, where the five qubits, Q0–Q4, are interconnected by the central bus resonator. c An instance of the experimental sequences for fulfilling the QGAN algorithm to learn the classical XOR gate. Both G and D are parameterized quantum circuits consisting of n layers of the multiqubit entangling gate UENT and n + 1 single-qubit rotations \({\theta }_{j,l,m}^{x/z}\), where l = n + 1 is the layer index of single-qubit rotations, m ∈ {G, D}, and the superscript (x or z) refers to the axis in the Bloch sphere around which the state of Qj is rotated by the angle θ. Shown is the training sequence on G to optimize its parameter \({\theta }_{3,1,{\rm {G}}}^{x}\) based on the quantum gradient subroutine, which includes two Hadamard gates (H), two controlled rotation gates, and a π/2 rotation around x-axis (X/2). In this instance, both Q1–Q2 and Q3–Q4 store the input label, and D’s output score is encoded in Q1 by \({S}_{n}^{{{{\rm{D}}}},{{{\rm{R/G}}}}}=\langle {\sigma }_{1}^{z}\rangle /2+1/2\), which can be obtained by directly measuring Q1. Q0’s \(\langle {\sigma }_{0}^{z}\rangle\) gives the score derivative with respect to the rotational angle parameter right before the first controlled rotation gate, i.e., \(\partial \langle {\sigma }_{1}^{z}\rangle /\partial {\theta }_{3,1,{\rm {G}}}^{x}=-\langle {\sigma }_{0}^{z}\rangle\) for the sequence displayed here. The first controlled rotation gate can be either a controlled X (CNOT) or controlled Z (CZ) gate depending on the single-qubit rotation axis it follows as shown in the lower right box.

Full size image

Specifically, denoting the sets of parameters constructing G and D as \({\overrightarrow{\theta }}_{{{{\rm{G}}}}}\) and \({\overrightarrow{\theta }}_{{{{\rm{D}}}}}\), respectively, the loss function V is written as

$$V=\frac{1}{N}\mathop{\sum }\limits_{n=1}^{N}\left[{S}_{n}^{{{{\rm{D}}}},{{{\rm{R}}}}}({\overrightarrow{\theta }}_{{{{\rm{D}}}}})-{S}_{n}^{{{{\rm{D}}}},{{{\rm{G}}}}}({\overrightarrow{\theta }}_{{{{\rm{D}}}}},{\overrightarrow{\theta }}_{{{{\rm{G}}}}})\right],$$

where N is the total number of data samples selected for training and \({S}_{n}^{{{{\rm{D}}}},{{{\rm{R}}}}}\) (\({S}_{n}^{{{{\rm{D}}}},{{{\rm{G}}}}}\)) represents the score of the nth data sample from R (G) evaluated by D. G and D are trained alternately with D being trained first. In D’s turn, we maximize the loss function by iteratively optimizing \({\overrightarrow{\theta }}_{{{{\rm{D}}}}}\) according to \({\overrightarrow{\theta }}_{{{{\rm{D}}}}}^{i+1}={\overrightarrow{\theta }}_{{{{\rm{D}}}}}^{i}+{\alpha }_{{{{\rm{D}}}}}{\nabla }_{{\overrightarrow{\theta }}_{{{{\rm{D}}}}}}V\), where i is the iteration step index and \({\nabla }_{{\overrightarrow{\theta }}_{{{{\rm{D}}}}}}V\) denotes the gradient vector of the loss function at the ith step; we train G by minimizing the square of the loss function with an iteration relation \({\overrightarrow{\theta }}_{{{{\rm{G}}}}}^{i+1}={\overrightarrow{\theta }}_{{{{\rm{G}}}}}^{i}-{\alpha }_{{{{\rm{G}}}}}{\nabla }_{{\overrightarrow{\theta }}_{{{{\rm{G}}}}}}{V}^{2}\). The learning rates can be adjusted by tuning αD and αG which are typically on the order of unity.

An important quantity that plays a vital role in training our QGAN is the gradient of the loss function with respect to a given parameter. Interestingly, owing to the special structures of our quantum circuits for the generator and the discriminator, a common approach to obtain such a gradient is to shift the corresponding parameter by ±π/2 and measure the loss function at the shifted values24. In our experiment, we employ an effective quantum method—the Hadamard test quantum algorithm25—to obtain the gradient for the first time. This algorithm can reduce half of the time in comparison with the common approach to finish the training, at the expense of an additional auxiliary qubit and two controlled gates (see Supplementary Note 4 for more details). At each round of the training process, the parameters of the discriminator (or generator) are updated simultaneously after the gradients for all parameters are obtained, and a quantum process tomography (QPT) is performed to characterize the overlap fidelity between the generated data based on the updated parameters and the true data.

Experimental implementation of QGAN

The above mentioned QGAN is experimentally realized on a superconducting quantum processor using five frequency-tunable transmon qubits labeled as Qj for j = 0–4, where all qubits are interconnected by a central bus resonator as illustrated in Fig. 1b. The role arrangement of Q0–Q4 can be visualized by the exemplary experimental sequence shown in Fig. 1c. Q0 is to assist the quantum gradient subroutine. Q1–Q2 stores the label which is passed to D, with the output score encoded in Q1 by \({S}_{n}^{{{{\rm{D}}}},{{{\rm{R/G}}}}}=\langle {\sigma }_{1}^{z}\rangle /2+1/2\). For the experimental instances with G inserted, Q3–Q4 also stores the label as the input to G and the output data sample from G is passed to D via Q3; for the experimental instances with R in replacement of G, only Q3 stores the data sample from R as designated by the label. Details of the device parameters can be found in the “Methods” section and Supplementary Note.

By tuning the qubits on resonance but detuned from the bus resonator in frequency, these qubits can be all effectively connected, which enables the flexible realizations of the multiqubit entangling gates among arbitrarily selected qubits. The all-to-all interactions are described in the dispersive regime by the effective Hamiltonian \({H}_{{{{\rm{I}}}}}=\sum {\lambda }_{jk}({\sigma }_{j}^{+}{\sigma }_{k}^{-}+{\sigma }_{j}^{-}{\sigma }_{k}^{+})\), where \({\sigma }_{j}^{+}\) (\({\sigma }_{j}^{-}\)) denotes the raising (lowering) operator of Qj, and λjk is the effective coupling strength between Qj and Qk mediated by the bus resonator. Evolution under this Hamiltonian for an interaction time τ leads to the entangling operator with the form of \({U}_{{{{\rm{ENT}}}}}={{\rm {e}}}^{-i{H}_{{{{\rm{I}}}}}\tau }\), which can steer the interacting qubits into highly entangled state. In our QGAN, the parameterized quantum circuits that comprise G and D leverage the naturally available multiqubit UENTs, with the interaction time of the two-qubit UENT fixed at around 50 ns for G and the three-qubit one fixed at around 55 ns for D. We stress that, compared to architectures with limited connectivity8,9,26, the all-to-all connectivity for the device used in this experiment could reduce the total circuit depths (hence the running time) in implementing both the generator and discriminator, which is a crucial merit given that the coherence time is limited.

As laid out in Fig. 1c, the entangling operators UENT are interleaved with the single-qubit X and Z rotations, which successively rotate Qj around x- and z-axis in the Bloch sphere by angles of \({\theta }_{j,l,m}^{x}\) and \({\theta }_{j,l,m}^{z}\), where l is the layer index and m ∈ {G, D}. The lengths of the X and Z rotations are fixed at 30 and 20 ns, respectively. Taking into account the experimental imperfections, we perform numerical simulations to decide the depths of the interleaved layers consisting of UENT and the single-qubit rotations, for a balance between the learning fidelity and efficiency, see Supplementary Discussion for the discussion of the circuit depth. For example, to learn the XOR gate, the circuit layer depths are set to be n = 2 and 3 for G and D, respectively, as shown in Fig. 1c.

The QGAN learning process is guided by the gradient of the loss function with respect to \({\overrightarrow{\theta }}_{{{{\rm{G}}}}}\) and \({\overrightarrow{\theta }}_{{{{\rm{D}}}}}\). To obtain these gradients, we adopt the method of Hadamard test14,25, which is illustrated in the sequence instance in Fig. 1c. For the partial derivative with respect to the parameter \({\theta }_{j,l,m}^{x}\) (\({\theta }_{j,l,m}^{z}\)), we insert the first controlled-X (Z) gate right after the single-qubit X (Z) rotation containing this parameter, with Qj as the target. The second controlled-Z gate is applied at the end of the training sequence with Q1 as the target. The partial derivative of Q1’s \(\langle {\sigma }_{1}^{z}\rangle\), which relates to D’s output score, is given by \(\partial \langle {\sigma }_{1}^{z}\rangle /\partial {\theta }_{j,l,m}^{x(z)}=-\langle {\sigma }_{0}^{z}\rangle\), which can be directly obtained by measuring Q0 and used in computing the gradient of the loss function. More details about the experimental realizations of the controlled-X (Z) gates, as well as the theoretical and experimental verifications of the quantum gradient method are presented in Supplementary Note 4.

Learning an arbitrary single-qubit quantum state

To benchmark the functionality of the quantum gradient method and the learning efficiency of our QGAN circuit, we first train an arbitrary mixed state as data which is a simulation of quantum channel. As shown in the inset of Fig. 2a, the mixed state for Q3 reads \({\rho }_{{{{\rm{R}}}}}=\left(\begin{array}{ll}0.7396&0.0431+0.3501i\\ 0.0431-0.3501i&0.2604\end{array}\right)\), which is generated by applying two single-qubit X rotations (with the rotation angles of 1.35 on Q3 and 0.68 on Q4) followed by the UENT gate on Q3 and Q4. Correspondingly, G is set up with a single layer and two parameters describing the single-qubit X rotation angles during the training, while D remains the one shown in Fig. 1c with 3 layers and all 18 parameters being trained. The trajectories of the loss function and scores of data from R/G during the training process are recorded and plotted in Fig. 2a. We optimize D at the beginning of the training to enlarge the distance between SD,R and SD,G. At the end of this turn, D can discriminate datasets from R and G with the maximum probability. In G’s turn, SD,G moves towards SD,R which means that G is learning the behavior of R. Each turn ends when the optimal point of the loss function is reached, or the iteration number goes over a preset limit. As the adversarial learning process goes on, the value of the loss function oscillates from turn to turn and eventually converges to 0 indicating that the learning arrives at a Nash equilibrium point, where G is able to produce a mixed state ρG which resembles ρR and D can no longer distinguish between them7,14. The training process is characterized by the similarity between datasets generated by G and R, which is quantified by the state fidelity \(F({\rho }_{{{{\rm{R}}}}},{\rho }_{{{{\rm{G}}}}})={{{\rm{Tr}}}}(\sqrt{{\rho }_{{{{\rm{R}}}}}}{\rho }_{{{{\rm{G}}}}}\sqrt{{\rho }_{{{{\rm{R}}}}}})\), As shown in Fig. 2a, The average fidelity increases rapidly with the iteration steps, indicating the effectiveness of the adversarial learning. The density matrices ρR and the final ρG are plotted in Fig. 2b, which yields a state fidelity of around 0.999. We mention that the QGAN demonstrated in our experiment is distinct from quantum tomography or state preparation in essential ways. Here, we carry out the tomography process merely to benchmark the performance of the QGAN. In practical applications of QGAN with more qubits, this tomography process is not necessary and one may use other more efficient approaches to measure the performance.

Fig. 2: QGAN performance in learning a mixed state.
figure 2

a Tracking of the loss function V, the output scores SD,R/G, and the state fidelity between R/G’s output states F during the adversarial training procedure with learning rates αD = 0.8 and αG = 0.6. The alternate training stages of D and G are marked by red and white regions, respectively. In each stage, the maximum step number is limited to 50 for D and 100 for G. Inset: the quantum circuit for generating ρR for Q3. The same circuit is also used for G, with random initial guesses for the two rotational angles which are then optimized. b Elements of the real and imaginary parts of the output density matrices of R(G). The numbers in the parentheses denotes the corresponding values for G.

Full size image

Learning the statistics of an XOR gate

Now we apply the recipe to train the QGAN to replicate the statistics of an XOR gate, which is a classical gate with input–output rules 00 → 0, 01 → 1, 10 → 1, and 11 → 0. The input bit values store as labels in Q1 and Q2, which is performed to let the discriminator know the corresponding input state of the state generated by the generator. We use the computational basis state \(\left|0\right\rangle\) and \(\left|1\right\rangle\) to encode the classical data 0 and 1, respectively. We randomly initialize the parameters of both D and G, and then update them alternately following the rules outlined above. The trajectories of the key parameters benchmarking the QGAN performance during the training process are plotted in Fig. 3a, with the evolutions of two representative parameters constructing D and G shown in Fig. 3b. Again, the loss function exhibits a typical oscillation during the adversarial process, and the training reaches its equilibrium after about 190 steps with an average state fidelity of 0.927. In addition, after training G successfully exhibits a truth table close to that of an XOR gate, as shown in the inset of Fig. 3a. Note that the fidelity of trained XOR gate is lower than the fidelity of the above mentioned single qubit mixed state. Due to the complexity of learning task, generator consisting of more layers and parameters is employed for training XOR gate, which would introduce more two-qubit gate infidelities and decoherence error during the learning.

Fig. 3: QGAN performance in learning the XOR gate.
figure 3

a Tracking of the loss function V, the averaged output scores \({\bar{S}}^{{{{\rm{D}}}},{{{\rm{R/G}}}}}\), and the averaged state fidelity between R/G’s output states \(\bar{F}\) during the adversarial training process with learning rates αD = 1.0 and αG = 1.5. The blue dashed line denotes the training fidelity of 0.9. The maximum step number is limited to 50 for both G and D. \({\bar{S}}^{{{{\rm{D}}}},{{{\rm{R/G}}}}}\) and \(\bar{F}\) are averaged over four possible inputs. Inset: The truth table of G after training in comparison with that of the XOR gate. b Trajectories of two representative parameters constructing D and G, \({\theta }_{3,1,{\rm {D}}}^{x}\) and \({\theta }_{3,1,{\rm {G}}}^{x}\), during the QGAN training. All parameters in G and D are initialized randomly between 0 and π and optimized alternately during the training.

Full size image

Discussion

We have experimentally implemented a multi-qubit QGAN equipped with a quantum gradient algorithm on a programmable superconducting processor. The results demonstrate the feasibility of QGAN in learning data with both classical and quantum statistics for small system sizes. The parameterized quantum circuits for constructing quantum generators and discriminators do not require accurate implementations of specific quantum logics and can be achieved on the near-term quantum devices across different physical platforms. QGAN has far-reaching effects in solving the quantum many-body problem, which can directly extend to the optimal control and self-guided quantum tomography, especially when the system size goes large27,28. Our implementation paves the way to the much-anticipated computing paradigm with combined quantum-classical processors, and holds the intriguing potential to realize practical quantum supremacy9 with noisy intermediate-scale quantum devices29.

We note that there might be challenges with the random initialization and hardware efficient forms of G and D with large depth. For instance, for larger circuits we may need larger depths to gain enough representation power. As a result, the coherence time in our experiment needs to be increased. Moreover, another possible challenge for larger circuits is the so called “barren plateaus” problem, namely that the gradient might be vanishing for most of the parameter regions (see ref. 20,21,22,23 for more details). In fact, these challenges are the common ones facing most of the current experiments on variational quantum circuits. We also would like to mention that when scale beyond a handful of qubits, G and D can be replaced by deep quantum netural networks30 and the corresponding gradient may as well be efficiently evaluated by the backward propagation algorithm31, similar to the case of training classical deep neural networks.

Methods

Details about the quantum device

Our experimental device is a superconducting circuit consisting of 20 transmon qubits interconnected by a central bus resonator with frequency fixed at around ωR/2π ≈ 5.51 GHz. Five qubits, denoted as Qj for j = 0–4, are actively used in this work. The frequencies of the used qubits are carefully arranged to minimize any possible unwanted interactions and crosstalk errors among qubits during single-qubit operations. Each qubit has its own microwave control and flux bias lines for implementations of XY and Z rotations, respectively. Meanwhile, each qubit is dispersively coupled to its own readout resonator for qubit-state measurement, and all the qubits can be measured simultaneously using the frequency-domain multiplexing technique.

Multi-qubit entangling gates generation

The multi-qubit entangling gates that comprise G and D in our QGANs are generated by tuning all the involved qubits on-resonance at around 5.165 GHz, which is detuned from the resonator frequency by 345 MHz. Single-qubit phase gates, which are realized by amplitude-adjustable Z square pulses with a width of 20 ns, are added on each qubit before and after the interaction process to cancel out the dynamical phases accumulated during it. In our experiment, the two- and three-qubit entangling gates contain Q3, Q4 and Q1, Q2, Q3 respectively. The characteristic interaction time tgate is fixed at π/4∣λ∣, where λ is negative and approximately equals to \({\widetilde{g}}^{2}\)/Δ. \(\widetilde{g}\) is defined as the average qubit-resonator coupling strength and Δ denotes the detuning between the interaction frequency and resonator frequency. λ/2π are around −2.48 and −2.27 MHz for the two- and three-qubit cases, respectively.