Abstract
As superconducting quantum circuits scale to larger sizes, the problem of frequency crowding proves a formidable task. Here we present a solution for this problem in fixed-frequency qubit architectures. By systematically adjusting qubit frequencies post-fabrication, we show a nearly tenfold improvement in the precision of setting qubit frequencies. To assess scalability, we identify the types of “frequency collisions” that will impair a transmon qubit and cross-resonance gate architecture. Using statistical modeling, we compute the probability of evading all such conditions, as a function of qubit frequency precision. We find that, without post-fabrication tuning, the probability of finding a workable lattice quickly approaches 0. However, with the demonstrated precisions it is possible to find collision-free lattices with favorable yield. These techniques and models are currently employed in available quantum systems and will be indispensable as systems continue to scale to larger sizes.
Similar content being viewed by others
Introduction
Realizing robust large-scale quantum information processors is one of the foremost challenges in quantum science. Many practical applications have been proposed for robust quantum computers, including estimating the ground state energy of chemical compounds and implementing machine learning algorithms1,2,3,4,5,6,7,8. Quantum advantage relative to classical computers can be realized without full fault tolerance, but requires large quantum circuits that a classical computer cannot simulate9. Recent demonstrations have shown qubit circuits nearly at the threshold for demonstrating quantum advantage10. Much work remains in order to realize fault-tolerant quantum processors; however, scale-up of solid-state quantum circuits has shown consistent and ongoing progress11,12,13,14,15,16,17,18,19,20. As the qubit circuits are scaled up, they must maintain high one- and two-qubit gate fidelities, high qubit connectivity, and low cross-talk error, which can be measured in a holistic sense via the quantum volume of the circuit21,22. Lattices of fixed-frequency transmon qubits represent a promising architecture for building systems of larger sizes10. A growing number of systems at the 20–50-qubit scale are now available to users through cloud access. Fixed-frequency transmons are largely insensitive to charge or flux noise and have achieved coherence times of 100 μs and growing. A variety of technical challenges confront further system scaling, including improving three-dimensional circuit integration and fast readout. High on the list of such challenges is the issue of “frequency crowding.”
The cross-resistance (CR) gate, a hardware-efficient all-microwave gate23,24,25,26, is readily used to entangle fixed-frequency transmons with gate fidelities >99%, approaching the threshold for fault-tolerant codes27. To achieve these fidelities, the CR gate needs not only high coherence qubits but also a precise setting of the qubits’ frequencies. The CR gate activates a ZX interaction by driving one “control” qubit with a microwave pulse at the other “target” qubit’s transition frequency. The magnitude of the ZX as well as other Hamiltonian terms depends on the relative frequencies of the two qubits28,29. Diminished ZX magnitude increases gate time, while other terms such as ZZ add gate errors. Neighboring qubits having the wrong detuning will exhibit a frequency collision in which the ZX may be suppressed or other undesirable effects arise.
Maintaining high gate fidelities for all pairs in a lattice will require solving this frequency-crowding problem by precise setting of qubit frequencies to specified values, as characterized by a standard deviation σf. To achieve low σf, the tunnel-junction conductance must be controlled with high precision. Transmon frequency f01 follows \(h{f}_{01}\simeq \sqrt{8{E}_{J}{E}_{C}}-{E}_{C}\), where Josephson energy \({E}_{J}=\frac{\hslash {I}_{{{{\rm{c}}}}}}{2e}\) is many times greater than charging energy \({E}_{C}=\frac{{e}^{2}}{2C}\)30. In typical transmons, a photolithographically defined capacitance C has dimensions in the tens to hundreds of microns and varies little from qubit to qubit. The critical current Ic is set by a tunnel barrier of area ~100 × 100 nm and thickness a few nm and is thus challenging to fabricate with precision better than a few percent31,32,33,34,35. However, tunnel barrier resistance Rn is readily measurable to precision better than 0.1% and relates to Ic according to the Ambegaokar–Baratoff relation \({I}_{{{{\rm{c}}}}}=\frac{\pi {{\Delta }}}{2e{R}_{{{{\rm{n}}}}}}\) (where Δ is the superconducting gap energy)36. We expect imprecision in resistance σR to produce a corresponding imprecision in frequency \({\sigma }_{f}=\frac{1}{2}\frac{{\sigma }_{R}}{\left\langle R\right\rangle }\cdot \left\langle f\right\rangle\), where \(\left\langle f\right\rangle\) and \(\left\langle R\right\rangle\) are the mean values of frequency and resistance, respectively. We can therefore measure Rn before a chip is cooled in order to assess qubit frequency imprecision. The best demonstrated precision in setting Rn at the time of fabrication is 2%34. A 2% variation in Rn indicates a fractional σf of 1%.
Careful design of lattices can enable error correction codes while at the same time minimizing the likelihood of “frequency collisions” and therefore the required σf for fabrication yield37,38. Yet even the most robust designs require a fractional σf of 0.25–0.5%, which represents a factor of 2–4 improvement over the best literature results. To overcome such limits will require rework of individual qubits’ tunnel junctions after fabrication. Thermal anneal has been shown to increase tunnel resistance Rn, and laser heating has been demonstrated as a highly localized rework tool39,40,41,42,43,44. However, the inherent variability of the anneal process itself must be overcome, and qubit frequency control utilizing such techniques at scale has never been presented in the literature.
In this paper, we introduce an adaptive post-fabrication trimming technique that we use to incrementally adjust Rn on a qubit-by-qubit basis, thereby overcoming inherent variability in both initial qubit fabrication and the laser anneal. We demonstrate this improvement in qubit frequency precision clearly in terms of narrowed frequency distributions. Crucially, we demonstrate qubit frequency imprecision σf of the same magnitude as the imprecision of predicting f01 from Rn. To estimate the scalability of this technique for the fabrication of error-corrected lattices, we employ a statistical yield model based on σf relative to specific collision bounds. This model predicts the severity of the frequency-crowding problem for different topologies and scales of error-corrected multi-qubit lattices as a function of code distance. The model demonstrates that, using conventional transmon fabrication, scaled-up qubit lattices will fail to evade frequency collisions. In contrast, our trimming technique achieves adequate σf for scalable fabrication of distance-3 through distance-7 heavy-square and heavy-hexagon codes. In particular, this technique enables the high yield fabrication of the distance-3 and distance-5 heavy-hexagon lattices currently deployed as IBM cloud connected systems22.
Results
Frequency precision σ f from transmon fabrication
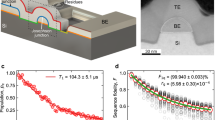
To assess the σf resulting from qubit fabrication, we developed a test vehicle containing a large number of identically fabricated qubits (Fig. 1). We cooled the chip in a dilution refrigerator and used dispersive readout through half-wave microwave resonators to measure qubit frequencies45. We measured the frequencies of 31 qubits to a precision better than 100 kHz using a Ramsey fringe method. The qubit frequencies had random variation σf = 132.3 MHz (Fig. 1) or 2.3% of the median frequency. After warming the qubits to room temperature, we measured their junction resistances. The standard deviation σR was 365 Ω, 4.6% of the median Rn. Fractional σf is exactly half of fractional σR, as expected from Transmon theory and the Ambegaokar–Baratoff relation. A plot of Rn against transmon frequency (Fig. 1) fits a power law of approximately \(-\frac{1}{2}\) power, as expected from theory. To further assess the fidelity of the frequencies to this f-vs-Rn correlation, we show the residual scatter after subtracting the fit line. This appears in the inset in Fig. 1 and exhibits a standard deviation 14.5 MHz or 0.25% of the qubit median frequency. Following transmon theory and the Ambegaokar–Baratoff relation, this residual scatter could indicate a qubit-to-qubit variation of up to 0.5% in superconducting gap Δ or qubit capacitance C. Small systematic errors in measuring Rn, for instance, due to substrate conductance, could also contribute. As we discuss below, future scaling of superconducting quantum logic circuits will require improvements in σf and therefore better control of these parameters.
a False-colored image of test-vehicle chip. Thirty-six fixed-frequency transmon qubits, each including a 500 × 320 micron planar capacitor (green) and a ~0.1 × 0.1 micron Al/AlOx/Al tunnel junction, are prepared identically on a 20 × 10 mm Si substrate. A half-wavelength coplanar waveguide resonator at each qubit (red) enables dispersive readout. Resonators are frequency-multiplexed in groups of 12 per feedline (blue). b Plot of transmon frequency vs Rn, and power-law fit of pre-tuned population. Inset histogram (10 MHz bins) shows residual scatter in frequency relative to fit line. c Distributions of qubit frequencies. Initial median was 5.7025 GHz and initial spread was σf = 132.3 MHz (red histogram, 70 MHz bins). Using selective laser anneal (Fig. 2), we prepared these qubits into two distinct frequency populations with medians 5.430 and 5.7046 GHz (black histograms, 10 MHz bins). Each population is outlined by a Gaussian curve centered at its local median frequency. Combined spread is σf = 14.0 MHz.
Tuning using selective laser anneal
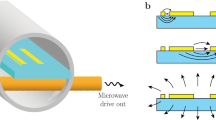
To reduce σf, we developed a technique for selective laser anneal to shift tunnel resistance Rn by pre-calibrated increments (see “Methods” and Fig. 2). We demonstrate the achievable frequency control of this technique by shifting the 31 measured qubits into a two-frequency pattern. We employed an Rn vs f correlation (Fig. 1) to designate the target resistances. We shifted 16 junctions to one Rn group and 15 to another Rn group. After tuning, the group of 16 junctions had median resistance 7.984 kΩ and the group of 15 had median resistance 8.798 kΩ. The 31 junctions clustered around these medians with an overall precision of σR = 51 Ω, about 0.61%. In a dilution refrigerator, we remeasured the frequencies of the qubits in the two groups. A change in fridge instrumentation degraded the readout signal-to-noise ratio of two of the qubits, so that their remeasurement (using continuous-wave spectroscopy) had frequency precision of only 2 MHz. The others were remeasured in the same way as in the first cooldown. The resulting frequencies appear in Fig. 1. The two frequency groups are approximately normally distributed and have medians f0,1 = 5.430 GHz and f0,2 = 5.7046 GHz. Calculating \({\sigma }_{f}=\sqrt{\left\langle {({f}_{i}-{f}_{0,j})}^{2}\right\rangle }\), where f0,j represents f0,1 or f0,2 as appropriate for a given qubit Qi, we assess the overall precision σf = 14.0 MHz. This imprecision is nearly identical to the residual scatter from the f(R) fit line (Fig. 1), which guided the tuning, and the fractional precision \({\sigma }_{f}/\left\langle f\right\rangle =\) 0.25% is slightly better than half of the fractional precision in setting Rn. Drift in Rn reported in the literature39 does not appear to be a limiting factor in this study. As we show in “Methods,” the laser-anneal tuning technique is capable of precisions of 0.3% in Rn. In future work, the imprecision of 14.5 MHz in predicting f from Rn could be made the limiting imprecision in σf.
a Schematic of the apparatus. A 532 nm (frequency doubled) diode-pumped solid-state laser is used as the laser annealing source. Active power calibration is accomplished via a half-wave plate and PBS combination, with feedback from a Si-PD. A piezoelectric mirror mount actively aligns the beam to the junction center via image pattern recognition. The beam is shaped into a four spot pattern in an intermediate image plane by a diffractive beam splitter, to avoid direct illumination of the junction. The illumination pattern is condensed 4× using a dual-objective relay imaging set-up51,53. Inset with 10 μm scale bar shows typical qubit junction and surrounding substrate heated by four Gaussian beam spots of diameter ~4 μm. b Adaptive anneal progression toward Rn targets in 20 tunnel junctions. Greater fractional tuning requires greater anneal powers or durations. Incremental exposure (anneal number) permits tracking the resistance change so as to monotonically approach a target resistance and not overshoot it. In this demonstration, colors blue, green, and red correspond to laser powers 1.74, 1.85, and 1.96 W, respectively. Rn shift was calibrated separately for each power. Single anneals lasted ~0.3–8 s. Total durations were ~8–22 s. SHG second harmonic generation, PBS polarizing beam splitter, Si-PD silicon photodiode, AM alignment mirror, BS beam splitter, TEC thermoelectric cooler.
Discussion
Our post-fabrication trimming reduced σf by 9.5× compared to initial fabrication. To assess whether this level of precision is sufficient to reliably prepare lattices of fixed-frequency transmons capable of error-correcting codes, we must quantify the frequency-crowding problem. Transmon qubits are weakly anharmonic and have decreasing transition energies at higher levels. Therefore, degeneracies among the \(\left|0\right\rangle \to \left|1\right\rangle\), \(\left|1\right\rangle \to \left|2\right\rangle\), and \(\left|0\right\rangle \to \left|2\right\rangle\) transitions of nearby qubits can all contribute to frequency collisions. We must consider the relative frequencies of both nearest neighbors and next nearest neighbors in the lattice28,46,47. Figure 3 illustrates the relative positions of nearest-neighbor and next-nearest-neighbor qubits in a section of lattice, and Table 1 lists the seven cases most likely to lead to gate errors28. We can think of them qualitatively as follows: Type 1 causes hybridization of states in Qj and Qk, while in type 2 the CR pulse excites Qj into the non-computational \(\left|2\right\rangle\) state. Type 3 excites Qk to the \(\left|2\right\rangle\) state but does not require a CR tone. In condition 4, ZX is weak, which implies long gate times and increased gate error28,29. In type 5, the CR gate addresses an additional neighboring qubit. In type 6, when one qubit is the target of a CR gate, its next nearest neighbor leaks to the \(\left|2\right\rangle\) state. In type 7, Qj acts as the control, Qi or Qk as the target, and the third qubit constitutes a “spectator.” An excited-state spectator can emit a photon that combines with photons in the CR pulse to excite Qj into the \(\left|2\right\rangle\) state.
Lattices are capable of d = 5 codes. Patterns of qubit frequencies avoid all conditions in Table 1. Statistical model is applied to these examples and to equivalent lattices at d = 3 and d = 7 (see Supplementary Figs. 1–9). Square lattice includes 49 qubits in a 5-frequency pattern. Heavy-square lattice includes 73 qubits in 3-frequency pattern. Heavy-hexagon lattice includes 65 qubits in 3-frequency pattern. In a portion of the heavy-hexagon lattice, we indicate qubits’ intended gate roles: control (black circles) or target (white circles), as well as code roles: data (D), ancilla (A), or flag (F)37. Inset shows relative positions of qubits for collision definitions of Table 1. Qj is coupled to nearest-neighbors Qi and Qk. Qubits Qi and Qk are next nearest neighbors.
Around each of the frequency collisions described in Table 1, we can designate a window of undesired frequencies. This breaks the frequency space into allowed and forbidden regions. Type 4 listed in Table 1 defines forbidden zones where ZX coupling is too low. For the other six conditions, we forbid regions where the frequency collision is the dominant source of gate error. Existing multi-qubit systems with CR gates typically exhibit two-qubit gate errors of 1–2% regardless of frequency15,46. Reference 28 considers an effective Hamiltonian model for the CR gate, as a function of the relative frequency of control and target qubits. From this model, we estimate the frequency windows for nearest-neighbor collisions (Table 1, types 1–3). Within these windows, assuming typical gate parameters of 30–50 MHz drive amplitude and 200–400 ns duration, we expect errors exceeding ~1%. Here we make an assumption that similar bounds apply to next-nearest-neighbor interactions (types 5–7). Future lattice scaling will benefit from defining frequency collisions precisely to achieve specific quantum volume or error-correction thresholds. Such work can exploit numerical models22,48 that find CR gate error as a function of frequency, coupling, and rate.
A useful lattice of qubits should enable high quantum volume and fault-tolerant operation while avoiding all of the frequency collisions and forbidden regions presented in Table 1. Both lattice layout and the pattern of qubit frequencies are relevant. We consider three types of lattices: square, “heavy square” and “heavy hexagon” (Fig. 3). Lattices comprise qubits and two-qubit connections, each qubit being linked to no more than four neighbors. In many practical implementations, these links comprise microwave-resonant buses. A square lattice facilitates “surface code” fault-tolerant codes49. Recent literature describes hybrids of the surface code with Bacon–Shor-type codes, which can be employed in heavy-hexagon and heavy-square lattices to achieve fault tolerance, albeit with lower error thresholds than the surface code37. In addition to the data and ancilla qubit roles employed in the surface code, these hybrid codes assign a portion of the lattice as “flag” qubits.
In the square lattice, every qubit in the bulk of the lattice lies on a degree-four vertex, while some at edges have degree two or degree three. If we populate the square lattice with five distinct frequencies of qubits, f5 > f4 > f3 > f2 > f1, with appropriate spacing between the frequencies, we can avoid all the forbidden regions of Table 113. In Fig. 3, we illustrate this pattern for a square lattice capable of a distance-5 (d = 5) rotated surface code. Condition 4 of Table 1 requires fcontrol > ftarget, so the pattern also fixes the direction of CNOT gate for each pair.
In contrast to the square lattice, the heavy-square lattice includes both degree-two and degree-four vertices in the bulk. Degree-one, degree-two, or degree-three vertices appear at the edges. We take advantage of this pattern to make all the degree-two vertices control qubits, using a three-frequency pattern f3 > f2 > f1. Since every control qubit (frequency f3) is linked to at most two target qubits, we need only two properly chosen target-qubit frequencies (f1 and f2) to satisfy conditions 5–7 of Table 1, as shown in Fig. 3. A third type of lattice, the heavy hexagon, uses a similar scheme. Here the bulk of the lattice includes degree-three and degree-two vertices. Additional degree-two and degree-one vertices lie at the edges. In this lattice, all of the frequency collisions and forbidden regions can be satisfied using only three frequencies f3 > f2 > f1, with all control qubits residing on degree-two vertices with frequency f3.
We use a Monte Carlo model to quantify the frequency crowding in each lattice type. We sample the qubits at random frequencies drawn from normal distributions characterized by σf and count the collisions defined in Table 1 (see “Methods” and Fig. 6). In Fig. 4, we show the mean number of frequency collisions predicted by the Monte Carlo model for each lattice type and frequency pattern, as a function of σf. As σf → 0, the lattice approaches the ideal patterns of Fig. 3 and has zero frequency collisions. As σf increases, the number of frequency collisions rises steadily. As σf → f01 − f12, the different conditions appearing in Table 1 all become likely, and a limiting number of frequency collisions is reached. Yield follows the inverse trend, as seen in Fig. 4. As σf increases, the likelihood of finding a “collision-free” chip falls off sharply. While the step sizes between frequency setpoints f1 to f5 are important, absolute values of setpoints are not. Setting f1 = 5.0, f2 = 5.07, and f3 = 5.14 GHz works as well as f1 = 5.05, f2 = 5.12, and f3 = 5.19 GHz.
Results of Monte Carlo simulation (see “Methods”). Simulation was applied to the lattices and frequency patterns shown in Fig. 3, capable of distance-5 codes, as well as to d = 3 and d = 7 scale lattices of square, heavy-square, or heavy-hexagon type (See Supplementary Figs. 1–9 for lattice layouts and Table 2 for numbers of qubits.). a Average number of collisions. b Fraction of cases having zero frequency collisions. Color-coded dotted lines are fits of each lattice yield to expression \({\left[\int\nolimits_{-\infty }^{({{\Delta }}f/{\sigma }_{f})}{e}^{-\frac{1}{2}{x}^{2}}dx\right]}^{N}\), where N is the number of qubits and ±Δf defines an allowable window around frequency set points (see Table 2). Using this expression, two solid red lines predict yield for the heavy-hexagon lattice type at 300 and 1000 qubits, using Δf = 27.99 and 26.32 MHz, respectively. See Fig. 5 for estimation of Δf as a function of qubit number.
The yield and mean collision number are a function of the several different collision types and bounds, so they are not readily susceptible to an analytic formulation. However, we can propose a simplified model for yield: in order for a lattice to be collision-free, every qubit in the lattice must fall within some frequency “window” ±Δf relative to its setpoint. Presuming the qubit frequencies are normally distributed, the probability of this occurring goes as the cumulative distribution function, raised to the power N, where N is the number of qubits: \({\left[\int\nolimits_{-\infty }^{({{\Delta }}f/{\sigma }_{f})}{e}^{-\frac{1}{2}{x}^{2}}{\rm{d}}x\right]}^{N}\). In the yield plot in Fig. 4, we fit this expression to find Δf for each lattice.
These model results allow us to predict how different lattice types and frequency patterns will respond to fabrication imprecision. As shown in Fig. 4, if imprecision σf is >30 MHz, any d = 5 lattice will exhibit >10 frequency collisions of one or another of the types listed in Table 1, causing the affected gates to have error rates above ~1%. However, if σf = 10 MHz then on average the d = 5 square lattice will exhibit 5 frequency collisions, while the heavy-square and heavy-hexagon lattices will exhibit 0.1 frequency collision. Considered in terms of yield, we see from Fig. 4 that if σf = 10 MHz, then for a d = 5 device, a square lattice with 5-frequency pattern has a 0.8% likelihood to be collision free, whereas a heavy-square lattice with 3-frequency pattern has 90% likelihood and heavy hexagon with 3-frequency pattern has 92% likelihood. Alternatively we can ask, how well do we have to control σf? If we seek a 10% yield, then Fig. 4 indicates that, for a d = 5 device, a square lattice with 5-frequency pattern requires σf < 8 MHz, whereas a heavy-square lattice with 3-frequency pattern requires σf = 16 MHz and heavy hexagon with 3-frequency pattern requires σf = 17 MHz. Although the square lattice requires 10–20% fewer qubits than the other types at each distance d, it requires far better frequency precision.
The as-fabricated σf seen in Fig. 1 is 132.3 MHz (see “Results”). The Monte Carlo modeling finds that for a heavy-hexagon lattice at d = 3 scale this σf can enable 0.1% yield of collision-free chips. Other lattice types and larger scales will all have yield ≪0.1%. The re-tuned σf = 14.0 MHz demonstrated in Fig. 1 will improve the yield in all types of lattice. Predictions of the Monte Carlo model for σf = 14.0 MHz appear in Table 2. At d = 5 scale, the heavy-hexagon and heavy-square lattices and 3-frequency patterns should be collision-free nearly one-third of the time, while at d = 7 scale the yield is about four times smaller, still reasonable for prototype systems.
As seen from the Monte Carlo analysis, the laser-anneal rework method can scale to the >100 qubit size, enabling a well-chosen lattice and frequency pattern to implement d = 7 error-correction codes free of frequency crowding. To examine needs for the next generation of chips up to the 1000-qubit level, we can coarsely estimate requirements by extrapolating the fixed window model for the heavy-hexagon lattice as shown in Fig. 5. While the σf = 14.0 MHz demonstrated here enables practical yield up to the 100–200 qubit scale, it is clear that roughly a factor of two further improvement is needed to scale toward 1000 qubits. Since this precision is also better than the resistance-to-frequency prediction precision shown in this work, development of further refinements in tuning and frequency prediction approaches will be necessary as the scale of fixed-frequency transmon circuits surpass the 100 qubit milestone.
Fixed window size model. (Back curves, left axis) Model yields for σf ranging from the 14 MHz demonstrated in this work to 6 MHz that would optimize future scaling yield beyond the 1000Q level. (Red points and curve, right axis) Fixed window size fits to the d = 3, d = 5, and d = 7 heavy-hexagon lattice, as well as a fit of these values to expression \(A+B\cdot {{\mathrm{log}}}\,(N)\), extrapolated from 20 to 1000 qubits. This trend illustrates varying frequency-crowding constraints as a function of lattice size.
Methods
Chip fabrication
A chip of the kind used to determine σf and to test our laser-anneal rework process appears in Fig. 1. All microwave elements comprise Nb films ~200 nm thick on a silicon substrate. Each qubit is coupled to a readout resonator but is not directly coupled to any nearby qubits. All transmon capacitors are identical. Junctions are fabricated using identical electron-beam lithographic patterns and deposited simultaneously using double-angle deposition and oxidation50. The individual qubit design is similar to that used in ref. 27 with anharmonicity f12 − f01 ≃ −330 MHz. Junctions have linear dimension ~100 nm and are designed for Ic of ~30 nA. During packaging, we accidentally damaged 3 of the 36 qubits and found these to be non-functional when cooled in a dilution refrigerator. We left 2 of the remaining 33 qubits un-tuned as experimental controls, so that our tuning demonstration includes 31 qubits.
Tuning using selective laser anneal
We have built an integrated junction rework system that can measure and modify the junction resistance. Figure 2 shows a schematic of our laser annealing system, which we call Laser Annealing of Stochastically Impaired Qubits (LASIQ). The laser output is generated by a diode-pumped solid-state laser, frequency doubled to 532 nm. Active power control of the anneal beam from approximately 1.7 to 2 W is performed using a piezo-rotary mounted waveplate and polarizing beam splitter, which is adaptively adjusted based on a pick-off beam measured on a downstream silicon photodiode. A precision-timed shutter exposes the device for 0.3–10 s, and beam alignment is performed using a mechanical mirror mount, which directs the beam via pattern recognition to the transmon junction center. To achieve a more consistent anneal, the beam is shaped into a four-spot pattern, which avoids directly illuminating the junction but uniformly heats the surrounding substrate51.
By careful control of laser power and pulse duration, we use this system to adjust Rn. This process overcomes the imprecision due to transmon fabrication, with a residual imprecision σf due to the rework process. To develop the process, we prepared a set of 126 junctions identical to qubit junctions and measured their response to a range of laser powers and exposure times. We recorded Rn shifts up to 15% relative to initial Rn for total anneal durations varying from 2 to 80 s and laser powers varying from 1.6 to 2 W. Response to laser power in particular was highly nonlinear. Based on these empirical calibrations of Rn shift to power and exposure, we established a qubit tuning process: We first measure the transmon junction’s Rn using four-point probing of the transmon capacitor pads at 25 °C. Using a f(Rn) prediction based on a previously determined correlation curve (Fig. 1), we assign the junction a target resistance corresponding to the target frequency in a multiqubit chip lattice. Because the anneal can shift Rn in only one direction, the target must be higher than the initial Rn. We anneal the qubit junction using laser power and duration chosen from our calibration set, then remeasure its Rn. By remeasuring after each anneal, we can adjust for random variation in the amount of Rn shift. A junction requiring large shifts in Rn may require repeated anneals to reach its target, as shown in Fig. 2. The control algorithm increases the resistance until the measured value is within 0.3% of the target value. In a separate trial of tuning precision, >300 junctions were tuned to target Rns ranging from 0.4 to 14.5% above their initial values and landed successfully within this 0.3% margin. We observed this precision to be independent of the target Rn. We expect 0.3% imprecision in Rn to introduce 0.15% imprecision in transmon frequency.
Monte Carlo frequency-crowding model
Using a Monte Carlo model, we can estimate the incidence of frequency collisions in a lattice as a function of σf. We assume that imperfect frequency setting will distribute qubit frequencies normally around their design frequencies with standard deviation σf. For lattices of the type shown in Fig. 3, we designate 3–5 frequencies f1, f2, f3, f4, f5 spaced at regular intervals in the pattern shown. We set f1 = 5 GHz, similar to real-world transmons22,52. We sample the qubit frequencies randomly around these values and count the collisions throughout the lattice, as listed in Table 1. To avoid unnecessary counting of type 4, we designate the higher-frequency qubit of every pair to be the control for that gate pair. This process is illustrated in Fig. 6. We repeat the frequency assignment and counting to build statistics for a given lattice and frequency pattern. We then repeat the model for a range of σf values from 0 to 150 MHz. We repeat the entire process over a range of frequency spacings to find the spacing that minimizes frequency collisions at each value of σf. As a function of σf, we can then extract (1) the mean number of total collisions in the lattice and (2) the fraction of repetitions that result in zero collisions (yield). Our simulations used 1000 repetitions except to find yield <1% in d = 5 lattices and <0.2% in d = 3 lattices, which used 4000 repetitions, and in d = 7 lattices to find mean collisions for σf < 16 MHz or yield >50% (100 repetitions) or to find mean collisions for σf > 16 MHz (40 repetitions).
Left: Square lattice, d = 3 with 5-frequency pattern of Fig. 3: f1 = 5.00, f2 = 5.07, f3 = 5.14, f4 = 5.21, f5 = 5.28 GHz. To model the lattice statistically, treat the frequencies f1 to f5 as means of distributions. Right: Mean frequencies and normal distributions characterized by σf. For each position in the lattice, sample from the local distribution. Choose random frequencies in this fashion, count collisions as described in Table 1, and repeat to gather statistical sample. Process is repeated for differing spacings between mean frequencies f1 to f5 and for different distribution widths σf.
Data availability
The experimental data presented in this manuscript are available from the corresponding author upon reasonable request.
References
Kandala, A. et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242–246 (2017).
Havlíček, V. et al. Supervised learning with quantum-enhanced feature spaces. Nature 567, 209–212 (2019).
Hempel, C. et al. Quantum chemistry calculations on a trapped-ion quantum simulator. Phys. Rev. X 8, 031022 (2018).
Colless, J. et al. Computation of molecular spectra on a quantum processor with an error-resilient algorithm. Phys. Rev. X 8, 011021 (2018).
Nam, Y. et al. Ground-state energy estimation of the water molecule on a trapped-ion quantum computer. npj Quantum Inf. 6, 1–6 (2020).
Arute, F. et al. Hartree-Fock on a superconducting qubit quantum computer. Science 369, 1084–1089 (2020).
Argüello-Luengo, J., González-Tudela, A., Shi, T., Zoller, P. & Cirac, J. I. Analogue quantum chemistry simulation. Nature 574, 215–218 (2019).
McArdle, S., Endo, S., Aspuru-Guzik, A., Benjamin, S. C. & Yuan, X. Quantum computational chemistry. Rev. Mod. Phys. 92, 015003 (2020).
Kandala, A. et al. Error mitigation extends the computational reach of a noisy quantum processor. Nature 567, 491–495 (2019).
Córcoles, A. D. et al. Challenges and opportunities of near-term quantum computing systems. Proc. IEEE 1–15 https://doi.org/10.1109/JPROC.2019.2954005 (2019).
Chow, J. M. et al. Implementing a strand of a scalable fault-tolerant quantum computing fabric. Nat. Commun. 5, 4015 (2014).
Córcoles, A. et al. Demonstration of a quantum error detection code using a square lattice of four superconducting qubits. Nat. Commun. 6, 6979 (2015).
Gambetta, J. M., Chow, J. M. & Steffen, M. Building logical qubits in a superconducting quantum computing system. npj Quantum Inf. 3, 2 (2017).
Takita, M. et al. Demonstration of weight-four parity measurements in the surface code architecture. Phys. Rev. Lett. 117, 210505 (2016).
Takita, M., Cross, A. W., Córcoles, A. D., Chow, J. M. & Gambetta, J. M. Experimental demonstration of fault-tolerant state preparation with superconducting qubits. Phys. Rev. Lett. 119, 180501 (2017).
Kelly, J. et al. State preservation by repetitive error detection in a superconducting quantum circuit. Nature 519, 66–69 (2015).
Risté, D. et al. Detecting bit-flip errors in a logical qubit using stabilizer measurements. Nat. Commun. 6, 6983 (2015).
Ofek, N. et al. Extending the lifetime of a quantum bit with error correction in superconducting circuits. Nature 536, 441–445 (2016).
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Kjaergaard, M. et al. Superconducting qubits: current state of play. Annu. Rev. Condens. Matter Phys. 11, 369–395 (2020).
Cross, A. W., Bishop, L. S., Sheldon, S., Nation, P. D. & Gambetta, J. M. Validating quantum computers using randomized model circuits. Phys. Rev. A 100, 032328 (2019).
Jurcevic, P. et al. Demonstration of quantum volume 64 on a superconducting quantum computing system. Preprint at https://doi.org/10.1088/2058-9565/abe519 (2020).
Chow, J. M. et al. Simple all-microwave entangling gate for fixed-frequency superconducting qubits. Phys. Rev. Lett. 107, 080502 (2011).
Chow, J. M. et al. Universal quantum gate set approaching fault-tolerant thresholds with superconducting qubits. Phys. Rev. Lett. 109, 060501 (2012).
de Groot, P. C. et al. Selective darkening of degenerate transitions for implementing quantum controlled-NOT gates. N. J. Phys. 14, 073038 (2012).
Rigetti, C. & Devoret, M. Fully microwave-tunable universal gates in superconducting qubits with linear couplings and fixed transition frequencies. Phys. Rev. B 81, 134507 (2010).
Sheldon, S., Magesan, E., Chow, J. M. & Gambetta, J. M. Procedure for systematically tuning up crosstalk in the cross resonance gate. Phys. Rev. A 93, 060302 (2016).
Magesan, E. & Gambetta, J. M. Effective Hamiltonian models of the cross-resonance gate. Phys. Rev. A 101, 052308 (2020).
Ware, M. et al. Cross-resonance interactions between superconducting qubits with variable detuning. Preprint at http://arxiv.org/abs/1905.11480v1 (2019).
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).
Potts, A., Parker, G., Baumberg, J. & de Groot, P. CMOS compatible fabrication methods for submicron Josephson junction qubits. IEE Proc. Sci. Meas. Technol. 148, 225–228 (2001).
Wu, X. et al. Overlap junctions for high coherence superconducting qubits. Appl. Phys. Lett. 111, 032602 (2017).
Costache, M. V., Bridoux, G., Neumann, I. & Valenzuela, S. O. Lateral metallic devices made by a multiangle shadow evaporation technique. J. Vac. Sci. Technol. B 30, 04E105 (2012).
Kreikebaum, J. M., O’Brien, K. P., Morvan, A. & Siddiqi, I. Improving wafer-scale Josephson junction resistance variation in superconducting quantum coherent circuits. Supercond. Sci. Technol. 33, 06LT02 (2020).
Foroozani, N. et al. Development of transmon qubits solely from optical lithography on 300 mm wafers. Quantum Sci. Technol. 4, 025012 (2019).
Ambegaokar, V. & Baratoff, A. Tunneling between superconductors. Phys. Rev. Lett. 10, 486–489 (1963).
Chamberland, C., Zhu, G., Yoder, T. J., Hertzberg, J. B. & Cross, A. W. Topological and subsystem codes on low-degree graphs with flag qubits. Phys. Rev. X 10, 011022 (2020).
Chow, J. M., Magesan, E., Steffen, M., Gambetta, J. M. & Takita, M. Reducing qubit frequency collisions through lattice design. US patent (10,622,536) US20200161529A1 (2020).
Koppinen, P. J., Väistö, L. M. & Maasilta, I. J. Complete stabilization and improvement of the characteristics of tunnel junctions by thermal annealing. Appl. Phys. Lett. 90, 053503 (2007).
Granata, C. et al. Trimming of critical current in niobium Josephson devices by laser annealing. J. Phys. Conf. Ser. 97, 012110 (2008).
Muthusubramanian, N. et al. Local trimming of transmon qubit frequency by laser annealing of Josephson junctions. In American Physical Society March Meeting B29.015 (American Physical Society, 2019).
Oliva, A. & Monaco, R. Annealing properties of high quality Nb/Al-AlOx/Nb tunnel junctions. IEEE Trans. Appl. Supercond. 4, 25–32 (1994).
Lehnert, T., Billon, D., Grassl, C. & Gundlach, K. H. Thermal annealing properties of Nb-Al/AlOx-Nb tunnel junctions. J. Appl. Phys. 72, 3165–3168 (1992).
Rosenblatt, S., Orcutt, J. S. & Chow, J. M. Laser annealing qubits for optimized frequency allocation. US patent 10340438B2 (2019).
Blais, A., Huang, R.-S., Wallraff, A., Girvin, S. M. & Schoelkopf, R. J. Cavity quantum electrodynamics for superconducting electrical circuits: an architecture for quantum computation. Phys. Rev. A 69, 062320 (2004).
McKay, D. C., Sheldon, S., Smolin, J. A., Chow, J. M. & Gambetta, J. M. Three-qubit randomized benchmarking. Phys. Rev. Lett. 122, 200502 (2019).
Malekakhlagh, M., Magesan, E. & McKay, D. C. First-principles analysis of cross-resonance gate operation. Phys. Rev. A 102, 042605 (2020).
Sundaresan, N. et al. Reducing unitary and spectator errors in cross resonance with optimized rotary echoes. PRX Quantum 1, 020318 (2020).
Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012).
Dolan, G. J. Offset masks for lift-off photoprocessing. Appl. Phys. Lett. 31, 337–339 (1977).
Rosenblatt, S. & Orcutt, J. S. Laser annealing of qubits with structured illumination. US patent 10170681B1 (2019).
Sheldon, S. et al. Characterizing errors on qubit operations via iterative randomized benchmarking. Phys. Rev. A 93, 012301 (2016).
Orcutt, J. S. Laser annealing of qubits using a diffractive beam splitter. US patent application (application pending) (2021).
Acknowledgements
We acknowledge funding from the Intelligence Advanced Research Projects Activity (IARPA) under contract W911NF-16-1-0114, for the multi-qubit test vehicle and frequency-vs-resistance correlation studies. We thank N. Bronn, M. Carroll, C. Chamberland, A. Cross, J. Gambetta, J. Ku, M. Malekakhlagh, D. McKay, B. Plourde, E. Pritchett, A. Rosenbluth, M. Takita, J. Timmerwilke, and G. Zhu for helpful discussions. We thank E. Porter for coding assistance, Y. Martin and R. Haight for assistance in constructing the laser optics, and R. Patel for photomicroscopy.
Author information
Authors and Affiliations
Contributions
J.B.H. developed the Monte Carlo model with input from J.A.S. and along with J.S.O. analyzed its results. E.M. developed theory to define frequency collisions. J.B.H., J.S.O., and J.M.C. conceived the experiment. V.P.A. and J.B.H. designed the device, and V.P.A. and M.B. fabricated it. M.S. developed apparatus and procedures used for qubit measurement. J.B.H. and M.S. measured the qubit frequencies and J.B.H. analyzed the data. J.-B.Y. and E.J.Z. measured and analyzed room-temperature resistance data. J.S.O., S.R., and E.J.Z. conceived and developed the LASIQ tuning method. J.S.O. and E.J.Z. built the LASIQ apparatus. E.J.Z. undertook the tuning experiments. J.B.H, J.S.O., and E.J.Z. prepared the manuscript, with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hertzberg, J.B., Zhang, E.J., Rosenblatt, S. et al. Laser-annealing Josephson junctions for yielding scaled-up superconducting quantum processors. npj Quantum Inf 7, 129 (2021). https://doi.org/10.1038/s41534-021-00464-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-021-00464-5
This article is cited by
-
Advanced CMOS manufacturing of superconducting qubits on 300 mm wafers
Nature (2024)
-
High-threshold and low-overhead fault-tolerant quantum memory
Nature (2024)
-
Alternating-bias assisted annealing of amorphous oxide tunnel junctions
Communications Materials (2024)
-
Scalable interconnection using a superconducting flux qubit
Scientific Reports (2024)
-
Experimental error suppression in Cross-Resonance gates via multi-derivative pulse shaping
npj Quantum Information (2024)