Introduction

Quantum physics and technology with continuous variables (CVs)1 has achieved noticeable progress recently. A potential advantage of CVs is the in-principle unlimited energy and information capacity of a single oscillator mode. In order to fully gain the benefits of CVs and to achieve universal quantum processing one requires an access to a nonlinear operation2,3, that is, at least a cubic potential. In addition, the CV quantum information processing can be greatly simplified and stabilized if variable higher-order potentials are available4. Variability of nonlinear gates can also help to overcome limits for fault tolerance5. Nanomechanical systems profit from a straightforward feasible way to achieve the nonlinearity by inducing a controllable classical nonlinear force of electromagnetic nature on a linear mechanical oscillator6,7,8. Such a nonlinear force needs to be fast, strong, and controllable on demand to access different nonlinearities required for an efficient universal CV quantum processing. Therefore, the field of optomechanics9,10,11,12 is a promising candidate to provide the key element for the variable on-demand nonlinearity. Optomechanical systems have reached a truly quantum domain recently, demonstrating the effects ranging from the ground state cooling13,14 and squeezing15,16 of the mechanical motion to the entanglement of distant mechanical oscillators17,18. Of particular interest are the levitated systems in which the potential landscape of the mechanical motion is provided by a highly developed device—an optical tweezer19,20,21,22. Levitated systems have proved useful in force sensing23,24, studies of quantum thermodynamics25,26,27, testing fundamental physics28,29,30, and probing quantum gravity31,32. From the technical point of view, the levitated systems have recently demonstrated noticeable progress in the controllability and engineering, particularly, cooling toward33,34,35,36 and eventually reaching the motional ground state37. Further theoretical studies of preparation of entangled states of levitated nanoparticles are underway38,39. Besides the inherently nonlinear optomechanical interaction met in the standard bulk optomechanical systems the levitated ones possess the attractive possibility of engineering the nonlinear trapping potential26,37,40,41,42,43,44. Moreover, the trapping potentials can be made time-dependent and manipulated at rates exceeding the rate of mechanical decoherence and even the mechanical frequency45. In this manuscript, we assume a similar possibility to generate the nonlinear potential for a mechanical motion and control it in a fast way (faster than the mechanical frequency). Our findings do not rely on the specific method of how the nonlinearity is created.

Here we propose a broadly applicable nonlinear stroboscopic method to achieve high-order nonlinearity in optomechanical systems with time- and space-variable external force. The method builds on the possibility to control the nonlinear part of the mechanical potential landscape and introduce it periodically, adjusted in time with the mechanical harmonic oscillations. Such periodic application inhibits the effect of the free motion and the restoring force terms in the Hamiltonian and allows approaching the state arising from the nonlinear potential only. This is achieved similarly to how a stroboscopic measurement enables a quantum nondemolition detection of displacement46,47. To prove feasibility of the method, we theoretically investigate realistic dynamics of a levitated nanoparticle in the presence of simultaneously a harmonic and a strong, stroboscopically applied, nonlinear potentials enabled by the engineering of the trapping beam. To run numerical simulations, we advance the theory of optomechanical systems beyond the covariance matrix formalism appropriate for Gaussian states. Using direct Fock-basis and Suzuki-Trotter48 simulations we model the simultaneous action of the nonlinear potential and harmonic trap, and obtain the Wigner functions (WFs) of the quantum motional states achievable in this system. We predict very nonclassical negative WFs49,50 generated by highly nonlinear quantum-mechanical evolution for time shorter than one mechanical period. The oscillations of WF reaching negative values, in accordance with estimates based on unitary dynamics, witness that the overall quantum state undergoes unitary transformation \(\exp ({\rm{i}}V(\hat{x})\tau )\) sufficient for universal quantum processing2. To justify it, we prove a nonlinear combination of the canonical quadratures of the mechanical oscillator to be squeezed below the ground state variance which is an important prerequisite of this state being a resource for the measurement-based quantum computation51,52. For numerical simulations, we focus our attention to realistic version of the key nonlinearity, namely the cubic one with V(x) ∝ x3, and find good agreement of the predictions based on experimentally feasible dynamics with the lossless and noiseless unitary approximation. The method allows straightforward extension to more complex nonlinear potentials which can be used for flexible generation of other resources for nonlinear gates and their applications4,52. In comparison with simultaneously developed superconducting quantum circuits53, an advantage of our approach stems from a much larger flexibility of nonlinear potentials. Stroboscopic driving of an optomechanical cavity in a linear regime was considered in ref. 54 for the purpose of cooling and Gaussian squeezing of the mechanical mode.

Results

The nonlinear stroboscopic protocol

To implement the stroboscopic method, it is possible to versatilely use a levitated nanoparticle45 with optical6, electric7 or magnetic8 trapping. It is also possible to use a mirror equipped with a fully optical spring55, or a membrane with electrodes allowing its nonlinear actuation and driving56. In any of such systems, the mechanical mode can be posed into nonlinear potential V(x), particularly, the cubic potential V3(x) ∝ x3 for the pioneering test. In this manuscript, we focus on the experimental parameters peculiar to the levitated nanoparticles36,37, although the principal results remain valid for the other systems as well. We also focus here solely on the evolution of the mechanical mode of the optomechanical cavity, assuming that the coupling to the optical cavity mode (blue in Fig. 1) is switched off.

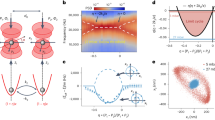
Fig. 1: Scheme of the proposed stroboscopic method.
figure 1

a A levitated optomechanical system as an illustration of mechanical oscillator in a nonlinear potential. A dielectric subwavelength particle (P) is trapped by a tweezer (not shown). The particle feels a total potential U(x) = Ωmx2/4 + α(t)V(x) that is a sum of the quadratic (green) and the nonlinear (orange, here: cubic) parts, both provided by the trapping beam. The particle can be placed inside a high-Q cavity and probed by the laser light. b, c Stroboscopic application of nonlinear potential. The nonlinear part of the potential is switched on for only a short fraction of the mechanical period (orange segments). The quadratic trapping potential (green segments) is present throughout all the evolution. d Suzuki-Trotter simulation of stroboscopic evolution of the mechanical mode. In the figure, orange segments represent action of the nonlinear potential, empty and filled green segments correspond, respectively, to unitary and damped harmonic evolution.

Full size image

The mechanical mode is a harmonic oscillator of eigenfrequency Ωm, described by position and momentum quadratures, respectively, \(\hat{x}\) and \(\hat{p}\), normalized such that \(\left[\hat{x},\hat{p}\right]=2{\rm{i}}\). The oscillator is coupled to a thermal bath at rate ηm. We also assume fast stroboscopic application of an external nonlinear potential α(t)V(x) with a piecewise constant α(t) illustrating the possibility to periodically switch the nonlinear potential on and off as depicted at Fig. 1(a). The Hamiltonian of the system, therefore, reads (ћ = 1)

$$\hat{H}=\hat{H}_{\rm{HO}}+\alpha (t)V(\hat{x}),\quad \hat{H}_{\rm{HO}}=\frac{1}{4}{{\Omega }}_{\rm{m}}({\hat{x}}^{2}+{\hat{p}}^{2}),$$
(1)

To illustrate the key idea behind the stroboscopic method, we first examine the regime of absent mechanical damping and decoherence. In this case, the unitary evolution of the oscillator is given by \(\rho (t)=\hat{U}(t,{t}_{0})\rho ({t}_{0}){\hat{U}}^{\dagger }(t,{t}_{0})\), with \(\hat{U}(t+\delta t,t)=\exp [-{\rm{i}}\hat{H}\delta t]\). When the nonlinearity is switched on permanently (α(t) = α0), the free evolution dictated by HHO mixes the quadratures of the oscillator which prohibits the resulting state from possessing properties of the target nonlinear quantum state arising purely from V(x) regardless of the nonlinearity strength (see Supplementary Note 4 for more details). Willing to obtain a unitary transformation as close to \(\exp [-{\rm{i}}V(\hat{x})\tau ]\) as possible despite a constant presence of \(\hat{H}_{\mathsf{HO}}\), we assume that the nonlinearity is repeatedly switched on for infinitesimally short intervals of duration τ. If the duration τ is sufficiently short for the harmonic evolution to be negligible, the resulting evolution during τ is approximately purely caused by the V(x) part of the Hamiltonian. To enhance the magnitude of the effect of the nonlinear potential, \(V(\hat{x})\) we can apply it every 2π/Ωm for short enough intervals as shown in Fig. 1b, c) . This allows to establish an effective rotating frame within which the nonlinearity is protected from the effect of harmonic evolution. Realistically, the stroboscopic application corresponds to α(t) = ∑kδτ(t − 2πk/Ωm), with \(k\in {\mathbb{Z}}\), where δτ is a physical approximation of Dirac delta function with width τ much shorter than the period of mechanical oscillations: τΩm ≪ 1. Then we can consider the evolution over a number M of harmonic oscillations as consisting of subsequent either purely harmonic or purely nonlinear steps, and the evolution operator can be approximately written as

$$\begin{array}{ll}\hat{U}(t+MT_{\mathsf{m}},t)={\left[\hat{U}(t+T_{\mathsf{m}},t)\right]}^{M}\approx {\left\{\exp [-{\rm{i}}\hat{H}_{\mathsf{HO}}T_{\mathsf{m}}]\exp [-{\rm{i}}V(\hat{x})\tau ]\right\}}^{M}\\ \qquad\qquad\qquad\,\,\,=\exp [-{\rm{i}}MV(\hat{x})\tau ].\end{array}$$
(2)

For the last equality we used the fact that the unitary harmonic evolution through a single period of oscillations is an identity map: \({\hat{U}}_{\mathsf{HO}}(t+T_{\mathsf{m}},t)\equiv \exp [-{\rm{i}}{\hat{H}}_{\mathsf{HO}}T_{\mathsf{m}}]\,=\,{\hat{{\mathbb{1}}}}\). Motion of a real mechanical oscillator can be approximated by a harmonic unitary evolution with good precision because of very high quality of mechanical modes of optomechanical systems35,36,57. Equation (2) shows that the effect of sufficiently short pulses of the strong nonlinear potential timed to be turned on precisely once per a period of mechanical oscillations M times, is equivalent to an M-fold increase of the nonlinearity.

A further improvement is possible by noting that undamped harmonic evolution over a half period simply flips the sign of the two quadratures \(({\hat{x}},{\hat{p}})\,\mapsto\, {-({\hat{x}},{\hat{p}})}\). Therefore, it is possible to similarly apply the potential twice per period, switching its sign each second time. This can be formalized as setting \(\alpha (t)={\sum }_{k}{(-1)}^{k}{\delta }_{\tau }(t-\pi k/{{\Omega }}_{\mathsf{m}}),\,k\,\in \,{\mathbb{Z}}\). In this case,

$$\hat{U}(t+T_{\mathsf{m}},t)={{\rm{e}}}^{-{\rm{i}}\hat{H}_{\mathsf{HO}}T_{\mathsf{m}}/2}{{\rm{e}}}^{+{\rm{i}}V(\hat{x})\tau }{{\rm{e}}}^{-{\rm{i}}\hat{H}_{\mathsf{HO}}T_{\mathsf{m}}/2}{{\rm{e}}}^{-{\rm{i}}V(\hat{x})\tau }={{\rm{e}}}^{-2{\rm{i}}V(\hat{x})\tau },$$
(3)

and therefore, after M periods

$$\hat{U}(t+MT_{\mathsf{m}},t)=\exp [-{\rm{i}}\cdot 2M\cdot V(\hat{x})\tau ].$$
(4)

The idealized scheme proposed above in reality faces two potentially deteriorative factors: the finiteness of the duration of the nonlinearity τ, and the mechanical decoherence caused by the thermal environment. We take a proper account of these two factors by considering the evolution as consisting of two kinds: (i) unitary undamped dynamics in a sum of the quadratic and nonlinear potentials, (ii) damped harmonic evolution between those. These two kinds of evolution are subsequently repeated, as shown in Fig. 1b, c. We develop an advanced method based on Suzuki-Trotter simulation (STS) to simulate the quantum state of a realistic optomechanical system after the application of our proposed protocol. It is worth noting that the STS is typically used to approximately achieve a novel evolution \(\hat{U}\) from experimentally available exact unitaries58,59. In our work, we use STS to simulate and justify that the experimentally available compound evolution \(\hat{U}\) can approximate one of its building blocks \(\hat{U}_{\mathsf{NL}}(\delta t)\equiv \exp (-{\rm{i}}V(x)\delta t)\). To verify the convergence of STS we also perform simulations in the Fock-state basis that allow direct computation of the propagator corresponding to the Hamiltonian (1). Fock-state-basis simulations unfortunately do not grant access to phase-space distributions such as WF60 which makes use of STS the primary strategy. Excellent agreement between the very distinct methods (STS and Fock-state-basis simulations) indicates that our results are correct. The details of the simulation methods are presented in Supplementary Notes 1 and 2.

We omit damping and thermal decoherence during the fast unitary action of the combined potential. Such applications are assumed to happen every half of a mechanical oscillation and have durations much shorter than the mechanical period, therefore, due to high quality of state-of-the-art mechanical oscillators, such omission is justified. The joint action is simulated using STS and verified by Fock-state-basis simulation. Between the applications of the nonlinear potential V(x) the mechanical oscillator experiences damped harmonic evolution described by the linear Heisenberg-Langevin equations

$$\dot{x}={{\Omega }}_{\mathsf{m}}p;\quad \dot{p}=-{{\Omega }}_{\mathsf{m}}x-\eta _{\mathsf{m}}p+\sqrt{2\eta _{\mathsf{m}}}\xi ,$$
(5)

where ξ is the quantum Langevin force, obeying \(\left[\xi (t),x(t)\right]={\rm{i}}\sqrt{2\eta_{\mathsf{m}}}\) and \(\frac{1}{2}\left\langle \left\{\xi (t),\xi (t^{\prime} )\right\}\right\rangle =(2n_{\mathsf{th}}+1)\delta (t-t^{\prime} )\) with nth being the mean occupation of the bath. The experimentally accessible value of the heating rate Hm is given by Hm = ηmnth. The density matrix ρ(Tm/2) of the particle after half of a period of oscillations including the action of the nonlinear potential and subsequent damping can be formally written as

$$\rho (\tau )={\mathcal{N}}\left[\rho (0)\right]={\mathcal{D}}\left[\hat{U}(\tau ,0)\rho (0){\hat{U}}^{\dagger }(\tau ,0)\right].$$
(6)

where \(\hat{U}(\tau ,0)\) describes the particle’s unitary dynamics in combined potential, and \({\mathcal{D}}[\,\bullet \,]\) indicates the mapping performed by the damping. Generalization of (6) to include the second half of the period, and the subsequent generalization to multiple periods, is straightforward.

Using these advanced numerical tools, further elaborated in “Methods” we evaluate the quantum state of the mechanical oscillator after the protocol and explore the limits of the achievable nonlinearities in the optomechanical systems that are accessible now or are within reach.

Application to the cubic nonlinearity

Motivated by the role of cubic nonlinearity for the universal continuous-variable quantum processing, we illustrate the devised method by numerically evaluating the evolution of a levitated particle under a stroboscopic application of a cubic potential V(x) ∝ x3. The nonlinear phase gate e−iV(x) is a limit case of motion, it modifies only momentum of the object without any change of its position. This nondemolition aspect is crucial for use in universal quantum processing. A nonlinear phase state (particularly, the cubic phase state introduced in3) as the outcome of evolution of the momentum eigenstate \(\left|p=0\right\rangle\) in a nonlinear potential V(x) is defined as

$$\left|{\gamma }_{V}\right\rangle \propto \int {\rm{d}}x\ {{\rm{e}}}^{{\rm{i}}V(x)\tau }\left|x\right\rangle ,$$
(7)

where V(x), is a highly nonlinear potential, and \(\left|x\right\rangle\) the position eigenstate \(\hat{x}\left|x\right\rangle =x\). The state (7) requires an infinite squeezing possessed by the ideal momentum eigenstate before the nonlinear potential is applied. More physical is an approximation of this state obtained from a finitely squeezed thermal state ρ0(r, n0), ideally, vacuum, by the application of V:

$$\rho (V,r,{n}_{0})={{\rm{e}}}^{{\rm{i}}V(\hat{x})\tau }{\rho }_{0}(r,{n}_{0}){{\rm{e}}}^{-{\rm{i}}V(\hat{x})\tau }.$$
(8)

The initial state ρ0 is the result of squeezing a thermal state with initial occupation n0

$${\rho }_{0}(r,{n}_{0})=\hat{S}(r){\rho }_{0}(0,{n}_{0}){\hat{S}}^{\dagger }(r)$$
(9)

where \(\hat{S}(r)=\exp [\frac{1}{2}{r}^{* }{(\hat{a})}^{2}-\frac{1}{2}r{({\hat{a}}^{\dagger })}^{2}]\) is a squeezing operator (\(\hat{a}=(\hat{x}+{\rm{i}}\hat{p})/2\)), and the initial state ρ0 is thermal with mean occupation n0. Phase of the squeezing parameter r = ∣r∣eiθ determines the squeezing direction. When n0 = 0, ∣r∣ → +∞, and θ = π, the initial state is infinitely squeezed in p, and Eq. (8) approaches the ideal cubic state (7).

The quantum state obtained as a result of the considered sequence of interactions approximates the ideal state given by Eq. (7). The quality of the approximation can be assessed by evaluating the variance of a nonlinear quadrature p − λ x2, or the cuts of the WFs of the states. A reduction in nonlinear quadrature variance below the vacuum is a necessary condition for application of these states in nonlinear circuits51,52. On the other hand, the phase-space interference fringes of the WF reaching negative values are a very sensitive witness of quantum non-Gaussianity of the states used in the recent experiments61,62,63,64. Fidelity happens to be an improper measure of the success of the preparation of the quantum resource state65 because it does not predict either applicability of these states as resources or their highly nonclassical aspects.

A noise reduction in the cubic phase gate can be a relevant first experimental test of the quality of our method. The approximate cubic state obtained from a squeezed thermal state (that is, the state (8) with V(x) = γx3/(6τ)) should possess arbitrary high squeezing in the variable p − λ x2 for n0 = 0 given sufficient squeezing of the initial mechanical state. The state (8) obtained from a squeezed in momentum state, has the following variance of the nonlinear quadrature

$${\sigma }_{3}^{\rho }(\lambda )\equiv {\rm{Tr}}(\rho {\left(\hat{p}-\lambda {\hat{x}}^{2}\right)}^{2})-{\left({\rm{Tr}}\rho (\hat{p}-\lambda {\hat{x}}^{2})\right)}^{2}=\frac{v_{\mathsf{th}}}{{s}^{2}}+2{\left(\lambda -\gamma \right)}^{2}{\left({s}^{2}v_{\mathsf{th}}\right)}^{2},$$
(10)

where vth = 2n0 + 1 is the variance of each canonical quadrature in the initial thermal state before squeezing, and s = er is the magnitude of squeezing. An important threshold is the variance of the nonlinear quadrature attained at the vacuum state (n0 = 0, s = 1)

$${\sigma }_{3}^{\rm{vac}}(\lambda )=1+2{\lambda }^{2}.$$
(11)

Application of a unitary cubic evolution to the initial vacuum state displaces this curve along the λ axis by γ. Further, as follows from Eq. (10), squeezing the initial state allows reducing the minimal value of σ3, and increase of the initial occupation n0 causes also increase of σ3. Suppression of fluctuations in the nonlinear quadrature is a convenient figure of merit because it is a direct witness of the applicability of the quantum state as a resource for measurement-based quantum information processing51,52 and a witness of non-classicallity66. It can be evaluated in an optomechanical system with feasible parameters using pulsed optomechanical interaction66 without a full quantum state tomography.

In Fig. 2a, we show the variance σ3 at the instants t = MTTm/2. Each of the curves takes into account also the interaction with the thermal environment lasting Tm/2 after each application of the nonlinearity. The heating rate parameter H0 = 4πHm/Ωm assumes value H0 = 2 × 10−3. For an oscillator of eigenfrequency Ωm = 2π × 100 kHz and Q = 106 is equivalent to occupation of the environment equal to nth ≈ 107 phonons. This is the equilibrium occupation of such an oscillator at the temperature of 50 K. A recent experiment of ground state cooling of a levitated nanoparticle37 reported the heating rate corresponding to H ≈ 102H0. A proof of robustness of the method against such heating is in the Supplementary Note 3.

Fig. 2: Results of the simulations.
figure 2

Results of stroboscopic application of cubic nonlinear potential V = γx3/(6τ) to the squeezed thermal state (initial occupation n0 = 0.05, squeezing s = 1.2) over multiple (MT = 1, 2, or 3) halves of mechanical periods. a Squeezing of nonlinear quadrature. Thick lines correspond to stroboscopic method with realistic parameters and thermal noise, thin lines, to purely unitary application of the nonlinearity. Dashed lines correspond to the result of evolution driven by the full Hamiltonian \(\hat{H}\) (1) from the same initial state over time τ, 2τ, and 3τ respectively. b Wigner function of motional states. Solid lines correspond to the same states from (a). Cyan line with markers (overlapping with solid red line) shows the unitary application of nonlinearity. Other parameters are as follows: potential stiffness γ = γ0 = 0.2, application duration τΩm = Θ = Θ0 = π/100, environmental thermal heating rate parameter H0 = 4πHm/Ωm = 0.002.

Full size image

Thin lines with markers show the analytic curves defined by Eq. (10) for the corresponding values of γ. The good quantitative correspondence between the approximate states resulting from the realistic stroboscopic application of nonlinear potential and the analytic curves again proves the validity of the stroboscopic method. Importantly, each of the curves has an area where it lies below the corresponding ground-state level σ3vac. This means each of the corresponding states gives advantage over vacuum if used as ancilla for the cubic gate. The dashed lines show the simulated quantum states obtained from the same initial state by longer unitary evolution according to the full Hamiltonian from Eq. (1), that is \({{\rm{e}}}^{-{\rm{i}}\hat{H}n\tau }\rho {{\rm{e}}}^{{\rm{i}}\hat{H}n\tau }\) where n = 1, 2, 3 for blue, yellow and red correspondingly. Further divergence from ideal than that of the ones corresponding to the stroboscopic method witnesses an advantage of the latter in generation of the resource for the measurement-based computation.

The stroboscopic application of a fixed limited gain nonlinearity, therefore, indeed allows amplification of nonlinearity in accordance with Eq. (4). Importantly, even despite requiring longer evolution in a noisy environment, the stroboscopic method allows better amplification than a unitary longer application of the nonlinearity in presence of the free evolution (\(\propto \!{\hat{p}}^{2}\)) and harmonic (\(\propto \!{\hat{x}}^{2}\)) terms in the Hamiltonian.

The non-Gaussian character of the prepared quantum state can be witnessed via its WF W(x, p) which for a quantum state ρ reads67

$$W(x,p)=\frac{1}{2\pi }{\int \nolimits_{-\infty }^{\infty }}{\rm{d}}y\ {{\rm{e}}}^{-{\rm{i}}py}\left\langle x+y| \rho | x-y\right\rangle .$$
(12)

WF shows a quasiprobability distribution over the phase space spanned by position x and momentum p and its negativity is a prerequisite of the non-classicallity of a quantum state. In Fig. 2b are WFs W(0, p) of the mechanical oscillator computed for the same approximate states as in the panel (a). The WF of an ideal cubic phase state, i.e. the state given by Eq. (7) for V(x) = x3γ/(6τ), reads3,50

$$W_{\mathsf{CPS}}(x,p)\propto {\rm{Ai}}\left[{\left(\frac{4}{\gamma }\right)}^{1/3}\left(\gamma {x}^{2}-p\right)\right],$$
(13)

where Ai(x) is the Airy function. This function with apparent non-Gaussian shape in the phase space exhibits fast oscillations reaching negative values in the positive momentum for any γ > 0. The WFs of the states obtained by application of the stroboscopic protocol approach the one of Eq. (8). Each of them exhibits areas with negative values which proves quantum non-Gaussian character of the resulting state. Moreover, with increased number of stroboscopic applications involved, the resulting approximate state corresponds to stronger nonlinearity. For the last curve where MT = 3 we also show the result of an idealized instantaneous unitary application of an equal total nonlinearity by a cyan line with markers which is indistinguishable from the line for the approximate evolution. For this pair of curves we also have an estimate for the overlap \({\rm{Tr}}[\rho_{\mathsf{red}}\rho_ {\mathsf{cyan}}]/{\rm{Tr}}[\rho_ {{\mathsf{cyan}}}^{2}]=0.9877\). Despite an excellent overlap of the ideal and approximate WFs, the important resource, squeezing σ3 shows a noticeable deviation from the ideal scenario. It is for this reason that we choose the squeezing σ3 as the main figure of merit for the protocol.

Discussion

In this article, we have proposed and theoretically analyzed a protocol to create a nonlinear motional state of the mechanical mode of an optomechanical system with controllable nonlinear mechanical potential. The method uses the possibility to apply the nonlinear potential to the motion of mechanical object in a stroboscopic way, twice per a period of oscillations. This way of application allows reducing the deteriorative effect of the free oscillations and approach the effect of pure action of nonlinear potential. In contrast to other methods of creating nonclassical states by a continuous evolution in presence of nonlinear terms in the Hamiltonian68,69,70, our method allows approaching the states that approximate evolution according to the unitary eiV(x) where V(x) is the nonlinear potential profile. We tested our method on a cubic nonlinearity \(\propto \!{\hat{x}}^{3}\) though the method is applicable to a wide variety of nonlinearities. Our simulations prove that application of the protocol allows one to obtain the squeezing in the nonlinear quadrature below the shot-noise level even if the initial state of the particle is not pure. The nonlinear state created in a stroboscopic protocol clearly outperforms as a resource the vacuum for which the bound (11) holds. Moreover, the stroboscopic states approximate the one defined by Eq. (8) obtained in absence of the free rotation and thermal decoherence. We also verify that the stroboscopic application of the cubic nonlinear potential generates nonclassical states under conditions that are further from optimal than the ones of Fig. 2. In particular, we find that the heating rate Hm can be increased approximately 100-fold until the curve σ3(λ) fails to overcome the vacuum boundary 1 + 2λ2. We are able to prove that when the duration of the application τ is increased tenfold such that the corresponding product V(x)τ remains constant, (that is, a less stiff potential is applied stroboscopically for proportionally longer time intervals), the resulting nonlinear state as well shows squeezing in σ3. This proves robustness of the method to the two major imperfections.

We have shown the method to work for the parameters inspired by recent results demonstrated by the levitated optomechanical systems71,72. The optical trap with a cubic potential has been already used in the experiments43,44. Levitated systems73, including electromechanical systems74, have recently shown significant progress in the motional state cooling35,36,37 and feedback-enhanced operation34 which lays solid groundwork of the success of the proposed protocol. The authors of ref. 44 report the experimental realization of the potential V(X) = μX3/6 with μ ≈ 8kBTμm−3, where \(X=x\sqrt{\hslash /(2m{{\Omega }}_{\mathsf{m}})}\) is the dimensional displacement of the oscillator, m is its mass, kBis the Boltzmann constant and T temperature. From this value we can make a very approximate estimate for the nonlinear gain γ = μ(ћ/(2mΩm))3/2τ ≈ 1.2 × 10−3 assuming duration τ = π/(50Ωm), temperature T = 300 K, frequency Ωm = 2π × 1 kHz, and a mass m = 4 × 10−15 g of a silica nanoparticle of 70 nm radius.

Experimental implementation of the proposed method can guarantee preparation of a strongly non-Gaussian quantum motional state. Further analysis of such a state will require either a full state tomography or better suited well-tailored methods to prove the nonclassicality75. An analysis of the estimation of the nonlinear mechanical quadrature variance via pulsed optomechanical interaction can be found in ref. 66. The optical read out can be improved using squeezed states of light76. This experimental step will open applications of the proposed method to other nonlinear potentials relevant for quantum computation4,51,52,77, quantum thermodynamics78,79 and quantum force sensing80,81.

In our simulations, we focused solely on the dynamics of the mechanical mode and assumed the conventional optomechanical interaction absent. This interaction, well developed in recent years, provides a sufficiently rich toolbox that allows incorporation of the mechanical mode into the optical circuits of choice9. As an option, a prepared nonlinear state can be transferred to traveling light pulse76 using optomechanical driving. In a more complicated scenario, one can add optomechanical interaction to the stroboscopic evolution to obtain even richer dynamics. A complete investigation of such dynamics, however, goes beyond the scope of the present research focused on the preparation of nonlinear motional states.

In parallel with the experimental verification, the stroboscopic method can be used to analyze other higher-order mechanical nonlinearities such as V(x) ∝ x4 or tilted double-well potentials required for tests of recently disputed quantum Landauer principle82, counter-intuitive Fock state preparation83 and approaching macroscopic superpositions84,85,86,87.

Methods

Tools of numerical simulations

The Eq. (6) approximates the damped evolution of an oscillator in a nonlinear potential by a sequence of individual stages of harmonic, nonlinear and damped harmonic evolution (see Fig. 1). Below we elaborate on how it is possible to simulate such dynamics using WF in the phase space, density matrix in position, momentum and Fock basis.

First, we evaluate the action of the nonlinearity during the stroboscopic pulse. While the nonlinearity is on, the Hamiltonian of the system reads

$$\hat{H}=\hat{H}_{\mathsf{HO}}+V(\hat{x})={\hat{H}}_{p}+{\hat{H}}_{x},$$
(14)

where \({\hat{H}}_{p}=\frac{{{\Omega }}_{\mathsf{m}}}{4}{\hat{p}}^{2},\) and \({\hat{H}}_{x}=\frac{{{\Omega }}_{\mathsf{m}}}{4}{\hat{x}}^{2}+\frac{\gamma }{6}{\hat{x}}^{3}.\)

Our important simulation tool is the STS (see ref. 48) for \(\hat{U}\)

$$\hat{U}(t+\tau ,t)={\left[\exp [-{\rm{i}}(\hat{H}_{\mathsf{HO}}+V(\hat{x}))\frac{\tau }{N}]\right]}^{N}={\left[\hat{U}_{\mathsf{HO}}(\frac{\tau }{N})\hat{U}_{\mathsf{NL}}(\frac{\tau }{N})+O\left({\left(\frac{\tau }{N}\right)}^{2}\right)\right]}^{N},$$
(15)

where \(\hat{U}_{\mathsf{HO}}(\delta t)\equiv \exp (-{\rm{i}}H_{\mathsf{HO}}\delta t)\), \(\hat{U}_{\mathsf{NL}}(\delta t)\equiv \exp (-{\rm{i}}V(x)\delta t)\), N is called the Trotter number. The accuracy of the approximation is, thereby, increasing with decreasing τ/N. Despite τ being now sufficiently large to take into account noticeable free rotation through an angle Ωmτ in the phase space, we still assume that τ is much shorter than the mechanical decoherence timescale, set by the heating rate Hm. This is well justified for the current experiments33,36,37, also see Supplementary Note 2. The STS requires the summands forming the Hamiltonian to be self-adjoint which is not always the case of V(x), in particular V(x) ∝ x3. We take the necessary precautions by considering such nonlinearities over only short time in a finite region of the phase space. Thus we cautiously take care of the quantum motional state being limited to this finite region. To further verify the correctness of numerics via STS, we cross-check it using numerical simulations in Fock-state basis.

Equation (14) shows the two possibilities to split the full Hamiltonian into summands to use the STS. We use these two possibilities to compute independently the mechanical state in order to verify the correctness of the STS in Supplementary Note 1.

First, we start from a squeezed thermal state ρ(0), which has a representation by the WF in the phase space

$$W_{\mathsf{th}}(x,p;{n}_{0},s)=\frac{\exp \left(-\frac{1}{2}\left[\frac{{\left(x/s\right)}^{2}+{\left(ps\right)}^{2}}{2{n}_{0}+1}\right]\right)}{2\pi (2{n}_{0}+1)}.$$
(16)

The WF corresponding to a quantum state ρ is defined67 as

$$W(x,p)=\frac{1}{2\pi }{\int \nolimits_{-\infty }^{\infty }}{\rm{d}}y\ {{\rm{e}}}^{-{\rm{i}}py}\left\langle x+y| \rho | x-y\right\rangle ,$$
(17)

and the corresponding density matrix element can be obtained from the WF by an inverse Fourier transform. It is therefore possible to extend this approach to any W(x, p) beyond the Gaussian states.

The evolution of a state ρ under action of a Hamiltonian proportional to a quadrature \(\hat{q}\) can be straightforwardly computed in the basis of this quadrature, where it amounts to multiplication of density matrix elements with c-numbers:

$$\left\langle q\right|{{\rm{e}}}^{-{\rm{i}}{\hat{H}}_{q}(\hat{q})t}\rho {{\rm{e}}}^{{\rm{i}}{\hat{H}}_{q}(\hat{q})t}\left|q^{\prime} \right\rangle =\left\langle q| \rho | q^{\prime} \right\rangle {{\rm{e}}}^{-{\rm{i}}({H}_{q}(q)-{H}_{q^{\prime} }(q^{\prime} ))t}.$$
(18)

In particular, the nonlinear evolution reads

$$\left\langle x\right|\hat{U}_{\mathsf{NL}}(\delta t)\rho {\hat{U}}^{\dagger }_{\mathsf{NL}}(\delta t)\left|x^{\prime} \right\rangle =\left\langle x\right|\rho \left|x^{\prime} \right\rangle {{\rm{e}}}^{-{\rm{i}}[V(x)-V(x^{\prime} )]\delta t}.$$
(19)

The undamped harmonic evolution driven by \(\hat{H}_{\mathsf{HO}}\) can be represented by the rotation of WF in the phase space. A unitary rotation through an angle θ = Ωmδt in the phase space maps the initial WF W(x, p; t) onto the final W(x, p; t + δt) as

$$W(x,p;t+\delta t)=W(x\cos \theta -p\sin \theta ,p\cos \theta +x\sin \theta ;t).$$
(20)

The unitary transformation of the density matrix can be as well computed in the Fock state basis.

Finally, damped harmonic evolution of a high-Q harmonic oscillator over one half of an oscillation can also be evaluated in the phase space as a convolution of the initial WF W(x, p; t) with a thermal kernel

$$W(x,p;t+\frac{\pi }{{{\Omega }}})={\iint\nolimits_{-\infty }^{\infty }}{\rm{d}}u\ {\rm{d}}v\ {W}_{i}(x-u,p-v;t)W_{\mathsf{B}}(u,v),$$
(21)

where the expression for the kernel reads

$$W_{\mathsf{B}}(u,v)=\frac{1}{2\pi \sigma_{\mathsf{th}}}\exp \left[-\frac{{u}^{2}+{v}^{2}}{2\sigma_{\mathsf{th}}}\right],$$
(22)

with σth = (2nth + 1)2πηm/Ωm, where nth ≈ kBT/(ћΩm) is the thermal occupation of the bath set by its temperature T. In terms of the heating rate Hm, σth = 4πHm/Ωm. Equation (21) is obtained by solving the joint dynamics of the oscillator and bath followed by tracing out the latter. The detailed derivation of Eq. (21) can be found in Supplementary Note 2.

Using these techniques, one can evaluate the action of the map \({\mathcal{N}}\) defined by Eq. (6) on the state of the quantum oscillator. This yields the quantum state of the particle after one half of a mechanical oscillation. Repeatedly applying the same operations, one can obtain the state after multiple periods of the mechanical oscillations. Our purpose is then to explore the limits of the achievable nonlinearities in optomechanical systems that are accessible now or are within reach.