Abstract
A key open question in quantum computing is whether quantum algorithms can potentially offer a significant advantage over classical algorithms for tasks of practical interest. Understanding the limits of classical computing in simulating quantum systems is an important component of addressing this question. We introduce a method to simulate layered quantum circuits consisting of parametrized gates, an architecture behind many variational quantum algorithms suitable for near-term quantum computers. A neural-network parametrization of the many-qubit wavefunction is used, focusing on states relevant for the Quantum Approximate Optimization Algorithm (QAOA). For the largest circuits simulated, we reach 54 qubits at 4 QAOA layers, approximately implementing 324 RZZ gates and 216 RX gates without requiring large-scale computational resources. For larger systems, our approach can be used to provide accurate QAOA simulations at previously unexplored parameter values and to benchmark the next generation of experiments in the Noisy Intermediate-Scale Quantum (NISQ) era.
Similar content being viewed by others
Introduction
The past decade has seen a fast development of quantum technologies and the achievement of an unprecedented level of control in quantum hardware1, clearing the way for demonstrations of quantum computing applications for practical uses. However, near-term applications face some of the limitations intrinsic to the current generation of quantum computers, often referred to as Noisy Intermediate-Scale Quantum (NISQ) hardware2. In this regime, a limited qubit count and absence of quantum error correction constrain the kind of applications that can be successfully realized. Despite these limitations, hybrid classical-quantum algorithms3,4,5,6 have been identified as the ideal candidates to assess the first possible advantage of quantum computing in practical applications7,8,9,10.
The Quantum Approximate Optimization Algorithm (QAOA)5 is a notable example of variational quantum algorithm with prospects of quantum speedup on near-term devices. Devised to take advantage of quantum effects to solve combinatorial optimization problems, it has been extensively theoretically characterized11,12,13,14,15,16, and also experimentally realized on state-of-the-art NISQ hardware17. While the general presence of quantum advantage in quantum optimization algorithms remains an open question18,19,20,21, QAOA has gained popularity as a quantum hardware benchmark22,23,24,25. As its desired output is essentially a classical state, the question arises whether a specialized classical algorithm can efficiently simulate it26, at least near the variational optimum. In this paper, we use a variational parametrization of the many-qubit state based on Neural Network Quantum States (NQS)27 and extend the method of ref. 28 to simulate QAOA. This approach trades the need for exact brute force exponentially scaling classical simulation with an approximate, yet accurate, classical variational description of the quantum circuit. In turn, we obtain an heuristic classical method that can significantly expand the possibilities to simulate NISQ-era quantum optimization algorithms. We successfully simulate the Max-Cut QAOA circuit5,11,17 for 54 qubits at depth p = 4 and use the method to perform a variational parameter sweep on a 1D cut of the parameter space. The method is contrasted with state-of-the-art classical simulations based on low-rank Clifford group decompositions26, whose complexity is exponential in the number of non-Clifford gates as well as tensor-based approaches29. Instead, limitations of the approach are discussed in terms of the QAOA parameter space and its relation to different initializations of the stochastic optimization method used in this work.
Results
The Quantum Approximate Optimization Algorithm
The Quantum Approximate Optimization Algorithm (QAOA) is a variational quantum algorithm for approximately solving discrete combinatorial optimization problems. Since its inception in the seminal work of Farhi, Goldstone, and Gutmann5,12, QAOA has been applied to Maximum Cut (Max-Cut) problems. With competing classical algorithms30 offering exact performance bounds for all graphs, an open question remains—can QAOA perform better by increasing the number of free parameters?
In this work, we study a quadratic cost function31,32 associated with a Max-Cut problem. If we consider a graph G = (V, E) with edges E and vertices V, the Max-Cut of the graph G is defined by the following operator:
where wij are the edge weights and Zi are Pauli operators. The classical bitstring \({\mathcal{B}}\) that minimizes \(\left\langle {\mathcal{B}}\right|{\mathcal{C}}\left|{\mathcal{B}}\right\rangle\) is the graph partition with the maximum cut. QAOA approximates such a quantum state through a quantum circuit of predefined depth p:
where \(\left|+\right\rangle\) is a symmetric superposition of all computational basis states: \(\left|+\right\rangle ={H}^{\otimes N}{\left|0\right\rangle }^{\otimes N}\) for N qubits. The set of 2p real numbers γi and βi for i = 1…p define the variational parameters to be optimized over by an external classical optimizer. The unitary gates defining the parametrized quantum circuit read \({U}_{B}(\beta )={\prod }_{i\in V}{e}^{-i\beta {X}_{i}}\) and \({U}_{C}(\gamma )={e}^{-i\gamma {\mathcal{C}}}\).
Optimal variational parameters γ and β are then found through an outer-loop classical optimizer of the following quantum expectation value:
It is known that, for QAOA cost operators of the general form \({\mathcal{C}}={\sum }_{k}{{\mathcal{C}}}_{k}({Z}_{1},\ldots ,{Z}_{N})\), the optimal value asymptotically converges to the minimum value:
where Cp is the optimal cost value at QAOA depth p and \({\mathcal{B}}\) are classical bit strings. With modern simulations and implementations still being restricted to lower p-values, it is unclear how large p has to get in practice before QAOA becomes comparable with its classical competition.
In this work we consider 3-regular graphs with all weights wij set to unity at QAOA depths of p = 1, 2, 4.
Classical variational simulation
Consider a quantum system consisting of N qubits. The Hilbert space is spanned by the computational basis \(\{\left|{\mathcal{B}}\right\rangle :{\mathcal{B}}\in {\{0,1\}}^{N}\}\) of classical bit strings \({\mathcal{B}}=({B}_{1},\ldots ,{B}_{N})\). A general state can be expanded in this basis as \(\left|\psi \right\rangle ={\sum }_{{\mathcal{B}}}\psi ({\mathcal{B}})\left|{\mathcal{B}}\right\rangle\). The convention \({Z}_{i}\left|{\mathcal{B}}\right\rangle ={(-1)}^{{B}_{i}}\left|{\mathcal{B}}\right\rangle\) is adopted. In order to perform approximate classical simulations of the QAOA quantum circuit, we use a neural-network representation of the many-body wavefunction \(\psi ({\mathcal{B}})\) associated with this system, and specifically adopt a shallow network of the Restricted Boltzmann Machine (RBM) type33,34,35:
The RBM provides a classical variational representation of the quantum state27,36. It is parametrized by a set of complex parameters θ = {a, b, W}—visible biases a = (a1, …, aN), hidden biases \({\bf{b}}=({b}_{1},\ldots ,{b}_{{N}_{\text{h}}})\) and weights W = (Wj,k: j = 1…N, k = 1…Nh). The complex-valued ansatz given in Eq. (5) is, in general, not normalized.
We note that the N-qubit \(\left|+\right\rangle\) state required for initializing QAOA can always be exactly implemented by setting all variational parameters to 0. That choice ensures that the wavefunction ansatz given in Eq. (5) is constant across all computational basis states, as required. The advantage of using the ansatz given in Eq. (5) as an N-qubit state is that a subset of one- and two-qubit gates can be exactly implemented as mappings between different sets of variational parameters \(\theta \mapsto \theta ^{\prime}\). In general, such mapping corresponding to an abstract gate \({\mathcal{G}}\) is found as the solution of the following nonlinear equation:
for all bit strings \({\mathcal{B}}\) and any constant C, if a solution exists. For example, consider the Pauli Z gate acting on qubit i. In that case, Eq. (6) reads \({e}^{{a}_{i}^{\prime}{B}_{i}}=C{(-1)}^{{B}_{i}}{e}^{{a}_{i}{B}_{i}}\) after trivial simplification. The solution is \({a}_{i}^{\prime}={a}_{i}+i\pi\) for C = 1, with all other parameters remaining unchanged. In addition, one can exactly implement a subset of two-qubit gates by introducing an additional hidden unit coupled only to the two qubits in question. Labeling the new unit by c, we can implement the RZZ gate relevant for QAOA. The gate is given as \(RZZ(\phi )={e}^{-i\phi {Z}_{i}{Z}_{j}}\propto \,\text{diag}\,(1,{e}^{i\phi },{e}^{i\phi },1)\) up to a global phase. The replacement rules read:
where \({\mathcal{A}}(\phi )\) = Arccosh \(\left({e}^{i\phi }\right)\) and C = 2. Derivations of replacement rules for these and other common one and two-qubit gates can be found in Sec. Methods.
Not all gates can be applied through solving Eq. (6). Most notably, gates that form superpositions belong in this category, including \({U}_{B}(\beta )={\prod }_{i}{e}^{-i\beta {X}_{i}}\) required for running QAOA. This happens simply because a linear combination of two or more RBMs cannot be exactly represented by a single new RBM through a simple variational parameter change. To simulate those gates, we employ a variational stochastic optimization scheme.
We take \({\mathcal{D}}(\phi ,\psi )=1-F(\phi ,\psi )\) as a measure of distance between two arbitrary quantum states \(\left|\phi \right\rangle\) and \(\left|\psi \right\rangle\), where F(ϕ, ψ) is the usual quantum fidelity:
In order to find variational parameters θ, which approximate a target state \(\left|\phi \right\rangle\) well (\(\left|{\psi }_{\theta }\right\rangle \approx \left|\phi \right\rangle\), up to a normalization constant), we minimize \({\mathcal{D}}({\psi }_{\theta },\phi )\) using a gradient-based optimizer. In this work we use the Stochastic Reconfiguration (SR)37,38,39 algorithm to achieve that goal.
For larger p, extra hidden units introduced when applying UC(γ) at each layer can result in a large number of associated parameters to optimize over that are not strictly required for accurate output state approximations. So to keep the parameter count in check, we insert a model compression step, which halves the number of hidden units immediately after applying UC doubles it. Specifically we create an RBM with fewer hidden units and fit it to the output distribution of the larger RBM (output of UC). Exact circuit placement of compression steps are shown on Fig. 1 and details are provided in Methods. As a result of the compression step, we are able to keep the number of hidden units in our RBM ansatz constant, explicitly controlling the variational parameter count.
A schematic representation of the QAOA circuit and our approach to simulating it. The input state is trivially initialized to \(\left|+\right\rangle\). Next, at each p, the exchange of exactly (UC) and approximately (RX(β) = e−iβX) applicable gates is labeled (see Sec. Methods). As noted in the main text, each (exact) application of the UC gate leads to an increase in the number of hidden units by ∣E∣ (the number of edges in the graph). In order to keep that number constant, we "compress" the model (see Sec. Methods), indicated by red dashed lines after each UC gate. The compression is repeated at each layer after the first, halving the number of hidden units each time, immediately after doubling it with UC gates. After the final layer, the RBM is parametrized by θopt, approximating the final QAOA target state \(\left|{\boldsymbol{\gamma }},{\boldsymbol{\beta }}\right\rangle\).
Simulation results for 20 qubits
In this section we present our simulation results for Max-Cut QAOA on random regular graphs of order N40,41,42. In addition, we discuss model limitations and its relation to current state-of-the-art simulations.
QAOA angles γ, β are required as an input of our RBM-based simulator. At p = 1, we base our parameter choices on the position of global optimum that can be computed exactly (see Supplementary Note 1). For p > 1, we resort to direct numerical evaluation of the cost function as given in Eq. (1) from either the complete state vector of the system (number of qubits permitting) or from importance-sampling the output state as represented by a RBM. For all p, we find the optimal angles using Adam43 with either exact gradients or their finite-difference approximations.
We begin by studying the performance of our approach on a 20-qubit system corresponding to the Max-Cut problem on a 3-regular graph of order N = 20. In that case, access to exact numerical wavefunctions is not yet severely restricted by the number of qubits. That makes it a suitable test-case. The results can be found in Fig. 2.
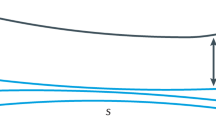
a The exact variational QAOA landscape at p = 1 of a random 20-qubit instance of a 3-regular graph is presented, calculated using the analytical cost formula (see Supplementary Note 1). The optimum is found using a gradient-based optimizer43 and marked. The restricted cut along the constant-β line and at optimal γ is more closely studied in panel b. b RBM-based output wavefunctions are contrasted with exact results. c A similar variational landscape cut is presented at p = 2. Optimal p = 2 QAOA parameters are calculated using numerical derivatives and a gradient-based optimizer. Parameters γ1, β1, and β2 are fixed at their optimal values while the cost function γ2-dependence is investigated. We note that our approach is able to accurately reproduce the increased proximity to the combinatorial optimum associated with increasing QAOA depth p. (The dashed line represents the minumum from p = 1 curve in panel b.).
In Fig. 2, we present the cost function for several values of QAOA angles, as computed by the RBM-based simulator. Each panel shows cost functions from one typical random 3-regular graph instance. We observe that cost landscapes, optimal angles and algorithm performance do not change appreciably between different random graph instances. We can see that our approach reproduces variations in the cost landscape associated with different choices of QAOA angles at both p = 1 and p = 2. At p = 1, an exact formula (see Supplementary Note 1) is available for comparison of cost function values. We report that, at optimal angles, the overall final fidelity (overlap squared) is consistently above 94% for all random graph instances we simulate.
In addition to cost function values, we also benchmark our RBM-based approach by computing fidelities between our variational states and exact simulations. In Fig. 3 we show the dependence of fidelity on the number of qubits and circuit depth p. While, in general, it is hard to analytically predict the behavior of these fidelities, we nonetheless remark that with relatively small NQS we can already achieve fidelities in excess of 92% for all system sizes considered for exact benchmarks.
Fidelities between approximate RBM variational states and quantum states obtained with exact simulation, for different values of p = 1, 2, 4 and number of qubits. QAOA angles γ, β we use are set to optimal values at p = 4 for each random graph instance. Ten randomly generated graphs are used for each system size. Error bars represent the standard deviation.
Simulation results for 54 qubits
Our approach can be readily extended to system sizes that are not easily amenable to exact classical simulation. To show this, in Fig. 4 we show the case of N = 54 qubits. This number of qubits corresponds, for example, to what implemented by Google’s Sycamore processor, while our approach shares no other implementation details with that specific platform. For the system of N = 54 qubits, we closely reproduce the exact error curve (see Supplementary Note 1) at p = 1, implementing 81 RZZ (e−iγZ⊗Z) gates exactly and 54 RX (e−iβX) gates approximately, using the described optimization method. We also perform simulations at p = 2 and p = 4 and obtain corresponding approximate QAOA cost function values.
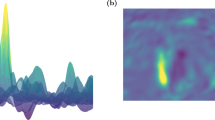
a Randomly generated 3-regular graphs with 54 nodes are considered at p = 1, 2, 4. At each p, all angles were set to optimal values (except for the final γp) for a smaller graph of 20 nodes for which optimal angles can be found at a much smaller computational cost. Cost dependence along this 1D slice of the variational landscape (a higher-dimensional analogue of panel a of Fig. 2) is investigated. The dashed line represents the exact cost at p = 1. Error bars were too small to be visible on the plot. At p = 2, this 54-qubit simulation approximately implements 162 RZZ gates and 108 RX gates while at p = 4 there are 324 RZZs and 216 RXs. b An array of final stochastic estimations of single-qubit fidelities (see Sec. Approximate gate application for formula) in the course of optimizer progress. The system presented consists of 54 qubits at p = 2 where exact state vectors are intractable for direct comparison. In these simulations, β1, β2, and γ1 are kept at their optimal values. Optimal γ2 value (for given β1, β2, γ1) is shown with a dashed line. We note that the fidelity estimates begin to drop approximately as γ2 increases beyond the optimal value. A similar qubit-by-qubit trend can be noticed across all system sizes and depths p we studied.
At p = 4, we exactly implement 324 RZZ gates and approximately implement 216 RX gates. This circuit size and depth is such that there is no available experimental or numerically exact result to compare against. The accuracy of our approach can nonetheless be quantified using intermediate variational fidelity estimates. These fidelities are exactly the cost functions (see Sec. Methods) we optimize, separately for each qubit. In Fig. 4 (panel b) we show the optimal variational fidelities (see Eq. (8)) found when approximating the action of RX gates with the RBM wavefunction. At optimal γ4 (minimum of p = 4 curve at Fig. 4, panel a), the lowest variational fidelity reached was above 98%, for a typical random graph instance shown at Fig. 4. As noted earlier, exact final states of 54-qubit systems are intractable so we are unable to report or estimate the full many-qubit fidelity benchmark results.
We remark that the stochastic optimization performance is sensitive to choices of QAOA angles away from optimum (see Fig. 4 right). In general, we report that the fidelity between the RBM state (Eq. (5)) and the exact N-qubit state (Eq. (2)) decreases as one departs from optimal by changing γ and β.
For larger values of QAOA angles, the associated optimization procedure is more difficult to perform, resulting in a lower fidelity (see the dark patch in Fig. 4, panel b). We find that optimal angles were always small enough not to be in the low-performance region. Therefore, this model is less accurate when studying QAOA states away from the variational optimum. However, even in regions with lowest fidelities, RBM-based QAOA states are able to approximate cost well, as can be seen in Figs. 2 and 4.
As an additional hint to the high quality of the variational approximation, we capture the QAOA approximation of the actual combinatorial optimum. A tight upper bound on that optimum was calculated to be Copt = −69 for 54 qubits by directly optimizing an RBM to represent the ground state of the cost operator defined in Eq. (3).
Comparison with other methods
In modern sum-over-Cliffords/Metropolis simulators, computational complexity grows exponentially with the number of non-Clifford gates. With the RZZ gate being a non-Clifford operation, even our 20-qubit toy example, exactly implementing 60 RZZ gates at p = 2, is approaching the limit of what those simulators can do26. In addition, that limit is greatly exceeded by the larger, 54-qubit system we study next, implementing 162 RZZ gates. State-of-the-art tensor-based approaches29 have been used to simulate larger circuits but are ineffective in the case of nonplanar graphs.
Another very important tensor-based method is the Matrix Product State (MPS) variational representation of the many-qubit state. This is is a low-entanglement representation of quantum states, whose accuracy is controlled by the so-called bond dimension. Routinely adopted to simulate ground states of one-dimensional systems with high accuracy44,45,46, extensions of this approach to simulate challenging circuits have also been recently put forward47. In Fig. 5, our approach is compared with an MPS ansatz. We establish that for small systems, MPS provides reliable results with relatively small bond dimensions. For larger systems, however, our approach significantly outperforms MPS-based circuit simulation methods both in terms of memory requirements (fewer parameters) and overall runtime. This is to be expected in terms of entanglement capacity of MPS wavefunctions, that are not specifically optimized to handle non-one-dimensional interaction graphs, as in this specific case at hand.
A range of MPS-based QAOA simulations are compared to our RBM ansatz performance on both 20-qubit and 54-qubit graphs at p = 2. In the 20-qubit case, we see quick convergence to the QAOA cost optimum with increasing bond dimension. Approximation ratio with of the RBM output is shown on the y-axis. However, on a 54-qubit graph, MPS accuracy increases approximately logarithmically with bond dimension. An approximation of the MPS bond dimension required for reaching RBM performance is extrapolated to be ≈1.5 × 104 which amounts to ~1010 free parameters.
For a more direct comparison, we estimate the MPS bond dimension required for reaching RBM performance at p = 2 and 54 qubits to be ~104 (see Fig. 5), amounting to ~1010 complex parameters (≈160 GB of storage) while our RBM approach uses ≈4500 parameters (≈70 kB of storage). In addition, we expect the MPS number of parameters to grow with depth p because of additional entanglement, while RBM sizes heuristically scale weakly (constant in our simulations) with p and can be controlled mid-simulation using our compression step. It should be noted that the output MPS bond dimension depends on the specific implementation of the MPS simulator, namely, qubit ordering and the number of “swap” gates applied to correct for the nonplanar nature of the underlying graph, and that a more efficient implementations might be found. However, determining the optimal implementation is itself a difficult problem and, given the entanglement of a generic circuit we simulate, it would likely produce a model with orders of magnitude more parameters than a RBM-based approach.
Discussion
In this work, we introduce a classical variational method for simulating QAOA, a hybrid quantum-classical approach for solving combinatorial optimizations with prospects of quantum speedup on near-term devices. We employ a self-contained approximate simulator based on NQS methods borrowed from many-body quantum physics, departing from the traditional exact simulations of this class of quantum circuits.
We successfully explore previously unreachable regions in the QAOA parameter space, owing to good performance of our method near optimal QAOA angles. Model limitations are discussed in terms of lower fidelities in quantum state reproduction away from said optimum. Because of such different area of applicability and relative low computational cost, the method is introduced as complementary to established numerical methods of classical simulation of quantum circuits.
Classical variational simulations of quantum algorithms provide a natural way to both benchmark and understand the limitations of near-future quantum hardware. On the algorithmic side, our approach can help answer a fundamentally open question in the field, namely whether QAOA can outperform classical optimization algorithms or quantum-inspired classical algorithms based on artificial neural networks48,49,50.
Methods
Exact application of one-qubit Pauli gates
As mentioned in the main text, some one-qubit gates gates can be applied exactly to the RBM ansatz given in Eq. (5). Here we discuss the specific case of Pauli gates. Parameter replacement rules we use to directly apply one-qubit gates can be obtained by solving Eq. (6) given in the main text. Consider for example the Pauli Xi or NOTi gate acting on qubit i. It can be applied by satisfying the following system of equations:
for Bi = 0, 1. The solution is:
with all other parameters remaining unchanged.
A similar solution can be found for the Pauli Y gate:
with all other parameters remaining unchanged as well.
For the Pauli Z gate, as described in the main text, one needs to solve \({e}^{{a}_{i}^{\prime}{B}_{i}}={(-1)}^{{B}_{i}}{e}^{{a}_{i}{B}_{i}}\). The solution is simply
More generally, it is possible to apply exactly an arbitrary Z rotation gate, as given in matrix form as:
where the proportionality is up to a global phase factor. Similar to the Pauli Zi gate, this gate can be implemented on qubit i by solving \({e}^{{a}_{i}^{\prime}{B}_{i}}={e}^{i\varphi {B}_{i}}{e}^{{a}_{i}{B}_{i}}\). The solution is simply:
with all other parameters besides ai remaining unchanged. This expression reduces to the Pauli Z gate replacement rules for φ = π as required.
Exact application of two-qubit gates
We apply two-qubit gates between qubits k andlby adding an additional hidden unit (labeled by c) to the RBM before solving Eq. (6) from the main text. The extra hidden unit couples only to qubits in question, leaving all previously existing parameters unchanged. In that special case, the equation reduces to
An important two-qubit gate we can apply exactly are ZZ rotations. The gate RZZ is key for being able to implement the first step in the QAOA algorithm. The definition is:
where the proportionality factor is again a global phase. The related matrix element for a RZZkl gate between qubits k and l is \(\left\langle {B}_{k}^{\prime}{B}_{l}^{\prime}\right|RZ{Z}_{kl}(\varphi )\left|{B}_{k}{B}_{l}\right\rangle ={e}^{i\varphi {B}_{k}\oplus {B}_{l}}\) where ⊕ stands for the classical exclusive or (XOR) operation. Then, one solution to Eq. (15) reads:
where \({\mathcal{A}}(\varphi )\) = Arccosh \(\left({e}^{i\varphi }\right)\) and C = 2.
Approximate gate application
Here we provide model details and show how to approximately apply quantum gates that cannot be implemented through methods described in sec. Exact application of one-qubit Pauli gates. In this work we use the Stochastic Reconfiguration (SR)37 algorithm to approximately apply quantum gates to the RBM ansatz. To that end, we write the “infidelity” between our RBM ansatz and the target state ϕ, \({\mathcal{D}}({\psi }_{\theta },\phi )=1-F({\psi }_{\theta },\phi )\), as an expectation value of an effective hamiltonian operator \({H}_{\,\text{eff}\,}^{\phi }\):
We call the hermitian operator given in Eq. (18) a “hamiltonian” only because the target quantum state \(\left|\psi \right\rangle\) is encoded into it as the eigenstate corresponding to the smallest eigenvalue. Our optimization scheme focuses on finding small parameter updates Δk that locally approximate the action of the imaginary time evolution operator associated with \({H}_{\,\text{eff}\,}^{\phi }\), thus filtering out the target state:
where C is an arbitrary constant included because our variational states (Eq. (5), main text) are not normalized. Choosing both η and Δ to be small, one can expand both sides to linear order in those variables and solve the resulting linear system for all components of Δ, after eliminating C first. After some simplification, one arrives at the following parameter at each loop iteration (indexed with t):
where stochastic estimations of gradients of the cost function \({\mathcal{D}}({\psi }_{\theta },\phi )\) can be obtained through samples from ∣ψθ∣2 at each loop iteration through:
Here, \({{\mathcal{O}}}_{k}\) is defined as a diagonal operator in the computational basis such that \(\left\langle {\mathcal{B}}\right|^{\prime} {{\mathcal{O}}}_{k}\left|{\mathcal{B}}\right\rangle =\frac{\partial {\mathrm{ln}}\,{\psi }_{\theta }}{\partial {\theta }_{k}}\ {\delta }_{{\mathcal{B}}^{\prime} {\mathcal{B}}}\). Averages over ψ are commonly defined as \({\langle \cdot \rangle }_{\psi }\equiv \left\langle \psi \right|\cdot \left|\psi \right\rangle /\langle \psi | \psi \rangle\). Furthermore, the S-matrix appearing in Eq. (20) reads:
and corresponds to the Quantum Geometric Tensor or Quantum Fisher Information (also see ref. 51 for a detailed description and connection with the natural gradient method in classical machine learning52).
Exact computations of averages over N-qubit states ψθ and ϕ at each optimization step range from impractical to intractable, even for moderate N. Therefore, we evaluate those averages by importance-sampling the probability distributions associated with the variational ansatz ∣ψθ∣2 and the target state ∣ϕ∣2 at each optimization step t. All of the above expectation values are evaluated using Markov Chain Monte Carlo (MCMC)38,39 sampling with basic single-spin flip local updates. An overview of the sampling method can be found in ref. 53. In order to use those techniques, we rewrite Eq. (21) as:
In our experiments with less than 20 qubits, we take 8000 MCMC samples from four independent chains (totaling 32,000 samples) for gradient evaluation. Between each two recorded samples, we take N MCMC steps (for N qubits). For the 54-qubit experiment, we take 2000 MCMC samples four independent chains because of increased computational difficulty of sampling. The entire Eq. (23) is manifestly invariant to rescaling of ψθ and ϕ, removing the need to ever compute normalization constants. We remark that the prefactor in Eq. (23) is identically equal to the fidelity given in Eq. (8) in the main text.
allowing us to keep track of cost function values during optimization with no additional computational cost.
The second step consists of multiplying the variational derivative with the inverse of the S-matrix (Eq. (22)) corresponding to a stochastic estimation of a metric tensor on the hermitian parameter manifold. Thereby, the usual gradient is transformed into the natural gradient on that manifold. However, the S-matrix is stochastically estimated and it can happen that it is singular. To regularize it, we replace S with S + \(\epsilon {\mathbb{1}}\), ensuring that the resulting linear system has a unique solution. We choose ϵ = 10−3 throughout. The optimization procedure is summarized in Supplementary Note 2.
In order to keep the number of hidden units reasonable, we employ a compression step at each QAOA layer (after the first). Immediately after applying the UC(γk) gate in layer k to the RBM ψθ (and thereby introducing unwanted parameters), we go through the following steps:
-
(1)
Construct a new RBM \({\widetilde{\psi }}_{\theta }\).
-
(2)
Initialize \({\widetilde{\psi }}_{\theta }\) to exactly represent the state \({U}_{C}\left(\frac{1}{k}{\sum }_{j\le k}{\gamma }_{j}\right)\left|+\right\rangle\). Doing this introduces half the number hidden units that are already present in ψθ.
-
(3)
Stochastically optimize \({\widetilde{\psi }}_{\theta }\) to approximate ψθ (using algorithm in Supplementary Note 2) with ϕ → ψθ and \(\psi \to {\widetilde{\psi }}_{\theta }\).
In essence, we use the optimization algorithm with the “larger” ψθ as the target state ϕ. The optimization results in a new RBM state with fewer hidden units that closely approximates the old RBM with fidelity > 0.98 in all our tests. We then proceed to simulate the rest of the QAOA circuit and apply the same compression procedure again when the number of parameters increases again. The exact schedule of applying this procedure in the context of different QAOA layers can be seen on Fig. 1.
We choose the initial state for the optimization as an exactly reproducible RBM state that has non-zero overlap with the target (larger) RBM. In principle, any other such state would work, but we heuristically find this one to be a reliable choice across all p-values studied. Alternatively, one can just initialize \(\widetilde{{\psi }_{\theta }}\) to \({U}_{C}\left(\gamma ^{\prime} \right)\left|+\right\rangle\) with \(\gamma ^{\prime} ={\text{argmax}}_{\gamma }\ F\left({\psi }_{\theta },{U}_{C}(\gamma )\left|+\right\rangle \right)\), using an efficient 1D optimizer to solve for \(\gamma ^{\prime}\) before starting to optimize the full RBM.
Data availability
The authors declare that the data supporting the findings of this study are available within the paper.
Code availability
Our Python code is available on GitHub to reproduce the results presented in this paper through the following URL: github.com/Matematija/QubitRBM.
References
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2, 79 (2018).
Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 1–7 (2014).
Farhi, E. & Neven, H. Classification with quantum neural networks on near term processors. Preprint at https://arxiv.org/abs/1802.06002 (2018).
Farhi, E., Goldstone, J. & Gutmann, S. A Quantum Approximate Optimization Algorithm. Preprint at https://arxiv.org/abs/1411.4028 (2014).
Grant, E. et al. Hierarchical quantum classifiers. npj Quantum Inf. 4, 1–8 (2018).
Aspuru-Guzik, A., Dutoi, A. D., Love, P. J. & Head-Gordon, M. Chemistry: simulated quantum computation of molecular energies. Science 309, 1704–1707 (2005).
O’Malley, P. J. et al. Scalable quantum simulation of molecular energies. Phys. Rev. X 6, 031007 (2016).
Biamonte, J. et al. Quantum machine learning. Nature 549, 195–202 (2017).
Lloyd, S. Universal quantum simulators. Science 273, 1073–1078 (1996).
Wang, Z., Hadfield, S., Jiang, Z. & Rieffel, E. G. Quantum approximate optimization algorithm for MaxCut: a fermionic view. Phys. Rev. A 97, 022304 (2018).
Farhi, E., Goldstone, J. & Gutmann, S. A Quantum Approximate Optimization Algorithm applied to a bounded occurrence constraint problem. Preprint at https://arxiv.org/abs/1412.6062 (2014).
Lloyd, S. Quantum approximate optimization is computationally universal. Preprint at https://arxiv.org/abs/1812.11075 (2018).
Jiang, Z., Rieffel, E. G. & Wang, Z. Near-optimal quantum circuit for Grover’s unstructured search using a transverse field. Phys. Rev. A 95, 062317 (2017).
Hadfield, S. et al. From the quantum approximate optimization algorithm to a quantum alternating operator ansatz. Algorithms 12, 34 (2019).
Zhou, L., Wang, S. T., Choi, S., Pichler, H. & Lukin, M. D. Quantum Approximate Optimization Algorithm: performance, mechanism, and implementation on near-term devices. Phys. Rev. X 10, 21067 (2020).
Harrigan, M. P. et al. Quantum approximate optimization of non-planar graph problems on a planar superconducting processor. Nat. Phys. 17, 332–336 (2021).
Santoro, G. E., Martoňák, R., Tosatti, E. & Car, R. Theory of quantum annealing of an Ising spin glass. Science 295, 2427–2430 (2002).
Rønnow, T. F. et al. Defining and detecting quantum speedup. Science 345, 420–424 (2014).
Guerreschi, G. G. & Matsuura, A. Y. QAOA for Max-Cut requires hundreds of qubits for quantum speed-up. Sci. Rep. 9, 1–7 (2019).
Bravyi, S., Kliesch, A., Koenig, R. & Tang, E. Obstacles to variational quantum optimization from symmetry protection. Phys. Rev. Lett. 125, 260505 (2020).
Pagano, G. et al. Quantum approximate optimization of the long-range Ising model with a trapped-ion quantum simulator. Proc. Natl Acad. Sci. USA 117, 25396–25401 (2020).
Bengtsson, A. et al. Improved success probability with greater circuit depth for the Quantum Approximate Optimization Algorithm. Phys. Rev. Appl. 14, 034010 (2020).
Willsch, M., Willsch, D., Jin, F., De Raedt, H. & Michielsen, K. Benchmarking the quantum approximate optimization algorithm. Quantum Inf. Process. 19, 1–24 (2020).
Otterbach, J. S. et al. Unsupervised machine learning on a hybrid quantum computer. Preprint at https://arxiv.org/abs/1712.05771 (2017).
Bravyi, S. et al. Simulation of quantum circuits by low-rank stabilizer decompositions. Quantum 3, 181 (2019).
Carleo, G. & Troyer, M. Solving the quantum many-body problem with artificial neural networks. Science 355, 602–606 (2017).
Jónsson, B., Bauer, B. & Carleo, G. Neural-network states for the classical simulation of quantum computing. Preprint at https://arxiv.org/abs/1808.05232 (2018).
Villalonga, B. et al. Establishing the quantum supremacy frontier with a 281 Pflop/s simulation. Quantum Sci. Technol. 5, 034003 (2020).
Goemans, M. X. & Williamson, D. P. Improved approximation algorithms for maximum cut and satisflability problems using semidefinite programming. J. ACM 42, 1115–1145 (1995).
Lucas, A. Ising formulations of many NP problems. Front. Phys. 2, 1–14 (2014).
Barahona, F. On the computational complexity of ising spin glass models. J. Phys. A Math. Gen. 15, 3241–3253 (1982).
Hinton, G. E. Training products of experts by minimizing contrastive divergence. Neural Comput. 14, 1771–1800 (2002).
Hinton, G. E. & Salakhutdinov, R. R. Reducing the dimensionality of data with neural networks. Science 313, 504–507 (2006).
Lecun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
Melko, R. G., Carleo, G., Carrasquilla, J. & Cirac, J. I. Restricted Boltzmann machines in quantum physics. Nat. Phys. 15, 887–892 (2019).
Sorella, S. Green function monte carlo with stochastic reconfiguration. Phys. Rev. Lett. 80, 4558–4561 (1998).
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H. & Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 21, 1087–1092 (1953).
Hastings, W. K. Monte carlo sampling methods using Markov chains and their applications. Biometrika 57, 97–109 (1970).
Steger, A. & Wormald, N. C. Generating random regular graphs quickly. Comb. Probab. Comput. 8, 377–396 (1999).
Kim, J. H. & Vu, V. H. Generating random regular graphs. in Proc. of the 35th annual ACM symposium on Theory of computing 213–222 (Association for Computing Machinery, 2003).
Hagberg, A. A., Schult, D. A. & Swart, P. J. Exploring network structure, dynamics, and function using NetworkX. in 7th Python Sci. Conf. (SciPy 2008), 11–15 (Pasadena, CA USA, 2008) https://networkx.org/documentation/stable/citing.html.
Kingma, D. P. & Ba, J. L. Adam: a method for stochastic optimization. in 3rd Int. Conf. Learn. Represent. ICLR 2015 - Conf. Track Proc. (San Diego, CA, USA, 2015) https://dblp.org/db/conf/iclr/iclr2015.html.
White, S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863–2866 (1992).
Vidal, G. Efficient classical simulation of slightly entangled quantum computations. Phys. Rev. Lett. 91, 147902 (2003).
Vidal, G. Efficient simulation of one-dimensional quantum many-body systems. Phys. Rev. Lett. 93, 040502 (2004).
Zhou, Y., Stoudenmire, E. M. & Waintal, X. What Limits the Simulation of Quantum Computers? Phys. Rev. X 10, 041038 (2020).
Gomes, J., Eastman, P., McKiernan, K. A. & Pande, V. S. Classical quantum optimization with neural network quantum states. Preprint at https://arxiv.org/abs/1910.10675 (2019).
Zhao, T., Carleo, G., Stokes, J. & Veerapaneni, S. Natural evolution strategies and variational Monte Carlo. Mach. Learn. Sci. Technol. 2, 2–3 (2020).
Hibat-Allah, M., Inack, E. M., Wiersema, R., Melko, R. G. & Carrasquilla, J. Variational Neural Annealing. Preprint at https://arxiv.org/abs/2101.10154 (2021).
Stokes, J., Izaac, J., Killoran, N. & Carleo, G. Quantum natural gradient. Quantum 4, 269 (2020).
Amari, S. I. Natural gradient works efficiently in learning. Neural Comput. 10, 251–276 (1998).
Newman, M. E. J. & Barkema, G. T.Monte Carlo Methods in Statistical Physics (Oxford University Press, 1999).
Harris, C. R. et al. Array programming with NumPy. Nature 585, 357–362 (2020).
Virtanen, P. et al. SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat. Methods 17, 261–272 (2020).
Gidney, C., Bacon, D. & The Cirq Developers. quantumlib/Cirq: A python framework for creating, editing, and invoking Noisy Intermediate Scale Quantum (NISQ) circuits. https://github.com/quantumlib/Cirq (2018).
Torlai, G. & Fishman, M. PastaQ.jl: Package for Simulation, Tomography and Analysis of Quantum Computers. https://github.com/GTorlai/PastaQ.jl (2020).
Fishman, M., White, S. R. & Stoudenmire, E. M. The ITensor software library for tensor network calculations. Preprint at https://arxiv.org/abs/2007.14822 (2020).
Hunter, J. D. Matplotlib: a 2D graphics environment. Comput. Sci. Eng. 9, 99–104 (2007).
Acknowledgements
We thank S. Bravyi for enlightening discussions and M. Fishman for insights into MPS simulations. Numerical simulations were performed using NumPy54, SciPy55, Google Cirq56, and PastaQ57,58 for MPS simulations. Random graph generation was done with NetworkX40,42. Plots were generated using Matplotlib59. M.M. acknowledges support from the CCQ graduate fellowship in computational quantum physics. The Flatiron Institute is a division of the Simons Foundation.
Author information
Authors and Affiliations
Contributions
G.C. conceived the main idea and co-wrote the manuscript. M.M. developed the idea further, wrote the computer code, executed the numerical simulations. and co-wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Medvidović, M., Carleo, G. Classical variational simulation of the Quantum Approximate Optimization Algorithm. npj Quantum Inf 7, 101 (2021). https://doi.org/10.1038/s41534-021-00440-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-021-00440-z
This article is cited by
-
Quantum harmonic oscillator model for simulation of intercity population mobility
Journal of Geographical Sciences (2024)
-
HASM quantum machine learning
Science China Earth Sciences (2023)
-
A review on quantum computing and deep learning algorithms and their applications
Soft Computing (2023)
-
Solving MaxCut with quantum imaginary time evolution
Quantum Information Processing (2023)
-
Empirical performance bounds for quantum approximate optimization
Quantum Information Processing (2021)