Abstract
While in classical mechanics the mean error of a measurement is solely caused by the measuring process (or device), in quantum mechanics the operator-based nature of quantum measurements has to be considered in the error measure as well. One of the major problems in quantum physics has been to generalize the classical root-mean-square error to quantum measurements to obtain an error measure satisfying both soundness (to vanish for any accurate measurements) and completeness (to vanish only for accurate measurements). A noise-operator-based error measure has been commonly used for this purpose, but it has turned out incomplete. Recently, Ozawa proposed an improved definition for a noise-operator-based error measure to be both sound and complete. Here, we present a neutron optical demonstration for the completeness of the improved error measure for both projective (or sharp) as well as generalized (or unsharp) measurements.
Similar content being viewed by others
Introduction
Precise knowledge of the mean error of a measurement is vital, both in classical mechanics, and even more in quantum mechanics, where it is essential in the development of emerging technologies such as quantum information processing, quantum computing or the quantum internet1. Extending the classical notion of root-mean-square (rms) error, which has been broadly accepted as the standard definition for the mean error of measurement, to quantum measurements is a highly challenging and a non-trivial task2,3,4,5,6,7,8. A noise-operator-based error measure has been commonly used as a sound error measure generalizing the classical root-mean-square error. The noise-operator was first used in attempts to prove Heisenberg’s uncertainty relation9 for approximate simultaneous measurements of pairs of non-commuting observables10,11,12. The noise-operator-based quantum root-mean-square (q-rms) error, defined as the root-mean-square of the noise operator, indicates how closely a meter observable ‘tracks’ the observable to be measured. In more recent developments the noise-operator-based q-rms error was used to reformulate Heisenberg’s error-disturbance relation to be universally valid2,13 and made the conventional relation testable. The validity of the reformulated relation as well as the violation of the conventional relation was observed first in neutronic14,15,16,17,18 and in photonic19,20,21,22,23 systems for successive spin measurements. However, Busch, Heinonen, and Lahti (BHL) found a case where the noise-operator-based quantum root-mean-square error shows incompleteness24, and brought about a debate on the use of the noise-operator7, until Ozawa recently brought a satisfactory solution25. It is the purpose of this work to briefly recapitulate the argument of BHL24, Ozawa’s improved definition of a sound and complete noise-operator-based q-rms error25, and to present a neutron optical experiment that demonstrates the completeness of improved noise-operator-based q-rms error. At this point, we want to emphasize that the improved error notion maintains the previously obtained universally valid uncertainty relations and their experimental confirmations without changing their forms and interpretations25.
Results
Theory
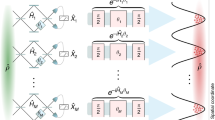
The noise-operator-based quantum root-mean-square (q-rms) error26 of a measuring process M, on quantum instrument \({\mathcal{I}}\), is denoted as \({\varepsilon }_{{\rm{NO}}}(A)=\left\langle \psi ,\xi \right|N{(A,{\bf{M}})}^{2}{\left|\xi ,\psi \right\rangle }^{1/2}\), where the noise-operator N(A, M) describes how accurately the value of an observable A is transferred to the meter observable MA, during the evolution U(t) of the composite system: N(A, M) = U(t)†(\({\mathbb{1}}\) ⊗ MA)U(t) − A ⊗ \({\mathbb{1}}\). Here A is an observable of a system S in state \(\left|\psi \right\rangle\) of Hilbert space \({\mathcal{H}}\), and MA is the observable representing the meter of the observer in the probe system (measurement device) P in initial state \(\left|\xi \right\rangle\) of Hilbert space \({\mathcal{K}}\). Moreover, U(t) is the unitary evolution of the composite quantum system S + P. This concept, introduced in27, is usually referred to as indirect measurement model of measuring process M and schematically illustrated in Fig. 1.
In the Heisenberg picture, we shall write A(0) = A ⊗ \({\mathbb{1}}\) and MA(t) = U(t)†(\({\mathbb{1}}\) ⊗ MA)U(t). The POVM Π of the measuring process M is defined by \({{\Pi }}(x)=\left\langle \xi \right|{{\rm{P}}}^{{M}_{A}(t)}(x)\left|\xi \right\rangle\), where \({{\rm{P}}}^{{M}_{A}(t)}(x)\) is the spectral projection of MA(t) for eigenvalues x. The moment operator M of the POVM Π is defined by M = ∑xx Π(x), and the second moment operator M(2) of the POVM Π is defined by M(2) = ∑xx2 Π(x). The measurement is called a sharp measurement of M if Π is projection-valued. In this case, we have Π(x) = PM(x) and M(2) = M2. Otherwise, the measurement is called an unsharp (or generalized) measurement of M; in this case we have M(2) > M2. An important property of εNO(A) is that it is determined by (moment operators of) the POVM Π of M in such a way that
This property and its consequence are to be studied in the present experiment.
After numerous successful experimental demonstrations of error-disturbance uncertainty relations based on the noise-operator-based q-rms error2,13,14,19,20,26, Busch, Lahti, and Werner (BLW)7 raised a reliability problem for quantum generalizations of the classical root-mean-square error. They compared the noise-operator-based q-rms error with the Wasserstein 2-distance, an error measure based on the distance between probability measures, and pointed out several discrepancies between them in favor of the latter.
In order to reconcile the conflict, Ozawa introduced four requirements for a valid definition of error measure ε generalizing the classical rms error25:
-
(i)
Operational definability: The error measure is definable by the POVM Π of measuring process M with A and \(\left|\psi \right\rangle\), i.e., \(\varepsilon =\varepsilon (A,{{\Pi }},\left|\psi \right\rangle )\).
-
(ii)
Correspondence principle: If A(0) and MA(t) commute, \(\varepsilon (A,{{\Pi }},\left|\psi \right\rangle )\) equals the classical rms error determined by the joint probability distribution of A(0) and MA(t).
-
(iii)
Soundness: The error measure ε should vanish for any accurate measurements.
-
(iv)
Completeness: The converse of soundness—a measurement should be accurate if the error measure ε vanishes.
Any reliable error measure should satisfy the soundness, while sound and complete error measures completely characterize accurate measurements. Ozawa25 showed that the noise-operator-based q-rms error satisfies requirements (i)–(iii), so that it is a sound generalization of the classical rms error. In fact, Eq. (1) ensures (i), and (ii) follows from the property of the joint probability distribution of A(0) and MA(t). It is further shown that every error measure satisfying (ii) automatically satisfies (iii)25. It was also shown that any error measures based on the distance of probability measures, including the Wasserstein 2-distance, satisfy (i) and (iii) but do not satisfy (ii) nor (iv)25. Hence, discrepancies between the two error measures are not caused by the unsoundness of the noise-operator-based q-rms error, but rather caused by the incompleteness of the Wasserstein 2-distance. Thus, the reliability problem for the noise-operator-based q-rms error has been solved. The error-disturbance relation formulated by the noise-operator-based q-rms error correctly describes the existence of the unavoidable error and disturbance25.
Counter-example
It is well known that the classical rms error is sound and complete for classical measurements. Thus, (ii) ensures that the noise-operator-based q-rms error is not only sound but also complete for any measurement such that A(0) and MA(t) commute. However, the noise- operator-based q-rms error does not satisfy the completeness, (iv), in general.
It is shown by BHL24 that there exists a measuring process M with \({\varepsilon }_{{\rm{NO}}}(A,{{\Pi }},\left|\psi \right\rangle )=0\), whereas M does not accurately measure A. However, a vanishing error is only expected for an accurate measurement for the completeness of the error measure. Here, we do not give the original counter-example but the slightly simplified version as stated in ref. 25. Consider measurement of the observable A in a two-level system in the initial state \(\left|\psi \right\rangle\) with measuring process described by a POVM Π with the moment operator M given as follows.
First, we consider the sharp measurement of M with the POVM Π1. In this case, one obtains Π1(x) = PM(x) and M(2) = M2, so that
However, this particular measurement is not accurate, since A and M have disjoint spectra. The operator A has spectral decomposition \(A={\sum }_{i}{a}_{i}\left|{a}_{i}\right\rangle \left\langle {a}_{i}\right|\), with eigenvalues ai = {2, 0} and normalized eigenvectors \(\left|{a}_{i}\right\rangle =1/\sqrt{2}{(1,\pm\!1)}^{T}=\left|\pm\!x\right\rangle\), while \(M={\sum }_{i}{m}_{i}\left|{m}_{i}\right\rangle \left\langle {m}_{i}\right|\), with eigenvalues \({m}_{i}=\{\pm \!\sqrt{2}\}\) and normalized eigenvectors \(\left|{m}_{i}\right\rangle =\{\frac{1}{\sqrt{4+2\sqrt{2}}}{(1+\sqrt{2},1)}^{T},\frac{1}{\sqrt{4-2\sqrt{2}}}{(1-\sqrt{2},1)}^{T}\}\). With PA(2), being the projector associated with eigenvalue 2, that is \(\left|+x\right\rangle \left\langle +x\right|\equiv {{\rm{P}}}^{{\sigma }_{x}}(1)\), which finally gives \(\left\langle +z\right|{{\rm{P}}}^{{\sigma }_{x}}(1)\left|+z\right\rangle =\frac{1}{2}\). We can then write \(\left\langle \psi \right|{{\rm{P}}}^{A}(2)\left|\psi \right\rangle =\frac{1}{2}\,\ne \,\left\langle \psi \right|{{{\Pi }}}_{1}(2)\left|\psi \right\rangle =0\) to express the inaccuracy of the measurement. Thus, the measurement with the POVM Π1 = PM does not accurately measure A but \({\varepsilon }_{{\rm{NO}}}(A,{{{\Pi }}}_{1},\left|\psi \right\rangle )=0\).
Secondly, we consider the unsharp measurement of M with POVM Π2 given by
for which we have M = 2Π2(2) − 2Π2( − 2), so that the POVM Π2 is an unsharp measurement of M. Then, we have M(2) = 41 and M2 = 21. Thus, we have \({\varepsilon }_{{\rm{NO}}}(A,{{{\Pi }}}_{2},\left|\psi \right\rangle )=\sqrt{2}.\) Since
the value \({\varepsilon }_{{\rm{NO}}}(A,{{{\Pi }}}_{2},\left|\psi \right\rangle )=\sqrt{2}\) will be revised when the value \({\varepsilon }_{{\rm{NO}}}(A,{{{\Pi }}}_{1},\left|\psi \right\rangle )=0\) is revised for the completeness of the error measure.
Definition and predictions of locally uniform quantum root-mean-square error
To remedy the incompleteness of the noise-operator-based q-rms error, Ozawa25 proposed a modification of its definition to satisfy all of the requirements (i)–(iv) including completeness. For any \(t\in {\mathbb{R}}\) the quantum root-mean-square (q-rms) error profile εt for A and Π in \(\left|\psi \right\rangle\) is defined as
In order to obtain a numerical error measure the locally uniform q-rms error \(\overline{\varepsilon }\) is defined as
Then \(\overline{\varepsilon }\) is a sound and complete q-rms error. For the given example from Eq. (2), with A, Π1, and \(\left|\psi \right\rangle\), we get
for the sharp M measurement described by the POVM Π1. The relation \(\overline{\varepsilon }(A,{{\Pi }},\left|\psi \right\rangle )=2\) correctly indicates that the measurement of A described in the example above is not an accurate measurement. For the unsharp M measurement described by the POVM Π2, one gets
Thus, the value \({\epsilon }_{{\rm{NO}}}(A,{{{\Pi }}}_{2},\left|\psi \right\rangle )=\sqrt{2}\) is revised as \(\overline{\epsilon }(A,{{{\Pi }}}_{2},\left|\psi \right\rangle )\ =\ \sqrt{6}\) for the completeness of the error measure \(\overline{\epsilon }\).
In addition to (i)–(iv), the locally uniform q-rms error \(\overline{\varepsilon}\) is shown to have the following two properties:
-
(v)
Dominating property: The error measure ε dominates the noise-operator-based q-rms error, that is \({\varepsilon }_{{\rm{NO}}}(A,{{\Pi }},\left|\psi \right\rangle )\le \varepsilon (A,{{\Pi }},\left|\psi \right\rangle )\).
-
(vi)
Conservation property for dichotomic measurements: The error measure ε coincides with the noise-operator-based q-rms error εNO for dichotomic measurements, i.e., \({\varepsilon }_{{\rm{NO}}}(A,{{\Pi }},\left|\psi \right\rangle )=\varepsilon (A,{{\Pi }},\left|\psi \right\rangle )\) if A2 = M(2) = 1.
Property (v) ensures that all the universally valid error-disturbance relations for εNO also hold for \(\overline{\varepsilon}\). Thus the improved notion maintains all previously obtained universally valid uncertainty relations and their experimental confirmations carried out for dichotomic measurements14,15,16,17,18 without changing their forms and interpretations, in contrast to a prevailing view that a state-dependent formulation for measurement uncertainty relation is not tenable7.
Experimental
Here, we present a neutron polarimetric measurement of the quantum root-mean-square (q-rms) error profile εα, resulting in determination of the locally uniform q-rms error \(\overline{\epsilon }\), for the POVM Π1 (the sharp measurement of M) and the POVM Π2 (an unsharp measurement of M), as given in Eqs. (7) and (8) to demonstrate the completeness property and thereby confirm the resolution of the inconsistency in question.
The experiment was performed at the polarimeter instrument NepTUn (NEutron Polarimeter TU wieN), located at the tangential beam port of the 250 kW TRIGA Mark II research reactor at the Atominstitut - TU Wien, in Vienna, Austria. A schematic illustration of the setup is given in Fig. 2. An incoming monochromatic neutron beam, reflected from a pyrolytic graphite crystal, with mean wavelength λ ≃ 2.02 Å (Δλ/λ ≃ 0.02) is polarized along the vertical (+z) direction by refraction from a CoTi multilayer array, hence on referred to as supermirror. The neutron polarimetric setup consists of three stages, as indicated in Fig. 2. The blue stage indicates the preparation of the incident state \(\left|\psi \right\rangle =\left|+z\right\rangle\), which is reflected from the polarizer (first super mirror). In the red stage the state evolution of initial state \(\left|\psi \right\rangle =\left|+z\right\rangle\) as \(\left|\psi (t)\right\rangle ={e}^{-{\rm{i}}tA}\left|\psi \right\rangle \ \to \ {e}^{({\rm{i}}\alpha {\sigma }_{x})/2}\left|\psi \right\rangle \equiv \left|\psi (\alpha )\right\rangle\) is induced, due to rotation by angle α about the x-axis (note that the error profile ϵα is a function of the rotation angle α). The Larmor precession inside direct current (DC) coil 1 is induced by the static magnetic field \({B}_{x}^{(\alpha )}\).
The setup consists of three regions: Blue: preparation of the initial state \(\left|\psi \right\rangle ={(1,0)}^{T}\equiv \left|+z\right\rangle\). Red: preparation of the evolved state \(\left|\psi (t)\right\rangle ={e}^{-{\rm{i}}tA}\left|\psi \right\rangle \to \ \left|\psi (\alpha )\right\rangle ={e}^{-{\rm{i}}t{\sigma }_{x}}\left|\psi \right\rangle ={e}^{({\rm{i}}\alpha {\sigma }_{x})/2}\left|\psi \right\rangle\). Green: Measurement of A2, M2 and M in state \(\left|\psi (\alpha )\right\rangle\), \(\ \left|\psi (\alpha +\pi )\right\rangle\) and \(\left|+x\right\rangle\), respectively. Projective (sharp) measurements are realized by applying projectors \({P}^{M}(\pm \!\sqrt{2})\) and generalized (unsharp) in terms of POVM by randomized sequences of PM and \({{\rm{P}}}^{{\sigma }_{x}}\). Bloch spheres above setup indicate the evolution of initial state \(\left|\psi (\alpha )\right\rangle\) and measured projectors PM and \({{\rm{P}}}^{{\sigma }_{x}}\).
In the green stage, a projective (or sharp) measurement of M is performed first, in order to demonstrate the counter example \({\varepsilon }_{t}(A,{{{\Pi }}}_{1},\left|\psi (t)\right\rangle )=2| \sin t|\) from25. The Π1 measurement has two possible outcomes, namely \(m=+\sqrt{2}\) and \(m=-\sqrt{2}\), corresponding to measurement operators \({{{\Pi }}}_{1}(\pm \!\sqrt{2})={{\rm{P}}}^{M}(\pm \!\sqrt{2})=\frac{1}{2}({\mathbb{1}}\pm {\sigma }_{m})\), with \({\sigma }_{m}=\frac{1}{\sqrt{2}}{\sigma }_{z}+\frac{1}{\sqrt{2}}{\sigma }_{x}\). The error-profile \({\varepsilon }_{\alpha }(A,{{{\Pi }}}_{1},\left|\psi (\alpha )\right\rangle )\) is obtained by measuring expectation values of A2, M2 and M in state \(\left|\psi (\alpha )\right\rangle\) and of M in auxiliary states \(\left|\psi (\alpha +\pi )\right\rangle\) and \(\left|+x\right\rangle\) (see the “Methods” section for details of the experimental realization of sharp M measurement process). The combined action of DC-coil 2 and the analyzer (second super mirror) realizes the respective projector.
In addition to the sharp measurement, we also realized a generalized (or unsharp) measurement of M in terms of a positive-operator-valued measures (POVM) elements \({{{\Pi }}}_{2}(\pm \!2)=\frac{1}{2}({\mathbb{1}}\pm \frac{1}{2}{\sigma }_{x}\pm \frac{1}{2}{\sigma }_{z})\), yielding q-rms error profile \({\varepsilon }_{\alpha }(A,{{{\Pi }}}_{2},\left|\psi (\alpha )\right\rangle )\). This is achieved by a randomized combination of projectors of \({{\rm{P}}}^{M}(\pm \!\sqrt{2})\) together with a contribution of a ’no-measurement’, realized by the ±x projectors, denoted as \({{\rm{P}}}^{{\sigma }_{x}}(\pm \!1)\), which gives (\(\left\langle \psi (\alpha )\right|{{\rm{P}}}^{{\sigma }_{x}}({\pm} \!{1})\left|\psi (\alpha )\right\rangle =\frac{1}{2}\) for all α ∈ [0, 2π]) (see the “Methods” section for experimental details of the POVM realization).
Figure 3a gives a Bloch sphere depiction of projectors \({{{\Pi }}}_{1}(\pm \!\sqrt{2})={{\rm{P}}}^{M}(\pm \!\sqrt{2})\) and POVM elements Π2( ± 2). The finally recorded intensity was about 350 neutrons s−1 at a beam cross-section of 10 (vertical) × 5 (horizontal) mm2. A 3He detector with high efficiency (more than 99 %) is used for count rate detection. To avoid unwanted depolarization, a static guide field pointing in the +z-direction with a strength of about 10 Gauss is produced by rectangular Helmholtz coils. In addition, the guide field induces Larmor precession, which, together with two appropriately tuned DC coils, enables state preparation of \(\left|\psi (\alpha )\right\rangle\) and projective or generalized measurements Π1 and Π2.
a Bloch sphere depiction of projectors \({{{\Pi }}}_{1}(\pm \!\sqrt{2})={{\rm{P}}}^{M}(\pm \!\sqrt{2})\) of sharp, and POVM elements Π2( ± 2) of unsharp measurement. b Expectations values of \(\left\langle \psi (\alpha )\right|{{{\Pi }}}_{1}(\pm \!\sqrt{2})\left|\psi (\alpha )\right\rangle =\left\langle \psi (\alpha )\right|{{\rm{P}}}^{M}(\pm \!\sqrt{2})\left|\psi (\alpha )\right\rangle\) for projective and \(\left\langle \psi (\alpha )\right|{{{\Pi }}}_{2}({\pm} \!{2})\left|\psi (\alpha )\right\rangle\) for generalized POVM in state \(\left|\psi (\alpha )\right\rangle\) with measurement time tmeas = 100 s. (error-bars represent ±1 st. dev.).
Experimental results of expectations values 〈ψ(α)∣Πi(±mi)∣ψ(α〉) (with i = 1, 2 and \({m}_{i}=\{\sqrt{2},2\}\)), that is \(\langle \psi (\alpha )| {{{\Pi }}}_{1}(\pm \!\sqrt{2})| \psi (\alpha \rangle )=\langle \psi (\alpha )| {{\rm{P}}}^{M}(\pm \!\sqrt{2})| \psi (\alpha \rangle )\) of projective (sharp) measurements and 〈ψ(α)∣Π2( ± 2)∣ψ(α〉) of generalized (unsharp) POVM are plotted in Fig. 3b. See the “Methods” section for details of the measurement procedure.
The final results for the error profile for projective M measurement and \({\varepsilon }_{\alpha }(A,{{{\Pi }}}_{2},\left|\psi (\alpha )\right\rangle )\) for generalized measurements (POVM), are plotted in Fig. 4. For the initial state \(\left|\psi \right\rangle =\left|+z\right\rangle\), which corresponds to α = 0, the q-rms error profile of the sharp (projective) measurement is zero; \({\varepsilon }_{\alpha }(A,{{{\Pi }}}_{1},\left|\psi (\alpha =0)\right\rangle )=0\), as expected from the counter-example from Eq. (3). The maximum value of εα = 2 is obtained for α = π, namely \({\varepsilon }_{\alpha }(A,{{{\Pi }}}_{1},\left|\psi (\alpha =\pi )\right\rangle )=2\). From this we infer the value of the locally uniform q-rms error\(\overline{\varepsilon }(A,{{{\Pi }}}_{1}\ \left|\psi \right\rangle )={{\sup}}{\varepsilon }_{\alpha }(A,{{{\Pi }}}_{1},\left|\psi (\alpha )\right\rangle )\) as \(\overline{\varepsilon }(A,{{{\Pi }}}_{1},| \psi )=2\). As can be seen from Fig. 4, the theoretical prediction for the error profile \({\varepsilon }_{\alpha }(A,{{{\Pi }}}_{1},\left|\psi (\alpha )\right\rangle )=2| \sin \frac{\alpha }{2}|\) are evidently reproduced for all values of α ∈ [0, 2π].
Green data points represent quantum root-mean-square (q-rms) error profile \({\varepsilon }_{\alpha }(A,{{{\Pi }}}_{1},\left|\psi (\alpha )\right\rangle )\) (projective) and red data points represent \({\varepsilon }_{\alpha }(A,{{{\Pi }}}_{2},\left|\psi (\alpha )\right\rangle )\) (POVM), for different evolved states \(\left|\psi (\alpha )\right\rangle\) with measurement time tmeas = 100 sec (error-bars represent ±1 st. dev.). Locally uniform q-rms error \(\overline{\varepsilon }(A,{{{\Pi }}}_{1},| \psi )=2\) (projective) and \(\overline{\varepsilon }(A,{{{\Pi }}}_{2},| \psi )=\sqrt{6}\) (POVM) are represented by green and red line, respectively.
The generalized (unsharp) measurement in terms of POVMs also reproduces the theoretical predictions of the q-rms error profile \({\varepsilon }_{\alpha }(A,{{{\Pi }}}_{2},\left|\psi (\alpha )\right\rangle )=\sqrt{4-2\cos \alpha }\), with minimum value \({\varepsilon }_{\alpha }(A,{{{\Pi }}}_{2},\left|\psi (\alpha =0,\ 2\pi )\right\rangle )=\sqrt{2}\) and maximum value \({\varepsilon }_{\alpha }(A,{{{\Pi }}}_{2},\left|\psi (\alpha =\pi )\right\rangle )=\sqrt{6}=\overline{\varepsilon }(A,{{{\Pi }}}_{2},\left|\psi \right\rangle )\), the locally uniform q-rms error. The higher values of the POVM error profile (meaning \({\varepsilon }_{\alpha }(A,{{{\Pi }}}_{2},\left|\psi (\alpha )\right\rangle )\,>\,{\varepsilon }_{\alpha }(A,{{{\Pi }}}_{1},\left|\psi (\alpha )\right\rangle )\) for all α ∈ [0, 2π]) are caused by the unsharp character of the POVM measuring process.
Discussion
As seen already from Eq. (1) the error \(\varepsilon (A,{{\Pi }},\left|\psi \right\rangle )\) depends on the choice of the respective POVM Π that realizes a particular measurement. From a physical point of view one might ask which measurement is optimal? Although individual expectation values (mean values) are the same for sharp (projective) and unsharp (POVM) realizations of the same measurement M, regarding measurement error of single measurements, sharp measurements are always superior compared to unsharp measurements. However in the case of joint, simultaneous (or successive) measurements, where an optimal error-error (or error-disturbance) trade-off is obtained, unsharp measurements are able to outperform sharp measurements18,28.
Generalized (or unsharp) measurements are of high importance in the emerging field of quantum metrology and quantum information processing and are foreseen to be vital in future applications within these fields. Our implementation of generalized measurements, that is a randomized combination of projectors together with a contribution of a ‘no-measurement’, applied here, is more direct (compact) and more efficient compared to methods used in previous experiments18,29. This technique will be applied in future experiments studying noise-disturbance trade-off relations in successive generalized measurements30.
For the operational accessibility of the locally uniform q-rms error in the general case, it is supposed that the unitary operator e−itA can be implemented canonically. This assumption is often made in quantum measurement theory. A justification is given by Ozawa13 (pp. 375–376) as follows. It is a standard assumption that for any observable A in a system S, we can implement the coupling A ⊗ P for a fixed time interval to a one-dimensional system P with the canonical observables Q, P with [Q, P] = iℏ to realize the unitary evolution e−iA⊗P of S + P. This assumption is commonly accepted, for instance, in implementing weak measurements31. Then, preparing P in the momentum eigenstate \(\left|t\right\rangle =\left|P=t\right\rangle\), we have
for any \(\left|\psi \right\rangle\). Thus, the unitary evolution e−itA of S can be operationally implemented in principle. Note that the general case where P is prepared in an arbitrary state \(\left|\phi \right\rangle\) instead of \(\left|t\right\rangle =\left|P=t\right\rangle\) was discussed by Ozawa25 (p. 7, the remark following Theorem 3).
To conclude, despite numerous successful experimental demonstrations of error-disturbance uncertainty relations based on the noise-operator-based q-rms error2,13,14,19,20,26, Busch, Lahti, and Werner7 brought about a debate on the use of the noise-operator-based q-rms error. Ozawa25 showed that the noise-operator-based q-rms error εNO is a sound error measure extending the classical rms error, and redefine it to be a sound and complete error measure, called the locally uniform q-rms error \(\overline{\varepsilon }\), by modifying the value for the measurements without satisfying [A(0), MA(t)] = 0. By the domination property \({\varepsilon }_{{\rm{NO}}}\le \overline{\varepsilon }\), the error-disturbance relation holds for the sound and complete error measure \(\overline{\varepsilon }\) with the same form as Ozawa’s original error-disturbance relation for εNO. Thus, we already have a universally valid error-disturbance relation with a sound and complete quantum extension of the classical rms error, whereas the original error-disturbance relation with the noise-operator-based q-rms error is stronger than the improved relation.
A problem remains as to the experimental accessibility of the improved error measure \(\overline{\varepsilon }\). It was shown that \({\varepsilon }_{{\rm{NO}}}=\overline{\varepsilon }\) holds for dichotomic measurements, often considered as the common case with regard to applications, for which the validity has been confirmed by many experiments14,19,20, and for measurements satisfying [A(0), MA(t)] = 0. However, our aim is to study the experimental behavior of \(\overline{\varepsilon }\) for non-dichotomic measurements without satisfying [A(0), MA(t)] = 0. In this paper, we present an experimental study of the improved error measure for measurements such that \(\overline{\varepsilon }\,\ne \,{\varepsilon }_{{\rm{NO}}}\), and the operational accessibility of the improved error measure is confirmed. Measuring the improved error of measurements of higher dimensional systems, which is operationally feasible, in principle, as discussed above, is a challenging problem in future studies.
Methods
Three-state-method and time evolution
In order to experimentally demonstrate the completeness of \(\overline{\varepsilon }\), Eqs. (7) and (8) need to be expressed in terms of experimentally accessible quantities, i.e., expectation values. This can be achieved by applying the well known three-state-method26 for generalized measurements13 (p.383) to obtain the state-dependent q-rms error profile \({\varepsilon }_{t}(A,{{\Pi }},\left|\psi (t)\right\rangle )\) from
where M(2) denotes the second moment of Π, given by M(2) = ∑xx2 Π(x). The first term of Eq. (9) can be symmetrized, applying the operator identity
which gives
The q-rms error-profile for all evolved states \(\left|\psi (\alpha )\right\rangle \left.\right)\) is calculated using the three-state method (see Supplementary Note 1 for the individual measurement results of all terms from Eq. (12)).
Next, we analyze the time evolution of the initial state \(\left|\psi \right\rangle ={(1,0)}^{T}\equiv \left|+z\right\rangle\), dependent on A, as expressed in Eq. (5). The observable A can be decomposed as A = \(\mathbb{1}\) + σx. Hence, the time evolution of the initial state yields
which is simply a rotation about the x-axis by an angle α (see Bloch sphere in Fig. 2). Thus the parametrization has changed from time t to an (experimentally adjustable) spinor rotation angle α.
Projective measurement of M
In order to demonstrate the counter example from Eq. (2), a sharp measurement of M is required. The decomposition of M into projectors is denoted as
where
with
Therefore, the error-profile \({\varepsilon }_{\alpha }^{2}(A,{{{\Pi }}}_{1},\left|\psi (\alpha )\right\rangle )\) yields
which finally gives
with locally uniform q-rms error \(\overline{\varepsilon }(A,{{{\Pi }}}_{1},\left|\psi \right\rangle )=2\), as predicted in ref. 25. Note that only for dichotomic measurements the first two terms of Eq. (17) are unity and the error profiles become α-independent (see Supplementary Note 1 for experimental details and results of all individual expectation values of the sharp M-measurement).
Generalized measurement of M
In addition, we performed generalized (unsharp) measurements, described by POVM Π2, to determine the q-rms error profile \(\overline{\varepsilon }(A,{{{\Pi }}}_{2},\left|\psi \right\rangle )\), where a decomposition of M in terms of POVM elements is applied, which is found as
The expectation value of M is expressed as
with probabilities \(p[{{{\Pi }}}_{2}(2),\psi (\alpha )]={\rm{Tr}}({{{\Pi }}}_{2}(2)\ {\rho }_{\alpha })\) and \(p[{{{\Pi }}}_{2}(-2),\psi (\alpha )]={\rm{Tr}}({{{\Pi }}}_{2}(-2)\ {\rho }_{\alpha })\), with \({\rho }_{\alpha }=\left|\psi (\alpha )\right\rangle \left\langle \psi (\alpha )\right|\), being the probabilities of obtaining the respective results. The individual POVM elements are given by Eq. (4), with M(2) = 4 \({\mathbb{1}}\) ≠ M2 = 2 \({\mathbb{1}}\). This accounts for a generalized measurement (with Π2(2) + Π2(−2) = \({\mathbb{1}}\), obeying the completeness relation of POVMs). Applying the definition of the q-rms error profile εα from Eq. (17) evidently reproduces the predictions for q-rms error profile
and for the locally uniform q-rms error we get \(\overline{\varepsilon }(A,{{{\Pi }}}_{2},\left|\psi \right\rangle )=\sqrt{6}\).
In the actual experiment the noisy POVM is realized by a randomized combination of a projective measurement of \({\sigma }_{m}=\frac{1}{\sqrt{2}}{\sigma }_{z}+\frac{1}{\sqrt{2}}{\sigma }_{x}\) and a ‘no-measurement’. The probability \(p[{{{\Pi }}}_{2},\psi (\alpha )]={\rm{Tr}}({{{\Pi }}}_{2}\left|\psi (\alpha )\right\rangle \left\langle \psi (\alpha )\right|)\), is measured by the projectors of σm, denoted as \({{\rm{P}}}^{{\sigma }_{m}}\), that is \(\left\langle \psi (\alpha )\right|{{\rm{P}}}^{{\sigma }_{m}}\left|\psi (\alpha )\right\rangle\), together with a contribution of a no-measurement. The ‘no-measurement’, (identity) is simply a measurement of spin operators, that are orthogonal to the plane spanned by the of the evolved states \(\left|\psi (\alpha )\right\rangle\), namely \(\left\langle \psi (\alpha )\right|{{\rm{P}}}^{{\sigma }_{x}}({\pm}\! {1})\left|\psi (\alpha )\right\rangle =\left\langle \psi (\alpha )\left|{\pm}\! {x}\right\rangle \left\langle {\pm} \!{x}\right|| \psi (\alpha )\right\rangle =\frac{1}{2}\) for all α ∈ [0, 2π], and therefore add up to identity. We can thus rewrite the POVM elements as
with \({\gamma }_{1}=\frac{1}{4}(2-\sqrt{2})\) as the weight for the ‘no-measurement’ and \({\gamma }_{2}=\frac{1}{\sqrt{2}}\) as weight of the projector. Experimentally this is achieved, for example in the \({\rm{Tr}}({{{\Pi }}}_{2}(2){\rho }_{\alpha })\) measurement, by controlling the current in DC coil 2 with a random generator, where with a frequency of 10 Hz either the current \({I}_{m}^{+}\) for the \({{\rm{P}}}^{{\sigma }_{m}}(1)\) measurement or \({I}_{{\rm{no}}}^{\pm }\) for one of the two orthogonal spin components of the ‘no-measurement’ is randomly chosen. The respective probabilities are given by \(p({I}_{{\rm{no}}}^{+})=p({I}_{{\rm{no}}}^{-})=\frac{1}{2}\frac{{\gamma }_{1}}{{\gamma }_{1}+{\gamma }_{2}}\) and \(p({I}_{m})=\frac{{\gamma }_{2}}{{\gamma }_{1}+{\gamma }_{2}}\).
The same procedure is applied to the measurement of expectation values \(\left\langle \psi (\alpha )\right|(A-{\mathbb{1}})\ M\ (A-{\mathbb{1}})\left|\psi (\alpha )\right\rangle\) and \(\left\langle \psi (\alpha )\right|A\ M\ A\left|\psi (\alpha )\right\rangle\). To obtain the results of \(\left\langle \psi (\alpha )\right|{A}^{2}\left|\psi (\alpha )\right\rangle\) and \(\left\langle \psi (\alpha )\right|{M}^{2}\left|\psi (\alpha )\right\rangle\) the expectation values of projector onto \(\left|+x\right\rangle\) and identity have to be measured (see Supplementary Note 1 for experimental results of all individual expectation values of the unsharp M-measurement).
Data availability
All data that support the findings and plots within this paper are available from the corresponding author upon request.
References
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–511 (2019).
Ozawa, M. Universally valid reformulation of the heisenberg uncertainty principle on noise and disturbance in measurement. Phys. Rev. A 67, 042105 (2003).
Hall, M. J. W. Prior information: how to circumvent the standard joint-measurement uncertainty relation. Phys. Rev. A 69, 052113 (2004).
Branciard, C. Error-tradeoff and error-disturbance relations for incompatible quantum measurements. Proc. Natl. Acad. Sci. USA 17, 6742–6747 (2013).
Busch, P., Lahti, P. & Werner, R. F. Proof of Heisenberg’s error-disturbance relation. Phys. Rev. Lett. 111, 160405 (2013).
Busch, P., Lahti, P. & Werner, R. F. Heisenberg uncertainty for qubit measurements. Phys. Rev. A 89, 012129 (2014).
Busch, P., Lahti, P. & Werner, R. F. Colloquium: quantum root-mean-square error and measurement uncertainty relations. Rev. Mod. Phys. 86, 1261–1281 (2014).
Buscemi, F., Hall, M. J., Ozawa, M. & Wilde, M. M. Noise and disturbance in quantum measurements: an information-theoretic approach. Phys. Rev. Lett. 112, 050401 (2014).
Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 43, 172–198.
Arthurs, E. & Kelly, J. L. On the simultaneous measurement of a pair of conjugate observables. Bell Labs Tech. J. 44, 725–729 (1965).
Yamamoto, Y. & Haus, H. A. Preparation, measurement and information capacity of optical quantum states. Rev. Mod. Phys. 58, 1001–1020 (1986).
Arthurs, E. & Goodman, M. S. Quantum correlations: a generalized Heisenberg uncertainty relation. Phys. Rev. Lett. 60, 2447–2449 (1988).
Ozawa, M. Uncertainty relations for noise and disturbance in generalized quantum measurements. Ann. Phys. 311, 350–416 (2004).
Erhart, J. et al. Experimental demonstration of a universally valid error-disturbance uncertainty relation in spin-measurements. Nat. Phys. 8, 185–189 (2012).
Sulyok, G. et al. Violation of Heisenberg’s error-disturbance uncertainty relation in neutron-spin measurements. Phys. Rev. A 88, 022110 (2013).
Demirel, B., Sponar, S., Sulyok, G., Ozawa, M. & Hasegawa, Y. Experimental test of residual error-disturbance uncertainty relations for mixed spin-1/2 states. Phys. Rev. Lett. 117, 140402 (2016).
Sulyok, G. & Sponar, S. Heisenberg’s error-disturbance uncertainty relation: Experimental study of competing approaches. Phys. Rev. A 96, 022137 (2017).
Demirel, B., Sponar, S., Abbott, A. A., Branciard, C. & Hasegawa, Y. Experimental test of an entropic measurement uncertainty relation for arbitrary qubit observables. New J. Phys. 21, 013038 (2019).
Rozema, L. A. et al. Violation of Heisenberg’s measurement-disturbance relationship by weak measurements. Phys. Rev. Lett. 109, 100404 (2012).
Baek, S.-Y., Kaneda, F., Ozawa, M. & Edamatsu, K. Experimental violation and reformulation of the Heisenberg’s error-disturbance uncertainty relation. Sci. Rep. 3, 2221 (2013).
Kaneda, F., Baek, S.-Y., Ozawa, M. & Edamatsu, K. Experimental test of error-disturbance uncertainty relations by weak measurement. Phys. Rev. Lett. 112, 020402 (2014).
Ringbauer, M. et al. Experimental joint quantum measurements with minimum uncertainty. Phys. Rev. Lett. 112, 020401 (2014).
Mao, Y.-L. et al. Error-disturbance trade-off in sequential quantum measurements. Phys. Rev. Lett. 122, 090404 (2019).
Busch, P., Heinonen, T. & Lahti, P. Noise and disturbance in quantum measurement. Phys. Lett. A 320, 261–270 (2004).
Ozawa, M. Soundness and completeness of quantum root-mean-square errors. npj Quantum Inf. 5, 1 (2019).
Ozawa, M. Universal uncertainty principle in the measurement operator formalism. J. Opt. 7, 672 (2005).
Ozawa, M. Quantum measuring processes of continuous observables. J. Math. Phys. 25, 79–87 (1984).
Abbott, A. A. & Branciard, C. Noise and disturbance of qubit measurements: An information-theoretic characterization. Phys. Rev. A 94, 062110 (2016).
Sponar, S. et al. Experimental test of entropic noise-disturbance uncertainty relations for three-outcome qubit measurements. Phys. Rev. Res. 3, 023175 (2021).
Baek, K. & Son, W. Entropic uncertainty relations for successive generalized measurements. Mathematics 4, 41–53 (2016).
Aharonov, Y., Albert, D. Z. & Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 60, 1351–1354 (1988).
Acknowledgements
This work was supported by the Austrian science fund (FWF) Projects No. P 30677-N36 and P 27666-N20. M.O. acknowledges the support of the IRI-NU collaboration. Y.H. is partly supported by KAKENHI Project No. 18H03466.
Author information
Authors and Affiliations
Contributions
S.S., M.O., and Y.H. conceived the experiment; S.S. and A.D. carried out the experiment; S.S. and A.D. analysed the data; all authors co-wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sponar, S., Danner, A., Ozawa, M. et al. Neutron optical test of completeness of quantum root-mean-square errors. npj Quantum Inf 7, 106 (2021). https://doi.org/10.1038/s41534-021-00437-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-021-00437-8