Introduction

Quantum machine learning is an emerging field that has attracted much attention recently. The major algorithmic breakthrough was an algorithm invented by Harrow–Hassidim-Lloyd1. This algorithm has been further developed to more sophisticated machine learning algorithms2,3. However, a quantum computer that is capable of executing those algorithms is yet to be realized. At present, noisy intermediate-scale quantum (NISQ) devices4, which consist of several tens or hundreds of noisy qubits, are the most advanced technology. Although their performance is limited compared to the fault-tolerant quantum computer, simulation of the NISQ devices with 100 qubits and sufficiently high gate fidelity are beyond the reach for the existing supercomputer and classical simulation algorithms5,6,7. This fact motivates us to explore its power for solving practical problems.

Many NISQ algorithms for machine learning have been proposed in recent works8,9,10,11,12,13,14,15,16,17. Almost all of the algorithms require us to evaluate an expectation value of an observable, which is sometimes troublesome to measure by sampling, for example with superconducting or trapped-ion qubits. On the other hand, NMR can evaluate the expectation value with a one-shot experiment owing to its use of a vast number of duplicate quantum systems. It is, therefore, a great testbed for those algorithms. A major weakness of NMR is that its initialization fidelity is quite low; at the thermal equilibrium of room temperature, the proton spins can effectively be described with a density matrix \({\rho }_{{\rm{eq}}}=\frac{1}{2}(I+\epsilon {I}_{{\rm{z}}})\) with ϵ ≈ 10−5. Nevertheless, ensemble spin systems can exhibit complex quantum dynamics that are classically intractable. For example, the dynamical phase transition between localization and delocalization has been observed in polycrystalline adamantane along with tens of correlated proton spins18. Discrete time-crystalline order has been observed in disordered19 and ordered20,21 spin systems. Also, it has been shown that general dynamics of NMR are classically intractable under certain complexity conjecture22,23. These facts strengthen our motivation to use NMR for NISQ algorithms.

In this work, we employ NMR for machine learning. Specifically, we implement the kernel-based algorithm which utilizes the quantum state as a feature vector and is a variant of theoretical proposals8,9,24. Ref. 25 has recently proved that this approach has a rigorous advantage over classical computation in a specific task. The experimental verification has been provided in refs. 15,26 using either superconducting qubits or the photonic system. Our strategy to use the NMR is advantageous in that we can estimate the value of the kernel, which is the inner product of two quantum states, by single-shot experiments. Moreover, the dimension of the Hilbert space employed in this work greatly exceeds the number of training data. We perform simple regression and binary classification tasks using the dynamics of nuclear spins in a polycrystalline adamantane sample, and observe that the performance of the trained model becomes better as more spins are involved in the dynamics. Also, to carry out the performance analysis of our approach without the inevitable effect of noise in experiments, we present numerical simulations of 20 spin dynamics, which well agree with the experimental results. We employ one of the largest quantum systems to date for a quantum machine learning experiment in this work with the single-shot setting that enables the use of a large quantum system.

Results

Kernel methods in machine learning

In machine learning, one is asked to extract some patterns, or features, in a given dataset3,27. It is sometimes useful to pre-process them beforehand to achieve the objective. For example, a speech recognition task might become easier when we work in the frequency domain; in this case, the useful pre-processing would be the Fourier transform. The space in which such pre-processed data live is called feature space. For a given set of data \({\{{{\boldsymbol{x}}}_{i}\}}_{i = 1}^{{N}_{{\rm{d}}}}\subset {{\mathbb{R}}}^{D}\), a feature space mapping ϕ(x) constructs the data in the feature space \({\{{\boldsymbol{\phi }}({{\boldsymbol{x}}}_{i})\}}_{i = 1}^{{N}_{{\rm{d}}}}\subset {{\mathbb{R}}}^{{D}_{{\rm{f}}}}\). The feature map has to be carefully taken to maximize the performance in e.g. classification tasks.

Kernel methods are a powerful tool in machine learning. It uses a distance measure of two inputs defined as a kernel, \(k:{{\mathbb{R}}}^{{D}_{{\rm{f}}}}\times {{\mathbb{R}}}^{{D}_{{\rm{f}}}}\to {\mathbb{R}}\). For example, a kernel can be defined as an inner product of two feature vectors:

$$k({{\boldsymbol{x}}}_{i},{{\boldsymbol{x}}}_{j})={\boldsymbol{\phi }}{({{\boldsymbol{x}}}_{i})}^{T}{\boldsymbol{\phi }}({{\boldsymbol{x}}}_{j}).$$
(1)

Many machine learning models, such as support vector machine or linear regression, can be constructed using the kernel only, that is, we do not have to explicitly hold ϕ(x). This dramatically reduces the computational cost when the feature ϕ(x) lives in a high-dimensional space. The direct approach that computes and stores ϕ(x) for all training data x would demand the computational resource that is at least proportional to Nd and Df ≫ Nd just for storing them, whereas the kernel method only requires us to store a Nd × Nd kernel matrix with its (i, j) elements being k(xi, xj).

Implementing kernel by NMR

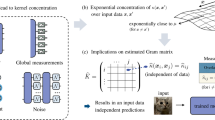
In NMR, we can prepare a data-dependent operator A(xi) by applying a data-dependent unitary transformation U(xi) on the initial z-magnetization \({I}_{{\rm{z}}}=\mathop{\sum }\nolimits_{\mu = 1}^{n}{I}_{{\rm{z}},\mu }\), that is, A(xi) = U(xi)IzU†(xi). Here, Iα,μ(α = x, y, z) is the α-component of the spin operator of the μ-th spin and n represents the number of spins. A(xi) with a sufficiently large n is generally intractable by classical computers22,23. We employ this operator A(xi) as a feature map ϕNMR(xi). A(xi) can be regarded as a vector, for example, by expanding A(xi) as a sum of Pauli operators. For an n-spin-1/2 system, A(xi) is a vector in \({{\mathbb{R}}}^{{4}^{n}}\). The dynamics of NMR can involve tens of spins maintaining its coherence18,28,29,30, which means we can employ an approximately 4O(10) dimensional feature vector for machine learning. Although the high-dimensional feature space does not always mean superiority in machine learning tasks, the fact that we can work with the feature space which has been intractable with a classical computer motivates us to explore its power.

The kernel method opens up a way to exploit A(xi) directly for machine learning purposes. While we cannot evaluate each element of A(xi) because it takes an exponential amount of time, we can evaluate the inner product of two feature vector A(xi) and A(xj) efficiently. The Frobenius inner product between two operators A(xi) and A(xj) is \({\text{Tr}}\left({A}({{\boldsymbol{x}}}_{i}){A}({{\boldsymbol{x}}}_{j})\right)\), which we employ as our NMR kernel function kNMR(xi, xj) in this work. Noting that,

$$\,{\text{Tr}}\,\left(A({{\boldsymbol{x}}}_{i})A({{\boldsymbol{x}}}_{j})\right)=\,{\text{Tr}}\,\left({U}^{\dagger }({{\boldsymbol{x}}}_{j})U({{\boldsymbol{x}}}_{i}){I}_{{\rm{z}}}{U}^{\dagger }({{\boldsymbol{x}}}_{i})U({{\boldsymbol{x}}}_{j}){I}_{{\rm{z}}}\right),$$
(2)

and also at the thermal equilibrium, the density matrix of spin systems is \({\rho }_{{\rm{eq}}}\approx \frac{1}{{2}^{n}}\left(I+\epsilon {I}_{{\rm{z}}}\right)\) assuming ϵ ≪ 1, we obtain,

$$\,{\text{Tr}}\,\left(A({{\boldsymbol{x}}}_{i})A({{\boldsymbol{x}}}_{j})\right)\propto \,{\text{Tr}}\,\left({U}^{\dagger }({{\boldsymbol{x}}}_{j})U({{\boldsymbol{x}}}_{i}){\rho }_{{\rm{eq}}}{U}^{\dagger }({{\boldsymbol{x}}}_{i})U({{\boldsymbol{x}}}_{j}){I}_{{\rm{z}}}\right).$$
(3)

The right hand side can be measured experimentally by first evolving the system at thermal equilibrium with U(xi) and then with U†(xj), and finally measuring Iz. A similar protocol is also used for measuring out-of-time-ordered correlator (OTOC)31,32, which is considered as a certain complexity measure of quantum many-body systems.

Experimental

We propose to use U(x) for an input \({\boldsymbol{x}}={\{{x}_{j}\}}_{j = 1}^{D}\) that takes the form of,

$$U\left({\boldsymbol{x}}\right)={e}^{-iH({x}_{D})\tau }\cdots {e}^{-iH({x}_{2})\tau }{e}^{-iH({x}_{1})\tau },$$
(4)

where τ is a hyperparameter that determines the performance of this feature map, and H(xj) is an input-dependent Hamiltonian (Fig. 1b). In this work, we choose H(xj) to be

$$H({x}_{j})={e}^{-i{x}_{j}{I}_{{\rm{z}}}}\mathop{\sum}\limits_{\mu <\nu }{d}_{\mu \nu }\left({I}_{{\rm{y}},\mu }{I}_{{\rm{y}},\nu }-{I}_{{\rm{x}},\mu }{I}_{{\rm{x}},\nu }\right){e}^{i{x}_{j}{I}_{{\rm{z}}}},$$
(5)

where Iα = ∑μIα,μ. The Hamiltonian H(0) can approximately be constructed from the dipolar interaction among nuclear spins in solids with a certain pulse sequence18,33,34 shown in Fig. 1b. See “Methods” for details. Shifting the phase of the pulse by x provides us H(x) for general x. This Hamiltonian with xj = 0 created in adamantane has been shown to have a delocalizing feature in refs. 18,28,29,30, which makes it appealing as we wish to involve as many spins as possible in the dynamics.

Fig. 1: Experimental setups.
figure 1

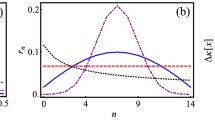
a Adamantane molecule. The white and pink balls represent hydrogen and carbon atoms, respectively. b Quantum circuit and pulse sequence employed in this work to realize evaluation of kNMR(xi, xj). The top right shows a pulse sequence for x1 = 0, where X and \(\bar{{\rm{X}}}\) represent +π/2 and −π/2 pulses along x-axis, respectively. In the experiment, Δ and \({{\Delta }}^{\prime}\) are set 3.5 μs and 8.5 μs, respectively. c NMR kernel employed in this work. d Fourier transform of (c) which corresponds to the obtained 1H multiple-quantum spectra for N = 1 to N = 6. Red line is Gaussian \(a\exp (-{m}^{2}/K)\) fitted to the spectra using a and K as fitting parameters. The Gaussian is fitted only to even m data points. K is the cluster size of the system18,30,33.

Full size image

To illustrate character of the kernel function, we show the shape of the kernel for one-dimensional input x obtained with this sequence setting τ = Nτ1 where τ1 = 60 μs and N = 1, 2, ⋯ , 6 as Fig. 1c. In this experiment, the overall unitary dynamics applied to the system is \({U}^{\dagger }({x}_{j})U({x}_{i})={e}^{iH({x}_{j})\tau }{e}^{-iH({x}_{i})\tau }={e}^{-i{x}_{j}{I}_{{\rm{z}}}}{e}^{iH(0)\tau }{e}^{-i({x}_{i}-{x}_{j}){I}_{{\rm{z}}}}{e}^{-iH(0)\tau }{e}^{i{x}_{i}{I}_{{\rm{z}}}}\). Since the initial state has only Iz element and the final observable is also Iz, we can omit \({e}^{i{x}_{i}{I}_{{\rm{z}}}}\) and \({e}^{-i{x}_{j}{I}_{{\rm{z}}}}\) operations in the experiment. We, therefore, show the value of the kernel as a function of xi − xj in Fig. 1c. The decay of the intensity of the signal with increasing N is due to decoherence. The number of spins involved in this dynamics can be inferred by the Fourier transform of the signal in Fig. 1c with respect to xi − xj. This is because the z-rotation \({e}^{-i({x}_{i}-{x}_{j}){I}_{{\rm{z}}}}\) after the forward dynamics e−iH(0)τ induces a phase \({e}^{-im^{\prime} ({x}_{i}-{x}_{j})}\) to terms in the form of \({I}_{\pm }^{\otimes m}\) which appears in the density matrix of the system, where m and \(m^{\prime}\) are integers, \(| m^{\prime} | \le m\), and I± = Ix ± iIy. This Fourier spectra is called multiple-quantum spectra18,30,31, from which we can extract a cluster size K, which can be considered as the effective number of spins involved in the dynamics, by fitting it with Gaussian distribution \(\exp (-{m}^{2}/K)\)18,30,33. We show the Fourier transform of the measured NMR kernel (Fig. 1c) along with corresponding K in Fig. 1d. We can conclude that, for N > 5, 6, the dynamics involve 25 spins, which corresponds to a feature space dimension of 425 ≈ 1015.

One-dimensional regression task

As the first demonstration, we perform the one-dimensional kernel regression task using the kernel shown in Fig. 1c. To evaluate the nonlinear regression ability of the kernel, we use \(y=\sin (2\pi x/50)\) and \(y=\frac{\sin (2\pi x/50)}{2\pi x/50}\), which will be refered to as sine and sinc function, respectively. We randomly drew 40 samples of x from [−45, 45] (in degrees) to construct the traning data set which consists of the input \({\{{x}_{j}\}}_{j = 1}^{40}\) and the teacher \({\{{y}_{j}\}}_{j = 1}^{40}\) calculated at each xj. The NMR kernel kNMR(xi, xj) is measured for each pair of data to construct the model by kernel ridge regression27. We let the model predict y for 64 x’s including the training data. The regularization strength was chosen to minimize the mean squared error of the result at the 64 evaluation data.

The result for the sine function is shown in Figure 2a, b. That for the sinc function is shown in “Methods”. Figure 3a shows the accuracy of learning evaluated by the mean squared error between the output from the trained model and true function. We see that the regression accuracy tends to increase with a larger N. For all N, the dimension of the feature space exceeds the number of data as the dynamics involve over 5 spins which corresponds to the Hilbert space dimension of 45 (see Fig. 1d). However, because of the deteriorating signal-to-noise ratio, the result also gets noisy with increasing N.

Fig. 2: Demonstration of one-dimensional regression task of \(y=\sin (2\pi x/50)\).
figure 2

a, b shows results for NMR kernel and numerically simulated kernel, respectively. The blue dots, green lines, red dashed lines represent the training data, the prediction of the trained model, and the function from which the function the training data are sampled.

Full size image
Fig. 3: Mean squared error of the trained models for the regression task of sine and sinc functions.
figure 3

a, b shows results for experimental NMR kernel and numerically simulated kernel, respectively.

Full size image

To certify the trend without the effect of noise, we conducted numerical simulations of 20-qubit dynamics with all-to-all random interaction in the form of Eq. (5), whose coupling strength, dij, are drawn uniformly from [−1, 1]. We set the evolution time τ = 0.01, 0.02, ⋯ , 0.06. Details of the numerical simulations are described in Methods. The result for the sine function is shown as Fig. 2g–l. For the sinc function, we place the result in “Methods”. The mean squared error of the prediction evaluated in the same manner is shown in Fig. 3b. We can see the performance gets better with increasing τ, which corresponds to increasing N in the experiment. This certifies the trend observed in the NMR experiment.

Two-dimensional classification task

As the second demonstration, we implement two-dimensional classification tasks. We employ the hard-margin kernel support vector machine27 and its implementation in scikit-learn35 for this task. We use two data sets which we call “circle” and “moon” data set generated by functions available in scikit-learn package35. They are depicted as dots in Fig. 4. A data set consists of pairs of input data point (x1, x2) ∈ [−45, 45]2 and its label y ∈ { − 1, +1}. For experimental simplicity, we have modified the generated (x1, x2) to be on a lattice. The NMR kernels with N = 1, 2, 3 are utilized in this task. We again conducted numerical simulations with the same setting as the previous section along with the experiment with τ = 0.03, 0.06, 0.09. The values of this numerical kernel are shown in the “Methods”.

Fig. 4: Demonstration of simple classification tasks.
figure 4

a Classification with the NMR kernel. Left and right panels respectively show the results for “circle” and “moon” data set. The red and blue dots represent inputs (x1, x2) with label y = +1 and y = −1, respectively. The background color indicates the decision function of the trained model. The number in each figure is the hinge loss after training defined as \(\frac{1}{{N}_{s}}\mathop{\sum }\nolimits_{i = 1}^{{N}_{s}}\max \{1-{\lambda }_{i}{y}_{i},0\}\) where Ns is the number of training data, and λi and yi are the output from the trained model and the teacher data corresponding to a training input xi. Top, middle, and bottom panels are the results with N = 1, 2, 3 NMR kernels, respectively. b Results from the numerically simulated quantum kernel. Top, middle, and bottom panels are the results with simulated kernel with τ = 0.03, 0.06, 0.09. All the other notations follow that of (a).

Full size image

The results are shown in Fig. 4. Also for this classification task, the dimension of feature space exceeds the number of data already at N = 1. Note that the evolution time, in this case, is doubled compared to the previous demonstration where the input is one-dimensional (see Eq. (4)), that is, the evolution time of N = 1 for two-dimensional input is equivalent to that of N = 2 for one-dimensional input. We also note that, for the moon dataset with N = 1 experimental NMR kernel, the kernel matrix was singular, and we did not obtain a reliable result. We reason this to the broadness of the kernel at N = 1.

For the circle data set with the experimental kernel, the best performance is achieved when N = 1. We believe this is because the task of classifying the circle dataset was too easy and did not need large feature space. This dataset can be completely classified, for example, by merely mapping two-dimensional data (x1, x2) to three-dimensional feature space \(({x}_{1},{x}_{2},{x}_{1}^{2}+{x}_{2}^{2})\). As for the moon dataset, the performance increased with increasing N. This can be attributed to the increasing dimension of the feature space.

Discussion

In the one-dimensional regression task, we observed the trend of better performance with longer evolution time. This can be explained by the shape of the kernel generated by the NMR dynamics, which is shown in Fig. 1c. As mentioned earlier, this experiment is essentially the Loschmidt echo, and the shape of the signal sharpens as the evolution time increases. The sharpness of the kernel can directly be translated to the representability of the model as it can be in the popular Gaussian kernel because this property allows the machine to distinguish different data more clearly. However, it also causes overfitting problems if the data points are sparse. The most extreme case is when we use a delta function as a kernel, where every training point is learned with the perfect accuracy while the trained model fails to predict for unknown inputs. In our experimental case, we did not observe any overfitting problem, which means that our training samples were dense enough for the sharpness of the kernel utilized in the model, and thus we observed an increasing performance from the improved representability of the kernel with longer evolution time. For the classification task, we observed the dataset-dependent trend with respect to the evolution time in the performance. We suspect that there is an optimal evolution time for this kind of task, which should be explored in future works. We believe the performance can also be improved by employing ensemble learning approach36.

We note that the shape of the kernel resembles the Gaussian kernel which is widely employed in many machine learning tasks. In fact, we can obtain better results using the Gaussian kernel as shown in “Methods”. More concretely, it can achieve mean squared error less than 10−5 for the regression tasks and hinge loss of order 10−5 for the classification tasks without fine tuning of a hyperparameter. While this fact casts a shadow on the usefulness of the NMR kernel used in this work, it is also true that the NMR dynamics evolved by general Hamiltonian cannot be simulated classically under certain complexity conjecture22,23. This leaves a possibility that the NMR kernel performs better than classical kernel in some specific cases. We also note that there is a quantum kernel that is rigorously advantageous over classical ones in a certain machine learning task25. More experiments using different Hamiltonians are required to test whether the "quantum” kernel has any advantage in machine learning tasks over widely used conventional kernels.

The previous research18,30,33 has shown that the cluster size can be brought up to over 1000 with more precise experiments. This indicates that the solid-state NMR is a platform well-suited to experimentally analyze the performance of kernel-based quantum machine learning. To extend the experiment to larger cluster sizes, we have to resolve the low initialization fidelity of nuclear spin systems, which is a major challenge faced by the NMR quantum information processing in general. We believe this can be overcome by the use of e.g., a technique called dynamic nuclear polarization37,38 where we initialize the nuclear spin qubits by transferring the polarization from initialized electrons.

To conclude, we proposed and experimentally tested a quantum kernel constructed by data-dependent complex dynamics of a quantum system. Experimentally, we used complex dynamics of 25 1H spins in adamantane to compute the kernel. This allowed us to achieve a scheme where the dimension of feature space greatly exceeds the number of data. We also stress that the spin dynamics of NMR is generally intractable by a classical computer22,23. Machine learning models for one-dimensional regression tasks and two-dimensional classification tasks were constructed with the proposed kernel. The experimental and numerical results showed similar results. Experiments along with numerical simulation also showed that the performance of the model tended to increase with longer evolution time, or equivalently, with a larger number of spins involved in the dynamics for certain tasks. It would be interesting to export this method to more quantum-oriented machine learning tasks. For example, one may be able to distinguish two dynamical phases of spin systems, such as localized and delocalized phases demonstrated in ref. 18, with the kernel support vector machine employed in this work. More experiments are needed to verify the power of this "quantum kernel” approach, but our results can be thought of as one of the baselines of this emerging field.

Note added—After the initial submission of this work, we became aware of related works on quantum kernel methods39,40.

Methods

Experimental details

A pulse sequence to realize H(0) is given in Supplementary Fig. 1. In the experiment, we set the length of π/2 pulse, τp, to 1.5 μs. For the waiting period, we used \({{\Delta }}^{\prime} =2{{\Delta }}+{\tau }_{p}\) with Δ = 3.5 μs, which makes the evolution time for a cycle, τ1, 60 μs. By repeating the sequence for N times, we can effectively evolve the spins with \({e}^{-iH({x}_{D})\tau }\) for τ = Nτ1. NMR spectroscopy with polycrystalline adamantane sample was performed at room temperature with OPENCORE NMR41, operating at a resonant frequency of 400.281 MHz for 1H nucleus observation.

Detail of numerical simulation

We drew the interaction strength, dμν, from uniform distribution on [− 1, 1] for all μ, ν. The evolution according to the Hamiltonian H(x) is approximated by the first-order Trotter formula, that is,

$${e}^{-iH(x)\tau }\approx {e}^{-ix{I}_{z}}{\left[\mathop{\prod}\limits_{\mu \,{<}\,\nu }{e}^{-i\tau {d}_{\mu ,\nu }({I}_{y,\mu }{I}_{y,\nu }-{I}_{x,\mu }{I}_{x,\nu })/M}\right]}^{M}{e}^{ix{I}_{z}}.$$
(6)

We set τ = 0.01, 0.02, ⋯ , 0.06 and τ/M = 0.001 in the simulation. In order to reduce the computational cost, we set \(A({\boldsymbol{x}})=U({\boldsymbol{x}}){\prod }_{\mu }\left(\frac{I}{2}+{I}_{z,\mu }\right){U}^{\dagger }({\boldsymbol{x}})\), which allows us to evaluate Tr(A(xi)A(xj)) by computing \({\left|\left\langle 0\right|{U}^{\dagger }({{\boldsymbol{x}}}_{j})U({{\boldsymbol{x}}}_{i})\left|0\right\rangle \right|}^{2}\), where \(\left|0\right\rangle\) is the ground state of Iz. Since we can compute this quantity by simulating dynamics of a 220-dimensional state vector, it is significantly easier than computing A(x) = U(x)IzU†(x) where we would need to simulate dynamics of 220 × 220 matrices. All simulations are performed with a quantum circuit simulator Qulacs42.

One-dimensional regression task

We show the results for the regression task of sinc function performed with the experimental NMR kernel and that of numerical simulations in Supplementary Fig. 2.

Comparison with Gaussian kernel

Here, we perform the same machine learning tasks with Gaussian kernel \(k({{\boldsymbol{x}}}_{i},{{\boldsymbol{x}}}_{j})=\exp \left(-\gamma \parallel {{\boldsymbol{x}}}_{i}-{{\boldsymbol{x}}}_{j}\parallel \right)\), where γ > 0 is a hyperparameter.

First, we perform kernel regressions of sine and sinc functions using a Gaussian kernel with γ = 0.02. Results are shown as Supplementary Fig. 3. Mean squared errors of the results are 1.3 × 10−6 and 6.1 × 10−8 for sine and sinc functions, respectively.

Secondly, we perform kernel support vector machine on circle and moon datasets using a Gaussian kernel with γ = 0.5. Results are shown as Supplementary Fig. 4. Hinge losses of the results are 7.9 × 10−5 and 5.2 × 10−5 for circle and moon datasets, respectively.

Kernel from the numerical simulations

The kernel computed from numerical simulations for one-dimensional input is shown as Supplementary Fig. 5. It is shown as a function of \(x-x^{\prime} \in \left[-\frac{\pi }{2},\frac{\pi }{2}\right]\). We can observe the similar features as the experimental one, such as the sharpening of the kernel with increasing evolution time.

Kernel for two-dimensional data

Let x = (x1, x2) and \({\boldsymbol{x}}^{\prime} =(x^{\prime} ,x^{\prime} )\) be two data points with which we wish to evaluate the kernel \(k({\boldsymbol{x}},{\boldsymbol{x}}^{\prime} )=k(\{{x}_{1},{x}_{2}\},\{x^{\prime} ,x^{\prime} \})\). We note that our experimental kernel satisfies the equality: \(k(\{{x}_{1},{x}_{2}\},\{x^{\prime} ,x^{\prime} \})=k(\{{x}_{1}-x^{\prime} ,{x}_{2}-x^{\prime} \},\{x^{\prime} -x^{\prime} ,0\})\). With this in mind, we define \({P}_{1}={x}_{1}-x^{\prime}\), \({P}_{2}={x}_{2}-x^{\prime}\), \({P}_{3}=x^{\prime} -x^{\prime}\). The value of the experimental and simulated kernel are sliced by the value of P3 and shown in Supplementary Figs. 6–8 and Supplementary Figs. 9–11, respectively.