Abstract
We solve the entanglement-assisted (EA) classical capacity region of quantum multiple-access channels (MACs) with an arbitrary number of senders. As an example, we consider the bosonic thermal-loss MAC and solve the one-shot capacity region enabled by an entanglement source composed of sender-receiver pairwise two-mode squeezed vacuum states. The EA capacity region is strictly larger than the capacity region without entanglement-assistance. With two-mode squeezed vacuum states as the source and phase modulation as the encoding, we also design practical receiver protocols to realize the entanglement advantages. Four practical receiver designs, based on optical parametric amplifiers, are given and analyzed. In the parameter region of a large noise background, the receivers can enable a simultaneous rate advantage of 82.0% for each sender. Due to teleportation and superdense coding, our results for EA classical communication can be directly extended to EA quantum communication at half of the rates. Our work provides a unique and practical network communication scenario where entanglement can be beneficial.
Similar content being viewed by others
Introduction
Communication channels model physical media for information transmission. In the case of a single-sender single-receiver channel, the Shannon capacity theorem1,2 concludes that a channel is essentially characterized by a single quantity—the channel capacity. As physical media obey quantum physics, the channel model eventually needs to incorporate quantum effects during the transmission, which has reshaped our understanding of communication. To begin with, the Shannon capacity has been generalized to the Holevo–Schumacher–Westmoreland classical capacity3,4,5. Quantum effects such as entanglement have also enabled nonclassical phenomena in communication, such as superadditivity6,7,8,9,10,11 and capacity-boost from entanglement-assistance (EA)12,13,14,15,16,17,18,19,20,21. Moreover, reliable transmission of quantum information is possible, established by the Lloyd–Shor–Devetak quantum capacity theorem22,23,24. Combining different types of information transmission, refs. 25,26 provide a capacity formula for the simultaneous trade-off of classical information (bits), quantum information (qubits), and quantum entanglement (ebits).
Despite their exact evaluation being prevented by the superadditivity dilemma, capacities of single-sender single-receiver quantum channels are well-understood. In particular, the benefits of entanglement in boosting the classical communication rates have been known since the pioneering theory works12,13,14,15,17 and recently experimentally demonstrated27 in a thermal-loss bosonic communication channel. The two-mode-squeezed-vacuum (TMSV) state is utilized as the entanglement source and functional quantum receivers are demonstrated, thanks to the practical protocol design in ref. 28. Further development of receiver designs29 and the application to covert communication30 have also been considered.
However, supported by the Internet, real-life communication scenarios, such as online lectures and online conferences, often involve multiple senders and/or receivers. As a common paradigm being studied in the literature31,32,33,34,35, the multiple-access channel (MAC) concerns multiple senders and a single receiver. Communication over a MAC is no longer characterized by a single rate, but a rate region with a trade-off between multiple senders. With the development of a quantum network36,37,38,39,40, quantum effects have also become relevant in such a communication scenario. In this regard, the classical capacity region of a quantum MAC was solved by Winter41, while the entanglement-assisted (EA) classical communication capacity region in the special case of a two-sender MAC was solved in ref. 17. Although superadditivity in the capacity region has also been found in a MAC42,43 and EA advantage in a classical MAC can be shown33, it is unclear how much advantage entanglement can provide for a quantum MAC in a direct communication scenario.
In this work, we present a thorough study of EA classical communication over a quantum MAC with an arbitrary number of senders. On the fundamental information-theoretic side, we prove the general EA classical capacity theorem for an s-sender (s ≥ 2) MAC, which has been conjectured in ref. 17 and yet not proven for the past decade. Next, we proceed to evaluate the EA rate region of the bosonic thermal-loss MAC, which models an optical or microwave communication scenario (see Fig. 1), and find rigorous advantages from entanglement. Finally, on the application layer, we propose practical protocols to realize the EA advantage in a bosonic thermal-loss MAC, and provide a variety of transmitter and receiver designs. Due to teleportation44 and superdense coding12, our results for EA classical communication can be directly extended to EA quantum communication at half of the rates. As bosonic thermal-loss MACs model various real-world communication networks, our EA communication scenario is widely applicable to radio frequency, deep space45, and wireless communication scenarios46.
The entanglement source distributes entangled pairs to each sender and the receiver, potentially via a quantum network. Each sender encodes its own message on its share and sends the signal to the receiver. The receiver decodes the messages of all senders by jointly measuring the received signals and the entanglement-assistance locally stored.
Results
General setting and main findings
In a MAC, multiple senders individually communicate with a single receiver. As shown in Fig. 1, besides a transmitter that sends encoded messages, each sender has access to entanglement pre-shared with the receiver, potentially through a ground-satellite and/or fiber-based quantum network. The receiver decodes all messages from the senders via a joint measurement on all received signals and the stored EA. Our first main result is an EA capacity theorem which quantifies the trade-off between the ultimate communication rates of different senders. The capacity formula has a form of conditional quantum mutual information, analogous to the classical formula2. We then give an explicit example of a bosonic thermal-loss MAC, which is widely applicable to practical communication scenarios. For example, it models the network depicted in Fig. 1, where multiple mobile devices are sending messages to a single base station. We evaluate its rate-region with the common TMSV entanglement source. Comparing it with the case without EA47, we find great advantages enabled by entanglement; Moreover, when the sources of all senders have equal and low brightness, we numerically find that the TMSV source is optimal at a corner rate point. As a benchmark, we derive bounds on the capacity region and design practical protocols, based only on off-the-shelf quantum optical elements, which can achieve quantum advantages from entanglement in the near-term.
EA classical capacity theorem for MAC
Multiple-access channels
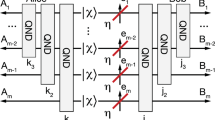
As depicted in Fig. 2, consider a MAC with s senders, each sending a message mk (1 ≤ k ≤ s) sampled from a message space Mk, therefore the overall message m = m1 ⋯ ms is sampled from the message space \(M={\otimes }_{k = 1}^{s}{M}_{k}\). To send each message mk, the kth sender performs a quantum operation \({{\mathcal{E}}}_{{m}_{k}}\) to produce a signal quantum system Ak. Following ref. 17, we introduce EA in the above communication scenario—namely the receiver has a reference system \({A}_{k}^{\prime}\) (idler) pre-shared as the EA with the kth sender.
The EA sources \(\hat{\phi }\) of the s senders are in a product state of Eq. (1). The s senders apply independent encoding modeled by quantum operations, i.e., sender k applies \({{\mathcal{E}}}_{{m}_{k}}\) on the signal state given the message mk. Denoting the entire message as m = m1 ⋯ ms, the encoded signal-idler is then in a state \({\hat{\sigma }}^{m}\). The senders’ encoded quantum systems A = A1 ⋯ As are sent through the MAC \({\mathcal{N}}\), leading to the output system B. The receiver applies the quantum operation \({\mathcal{D}}\) to decode the information from the joint state \({\hat{\beta }}^{m}\) of the output system B and the pre-shared reference systems \(A^{\prime} =A_1^{\prime} \cdots A_s^{\prime}\). We define Mk as the codeword space of each message mk, M as the overall codeword space of message m, and \({M}^{\prime}\) as the decoded codeword space. To facilitate the analysis, we denote the overall state \(\hat{{{\Xi }}}\) (Eq. (14)) over systems \(MA{A}^{\prime}\) right before the channel and the overall state \(\hat{\omega }\) (Eq. (15)) over systems \(MB{A}^{\prime}\) right before the decoding.
We consider the entanglement to be pairwise between each sender and the receiver such that the overall quantum state
is in a product form, where we have denoted A = A1 ⋯ As and \({A}^{\prime}={A}_{1}^{\prime}\cdots {A}_{s}^{\prime}\) as the overall systems.
After the encoding, the composite system A containing all of the quantum systems \({\{{A}_{k}\}}_{k = 1}^{s}\) is input to the MAC \({{\mathcal{N}}}_{A\to B}\), which outputs the quantum system B for the receiver to decode the messages jointly with the EA \({A}^{\prime}\). For convenience, we define a quantum state after the channel but without the encoding, \({\hat{\rho }}_{B{A}^{\prime}}=[{{\mathcal{N}}}_{A\to B}\otimes {\mathcal{I}}]({{\hat{\phi }}}_{A{A}^{\prime}}),\) where \({\mathcal{I}}\) is the identity channel modeling the ideal storage of the idler system. The formal analyses of the quantum-state evolution can be found in the Methods.
The performance metric of the above communication scenario is described by a vector of rates (R1, ⋯ , Rs), where Rk is the reliable communication rate between the kth sender and the receiver (see Methods, Section II of ref. 41, and Subsection III.A of ref. 17 for the formal definitions). These rates in general have non-trivial trade-offs with each other. In the case without EA, the capacity region is well-established by the pioneering work of Winter41 (see Supplementary Note 2).
To describe the rate region of the s-sender MAC, we will frequently divide the senders into two blocks, the block of interest indexed by a sequence J and the complementary block Jc. For example, when s = 2, we have four possible block divisions: {J = 1, Jc = 2}, {J = 2, Jc = 1}, and and two trivial cases \(\{J=12,{J}^{c}=\varnothing \}\), \(\{J=\varnothing ,{J}^{c}=12\}\). Any s-fold quantity can be written as a composition of the two blocks, e.g., message space M = M[J]M[Jc], with M[J] = ⊗ i∈JMi, \(M[{J}^{c}]={\otimes }_{i\in {J}^{c}}{M}_{i}\); similarly the message as m = m[J]m[Jc].
Capacity theorem
To present our EA-MAC capacity theorem for the scenario in Fig. 2, we introduce some entropic quantities. For a quantum system XYZ in a state \(\hat{\alpha }\), we define the quantum mutual information between X and Y as
where \(S{(X)}_{\hat{\alpha }}=S({\hat{\alpha }}_{X})=-{\rm{tr}}({\hat{\alpha }}_{X}{\log}_{2}{\hat{\alpha }}_{X})\) is the von Neumann entropy. Similarly, the quantum conditional mutual information between X and Z conditioned on Y
With the entropic quantities in hand, we can present our main theorem below (see Supplementary Note 3 for a proof).
Theorem 1
(EA-MAC capacity) The EA classical communication capacity region over an s-sender MAC \({\mathcal{N}}\) is given by the regularized union
where the “one-shot” capacity region \({{\mathcal{C}}}_{{\rm{E}}}^{(1)}({\mathcal{N}})\) is the convex hull of the union of “one-shot, one-encoding” regions
The “one-shot, one-encoding” rate region \({\tilde{{\mathcal{C}}}}_{{\rm{E}}}({\mathcal{N}},\hat{\phi })\) for the 2s-partite pure product state \({\hat{\phi }}_{A{A}^{\prime}}={\otimes }_{k = 1}^{s}{\hat{\phi }}_{{A}_{k}{A}_{k}^{\prime}}\) over \(A{A}^{\prime}\), is the set of rates (R1, ⋯ , Rs) satisfying the following 2s inequalities
where the conditional quantum mutual information is evaluated over the output state \({\hat{\rho }}_{B{A}^{\prime}}={{\mathcal{N}}}_{A\to B}\otimes {\mathcal{I}}({\hat{\phi }}_{A{A}^{\prime}})\).
Here we make some remarks about Theorem 1: First, if we only focus on the regularized capacity region \({{\mathcal{C}}}_{{\rm{E}}}({\mathcal{N}})\), then the convex hull in Eq. (3) is not necessary, as one can simply include the time-sharing over different inputs among the infinite number of channel uses; However, if one wants to formulate the “one-shot” capacity region \({{\mathcal{C}}}_{{\rm{E}}}^{(1)}({\mathcal{N}})\), then the convex hull is necessary to include potential time-sharing between any codes. Second, the capacity formula in ref. 17 can be considered as a special case of our theorem, as the regularized case does not need the convex hull in Eq. (3); indeed, at the end of ref. 17 our theorem is stated as a conjecture.
EA capacity region for a bosonic MAC
Bosonic thermal-loss MACs
In an optical or microwave communication scenario, the relevant MAC is a bosonic thermal-loss MAC depicted in Fig. 3. Upon the input modes \({\hat{a}}_{{A}_{1}}\cdots {\hat{a}}_{{A}_{s}}\) from the s senders, the MAC \({\mathcal{N}}\) first combines the modes through a beam splitter array to produce a mixture mode
while all other ports of the beam splitter array are discarded, here the weights {ηk} are non-negative and normalized. Then the mixture mode goes through a bosonic thermal-loss channel \({{\mathcal{L}}}^{\tau ,{N}_{{\rm{B}}}}\) described by the operator transform
where \({\hat{a}}_{E}\) denotes the environment mode in a thermal state with a mean photon number \(\langle {\hat{a}}_{E}^{\dagger }{\hat{a}}_{E}\rangle ={N}_{{\rm{B}}}/(1-\tau )\). This convention of fixing the mean photon number NB of the thermal noise mixed into the output mode \({\hat{a}}_{B}\) is widely used, e.g., in quantum illumination48,49.
In a bosonic MAC, the Hilbert space of the quantum systems is infinite-dimensional—an arbitrary number of photons can occupy a single mode due to the bosonic nature of light. To model a realistic communication scenario, we will consider an energy constraint on the mean photon number (brightness) of the signals modes
which is commonly adopted in bosonic communication28,47,50. Note that in general the energy of different senders can be different.
Without EA, the capacity region of the above bosonic MAC has been considered in ref. 47 for the two-user case. However, the generalization of the coherent state rate region therein to the s-sender case is straightforward, leading to a rate region specified by the following 2s inequalities,
where g(x) = (x + 1) log2(x + 1) − x log2(x) and J can be chosen arbitrarily. Moreover, a squeezing-based encoding scheme is shown to be advantageous over the coherent-state encoding; however, regardless of the encoding, the rate region is always bounded by the following set of outer bounds
which are derived by assuming a super receiver that can reverse the beam splitter array in the bosonic thermal-loss MAC. A second outer bound can be obtained from energetic considerations, which leads to the same form of Ineq. (8) with J being all users. As these outer bounds represent the upper limit of all encodings without EA, an EA rate region outside the rate region specified by the above outer bounds will demonstrate a strict advantage enabled by entanglement.
EA outer bounds
As the exact evaluation of the EA capacity region for the bosonic MAC is challenging, we first focus on outer bounds to obtain some insights. Similar to the case without EA, via reducing to the single-sender EA classical capacity, one can obtain outer bounds for the EA-MAC classical capacity region (See Methods for a proof). Explicitly, we have
where the explicit formula of the EA capacity \({C}_{{\rm{E}}}\left({N}_{{\rm{S}}};{{\mathcal{L}}}^{{\tau ,N}_{{\rm{B}}}}\right)\) over a bosonic thermal-loss channel \({{\mathcal{L}}}^{{\tau ,N}_{{\rm{B}}}}\), with the energy constraint NS, can be found in Eq. (18) of Methods. These outer bounds provide the upper limit of EA classical communication rates, and apply to arbitrary forms of entanglement source \(\hat{\phi }\) and encoding \(\{{{\mathcal{E}}}_{m}\}\).
Two-mode squeezed vacuum rate region
To obtain an explicit example of bosonic EA-MAC capacity region, we consider the entanglement source in Eq. (1) as a product of TMSV pairs, each with the wave-function
for 1 ≤ k ≤ s, where \(\left|n\right\rangle\) is the number state defined by \({\hat{a}}^{\dagger }\hat{a}\left|n\right\rangle =n\left|n\right\rangle\). In ref. 28, it has been shown that the TMSV state is optimal for single-sender single-receiver EA classical communication, therefore we expect the TMSV source to be good in the MAC case. Although, due to the complexity from the plurality of the senders, the exact union over the states in Eq. (3) for the EA-MAC classical capacity region is challenging to solve.
We evaluate the “one-shot, one-encoding” rate region \({\tilde{{\mathcal{C}}}}_{{\rm{E}}}({\mathcal{N}},{\hat{\phi }}^{{\rm{TMSV}}})\) in Ineqs. (4) for the product of TMSV source in Eq. (12). Although the evaluation of each Ineq. (4) is efficient thanks to the Gaussian nature of the state, the number of such inequalities 2s is exponential and therefore resource-consuming in practice. To showcase the capacity region, we choose s = 2, 3, which enable direct visualization as the rate region is two or three dimensional. In comparison, we also compute the classical coherent-state rate region in Ineq. (8) and the classical outer bound, specified jointly by Ineq. (9) and Ineq. (8) with J being all senders. Moreover, we can also compare \({\tilde{{\mathcal{C}}}}_{{\rm{E}}}({\mathcal{N}},{\hat{\phi }}^{{\rm{TMSV}}})\) with the EA outer bound in Ineqs. (11) and (10).
Three representative setups of parameters are chosen as examples. To begin with, we consider an intermediate channel noise NB = 20, identical to the case of microwave quantum illumination48,51; Furthermore, a noisy channel with sufficiently large noise NB = 104 is noteworthy as it provides a saturated EA advantage28; Finally, the long wavelength infrared domain with low noise NB = 0.1 is a relatively uncharted territory for EA communication, nevertheless also relevant for practical applications.
We begin with a two-sender case (s = 2). As shown in Fig. 4, in all the parameter settings being considered, we can see strict advantages of the EA capacity region (cyan solid) over the classical outer bound (black dashed), which is higher than the coherent-state rate region (black solid). We find that the advantage is larger when the noise NB is larger, comparing subplots (c) and (d). In particular, this advantage also holds when NS ≪ NB ≪ 1, which can happen in the long wavelength infrared domain, as shown in subplot (d).
Rates are normalized by the coherent-state bounds \({C}_{{\rm{coh}}}^{1}\), \({C}_{{\rm{coh}}}^{2}\) defined in Ineq. (8), evaluated in the scenario of: a microwave domain, τ = 0.01, NB = 20, NS,1 = NS,2 = 0.01, η1 = 1/3, η2 = 2/3. b microwave domain, τ = 0.01, NB = 20, η1 = η2 = 1/2, NS,1 = 0.001, NS,2 = 0.01. c a noisy channel, τ = 10−3, NB = 104, η1 = η2 = 1/2, NS,1 = 0.001, NS,2 = 0.01. d long wavelength infrared domain η1 = η2 = 1/2, τ = 0.001, NB = 0.1, NS,1 = 0.001, NS,2 = 0.01. The EA rate region in Ineq. (4) (cyan solid), evaluated on TMSV states, is bounded by the EA outer bound (magenta dashed) in Ineqs. (11) and (10); while the coherent-state rate region (black solid) given by Ineq. (8) is bounded by the classical outer bound (black dashed).
Comparing with the EA outer bound (magenta dashed), we see that in Fig. 4a the TMSV rate region (cyan solid) touches the EA outer bound (magenta dashed) at a corner point when \({R}_{2}/{C}_{{\rm{coh}}}^{2}={R}_{1}/{C}_{{\rm{coh}}}^{1}\) to the leading order. The gap is of the order of 10−5 relatively; therefore, at this point, the TMSV source is in fact optimal for the thermal-loss MAC being considered, for this symmetric case where the parameters NS,k ≪ 1 are identical among the senders. Note this holds although the transmissivities of the senders ηk are not equal. In other cases, when NS,1 ≠ NS,2, regardless of the values of ηk being equal, a strict gap between the TMSV rate region and the EA outer bound exists. This does not conclude that the TMSV encoding is inferior, though, as the outer bound is likely to be loose.
Furthermore, we consider a three-sender asymmetric case (s = 3), with unequal source brightness NS,1 = NS,2 ≠ NS,3. In Fig. 5, a gap emerges between the TMSV rate region (the region below the cyan surface) and the outer bound (the magenta surface), as we expected. An appreciable EA advantage remains as the EA capacity region is several times larger than the coherent state rate region (dark gray surface) and the classical outer bound (light gray surface).
The rates are normalized by the coherent state bounds \({C}_{{\rm{coh}}}^{1}\), \({C}_{{\rm{coh}}}^{2}\), and \({C}_{{\rm{coh}}}^{3}\) defined in Ineq. (8), evaluated in the scenario of microwave domain NS,1 = NS,2 = 0.1, NS,3 = 0.01, τ = 0.01, NB = 20, η1 = η2 = η3 = 1/3. The EA rate region in Ineq. (4) (cyan), evaluated on TMSV states, is bounded by the EA outer bound (magenta) in Ineqs. (11) and (10); while the coherent-state rate region (black) given by Ineq. (8) is bounded by the classical outer bound (light gray).
Now we further consider the scaling of the EA advantage observed above. As shown in Fig. 6, the advantage of the EA capacity (magenta) relative to the case without EA also diverges with log(NS), when the signal brightness NS is small and the noise NB is much larger than the signal brightness NS. Note that this advantage also holds for the case when NS ≪ NB < 1, as shown in Fig. 6b. This logarithmic diverging EA advantage in MACs is similar to the single-sender single-receiver case studied in ref. 28. Indeed, at the limit τ ≪ 1, NS ≪ 1, the relative ratio of the outer bound over the coherent-state rate
is also logarithmic in 1/NS,k when NB is small.
The dependence on source brightness NS,1 = NS,2 = NS of the EA advantage of the EA rate regions for two-sender MAC communication under the scenario of: a microwave domain η = 1/2, τ = 0.01, NB = 20; b long wavelength infrared domain η1 = η2 = 1/2, τ = 0.001, NB = 0.1. We plot R1 for sender 1 under conditions R1/R2 = ∞ (solid) and R1/R2 = 1 (dot-dashed). For TMSV, the two curves overlap. Note that R1/R2 = 0, ∞ are equivalent up to a swap due to the symmetry between the two senders; and for given R1/R2, \({R}_{2}/{C}_{{\rm{coh}}}^{2}={R}_{1}/{C}_{{\rm{coh}}}^{1}\). We also compare the EA rate region of TMSV (cyan) with the EA outer bound (magenta).
Protocol designs for the bosonic EA-MAC
In this section, we design a practical protocol to realize EA classical communication over the bosonic thermal-loss MAC. The protocol consists of phase-modulation encoding on the TMSV entanglement source and structured receiver designs.
Encoding and receiver designs
Similar to the single-sender single-receiver case, to encode a bit of information mk = 0, 1, the kth sender performs a phase modulation on the signal part of the TMSV pairs via a unitary \({{\mathcal{E}}}_{{m}_{k}}={e}^{i{m}_{k}\pi {\hat{a}}_{{A}_{k}}^{{}^{\dagger }}{\hat{a}}_{{A}_{k}}}\) to produce the quantum system Ak input to the MAC, while the idler part of the TMSV pair \({A}_{k}^{\prime}\) is pre-shared to the receiver side for EA. Here we have considered the binary phase-shift keying: the kth sender sends the bit message mk = 0, 1 by the same probability p0 = p1 = 1/2. To enable efficient decoding, we consider NR repetitions of such encoding—each message is repeatedly encoded on NR signal modes of a single sender.
The decoding process takes the output of the MAC \({\hat{a}}_{B}\) and the EA idlers \(\{{\hat{a}}_{{A}_{k}^{\prime}},1\le k\le s\}\) to decode the information {mk, 1 ≤ k ≤ s} of all the senders. Below we propose four receiver designs for the decoding. The basic element in the receiver design is the optical parametric amplifier (OPA), which upon input modes \({\hat{a}}_{R}\) and \({\hat{a}}_{I}\), produces two modes \({\hat{a}}_{R}^{\prime}=\sqrt{G}{\hat{a}}_{R}+\sqrt{G-1}{\hat{a}}_{I}^{\dagger },{\hat{a}}_{I}^{\prime}=\sqrt{G}{\hat{a}}_{I}+\sqrt{G-1}{\hat{a}}_{R}^{\dagger },\) where G is the gain of the OPA. An OPA transforms the phase-sensitive correlation between the input mode-pair into the photon number difference \({{\Delta }}\langle {\hat{a}}_{I}^{^{\prime} \dagger }{\hat{a}}_{I}^{\prime}\rangle \propto \sqrt{G(G-1)}2{\rm{Re}}\langle {\hat{a}}_{I}{\hat{a}}_{R}\rangle\), which is widely utilized to design receivers in EA applications, such as quantum illumination51 and the bipartite EA classical communication28. Moreover, one can use an OPA as a phase-conjugator to design a phase-conjugate receiver (PCR), as explained in ref. 28.
To decode all s messages, one can apply two different strategies, either decode them in a serial manner or in parallel. One can also base the receiver design on the direct OPA or on the phase-conjugation mechanism. These choices lead to four receiver designs—serial OPA receiver (OPAR), serial PCR, parallel OPAR and parallel PCR—as we summarize below (see details in Supplementary Note 1).
In the serially connected scheme, on the kth round, the signal output \({\hat{a}}_{{B}_{k-1}}^{\prime}\) from the (k − 1)th round and the idler \({\hat{a}}_{{A}_{k}^\prime}\) are input to an OPA. The idler mode output from the OPA is detected, by direct detection in serial OPAR or an interferometric detection in serial PCR, to decode the message from the kth sender. Meanwhile, the signal mode output from the OPA is further utilized in the next round. Note that after the kth round, the cross correlation between the signal mode with the other idler modes are almost intact; therefore, performing an OPA on the signal and another idler \({\hat{a}}_{{A}_{k^\prime}^{\prime}}\), one can decode the message from the \({k}^{\prime}\)th sender. Iterating this procedure on the remaining mode consecutively, one obtains a serial architecture for the receiver, as shown in Fig. 7a, b for the serial OPAR and serial PCR.
We can also adopt a parallel design for the receivers. As the thermal-loss channel in the MAC adds excess noise into the output, we expect that in the noisy case, splitting the received signal into s copies, each for the decoding of the message of a single sender, will still provide similar signal-to-noise ratios (SNR), when compared to the case without the splitting. In this way, each portion of the received signal can be utilized in parallel, in each individual OPA component in the parallel OPAR or in each phase-conjugation detection in the parallel PCR, to decode each message. As shown in Fig. 7c, d, we can design parallel-OPAR and parallel-PCR schemes.
Finally, we specify the choices of the gain in the OPA. Optimized with respect to the SNR, for OPAR the gains of the s OPAs are chosen to be \({G}_{k}=\sqrt{{N}_{{\rm{S}},k}}/\sqrt{{N}_{{\rm{B}}}(1+{N}_{{\rm{B}}})}\), 1 ≤ k ≤ s. For PCR the optimal gain turns out to be infinity; however, we find that the performance is saturated when (Gk − 1)NB ≫ NS,k for the kth sender, thus we choose a feasible value accordingly.
Receiver rate region evaluations
As the encoding and receivers are chosen, now the (soft-decoding) rate region is entirely obtained from the classical formula of conditional mutual information2 computed over the measurement outcome distribution (see Supplementary Note 1). As shown in Fig. 8, we compare the receiver rate regions with the classical coherent-state rate region in Ineq. (8) (black solid) and the classical outer bound in Ineq. (9) jointly and Ineq. (8) (black dashed) with J being all senders. We see that the performance of both OPAR and PCR can beat the classical coherent state rate region and the classical outer bound.
The rates are normalized by the coherent state bounds \({C}_{{\rm{coh}}}^{1}\), \({C}_{{\rm{coh}}}^{2}\) defined in Ineq. (8): a microwave domain NS,1 = NS,2 = 0.01, τ = 0.01, NB = 20, η1 = η2 = 1/2, NR = 2 × 104; b a noisy channel with NS,1 = NS,2 = 10−3, τ = 10−3, NB = 104, η = 1/2, NR = 107. To distinguish between the overlapping lines, we plot the serial receivers in thicker lines by contrast with the parallel receivers plotted narrowed. The gains of OPAR are given in the main text, and the gains of PCR are G = 2 for NB = 20 and G = 1 + 10−3 for NB = 104. We also compare the receiver rate region with the coherent-state rate (black solid) region and the classical outer bound (black dashed).
In Fig. 8, the performance of the OPAR (blue solid and red solid) is inferior to the PCR (purple solid and orange solid), with a gap that is more significant in Fig. 8a. This is because the PCR has a better SNR to the next order in NS compared with OPA, as found in the single-sender case in ref. 28 and confirmed in Fig. 9 here. As the brightness NS decreases in Fig. 8b, the gap between the PCR and OPAR almost diminishes. In Fig. 9, we see the rates of OPAR (blue and red) are lower than PCR (purple and orange), with a gap expanding as the brightness NS grows. We also find that the rate advantage of both the OPAR and PCR saturates to 3dB as the brightness NS decreases, consistent with the SNR advantage in quantum illumination48,49. This is because when the noise is large, the information rate is proportional to the SNR. Note that when the channel noise NB decreases, the theoretical EA advantage evaluated by TMSV remains substantial. However, the practical advantage allowed by our receivers diminishes as NB falls below 1. For NB = 0.1 (and smaller), there is no advantage for the proposed receivers, as shown in Fig. 9b. This leaves an open question that a feasible receiver that provides EA advantage in the low-noise scenario is hitherto elusive.
The dependence on source brightness NS,1 = NS,2 = NS of the EA advantage of the four receivers for two-sender MAC communication under the scenario of: a microwave domain η = 1/2, τ = 0.01, NB = 20; b long wavelength infrared domain η1 = η2 = 1/2, τ = 0.001, NB = 0.1. In the legend s, p refer to “serial” and “parallel”, respectively. The number of modes NR is fixed such that the SNR NRτNS/NB = 0.1 for sender i = 1, 2. We plot R1 for sender 1 under conditions R1/R2 = ∞ (solid) and R1/R2 = 1 (dot-dashed). Note that R1/R2 = 0, ∞ are equivalent up to a swap due to the symmetry between the two senders; and for given R1/R2, \({R}_{2}/{C}_{{\rm{coh}}}^{2}={R}_{1}/{C}_{{\rm{coh}}}^{1}\).
Discussion
In this paper, we have solved the capacity region of EA classical communication over a quantum MAC with an arbitrary number of senders. We also provide explicit encoding and decoding strategies that offer a practical route towards achieving quantum advantages in such network communication scenarios. Due to teleportation44 and super-dense coding12, the rate region of EA quantum communication is precisely half of the EA classical communication region; therefore, all of our results can be straightforwardly extended to the case of quantum communication. The explicit protocols can also be used for EA quantum communication via further combining with a teleportation protocol.
Many future directions can be explored. For example, multi-partite entanglement may be considered instead of the product form of Eq. (1) to assist the communication scenario, when the senders can collaborate in the entanglement distribution process. Another open question is whether one can have superadditivity phenomena in our EA capacity region of MACs.
Before closing, we discuss potential experimental realizations for the proposed EA-MAC communication systems. The basic setup will be similar to that in ref. 27, with entanglement generated by spontaneous parametric down-conversion in a nonlinear crystal. The receiver can be implemented with another nonlinear crystal to perform phase conjugation or parametric amplification. However, the challenge to demonstrate an entanglement advantage under the multiple-senders scenario is that the pump beams for different entanglement sources need to be frequency and phase locked. Moreover, each stored idler needs to be phase locked to its corresponding signal received from the MAC. Differential-phase encoding can potentially avoid the need for phase locking, which is subject to future studies.
Methods
Formal analysis of the EA-MAC
In the MAC communication scenario of Fig. 2, each encoded signal-idler is in a state \({\hat{\sigma }}_{{A}_{k}{A}_{k}^{\prime}}^{{m}_{k}}={{\mathcal{E}}}_{{m}_{k}}\otimes {\mathcal{I}}({\hat{\phi }}_{{A}_{k}{A}_{k}^{\prime}})\), where \({\mathcal{I}}\) is the identity channel modeling the ideal storage of the idler system. Denote the overall encoding operation as \({{\mathcal{E}}}_{m}={\otimes }_{k = 1}^{s}{{\mathcal{E}}}_{{m}_{k}}\), and the probability of sending each message as \({p}_{m}=\mathop{\prod }\nolimits_{k = 1}^{s}{p}_{{m}_{k}}\), the overall encoding can be described by the composite quantum state
where \({\hat{\sigma }}_{A{A}^{\prime}}^{m}={\otimes }_{k = 1}^{s}{\hat{\sigma }}_{{A}_{k}{A}_{k}^{\prime}}^{{m}_{k}}\equiv \left[{{\mathcal{E}}}_{m}\otimes {\mathcal{I}}\right]\left({\hat{\phi }}_{A{A}^{\prime}}\right)\) is the overall encoded state conditioned on message m and \(\left|m\right\rangle {\left\langle m\right|}_{M}\) is the classical register for message m.
After the encoding, all of the quantum systems from the s senders A are input to the MAC \({{\mathcal{N}}}_{A\to B}\), which outputs the quantum system B for the receiver to decode the messages jointly with the EA \({A}^{\prime}\). The overall state after the channel is
where \({\hat{\beta }}_{B{A}^{\prime}}^{m}=\left[{{\mathcal{N}}}_{A\to B}\otimes {\mathcal{I}}\right]\left({\hat{\sigma }}_{A{A}^{\prime}}^{m}\right)\).
The performance metric of a communication scenario over a MAC is described by a vector of rates (R1, ⋯ , Rs), where Rk is the reliable communication rate between the kth sender and the receiver. These rates in general have non-trivial trade-offs with each other. Formally, we define an (n, R1, ⋯ , Rs, ϵ) EA code by: the prior set \(\{{p}_{{{\boldsymbol{m}}}_{k}^{n}}\}\), the encoded quantum states \(\{{\hat{\sigma }}^{{{\boldsymbol{m}}}_{k}^{n}}\}\), 1 ≤ k ≤ s on the input An for n parallel channel uses, with each message \({{\boldsymbol{m}}}_{k}^{n}\in [{2}^{n{R}_{k}}]\), and the decoding positive operator-valued measure (POVM) \(\{{\hat{{{\Lambda }}}}_{{m}_{1}\cdots {m}_{s}}\}\) on \({{\boldsymbol{B}}}^{n}{{\boldsymbol{A}}}^{^{\prime} n}\) such that
We say that (R1, ⋯ , Rs) is an achievable rate vector if for all ϵ > 0, δ > 0 and sufficiently large n, there exists an (n, R1 − δ, ⋯ , Rs − δ, ϵ) EA code. The EA classical capacity region \({{\mathcal{C}}}_{{\rm{E}}}({\mathcal{N}})\) is defined to be the closure of the set of all achievable rate vectors. The regularized capacity \({{\mathcal{C}}}_{{\rm{E}}}({\mathcal{N}})\) is the union of all ℓ-letter one-shot capacity regions \({{\mathcal{C}}}_{{\rm{E}}}^{(1)}({{\mathcal{N}}}^{\otimes \ell })/\ell\), with integers ℓ ≥ 1. The one-shot capacity region \({{\mathcal{C}}}_{{\rm{E}}}^{(1)}({\mathcal{N}})\) is the convex closure of the subset of achievable rate vectors by (n, R1 − δ, ⋯ , Rs − δ, ϵ) codes that are generated from separable inputs among the n channel uses. Here “one-shot” is in the sense that the entanglement is constrained in a single channel use. For \(\ell\)-letter rates, the capacity region \({{\mathcal{C}}}_{{\rm{E}}}^{(1)}({{\mathcal{N}}}^{\otimes \ell })\) considers \({{\mathcal{N}}}^{\otimes \ell }\) as a single channel and allows codes with entanglement between ℓ uses of \({\mathcal{N}}\). In the case without EA, the capacity region is well-established by the pioneering work of Winter41 (see Supplementary Note 2).
Outer bounds for bosonic thermal-loss MAC
Now we provide the outer bound in Ineqs. (11) and (10) for the EA classical capacity region of the bosonic thermal-loss MAC. As we see in Fig. 3, the overall channel can be written as a concatenation of two parts, \({\mathcal{N}}={{\mathcal{L}}}^{\tau ,{N}_{{\rm{B}}}}\circ {{\mathcal{E}}}_{{\rm{MAC}}}\), where \({{\mathcal{E}}}_{{\rm{MAC}}}\) represents the beam splitter modeling the signal interference. From the bottleneck inequality, the overall communication rate is upper bounded by
the single-sender single-receiver EA classical capacity of the thermal-loss channel \({{\mathcal{L}}}^{\tau ,{N}_{{\rm{B}}}}\) with brightness \(\mathop{\sum }\nolimits_{k = 1}^{s}{\eta }_{k}{N}_{{\rm{S}},k}\). This is because for the channel \({{\mathcal{L}}}^{\tau ,{N}_{{\rm{B}}}}\), only a single mode signal \({\hat{a}}_{{A}_{{\rm{mix}}}}\) in Eq. (5) with brightness \(\left\langle {\hat{a}}_{{A}_{{\rm{mix}}}}^{\dagger }{\hat{a}}_{{A}_{{\rm{mix}}}}\right\rangle =\mathop{\sum }\nolimits_{k = 1}^{s}{\eta }_{k}{N}_{{\rm{S}},k}\) goes through. Explicitly, the capacity
with \({A}_{\pm }=(D-1\pm ({N}_{{\rm{S}}}^{\prime}-{N}_{{\rm{S}}}))/2\), \({N}_{{\rm{S}}}^{\prime}=\tau {N}_{{\rm{S}}}+{N}_{{\rm{B}}}\) and \(D=\sqrt{{({N}_{{\rm{S}}}+{N}_{{\rm{S}}}^{\prime}+1)}^{2}-4\tau {N}_{{\rm{S}}}({N}_{{\rm{S}}}+1)}\). This proves Ineq. (11).
As for the individual upper bounds for the senders in Ineq. (10), we consider a theoretical super-receiver with access to all of the output ports of the beam splitter part. The super-receiver performs the reverse of the beam splitter transform, after which the communication reduces to the single-sender scenario of which the information rate is bounded by each single-sender single-receiver EA classical capacity. Explicitly, we have
which proves Ineq. (10).
Data availability
The data that support the findings of this study are available upon reasonable request.
Code availability
The code used to generate data will be made available to the interested reader upon reasonable request.
References
Shannon, C. A mathematical theory of communication bell. Syst. Tech. J. 27, 379 (1948).
Cover, T. M. Elements of Information Theory (John Wiley, Sons, 1999).
Hausladen, P., Jozsa, R., Schumacher, B., Westmoreland, M. & Wootters, W. K. Classical information capacity of a quantum channel. Phys. Rev. A 54, 1869 (1996).
Schumacher, B. & Westmoreland, M. D. Sending classical information via noisy quantum channels. Phys. Rev. A 56, 131 (1997).
Holevo, A. S. The capacity of the quantum channel with general signal states. IEEE Trans. Inf. Theory 44, 269 (1998).
Hastings, M. B. Superadditivity of communication capacity using entangled inputs. Nat. Phys. 5, 255 (2009).
Smith, G. & Yard, J. Quantum communication with zero-capacity channels. Science 321, 1812 (2008).
Zhu, E. Y., Zhuang, Q. & Shor, P. W. Superadditivity of the classical capacity with limited entanglement assistance. Phys. Rev. Lett. 119, 040503 (2017).
Zhu, E. Y., Zhuang, Q., Hsieh, M.-H. & Shor, P. W. Superadditivity in trade-off capacities of quantum channels. IEEE Trans. Inf. Theory 65, 3973–3989 (2018).
Leditzky, F., Leung, D. & Smith, G. Dephrasure channel and superadditivity of coherent information. Phys. Rev. Lett. 121, 160501 (2018).
Fanizza, M., Kianvash, F. & Giovannetti, V. Quantum flags and new bounds on the quantum capacity of the depolarizing channel. Phys. Rev. Lett. 125, 020503 (2020).
Bennett, C. H. & Wiesner, S. J. Communication via one-and two-particle operators on einstein-podolsky-rosen states. Phys. Rev. Lett. 69, 2881 (1992).
Bennett, C. H., Shor, P. W., Smolin, J. A. & Thapliyal, A. V. Entanglement-assisted classical capacity of noisy quantum channels. Phys. Rev. Lett. 83, 3081 (1999).
Bennett, C. H., Shor, P. W., Smolin, J. A. & Thapliyal, A. V. Entanglement-assisted capacity of a quantum channel and the reverse shannon theorem. IEEE Trans. Inf. Theory 48, 2637 (2002).
Holevo, A. S. On entanglement-assisted classical capacity. J. Math. Phys. 43, 4326 (2002).
Shor, P. W. The classical capacity achievable by a quantum channelassisted by a limited entanglement. Quant. Info. Comput. 4, 537–545. Preprint at https://arxiv.org/abs/quant-ph/0402129 (2004).
Hsieh, M.-H., Devetak, I. & Winter, A. Entanglement-assisted capacity of quantum multiple-access channels. IEEE Trans. Inf. Theory 54, 3078 (2008).
Zhuang, Q., Zhu, E. Y. & Shor, P. W. Additive classical capacity of quantum channels assisted by noisy entanglement. Phys. Rev. Lett. 118, 200503 (2017a).
Wilde, M. M. & Hsieh, M.-H. The quantum dynamic capacity formula of a quantum channel. Quantum Inf. Process. 11, 1431 (2012a).
Wilde, M. M., Hayden, P. & Guha, S. Information trade-offs for optical quantum communication. Phys. Rev. Lett. 108, 140501 (2012a).
Zhuang, Q. Quantum-enabled communication without a phase reference. Phys. Rev. Lett. 126, 060502 (2021).
Lloyd, S. Capacity of the noisy quantum channel. Phys. Rev. A 55, 1613 (1997).
Shor, P. W. The quantum channel capacity and coherent information. in Lecture Notes, MSRI Workshop on Quantum Computation (2002).
Devetak, I. The private classical capacity and quantum capacity of a quantum channel. IEEE Trans. Inf. Theory 51, 44 (2005).
Wilde, M. M. & Hsieh, M.-H. The quantum dynamic capacity formula of a quantum channel. Quantum Inf. Process. 11, 1431 (2012b).
Wilde, M. M., Hayden, P. & Guha, S. Quantum trade-off coding for bosonic communication. Phys. Rev. A 86, 062306 (2012b).
Hao, S., Shi, H., Li, W., Zhuang, Q., and Zhang, Z. Entanglement-assisted communication surpassing the ultimate classical capacity, Preprint at https://arxiv.org/abs/2101.07482 (2021).
Shi, H., Zhang, Z. & Zhuang, Q. Practical route to entanglement-assisted communication over noisy bosonic channels. Phys. Rev. Applied 13, 034029 (2020).
Guha, S., Zhuang Q. & Bash, B. A. Infinite-fold enhancement in communications capacity using pre-shared entanglement. In IEEE International Symposium on Information Theory (ISIT), 1835–1839. IEEE. https://doi.org/10.1109/ISIT44484.2020.9173940 (2020)
Gagatsos, C. N., Bullock, M. S. & Bash, B. A. Covert capacity of bosonic channels. IEEE J. Sel. Area Inf. Theory 1, 555 (2020).
Laurenza, R. & Pirandola, S. General bounds for sender-receiver capacities in multipoint quantum communications. Phys. Rev. A 96, 032318 (2017).
Nötzel, J. Entanglement-enabled communication. IEEE J. Sel. Area Inf. Theory 1, 401 (2020).
Leditzky, F., Alhejji, M. A., Levin, J. & Smith, G. Playing games with multiple access channels. Nat. Commun. 11, 1 (2020).
Yard, J., Hayden, P. & Devetak, I. Capacity theorems for quantum multiple-access channels: Classical-quantum and quantum-quantum capacity regions. IEEE Trans. Inf. Theory 54, 3091 (2008).
Qi, H., Wang, Q. & Wilde, M. M. Applications of position-based coding to classical communication over quantum channels. J. Phys. A 51, 444002 (2018).
Kimble, H. J. The quantum internet. Nature 453, 1023 (2008).
Biamonte, J., Faccin, M. & De Domenico, M. Complex networks from classical to quantum. Commun. Phys. 2, 53 (2019).
Wehner, S., Elkouss, D. & Hanson, R. Quantum internet: a vision for the road ahead Science 362, eaam9288 (2018).
Kozlowski, W. & Wehner, S. Towards large-scale quantum networks. In Proc. Sixth Annual ACM International Conference on Nanoscale Computing and Communication. Association for Computing Machinery. 1–7 (New York, NY, USA, 2019).
Zhang, B. & Zhuang, Q. Entanglement formation in continuous-variable random quantum networks. npj Quantum Inf. 7, 33 (2021).
Winter, A. The capacity of the quantum multiple-access channel. IEEE Trans. Inf. Theory 47, 3059 (2001).
Czekaj, L. & Horodecki, P. Purely quantum superadditivity of classical capacities of quantum multiple access channels. Phys. Rev. Lett. 102, 110505 (2009).
Czekaj, L. Subadditivity of the minimum output entropy and superactivation of the classical capacity of quantum multiple access channels. Phys. Rev. A 83, 042304 (2011).
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and einstein-podolsky-rosen channels. Phys. Rev. Lett. 70, 1895 (1993).
Banaszek, K., Kunz, L., Jarzyna, M. & Jachura, M. Approaching the ultimate capacity limit in deep-space optical communication. In Proc. SPIE 10910, Free-Space Laser Communications XXXI 109100A. (eds) Hamid Hemmati, Don M. Boroson (International Society for Optics and Photonics, 2019).
Win, M. Z. & Scholtz, R. A. Ultra-wide bandwidth time-hopping spread-spectrum impulse radio for wireless multiple-access communications. IEEE Trans. Inf. Theory 48, 679 (2000).
Yen, B. J. & Shapiro, J. H. Multiple-access bosonic communications. Phys. Rev. A 72, 062312 (2005).
Tan, S.-H. et al. Quantum illumination with gaussian states. Phys. Rev. Lett. 101, 253601 (2008).
Zhuang, Q., Zhang, Z. & Shapiro, J. H. Optimum mixed-state discrimination for noisy entanglement-enhanced sensing. Phys. Rev. Lett. 118, 040801 (2017b).
Giovannetti, V., Garcia-Patron, R., Cerf, N. J. & Holevo, A. S. Ultimate classical communication rates of quantum optical channels. Nat. Photonics 8, 796 (2014).
Guha, S. & Erkmen, B. I. Gaussian-state quantum-illumination receivers for target detection. Phys. Rev. A 80, 052310 (2009).
Acknowledgements
This project is supported by the Defense Advanced Research Projects Agency (DARPA) under Young Faculty Award (YFA) Grant No. N660012014029, National Science Foundation (NSF) Engineering Research Center for Quantum Networks Grant No. 1941583 and NSF Grant No. OIA-2040575. Q.Z. also acknowledges Craig M. Berge Dean’s Faculty Fellowship of University of Arizona. Z.Z. is supported in part by NSF Grant No. ECCS-1920742 and No. CCF-1907918. Q.Z. thanks Moe Z. Win for helpful discussions.
Author information
Authors and Affiliations
Contributions
Q.Z. conceived of and designed the study. H.S. performed the calculations and generated the figures under the supervision of Q.Z. The coherent-state rate region and classical outer bounds without EA are derived by H.S. and Q.Z., with inputs from S.G. Theorem 1 is proven by H.S. and Q.Z., with contribution from M.-H.H. Q.Z., and Z.Z. proposed the receiver designs. H.S. and Q.Z. wrote the manuscript, with inputs from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shi, H., Hsieh, MH., Guha, S. et al. Entanglement-assisted capacity regions and protocol designs for quantum multiple-access channels. npj Quantum Inf 7, 74 (2021). https://doi.org/10.1038/s41534-021-00412-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-021-00412-3
This article is cited by
-
State transfer on the multi-access channel network
Quantum Information Processing (2024)