Abstract
High-precision, individually programmable manipulation of quantum particles is crucial for scaling up quantum information processing (QIP) systems such as laser-cooled trapped-ions. However, restricting undesirable “crosstalk” in optical manipulation of ion qubits is fundamentally challenging due to micron-level inter-ion separation. Further, inhomogeneous ion spacing and high susceptibility to aberrations at UV wavelengths suitable for most ion-species pose severe challenges. Here, we demonstrate high-precision individual addressing (λ = 369.5 nm) of Yb+ using a reprogrammable Fourier hologram. The precision is achieved through in-situ aberration characterization via the trapped ion, and compensating (to λ/20) with the hologram. Using an iterative Fourier transformation algorithm (IFTA), we demonstrate an ultra-low (<10−4) intensity crosstalk error in creating arbitrary pair-wise addressing profiles, suitable for over fifty ions. This scheme relies on standard commercial hardware, can be readily extended to over a hundred ions, and adapted to other ion-species and quantum platforms.
Similar content being viewed by others
Introduction
Programmable and precise control over individual quantum particles, such as laser-cooled trapped ions and neutral atoms, fundamentally enhances our capability to manipulate, probe, and create non-trivial quantum states. In particular, programming internal spin or qubit states of individual trapped ions1,2, spaced a few microns from each other in a linear Coulomb crystal, constitute a powerful platform for quantum information processing (QIP). Individual optical addressing of ions has recently enabled a plethora of challenging experiments, such as creating quantum gates between arbitrary pairs of ion qubits3,4,5,6,7 and engineering non-trivial quantum Hamiltonians for the simulation of strongly correlated many-body phenomena8,9. However, existing technical approaches suffer from scaling and other fundamental challenges, such as lacking independent control4,7,8,9,10,11,12 between the frequency and spatial position of the light, lacking simultaneous illumination capability on arbitrary sets of ions at the diffraction limit13,14, or requiring uniformly spaced ions3,5,6 not readily available in most ion traps15. Crucially, the stringent requirement of low crosstalk between the target ion and its neighbors in QIP experiments, especially for quantum error correction16, necessitates careful engineering and alignment of optical components to minimize aberrations. This problem is compounded by the need to use ultraviolet (UV) radiation for most ion species suitable for QIP1,17. Because, shorter wavelengths accumulate more aberrations for the same optical path mismatch from manufacturing imperfection, optics misalignment, and the use of spherical surfaces. Further, some of the commercial solutions6,18 are expensive and available only for a narrow range of wavelengths.
In this work, we demonstrate a scalable, arbitrary, reprogrammable, and precise individual-ion addressing scheme with in situ aberration-compensation. We adopt a Fourier-holographic19,20 optical addressing approach by employing a programmable amplitude hologram implemented with a commercially available Digital Micromirror Device (DMD). The hologram creates optical field profiles capable of simultaneously addressing arbitrary sets of ions, without changing the frequency of light. We validate high-quality, aberration-compensated optical engineering at λ ≈ 369.5 nm, by observing the fluorescence from the 2S1/2–2P1/2 transition of an Ytterbium ion (174Yb+) in a Paul trap21. This technique can readily be applied to most ion species, as commercial DMDs capable of handling several Watts of optical power are available for a wide wavelength range of 355 nm–2.5 μm. We use the ion for in situ characterization of aberrations, which are then compensated for with high precision (to λ/20 RMS) by feeding back onto the DMD hologram. An adaptation of the iterative Fourier transformation (IFTA) algorithm22 in generating the DMD holograms allows us to reach intensity crosstalk errors in 10−4–10−5 level for realistic inter-ion separation. This crosstalk error is comparable13 or about an order of magnitude lower6,23 than state-of-the-art trapped-ion QIP experiments, when compared at the same ratio of ion spacing to Gaussian spot size, and approaches error correction thresholds16,24. Significantly, our beam profile data indicate that the low error can be maintained while addressing arbitrary pairs in a chain of over a hundred ions with typical unequal spacings15. These results point to the inherent scalability of our approach compared to other existing technologies. The holographic addressing also allows for precise programming of the optical phase as well as the intensity of light, for applications such as phase-sensitive quantum gates25,26. Faster switching speed of MEMS-mirror technology used in DMD, compared to other hologram technology27, enables exploration of digital28 and digital-analog hybrid simulation29 protocols.
Results
Experimental setup
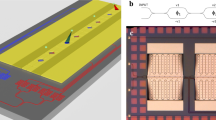
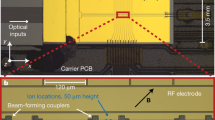
The 369.5 nm light illuminates a circular aperture on the DMD (Texas Instruments DLP9500UV) placed in the Fourier plane (FP) of a focusing lens L2 (f = 200mm), as shown in Fig. 1. The micromirror pitch is d = 10.8 μm and each micromirror can be toggled between two angles, behaving like a local binary light-switch. A binary amplitude grating (with periodicity a = 4d = 43.2 μm) is employed to modulate both the phase and amplitude of the electric field of light, EFP in the DMD plane (FP), such that the target electric field profile in the image plane EIP (with IP referring to either IP1 or IP2, shown in Fig. 1) can be generated with high accuracy. Thus, we operate the DMD as a programmable Fourier hologram. A pinhole placed in the image plane (IP1) of L2 allows us to choose a specific diffraction order (m = −1 here) of the DMD binary grating to propagate to the 174Yb+ ion, after a five times demagnification from IP1 to IP2. The ion is trapped in a Paul trap, with an axial (along y) and radial trapping frequencies of approximately 2π × 180 kHz and 2π × 400 kHz, respectively. We can model the total aberrations from the light source to IP by introducing an aberration phase map \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{IP}})}({\bf{x}})\) in FP, such that the optical Fourier transformation between the field EFP at FP and EIP at IP of a paraxial lens system of effective focal length f is modified (see Supplementary Information) to
Here, \({\bf{x}}^{\prime}\) and \({\bf{k}}^{\prime}\) denote the spatial coordinate and the wave vector at IP respectively, and \({\mathcal{F}}\) denotes Fourier transformation. The wave vector \({\bf{k}}^{\prime}\) is related to the spatial coordinate x at FP by \({\bf{x}}=\frac{\lambda f}{2\pi }{\bf{k}}^{\prime}\). The DMD hologram can then be programmed to imprint a spatial phase \((-{{{\Phi }}}_{{\rm{ab}}}^{({\rm{IP}})}({\bf{x}}))\) on the light to nullify the aberrations.
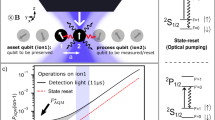
The s-polarized 369.5 nm output beam from the fiber is expanded by the collimating lens L1 to a 5 mm (1/e2 intensity radius) Gaussian beam illuminating a circular aperture on the DMD at an incident angle of ~24∘. A flip mirror can direct the light onto a camera C1 to monitor the optical intensity profile and characterize aberrations at IP1. A CMOS camera (C2) is used to detect fluorescence from the ion. The DMD beam is introduced into the fluorescence-imaging path through a polarizing beam splitter (PBS). Ion addressing and fluorescence collection are achieved using a shared off-the-shelf objective (Thorlabs LMU-5X-NUV) and an imaging lens L3. The effective focal length between the DMD FP and IP2 is 39.9 mm. Here, we choose a coordinate system convention where the beam is propagating along the z direction. A magnetic field \(B\hat{{\bf{x}}}\,(\approx \!2\,{\rm{G}})\) is applied to the ion to prevent it from going into a coherent dark state. An example DMD hologram and a simplified energy level diagram of 174Yb+ are shown at the bottom.
Aberration characterization
To realize diffraction-limited performance at an image plane, we first characterize the aberration phase map \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{IP}})}({\bf{x}})\), following a similar approach as in Zupancic et al.19, schematically shown in Figs 2 and 3. We let the light from two FP patches (Figs 2a and 3a), centered at x = 0 (center of the FP aperture) and x = Δ, consisting of a small number of DMD micromirrors, interfere in the image plane IP. The interference fringes are measured on the camera C1 for IP1 (Fig. 2b) or with the ion fluorescence for IP2 (Fig. 3b) for extracting the aberration phase \(({{{\Phi }}}_{{\rm{ab}}}^{({\rm{IP}})}({\boldsymbol{\Delta }})-{{{\Phi }}}_{{\rm{ab}}}^{({\rm{IP}})}({\bf{0}}))\) (see “Phase profile extraction in the intermediate image plane IP1” section). With the central patch as a reference, we vary Δ to scan the FP aperture on a grid in steps of dg to reconstruct the aberration phase map, after unwrapping the phases30 and interpolating between the grid lines. The FP patch sizes are chosen so as to get a good signal-to-noise ratio, while making sure that the optical phase does not vary appreciably (≪2π) within a patch. We choose the patch size empirically, such that the standard error in the ion fluorescence signal is approximately ten times smaller than the fringe contrast (Fig. 3b). This leads to about λ/50 uncertainty in phase estimation.
a–c The characterization of aberration phase maps \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{0}})}({\bf{x}})\) (top row) and \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{1}})}({\bf{x}})\) (bottom row). a DMD FP patches, as defined in the text. b Corresponding interference fringes at IP1, measured by the camera C1. The diffraction pattern from the OFF micromirrors (Supplementary Information) limits the region of interest (ROI) for phase extraction. Note that the two interference fringes are located at different positions on the camera C1. This is because a non-zero diffraction angle of the m = −1 order translates to a spatial offset of the beam at IP1. c Interpolated and unwrapped measured phase profiles (piston and tilts removed) reconstructed from respective interference fringes. d The measured residual aberration map without piston and tilt components and its histogram after correcting for \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{0}})}({\bf{x}})\) and \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{1}})}({\bf{x}})\). The histogram is based on re-sampled data from the interpolated phase map at each micromirror position. e First few Zernike coefficients of \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{0}})}({\bf{x}})\), \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{1}})}({\bf{x}})\), and the residual aberration. The error bars indicate the standard deviation from error propagation (Eq. (16)). f The amplitude profile of the beam (scaled to the maximum amplitude, see “Methods” section) illuminated on the DMD.
a Schematic of aberration measurement with a single 174Yb+ ion in a “four-rod” trap. b Interference fringes measured by observing the 2S1/2 − 2P1/2 fluorescence of the ion. For each value of phase ϕ2 of the scanning grating patch, in steps of π/8 from 0 to 4π (with the redundancy for a robust phase extraction), we acquire the fluorescence for 100 ms. The 369.5 nm light is red-detuned by ~20 MHz from resonance, for maximizing the signal-to-noise ratio while Doppler-cooling the ion. We estimate the peak optical intensity of the fringes on the ion to be about 0.5Isat, where Isat is the saturation intensity. Each data point is an average over five identical experiments, and error bars represent the standard error. Each solid line is a cosine wave at a fixed angular frequency of 1, reconstructed from the amplitude and phase ϕ obtained from fast Fourier Transform (FFT) of the data set. c The aberration phase map \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{2}})}({\bf{x}})\) (corresponding scanning patches for plots in b are superimposed). d The residual aberration phase map and normalized histogram (with the same method in Fig. 2b) after aberration compensation. e First few Zernike coefficients of \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{2}})}({\bf{x}})\) and the residual aberration, extracted in the same manner as in Fig. 2. f 369.5 nm single-ion addressing beam profile before (blue) and after (orange) the aberration correction, as measured (see Methods) by ion fluorescence. Error bars indicate the standard error over five repeated measurements. The beam profile is created by employing a grating over the entire FP aperture (diameter 600d), without any amplitude modulation. We scan the beam on the ion by adding a programmable tilt in the phase map. The spatial location of the beam (horizontal axis) at the ion is calculated from the known value of the tilt and the effective focal length. The effective NA here is 0.08 (the ideal Airy pattern is shown), corresponding to an Airy radius of 2.8 μm.
We characterize the total aberrations in terms of three phase maps: \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{0}})}({\bf{x}})\), \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{1}})}({\bf{x}})\), and \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{2}})}({\bf{x}})\), such that \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{IP1}})}({\bf{x}})={{{\Phi }}}_{{\rm{ab}}}^{({\rm{0}})}({\bf{x}})+{{{\Phi }}}_{{\rm{ab}}}^{({\rm{1}})}({\bf{x}})\) and \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{IP2}})}({\bf{x}})={{{\Phi }}}_{{\rm{ab}}}^{({\rm{0}})}({\bf{x}})+{{{\Phi }}}_{{\rm{ab}}}^{({\rm{2}})}({\bf{x}})\).
The measured phase maps are shown in Figs 2c and 3c, respectively, and the measured residual aberration phase maps after aberration correction are shown in Figs 2d and 3d.
The phase map \({{{\Phi }}}_{{\rm{ab}}}^{(0)}({\bf{x}})\) characterizes a majority of the total aberrations from the source up to IP1 with high precision. For this, we turn on all the micromirrors within the two patches (4 × 4 micromirrors each), as shown in Fig. 2a (top), and choose a grid size dg = 20d. We measure about 6.5λ (13π) peak–peak and 1.13(2)λ RMS phase aberrations (Fig. 2c, top), dominated by astigmatism (Zernike coefficient \({Z}_{2}^{-2}\)), as seen in Fig. 2e. In this manuscript, all phase aberration-specifications are reported after removing the “piston” (\({Z}_{0}^{0}\)) and “tilt” terms (\({Z}_{1}^{-1}\) and \({Z}_{1}^{1}\)), as piston is an inconsequential global phase, and tilts can be easily fixed by tilting a mirror placed in an FP.
The phase map \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{1}})}({\bf{x}})\) characterizes additional aberrations, up to IP1, caused by the non-zero diffraction angle of the m = −1 order of the DMD hologram. For this, we employ the binary grating (a = 4d), pre-compensated for \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{0}})}({\bf{x}})\), within two circular FP patches of diameter dp = 30d each, as shown in Fig. 2a (bottom), and choose the grid size dg = 25d. We measure about 0.45λ peak–peak and 0.09(1)λ RMS phase in \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{1}})}({\bf{x}})\) (Fig. 2c, bottom), validating our assumption that \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{0}})}({\bf{x}})\) characterizes the majority of aberrations. This \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{1}})}({\bf{x}})\) is again dominated by astigmatism (\({Z}_{2}^{-2}\)), which is the primary aberration (except the tilt) from an angled beam. We find that the residual aberrations up to IP1 (Fig. 2d), after compensating for \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{0}})}({\bf{x}})\) and \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{1}})}({\bf{x}})\), is 0.014λ RMS (0.15λ peak–peak), which falls below the standard error of 0.025λ.
The phase map \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{2}})}({\bf{x}})\) is measured with fluorescence from the ion, which behaves as a point detector because it is well-localized (estimated to be ~130 nm RMS at Doppler-cooling temperature) compared to the diffraction limit of 2.8 μm. Instead of moving the ion, we scan the phase difference (ϕ2 in Fig. 3b) between the two circular FP grating patches (dp = 100d, a = 4d, dg = 50d) to move the interference fringes across the ion. The 0.9λ peak–peak and 0.20(1)λ RMS aberrations in \({{{\Phi }}}_{{\rm{ab}}}^{({\rm{2}})}({\bf{x}})\) are compensated to a residual aberration of 0.05(2)λ RMS (Fig. 3d), resulting in a diffraction-limited spot at the ion, as demonstrated by measuring the beam profile using ion fluorescence in Fig. 3f. The residual aberrations in both IP1 (Fig. 2d) and IP2 (Fig. 3d) are lower than the standard manufacturing tolerance of precision lenses (λ/10 at 633 nm).
Amplitude characterization on DMD
The amplitude of the light illuminating the DMD FP, ∣EFP∣ (Fig. 2f) is characterized by measuring the intensity of reflected beams from a single patch (10 by 10 micromirrors), scanning across the FP with a grid size dg = 20d. The intensity is measured by C1 within the same ROI used in phase measurements described above (see “Methods” section).
Programming the DMD hologram
The binarization of the DMD hologram introduces errors in engineering the target electric field at the image plane. To mitigate errors due to binarization and optical aberrations, we adopt a deterministic iterative Fourier transformation algorithm (IFTA). Our algorithm is based on Wyrowski (1989)22 with two significant modifications. First, we introduce phase constraints at the image plane, making the algorithm suitable for QIP experiments requiring optical phase control25,26. Second, we incorporate the ability to account for aberrations and non-uniform illumination in the Fourier plane. The IFTA strives to minimize errors only inside a user-defined “signal window” in the image plane. A suitable spatial filter placed in IP1, such as a rectangular aperture, shields the ion chain from erroneous signals outside of this signal window.
In Fig. 4a, b, we schematically describe our algorithm and show a numerical simulation for creating a pair of Gaussian spots. Figure 4c shows experimental data taken with camera C1 in IP1 of pairs of Gaussian spots suitable for simultaneously addressing arbitrary pairs of ions with non-uniform spacing. A relative intensity crosstalk error below 10−4 is achieved at a distance of approximately 4wIP1 within a 400wIP1 × 10wIP1 signal window, where wIP1 is the spot size of the addressing Gaussian beam, limited by the numerical aperture. Crucially, this low-error rate is maintained over a large signal window of length ~400wIP1. This suggests that the low-error window can fit up to 400wIP1/4wIP1 = 100 ions. In Fig. 4d, we demonstrate high-quality optical addressing by directly observing ion-fluorescence at the center of the image plane IP2, while scanning the addressing beam along y between the center and the edge of a 120wIP2 × 10wIP2 = 480 μm × 40 μm signal window. While our measurements are limited by the signal-to-noise ratio of ion fluorescence (see “Methods” section) on camera C2, we expect the low-error rates to be transmitted to IP2. This is because, astigmatism (leading aberration) at a field point 240 μm away from the center of IP2 is independently estimated (using Zemax Optics Studio) to be about 0.02 in terms of the standard Zernike coefficient, smaller than the demonstrated aberration correction limit in Fig. 3e (Supplementary Table 2).
a Illustration of the iterative Fourier transformation algorithm (IFTA) for programming holograms to create two Gaussian spots. We first binarize the ideal, aberration-corrected, and gray-scale hologram (from Eq. (1), which has a Gaussian envelope of width wFP = 200d) by setting a dynamic threshold (Supplementary Information) on each mirror. The Fourier transformed profile in the image plane differs from the target profile due to this binarization. We numerically fix this error within a user-defined signal window at the image plane, by substituting the field profile with the target profile. The inverse Fourier transform of this modified profile results in another gray-scale hologram which will be binarized again in the next iteration. We iterate this procedure to achieve the numerical accuracy of the electric field within a small error of the target profile (N = 2000 iterations here). b Numerical simulation of two Gaussian addressing beams at the image plane with a binary hologram created by IFTA. c Intensity profile of Gaussian spots (wIP1 = 10 μm) measured by the camera C1 at IP1 suitable for addressing various pairs (A through E) in a chain of 53 174Yb+ ions. Expected equilibrium positions of ions are represented by black dots and superimposed on the image (with ×30 magnification, see Supplementary Information). The top panel shows a cross-section of the signal window (a close-up shown in the inset) from the high dynamic range (HDR) images shown in the bottom panel. Each HDR image is composed of five images with exposure times varying in steps of 10× from 120 μs to 1.2 s. d Fluorescence signal (see “Methods” section) of an 174Yb+ ion when illuminated by an addressing beam profile consisting of two Gaussian spots of waist wIP2 = 4 μm each. The beam is scanned on the ion identically as in Fig. 3f, and the shaded region indicates the standard error.
Discussions
In summary, we have demonstrated a high-quality, reprogrammable, ultraviolet, holographic, and individual optical addressing scheme with in situ aberration compensation for trapped ions. The flexibility of our approach facilitates the manipulation of ions with an irregular spacing, such as in Coulomb crystals, vastly extending the capabilities of most trapped-ion systems for QIP. The in situ aberration-compensation also eliminates the need for highly sensitive beam alignment that is often challenging, especially for high numerical apertures. Further, the ions can be addressed by non-Gaussian or “flat-top” beams that can potentially suppress intensity fluctuations critical for low-error quantum operations, especially with ions trapped in weak potentials31. For wavelengths that are not resonant with an atomic transition, we can extend our in situ aberration characterization by using coherent Raman transitions or phase shifts32 on ion-qubit states using Ramsey interferometry.
The intensity modulation profile (Fig. 4a) for addressing a pair of ions with two Gaussian beams is a Gaussian envelope with a sinusoidal modulation in the FP. The extent of the FP Gaussian envelope determines the beam waist wIP at IP, and the spatial frequency of the modulation (limited by the FP pixel size) determines the separation of the Gaussian spots at IP. Therefore, given a fixed ratio between wIP and the spacing of the neighboring addressing beams, the maximum number of addressable ions is fundamentally determined by the number of DMD micromirrors illuminated in the FP. By increasing the grating periodicity a, we can further increase the signal window to accommodate more than 100 ions (Supplementary Information).
To achieve a target intensity crosstalk of 10−4 or lower, wIP ≤ dm/4 (Fig. 4c), which determines the minimum required NA for the objective. Here, dm is the minimum separation between ions, determined by the trapping parameters33. For our Nion = 53 example, dm ≈ 2.4 μm, wIP ≈ dm/7 (Fig. 4c) requiring NA ≈ 0.6, although the minimum required NA ≈ 0.35 (for wIP = dm/4). We note that the aberration correction scheme adopted here has been demonstrated for up to NA = 0.8 imaging system19. For longer ion chains, a large field-of-view may necessitate the characterization of separate aberration phase maps for addressing various spatial regions. For Nion ≳ 100, the length of the ion chain increases to ~500 μm while dm ~ 3.5 μm (see trapping parameters in ref. 34) and the minimum required NA ≈ 0.3 which allows for a 500 μm field-of-view35.
By numerical simulation, we find that a deterministic hologram using our IFTA algorithm is capable of producing lower RMS errors within the user-defined signal window compared with a typical hologram using a probabilistic algorithm19, where a probability is assigned to each micromirror for binarization. We directly compare IFTA simulation results from Fig. 4b with the probabilistic algorithm for the same target in Fig. 5. Figure 5 show one instance (Fig. 5a) and an average of over 20 instances (Fig. 5b, c) of the simulated beam profile, respectively, in the image plane with the probabilistic algorithm. The accuracy of the electric field obtained with IFTA surpasses that with the probabilistic algorithm after about N ≈ 100 iterations and produces about an order of magnitude less intensity crosstalk after N ≈ 2000 iterations (Fig. 5b, c). The computational time for IFTA is proportional to N and is about 5 s for N = 2000 on a GPU (Nvidia RTX2070 Super).
a The simulated intensity profile at the image plane from the hologram generated by a randomized algorithm38 with the same target profile as in Fig. 4b. b Simulated electric field RMS error compared to the target profile Eideal within the signal window at the image plane versus the number of iterations N. c Cross-section of the simulated intensity and phase profiles along the ion chain direction (y), at x = 0. The phase is plotted for the regime that the intensity relative to the peak is larger than 10−3. Here, we compare IFTA (N = 2000 iterations) with a randomized algorithm and with the ideal target profile. The lower and upper bound of the shaded areas in b and c indicate the first and third quantities from 20 simulations with the randomized algorithm.
The DMD efficiency, defined as the ratio of usable power in the image plane signal window to input power on the DMD, is determined by several factors, including the efficiency of the user-defined amplitude grating, the number of addressing beams, and the efficiency of the fixed micromirror grating on the DMD chip (Supplementary Information). By turning on a uniform amplitude grating (a = 4d) across the FP aperture, we measure an efficiency of ~4.5% in the m = −1 diffraction order. For creating n addressing Gaussian beams with equal intensity in the image plane, the efficiency scales approximately as 1/n (i.e., 1/n2 per addressing beam), and is independent of the total number of ions, Nion in the system. Despite low efficiency due to the amplitude grating, the exquisite control over aberrations allows for high optical intensity at ions. For example, 1 mW, λ ≈ 369.5 nm resonant (for an Ytterbium ion) light incident on the DMD will result in an intensity I ≈ 1.1 × 108 Wm−2 ≈ 2.2 × 105Isat where Isat is the saturation intensity of the 2S1/2 − 2P1/2 transition, assuming a NA = 0.6 objective. As for a mode-locked laser, used in many QIP experiments, the finite frequency bandwidth will broaden the addressing beam profile compared to a continuous wave laser (Supplementary Information).
Apart from the higher power handling capability of DMDs (up to 10 W in the UV and higher for longer wavelengths), they can also be switched at a faster rate (>10 kHz) compared to other spatial light modulators, such as liquid crystal on silicon spatial light modulator (LCOS-SLM) (<1 kHz)27. Individual micromirrors of a DMD can be switched as fast as in 10 μs and can potentially be made even faster13. However, the data transfer rate between the DMD controller and the chip is currently a bottleneck. Megahertz rate light switching, required for some QIP experiments, can be achieved by using an acousto-optic modulator (AOM) in conjunction with the DMD. The relatively slow switching speed of the DMD compared to trapped-ion quantum gates36 increases the total algorithm time in a quantum experiment. The long coherence time of trapped-ion qubits37 in absence of any control light implies negligible decoherence compared to typical gate infidelities24, for example, an infidelity of \(\sim \!1-\exp \left(-(30{\rm{\mu s}}/10{\rm{s}})\right)\approx 3\times 1{0}^{-6}\) for an idling time of 30 μs and a coherence time of 10 s. However, other sources of error such as motional heating rate of the specific trap have to be taken into account to accurately quantify the impact of a longer algorithm time.
The experiments with ion fluorescence collection reported here suffer from an unwanted scattering of the resonant light (about 10% relative to the peak fluorescence of the addressing beam) from vacuum chamber windows leaking onto the imaging system, thus, reducing the signal-to-noise ratio of the ion fluorescence signal on the camera C2. The unwanted scattering also limited the maximum area or which we could characterize aberrations using the ion and thus reduced the NA to 0.08. The scattering problem can be mitigated by using separate directions for measurement and addressing. Also, experiments that don’t require addressing and measurement at the same time (for example state preparation by optical pumping) do not suffer from the scattering problem. The high-precision addressing capabilities demonstrated here open up exciting possibilities for new experiments, such as partial measurement of a quantum system at the level of a single qubit without decohering others.
Methods
Phase-profile extraction in the intermediate image plane IP1
The interference fringes in IP1 (in Fig. 2b for example) are sampled by the camera C1 as a 2D array. We crop the array within a region of interest (ROI) for phase extraction. The cropped array is denoted as Ixy(mp, np) where Δ ≡ (x, y) denotes the coordinate of the scanning patch relative to the reference patch in the DMD FP, and (mp, np) denotes the coordinates of camera pixels. Here, m and n denote the two spatial directions of the fringes on the camera. We first calculate the spectrum Sxy of Ixy with a 2D fast Fourier transformation (FFT),
Next, we apply a high-pass filter (HPF) to filter out the low spatial frequency background envelope of Ixy and retrieve the spatial frequency of the interference fringes \(({\kappa }_{m}^{xy},{\kappa }_{n}^{xy})\),
A robust estimate for \(({\kappa }_{m}^{xy},{\kappa }_{n}^{xy})\), that is insensitive to shot-to-shot fluctuations in the interference fringes, can be obtained by finding their linear functional dependence on the FP coordinates (x, y), as
Here, \(a,a^{\prime} ,b,b^{\prime}\) are fitting parameters. The relative negative sign between a and \(a^{\prime}\) is due to the fact that the camera is facing opposite to the beam pointing direction. From the two spatial frequencies, we can construct a complex plane wave fringe profile,
where (mc, nc) is the coordinate of the user-defined center of the interference fringes. The phase of the FP at (x, y) is computed from,
Zernike coefficients
Zernike polynomials, commonly used to describe optical aberrations, are a sequence of orthogonal polynomials defined within a unit circle. They are expressed in polar coordinates ρ and θ as
such that
The aberration phase map Φ(ρ, θ) can be expressed as a unique linear combination of Zernike polynomials,
We estimate the Zernike coefficients in our measured phase maps by uniformly sampling across the FP aperture (of radius \({r}_{{\rm{aperture}}}\)), as
Here,
The sample size N equals to the number of grid points in scanning the FP patches. In our experiments, we extract the Zernike coefficients (Eq. (13)) after averaging the phase maps over five repeated measurements. The uncertainty of the Zernike coefficients and the standard deviation δΦ(x, y) of the phase map are related through,
Amplitude characterization
The amplitude profile of the beam illuminating on the DMD ∣Ein(x)∣ is characterized by measuring its intensity, \(| {E}_{{\rm{in}}}({\bf{x}})| =\sqrt{I({\bf{x}})}\). We turn on all the micromirrors in a 10d × 10d patch and scanned on a dg = 20d grid on the DMD. We choose an ROI on the camera C1 (in IP1) to avoid diffraction from the OFF mirrors (as shown in 2b), and measure the total intensity on all pixels within the ROI. We subtract the contribution of OFF mirrors in the ROI, by taking another image with all micromirrors in the OFF position.
Ion fluorescence measurement
While measuring ion fluorescence (in Figs 2–4), we keep a weak Doppler-cooling beam on, shining perpendicularly to the DMD beam, in order to keep the ion cold and hence localized. We extract the fluorescence count due to the DMD beam only (n(DMD)), by taking into account the contributions from the side-Doppler-cooling fluorescence as well as unwanted reflections of these beams, as,
Here, n is the total count detected on a camera pixel. n(935off) denotes the count with the 935 nm repumper beam turned off, pumping the ion into the D3/2 dark state. Hence, n(935off) measures the unwanted reflection of the DMD and side-fluorescence beams. n(DMDoff) denotes the measured count with DMD beam turned off, and hence includes fluorescence and unwanted reflections from the side-Doppler-cooling beam. \({n}^{({\rm{DMD}}{\rm{off}}\& 935{\rm{off}})}\) denotes the measured count with the DMD and the 935 nm beams turned off, and hence includes the unwanted reflections from the side-Doppler-cooling beam. The error bars presented in the results here are calculated by propagating errors in each term in Eq. (17).
Data availability
The data sets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
References
Monroe, C. et al. Programmable quantum simulations of spin systems with trapped ions. Preprint at http://arxiv.org/abs/1912.07845 (2019).
Brown, K. R., Kim, J. & Monroe, C. Co-designing a scalable quantum computer with trapped atomic ions. npj Quant. Inf. 2, 1–10 (2016).
Egan, L. et al. Fault-tolerant operation of a quantum error-correction code. Preprint at http://arxiv.org/abs/2009.11482 (2020).
Friis, N. et al. Observation of entangled states of a fully controlled 20-qubit system. Phys. Rev. X 8, 021012 (2018).
Nam, Y. et al. Ground-state energy estimation of the water molecule on a trapped-ion quantum computer. npj Quant. Inf. 6, 1–6 (2020).
Debnath, S. et al. Demonstration of a small programmable quantum computer with atomic qubits. Nature 536, 63 (2016).
Monz, T. et al. Realization of a scalable shor algorithm. Science 351, 1068–1070 (2016).
Martinez, E. A. et al. Real-time dynamics of lattice gauge theories with a few-qubit quantum computer. Nature 534, 516–519 (2016).
Smith, J. et al. Many-body localization in a quantum simulator with programmable random disorder. Nat. Phys. 12, 907–911 (2016).
NAÈgerl, H. C. et al. Laser addressing of individual ions in a linear ion trap. Phys. Rev. A 60, 145 (1999).
Jurcevic, P. et al. Quasiparticle engineering and entanglement propagation in a quantum many-body system. Nature 511, 202–205 (2014).
Schindler, P. et al. A quantum information processor with trapped ions. N. J. Phys. 15, 123012 (2013).
Crain, S., Mount, E., Baek, S. & Kim, J. Individual addressing of trapped 171yb+ ion qubits using a microelectromechanical systems-based beam steering system. Appl. Phys. Lett. 105, 181115 (2014).
Wang, Y. et al. High-fidelity two-qubit gates using a mems-based beam steering system for individual qubit addressing. In Quantum 2.0, QW5B–1 (2020).
Steane, A. The ion trap quantum information processor. Appl. Phys. B 64, 623–643 (1997).
Parrado-Rodríguez, P., Ryan-Anderson, C., Bermudez, A. & Müller, M. Crosstalk suppression for fault-tolerant quantum error correction with trapped ions. Preprint at http://arxiv.org/abs/2012.11366 (2020).
Ozeri, R. et al. Errors in trapped-ion quantum gates due to spontaneous photon scattering. Phys. Rev. A 75, 042329 (2007).
Wasilousky, P. A. et al. Multi-channel phase-capable acousto-optic modulator (aom) and related methods. US Patent 9,915,851 (2018).
Zupancic, P. et al. Ultra-precise holographic beam shaping for microscopic quantum control. Optics Exp. 24, 13881–13893 (2016).
Čižmár, T., Mazilu, M. & Dholakia, K. In situ wavefront correction and its application to micromanipulation. Nat. Photonics 4, 388–394 (2010).
Olmschenk, S. et al. Manipulation and detection of a trapped yb+ hyperfine qubit. Phys. Rev. A 76, 052314 (2007).
Wyrowski, F. Iterative quantization of digital amplitude holograms. Appl. Optics 28, 3864–3870 (1989).
Mehta, K. K. et al. Integrated optical addressing of an ion qubit. Nat. Nanotechnol. 11, 1066–1070 (2016).
Ballance, C., Harty, T., Linke, N., Sepiol, M. & Lucas, D. High-fidelity quantum logic gates using trapped-ion hyperfine qubits. Phys. Rev. Lett. 117, 060504 (2016).
Sørensen, A. & Mølmer, K. Quantum computation with ions in thermal motion. Phys. Rev. Lett. 82, 1971 (1999).
Cirac, J. I. & Zoller, P. Quantum computations with cold trapped ions. Phys. Rev. Lett. 74, 4091 (1995).
Thalhammer, G., Bowman, R. W., Love, G. D., Padgett, M. J. & Ritsch-Marte, M. Speeding up liquid crystal slms using overdrive with phase change reduction. Optics Exp. 21, 1779–1797 (2013).
Blatt, R. & Roos, C. F. Quantum simulations with trapped ions. Nat. Phys. 8, 277–284 (2012).
Rajabi, F. et al. Dynamical hamiltonian engineering of 2d rectangular lattices in a one-dimensional ion chain. npj Quant. Inf. 5, 32 (2019).
Van der Walt, S. et al. scikit-image: image processing in python. PeerJ 2, e453 (2014).
Cetina, M. et al. Quantum gates on individually-addressed atomic qubits subject to noisy transverse motion. Preprint at http://arxiv.org/abs/2007.06768 (2020).
Lee, A. C. et al. Engineering large stark shifts for control of individual clock state qubits. Phys. Rev. A 94, 042308 (2016).
Dubin, D. H. E. Theory of structural phase transitions in a trapped coulomb crystal. Phys. Rev. Lett. 71, 2753–2756 (1993).
Pagano, G. et al. Cryogenic trapped-ion system for large scale quantum simulation. Quant. Sci. Technol. 4, 014004 (2018).
Pritchard, J., Isaacs, J. & Saffman, M. Long working distance objective lenses for single atom trapping and imaging. Rev. Sci. Instrum. 87, 073107 (2016).
Schäfer, V. et al. Fast quantum logic gates with trapped-ion qubits. Nature 555, 75–78 (2018).
Wang, P. et al. Single ion qubit with estimated coherence time exceeding one hour. Nat. Commun. 12, 1–8 (2021).
Zupancic, P. P. Dynamic holography and beamshaping using digital micromirror devices. Master’s thesis, LMU Münich, Grainer Lab Harvard (2013).
Acknowledgements
We thank Kaleb Ruscitti for helping with DMD hardware and codes, Thiago Bergamaschi and Joel Wallman for scientific discussions, and Anthony Vogliano for helping with the manuscript. We acknowledge financial support from a cooperative agreement with the US Army Research Laboratory (W911NF-17-2-0117), the Canada First Research Excellence Fund (CFREF), the Natural Sciences and Engineering Research Council of Canada Discovery (RGPIN-2018-05250) program, and NFRF Grant, Ontario Early Researcher Award, University of Waterloo, and Innovation, Science and Economic Development Canada (ISED).
Author information
Authors and Affiliations
Contributions
C.-Y.S. and R.I. conceived and designed the experiments. C.-Y.S., S.M., N.K., M.S., and R.H. performed the experiments. C.-Y.S. and S.M. analyzed the data. All authors contributed materials and analysis tools, and took part in writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shih, CY., Motlakunta, S., Kotibhaskar, N. et al. Reprogrammable and high-precision holographic optical addressing of trapped ions for scalable quantum control. npj Quantum Inf 7, 57 (2021). https://doi.org/10.1038/s41534-021-00396-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-021-00396-0
This article is cited by
-
Low cross-talk optical addressing of trapped-ion qubits using a novel integrated photonic chip
Light: Science & Applications (2024)
-
Preserving a qubit during state-destroying operations on an adjacent qubit at a few micrometers distance
Nature Communications (2024)
-
Design of scalable metalens array for optical addressing
Frontiers of Optoelectronics (2022)