Abstract
Our ability to trust that a random number is truly random is essential for fields as diverse as cryptography and fundamental tests of quantum mechanics. Existing solutions both come with drawbacks—device-independent quantum random number generators (QRNGs) are highly impractical and standard semi-device-independent QRNGs are limited to a specific physical implementation and level of trust. Here we propose a framework for semi-device-independent randomness certification, using a source of trusted vacuum in the form of a signal shutter. It employs a flexible set of assumptions and levels of trust, allowing it to be applied in a wide range of physical scenarios involving both quantum and classical entropy sources. We experimentally demonstrate our protocol with a photonic setup and generate secure random bits under three different assumptions with varying degrees of security and resulting data rates.
Similar content being viewed by others
Introduction
Randomness is an important resource in modern information science. It has a great number of applications, ranging from randomized sampling, simulations, randomized algorithms, and above all, cryptography. Many of these applications critically depend on the quality of random numbers, and therefore the design of high-quality random number generators (RNGs) is of utmost importance. There are many different sources of entropy that can be utilized for RNG designs. These range from simple to generate but hard to predict computer data (such as the movement of a mouse cursor on a computer screen or the time between user keystrokes) to seemingly random physical phenomena (such as thermal noise or the breakdown in Zener diodes1,2). In this regard, quantum mechanics offers the possibility of truly random events, such as nuclear decay or photons traveling through a semi-transparent mirror (see ref. 3 for a review on quantum RNGs).
The quality of RNGs is traditionally assessed with the help of statistical tests, or, more recently, machine learning4,5, which can verify that the produced string is virtually indistinguishable from a truly random string. In essence, however, such an approach to analyzing RNGs is problematic, because the statistical tests do not assume anything about the origin of the data they test. As an example, take the binary expansion of the number e—although the string created in this manner would pass many of the conventionally used statistical tests, it is obviously not suitable for cryptographic purposes. This ignorance of the process used to generate the tested random string opens a window to various security risks. Aside from malicious attacks on the RNG, such as inserting back-doors6 or displaying a simple bias towards certain strings7,8, its functioning can be compromised by a simple hardware malfunction, which is often hard to detect9.
Considerations such as these have recently resulted in a different approach to RNG designs based on quantum phenomena, where stronger forms of randomness certificates are possible10. Such quantum RNGs, introduced in ref. 11 and developed in refs. 12,13,14,15,16,17,18,19,20,21, are called device independent (DI-RNGs), because they assume very little about the hardware they use. The security proof for these devices is usually based on Bell-type arguments: the RNG is composed of several non-communicating parts and runs a set of randomness-generation rounds, which involve a predetermined quantum measurement. In a small, randomly chosen fraction of the run-time, the device is tested. In these test rounds, the ability of the devices to violate Bell-type inequalities is verified22,23. The violation of local-realism can be seen as a certificate that the devices use quantum measurements and their outcomes are fundamentally unpredictable. Since Bell-type arguments do not assume anything about the devices used apart from space-like separation, this approach can truly be seen as device-independent. The disadvantage of DI-RNGs lies in their implementation—loophole-free Bell violations have been achieved only recently and under very strict laboratory conditions24,25,26.
In an attempt to retain the randomness certification capabilities of DI-RNGs with less stringent experimental requirements, many semi-device-independent random number generators (SDI-RNGs) have been proposed27,28,29,30,31,32,33,34,35,36,37,38,39. Similar to DI-RNGs, SDI-RNGs include test rounds that are designed to certify the randomness of their output. However, to make the RNGs experimentally more feasible, reasonable assumptions about the functioning of some components of the RNG are made, such as a trusted source27,28,29,30,31,32,33,34 or measurement device37,38,39.
In this paper we present an approach to semi-device-independent randomness certification that allows for flexible assumptions about the workings of an RNG. What sets our work apart from other SDI-RNG proposals is that our framework is formulated in a high-level abstract language of trusted randomness sources. This allows us to certify randomness in a large number of practical implementations utilizing both quantum and classical entropy sources. Additionally, our framework can work with different levels of trust in particular parts of the RNG, without changing the protocol itself. This is in contrast to existing SDI-RNGs, where the protocol relies on a fixed set of assumptions about specific parts of the device. We showcase this flexibility using a photon source and a beam splitter as the source of entropy. Changing the assumptions on the photon source—whether it produces either single photons, coherent/thermal states, or is an unknown source characterized only by its average photon production rate—is possible in our framework, at the cost of changes in the amount of certifiable entropy. Unlike previous SDI-RNG designs, our implementation therefore comes with a user-defined security/production rate trade-off.
The paper is organized as follows. In the “General framework” section we introduce our general framework, which consis ts of three abstract models of entropy sources, and a general protocol to extract perfect randomness from them. We discuss methods to lower bound the entropy of strings obtained from our protocol in the section “Entropy estimation”. The section “Example: a photon through a beam-splitter” is devoted to a particular experiment implementing the described entropy sources with the use of a photon source and a beam splitter. Here we also discuss how different assumptions on the experimental setup change its description within our framework, which results in trade-off between security and randomness production rate. Finally, in the section “Experimental realization and results” we experimentally implement the entropy source described in the section “Example: A photon through a beam-splitter” and post-process its outcomes with three different sets of assumptions, based on the amount of trust placed on the photon source.
Results
General framework
In this section we introduce three different abstract models of randomness, with a decreasing level of trust and describe a protocol, which uses a trusted shutter to extract randomness from such sources.
Our basic assumption about the entropy source is that at regular time intervals, it produces a signal with probability p, and with probability 1 − p, no signal is produced. Such an assumption on the source is conceptually simple, very natural, and in fact many conventional entropy sources mentioned above, such as Geiger counters, thermal noise, or the breakdown in Zener diodes can be modeled in this way. One might argue that such an assumption on the source is too strong, because if one also assumes perfect and trusted signal detectors, extracting randomness from such a source is trivial—click events can be interpreted as "1” and no-click events as "0”. Entropy of such an output string is easily calculable and it can be post-processed into a perfectly random string. Indeed, early trusted commercial quantum RNGs can be described this way (e.g. IDQuantique40 using a photon source and a beam splitter as an entropy source). The main result of this work is that the above assumption on the entropy source can be made sufficient even in the case of partially untrusted measurement device.
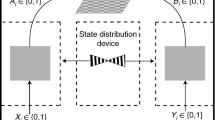
In order to achieve this, we add an additional component to the setup—a movable shutter, which can block the signal being sent from the source to the measurement device (see Fig. 1). We call this scenario a simple scenario and the source of entropy a simple source.
A simple entropy source, \({\mathcal{S}}\), emits a random signal with probability p. This signal is assumed to be unpredictable to any potential adversary. The signal can be blocked with the help of a movable shutter, \({\mathcal{A}}\), controlled via a binary variable x. The measurement device, \({\mathcal{D}}\), is assumed to be dishonest.
Taking the simple entropy source as a building block, we can generalize to a scenario referred to as a mixed source scenario, where the entropy source is a probabilistic mixture of multiple simple sources. Formally, we define a discrete (potentially infinite) probability distribution, γ = {γi}, γi ≥ 0∀i, ∑iγi = 1. We associate a simple source \({{\mathcal{S}}}_{i}\) with each γi. In the mixed source scenario, the simple source \({{\mathcal{S}}}_{i}\) is chosen with probability γi and subsequently a signal is sent with probability pi (see Fig. 2).
In the second scenario, the entropy source \({\mathcal{S}}\) (depicted by a dashed rectangle) is a probabilistic mixture of several (potentially infinitely many) simple sources \({{\mathcal{S}}}_{1},\ldots ,{{\mathcal{S}}}_{n}\). A random variable γ is used to choose a simple source \({{\mathcal{S}}}_{i}\), which emits a random signal with probability pi. The choice of source \({{\mathcal{S}}}_{i}\) in a given round is known to the measurement device \({\mathcal{D}}\) and the adversary, but not to the user. The random variable γ is constrained either by a fixed probability distribution or in a more general scenario by more general constraints (e.g. mean value).
The value of the random variable γ in each round is assumed to be known to the adversary and the measurement device, but unknown to the user. In order to derive bounds on the entropy produced, the variable γ has to be at least partially characterized. This characterization takes the form of a (potentially infinite) sequence of constraints, {fj(γ) = cj}. The strongest of such constraint sets is describing γ completely by specifying each γi. We study this special case separately; however, we show that the entropy of the RNG output can be lower bounded even for weaker characterizations of γ. In fact, this is possible already if the constraint set contains only a single (smooth) function (see section “Entropy estimation”).
Using such a high-level abstraction of the entropy sources is deliberate. It makes the extraction protocol presented below usable for a plethora of different experimental setups. The only requirement is that trusted randomness is produced in the form of a signal with probability p. The reason why the signal is unpredictable to the adversary varies from implementation to implementation. This makes the presented framework usable with both quantum sources of randomness, where randomness is guaranteed from inherent non-determinism of certain quantum measurements and classical sources, where some assumption about unavailability of certain data to the adversary must be made. In the particular experimental realization presented in section “Example: A photon through a beam-splitter”, the trusted randomness is obtained from the path a single photon takes traveling through a beam splitter, which is a genuinely random quantum event.
Before we describe our protocol for extracting perfect randomness from the sources described above, we list a number of required technical assumptions.
-
The shutter (\({\mathcal{A}}\)) can be reliably controlled by the user through their inputs x.
-
The user has access to a uniform random seed X uncorrelated to the devices. For example, this can be a private randomness source. Note that in this case we also naturally require that the output randomness \({H}_{\min }(Y| E)\) of the device is longer than ∣X∣. This can be always achieved by increasing the block size N and decreasing the testing rate q accordingly. Particularly, the protocol requires \(| X| =N{\mathcal{O}}(-q \, \mathrm{log}\,q)\) bits to choose the test rounds and their shutter settings. With large enough N it is sufficient to set \(q=\frac{1}{\sqrt{N}}\), which leads to \(| X| ={\mathcal{O}}(\sqrt{N}\mathrm{log}\,\sqrt{N})\) bits which are used to choose the test rounds, while a much longer output string of length \({H}_{\min }(Y| E)={\mathcal{O}}(N)\) is being produced. Another random string is required for final hashing. This string can however be re-used (see section “Experimental realization”); thus, randomness needed for its selection is negligible for large N or public randomness beacon41.
-
The entropy source \(({\mathcal{S}})\) is a passive element which does not change from round to round.
-
The measurement device (\({\mathcal{D}}\)) is memoryless, which together with the previous assumption implies that each round is identical and independently distributed. Note that the assumption of memoryless measurement devices is rather standard (and often hidden) in the literature, and appears in many contexts (e.g. QKD42, randomness generation32, and more generally, Bell inequality violations43). Nevertheless, methods have recently appeared (e.g. refs. 44 or 45), which allow to leave out this assumption. In particular, using these tools it is often possible to show that the amount of produced private entropy is almost the same as in the memoryless case.
-
In case of quantum entropy sources \(({\mathcal{S}})\) in which the signal state is in a superposition with no-signal state, the measurement device \(({\mathcal{D}})\) is described by a projector onto a basis that contains the no-signal state (see section “Example: A photon through a beam-splitter” for an example with coherent photon sources).
-
There is no communication between the devices besides the signal channel, and the laboratory is shielded from external eavesdroppers. In particular, neither the measurement device nor the source receive direct information about the shutter settings x.
As in any cryptographic protocol, if any of these assumptions cannot be met, the security of the final string cannot be guaranteed. The assumptions imply that the measurement device is left mostly uncharacterized; in particular, it may still be classically correlated with an adversary.
Now we are ready to present the protocol, which consists of two parts: data collection and post-processing. For practical purposes, the protocol is run in large batches of N rounds. For the full description, see Fig. 3. As is seen from the protocol, the user will use the testing rounds to obtain a statistical estimation of the workings of the device.
More precisely, the user will create a vector \(\hat{{\bf{S}}}\) as an estimate for S in Eq. (1), which will be filled out with observed experimental frequencies. This introduces an estimation error εe, which can be made arbitrarily small by increasing the number of rounds in a batch N, and the testing rate q. To keep the main text easier to read, we assume that the experimentalist has access to the actual probabilities in Eq. (1), and elaborate on the sampling error in Supplementary Note 1.
In the following section we describe the post-processing procedure. The goal is to estimate min-entropy \({H}_{\min }(Y| E)\) of the output string Y conditioned on the knowledge of the adversary E. Min-entropy \({H}_{\min }(Y| E)\) roughly describes the length of a perfectly random string obtainable from Y with the help of randomness extractors46. The lower bound on min-entropy is obtained by upper bounding the probability of the adversary to guess the outcome of a single randomness generating round (shutter open), denoted g*. The obtained upper bound depends on observed S, the type of the entropy source used—simple or mixed, with or without the full characterization of γ. Finally, guessing probability is related to min-entropy of the outcome Y as
where ∣Y∣ is the number of randomness generating rounds.
Entropy estimation
In this section we give a procedure to estimate the entropy of the data collected in the protocol described in the previous section. This is split into three parts based on the type of entropy source used.
The simplest case uses a simple entropy source \({\mathcal{S}}\) which sends a signal with probability p. Based on the assumptions introduced earlier, the strategy of the measurement device to click (i.e. behave as if it detected the signal) in a given round can be based only on whether the signal arrived or not, (i.e. a single bit of information). The response of a detector (whether to click or not to click) can also be described by a single bit. Therefore, the possible deterministic response functions, called deterministic detector strategies, can be described by a function S: {0, 1} ↦ {0, 1}, which maps a bit to a bit. There are only four functions of this type, which we call “Never Click” (SN) (both input bits are mapped to 0), “Always Click” (SY) (both input bits are mapped to 1), “Click Honestly” (SH) (0 is mapped to 0 and 1 is mapped to 1), “Click Dishonestly” (S¬H) (0 is mapped to 1 and 1 is mapped to 0). We represent these strategies by the observable behaviors of the measurement device using them, which can be expressed as vectors \(\left(P(\,\text{click}\,| {\it{x}}=0),\,{\it{P}}(\,\text{click}\,| {\it{x}}=1)\right)\):
General non-deterministic strategies can be described by response functions which, except for the information about the arriving photon, take an additional randomized input. It is easy to see that it is sufficient to consider a random input λ of 2 bits, which specifies which of the deterministic functions described above is being used in a given round. The observable statistics of such non-deterministic strategies can be therefore expressed as a convex combination of observable statistics of four deterministic strategies described in Eq. (3). The convex combination is described by a hidden variable λ. We assume that the value of λ is shared between the measurement device and the adversary in each round. Further, we assume that the values (Y, N, H, or ¬H) of the hidden variable λ are identically distributed throughout the rounds according to a probability distribution λY, λN, λH, λ¬H ≥ 0; λY + λN + λH + λ¬H = 1. The adversary tries to guess whether the measurement device clicked or not in each given round based on their knowledge of λ, and thus to guess the outcomes of the RNG.
Let us highlight the importance of the trusted movable shutter in our design. If the design did not contain it, then setting the random variable λ to be uniformly distributed over the strategies SN and SY would lead to the output of the RNG being uniformly random as well. It would therefore pass any statistical test with high probability, even though the adversary would posses its perfect copy, rendering it useless for any cryptographic purpose.
In order to safely bound the amount of the entropy produced, the user must assume that any deviation from the idealized honest scenario SH is correlated with information gained by the adversary. We measure the information gain by the adversary’s optimal guessing probability, g*, which is related to the min-entropy via \({g}^{* }={2}^{-{H}_{\min }(Y| E)}\). If in a given round the measurement device is following the strategies SN or SY, then the adversary can be certain of the output, but if SH or S¬H is used, the guessing probability is reduced to \(g:= \max (1-p,p)\).
Without loss of generality, let us assume that P(click∣x = 0) > P(click∣x = 1) (the other case can be treated similarly, due to the symmetry of the measurement device strategies). Then, Se = (α, β) can be written as the convex combination \(\frac{1}{2}(2\beta ,2\beta )+\frac{1}{2}(2\alpha -2\beta ,0)\). Note that the (2β, 2β) part can be obtained by the measurement device by using only the strategies SN or SY, i.e. without decreasing the adversary’s guessing probability. On the other hand, the (2α − 2β, 0) part can be obtained by using strategy SH only. In particular, this means that whenever our assumption holds, the adversary’s optimal strategy is to set λ¬H = 0, and their guessing probability can be obtained by solving the following optimization problem:
Since the first three constraints contain only three variables and take the form of equalities, we can directly solve them for λ{N,Y,H} to obtain
In order to satisfy the last constraint, λN,Y,H ≥ 0, the following needs to hold:
These six conditions are not independent, but they can be reduced to three conditions which are required for the existence of the solution (see Supplementary Note 2 for a geometric interpretation):
If these conditions are satisfied, the result of the optimization is
and \({H}_{\min }(Y| E)\ge -{\mathrm{log}\,}_{2}\left[1-\left(\alpha -\beta \right)\left(\frac{1-g}{p}\right)\right]| Y|\), where ∣Y∣ is the size of the output string Y.
Let us now turn to the more involved case of a probabilistic mixture of countably many simple sources. Recall that in this case the source \({\mathcal{S}}\) is a mixture of simple sources \({{\mathcal{S}}}_{i}\), characterized by a known probability distribution γ. Since the measurement device knows which source \({{\mathcal{S}}}_{i}\) is being used in a given round, it can produce different statistics Si for each source, and the overall observed statistics can be written as S = ∑iγiSi. Just like in the case of a single simple source, without loss of generality we assume that S = (α, β) satisfies α ≥ β. This assumption also implies (see the Supplementary Note 3) that in the optimal solution each Si = (αi, βi) satisfies αi ≥ βi, as well as the full set of conditions in Eq. (5). Thus, for each source \({{\mathcal{S}}}_{i}\) the produced statistics can be written as \({{\bf{S}}}_{i}={\lambda }_{i,Y}{S}_{Y}+{\lambda }_{i,N}{S}_{N}+{\lambda }_{i,H}{S}_{{H}_{i}}\), with SY = (1, 1), SN = (0, 0) being the constant strategies and \({{\bf{S}}}_{{H}_{i}}=({p}_{i},0)\) the honest strategy of the source \({{\mathcal{S}}}_{i}\). Since each source \({{\mathcal{S}}}_{i}\) produces entropy according to \({g}_{i}:= \max ({p}_{i},1-{p}_{i})\) and contributes to the overall guessing probability g* by \({g}_{i}^{* }={\lambda }_{i,Y}+{\lambda }_{i,N}+{\lambda }_{i,H}\cdot {g}_{i}\) weighted by γi, we have
Hence, the bound to the adversary’s guessing probability is given by the solution to the following linear program:
In order to formulate the solution to this optimization problem, let us introduce some notation. We start by dividing the set of all entropy sources \({\mathcal{S}}\) into two sets, \({{\mathcal{S}}}_{+}\) and \({{\mathcal{S}}}_{-}\). The source \({{\mathcal{S}}}_{i}\) belongs to \({{\mathcal{S}}}_{+}\) if and only if \({p}_{i}>\frac{1}{2}\), otherwise it belongs to \({{\mathcal{S}}}_{-}\). Let us also define N+ as the number of sources in the set \({{\mathcal{S}}}_{+}\) (including the possibility that N+ represents ∞). We will use positive integers i ≥1 to label the elements of \({{\mathcal{S}}}_{+}\), and negative integers i ≤ − 1 to label the elements of \({{\mathcal{S}}}_{-}\). This allows us to define \({N}_{-}=-| {{\mathcal{S}}}_{-}|\), where \(| {{\mathcal{S}}}_{-}|\) is the cardinality of \({{\mathcal{S}}}_{-}\) (again, potentially infinite). Then, without loss of generality, we will use the ordering of the sources in the set \({\mathcal{S}}\) such that ∀i > j, pi ≥ pj. We use the convention that unless specified otherwise, ∑i denotes the sum over all sources from \({\mathcal{S}}\). Last but not least, note that we deliberately left out the index i = 0, as it is used in a formulation of the solution and its proof.
Using the above notation, the solution of the optimization problem presented in Eq. (8) reads (see section “Known distribution analysis” for proof):
Here, if \({\sum }_{i\in {{\mathcal{S}}}_{+}}{\gamma }_{i}{p}_{i}\le \alpha -\beta\), then N = 0 and \({p}_{N}=\frac{1}{2}\), and otherwise N is defined to be the largest natural number such that
Again, the guessing probability g* allows us to lower bound the min-entropy of the output string Y of length ∣Y∣ as \({H}_{\min }(Y| E)\ge -| Y| {\mathrm{log}\,}_{2}({g}^{* })\).
In the more general case, the probability distribution γ, which chooses the simple source \({{\mathcal{S}}}_{i}\) to use in a given round, is not fully characterized, but is constrained by a set of functions, {fj(γ) = cj}. Formally, all the arguments from the previous case remain the same, except now the optimization needs to be done over the parameters γi as well. The maximization task can be stated as follows:
Since the functions fj are in principle arbitrary, the constraints might not be linear anymore and thus it might not be possible to efficiently solve the problem, even numerically. However, if the functions fj are smooth, for every fixed distribution γ, we are able to optimize over the variables {λ} according to the previous section. Therefore we can use the solution in Eq. (9) as the objective function, and the optimization problem becomes
Note that this is still not an easy optimization problem, because even if the functions fj are smooth, a minor change in the distribution of γi might lead to a change in the starting point of the summation in Eq. (10), as N is implicitly dependent on γi via Eq. (10).
To address this problem, let us change the perspective on N. Instead of N being an implicitly defined value dependent on γ, we will interpret it as a free parameter. Additionally, it can be shown (see section “Known distribution analysis”) that the maximum is obtained when the condition in Eq. (10) for γ is satisfied with equality. In such a case the objective function can be written in a simpler form (see Eq. (55)) and the optimization problem becomes
Note that if we fix the value of N, this maximization problem becomes much easier, because the target function is linear in γ. This yields a simple algorithm to find the solution of Eq. (13). One can simply solve the problem for each possible N ∈ {1, …, N+}, and take the overall maximum over the solutions as the final outcome.
This algorithm of course involves a potentially infinite number of optimization problems to solve, but for simple (e.g. linear) constraint functions fj it can be shown that there is a threshold value \({N}_{\max }\), such that it is not possible to satisfy both the conditions given by fj and \(\mathop{\sum }\nolimits_{i = N}^{{N}_{+}}{\gamma }_{i}{p}_{i}=(\alpha -\beta )\), whenever \(N \, > \, {N}_{\max }\). Last but not least, note that if the functions fj are linear, for each fixed value of N the optimization problem described in Eq. (13) is a linear program and thus can be solved efficiently. Additionally, in Appendix 4.3 we show that in case of a single linear constraint function f, feasible values of N are constrained to a small finite interval, which renders the optimization efficient. The solution to this optimization problem again yields the probability g* of the adversary to guess the outcome of a single generating round, which is related to min-entropy of output string Y as \(H(Y| E)\ge -| Y| {\mathrm{log}\,}_{2}({g}^{* })\).
Example: A photon through a beam splitter
In this section we describe a simple optical setup for randomness generation and analyze it with the help of our framework. The entropy source \({\mathcal{S}}\) consists of a photon source \({\mathcal{P}}{\mathcal{S}}\) emitting photons through a beam splitter \({\mathcal{BS}}\) with reflection probability π. Transmitted photons are coupled to a photon detector \({\mathcal{D}}\) and their path can be blocked by a movable shutter \({\mathcal{A}}\), which can be reliably controlled via a binary variable x. Reflected photons are discarded (see Fig. 4). We use this physical setup to showcase the assumption flexibility our framework allows for. First of all, the model that describes the entropy source in this setup depends on the assumption we place on the photon source \({\mathcal{P}}{\mathcal{S}}\).
The photonic entropy source \({\mathcal{S}}\) (depicted by a dashed rectangle) consists of a photon source \({\mathcal{P}}{\mathcal{S}}\) coupled to a beam splitter \({\mathcal{BS}}\) with the probability of reflection π and the probability of transmission 1 − π. Transmitted photons are interpreted as a random signal emitted from the entropy source, while the reflected photons are discarded. In order to extract randomness from such a source, we use a mostly uncharacterized and untrusted measurement device and a trusted shutter controlled by a binary variable x. According to the assumptions we place on the photon source \({\mathcal{P}}{\mathcal{S}}\), this photonic setup is able to realize all three different general scenarios that we introduced in the section “General framework”.
Single photon. If the photon source \({\mathcal{P}}{\mathcal{S}}\) produces a single photon on demand, the entropy source \({\mathcal{S}}\) is a simple entropy source with the probability p = 1 − π of sending a signal.
Known photon distribution. If the photon source \({\mathcal{P}}{\mathcal{S}}\) produces i photons with known probability γi, the source \({\mathcal{S}}\) is a mixture of simple sources \({{\mathcal{S}}}_{i}\) with pi = 1 − πi and mixing probability γ = {γi}.
Known mean number of photons. If the photon source is characterized only by the mean photon number μ, the setup corresponds to a source \({\mathcal{S}}\) which is a mixture of simple sources \({{\mathcal{S}}}_{i}\) with pi = 1 − πi and the mixing probability γ is constrained by ∑iiγi = μ.
While the single-photon source case can be easily seen to be a simple source, the other two cases require further explanation. Assume that the source produces an n-photon event, where n ≥ 2. Since the number of photons transmitted through the beam splitter can vary between 0 and n, the information available to the (photon-counting) measurement device is more complex than just binary information about receiving the signal or not. The response function of the measurement device is therefore potentially more complex than the four deterministic functions described in Eq. (3). In fact, there are 2n+1 different deterministic response functions assigning click/no-click measurement device events to the number of transmitted photons. In Supplementary Note 4, we show that in spite of this exponential increase, for each n there are only four response functions that yield the optimal guessing probability for the adversary. The first two are "Never Click" and "Always Click", which are fully deterministic and do not depend on the number of received photons. The third response function is labeled "Click Honestly". Using this response function, the measurement device clicks when a positive number of photons arrive and does not click when no photons arrive. The last response function is called "Click Dishonestly", and the measurement device clicks only when no photons arrive. These are exactly the four strategies that characterize a simple entropy source, since the measurement device decides only on the binary information whether it received a signal (i.e. non-zero number of photons) or not. Therefore, known photon distribution case can be characterized as a mixed source with known mixing probability γ and the known mean number of photons case as a mixed source with mixing probability constrained by mean photon number μ.
Note that in the setup described above we do not assume anything about the coherence of the photon source \({\mathcal{P}}{\mathcal{S}}\). In fact, in order to be able to describe the strategies available to the measurement device as in the above paragraph, the setup needs to fulfill one out of two assumptions. Either \({\mathcal{P}}{\mathcal{S}}\) produces states which are diagonal in the Fock basis (e.g. thermal states), or the measurement device is measuring in the Fock basis. In both cases, the mapping to the abstract mixed entropy sources is straightforward. Assuming that the state is diagonal in the Fock basis implies that the whole setup can be implemented with the use of classical sources of light. On the other hand, the Fock basis measurement assumption is very well motivated from the practical point of view and it allows us some leeway in the description of the \({\mathcal{P}}{\mathcal{S}}\). Namely, we do not require the source to produce a specific photonic state; it can be characterized solely by a probability distribution γ or its mean.
Now we are ready to formulate the upper bounds on the guessing probability g* of a single generating round in case of the known photon distribution and known mean number of photons, which can be related to min-entropy of the output string Y of the RNG protocol as \({H}_{\min }(Y| E)\ge -| Y| {\mathrm{log}\,}_{2}({g}^{* })\).
Let us first deal with the case of known photon distribution. According to the solution of the general case in Eq. (9), if \(\mathop{\sum }\nolimits_{i = 1}^{\infty }{\gamma }_{i}(1-{\pi }^{i}) \, > \, \alpha -\beta\), we need to find N, that is, the largest natural number such that \(\mathop{\sum }\nolimits_{i = N}^{\infty }{\gamma }_{i}(1-{\pi }^{i})\ge \alpha -\beta\). In this case, the optimal guessing probability is
Otherwise, if \(\mathop{\sum }\nolimits_{i = 1}^{\infty }{\gamma }_{i}(1-{\pi }^{i})\le \alpha -\beta\), the optimal guessing probability is
Finally, in what follows we assume that the photon source is characterized only by its mean photon number μ. This assumption requires us to solve an optimization problem of the form as in Eq. (13), where now the condition f(γ) = cγ reads
and pi = 1 − πi.
In the section “Mean photon number analysis” we show that the solution to this optimization problem contains only three non-zero probabilities γi:
for each feasible value of N = i, i ∈ {1, …, N+}. After plugging these values of γ0, γN, γN+1 into the target function, we obtain the optimal guessing probability:
The overall solution of Eq. (13) is \({\max }_{N}\{{g}_{N}^{* }\}\) where the the maximization is done over all feasible values of N. In the section “Mean photon number analysis” we show that in general there is only a finite number of feasible values N, and therefore the maximum always exists. Although the number of these values can still be prohibitively large, in the analysis of the data obtained from the experiment we conducted (see the section “Experimental realization and results”), only a single feasible value of N was encountered, making the analysis very efficient.
Last, but not least, in order to emphasize the flexibility of our framework, we discuss possible modifications of the optical setup described above. Notice that two probability distributions are characterized in the above setup. The first one is the photon number probability distribution γ and the second one is the beam splitter reflection probability π, or, more generally, binary distributions with probability of success 1 − πi associated with each photon number. The difference between them is that in our setup, the randomness resulting from the beam splitter events is assumed to be private, unlike γ, which is available to the adversary. Essentially, our framework can be seen as a procedure to certify randomness originating from the trusted source (in this case the beam splitter) in a noisy setup, where the noise is only partially characterized.
One can, however, assume that the photon emission is also a private random event characterized by γ. This is natural if the photon source \({\mathcal{P}}{\mathcal{S}}\) is coherent for example, since in this case it is impossible for the adversary to know the photon number in a given round before the measurement. In such a case, both the entropy originating from the beam splitter and the entropy of the photon source can be combined into a simple source with the probability of signal \(p=1-\mathop{\sum }\nolimits_{i = 1}^{\infty }{\gamma }_{i}(1-{\pi }^{i})\). Or, even more interestingly, the beam splitter can be left out from the setup altogether and assuming Fock measurements, the setup can be analyzed as a simple source with signal probability 1 − γ0. Note that a similar experiment was studied in two recent works32,47, but was analyzed by different techniques.
Experimental realization and results
We experimentally implemented the optical random number generation setup described in section “Example: A photon through a beam-splitter”. In the experimental implementation (see Fig. 5), the photon source \({\mathcal{P}}{\mathcal{S}}\) is a source of weak coherent pulses, the shutter \({\mathcal{A}}(x)\) is implemented with an electro-optic intensity modulator (IM), and the detection \({\mathcal{D}}\) is performed by a single-photon detector (SNSPD) and a counting logic (time tagger) to extract the output bit string. The details of the experiment and post-processing are presented in the section “Experimental realization”.
The proposed protocols are tested in an optical setup where weak coherent pulses of 8 ns duration at 5 MHz are generated by driving a laser diode with a signal generator (Pulse Streamer), and attenuating its power to ~1 photon per pulse. The photons (represented by the solid red line) are incident on a fiber beam splitter (BS) that discards the reflected photons. The transmitted photons are fast-switched via a fiber electro-optic intensity modulator (IM) that is driven by the digital output of the pulse streamer which provides the uniform random seed. The pulses at the output of the shutter (composed of the IM) are sent to a superconducting nanowire single-photon detector (SNSPD). The counts of the detector and a clock signal from the pulse streamer are recorded with a counting logic (quTAG time tagger), which allows one to extract coincidences for each pulse and generate the bit string.
The results of the experiment are summarized in Table 1. We see that while the actual rates of randomness generation depend on the level of trust into different parts of the experimental setup, even in the most adversarial scenario one can achieve rates comparable to less secure settings.
Discussion
In this paper, we have presented a framework to design and analyze semi-device-independent RNGs. In contrast with previous approaches, our framework does not require any fixed assumptions to be made on the workings of an RNG, can be applied in a very broad family of physical implementations, and can cover very different levels of trust placed on different parts of the RNG. The centerpiece of our approach consists of a shutter that can trustfully block the transmitted signal. This, in connection with some limited trust in the source and/or measurement devices, proves to be enough to certify randomness.
During the certification protocol, sample data are collected in order to characterize the behavior of the measurement devices during both shutter settings (open or closed). These sample data are subsequently used to calculate the probability that the adversary, who is classically correlated with the measurement devices, is able to guess the outcome of the measurements with open shutter. This calculation involves solving a number of optimization problems expressed as linear programs. The exact formulation and number of these linear programs depends on the level of trust we place into the entropy source. Three different trust levels are possible: (i) a simple source emits a signal with probability p; or the entropy source is a mixture of multiple such simple sources governed by a probability distribution γ, which is either (ii) fully characterized or (iii) partially characterized. The main benefit of our framework is that all three characterizations can be used with the same physical setup and can be seen as different levels of trust placed onto the entropy source.
We showcase the applicability of the framework by implementing a RNG using a weak coherent optical source and a beam splitter. This implementation allowed us to demonstrate an important property of our framework: flexibility in the assumptions made about specific parts of the device. We have data analyzed from a single experiment under three very different sets of assumptions on the source—true single photons, coherent states, and an unknown source characterized only by its average photon production rate. In all cases, we were able to extract high-quality random strings, but with significantly different rates. This is natural, as stronger assumptions on the source allow for better extraction rates at the cost of giving the adversary more possibilities to attack.
Our approach provides significant practical benefits for secure randomness generation. Using the same simple device, a user can make their own choice of the level of secrecy or production rate, just by choosing the appropriate post-processing strategy. Very interestingly, our results show that even for the most adversarial assumption on the source, i.e. trust only in the mean number of photons, rates of the same order of magnitude were achieved as with the rather strong assumption of a coherent source. The average number of photons produced by a source is testable in principle via its energy consumption, which provides a possible means to further strengthen the security of our framework. Our results pave the way towards practical and experimentally feasible semi-device-independent RNGs, which play a crucial role in the ongoing quantum information revolution.
Methods
Experimental realization
In this section we provide details for the experimental realization and post-processing. Recall that the experiment consists of a source of weak coherent pulses, electro-optic IM implementing the shutter, a single-photon detector (SNSPD) and a counting logic (see Fig. 5). In real-world network applications, clock synchronization of optical pulse trains and detectors would be straightforward. However, for the purposes of this demonstration, all electrical signals are generated by a Swabian instruments Pulse-Streamer 8/2. We drive a laser diode with 0.8 V analog pulses of 8 ns duration (limited by analog output bandwidth) at 5 MHz (limited by single-photon detection amplifier deadtime ~150 ns), attenuate the weak coherent pulses to ~1 photon per pulse, and are then incident through a fiber beam splitter with power transmission 0.5118 ± 0.0005. These pulses are fast-switched via a fiber lithium niobite electro-optic IM (EOSpace, Model AZ-0S5-10-PSA-SFA) driven by a digital output of the signal generator, which with probability q = 8/100 blocks the channel (i.e. TEST rounds with x = 1). A typical extinction ratio of 1/100 is observed and a slight thermal drift is calibrated for each 100,000 rounds of the experiment. The pulses are then routed to the detectors through a channel with lumped efficiency from switch to detectors of 0.9339 ± 0.00005. Detection is made by superconducting nanowire single-photon detectors with efficiency 0.9231 ± 0.0007. A QuTools QuTAG counting logic records time-tags from the detectors along with a clock signal from the signal generator, allowing coincidences for each pulse to be extracted using a 10 ns coincidence window, and the output bit string to be recovered.
Once the data are collected, we begin the post-processing on batches of size N = 100, 000. With probability 8/92 we randomly select some of the non-blocked rounds to be TEST rounds with x = 0 (such that the expected number of test rounds with x = 0 is the same as the expected number of test rounds with x = 1). Given the large number of total test rounds (~16, 000), we use the Chernoff–Hoeffding bound to calculate the test statistic \(\hat{S}\), see Eq. (1) with sampling error ε = 10−6. In particular, we give a conservative estimate of S and the probability that either α or β falls outside of the desired interval is 2ε (see Supplementary Note 1 for details). For each batch, we used \(\hat{S}\) to calculate an upper bound on the adversary’s guessing probability g*. We have performed separate estimations for the three scenarios; (i) a single-photon source, (ii) the photon number distributed according to a Poisson probability distribution with mean μ, and (iii) the photon number being μ on average. For cases (ii) and (iii), we used μ = 1.06 since it is an upper bound on the observed average photon number per pulse, and that yields the least amount of entropy.
For simplicity, the length of the output string Y was chopped to a constant size of ∣Y∣ = 83,000 per batch, which leads to a final lower bound on the entropy of the string Y, expressed as \({H}_{\min }(Y| E)\ge -83,000 \cdot {\mathrm{log}\,}_{2}({g}^{* })\). To extract the final random string Z from Y (see the protocol description in Fig. 3), a hashing function, in our case a random binary Toeplitz matrix, has been applied to Y. To keep the discussion clear, we shall focus on case (ii) of a known (Poisson) distribution. The remaining cases follow an analogous post-processing strategy. In order to reduce the amount of randomness needed, we only generated one Toeplitz matrix and re-used it for every batch. Indeed, the Leftover Hashing Lemma guarantees that when using a Toeplitz matrix of dimensions \(| Y| \times (-{\mathrm{log}\,}_{2}({g}^{* })+2\mathrm{log}\,\delta )\), the output string Z is at most δ-far in ℓ1-distance from being uniformly distributed48. We take δ = 2−100 ≈ 10−31, which implies that we can re-use the Toeplitz matrix ~1020 times and still maintain a ℓ1-distance from the uniform distribution of no more than 10−10.
Note that the estimates of entropy \({H}_{\min }(Y| E)\ge -83,000 \cdot {\mathrm{log}\,}_{2}({g}^{* })\) differ for different batches of data. This is because the entropy per bit \(-{\mathrm{log}\,}_{2}({g}^{* })\) is estimated separately for each batch, with different results. The experimental distribution of estimated min-entropies (per bit) can be seen in Fig. 6. However, in order to re-apply the same hash function to each batch, it is important to guarantee that all batches have their min-entropy lower bounded by the same value—this is because the output length of the hash function must be smaller than the total min-entropy of the input. If all batches were used, the total min-entropy in each string would have to be bounded by the min-entropy of the worst batch which can be rather low. Therefore it is advantageous to discard a (small) number of batches with low certified min-entropy, which increases the amount of min-entropy we can extract per batch, but decreases the number of batches. One can optimize the cutoff threshold min-entropy for each case in order to extract the maximum amount of randomness.
In the known photon number distribution scenario (ii), we chose a cutoff of 0.167 bits of entropy per physical bit, i.e., any batch whose estimated min-entropy was lower was simply discarded. Therefore, the Toeplitz matrix generated was of size 83,000 × 13,661. For demonstration purposes, we collected data from 1000 batches with each batch on average having an estimated 0.185 bits of entropy per physical bit. In all, 97.5% of the batches were calculated to be above the set threshold, resulting in a total of 13.2 Mbits of extracted randomness. All results are summarized in Table 1.
Finally, we carried out the industry-standard NIST randomness tests using an improved implementation presented in ref. 49. As expected, the processed output performed well in all of these tests.
Known distribution analysis
Here we derive the results presented in the section “Entropy estimation”. We need to find the solution to the following optimization problem:
Recall that we use the following notation: We start by dividing the set of all sources of entropy \({\mathcal{S}}\) into two sets, \({{\mathcal{S}}}_{+}\) and \({{\mathcal{S}}}_{-}\). The source \({{\mathcal{S}}}_{i}\) belongs to \({{\mathcal{S}}}_{+}\) if and only if \({p}_{i}>\frac{1}{2}\), otherwise it belongs to \({{\mathcal{S}}}_{-}\). We define N+ as the number of sources in the set \({{\mathcal{S}}}_{+}\) (including the possibility that N+ represents ∞). We use positive integers i ≥ 1 for indexing the elements of \({{\mathcal{S}}}_{+}\), and negative integers i ≤ − 1 for indexing the elements of \({{\mathcal{S}}}_{-}\). This allows us to define \({N}_{-}=-| {{\mathcal{S}}}_{-}|\), where \(| {{\mathcal{S}}}_{-}|\) is the cardinality of \({{\mathcal{S}}}_{-}\) (again, potentially infinite). Then, without loss of generality, we order the sources in the set \({\mathcal{S}}\) such that
We use a convention that unless specified otherwise, ∑i denotes the sum through all sources from \({\mathcal{S}}\). Last but not least, note that we deliberately left out the index i = 0, as it is used later in the proof.
Also recall that for the measured parameters to be physical, we require
Substituting the equality constrains of Eq. (21) together with Eq. (22), we can further simplify the optimization problem to
It is now easy to see that in order to find the maximum of Eq. (24), we need to set as many λi,H = 1 as possible, starting with ones with the highest parameter pi. Of course this needs to be done with the constraints presented in Eqs. (25)– (28) in mind.
Let us start with the simpler of two possibilities. If
then we can set λi,H = 1 for all i ∈ \({{\mathcal{S}}}_{+}\) (and therefore λi,N = λi,Y = 0 for all i ∈ \({{\mathcal{S}}}_{+}\)). It remains to show that we can find values for the other λ variables such that the solution fulfills all the constraints. Let us first treat the case of both sets \({{\mathcal{S}}}_{-}\) and \({{\mathcal{S}}}_{+}\) being non-empty. The other two special cases will be treated separately later. First, let us set for \(\forall i\in {{\mathcal{S}}}_{-}\)
Let us now show that this is indeed a valid assignment, i.e. 0 ≤ Δ ≤ 1. Although the positivity of Δ follows trivially from Eq. (29), the second inequality is a little more involved. In order to show that Δ ≤ 1, let us note that since Eq. (23) holds for each αi, βi, and pi (this is a necessary condition for the statistics produced by \({{\mathcal{S}}}_{i}\) to be physical), due to its linearity it also holds for α = ∑iαi, β = ∑iβi and p = ∑iγipi. Therefore, from Eq. (23) we get
which proves Δ ≤ 1. Using the values λi,H = 1 for i ∈ S+ and λi,H = Δ for i ∈ S−, it is straightforward to verify that the constraint in Eq. (25) is satisfied.
In order to satisfy Eq. (26) we need to show that
Note that because of Eq. (27), we have that \(\forall i\in {{\mathcal{S}}}_{-},(1-{{\Delta }})={\lambda }_{i,Y}+{\lambda }_{i,N}\). Therefore,
If \((1-{{\Delta }}){\sum }_{i\in {{\mathcal{S}}}_{-}}{\gamma }_{i}\ge \beta\), we can clearly find positive values of λi,Y and λi,N, such that \({\sum }_{i\in {{\mathcal{S}}}_{-}}{\gamma }_{i}{\lambda }_{i,Y}=\beta\) and \({\sum }_{i\in {{\mathcal{S}}}_{-}}{\gamma }_{i}{\lambda }_{i,N}=(1-{{\Delta }}){\sum }_{i\in {{\mathcal{S}}}_{-}}{\gamma }_{i}-\beta\) is positive; thus, all the constraints of our optimization problem are satisfied.
The first step to prove Eq. (32) is to show that
We have that
where \({p}_{-}=\frac{{\sum }_{i\in {{\mathcal{S}}}_{-}}{\gamma }_{i}{p}_{i}}{{\sum }_{i\in {{\mathcal{S}}}_{-}}{\gamma }_{i}}\), and \({p}_{+}=\frac{{\sum }_{i\in {{\mathcal{S}}}_{+}}{\gamma }_{i}{p}_{i}}{{\sum }_{i\in {{\mathcal{S}}}_{+}}{\gamma }_{i}}\). Notice that p is a convex combination of p− and p+ with p−≤p+, and therefore p− ≤ p ≤ p+. Then, it also holds that \({\sum }_{i\in {{\mathcal{S}}}_{-}}{\gamma }_{i}{p}_{i}={p}_{-}{\sum }_{i\in {{\mathcal{S}}}_{-}}{\gamma }_{i}\le p{\sum }_{i\in {{\mathcal{S}}}_{-}}{\gamma }_{i}\).
Now using Eq. (34) and (Eq. (23)) again, we get
Since \({{\mathcal{S}}}_{-}\) is non-empty, we have that \({\sum }_{i\in {{\mathcal{S}}}_{-}}{\gamma }_{i}{p}_{i} \, \ne \, 0\), which leads to
that is, Eq. (32) holds, which proves that it is possible to satisfy all conditions presented in Eqs. (25)–(28) while maximizing the guessing probability by a suitable choice of λ’s. Setting \({\lambda }_{i,H}=1,\forall i\in {{\mathcal{S}}}_{+}\) yields
Let us now return to the two special cases. First, assume that \({{\mathcal{S}}}_{+}\) is empty. In such a case Eq. (35) is not well defined (because in the definition of p+ we divide by 0). However, the goal of Eq. (35) is to prove Eq. (34), which in this case holds trivially, since \(p={\sum }_{i\in {{\mathcal{S}}}_{-}}{\gamma }_{i}{p}_{i}\) and \({\sum }_{i\in {{\mathcal{S}}}_{-}}{\gamma }_{i}=1\).
It remains to solve the case of \({{\mathcal{S}}}_{-}\) being empty. Then from Eq. (29) we have that p ≤ α − β. Simultaneously, from Eq. (31) we have that p ≥ α − β. Therefore, α − β = p, and in order to fulfill Eq. (25), we require λi,H = 1 for all i. Also, now we can use the identity α = p + β and Eq. (23) again to d + β ≤ p + β(1 − p), which allows a solution only for β = 0 (otherwise the observed point (α, β) is non-physical). With β = 0 it is easy to see that other constrains are satisfied as well and the maximum is equal to p. Note that this is in some sense an extreme case, since the observed point such as this can be obtained only with perfectly error-less devices in the limit of the infinite number of rounds.
Now we deal with the more interesting case of
In this case we cannot set λi,H = 1 for \(\forall i\in {{\mathcal{S}}}_{+}\), as this would violate condition of Eq. (25). If we are only concerned with the variables λi,H, it is clear that in the optimal case we could set
as sources in \({{\mathcal{S}}}_{-}\) does not contribute to the objective function in Eq. (24). Using this we can rewrite Eq. (24) into
Next—still only being concerned with λi,H—we argue that Eq. (41) is maximized by choosing λi,H = 1 for the largest pi (large i) and zero elsewhere, except for a single element with 0 < λi,H < 1. This can be seen from the fact that keeping the sum of ∑iγiλi,H ⋅ pi constant while minimizing ∑iγiλi,H (as it enters the maximization function with a negative sign) is the same as maximizing ∑iγiλi,H ⋅ pi while keeping ∑iγiλi,H constant, which is clearly achieved by choosing γiλi,H large for pi large and vice versa. In the following, we show that it is indeed possible to choose the values of λi,H according to this procedure, and satisfy all the constraints Eqs. (25)– (28), by providing an explicit assignment of all the λ variables in Eqs. (47)– (49).
To obtain the explicit assignment, let us first define the natural number N in the following implicit way
In case we have that \(\mathop{\sum }\nolimits_{i = N}^{{N}_{+}}{\gamma }_{i}{p}_{i}>\alpha -\beta\), we perform the following trick: we formally divide the box labeled N into two boxes, labeled N − 1 and N, both having the same pN. The new parameters \({\widetilde{\gamma }}_{N}\) and \({\widetilde{\gamma }}_{N-1}\) will be defined in the following way:
Note that both values are well defined, because \({\gamma }_{N}\in {{\mathcal{S}}}_{+}\), and thus \({p}_{N} \, > \, \frac{1}{2}\). All the boxes labeled by i < N are re-labeled i → i − 1, utilizing the so-far unused index i = 0. This new set of boxes will have the same properties as the old one, it is a mere change of mathematical description. For this new set it holds that
Now we are ready to state the values of the parameters λ that maximize g* in the following way:
with all other parameters given by the condition for their sum. In the above formulas, we use the definition
Note that this is well-defined, as \(\mathop{\sum }\nolimits_{i = {N}_{-}}^{N-1}{\widetilde{\gamma }}_{i}=0\) would imply that \({{\mathcal{S}}}_{-}\) is empty, as well as N = 1 and \(\widetilde{{\gamma }_{0}}=0\) (i.e. the first non-zero γi is γN, but we can always start the indexing from the first non-zero element, that is, γN = γ1). This in turn implies that \({\gamma }_{1}=\widetilde{{\gamma }_{1}}\) and Eq. (46) becomes \({\sum }_{i\in {{\mathcal{S}}}_{+}}{\gamma }_{i}{p}_{i}=\alpha -\beta\), which contradicts Eq. (39). Now the maximum guessing probability is
The only thing that needs to be shown is that ω ≤ 1, as its positivity is obvious from its definition presented in Eq. (50). This comes from the facts that N ≥ 1, \(p\mathop{\sum }\nolimits_{i = N}^{{N}_{+}}{\widetilde{\gamma }}_{i}\le \mathop{\sum }\nolimits_{i = N}^{{N}_{+}}{\widetilde{\gamma }}_{i}{p}_{i}\) (the argument is analogous to Eq. (34)) in combination with Eq. (23):
from which we have that
and therefore ω ≤ 1.
It remains to join Eqs. (38) and (51) into a single formula. It suffices to plug Eq. (44) into Eq. (51) and obtain
Note that if \({\sum }_{i\in {{\mathcal{S}}}_{+}}{\gamma }_{i}{p}_{i} \, > \, \alpha -\beta\), one needs to calculate N from Eqs. (42) and (43). In case \({\sum }_{i\in {{\mathcal{S}}}_{+}}{\gamma }_{i}{p}_{i}\le \alpha -\beta\), we simply set N = 0 and \({p}_{N}=\frac{1}{2}\) and obtain the solution presented in Eq. (38).
Last but not least, using the modified parameters \(\widetilde{{\gamma }_{i}}\), the solution can take the following simple form obtained by plugging Eq. (46) into Eq. (51):
with N explicitly defined by (46). This form is particularly useful in the derivation of the case with mixed sources with partially characterized γ, where we can show that in the optimal solution presented in Eq. (42) holds with equality and therefore \(\forall i,\,{\widetilde{\gamma }}_{i}={\gamma }_{i}\).
Mean photon number analysis
Here we derive the results presented in the last part of section “Example: a photon through a beam-splitter”. In the section “Entropy estimation” we have shown that the optimization problem associated with the scenario with partial information about the mixed entropy source can be stated as
We have also argued that the solution to this problem can be obtained by finding the maximum for each fixed value of N in the range {1, …, N+}, and the overall solution is the largest of these maxima. In order to proceed with the analytical solution of this problem, let us restrict to a single linear constraint function, cγ = ∑iaiγi, and reformulate the optimization problem using the Lagrange function for each fixed N,
with the half-plane conditions γi ≥ 0 for all i.
In order to find the maximum, we need to examine partial differentiation of Eq. (57) over all variables γi, τf, τN, τnorm. While the partial derivatives over τf, τN, τnorm are the required equality constraints of Eq. (56) for γ, f, and N, the partial derivatives over all γi have the following form:
Now we need to examine all the stationary points of Eq. (57). We will argue that on the stationary points, for each variable γi, the corresponding partial derivative is either equal to 0, or γi = 0 (so that the variable γi is actually on the boundary of its allowed interval). We first divide the {γi} into two sets: \({\partial }_{{\gamma }_{i}}{{\mathcal{L}}}_{N}=-{\tau }_{\mathrm {norm}}-{\tau }_{f}{a}_{i}\quad \,\text{if}\quad i<N\) (note that this set cannot contain all the variables, because it is impossible to find values of τ{norm, f, N} for which all partial derivatives presented in Eqs. (58) and (59) vanish), and Γb = {γi}⧹Γ0. Since by construction the variables in Γb have non-zero derivatives, by the extreme value theorem the maximum of Eq. (57) must be attained when these variables are on their boundary. This is when γi = 0, since all other constraints are taken care of with the derivatives \({\partial }_{\{{\tau }_{f},{\tau }_{N},{\tau }_{norm}\}}{{\mathcal{L}}}_{N}=0\). A maximum may therefore be found if for all γi ∈ Γb we have \({\partial }_{{\gamma }_{i}}{{\mathcal{L}}}_{N} \, < \, 0\) (i.e. the value of \({\mathcal{L}}\) is increasing towards the boundary of all γi ∈ Γb), and since \({{\mathcal{L}}}_{N}\) is linear in all γi this maximum would be a global one. The remaining issue is therefore to find the optimal set Γ0 for which the derivatives presented in Eqs. (58) and (59) vanish. We proceed to construct this optimal set by showing how alternative choices cannot be the optimal solution.
Further analysis now depends on the exact values of ai and pi. In the section “Experimental realization and results” we have shown that in our experiment, if we characterize the photon source with the mean number of photons only, the constraint function is μ = ∑iiγi. Therefore, we will focus on the case where {ai} is a non-negative, unbounded, and strictly increasing sequence, with our prime example being {ai = i}. Likewise {pi = 1 − πi} in our experimental section, so we require {pi} to be a non-negative strictly increasing sequence such that {pi/ai} is strictly decreasing. Since the sequence {ai} is unbounded, we need to have τf ≥ 0, otherwise both Eqs. (58) and (59) will become positive for some (large enough) value of i. One (trivial) solution is choosing τf = 0, which is only possible for τnorm ≥ 0 by Eq. (58). This would allow to have all γi for i < N potentially non-zero. But then Eq. (59) will become
If τN ≥ 2, then this equation is always negative, leading to γi = 0 for i ≥ N, which would violate the last constraint presented in Eq. (56). For smaller τN, assume \({\partial }_{{\gamma }_{i}}{{\mathcal{L}}}_{N}=0\) for some i. Then, since the {pi} are increasing, \({\partial }_{{\gamma }_{i+1}}{{\mathcal{L}}}_{N} \, > \, 0\). As we have argued above, that would not lead to a maximum, since γi ≥ 0, and the derivatives of the Γb variables should be negative. Therefore we conclude that τf > 0.
For i < N, Eq. (58) now reads τnorm = −τfai. Since all of the {ai} are different, this equation can only be satisfied for a single variable γi. Notice however that Eq. (58) is a decreasing function in i; therefore, in order to guarantee that all the non-zero partial derivatives \({\partial }_{{\gamma }_{i}}{{\mathcal{L}}}_{N}\) are negative, we must have τnorm = −a0τf. That is, γ0 ∈ Γ0 and γ0<i<N ∈ Γb, i.e. γi = 0 for 0 < i < N. Eq. (59) now reads:
Since we have two free parameters available (τf and τN), it is possible to achieve \({\partial }_{{\gamma }_{i}}{{\mathcal{L}}}_{N}=0\) for at most two different values of i. Notice that (ai − a0) > 0, and we have shown that τf > 0. Therefore (2 − τN) must be positive, or else all \({\partial }_{{\gamma }_{i\ge N}}{{\mathcal{L}}}_{N} \, < \, 0\). Furthermore, since {pi/ai} is strictly decreasing, then Eq. (61) is also strictly decreasing. Therefore, in order to satisfy Eq. (59) for two different γi and to have all the rest of the partial derivatives negative, it must hold that \({\partial }_{{\gamma }_{i = N}}{{\mathcal{L}}}_{N}=0\) and \({\partial }_{{\gamma }_{i = N}}{{\mathcal{L}}}_{N+1}=0\). The conditions cannot be solved for the rest, so γi>N+1 = 0.
Now, we know that Γ0 = {γ0, γN, γN+1} are the only non-zero variables. We can therefore use the original problem constraints to solve for the unknowns. Namely:
This linear system of equations is then solved. The only difficulty remaining is that, depending on the values of {ai} and {pi}, it is not at all clear that the solutions satisfy γi ≥ 0 for a given N. In fact, we will show that in our prime example, {ai = i}, cγ = μ, and {pi = 1 − πi}, only a finite number of N can satisfy the positivity constraints for γ. We therefore switch to this concrete example to finish this section. The solution to the linear system of equations reads
Note that γN is approaching infinity with increasing N. This means that only a finite number of values N need to be tested, as for sufficiently large N we have γN > 1 and the positivity constraints for γN+1 and γ0 cannot be satisfied. Therefore, the final guessing probability will be the maximum from the finite number of guessing probabilities of the form:
Data availability
Data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.
References
Somlo, P. I. Zener-diode noise generators. Electron. Lett. 11, 290 (1975).
Stipěvić, M. Fast nondeterministic random bit generator based on weakly correlated physical events. Rev. Sci. Instrum. 75, 4442–4449 (2004).
Herrero-Collantes, M. & Garcia-Escartin, J. C. Quantum random number generators. Rev. Mod. Phys. 89, 015004 (2017).
Mrazek, V., Sys, M., Vasicek, Z., Sekanina, L. & Matyas V. Evolving boolean functions for fast and efficient randomness testing. In Proc. of GECCO’18, 1302–1309 (2018).
Truong, N. D., Haw, J. Y., Assad, S. M., Lam, P. K. & Kavehei, O. Machine learning cryptanalysis of a quantum random number generator. IEEE Trans. Inf. Forensics Security 14, 403–414 (2019).
Checkoway, S. et al. On the practical exploitability of dual EC in TLS implementations. In Proc. USENIX Security 14, 319–335 (2014).
Heninger, N., Durumeric, Z., Wustrow, E. & Halderman, J. A. Minding your ps and qs: detection of widespread weak keys in network devices. In Proc. USENIX Security 12, 35–35 (2012).
Lenstra, A. K. et al. Ron was wrong, Whit is right. IACR Cryptology ePrint Archive, Report 2012/064 (2012).
Barker, E. & Kelsey, J. Recommendation for the entropy sources used for random bit generation. Special Publication (NIST SP) 800-90B (National Institute of Standards and Technology, 2012).
Pivoluska, M. & Plesch, M. Device independent random number generation. Acta Phys. Slovaca 64, 600 – 663 (2014).
Colbeck, R. Quantum And Relativistic Protocols For Secure Multi-Party Computation. PhD thesis, Trinity College, University of Cambridge (2009).
Pironio, S. et al. Random numbers certified by bell’s theorem. Nature 464, 1021–1024 (2010).
Fehr, S., Gelles, R. & Schaffner, C. Security and composability of randomness expansion from Bell inequalities. Phys. Rev. A 87, 012335 (2013).
Pironio, S. & Massar, S. Security of practical private randomness generation. Phys. Rev. A 87, 012336 (2013).
Bouda, J., Pawłowski, M., Pivoluska, M. & Plesch, M. Device-independent randomness extraction from an arbitrarily weak min-entropy source. Phys. Rev. A 90, 032313 (2014).
Plesch, M. & Pivoluska, M. Device-independent randomness amplification with a single device. Phys. Lett. A 378, 2938–2944 (2014).
Vazirani, U. & Vidick, T. Certifiable quantum dice: or, true random number generation secure against quantum adversaries. In Proc. STOC’12, 61–76 (2012).
Miller, C. A. & Shi, Y. Universal security for randomness expansion from the spot-checking protocol. SIAM J. Comput. 46, 1304–1335 (2017).
Bierhorst, P. et al. Experimentally generated randomness certified by the impossibility of superluminal signals. Nature 556, 223–226 (2018).
Liu, Y. et al. Device-independent quantum random-number generation. Nature 562, 548–551 (2018).
Brown, P. J., Ragy, S. & Colbeck, R. A framework for quantum-secure device-independent randomness expansion. IEEE Trans. Inf. Theory 66, 2964–2987 (2020).
Bell, J. S. On the Einstein Podolsky Rosen paradox. Physics 1, 195–200 (1964).
Brunner, N., Cavalcanti, D., Pironio, S., Scarani, V. & Wehner, S. Bell nonlocality. Rev. Mod. Phys. 86, 419–478 (2014).
Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Shalm, L. K. et al. Strong loophole-free test of local realism. Phys. Rev. Lett. 115, 250402 (2015).
Giustina, M. et al. Significant-loophole-free test of Bell’s theorem with entangled photons. Phys. Rev. Lett. 115, 250401 (2015).
Nie, Y.-Q. et al. Experimental measurement-device-independent quantum random-number generation. Phys. Rev. A 94, 060301 (2016).
Cao, Z., Zhou, H. & Ma, X. Loss-tolerant measurement-device-independent quantum random number generation. N. J. Phys. 17, 125011 (2015).
Lunghi, T. et al. Self-testing quantum random number generator. Phys. Rev. Lett. 114, 150501 (2015).
Bischof, F., Kampermann, H. & Bruß, D. Measurement-device-independent randomness generation with arbitrary quantum states. Phys. Rev. A 95, 062305 (2017).
Šupić, I., Skrzypczyk, P. & Cavalcanti, D. Measurement-device-independent entanglement and randomness estimation in quantum networks. Phys. Rev. A 95, 042340 (2017).
Brask, J. B. et al. Megahertz-rate semi-device-independent quantum random number generators based on unambiguous state discrimination. Phys. Rev. Appl. 7, 054018 (2017).
Passaro, E., Cavalcanti, D., Skrzypczyk, P. & Acín, A. Optimal randomness certification in the quantum steering and prepare-and-measure scenarios. N. J. Phys. 17, 113010 (2015).
Rusca, D. et al. Self-testing quantum random-number generator based on an energy bound. Phys. Rev. A 100, 062338 (2019).
Van Himbeeck, T. & Pironio, S. Correlations and randomness generation based on energy constraints. Preprint at https://arxiv.org/abs/1905.09117 (2019).
Xu, F., Shapiro, J. H. & Wong, F. N. C. Experimental fast quantum random number generation using high-dimensional entanglement with entropy monitoring. Optica 3, 1266–1269 (2016).
Cao, Z., Zhou, H., Yuan, X. & Ma, X. Source-independent quantum random number generation. Phys. Rev. X 6, 011020 (2016).
Avesani, M., Marangon, D. G., Vallone, G. & Villoresi, P. Source-device-independent heterodyne-based quantum random number generator at 17 gbps. Nat. Commun. 9, 5365 (2018).
Drahi, D. et al. Certified quantum random numbers from untrusted light. Phys. Rev. X 10, 041048 (2020).
ID Quantique What is the Q in QRNG? Random Number Generation White Paper (ID Quantique SA, 2020).
Kelsey, J., Brandão, L. T., Peralta, R. & Booth, H. A reference for randomness beacons: format and protocol version 2. NISTIR 8213 (National Institute of Standards and Technology, 2019).
McKague, M. Device independent quantum key distribution secure against coherent attacks with memoryless measurement devices. N. J. Phys. 11, 103037 (2009).
Scheidl, T. et al. Violation of local realism with freedom of choice. Proc. Natl Acad. Sci. USA 107, 19708–19713 (2010).
Dupuis, F. & Fawzi, O. Entropy accumulation with improved second-order term. IEEE Trans. Inf. Theory 65, 7596–7612 (2019).
Zhang, Y., Knill, E. & Bierhorst, P. Certifying quantum randomness by probability estimation. Phys. Rev. A 98, 040304 (2018).
Shaltiel, R. In Automata, Languages and Programming (eds. Aceto, L. et al.) 21–41 (Springer, 2011).
Van Himbeeck, T., Woodhead, E., Cerf, N. J., García-Patrón, R. & Pironio, S. Semi-device-independent framework based on natural physical assumptions. Quantum 1, 33 (2017).
Ma, X. et al. Postprocessing for quantum random-number generators: entropy evaluation and randomness extraction. Phys. Rev. A 87, 062327 (2013).
M, S. ýs, Ríha, Z. & Matyas, V. Algorithm 970: optimizing the nist statistical test suite and the Berlekamp-Massey algorithm. ACM Trans. Math. Softw. 43, 1–11 (2016).
Acknowledgements
We would like to thank Robert Fickler for discussions about the experimental realization and Marek Sýs for running the NIST randomness test on the data we acquired in the experiment. We would like to thank Ugo Zanforlin, Gerald Buller, Daniel White, and Cristian Bonato for their help with the experiment. M. Pivoluska, M. Plesch, and M.M. acknowledge Czech-Austrian project MultiQUEST (I3053-N27 and GF17-33780L). M. Pivoluska and M. Plesch additionally acknowledge the support of VEGA project 2/0136/19. M.F. acknowledges support from the Polish NCN grant Sonata UMO-2014/14/E/ST2/00020, the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program ERC AdG CERQUTE (grant agreement No 834266), the State Research Agency (AEI) TRANQI (PID2019-106888GB-I00/10.13039/501100011033), the Government of Spain (FIS2020-TRANQI; Severo Ochoa CEX2019-000910-S), Fundació Cellex, Fundació Mir-Puig, and Generalitat de Catalunya (CERCA, AGAUR). M.M., W.M., N.H.V., and C.F. acknowledge support from the QuantERA ERA-NET Co-fund (FWF Project I3773-N36) and the UK Engineering and Physical Sciences Research Council (EPSRC) (EP/P024114/1).
Author information
Authors and Affiliations
Contributions
E.A.A., M.F., M. Pivoluska, and M. Plesch formulated the initial idea; E.A.A., M.F., M. Pivoluska, M. Plesch, and N.R. developed the theory; C.F., N.H.V., W.M.C., and M.M. performed the experiment, E.A.A., M. Pivoluska, and M. Plesch analyzed data. All co-authors contributed to the preparation of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pivoluska, M., Plesch, M., Farkas, M. et al. Semi-device-independent random number generation with flexible assumptions. npj Quantum Inf 7, 50 (2021). https://doi.org/10.1038/s41534-021-00387-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-021-00387-1