Abstract
Quantum systems are promising candidates for sensing of weak signals as they can be highly sensitive to external perturbations, thus providing excellent performance when estimating parameters of external fields. However, when trying to detect weak signals that are hidden by background noise, the signal-to-noise ratio is a more relevant metric than raw sensitivity. We identify, under modest assumptions about the statistical properties of the signal and noise, the optimal quantum control to detect an external signal in the presence of background noise using a quantum sensor. Interestingly, for white background noise, the optimal solution is the simple and well-known spin-locking control scheme. Using numerical techniques, we further generalize these results to the case of background noise with a Lorentzian spectrum. We show that for increasing correlation time, pulse based sequences, such as CPMG, are also close to the optimal control for detecting the signal, with the crossover dependent on the signal frequency. These results show that an optimal detection scheme can be easily implemented in near-term quantum sensors without the need for complicated pulse shaping.
Similar content being viewed by others
Introduction
Quantum systems are extremely sensitive to the environment which makes them an ideal candidate as a sensor of weak external fields. Many promising candidates have been put forward as quantum sensors, such as defect centers in diamond or silicon carbide, SQUID-based sensors, atomic sensors, along with many others (see, e.g., ref. 1). A variety of sensing techniques have been developed which can be used to detect either the magnitude or the phase of the signal. In Ramsey interferometry2, a qubit is prepared in the equal superposition state and its oscillation frequency is sensitive to the splitting of the qubit, which depends on the external field to be sensed. This allows for the estimation of the magnetic field amplitude with sensitivity limited by the free-evolution dephasing time of the qubit, which can be enhanced through optimal control methods3. Similarly, detecting AC signals is possible with Ramsey and echo sequences, such as Carr–Purcell (CP)4 and dynamical decoupling5,6 sequences. These sequences can also be used for estimating frequencies of the signal7,8. For amplitude sensing, the typical figure of merit one considers when measuring the performance of a quantum sensor is the sensitivity, which characterizes the smallest external field that can be measured in a given amount of time1. This can be formulated in terms of the quantum Cramér–Rao bound, and has associated applications and limiting cases9,10,11,12,13.
While sensitivity is important for parameter estimation, it is less relevant for the signal detection. In this manuscript, we reformulate the quantum sensing problem in a manner consistent with the following decision theoretic question: How does one optimally detect the presence of a stochastic signal with a known spectrum in the presence of background noise? The detection of signals in the presence of noise has been extensively studied in the field of classical decision theory14. A highly relevant applied formulation determines how to optimally choose whether a time-varying signal was signal plus noise or noise only, which has broad applicability for detection systems, such as radar receivers15,16. This field of study was extended to the quantum domain by Helstrom17,18, who considered how to optimally choose between one of two density operators as the correct description of a receiver, and Holevo19, who considered the question of the optimal measurement to distinguish between one of two quantum states. Results following these works have placed bounds on the limits of quantum state20,21 and channel discrimination22,23,24,25,26. We build upon this early work but incorporate the filter function (FF) formalism originating from quantum control theory27,28,29,30 to answer this question of how to optimally detect signals, with a controllable quantum sensor. Unlike earlier works on state and channel discrimination that aim to identify the optimal measurements to distinguish two states/channels, our work is focused on identifying the control scheme that optimally separates the two cases.
Our model, as shown schematically in Fig. 1, considers a single qubit (or an ensemble of noninteracting qubits) with external fields that couple to the qubit through an energy splitting term and single-axis control on the transverse axis. We seek control protocols that minimize the average error rate of detecting the presence of a signal over background noise. In particular, we seek to detect band-limited signals that are of interest in signal processing, such as pulse-compressed radar31 and phase/frequency-modulated communications32 or radar33. We examine arbitrary single-axis time-dependent controls for this discrimination problem and show that, under certain assumptions on the background noise, the optimal control protocol is remarkably just a constant control with Rabi frequency corresponding to the maximum of the signal spectrum. This corresponds to what is traditionally known as spin-locking (SL) in the nuclear magnetic resonance literature34. The SL technique, along with its pulsed analogue, has been widely used in quantum sensing and noise spectroscopy applications8,35,36,37,38,39.
a The detection protocol. The qubit is initialized in an eigenstate of \(\hat{\sigma}_{x}\), \(\left|{\psi }_{{\rm{in}}}\right\rangle =\frac{1}{\sqrt{2}}(\left|0\right\rangle +\left|1\right\rangle )\) and evolves in the presence of a signal, background noise, and control. The measurement is done in the \(\hat{\sigma}_z\) basis after a Hadamard rotation. b Schematic picture for the detection setup. c The average probability of the occupation of state \(\left|0\right\rangle\) (denoted by \({P}_{\left|0\right\rangle }\)) decays as a function of time, with the decay rate dependent on the presence/absence of a signal. The detection is optimally performed at topt.
Results
Model
Let us consider a single qubit as a quantum sensor in the presence of a dephasing signal and noise. Assuming uniaxial control (along \(\hat{\sigma}_x\)) and under the rotating wave approximation, the qubit Hamiltonian in the rotating frame is given by
where Ω(t) is the Rabi frequency of an arbitrary time-dependent control in the rotating frame with respect to the drive frequency, the signal s(t) and background noise η(t) are both considered to be classical wide-sense stationary Gaussian stochastic processes, α denotes the ratio of the signal-to-noise power (SNR) and J2 is the total noise power. These stochastic processes have mean zero, \(\overline{s(t)}=\overline{\eta (t)}=0\) and two-point time correlations given by \(\overline{\eta (t)\eta ({t}^{\prime})}={g}_{\eta }(t-{t}^{\prime})\), \(\overline{s(t)s({t}^{\prime})}={g}_{s}(t-{t}^{\prime})\) and \(\overline{\eta (t)s({t}^{\prime})}=0\) with the normalization gη(0) = gs(0) = 1 and \(\overline{(\cdots \ )}\) denoting averaging over noise realizations. Alternatively, the noise correlations may also be represented in the frequency domain, using the power spectrum, \({S}_{\eta }(\omega )=\mathop{\int}\nolimits_{-\infty }^{\infty }{\mathrm{d}}\tau {g}_{\eta }(\tau ){e}^{-i\omega \tau }\), with the normalization \(\mathop{\int}\nolimits_{-\infty }^{\infty }{\mathrm{d}}\omega {S}_{\eta }(\omega )=2\pi\), and similarly for Ss(ω). In this manuscript, we consider two distinct types of noise for the background noise spectrum: white noise and Lorentzian. For white noise, we are able to derive the optimal control analytically. For a Lorentzian spectrum, corresponding to \({g}_{\eta }(t)={e}^{-| t| /{\sigma }_{t}}\), where σt denotes the correlation timescale, we find the optimal control protocols through numerical simulation. This noise spectrum is quite relevant to quantum sensing platforms such as nitrogen-vacancy centers in diamond40,41.
For our numerical simulations, we model the qubit sensor by time evolving the stochastic Liouville equation using a Trotter decomposition; see “Methods” for details. The signal power-spectrum Ss(ω) is chosen to be white cutoff, centered around a frequency ω0 and width 2δ0; see, e.g., Fig. 2a (in orange). This spectrum is chosen as an idealized band-limited stochastic signal commonly considered in signal processing. Note that the parameters considered in this manuscript are chosen to be in the regime of low SNR (α ≪ 1) and weak noise relative to the control (\(J/\max \{{{\Omega }}(t)\}\lesssim 1\)). The weak noise limit allows us to utilize the cumulant expansion to study the dynamics of the qubit.
a Background noise (blue) is considered to be nearly white (\(J{\sigma }_{t}=0.01\sqrt{30/\pi }\)), and the signal spectrum (orange) is white-cutoff centered around \({\omega }_{0}/J=10\sqrt{\pi /30}\) and width \(2{\delta }_{0}/J=3\sqrt{\pi /30}\), and SNR given by α = 0.05. For clarity of presentation, we use a mixed linear and logarithmic scale on the y-axis. The scale is linear between 0 ≤ y ≤ 0.01 and logarithmic for y > 0.01. b Dephasing under spin-locking, represented by outcome probability, \({P}_{\left|0\right\rangle }\), in the presence (orange) and absence (blue) of signal. The points and solid lines correspond to the outcome probabilities as calculated, using exact numerical simulation and SCA, respectively. c Comparison between spin-lock (black) driving at frequency ω = ω0 to the numerically optimal control [see Eq. (9)] until their respective detection time \({t}_{{\rm{s}}}={t}_{{{\Delta }}{P}_{\max }}\). d Maximum of the objective function, \({\mathcal{O}}={{\Delta }}{P}_{\left|0\right\rangle }\) [see Eq. (5)] at \({t}_{{\rm{s}}}={t}_{{\rm{{{\Delta }}}}{P}_{\max }}\) for different spin-lock driving frequencies, Ω(t) = Ω, as obtained from exact numerics (points) and from second cumulant expansion (line). Red dashed line shows \({{\mathcal{O}}}_{{\rm{opt}}}={\mathcal{O}}({\Omega}_{{\rm{opt}}},{t}_{{{\Delta }}{P}_{\max }})\) for the SCA-optimal control (plotted in red in c).
Detection protocol
The aim of this protocol is to optimally detect the presence of a stochastic signal with a known spectrum in the presence of background noise. This is in contrast to the goal of estimating some parameter of an AC or DC signal, as traditionally considered in quantum sensing1. The detection protocol can be described in three steps; schematically shown in Fig. 1. (i) Initialize: initialize the qubit in the state \(\left|+\right\rangle =\frac{1}{\sqrt{2}}(\left|0\right\rangle +\left|1\right\rangle )\). (ii) Sense: let the qubit evolve for sensing time ts in the presence of the Hamiltonian, H(t); see Eq. (1). (iii) Measure: rotate the qubit using a Hadamard gate (denoted as H) and measure in the \({\hat{\sigma }}_{z}\) basis. Record outcome as \(\left|0\right\rangle\) or \(\left|1\right\rangle\). The measurement outcome probability depends on the signal s(t), noise η(t), applied control Ω(t), and the sensing time ts. Examining the dephasing dynamics of a single qubit, it is straightforward to show \({P}_{\left|0\right\rangle }({t}_{{\rm{s}}})=\frac{1}{2}(1+{e}^{-\chi ({t}_{{\rm{s}}})})\). Clearly, the dephasing exponent depends on the presence or absence of a signal and is denoted χη+s or χη, with corresponding outcome probabilities labeled as \({P}_{\left|0\right\rangle ,\eta +{\rm{s}}}\) or \({P}_{\left|0\right\rangle ,\eta }\), respectively.
Optimizing the detection protocol
The optimal detection protocol {Ωopt, topt} that minimizes the average error rate Perr is given by a control function Ω(t) = Ωopt(t) and a corresponding optimal sensing time ts = topt. The average error rate Perr is defined as the average probability of false positive (FP) and false negative (FN) detections. In general, this error rate is dependent on the number of shots/repetitions Ns of the experiment in addition to the outcome probabilities \(\{{P}_{\left|0\right\rangle ,\eta +{\rm{s}}},{P}_{\left|0\right\rangle ,\eta }\}\). For single-shot (Ns = 1) detection experiments, the scenario considered by Helstrom in the early works on quantum state discrimination apply17,18. In this case, Perr is minimized by maximizing the separation between the outcome probabilities \({{\Delta }}{P}_{\left|0\right\rangle }={P}_{\left|0\right\rangle ,\eta }-{P}_{\left|0\right\rangle ,\eta +{\rm{s}}}\); see Supplementary Note I for derivation. For Ns > 1 shots, the average error rate can be rewritten in terms of cumulative distribution functions of the binomial distribution with an appropriately chosen threshold for detection. In general, this error rate is dependent on the number of shots, Ns, and does not admit a differentiable expression; see Supplementary Note I for details. Thus, for the simplicity of having a differentiable objective function for numerically optimizing the control function, as well as analytical insight, we choose to minimize the error rate for single-shot discrimination with the objective function chosen as \({\mathcal{O}}\equiv {{\Delta }}{P}_{\left|0\right\rangle }\). We also identify the corresponding single-shot optimal detection time for these protocols, \({t}_{{\rm{s}}}={t}_{\max {{\Delta }}P}\). We show that for the detection scenarios considered in this work, the optimal control schemes identified using this criteria (Ns = 1) also perform well for the case of multiple shots (Ns > 1), when compared to detection schemes without any control.
In this paper, we make no assumptions on the shape of the control function Ω(t), in order to obtain the optimal detection protocol. We derive analytical expressions for the objective function in the regime of weak signal, noise, and SNR, and use it as a heuristic for identifying the optimal control function for single-shot detection. Having identified these optimal control functions [Ωopt(t)] for detecting the stochastic signal of interest, we examine the performance of these detection schemes for the case of Ns > 1 shots and identify the Ns-dependent optimal sensing time for detection \({t}_{{\rm{opt}}}\equiv {t}_{{\rm{opt}},{N}_{{\rm{s}}}}\) that minimizes the average error rate; see “Methods” for details on the numerical procedure. The numerically optimized detection scheme is compared with the performance of some well-known protocols used in sensing (i) SL: \({{\Omega }}(t)={\rm{constant}}\); (ii) Carr, Purcell, Meiboom, and Gill (CPMG) pulse sequence: Ω(t) is given by a series of equidistant π-pulses separated by free-evolution periods of duration τCPMG; and (iii) Ramsey interferometry: Ω(t) = 0.
Dephasing in second cumulant approximation
Let us consider the dephasing of a qubit just in the presence of noise, setting s(t) = 0. The dynamics of the qubit in a weak noisy environment is well understood using the cumulant expansion30,42. The dephasing exponent, χη, can be obtained from the dynamics of \(\overline{\langle \hat{{\sigma }}_{x}(t)\rangle }={\rm{Tr}}\left[{\sigma }_{x}\rho (t)\right]\approx {e}^{-\chi (t)}{\langle \hat{\sigma }_{x}\rangle }_{0}\); \({\langle \hat{\sigma }_{x}\rangle }_{0}\) denoting the initial state. In the interaction frame of the control \({U}_{c}(t)={e}^{-i\frac{1}{2}{\hat{\sigma }}_{x}{{{\Lambda }}}_{t}}\), where \({{{\Lambda }}}_{t}=\mathop{\int}\nolimits_{0}^{t}{\mathrm{d}}\tilde{t}{{\Omega }}(\tilde{t})\), the dynamics are straightforwardly rewritten in terms of the cumulant expansion, \(\overline{\langle \hat{{\sigma }}_{x}(t)\rangle }={\rm{Tr}}[\exp (\mathop{\sum }\nolimits_{n = 1}^{\infty }\frac{{(-i)}^{n}}{n!}{C}^{(n)}(t))\rho (0)\hat{\sigma }_{x}]\); C(n) denoting the nth cumulant42. In the regime where the noise is weak, it is sufficient to terminate the series at the second cumulant (odd cumulants vanish trivially) to obtain the following expression for the decay,
where χη(t) is always real. In the frequency domain, Eq. (2) can be recast into an overlap between the noise spectrum and the FF, \({\chi }_{\eta }(t)=\frac{{J}^{2}}{2}\mathop{\int}\nolimits_{-\infty }^{\infty }\frac{{\mathrm{d}}\omega }{2\pi }{S}_{\eta }\left(\omega \right)| {F}_{t}\left(\omega \right){| }^{2}\). The FF is now given by the following expression,
where we use the symmetry of the noise spectrum, Sη(ω) = Sη(−ω). Note that the FFs have a normalization, \(\mathop{\int}\nolimits_{-\infty }^{\infty }\frac{{\mathrm{d}}\omega }{2\pi }| {F}_{t}(\omega ){| }^{2}=t\). Additional details regarding the derivation of the expressions for Ft(ω) and χη(t) are provided in “Methods”.
As an example, consider the limiting case when the background noise is white. In this case, \({g}_{\eta }(t-{t}^{\prime})\propto \delta (t-{t}^{\prime})\), which is the Dirac δ-function. To be consistent with our normalization [g(0) = 1], we define \(g(t)={\mathrm{lim}\,}_{\epsilon \to 0}{e}^{-| t| /\epsilon }\). However, to have a nonzero decay rate, we must rescale the noise power J2 such that, 2J2ϵ = γ is a constant. Now, χη is obtained straightforwardly from Eq. (2), \({\chi }_{\eta }(t)=\frac{1}{2}\gamma t\). This gives the standard T2 time for the qubit with T2 = 2/γ. The dephasing rate under white noise is constant regardless of the control Ω(t) applied. This is expected because the noise has the same amplitude for all frequencies (i.e., infinite bandwidth) and it is consistent with the well-known fact that it is impossible to suppress dephasing under white noise using control43.
In order to compare with numerics, it is convenient to switch to the discrete time picture, with time steps Δt = t/N, where N is the total number of steps, in addition to a piecewise constant control Ω = (Ω0, ⋯ , ΩN). Here, Eq. (2) becomes a Riemann sum and χη is a matrix expectation value. To this end, let us introduce (i) an N-dimensional vector for the control, \({{\boldsymbol{\Theta}}}_{t}=\frac{1}{\sqrt{N}}{\left[{e}^{-i{{{\Lambda }}}_{0}},{e}^{-i{{{\Lambda }}}_{{{\Delta }}t}},\cdots ,{e}^{-i{{{\Lambda }}}_{N{{\Delta }}t}}\right]}^{\mathrm{T}}\) with a normalization, \({{\boldsymbol{\Theta}}}_{t}^{\dagger }\cdot {{\boldsymbol{\Theta}}}_{t}=1\); and (ii) an N × N-dimensional symmetric Toeplitz matrix for the noise autocorrelation function, \({\left[{{\mathbb{G}}}_{\eta }\right]}_{ij}={g}_{\eta }\left(\left(i-j\right){{\Delta }}t\right)={\left[{{\mathbb{G}}}_{\eta }\right]}_{ji}\). Using these definitions, the expression for χ can now be written in a compact form,
The white-noise limit is recovered by setting \({{\mathbb{G}}}_{\eta }\) to be a diagonal matrix, \({\left[{{\mathbb{G}}}_{\eta }\right]}_{ii}=1\), and J2Δt = γ. We also note that in this discrete time notation, the FF [see Eq. (3)] is the Fourier series of Θ.
Optimization for detection in the SCA
Let us now describe the procedure for optimizing the control for detecting the signal. Both the signal and the noise cause the qubit to dephase, and the dephasing exponent is straightforwardly obtained in the second cumulant approximation (SCA), using Eq. (4). Since the signal and noise are uncorrelated, the decay in the presence of a signal is a sum, χη + s = χη + χs, where χs and χη are the decay exponents obtained from having just the signal or the noise present, respectively. Thus, the qubit decays at a faster rate in the presence of both signal and noise compared to just the background noise. In order to optimize for single-shot detection, we maximize over the difference between the two outcome probabilities, \({{\Delta }}{P}_{\left|0\right\rangle }\). We now have an effective heuristic for designing optimal detection controls that becomes optimal when the SCA applies. We define the following objective function,
We carry out the optimization as a two-step procedure: (i) optimize over control trajectories to obtain \({{\mathbf{\Omega }}}_{{\rm{opt}}}={{\rm{argmax}}}_{\{{\mathbf{\Omega}}\}}\left[\mathrm{log}\,{\mathcal{O}}({t}_{{\rm{s}}},\{{\mathbf{\Omega }}\})\right]\) for single-shot detection at a fixed detection time ts. Recall that the detection time sets the dimension of the control vector, \(\dim \left[{\mathbf{\Omega}}\right]={t}_{{\rm{s}}}/{{\Delta }}t\). In the limit of white background noise, we will obtain analytically the optimal control that maximizes \({\mathcal{O}}\). More generally, for arbitrary noise spectrum, the optimization is implemented using stochastic gradient descent (SGD) algorithms. We implement the SGD using the Adam optimization algorithm implemented in TensorFlow44,45. Note that it is also straightforward to add additional constraints on the variables that could be motivated by experimental requirements; e.g., maximum available power, see Supplementary Note III. (ii) Optimize over the time of detection, topt, which depends on the total number of shots Ns, to obtain the optimal detection protocol. For the case of single-shot detection, the optimal time is obtained using a grid search over different detection times ts to identify the optimal single-shot detection time, \({t}_{{{\Delta }}{P}_{\max }}={{\rm{argmax}}}_{{t}_{{\rm{s}}}}\left[{{\Delta }}{P}_{\left|0\right\rangle }({t}_{{\rm{s}}})\right]\). For Ns > 1 shots, we minimize the average error rate to identify the optimal time of measurement, \({t}_{{\rm{s}}}={t}_{{\rm{opt}},{N}_{{\rm{s}}}}\); see “Methods” for details on implementation. Therefore, we obtain the optimal detector in the SCA, which we denote as “SCA optimal”, with \({{\mathcal{O}}}_{{\rm{opt}}}={\mathcal{O}}({t}_{{\rm{opt}}},{{\mathbf{\Omega }}}_{{\rm{opt}}})\). See “Methods” for more details regarding the optimization procedure.
White background noise
Let us start by discussing the SCA-optimal protocol when the background noise is close to white, \({\sigma }_{t}\ll \min \{1/{\omega }_{0},1/{\delta }_{0}\}\). Here, we assume that the signal spectrum Ss(ω) is characterized by a peak at ω = ω0 and width ≈ 2δ0. This case allows us to compute the optimal control analytically. Dephasing in the absence of any signal, χη, is independent of the applied control, which simplifies the optimization objective \({\mathcal{O}}\) [see Eq. (5)]. Therefore, \({\mathcal{O}}\) can be maximized by maximizing χs given by a formula analogous to Eqs. (2) and (4). Examining the expression of χs in terms of FFs, the following bound is obtained,
where we use the normalization \(\mathop{\int}\nolimits_{-\infty }^{\infty }\frac{\mathrm{d}\omega }{2\pi }| {F}_{{t}_{{\rm{s}}}}(\omega ){| }^{2}={t}_{{\rm{s}}}\). In the following, we show that this upper bound on χs(ts) can be achieved in the limit of long times (ts ≫ 1/δ0), using a control that is constant in time, \({{\Omega }}(t)={{\rm{argmax}}}_{\omega }\left[S(\omega )\right]={\omega }_{0}\). This control scheme is commonly referred to as “spin-locking”.
A SL control scheme Ω(t) = Ω has the FF \({F}_{t}(\omega )=t{e}^{i({{\Omega }}-\omega )t/2}\,\text{sinc}\,\left[({{\Omega }}-\omega )\frac{t}{2}\right]\) and decay exponent
where, in the second step we approximate the sinc(ϵx) as a rectangular function. Alternatively, one can also use the approximation, \({{\rm{sinc}}}^{2}(\omega {t}_{{\rm{s}}}/2)\approx \frac{2\pi }{{t}_{{\rm{s}}}}\delta (\omega )\) in the limit ts → ∞ to arrive at the same conclusion as Eq. (8). Therefore, we see that the bound for χs(ts) [see Eq. (6)] can be saturated using a simple control protocol Ω(t) = ω0. While we have shown this result for a spectrum that has a maxima at ω = ω0, it is straightforward to specialize to the case of a white-cutoff signal spectrum (see Fig. 2a), in which case the optimal SL frequency is consistent with any frequency in the signal band. We emphasize the following subtlety in the derivation of Eq. (8): the sensing time (ts) of the detector is large compared to the inverse width of the signal spectrum, ts ≫ 1/δ0.
The SCA-optimal detection protocol at any particular sensing time ts with white background noise can also be calculated numerically without using time-consuming SGD-based optimizers. Since this control maximizes χs, it can be obtained from the eigenstructure of the correlation matrix \({{\mathbb{G}}}_{\mathrm{s}}\) [see Eq. (4)]. In fact, it is straightforward to show that \({\chi }_{\mathrm{s}}^{{\rm{opt}}}({t}_{{\rm{s}}})\le \frac{1}{2}{J}^{2}\alpha {t}_{{\rm{s}}}{{\Delta }}t{{\mathfrak{g}}}_{\max }\), where \({{\mathfrak{g}}}_{\max }\) (\({{\mathbf{\upphi }}}_{{t}_{{\rm{s}}}}^{\max }\)) denotes the largest eigenvalue (eigenvector) of the correlation matrix of the signal spectrum \({{\mathbb{G}}}_{\mathrm{s}}\). However, the eigenvector of the correlation matrix is not necessarily an allowed control protocol. Therefore, the SCA-optimal control protocol is obtained from identifying a control vector \({{\boldsymbol{\Theta}}}_{{t}_{{\rm{s}}}}^{{\rm{opt}}}=\frac{1}{\sqrt{N}}\left[{e}^{-i{{{\Lambda }}}_{0}},\ldots \, ,{e}^{-i{{{\Lambda }}}_{{t}_{{\rm{s}}}}}\right]\) with the largest overlap with \({{\mathbf{\upphi }}}_{{t}_{{\rm{s}}}}^{\max }\). Noting that the eigenspectrum of \({{\mathbb{G}}}_{\mathrm{s}}\) is doubly degenerate (denote them by i = ±), we can construct two possible SCA-optimal control vectors elementwise as
where the two possible optimal controls correspond to driving around ±ω0. Having constructed the SCA-optimal control for arbitrary sensing time ts, the optimal time of measurement for single-shot detection, \({t}_{{{\Delta }}{P}_{\max }}\) is obtained by maximizing \({\mathcal{O}}\) from Eq. (5). Now, we have the SCA-optimal control for detection \({{\boldsymbol{\Theta }}}_{{t}_{{{\Delta }}{P}_{\max }}}^{{\rm{opt}}}\), an example of which is shown in Fig. 2c.
We numerically simulate the performance of the sensing protocol for white background noise; the results are shown in Fig. 2. A nearly white background noise spectrum is obtained by choosing the correlation time to be small, \(J{\sigma }_{t}=0.01\sqrt{30/\pi }\ll J/{\delta }_{0}\). Figure 2b shows the observed outcome probability of state \(\left|0\right\rangle\), \({P}_{\left|0\right\rangle }\) as a function of sensing time ts. Both with and without the signal, \({P}_{\left|0\right\rangle }\) (shown in orange and blue) decays exponentially, with very good agreement between the exact dynamics (points) and SCA (solid line). We calculate the optimal time for detection \({t}_{{{\Delta }}{P}_{\max }}\) by maximizing the difference \({\mathcal{O}}\), see Eq. (5). In Fig. 2c, d, we examine the optimality of SL. Figure 2c compares SL to the numerically obtained SCA-optimal protocol, \({{\boldsymbol{\Theta }}}_{{t}_{{{\Delta }}{P}_{\max }}}^{{\rm{opt}}}\) [see Eq. (9)], up to their respective optimal times of measurement. Comparing the two control schemes, it is clear that SL is close to optimal. In fact, for long times of measurement, ts → ∞, \({{\boldsymbol{\Theta}}}_{{t}_{{\rm{s}}}\to \infty }^{{\rm{opt}}}\) converges to SL. However, at the optimal measurement time, \({t}_{{\rm{s}}}={t}_{{{\Delta }}{P}_{\max }}\), \({{\boldsymbol{\Theta}}}_{{t}_{{{\Delta }}{P}_{\max }}}^{{\rm{opt}}}\) remains distinct from SL, with oscillations around the spin-lock frequency. Figure 2d compares the performance of SL as a function of the Rabi frequency of the applied control Ω to the SCA-optimal detector. Comparing the performance of SL as obtained from exact numerics (blue dots) with that obtained for the SCA-optimal control (red dashed line), it is clear that SL may perform marginally better in practice, which we attribute to corrections to the dynamics beyond the SCA.
Lorentzian background noise
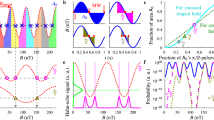
We now compare the performance of SL (Ω(t) = ω0) as a function of correlation time of the background noise. Specifically, we compare it to CPMG with τCPMG = π/ω0 and Ramsey interferometry, Ω(t) = 0. We also numerically obtain the SCA-optimal control protocol using SGD-based optimizers, and compare its shape with these protocols. The results are shown in Figs. 3 and 4. One of the important takeaways from the numerical optimization of the objective function \({\mathcal{O}}\) is that the SCA-optimal protocol depends on the correlation time σt. The control obtained from the SGD is close to SL for short correlation times; however, for correlation times longer than a crossover scale, CPMG performs better (see Fig. 3b). In Fig. 3a, we show the numerical optimized control sequence for increasing correlation times Jσt = 0.03, 0.19, and 1.17. Clearly, the SCA-optimal control has close resemblance to CPMG for Jσt = 1.17. Interestingly, in some cases, the SGD-based optimizer also finds control schemes that are neither CPMG or SL; see “Discussion” in Supplementary Note III accompanying Supplementary Figs. 2 and 3.
a Different SCA-optimal control schemes from the SGD-based optimizer for increasing correlation times Jσt = 0.03, 0.19, and 1.17. The signal is at \({\omega }_{0}/J=10\sqrt{\pi /30}\). b Comparison of the maximum of the objective function \({\mathcal{O}}\) [see Eq. (5)] as a function of background noise correlation, σt, in comparison to SL and CPMG sequences with their corresponding detection times set to \({t}_{{\rm{s}}}={t}_{{{\Delta }}{P}_{\max }}\). The signal is the same as in a. The SCA-optimal control (shown as red circles) exhibits a crossover at \({\sigma }_{t}={\sigma }_{t}^{{\rm{cross}}}\) (pink plus). It is close to SL (solid black line) when \({\sigma }_{t}\,<\,{\sigma }_{t}^{{\mathrm{cross}}}\), and crossing over to CPMG (solid blue line) when \({\sigma }_{t}\,>\,{\sigma }_{t}^{{\rm{cross}}}\). c The inverse of the crossover correlation time, \(1/{\sigma }_{t}^{{\rm{cross}}}\) as a function of the center of the signal frequency ω0 keeping the SNR α fixed. The dashed line is a linear fit to the points.
Signal is chosen centered at \({\omega }_{0}/J=10\sqrt{\pi /30}\) and the background noise has the correlation time Jσt = 1.17. a The different protocols shown here are chosen for the detection time \({t}_{{\rm{s}}}={t}_{{\rm{opt}},{N}_{{\rm{s}}}}\) that minimizes the average error rate for Ns = 100. b Average error rates for classification of the presence or absence of the signal given by the average probability of false positive and false negative outcomes, as a function of the number of shots of the protocol (see Fig. 1). For a given number of shots, the threshold for the detector is chosen to minimize the total probability of FP and FN outcomes.
The crossover correlation timescale for CPMG to perform better than SL approximately scales as a power law with the signal frequency, \({\sigma }_{t}^{{\rm{cross}}} \sim 1/{\omega }_{0}\) (see Fig. 3c). The better performance of CPMG compared to SL for longer correlation times can be understood qualitatively from the shape of their corresponding FFs (Supplementary Figs. 2 and 3). While the FF for SL has all of its weight close to ω0, CPMG has some weight also at the odd harmonics of ω0 (refs. 46,47). In addition, the amplitude of the FF for CPMG at frequencies ω < ω0 is lower compared to SL; see, e.g., Supplementary Fig. 1. Since the background spectrum is Lorentzian and Sη(ω) decays at higher frequencies, this leads to \({\chi }_{\eta }^{{\rm{CPMG}}}\,<\,{\chi }_{\eta }^{{\rm{SL}}}\); unlike when the background is white where the χη is independent of the control. The optimization objective depends on χs/η in a nonlinear fashion [see Eq. (5)] which increases with either decreasing χη or increasing χs. Even though for the signal spectrum \({\chi }_{{\rm{s}}}^{{\rm{CPMG}}}\,<\,{\chi }_{{\rm{s}}}^{{\rm{SL}}}\), the smaller value of \({\chi }_{\eta }^{{\rm{CPMG}}}\) leads to a larger \({\mathcal{O}}\). It is interesting to note that in the presence of experimentally motivated constraints, such as maximum available power, the optimal protocol interpolates between CPMG (instantaneous π-pulses) and SL (Supplementary Fig. 4).
Let us now discuss the performance of the different control schemes as obtained from exact numerical simulation taking into account Ns > 1 measurement shots, see Fig. 4. We compare the performance of SL, CPMG, SCA-optimal, and Ramsey schemes at their respective optimal detection times; the controls are shown in Fig. 4a, with corresponding FFs shown in Supplementary Fig. 1. The optimal detection times are obtained for each control scheme by minimizing the average error rate for a given Ns; see “Methods” for details. Choosing the threshold such that the average of probability of FP (type I error) and FN (type II error) is minimum, we plot the error rate as a function of the number of measurements in Fig. 4b; a better detector is characterized by lower error rates. Rather surprisingly, even when the correlation time is large Jσt = 1.17, the performance of CPMG and SL remains fairly close to each other, with SL still performing marginally better. The optimal control scheme obtained in the SCA (see Fig. 3a) also performs equally well (although not better) in comparison to the standard protocols. This is likely due to the fact that the SGD-based optimization is done under the assumption that the SCA holds. However, non-negligible contributions from higher cumulants to the dephasing rate leads to deviations from the SCA, which may lead to better performance of SL. This also reveals some general robustness in the optimality of SL as a detection protocol for the signal.
Discussion
In this work, we discuss the performance of different control schemes for detecting a known signal in the presence of certain background noise environments and show that a SL drive is close to optimal in all cases we considered. This work opens up a potentially exciting use case for currently available quantum sensor hardware. These detectors can be used to identify signals in electromagnetic fields, where the detection bandwidth is only limited by the frequency range of the control drive.
These results suggest several directions for future work. We only considered the dynamics in the SCA, where we are able to show the near optimality of SL. We did not take into account the role of the higher cumulants, as they do not play a significant role at optimal detection time. However for qubits with higher T2 times and larger signal power, it will be essential to consider its role for determining optimal controls for detection. Another possibility is to consider the performance of detection protocols when the signal or noise is non-gaussian and/or nonstationary. Furthermore, we have considered the control drive to be on resonance. Any detuning will result in a two-dimensional control in the rotating frame, with controls along both \({\hat{\sigma }}_{x}\) and \({\hat{\sigma }}_{y}\). The optimal detection protocol in the presence of detuning will be a topic of future work, and will point to more robust protocols for detection. In addition, we have not considered any errors in the implementation of the control unitaries. Unlike the scenarios described in this work, the optimized control sequences may possibly significantly outperform SL and CPMG in the presence of control noise. Finally, we have considered only a single qubit or a noninteracting ensemble of qubits as the sensor and do not consider the role of entanglement, which may provide an enhancement in sensing beyond that available classically.
Methods
Dynamical simulation of a noisy qubit
The dynamics of the qubit is modeled numerically by an exact noisy quantum simulation and control library—“Mezze”48, which uses a stochastic Liouville equation formalism with a Trotter decomposition49. For our simulations, we fix the noise power J2 = 30/π ≈ 9.549 and rescale all frequencies and timescales in units of J. We also keep fixed the SNR α = 0.05 and Trotter time-step Δt = 10−3.
Filter function in the second cumulant approximation
We derive the expression for the decay exponent χ(t) and FF, Ft(ω) defined in Eqs. (2) and (3) in the main text. For the purposes of this section, we set s(t) = 0, and follow the steps outlined in refs. 30,42. Taking the definition of the Hamiltonian in Eq. (1) from the main text and transforming to an interaction picture with respect to the control, \({U}_{c}(t)={e}^{-i\frac{1}{2}\hat{\sigma }_{x}{{{\Lambda }}}_{t}}\) we have,
where \({{{\Lambda }}}_{t}=\mathop{\int}\nolimits_{0}^{t}{\mathrm{d}s}\,{{\Omega }}(s)\). We define an alternate Hamiltonian, \(\tilde{H}(s)\)30,42,
and now, we are ready to write down the time evolution of a particular observable. Of interest to us is the evolution of σx(t) with a particular initial state ρ(0). Noting that the observable σx and the initial state \(\rho (0)=\left|+\right\rangle \left\langle +\right|\) are unchanged in the interaction picture given by Uc(t), we have under time evolution with \({U}_{I}(t)={\mathcal{T}}\left[\exp \left(-i\mathop{\int}\nolimits_{0}^{t}{\mathrm{d}}s\,{H}_{I}(s)\right)\right]\),
where we have averaged over noise realizations. Now, we can expand the exponential in the cumulant expansion,
The odd cumulants in the sum vanish since HI ∝ η(t), and we assume that the noise is gaussian with vanishing mean.
Second cumulant approximation
When the noise is weak, it is sufficient to approximate the time-ordered exponential up to the second cumulant. We have the expression for the second cumulant,
where, to simplify Eq. (17) to Eq. (18), we use the definitions of \(\tilde{H}(t)\) from Eq. (12) and splitting the integrals around t = 0. In addition, to go from Eq. (19) to Eq. (20), we use the fact that σxHI(t)σx = −HI(t). The integrand can be further simplified using,
Averaging over noise realizations, and noting that \(\overline{\eta ({t}_{1})\eta ({t}_{2})}={g}_{\eta }({t}_{1}-{t}_{2})\), with g(t) being an even function, the second cumulant can be expressed as a convolution between the correlation function and control-dependent terms. Noting that the term ∝ \(\hat{\sigma}_x\) in C(2)(t) vanishes because the noise correlation is an even function [gη( − t) = gη(t)], the second cumulant can be simplified to
We utilize the second cumulant to express the expectation value given in Eq. (15) as
The decay function χ(t) = C(2)(t)/2 characterizes the decoherence rate of the system and is explicitly given by
where we have used \({S}_{\eta }(\omega )=\mathop{\int}\nolimits_{-\infty }^{\infty }\mathrm{d}\tau {g}_{\eta }(\tau ){e}^{-i\omega \tau }\) and \(g(\tau )=\frac{1}{2\pi }\mathop{\int}\nolimits_{-\infty }^{\infty }\mathrm{d}\omega {S}_{\eta }(\omega ){e}^{i\omega \tau }\). Note that \({F}_{t,+}(\omega )={[{F}_{t,-}(-\omega )]}^{* }\), which means that if S(ω) = S(−ω), the expression for χ can be further simplified by introducing Ft(ω) introduced in Eq. (2). This completes the derivation for expressions of χ(t) and F(ω), as defined in Eq. (2) in the main text.
Optimization of the objective function
We use a two-step numerical optimization to find the Ωopt that maximizes \({{\Delta }}{P}_{\left|0\right\rangle }=\frac{1}{2}{e}^{-{\chi }_{\eta }}(1-{e}^{-{\chi }_{{\rm{s}}}})\). Specifically, we do a grid search over different sensing times, ts, and for each choice of ts, we find the control schedule that optimizes the objective function. Since the cost function is differentiable, we use the Adam44 optimizer with default parameters in TensorFlow to optimize the object function taking advantage of graphical processing units to accelerate the optimization procedure. Moreover, we constrain [Ω]i to be positive for all values of i. We either run the optimization for 10,000 iterations, or stop if the magnitude of the difference of the objective function values separated by 1000 iterations is <10−6. In all the optimizations performed in this work, we discretize the control to \(J{{\Delta }}t=(\sqrt{30/\pi })0.01\). We repeat this procedure for different choices of ts from 300Δt to 1300Δt in increments of 10Δt. We then choose a ts that has the optimal objective value.
After finishing this two-step optimization, we evaluate \({{\Delta }}{P}_{\left|0\right\rangle }\) at the optimal time with the optimal control by interpolating the results to a finer discretization of \(J{{\Delta }}t=(\sqrt{30/\pi })0.001\), and compare it to the value of \({{\Delta }}{P}_{\left|0\right\rangle }\) with CPMG and spin-lock control schemes. For single-shot detection, we obtain the best time for CPMG and spin-lock control schemes by numerically evaluating the \({{\Delta }}{P}_{\left|0\right\rangle }\), using discretized control with \({{\Delta }}t=(\sqrt{30/\pi })0.001\) and varying the sensing times, ts, from 3000Δt to 13,000Δt in increments of 100Δt. See Supplementary Note III for a discussion on imposing additional constraints on Ω.
Calculating \({t}_{{\rm{opt}},{N}_{{\rm{s}}}}\) by minimizing the average error rate
For a given number of measurements Ns, the optimal detection time \({t}_{{\rm{opt}},{N}_{{\rm{s}}}}\) for a particular control scheme is obtained by minimizing the average error rate Perr, which is used to obtain Fig. 4. A particular control scheme is characterized by outcome probabilities as a function of the sensing time ts, in the presence \(\left[{P}_{\left|0\right\rangle ,\eta +{\rm{s}}}({t}_{{\rm{s}}})\right]\) or absence \(\left[{P}_{\left|0\right\rangle ,\eta }({t}_{{\rm{s}}})\right]\) of a signal.
Given Ns measurement shots, the number of \(\left|0\right\rangle\) measurement outcomes (N0) is drawn from the corresponding binomial distribution: \(B({N}_{0},{N}_{{\rm{s}}},{P}_{\left|0\right\rangle ,\eta +{\rm{s}}})\) or \(B({N}_{0},{N}_{{\rm{s}}},{P}_{\left|0\right\rangle ,\eta })\) depending on whether the signal is present or absent, respectively. Given a threshold for detection \(\tilde{N}\) (i.e., \({N}_{0}\,<\,\tilde{N}\) to detect the signal), the average error rate of the detection is a function of the outcome probabilities \(\{{P}_{\left|0\right\rangle ,\eta }({t}_{{\rm{s}}}),{P}_{\left|0\right\rangle ,\eta +{\rm{s}}}({t}_{{\rm{s}}})\}\) and is defined as,
where, \(B({N}_{0},{N}_{{\rm{s}}},P)=\left(\begin{array}{c}{N}_{{\rm{s}}}\\ {N}_{0}\end{array}\right){P}^{{N}_{0}}{(1-P)}^{({N}_{{\rm{s}}}-{N}_{0})}\) denotes the binomial distribution. Clearly, the average error rate is a function of the detection time ts and the threshold \(\tilde{N}\). To identify the optimal time of detection that minimizes Perr, we follow a two-step procedure,
-
(i)
Given ts, the threshold is identified to minimize \({P}_{{\rm{err}}}({t}_{{\rm{s}}},\tilde{N})\),
$${N}_{{\rm{th}}}({t}_{{\rm{s}}})=\mathop{{\rm{argmin}}}\limits_{\tilde{N}}\left[{P}_{{\rm{err}}}({t}_{{\rm{s}}},\tilde{N})\right]$$(28) -
(ii)
Having identified the threshold Nth as a function of ts, the optimal time of detection can be identified through a simple grid search,
$${t}_{{\rm{opt}},{{\rm{N}}}_{{\rm{s}}}}=\mathop{{\rm{argmin}}}\limits_{{t}_{{\rm{s}}}}\left[{P}_{{\rm{err}}}\left({t}_{{\rm{s}}},{N}_{{\rm{th}}}({t}_{{\rm{s}}})\right)\right]$$(29)
Therefore, we have identified the optimal detection time \({t}_{{\rm{opt}},{N}_{{\rm{s}}}}\) for a particular control scheme, given the number of shots Ns.
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
Code availability
The codes used for producing data used in this study are available from the corresponding author on reasonable request.
References
Degen, C. L., Reinhard, F. & Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 89, 035002 (2017).
Ramsey, N. F. A molecular beam resonance method with separated oscillating fields. Phys. Rev. 78, 695–699 (1950).
Poggiali, F., Cappellaro, P. & Fabbri, N. Optimal control for one-qubit quantum sensing. Phys. Rev. X 8, 021059 (2018).
Carr, H. Y. & Purcell, E. M. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys. Rev. 94, 630–638 (1954).
Viola, L. & Lloyd, S. Dynamical suppression of decoherence in two-state quantum systems. Phys. Rev. A 58, 2733–2744 (1998).
Viola, L., Knill, E. & Lloyd, S. Dynamical decoupling of open quantum systems. Phys. Rev. Lett. 82, 2417–2421 (1999).
Fedder, H. et al. Towards t1-limited magnetic resonance imaging using rabi beats. Appl. Phys. B 102, 497–502 (2011).
Aiello, C. D., Hirose, M. & Cappellaro, P. Composite-pulse magnetometry with a solid-state quantum sensor. Nat. Commun. 4, 1419 (2013).
Braunstein, S. L., Caves, C. M. & Milburn, G. Generalized uncertainty relations: theory, examples, and lorentz invariance. Ann. Phys. 247, 135–173 (1996).
Braunstein, S. L. & Caves, C. M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 72, 3439–3443 (1994).
Paris, M. G. A. Quantum estimation for quantum technology. Int. J. Quantum Inf. 07, 125–137 (2009).
Tsang, M., Wiseman, H. M. & Caves, C. M. Fundamental quantum limit to waveform estimation. Phys. Rev. Lett. 106, 090401 (2011).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum metrology. Phys. Rev. Lett. 96, 010401 (2006).
Wald, A. Contributions to the theory of statistical estimation and testing hypotheses. Ann. Math. Stat. 10, 299–326 (1939).
Peterson, W., Birdsall, T. & Fox, W. The theory of signal detectability. IRE Trans. Inf. Theory 4, 171–212 (1954).
Marcum, J. A statistical theory of target detection by pulsed radar. IRE Trans. Inf. Theory 6, 59–267 (1960).
Helstrom, C. W. Detection theory and quantum mechanics. Inf. Control 10, 254 – 291 (1967).
Helstrom, C. W. Quantum detection and estimation theory. J. Stat. Phys. 1, 231–252 (1969).
Holevo, A. Statistical decision theory for quantum systems. J. Multivar. Anal. 3, 337–394 (1973).
Audenaert, K. M. R. et al. Discriminating states: the quantum chernoff bound. Phys. Rev. Lett. 98, 160501 (2007).
Calsamiglia, J., Muñoz-Tapia, R., Masanes, L., Acin, A. & Bagan, E. Quantum Chernoff bound as a measure of distinguishability between density matrices: application to qubit and Gaussian states. Phys. Rev. A 77, 032311 (2008).
Acín, A. Statistical distinguishability between unitary operations. Phys. Rev. Lett. 87, 177901 (2001).
Sacchi, M. F. Optimal discrimination of quantum operations. Phys. Rev. A 71, 062340 (2005).
Wang, G. & Ying, M. Unambiguous discrimination among quantum operations. Phys. Rev. A 73, 042301 (2006).
Hayashi, M. Discrimination of two channels by adaptive methods and its application to quantum system. IEEE Trans. Inf. Theory 55, 3807–3820 (2009).
Harrow, A. W., Hassidim, A., Leung, D. W. & Watrous, J. Adaptive versus nonadaptive strategies for quantum channel discrimination. Phys. Rev. A 81, 032339 (2010).
Kofman, A. G. & Kurizki, G. Universal dynamical control of quantum mechanical decay: modulation of the coupling to the continuum. Phys. Rev. Lett. 87, 270405 (2001).
Cywiński, L., Lutchyn, R. M., Nave, C. P. & Das Sarma, S. How to enhance dephasing time in superconducting qubits. Phys. Rev. B 77, 174509 (2008).
Hayes, D., Khodjasteh, K., Viola, L. & Biercuk, M. J. Reducing sequencing complexity in dynamical quantum error suppression by walsh modulation. Phys. Rev. A 84, 062323 (2011).
Paz-Silva, G. A. & Viola, L. General transfer-function approach to noise filtering in open-loop quantum control. Phys. Rev. Lett. 113, 250501 (2014).
Cook, C. E. Pulse compression-key to more efficient radar transmission. Proc. IRE 48, 310–316 (1960).
Sklar, B. Digital Communications: Fundamentals and Applications (Prentice-Hall PTR, Upper Saddle River, New Jersey, 2001).
Stove, A. G. Linear fmcw radar techniques. IEE Proceedings F (Radar and Signal Processing), 139, 343–350 (IET, 1992).
Levitt, M. H. Spin Dynamics: Basics of Nuclear Magnetic Resonance 2nd edn (Wiley, 2008).
Hirose, M., Aiello, C. D. & Cappellaro, P. Continuous dynamical decoupling magnetometry. Phys. Rev. A 86, 062320 (2012).
Loretz, M., Rosskopf, T. & Degen, C. L. Radio-frequency magnetometry using a single electron spin. Phys. Rev. Lett. 110, 017602 (2013).
Collin, E. et al. Nmr-like control of a quantum bit superconducting circuit. Phys. Rev. Lett. 93, 157005 (2004).
Slichter, D. H. et al. Measurement-induced qubit state mixing in circuit qed from up-converted dephasing noise. Phys. Rev. Lett. 109, 153601 (2012).
Yan, F. et al. Spectroscopy of low-frequency noise and its temperature dependence in a superconducting qubit. Phys. Rev. B 85, 174521 (2012).
Klauder, J. R. & Anderson, P. W. Spectral diffusion decay in spin resonance experiments. Phys. Rev. 125, 912–932 (1962).
Bar-Gill, N. et al. Suppression of spin-bath dynamics for improved coherence of multi-spin-qubit systems. Nat. Commun. 3, 858 (2012).
Paz-Silva, G. A., Norris, L. M. & Viola, L. Multiqubit spectroscopy of gaussian quantum noise. Phys. Rev. A 95, 022121 (2017).
Viola, L., Knill, E. & Lloyd, S. Dynamical decoupling of open quantum systems. Phys. Rev. Lett. 82, 2417–2421 (1999).
Kingma, D. P. & Ba, J. Adam: A method for stochastic optimization. 3rd International Conference on Learning Representations, {ICLR} 2015, Conference Track Proceedings (San Diego, CA, USA, 2015).
Abadi, M. et al. Tensorflow: large-scale machine learning on heterogeneous distributed systems. 12th {USENIX} symposium on operating systems design and implementation (OSDI 16) pp. 265–283 (2016).
Álvarez, G. A. & Suter, D. Measuring the spectrum of colored noise by dynamical decoupling. Phys. Rev. Lett. 107, 230501 (2011).
Ajoy, A., Álvarez, G. A. & Suter, D. Optimal pulse spacing for dynamical decoupling in the presence of a purely dephasing spin bath. Phys. Rev. A 83, 032303 (2011).
Mezze. A toolbox for simulating open quantum system dynamics (2020). https://github.com/mezze-team/mezze.
Suzuki, M. Decomposition formulas of exponential operators and lie exponentials with some applications to quantum mechanics and statistical physics. J. Math. Phys. 26, 601–612 (1985).
Acknowledgements
The authors would like to thank Mohammad Hafezi, Jeff Barnes, Colin Trout, and Timothy Sweeney for useful discussions. P.T., K.M.S., G.D.Q., and B.C. also acknowledge funding from the Internal Research and Development program of the Applied Physics Laboratory. This work was subsequently supported in part by the U.S. Department of Energy(DOE), Office of Science, Office of Advanced Scientific Computing Research (ASCR) Quantum Computing Application Teams program, under fieldwork proposal number ERKJ347. A.S. gratefully acknowledges support from ARO-MURI and Physics Frontier Center by National Science Foundation at the JQI.
Author information
Authors and Affiliations
Contributions
B.D.C. conceived and supervised the project. P.T. and K.M.S. did the analytical and numerical simulation of qubit dynamics. G.D.Q. contributed to the analysis using filter functions. A.S. developed the numerical optimization procedure to obtain the optimal control protocols. All authors contributed to the discussion of results and writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Titum, P., Schultz, K., Seif, A. et al. Optimal control for quantum detectors. npj Quantum Inf 7, 53 (2021). https://doi.org/10.1038/s41534-021-00383-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-021-00383-5
This article is cited by
-
Control-enhanced non-Markovian quantum metrology
Communications Physics (2024)
-
Quantum control for time-dependent noise by inverse geometric optimization
Science China Physics, Mechanics & Astronomy (2024)
-
Analysis of multi-photon quantum radar cross section for targets in atmospheric medium
Quantum Information Processing (2024)