Abstract
Entanglement engineering plays a central role in quantum-enhanced technologies, with potential physical platforms that outperform their classical counterparts. However, free electrons remain largely unexplored despite their great capacity to encode and manipulate quantum information, due in part to the lack of a suitable theoretical framework. Here we link theoretical concepts from quantum information to available free-electron sources. Specifically, we consider the interactions among electrons propagating near the surface of a polariton-supporting medium and study the entanglement induced by pair-wise coupling. These correlations depend on the controlled interaction interval and the initial electron bandwidth. We show that long interaction times of broadband electrons extend their temporal coherence. This in turn is revealed through a widened Hong–Ou–Mandel peak and is associated with an increased entanglement entropy. We then introduce a discrete basis of electronic temporal modes and discriminate between them via coincidence detection with a shaped probe. This paves the way for ultrafast quantum information transfer by means of free electrons, rendering the large alphabet that they span in the time domain accessible.
Similar content being viewed by others
Introduction
Quantum degrees of freedom occupy a large parameter space compared with their classical counterparts. This property renders them challenging for simulation on classical computers. Nonetheless, it also endows them with a vast information capacity, useful for novel computational and metrologic paradigms1,2,3. Entangled photon pairs have long been the work-horse of quantum enhancement demonstrations in the optical arena, with applications in metrology4,5, imaging6,7,8,9,10,11, and spectroscopy11,12,13,14. A key concept in the generation of such useful states is initiation of well-monitored interactions between continuous variables. The latter exhibit rich entanglement spectra and large state space on which information can be recorded and accessed15,16,17,18,19. These concepts have not yet been addressed in the well-established field of free-electron-based metrology techniques, such as spectroscopy and microscopy20. Designing controlled entanglement of free-electron sources constitutes the main challenge, and this is precisely what we address here.
Extraordinary electron-beam-shaping capabilities have been recently demonstrated in electron microscopes combining ultrafast optics elements21,22,23. Revolutionary concepts such as free-electron qubits24 and cavity-induced quantum control25,26,27 are becoming available, pointing toward the emergence of next-generation quantum light–electron technologies. While photons maintain coherence over large distances, electrons decohere rapidly due to their strong environmental coupling. Combined with the control schemes mentioned above, this suggests that isolated electrons provide valuable quantum probes when selectively exposed to targets of interest. We show that electrons passing by polariton-supporting media can experience geometrically controlled interaction resulting in entanglement. This effect is closely related to Amperean pairing of electrons discussed in refs. 28,29,30, shown here to induce an entangled Einstein–Podolsky–Rosen state in the long interaction time limit.
Here, we study the quantum correlations generated by abrupt interactions of electron pairs with a neighboring medium, as depicted in Fig. 1, for a controlled time interval TI. We explore the transient state generated by abrupt interactions, as well as the steady-state limit in the perturbative regime. By varying two control parameters—interaction time TI and initial electron bandwidth σe—we effectively scan the degree of entanglement. The entanglement in the longitudinal dimension is characterized by the Schmidt decomposition of the wave function. We then calculate the coincidence probability and display it versus the degree of entanglement. We denote the resulting eigenstate electronic temporal modes (ETMs) in analogy to their photonic counterparts31,32. Finally, we propose a technique that is useful for real-time discrimination between ETMs, essential for state tomography and related quantum information processing applications.
a An uncorrelated electron pair \(\left|{{{\Psi }}}_{0}\right\rangle\) propagates parallel to the planar surface of a polariton-supporting film of length L along the propagation direction, transverse width lx ≫ L, and thickness d = 1nm. b Initial distribution of the longitudinal momentum component, centered around k0 with \({\sigma }_{\,\text{e}\,}^{2}\) spread. c Spatial orientation of the variance in the transverse momentum spread \({\sigma }_{x,y}^{2}\). After an interaction time TI, a correlated pair \(\left|{{\Psi }}\left({T}_{\text{I}}\right)\right\rangle\) is obtained.
Results
The pair amplitude
The electron-pair amplitude is obtained from the underlying electron–polariton coupling. We consider free electrons traveling with mean momentum k0, as depicted in Fig. 1. The full Hamiltonian is given by three contributions: \({\mathcal{H}}={{\mathcal{H}}}_{\text{e}}+{{\mathcal{H}}}_{\phi }+{{\mathcal{H}}}_{\text{e}-\phi }\). The electrons kinetic term is described by \({{\mathcal{H}}}_{\text{e}}\), the electromagnetic field degrees of freedom combined with the surface polaritons are contained in \({{\mathcal{H}}}_{\phi }\)33,34, and the electron–field coupling is \({{\mathcal{H}}}_{\text{e}-\phi }\) (see the “Methods” section). Two initially distinguishable electrons illustrated in Fig. 1 are assumed to be prepared in a statistically independent state, described by the product state \(\left|{{{\Psi }}}_{0}\right\rangle =\int_{{{\Omega }}}d{{\boldsymbol{k}}}_{1}d{{\boldsymbol{k}}}_{2}{\alpha }_{{s}_{1}}^{\left(1\right)}\left({{\boldsymbol{k}}}_{1}\right){\alpha }_{{s}_{2}}^{\left(2\right)}\left({{\boldsymbol{k}}}_{2}\right){c}_{{s}_{1}}^{\dagger }\left({{\boldsymbol{k}}}_{1}\right){c}_{{s}_{2}}^{\dagger }\left({{\boldsymbol{k}}}_{2}\right)\left|{{\emptyset}}\right\rangle\). Here \({c}_{{s}_{i}}^{\dagger }\left({{\boldsymbol{k}}}_{i}\right)\) represents a creation operator of an electron state with momentum ki and spin si, s1 ≠ s2 are known polarizations, Ω is the integration domain, and \(\left|{{\emptyset}}\right\rangle\) denotes a state without electrons. The single-electron amplitude \({\alpha }_{{s}_{i}}^{\left(i\right)}\left({{\boldsymbol{k}}}_{i}\right)\) is determined by the preparation process, and we assume it to be a Gaussian centered around k0 along the propagation axis in our calculations. The opposite spin polarizations allow one to address each electron separately and play a central role in quantum-enhanced metrology protocols (elaborated in the “Methods” section). As the electrons pass in vicinity to the film, they exchange energy via the medium. The interaction mediated by the polaritons decays exponentially with the distance from the medium, validating the use of perturbative approach (see Sec. S1 of the SI). Expanding the evolution in the interaction picture to second order, we obtain the electron-pair wave function in its generic form
where λ labels a set of control parameters. In the present configuration, λ parametrizes the dimensionless interaction time TI and the initial electron bandwidth σe. We are interested in the dynamics of the longitudinal component of the electron pair \(\left({k}_{1},{k}_{2}\right)\). By tracing the transverse momenta, we obtain an expression for \({{{\Phi }}}_{{s}_{1},{s}_{2}}^{\lambda }\left({k}_{1},{k}_{2}\right)\), which we denote as the pair amplitude (see Eq. (5) in the “Methods” section). The pair amplitude exhibits continuous variable entanglement throughout most of the explored parameter space.
Entanglement spectrum and ETMs
It is useful to explore the parameter space of the pair amplitude by performing a Schmidt decomposition. The Schmidt–Mercer theorem allows us to express an inseparable state as a superposition of separable ones,
where spin labels are omitted for brevity. The longitudinal eigenstates \(\left\{{\psi }_{n},{\phi }_{n}\right\}\) appear in pairs of ETMs. If the state ψn is detected, its counterpart occupies the state ϕn with absolute certainty. The eigenvalues pn reflect the probability of detecting the nth mode.
The joint momentum representation of the pair amplitude is displayed in Fig. 2a for the selected values of the control parameters (i.e., a dimensionless interaction time TI and the electron bandwidth σeλp). The dimensionless interaction time is given by \({T}_{\text{I}}=L{\lambda }_{\text{C}}/\beta {\lambda }_{\text{p}\,}^{2}\), where β = v/c is the electron velocity relative to that of the speed of light, λC is the electron Compton wavelength, L is the length of the medium along the main propagation direction, and λp is the polariton wavelength in the film (see Sec. S1 of SI). We employ the collision (Rényi) entropy \({H}_{2}\left[\lambda \right]=-\mathrm{log}\,\left({\sum }_{n}{p}_{n}^{2}\right)\) and Schmidt number \(\kappa \equiv {2}^{{H}_{2}\left[\lambda \right]}\) as measures for entanglement16,17,35,36. The entropy quantifies the degree of uncertainty with respect to the instantaneous ETM, while κ is the effective number of participating ETMs. Sweeping the control parameters throughout the entire dynamical range reveals two opposite highly correlated regimes, as depicted in Fig. 2b, c. For large σeλp and TI, we observe increasing entanglement and correlated momenta due to energy conservation combined with long exchange times. The corresponding amplitude is captured in Φ1 of Fig. 2a, in agreement with the results reported for photonic counterpart16. For short interaction times, narrow-band electrons present anticorrelated momenta that resembles the enhanced features in the loss–gain map presented in ref. 25, due to increased light–electron coupling27. Because of the short interaction time, large energy fluctuations are introduced in the joint system frame (electrons + film), enabling a wide range of anticorrelated momenta visible in Φ5 of Fig. 2a. In this regime, we observe a rapidly growing degree of entanglement, captured by the growing number of participating ETMs. The transition between the positively and negatively correlated regimes is characterized by a very low Schmidt number \(\left(\kappa \approx 1\right)\). This corresponds to an almost separable state, for which a single ETM is required, corresponding to Φ3 in Fig. 2a. In this regime, the electrons can be regarded as approximately disentangled for all practical purposes. The entanglement spectrum plotted in Fig. 2d is obtained from the Schmidt decomposition of the amplitude displayed in the extreme left of Fig. 2e, for which κ ≈ 6. The first (lowest order) three ETMs are visualized along with their corresponding cross-sections.
a The bare pair amplitude \({{{\Phi }}}_{{s}_{1},{s}_{2}}^{\lambda }\left({k}_{1},{k}_{2}\right)\) is presented for selected control-parameter values, covering the key areas of the dynamical range. The amplitudes labeled Φi are calculated at the dimensionless interaction times \({T}_{\text{I}}=\left(1{0}^{-2},1{0}^{-3},1{0}^{-5},1{0}^{-5},1{0}^{-5}\right)\), with bandwidths \({\sigma }_{\text{e}}=\frac{2\pi }{{\lambda }_{\text{p}}}\left(2,2,2,1/2,1/20\right)\), respectively. b Collision entropy versus TI and σe, covering the entire dynamical range from correlated \(\left({{{\Phi }}}_{1}\right)\) to anticorrelated \(\left({{{\Phi }}}_{5}\right)\) momenta. c Variation of the Schmidt number κ along the dotted curve displayed in b, exposing the short time mode meshing of narrow-band electrons. d Schmidt spectrum of the amplitude displayed in e \(\left(\kappa \approx 6\right)\). The corresponding eigenstates are displayed in the inset with matching colors. e Pair amplitude in joint momentum space, where we display the first (lowest order) three modes.
Coincidence detection
A common approach to probe quantum correlations is by measuring the coincidence probability \({{\mathcal{P}}}_{{\boldsymbol{12}}}\left(\delta l\right)=\int {\rm{d}}t\ {\rm{d}}\tau \langle {{{\Psi }}}_{{\boldsymbol{1}}}^{\dagger }\left(t\right){{{\Psi }}}_{{\boldsymbol{2}}}^{\dagger }\left(t+\tau \right){{{\Psi }}}_{{\boldsymbol{2}}}\left(t+\tau \right){{{\Psi }}}_{{\boldsymbol{1}}}\left(t\right)\rangle\), assuming an experimental set-up as sketched in Fig. 3a. We consider balanced beam splitters (BSs) and obtain
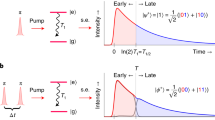
where n,m label ETMs and \({{\mathcal{I}}}_{nm}\left(\delta l\right)=\int {\rm{d}}k\;{\phi }_{n}^{* }\left(k\right){\phi }_{m}\left(k\right){{\rm{e}}}^{-\frac{i}{\hslash }{E}_{k}\delta l/{\boldsymbol{v}}}\) (see Sec. S3 of the SI). Figure 3b displays \({{\mathcal{P}}}_{12}\left(\delta l\right)\) as a function of the BS displacement, arranged in growing degree of entanglement. The probability ranges from 1/2 (completely random) to unity (utterly antibunched) due to two-particle interference in the Mach–Zehnder interferometer depicted in Fig. 3a. Two-particle interference plays a crucial role in Hong–Ou–Mandel (HOM) interferometry, where a Pauli dip is revealed37,38,39. In the left panel of Fig. 3b, we scan TI while fixing σe = 4π/λp in the broadband range. Interestingly, we find that for the higher degree of entanglement the probability peak extends over a wider range of δl. This can be attributed to temporal expansion of the electron wave function due to long interaction times. In the inset, we see that κ grows with TI in a piecewise linear manner, providing a valuable design tool for a desired target state (see Sec. S3 of the SI). On the right panel, σe is varied while TI is fixed in the long interaction range and a similar behavior is found. We find that \(\kappa \propto {\sigma }_{\,\text{e}\,}^{2}\), which is a direct consequence of the initial Gaussian wave packet, together with the emergent linear relations of κ and the interaction time.
a Incoming electron pairs are separated by an electron beam splitter (BS) and subsequently combined by another BS with controllably scanned position, providing a relative path difference δl. The two output ports D1 and D2 are measured in coincidence. b Coincidence probability \({{\mathcal{P}}}_{{\boldsymbol{12}}}\) for varying path difference δl/λp and Schmidt number (degree of entanglement). The left panel corresponds to varying interaction time for fixed σe = 4π/λp. In the right panel, the dimensionless time is fixed to TI = 5 × 10−3 while the initial bandwidth is scanned. The insets show the relations between the control parameters and the Schmidt number.
In Fig. 4a, the coincidence detection (HOM interference) of the instantaneous incoming ETM with a known probe mode labeled ϕp is presented. The first three ETMs are extracted from the Schmidt decomposition of the amplitude displayed in Fig. 2e. These modes are the eigenstates of the reduced single-electron density matrix, therefore in each realization one such mode is detected with probability pn. When the incoming mode matches the shaped probe mode, the coincidence signal exhibits a peak for a vanishing path difference, as depicted in Fig. 4b. By counting the appearance rate of each mode separately, we can deduce the probability vector pn and thus characterize the quantum state. Beyond state tomography, this could also be used in coincidence with parallel operations on its ETM twin, realizing more sophisticated information processing protocols.
a An incoming electron pair prepared in a superposition of ETMs is separated by a first BS, then combined with a (shaped) probe mode ϕp and finally measured in coincidence. b Coincidence outcomes of the probe with three possible incoming modes \(n,p\in \left\{1,2,3\right\}\), as a function of path difference δl. The interference pattern displays increased response for identical probe and incoming ETM.
Discussion
Near fields evolving at the surface of polariton-supporting materials provide a novel approach to generate and shape quantum correlations in charged particles, and in particular in free electrons. While such pairing mechanisms are suppressed in matter due to ambient noise (e.g., thermal), electrons structured in a beam undergo significantly less scattering events, thus enabling coherent interactions to persist over longer space–time intervals. We have shown that electron pairs near polariton-supporting material boundaries undergo nontrivial coupling that generates entanglement. Such correlations are mathematically expressed by the apparent inseparability of the pair amplitude in Eq. (1), giving rise to the results displayed in Fig. 2. The Schmidt decomposition allows us to express the pair amplitude using a set of factorized states, providing useful measures for bipartite entanglement16,17,40,41,42,43,44,45,46. This framework reveals simple relations between the control parameters and the resulting evolution of quantum correlations in the above configuration. Such properties are desirable for entanglement engineering.
The large Hilbert space dimensionality occupied by the ETMs renders them appealing ultrafast quantum information carriers. This has potential applications in quantum-enhanced electron metrology, as proposed using optical set-ups14,47. For example, measuring the momentum of one of the electrons in the pair and the position of the other, one may obtain super-resolved imaging. Such class of quantum enhancements benefits from the fact that single-particle (local) observables are not Fourier conjugates of the (extended) composite state. This work raises multiple open questions concerning vicarious temperature effects, the imprint of the medium topology on the entanglement spectrum, entanglement along the transverse plane, and higher-order electron-matter quantum correlations. These are just a few examples of the emerging field of quantum free-electron metrology. From the information theoretic point of view, the large alphabet spanned by ETMs promotes their candidacy for electron-beam quantum information processing and communication tasks. This raises questions regarding information capacity of the channel in the presence of noise, providing a direction for future study.
Methods
Electron source
First, it is useful to discuss the importance of distinguishability in the initial product state \(\left|{{{\Psi }}}_{0}\right\rangle =\int_{{{\Omega }}}{\rm{d}}{{\boldsymbol{k}}}_{1}{\rm{d}}{{\boldsymbol{k}}}_{2}{\alpha }_{{s}_{1}}^{\left(1\right)}\left({{\boldsymbol{k}}}_{1}\right){\alpha }_{{s}_{2}}^{\left(2\right)}\left({{\boldsymbol{k}}}_{2}\right){c}_{{s}_{1}}^{\dagger }\left({{\boldsymbol{k}}}_{1}\right){c}_{{s}_{2}}^{\dagger }\left({{\boldsymbol{k}}}_{2}\right)\left|{{\emptyset}}\right\rangle\). In order to benefit from the entangled state in a quantum-metrological sense, one crucially relies on the ability to address each of the particles separately, thus exposing nonlocal effects (e.g., photon polarization13,16). By addressing each particle separately using a specified degree of freedom (here the spin), one can measure conjugate quantities—such as the momentum of one and the position of the other—with increased sensitivity48,49. (Complementary to quantum correlations of indistinguishable fermions revealed by the Slater rank50.) We consider the initial state to be prepared using a spin polarized electron source, allowing separate single-particle manipulation prior to the interaction51,52,53. One way to attempt such state preparation is by energy sorting electrons ionized by a pulse sequence that generates altering spin polarization54,55.
Pair-amplitude derivation
The pair amplitude is obtained perturbatively in the interaction picture (Sec. S1 of the SI). The full Hamiltonian of the system contains three contributions: \({\mathcal{H}}={{\mathcal{H}}}_{\text{e}}+{{\mathcal{H}}}_{\phi }+{{\mathcal{H}}}_{\text{e}-\phi }\). The electrons kinetic term is given by \({{\mathcal{H}}}_{\text{e}}={\sum }_{{\boldsymbol{k,s}}}{\epsilon }_{{\boldsymbol{k}}}{c}_{{\boldsymbol{k,}}s}^{\dagger }{c}_{{\boldsymbol{k,}}s}\), where the operator \({c}_{{\boldsymbol{k}},s}\left({c}_{{\boldsymbol{k}},s}^{\dagger }\right)\) creates (annihilates) an electronic mode with momentum k and spin s obeying the anticommutation relations \(\left\{{c}_{{\boldsymbol{k}},s},{c}_{{\boldsymbol{k}}^{\prime} ,s^{\prime} }\right\}={\delta }_{{\boldsymbol{k}}{\boldsymbol{k}}^{\prime} }{\delta }_{ss^{\prime} }\). The term \({{\mathcal{H}}}_{\phi }\) describes the electromagnetic-field degrees of freedom combined with the surface polaritons in the framework of macroscopic quantum electrodynamics33,34. The electron–field coupling is expressed using the Hamiltonian34,56
where λC = h/mec is the Compton wavelength of the electron, while e and me are its charge and mass, respectively. We have employed the Weyl gauge, setting the scalar potential to zero and introduced \({\bf{A}}\left({\bf{q}}\right)\), the vector field operator in momentum space. The vector field in macroscopic quantum electrodynamics is expressed in terms of the Green tensor, encapsulating the geometric and spectral properties of the medium. Proceeding to calculate the first nontrivial order (second), we obtain the general form of Eq. (1). We consider Gaussian initial states of mean distance y0 = 5 nm from the thin film and σy = 0.5 nm (see Fig. 1). Taking the long lx limit and choosing \({\sigma }_{x}=\frac{2\pi }{{\lambda }_{\text{p}}}\), we trace the transverse components and obtain
Here, \({\mathcal{N}}\) is a normalization constant, T is the interaction time, and \(\chi \left(q\right)\) is obtained by tracing the lateral wave vector \({{\boldsymbol{q}}}_{\parallel }=\left({q}_{x},{q}_{y}\right)\) in the interaction picture (Sec. S1 of SI). Additionally, we have invoked the nonrecoil approximation for small momentum exchanges relative to k0, resulting in a linear electron–energy exchange ϵk+q − ϵk ≈ \(\hbar\)q ⋅ v, where q is the polariton wave vector and v is the electron velocity.
ETM calculation
To find the set of ETMs \(\left\{{\psi }_{n},{\phi }_{n}\right\}\) and their weights pn, we solve the integral eigenvalue equations \({p}_{n}{\psi }_{n}\left(k\right)=\int {\rm{d}}k^{\prime} \ {K}_{1}\left(k,k^{\prime} \right){\psi }_{n}\left(k^{\prime} \right)\) and \({p}_{n}{\phi }_{n}\left(k\right)=\int {\rm{d}}k^{\prime} \ {K}_{2}\left(k,k^{\prime} \right){\phi }_{n}\left(k^{\prime} \right)\) (Sec. S2 of SI). The kernels, which are found from the reductions \({K}_{1}\left(k,k^{\prime} \right)=\int {\rm{d}}{k}_{2}\ {{{\Phi }}}_{{s}_{1}{s}_{2}}^{\lambda }\left(k,{k}_{2}\right){{{\Phi }}}_{{s}_{1}{s}_{2}}^{\lambda * }\left(k^{\prime} ,{k}_{2}\right)\) and \({K}_{2}\left(k,k^{\prime} \right)=\int {\rm{d}}{k}_{1}\ {{{\Phi }}}_{{s}_{1}{s}_{2}}^{\lambda }\left({k}_{1},k\right){{{\Phi }}}_{{s}_{1}{s}_{2}}^{\lambda * }\left({k}_{1},k^{\prime} \right)\), can be interpreted as single-electron correlation functions. To obtain the Schmidt spectrum and characterize the degree of entanglement, we discretize the kernels and numerically solve the integral eigenvalue equations. We have used a 800 × 800 discretization of the kernel and repeated the procedure for each control parameter separately. The pair amplitude used for the generation of the kernels involves integration over the polariton degrees of freedom. We have done this numerically for each set of control parameters λ using straightforward numerical integration of Eq. (5) on a uniform grid. The step size was varied to satisfy the convergence of the Schmidt number. The convergence criterion adopted in this scheme is \(\max \left\{2\left({\kappa }_{N+1}-{\kappa }_{N}\right)/\left({\kappa }_{N+1}+{\kappa }_{N}\right)\right\}\le 0.05\), where N is the number of data points within a constant range in the given kernel size.
Data availability
The main results of this manuscript are composed of analytical and numerical calculations. All data generated, analyzed, or required to reproduce the results of this study are included in this article and its Supplementary Information file.
References
Helstrom, C. W. Quantum detection and estimation theory. J. Stat. Phys. 1, 231–252 (1969).
Helstrom, C. W. Resolution of point sources of light as analyzed by quantum detection theory. IEEE Trans. Inf. Theory 19, 389–398 (1973).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information: 10th Anniversary Edition (Cambridge University Press, 2010).
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photonics 5, 222–229 (2011).
Dowling, J. P. Quantum optical metrology-the lowdown on high-n00n states. Contemp. Phys. 49, 125–143 (2008).
Beskrovnyy, V. N. & Kolobov, M. I. Quantum limits of super-resolution in reconstruction of optical objects. Phys. Rev. A 71, 043802 (2005).
Kolobov, M. I. The spatial behavior of nonclassical light. Rev. Mod. Phys. 71, 1539–1589 (1999).
Brida, G., Genovese, M. & Berchera, I. R. Experimental realization of sub-shot-noise quantum imaging. Nat. Photonics 4, 227–230 (2010).
Rozema, L. A. et al. Scalable spatial superresolution using entangled photons. Phys. Rev. Lett. 112, 223602 (2014).
Israel, Y., Tenne, R., Oron, D. & Silberberg, Y. Quantum correlation enhanced super-resolution localization microscopy enabled by a fibre bundle camera. Nat. Commun. 8, 14786 (2017).
Asban, S., Dorfman, K. E. & Mukamel, S. Quantum phase-sensitive diffraction and imaging using entangled photons. Proc. Natl Acad. Sci. USA 116, 11673–11678 (2019).
Mukamel, S. et al. Roadmap on quantum light spectroscopy. J. Phys. B At. Mol. Opt. Phys. 53, 072002 (2020).
Dorfman, K. E., Schlawin, F. & Mukamel, S. Nonlinear optical signals and spectroscopy with quantum light. Rev. Mod. Phys. 88, 045008 (2016).
Schlawin, F., Dorfman, K. E. & Mukamel, S. Entangled two-photon absorption spectroscopy. Acc. Chem. Res. 51, 2207–2214 (2018).
Hong, C. K. & Mandel, L. Theory of parametric frequency down conversion of light. Phys. Rev. A 31, 2409–2418 (1985).
Law, C. K., Walmsley, I. A. & Eberly, J. H. Continuous frequency entanglement: effective finite hilbert space and entropy control. Phys. Rev. Lett. 84, 5304–5307 (2000).
Law, C. K. & Eberly, J. H. Analysis and interpretation of high transverse entanglement in optical parametric down conversion. Phys. Rev. Lett. 92, 1–4 (2004).
Mair, A., Vaziri, A., Weihs, G. & Zeilinger, A. Entanglement of the orbital angular momentum states of photons. Nature 412, 313 (2001).
Fickler, R., Krenn, M., Lapkiewicz, R., Ramelow, S. & Zeilinger, A. Real-time imaging of quantum entanglement. Sci. Rep. 3, 1–5 (2013).
García de Abajo, F. J. Optical excitations in electron microscopy. Rev. Mod. Phys. 82, 209–275 (2010).
Vanacore, G. M. et al. Attosecond coherent control of free-electron wave functions using semi-infinite light fields. Nat. Commun. 9, 2694 (2018).
Vanacore, G. M. et al. Ultrafast generation and control of an electron vortex beam via chiral plasmonic near fields. Nat. Mater. 18, 573–579 (2019).
Madan, I. et al. Holographic imaging of electromagnetic fields via electron-light quantum interference. Sci. Adv. 5, eaav8358 (2019).
Reinhardt, O., Mechel, C., Lynch, M. & Kaminer, I. Free-electron qubits. In Conference on Lasers and Electro-Optics, OSA Technical Digest FF1F.6 (Optical Society of America, 2019).
Kfir, O. Entanglements of electrons and cavity photons in the strong-coupling regime. Phys. Rev. Lett. 123, 103602 (2019).
Wang, K. et al. Coherent interaction between free electrons and a photonic cavity. Nature 582, 50–54 (2020).
Kfir, O. et al. Controlling free electrons with optical whispering-gallery modes. Nature 582, 46–49 (2020).
Lee, S.-S., Lee, P. A. & Senthil, T. Amperean pairing instability in the u(1) spin liquid state with fermi surface and application to κ–(BEDT–TTF)2cu2(CN)3. Phys. Rev. Lett. 98, 067006 (2007).
Lee, P. A. Amperean pairing and the pseudogap phase of cuprate superconductors. Phys. Rev. X 4, 031017 (2014).
Schlawin, F., Cavalleri, A. & Jaksch, D. Cavity-mediated electron-photon superconductivity. Phys. Rev. Lett. 122, 133602 (2019).
Brecht, B., Reddy, D. V., Silberhorn, C. & Raymer, M. G. Photon temporal modes: a complete framework for quantum information science. Phys. Rev. X 5, 041017 (2015).
Raymer, M. G. & Walmsley, I. A. Temporal modes in quantum optics: then and now. Phys. Scr. 95, 064002 (2020).
Buhmann, S. Y. Dispersion Forces I (Springer-Verlag, 2012).
Dung, H. T., Knöll, L. & Welsch, D.-G. Three-dimensional quantization of the electromagnetic field in dispersive and absorbing inhomogeneous dielectrics. Phys. Rev. A 57, 3931–3942 (1998).
Rényi, A. On measures of entropy and information. In Proc. Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics, 547–561 (University of California Press, 1961).
Müller-Lennert, M., Dupuis, F., Szehr, O., Fehr, S. & Tomamichel, M. On quantum Rényi entropies: a new generalization and some properties. J. Math. Phys. 54, 122203 (2013).
Bocquillon, E. et al. Coherence and indistinguishability of single electrons emitted by independent sources. Science 339, 1054–1057 (2013).
Giovannetti, V., Frustaglia, D., Taddei, F. & Fazio, R. Electronic Hong-Ou-Mandel interferometer for multimode entanglement detection. Phys. Rev. B 74, 115315 (2006).
Neder, I. et al. Interference between two indistinguishable electrons from independent sources. Nature 448, 333–337 (2007).
Ekert, A. & Knight, P. L. Entangled quantum systems and the Schmidt decomposition. Am. J. Phys. 63, 415–423 (1995).
Parker, S., Bose, S. & Plenio, M. B. Entanglement quantification and purification in continuous-variable systems. Phys. Rev. A 61, 032305 (2000).
Giedke, G., Wolf, M. M., Krüger, O., Werner, R. F. & Cirac, J. I. Entanglement of formation for symmetric Gaussian states. Phys. Rev. Lett. 91, 107901 (2003).
Straupe, S. S. et al. Self-calibrating tomography for angular Schmidt modes in spontaneous parametric down-conversion. Phys. Rev. A 87, 042109 (2013).
Laskowski, W., Richart, D., Schwemmer, C., Paterek, T. & Weinfurter, H. Experimental Schmidt decomposition and state independent entanglement detection. Phys. Rev. Lett. 108, 240501 (2012).
Sciara, S., Lo Franco, R. & Compagno, G. Universality of Schmidt decomposition and particle identity. Sci. Rep. 7, 44675 (2017).
Giddings, S. B. & Rota, M. Quantum information or entanglement transfer between subsystems. Phys. Rev. A 98, 062329 (2018).
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photonics 5, 222–229 (2011).
Howell, J. C., Bennink, R. S., Bentley, S. J. & Boyd, R. W. Realization of the einstein-podolsky-rosen paradox using momentum- and position-entangled photons from spontaneous parametric down conversion. Phys. Rev. Lett. 92, 210403 (2004).
Saunders, D. J., Jones, S. J., Wiseman, H. M. & Pryde, G. J. Experimental EPR-steering using bell-local states. Nat. Phys. 6, 845–849 (2010).
Schliemann, J., Cirac, J. I., Kuś, M., Lewenstein, M. & Loss, D. Quantum correlations in two-fermion systems. Phys. Rev. A 64, 022303 (2001).
Kohashi, T., Konoto, M. & Koike, K. High-resolution spin-polarized scanning electron microscopy (spin SEM). J. Electron Microsc. 59, 43–52 (2009).
Kuwahara, M. et al. Development of spin-polarized transmission electron microscope. J. Phys. Conf. Ser. 298, 012016 (2011).
Kohashi, T. Chapter two - spin-polarized scanning electron microscopy. In Advances in Imaging and Electron Physics 83–125 (Elsevier, 2015).
Barth, I. & Smirnova, O. Spin-polarized electrons produced by strong-field ionization. Phys. Rev. A 88, 013401 (2013).
Hartung, A. et al. Electron spin polarization in strong-field ionization of xenon atoms. Nat. Photonics 10, 526–528 (2016).
Dressel, M. & Grüner, G. Electrodynamics of Solids: Optical Properties of Electrons in Matter (Cambridge University Press, 2002).
Acknowledgements
We gratefully acknowledge help from Noa Asban on the graphical illustrations. This work has been supported in part by the Spanish MINECO (MAT2017-88492-R and SEV2015-0522), the European Research Council (Advanced Grant 789104-eNANO), the European Commission (Graphene Flagship 696656), the Catalan CERCA Program, and Fundació Privada Cellex.
Author information
Authors and Affiliations
Contributions
Both authors have contributed equally to this work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Asban, S., García de Abajo, F.J. Generation, characterization, and manipulation of quantum correlations in electron beams. npj Quantum Inf 7, 42 (2021). https://doi.org/10.1038/s41534-021-00376-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-021-00376-4
This article is cited by
-
Extremal quantum correlation generation using a hybrid channel
Scientific Reports (2023)