Abstract
Spin-dependent photogalvanic effect (PGE) in low-dimensional magnetic systems has recently attracted intensive attention. Based on first-principle transport calculations and symmetry analyses, we propose a robust scheme to generate pure spin current by PGE in centrosymmetric materials with spin polarization antisymmetry. As a demonstration, the idea is successfully applied to a photoelectric device constructed with a zigzag graphene nanoribbon (ZGNR), which has intrinsic antiferromagnetic coupling between the two edges and spin degenerate band structure. It suggests that spin splitting is not a prerequisite for pure spin current generation. More interestingly, by further introducing external transverse electric fields to the two leads to lift the spin degeneracy, the device may behave multifunctionally, capable of producing fully spin-polarized current or pure spin current, depending on whether the fields in the two leads are parallel or antiparallel. Very importantly, our scheme of pure spin current generation with PGE is not limited to ZGNR and can be extended to other two-dimensional (2D) centrosymmetric magnetic materials with spin polarization antisymmetry, suggesting a promising category of 2D platforms for PGE-based pure spin current generation.
Similar content being viewed by others
Introduction
The photogalvanic effect (PGE), characterized by a finite direct electric current produced in materials lacking space inversion symmetry by the light illumination without any applied bias voltage, has great potential in the field of the photoelectric devices due to the great advantages of its self-powered function1,2,3,4,5,6,7,8,9. This important concept is first predicted by Pikus and Belinicher independently1,2, and then quickly observed in tellurium crystal in experiment3, followed by considerable investigations since then4,5,6,7,8,9,10,11,12,13,14,15,16,17. Inspired by the recent progress in the fields of two-dimensional (2D) semiconductors and ferromagnets with atomic thickness18,19,20,21,22,23,24,25, substantial efforts have also been made in generating photocurrent by PGE in 2D materials, where the structures are designed to lack structural inversion symmetry purposely by various ways, such as atom doping26, chemical decoration27, heterojunction28, and gate voltage29, etc.
In spintronics, the generation of fully spin-polarized current and pure spin current without accompanying net charge current is a fundamental, but critical task in developing future spin-based devices30,31. To date, the scaling of the traditional electronic devices has almost reached the bottleneck in semiconductor industry. Fortunately, the successive discoveries of the intrinsic magnetism in 2D materials have provided a new platform for low-dimensional spintronics22. These theoretical and experimental advances have also intrigued more research efforts on the PGE-induced spin-dependent transport in these 2D magnetic systems or their hybrid systems, especially for the generation of the fully spin-polarized current and pure spin current27,28,32,33. For example, Xie et al. have theoretically proposed a spin battery that induces pure spin current by PGE based on Ni/phosphorene/Ni junction28. Very recently, we have also designed a spin-photovoltaic device based on silicene nanoribbon with asymmetric hydrogenation that breaks the structural inversion symmetry, in which a fully spin-polarized current and pure spin current is obtained27. Besides ferromagnetic systems, PGE-induced pure spin current is also predicted in antiferromagnetically ordered hexagonal SiC zigzag nanoribbons33. However, in all the above systems, the conditions for obtaining pure spin current are extremely strict since it can be achieved only by precisely tuning the photons at specific energy or specific polarization/helicity angle, which is rather difficult in practice. In addition, previous attention was mainly focused on magnetic materials with spin splitting in the energy band structure. In magnetic systems with Cs symmetry, it is interesting that pure spin current is predicted at special polarization angles 0∘, 90∘, and 180∘; however, it demands an external magnetic field applied to one of the ferromagnetic leads to achieve an antiparallel magnetic configurations of the two leads27,28. A natural question to ask is that, are there schemes for pure spin current generation with PGE that are not limited to any particular photon energy or polarization angle, not limited to materials with spin splitting band structures, and demand no external magnetic fields?
In this work, we intend to provide a solution for this problem. We theoretically propose a class of spin photogalvanic devices for pure spin current generation with PGE based on AFM semiconductors, in which the whole structure holds spatial inversion symmetry while the real-space charge distribution of neither the spin-up state nor the spin-down state holds spatial inversion symmetry. One typical example is zigzag graphene nanoribbons (ZGNRs) which have special localized edge states, with the two edges antiferromagnetically coupled. Here, we take 6-ZGNR which has six zigzag carbon chains as an example. It is found that, under the illumination of the polarized light, pure spin current can be robustly generated, neither dependent of the photon energy nor dependent of the polarization feature of the light. The robustness is ascribed to the spatial inversion symmetry and spin density inversion antisymmetry. In addition, by applying an external transverse electric filed, the symmetry of the spin-dependent density of the ZGNR can be significantly modulated, providing a possible way for tuning the photocurrent generation. We find that, when two antiparallel electric fields with the same magnitude are applied to the two leads, pure spin current can still be robustly generated by PGE due to the preservation of spin density antisymmetry. In contrast, when the fields in the two leads are changed to parallel, fully spin-polarized photocurrent can be achieved. Thus, by reversing the electrical fields in the two leads, the ZGNR can be conveniently tuned to achieve fully spin-polarized current and pure spin current, realizing two ideal goals in spintronics. Further, we demonstrate that pure spin current generation scheme with PGE proposed in this work can be extended to other antiferromagnets with spatial inversion symmetry and bilayer 2H-VSe2 is provided as example of 2D A-type van der Waals (vdWs) antiferromagnets for the extension.
Results and discussion
Electronic structures of 6-ZGNR without and with applying gate voltages
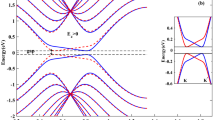
The photocurrent of two antiferromagnetic systems, namely, a ZGNR and a bilayer 2H-VSe2, will be studied. As an example, the photoelectric device constructed with 6-ZGNR is shown in Fig. 1. It is divided into three parts: left lead (L), right lead (R), and scattering region (S). The edge dangling bonds are passivated by hydrogen atoms. The scattering region is chosen to contain 11.5 unit cells with length 28.29 Å so that it is centrosymmetric. To produce photocurrent, light is normally irradiated at the region containing 5.5 unit cells marked by the dashed line box. Before analyzing the photon-induced spin transport properties of the proposed spin photogalvanic device, we first investigate the electronic structures of 6-ZGNR used for constructing the device with and without applying the transverse electric field. The transverse electrical field is applied by setting a gate voltage +Vg/2 at one edge and −Vg/2 at the opposite edge along the transverse direction34, thus, the strength and direction of the transverse electrical field are indicated by the magnitude and sign of Vg, respectively. Without applying a gate voltage, namely, Vg = 0 V, our results show that the ground state of 6-ZGNR is an AFM state, characterized by ferromagnetic coupling along each edge and antiferromagnetic coupling between the two edges. The spin-polarized band structure shows that spin-up and spin-down states are exactly degenerate and both exhibit semiconducting character with a direct band gap of 0.62 eV, which is seen in Fig. 2a. These results are in good agreement with previous studies32. By further investigating the spin-resolved edge states at the valence band maximum (VBM) and conduction band minimum (CBM) shown in Fig. 2b, it is clearly seen that spin-up edge states ∣Ψ↑(r)∣ in the valence band are localized at the bottom edge, while spin-down edge states ∣Ψ↓(r)∣ are localized at the top edge. On the contrary, in the conduction band, ∣Ψ↑(r)∣ are localized at the top edge, while ∣Ψ↓(r)∣ are localized at the bottom edge. Due to these unique localization features of the edge states, by applying a positive transverse electrical field penetrating from the top edge to the bottom edge, the edge states of the two spin components in the bottom edge increase in potential energy while those in the top edge decrease, which causes the spin-up gap to decrease and spin-down gap to increase (see Fig. 2a, c). This phenomenon becomes more remarkable with the increase of the gate voltages and half-metallicity emerges at a critical gate voltage Vg ~ 10 V, with spin-up bands crossing the Fermi level. The situation is reversed with the sign reverse of the gate voltage and half-metallicity with spin-down bands crossing the Fermi level is induced. An interesting observation is that after one spin channel becomes metallic, the band gap of the other spin channel drops suddently, as seen from Fig. 2c. This can be understood as follows. Within the Hubbard model, i.e., \(H=-t{\sum }_{\langle i,j\rangle ,\sigma }[{c}_{i\sigma }^{\dagger }{c}_{j\sigma }+\mathrm{h.c.}]+U{\sum }_{i}{n}_{i\uparrow }{n}_{i\downarrow }\), the band gap is proportional to the Coulomb interaction parameter U. Here, with the increase of postive gate voltage (similar for negative gate voltage), for the spin-down channel, the gap increases nearly linearly first, this is due to the linear shift in potential energy from the external field. If there were no changes in the states and no charge redistribution, then this linear increase trend would continue. However, due to the charge redistribution, the increasing trend deviate from the linear curve. At ~10 V, the band gap in the spin-up channel closes, and it becomes metallic. The screening effects from the metallic spin-up electrons greatly reduces the effective Coulomb interaction parameter U and leads to the sudden decrease of gap in the spin-down channel.
The a top view and b front view of the proposed spin photogalvanic device model based on 6-ZGNR. \({{\bf{e}}}_{{\bf{1}}}=\hat{z}\) and \({{\bf{e}}}_{{\bf{2}}}=-\hat{x}\) are two polarized vectors that determine the incident direction of the polarized light. The red spiral arrows denote the applied polarized light. A is the electromagnetic vector potential and θ is the polarization angle of the polarized light. The black dashed line denotes the mirror plane. c Three gate configurations: ZZ, PP, and PN. Here, ZZ denotes that there is no gate voltage applied in device. PP (PN) denotes that a positive (positive) gate voltage is applied in the left lead and a positive (negative) gate voltage is applied in the right lead.
a Spin-polarized band structures of 6-ZGNR at different in-plane gate voltages Vg. The dark-pink and blue colors denote spin-up (↑) and spin-down (↓) states, respectively. b The real-space wave function distributions of the edge states of the 6-ZGNR. c The gate voltage dependence of the band gap for the spin-up (↑) and spin-down (↓) states. The gray shaded areas denote that half-metallicity can be induced.
Spin photogalvanic device based on 6-ZGNR
Note that spin polarization and spatial inversion asymmetry of the states in each spin channel are essential conditions to achieve photon-induced spin transport by PGE. Obviously, the pristine 6-ZGNR satisfies the above criteria, thus we will study its spin-dependent PGE in the following. In addition, it is worth noting that the introduction of an external electric field in ZGNR not only leads to spin splitting, but also changes the symmetry of the electronic structure of the pristine system due to the redistribution of the spin-dependent charge density. Thus, the gate voltage provides a strategy for tuning the symmetry of the spin polarization and subsequently the spin-dependent photocurrent generation by PGE in ZGNR. In this regard, we construct a dual-gated optoelectronic device based on 6-ZGNR, as shown in Fig. 1a, b. In-plane gates are applied symmetrically in the left and right leads, and parts of the scattering region. The signs of the gate voltages in two leads can be switched individually. Thus, as shown in Fig. 1c, three gate configurations including zero:zero (ZZ), positive:positive (PP), and positive:negative (PN) gate voltages for the two leads will be considered.
Firstly, we consider the case of “ZZ” configuration in which no gate voltages are applied in both leads. Figure 3a, b shows the total charge ρ(0) = ρ↑ + ρ↓ and spin density ρs(0) = ρ↑ − ρ↓, respectively. Here, ρ↑ (ρ↓) is spin-up (-down) charge density and 0 in the bracket denotes zero gate voltage. It is found that, the total charge density exhibits perfect spatial inversion symmetry, which is determined by the structure being of D2h point group. However, for the spin-dependent charge densities, both two spin channels exhibit mirror symmetry (Cs symmetry) with respect to the black dashed line in the device model (see Fig. 1a), but no inversion symmetry, which means that they are not invariant under the spatial inversion operation for each spin component itself. It has already demonstrated that a finite photocurrent can be generated in the systems with Cs symmetry and no inversion symmetry by PGE27,28,35. This means that, although the system has spatial inversion symmetry in structure, spin-dependent photocurrent can be induced by PGE when the inversion symmetry of the charge density for each spin component is broken. Indeed, our numerical results confirm this speculation. Figure 4a, b presents the spin-up (I↑), spin-down (I↓) photocurrents, and the total charge photocurrent (Ic = I↑ + I↓) as functions of polarization angle θ and helicity angle φ under the irradiation by linearly polarized light (LPL) and elliptically polarized light (EPL), respectively, with photon energy Eph = 0.65 eV slightly larger than the intrinsic band gap of 6-ZGNR. It is clearly seen that both I↑ and I↓ are finite and present a sinusoidal relationship with 2θ (2φ) by LPL (EPL), which is a unique characteristic of the linear (circular) PGE in the material with Cs symmetry35. More interestingly, spin-up and spin-down photocurrents always have the same magnitude but opposite signs, which results in a vanished total charge current Ic and a finite spin current (Is = I↑ − I↓). Therefore, pure spin current without any accompanying charge current is generated by PGE. We also note that the photocurrent induced by EPL is an order of magnitude larger than that induced by LPL. This phenomenon is not a general result, and it is highly related to the electrnonic and structural information of the studied systems. Furthermore, our further investigations demonstrate that the same features are observed at increasing photon energies. Specifically, the spin dependent and total charge photocurrents as a function of photon energy under LPL/EPL with θ/φ = 45∘ are shown in Supplementary Fig. 1. It means the robust generation of the pure spin current in the sense that it is insensitive either to the photon energy or to the polarization angle and type of the light. Of course, the photon energy should be larger than the band gap of the system, since below which electrons can not be excited from the valence band to the conduction band, thus no photocurrent can be induced.
a The charge density ρ(0) and b the spin density ρs(0) of 6-ZGNR without any gate voltage. A positive (negative) value denotes spin-up (-down) component. The gate voltage-induced c charge density difference Δρ = ρ(Vg) − ρ(0) and d spin density difference Δρs = ρs(Vg) − ρs(0) in “PP” configuration. The gate voltage-induced e Δρ and f Δρs in “PN” configuration. Vg is set to 12 V.
The spin-up (I↑), spin-down (I↓), and total charge photocurrents (Ic) under a LPL and b EPL with photon energy Eph = 0.65 eV in “ZZ” configuration. θ (φ) denotes the polarization (helicity) angle of the linearly (elliptically) polarized light. φ = 45∘ and 135∘ correspond to right and left circularly polarized light, respectively. c Schematic plot of the photocurrent generation in AFM ZGNR. The orange and black areas denote the edge state bands of the nanoribbon. The real space representation of the photocurrent generation is shown by a schematic plot for d spin-up channel and e spin-down channel. “Upper” and “lower” mean the upper edge and lower edge of the ribbon, while v and c mean the locations of the edge states in the valence band and the conduction band, respectively. θ is the angle between the incoming and outgoing electron momentum p and the vector potential A.
To clearly understand the physical origin of the pure spin current generation in 6-ZGNR, we first present the general process of the photocurrent in spin photogalvanic device by the schematic diagram in Fig. 4c. Under the irradiation of the light with photon energy larger than the optical gap, the spin-up and spin-down electrons will be excited from the valence bands to the conduction bands. Then the electrons excited will further move to the left and right leads due to the nonequilibrium between the scattering region and the leads (we call this outgoing process). At the same time, the holes left in the scattering region will be filled by the electrons coming from the left and right leads (incoming process). The above processes are denoted by the red and blue dashed arrows as shown in Fig. 4c, where red and blue colors denote spin-up and spin-down components, respectively. For each lead, the net photocurrent is determined by the sum of current components induced in the incoming and outgoing processes, occurring in the valence band and conduction band, respectively.
Now we will understand why the photocurrents of the spin-up and spin-down components always have the same magnitude, and opposite signs phenomelogically by the schematic diagrams in Fig. 4d, e. We first focus on the spin-up photocurrent induced by the excitation of electrons between the edge states of the valence bands and conduction bands. Suppose the spin-up edge states in the valence band are located at the lower edge, then those in the conduction band are located at the upper edge (see Fig. 4d). When the electrons in the valence band are excited into the conduction band, they will move from the lower edge to the upper edge in real space. In a sense, the polarization direction plays the role of tuning the relative probability of the electrons incoming from (or outgoing to) the two leads. As indicated in Fig. 4d, the polarization angle θ measured between the incoming or outgoing electron momentum p and the vector potential A for the two leads will be supplementary. According to Eq. (4), it will add a positive or negative term to the Hamiltonian for the electrons from the two leads, respectively. It can be reasonably supposed that it is easier for the electrons from one lead with an obtuse angle θ(>90∘) than the other lead with an acute angle 180∘ − θ(<90∘) to come into (leave from) the central region, then for the case shown in Fig. 4d, the current flowing in from the left lead will be larger than that from the right lead, and current flowing out to the right lead will be larger than that flowing out to the left lead, as indicated by the thickness of the curves showing the photocurrent. In this case, the net spin-up photocurrent will flow from the left lead to the right lead. For the spin-down component, since the spin-down edge states in the valence band are located at the upper edge and those in the conduction band are located at the lower edge, the excitation process will be like that shown in Fig. 4e and the electrons will flow from the upper edge to the lower edge. In addition, the incoming current from the right lead will be larger than that from the left lead and the outgoing current to the left lead will be larger than that to the right lead. The net spin-down photocurrent will flow from the right lead to the left lead. Since the spin-up and spin-down edge states in either the valence band or the conduction band are exactly degenerate both in energy and in real space, all the current components everywhere in the device for the two spin channels will be exactly equal in magnitude and opposite in flow direction. Of course, for each spin component, besides the edge states, the bulk states will also participate. However, since the bulk states at each energy for the two spin channels have exactly the same real space distribution, the photocurrent contributed by them for the two spin channels will also take the same magnitude and opposite directions. Thus, pure spin current will be generated, independent of the polarization angle.
For θ = 90∘, the two incoming (outgoing) components from (to) the two leads will be equal, leading to zero current for both spin channels. For θ < 90∘, the left flowing component for both spin channels will be larger than the right flowing one, thus the direction of the pure spin current will be reversed. As for θ = 0∘ and 180∘, since the polarization direction is parallel to the incoming direction of the electrons from the leads, the probability from one edge to the other one will be zero, thus the current for both spin channels will be zero. Very interesting is the case θ = 90∘. Although for each spin component in each lead, the incoming component and the outgoing component cancels each other exactly, thus the total pure spin current is zero, pure spin current can still be locally detected everywhere at the edges, since the incoming path and the outgoing path are located at the upper edge and lower edge, respectively.
The above phenomenon can further be understood by symmetry analyses. It is well known that PGE is a nonlinear and asymmetry-induced optical effect. The photocurrent is proportional to the quadratic relation of the electric filed of the irradiated light, namely, I ~ −βEE*, where β is the PGE coefficient28. The generation of the PGE-induced current is due to the broken inversion symmetry of the PGE coefficient, i.e., β(r) ≠ β(−r), which generally occurs in polar or p–n hybrid systems that lack inversion center. Note that, for spin-polarized systems, β(r) is spin dependent, thus β(r) = β↑(r) + β↓(r), where β↑(r) and β↓(r) are the spin-up and spin-down components of the PGE coefficient, respectively. For an AFM system with inversion symmetry we have spin-dependent charge density ρ↑(r) = ρ↓(−r) and ρσ(r) ≠ ρσ(−r) with σ = ↑, ↓, and total charge density ρc(r) = ρc(−r). It is well known that the fundamental physical properties of a system are determined by its charge density. Thus, we can get β↑(r) = β↓(−r) and βσ(r) ≠ βσ(−r) due to the spin rotation symmetry SU(2). This means that we will have I↑ ≠ 0 and I↓ ≠ 0, but I↑ + I↓ = 0.
Gate-controlled spin photogalvanic transport behaviors
The application of the gate voltage will lead to the charge redistribution and a significant spin splitting in the band structure, which creates a possibility to further tune the PGE effect on 6-ZGNR. In the following, we discuss the gate effect when a gate voltage of Vg = 12 V with “PP” configuration and “PN” configuration are applied in the device. Figure 3c–f presents the Vg-induced charge density difference Δρ, and spin density difference Δρs in “PP” and “PN”configurations. For the “PP” case, as shown in Fig. 3c, d, we find that both Δρ and Δρs exhibit mirror symmetry due to the introduction of two symmetric electric fields with same magnitude and direction, indicating that the inversion symmetry of the total charge density ρ is broken and further switches to Cs symmetry, while the charge density for each spin component (ρ↑ and ρ↓) still holds Cs symmetry. In contrast to “PP” configuration, “PN” configuration presents a different situation. As shown in Fig. 3e, f, it is seen that Δρ is symmetric and Δρs is antisymmetric with respect to the inversion center along any direction, which means that the inversion symmetry in the total charge density and inversion antisymmetry in the spin-dependent density are retained, when two antiparallel electric fields are introduced. These particular symmetries will result in very interesting spin transport behavior under light irradiation, as shown below.
We then study the PGE of the “PP” configuration. When Vg = 12 V is applied in the device, both leads now become half-metal with metallicity for the spin-up channel and a band gap of 0.86 eV for the spin-down channel (see Fig. 2a), while the illuminated part of the scattering region, represented by the red dotted line in Fig. 1a, presents semiconducting character since there is no gate voltage applied in this part. The whole photoelectric device thus forms a half-metal/semiconductor/half-metal (HM/S/HM) structure. Figure 5a, b shows the spin-dependent photocurrents (I↑, I↓) and total charge photocurrent (Ic) as functions of polarization angle θ, and helicity angle φ under LPL and EPL with photon energy Eph = 0.65 eV, respectively. It is found that I↑ varies as a function of \(\sin (2\theta )\) or \(\sin (2\varphi )\), while I↓ is always zero. Consequently, the total charge photocurrent is equal to that of spin-up component and also presents a sinusoidal relationship with 2θ or 2φ, demonstrating a fully spin-polarized current generated by PGE. This phenomenon can be well understood by a schematic plot in Fig. 6a. Under the light irradiation with photon energy slightly larger than the band gap of the pristine 6-ZGNR, only spin-up electrons are excited and involved in the whole photocurrent generation process due to the spin matching of the corresponding energy range between the scattering region and the leads, resulting in a single spin flow. When the photon energy is larger than the spin-down gap of the half-metallic lead, both spin-up and spin-down electrons will be involved in the photocurrent generation progress, since the leads and the scattering region have spin matching states in the corresponding energy range for both spin-up and spin-down channels (see Fig. 6b). Therefore, each spin contributes a photocurrent. This is demonstrated in Supplementary Fig. 2. Note that the spin-dependent and total charge photocurrents always have a sine dependence on 2θ or 2φ, regardless of the photon energy, which is consistent with the previous symmetry analysis, where the distribution of both the charge density and spin density holds Cs symmetry.
The schematic plot of spin photocurrent generation occurring at: a the photon energy slightly larger than the band gap and b the photon energy much larger than the band gap in “PP” configuration. The schematic plot of spin photocurrent generation occurring at: c the photon energy slightly larger than the band gap and d the photon energy much larger than the band gap in “PN” configuration.
Next, we discuss the PGE of the “PN” configuration. Figure 5c, d display the spin-dependent and total charge photocurrent by LPL and EPL with Eph = 0.65 eV, respectively. It is found that both I↑ and I↓ are finite and still present sine dependence on 2θ or 2φ, but there is significant shift along the vertical axis compared with the case without applying any gate voltage. In this case, the spin-dependent photocurrent \({I}_{\uparrow /\downarrow }=\pm\! a\sin (2\theta )\pm b\) or \({I}_{\uparrow /\downarrow }=\pm\! a\sin (2\varphi )\pm b\). Meanwhile, we notice that although the magnitude a and the shift b are different for the LPL and EPL cases, as seen from the Fig. 5c, d, I↑ and I↓ always have the same magnitude but opposite sign, meaning that a finite pure spin current is always generated, independent of the polarization/helicity angle or the polarization type. This is due to the inversion antisymmetry of the spin density and the inversion symmetry of the total charge density with respect to the inversion center. Similar curves for higher photon energy are presented in Supplementary Fig. 3, all unambiguously giving rise to pure spin current. Obviously, in contrast to the “PP” configuration, both spin-up and spin-down electrons are involved in the generation of the photocurrent in the “PN” configuration. However, there is a slight difference in the photocurrent generation for low and high photon energy excitations. For a photon energy slightly larger than the band gap of the illumination region, the flowing of the spin-up electrons only occur in the region between the left lead and the scattering region, while the spin-down electrons only occur in the region between the right lead and the scattering region. This is because the left lead only provides transport channels for the spin-up electrons, while the right lead only provides transport channels for the spin-down electrons, as determined by the band structure shown in Fig. 6c. With a larger photon energy, both spin-up and spin-down electrons are involved in all flowing paths between two leads and the scattering region (see Fig. 6d).
It has been demonstrated that an extremely high electric field is required to achieve half-metallicity in ZGNR36,37, which is almost impractical in present industrial technology. Thus, it is essential to demonstrate if these unique features can be obtained by decreasing the gate voltage. To this end, we calculate the photocurrent for “PP” and “PN” configurations at Vg = 5 V. The results show that the photocurrent behaves in the same way as that at Vg = 12 V, as shown in Supplementary Fig. 4. This is because the magnitude change of the gate voltage only affects the degree of spin splitting of the leads, and does not affect the symmetries of the spin density and the total charge density.
Extension to known 2D centrosymmetrical antiferromagnets
Note that this mechanism can be ubiquitously applied to other quasi-1D nanoribbons based on column-IV 2D materials, which also exhibit ZGNR-like AFM edge states, such as silicene38, germanene39, and stanene34. More generally, it is also applicable to any antiferromagnets with spatial inversion symmetry, such as 2D A-type AFM vdWs materials. In the following, we study the PGE in bilayer 2H-VSe2 (ref. 40), which is a 2D A-type vdW structure with intralayer ferromagnetism and interlayer antiferromagnetism. Figure 7a and Supplementary Fig. 5 show the layer-projected density of states (DOS) and the spin-polarized band structure of the bilayer 2H-VSe2, respectively. It is found that spin-up and spin-down states are degenerate and exhibit semiconducting character with an indirect band gap of 0.34 eV, which agrees well with previous study40,41. Moreover, it shows that, in the bilayer 2H-VSe2, spin-up states in VBM are contributed by the second VSe2 layer (L2), while spin-down states are contributed by the first VSe2 layer (L1). However, in the CBM, spin-up states are contributed by L1, while spin-down states are contributed by L2. Based on these unique properties that are similar to the edge states in ZGNR, half-metallicity can also be achieved in the bilayer 2H-VSe2 by applying a proper external vertical electric field40. More importantly, the spin density in Fig. 7b shows that it is antiferromagnetic coupled between the two layers and the charge densities of the two spin components are always antisymmetric under the inversion operation. This unique feature unambiguously demonstrates that the robust generation of pure spin current will occur in this system. We have carried out photocurrent calculations for the spin photogalvanic device based on bilayer 2H-VSe2, as shown in Supplementary Fig. 6, in which the spatial inversion symmetry is maintained. It is periodic in both in-plane directions and the transport direction is along the zigzag direction. The results show that pure spin current is obtained, independent of polarization/helicity angle and the photon energy (see Fig. 7c, d). From theses results, we can conclude that the generation of pure spin current in centrosymmetric material originates from the spin polarization antisymmetry.
a The layer-projected DOS of the bilayer 2H-VSe2. L1 (L2) denotes the first (second) layer of bilayer VSe2. Positive (negative) value of DOS represents spin-up (-down) component. b The spin density of the bilayer 2H-VSe2. The spin-dependent and total charge photocurrent under c LPL and d EPL with Eph = 0.65 eV.
Finally, we note that the irradiated region is chosen as small as nanometers in the examples above mainly because of computation capability consideration. For practical devices, both the system size and irradiated region can be much larger for easier experimental realization. Specifically, if part atoms of the leads are also under irradiation to increase the irradiated region size, the magnitude of pure spin current will be increased since more electrons are excited. In addition, in real implementation, there may be a number of factors that affect the possibility to observe the predicted effect, such as temperature, ribbon width, and disorder, etc. Anyhow, the predicted effect only depends on whether the system is a centrosymmetric antiferromagnet. For the ZGNRs, according to a recent experimental report, the antiferromagnetic order can persist up to 7 nm in ribbon width under room temperature42. When the ribbon width is larger than 7 nm, it will turn to a ferromagnetic metal. Edge disorder is a little more intricate factor since it may break the centrosymmetry of the structure, which is the basis of the scheme. However, if the concentration of disorder is sufficiently low, it can be predicted that the effect will be negligible. Moreover, with the development of fabrication techniques, especially the atomically precise control of structure design, the disorders at the edges can be well controlled and atomically perfect graphene edges can be achieved43. Based on these facts, by choosing the ribbon width to be smaller than 7 nm and careful control over the edge disorder, it will be able to observe the pure spin current produced with PGE in ZGNRs.
In conclusion, based on first-principle transport calculations, we show a robust route to generate pure spin current in antiferromagnetic systems with PGE, in which space inversion symmetry is maintained in the structure, but is broken in the charge distribution for each spin channel. Due to the structural inversion symmetry and spin polarization antisymmetry, the charge photocurrent induced by the PGE must vanish, while a finite spin-dependent photocurrent is still generated, resulting in a pure spin current without any accompanying charge current. By taking a device constructed with 6-ZGNR as an example, we demonstrate that pure spin current can be robustly generated, neither dependent of the photon energy, nor dependent of the polarization feature of the applied polarized light. More interestingly, the device can be tuned to switch between two states of producing fully spin-polarized current and producing pure spin current, two ideal goals to be realized in spintronics, by applying two parallel or antiparallel external transverse electric fields to the two leads. The results highlight the importance of spin polarization antisymmetry in centrosymmetric magnetic semiconductors as an effective mechanism to robustly generate pure spin current by PGE, as further confirmed by the study on 2H-VSe2 bilayer, a 2D A-type vdW antiferromagnet. Given the recent experimental and theoretical discoveries of 2D antiferromagnetic materials with spin polarization antisymmetry40,44,45, PGE-induced pure spin current will be easily realized in them.
Methods
Details on DFT calculations
All structure relaxations are performed by the Vienna ab initio simulation package46,47,48, which is based on density functional theory (DFT) using the projector-augmented wave method and a plane wave basis set. The plane wave energy cutoff is set to 500 eV. The exchange and correlation functional is adopted in the generalized gradient approximation with Perdew–Burke–Ernzerhof (PBE) form for ZGNR and PBE + U with Dudarev-type for bilayer 2H-VSe2 system40,49,50. A 1 × 1 × 21 and 16 × 1 × 16 Monkhorst-Pack k-point mesh is adopted in the structure relaxation for ZGNR and VSe2 unit cells, respectively. To eliminate the interaction from the neighboring images a vacuum region of no <15 Å is applied in the slab direction. The relaxation process goes on until the residual force on each atom is <1 meV/Å. The photocurrent calculations are performed by the NanoDcal package51,52, which combines DFT and nonequilibrium Green’s function for quantum transport study. A double-zeta-polarized basis set is adopted for describing the electron wave function. Moreover, the energy cutoff is 200 Ry and the k-point grids of the electrodes for ZGNR and VSe2 are 1 × 1 × 100 and 11 × 1 × 100, respectively.
Theoretical formalism of photocurrent for nanoscale photovoltaic device
For an electron–photon coupled transport system the total Hamiltonian can be defined by53
where m0 is the electron mass, e is the elementary charge, A is the space- and time-dependent electromagnetic vector potential of the light, p is the electronic momentum operator, B(r, t) = ∇ × A(r, t) is the magnetic field operator, and V(r) is the electrostatic potential. Equation (1) can be divided into two parts, i.e.,
and
where He is the electron Hamiltonian of the system without the electromagnetic interaction and He–p is the Hamiltonian with the electromagnetic interaction included. For He–p, the first two terms is linearly dependent on A(r, t), while the last term is quadratically dependent on it. Compared with the A terms, the effect of the A2 term can be neglected for ordinary light sources since the light intensity is sufficiently low. Furthermore, the ratio of the second term over the first term is of the order of a0/λ (a0 and λ are the Bohr radius and the wavelength of the light, respectively) and a0/λ ≪ 1, since a0 is generally much smaller than λ (ref. 53). Thus the second term \(\frac{e}{{m}_{0}}{\bf{S}}\cdot {\bf{B}}({\bf{r}},t)\) can also be neglected, leaving the electron–photon interaction term as
Actually, He–ph is neglected in the self-consistent Hamiltonian calculation of the two probe system and then is regarded as a perturbation in the photocurrent calculation after the self-consistent electron Hamiltonian He is obtained. The photocurrent flowing from the central region to the lead α can be then expressed as32,54
where the effective transmission function
Here, α(L, R) and σ(↑, ↓) denote the lead and spin indexes, respectively. Γα is the line-width function of the lead α describing the coupling between the scattering region and the lead α. \({G}_{\mathrm{ph}}^{\,{<}\,( \,{>}\,)}\) is the lesser (greater) Green’s function of the scattering region with the electron–photon interaction taken into consideration in the first-order Born approximation55. More details on the theoretical formalism are found in ref. 54. The polarization of the polarized light can be characterized by a complex vector A. For LPL, the polarization vector is defined as \({\bf{A}}=\cos (\theta ){{\bf{e}}}_{{\bf{1}}}+\sin (\theta ){{\bf{e}}}_{{\bf{2}}}\), where e1 and e2 are two perpendicular unit vectors for defining the propagation direction of light according to the right hand rule, and θ is the polarization angle formed by the polarized direction with respect to the vector e1. As for EPL, the polarization vector is defined as \({\bf{A}}=\cos (\varphi ){{\bf{e}}}_{{\bf{1}}}+i\sin (\varphi ){{\bf{e}}}_{{\bf{2}}}\), where φ determines the helicity of the EPL.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The code used in this paper are available from the corresponding author upon reasonable request.
References
Ivchenko, E. L. & Pikus, G. E. New photogalvanic effect in gyrotropic crystals. JETP Lett. 27, 640 (1978).
Belinicher, V. Space-oscillating photocurrent in crystals without symmetry center. Phys. Lett. A 66, 213–214 (1978).
Asnin, V. et al. Observation of a photo-emf that depends on the sign of the circular polarization of the light. JETP Lett. 28, 74–77 (1978).
Ganichev, S. D. & Prettl, W. Spin photocurrents in quantum wells. J. Phys. Condens. Matter 15, R935 (2003).
Ganichev, S. D. et al. Zero-bias spin separation. Nat. Phys. 2, 609–613 (2006).
Zhou, B. & Shen, S.-Q. Deduction of pure spin current from the linear and circular spin photogalvanic effect in semiconductor quantum wells. Phys. Rev. B 75, 045339 (2007).
Dhara, S., Mele, E. J. & Agarwal, R. Voltage-tunable circular photogalvanic effect in silicon nanowires. Science 349, 726–729 (2015).
Li, J. & Haney, P. M. Circular photogalvanic effect in organometal halide perovskite ch3nh3pbi3. Appl. Phys. Lett. 109, 193903 (2016).
de Juan, F., Grushin, A. G., Morimoto, T. & Moore, J. E. Quantized circular photogalvanic effect in weyl semimetals. Nat. Commun. 8, 1–7 (2017).
Ganichev, S., Ketterl, H., Prettl, W., Ivchenko, E. & Vorobjev, L. Circular photogalvanic effect induced by monopolar spin orientation in p-gaas/algaas multiple-quantum wells. Appl. Phys. Lett. 77, 3146–3148 (2000).
Král, P., Mele, E. J. & Tománek, D. Photogalvanic effects in heteropolar nanotubes. Phys. Rev. Lett. 85, 1512–1515 (2000).
He, X. W. et al. Anomalous photogalvanic effect of circularly polarized light incident on the two-dimensional electron gas in alxga1−xN/GaN heterostructures at room temperature. Phys. Rev. Lett. 101, 147402 (2008).
Mal’shukov, A. G. Equilibrium circular photogalvanic effect in a hybrid superconductor-semiconductor system. Phys. Rev. Lett. 107, 146603 (2011).
Gao, Y., Zhang, Y. & Xiao, D. Tunable layer circular photogalvanic effect in twisted bilayers. Phys. Rev. Lett. 124, 077401 (2020).
Xu, S.-Y. et al. Electrically switchable berry curvature dipole in the monolayer topological insulator wte2. Nat. Phys. 14, 900–906 (2018).
Yuan, H. et al. Generation and electric control of spin-valley-coupled circular photogalvanic current in wse2. Nat. Nanotechnol. 9, 851–857 (2014).
Ji, Z. et al. Spatially dispersive circular photogalvanic effect in a weyl semimetal. Nat. Mater. 18, 955–962 (2019).
Li, L. et al. Black phosphorus field-effect transistors. Nat. Nanotechnol. 9, 372 (2014).
Manzeli, S., Ovchinnikov, D., Pasquier, D., Yazyev, O. V. & Kis, A. 2d transition metal dichalcogenides. Nat. Rev. Mater. 2, 17033 (2017).
Jariwala, D., Sangwan, V. K., Lauhon, L. J., Marks, T. J. & Hersam, M. C. Emerging device applications for semiconducting two-dimensional transition metal dichalcogenides. ACS Nano 8, 1102–1120 (2014).
Splendiani, A. et al. Emerging photoluminescence in monolayer mos2. Nano Lett. 10, 1271–1275 (2010).
Gibertini, M., Koperski, M., Morpurgo, A. & Novoselov, K. Magnetic 2d materials and heterostructures. Nat. Nanotechnol. 14, 408–419 (2019).
Gong, C. et al. Discovery of intrinsic ferromagnetism in two-dimensional van der waals crystals. Nature 546, 265–269 (2017).
Huang, B. et al. Layer-dependent ferromagnetism in a van der waals crystal down to the monolayer limit. Nature 546, 270–273 (2017).
Yu, W. et al. Chemically exfoliated vse2 monolayers with room-temperature ferromagnetism. Adv. Mater. 31, 1903779 (2019).
Xie, Y., Zhang, L., Zhu, Y., Liu, L. & Guo, H. Photogalvanic effect in monolayer black phosphorus. Nanotechnology 26, 455202 (2015).
Jiang, P. et al. Robust generation of half-metallic transport and pure spin current with photogalvanic effect in zigzag silicene nanoribbons. J. Phys. Condens. Matter 31, 495701 (2019).
Xie, Y. et al. Two-dimensional photogalvanic spin-battery. Phys. Rev. Appl. 10, 034005 (2018).
Yuan, H. et al. Generation and electric control of spin-valley-coupled circular photogalvanic current in wse2. Nat. Nanotechnol. 9, 851 (2014).
Zhang, S., Levy, P. & Fert, A. Mechanisms of spin-polarized current-driven magnetization switching. Phys. Rev. Lett. 88, 236601 (2002).
Wang, D.-K., Sun, Q.-f. & Guo, H. Spin-battery and spin-current transport through a quantum dot. Phys. Rev. B 69, 205312 (2004).
Tao, X. et al. h-bn/graphene van der waals vertical heterostructure: a fully spin-polarized photocurrent generator. Nanoscale 10, 174–183 (2018).
Chen, J. et al. Photogalvanic effect induced fully spin polarized current and pure spin current in zigzag sic nanoribbons. Phys. Chem. Chem. Phys. 20, 26744–26751 (2018).
Marin, E. G., Marian, D., Iannaccone, G. & Fiori, G. Tunnel-field-effect spin filter from two-dimensional antiferromagnetic stanene. Phys. Rev. Appl. 10, 044063 (2018).
Ganichev, S. D. et al. Removal of spin degeneracy in p-sige quantum wells demonstrated by spin photocurrents. Phys. Rev. B 66, 075328 (2002).
Son, Y.-W., Cohen, M. L. & Louie, S. G. Half-metallic graphene nanoribbons. Nature 444, 347 (2006).
Kan, E.-J., Li, Z., Yang, J. & Hou, J. Will zigzag graphene nanoribbon turn to half metal under electric field? Appl. Phys. Lett. 91, 243116 (2007).
Kang, J., Wu, F. & Li, J. Symmetry-dependent transport properties and magnetoresistance in zigzag silicene nanoribbons. Appl. Phys. Lett. 100, 233122 (2012).
Yang, K., Cahangirov, S., Cantarero, A., Rubio, A. & D’Agosta, R. Thermoelectric properties of atomically thin silicene and germanene nanostructures. Phys. Rev. B 89, 125403 (2014).
Gong, S.-J. et al. Electrically induced 2d half-metallic antiferromagnets and spin field effect transistors. Proc. Natl. Acad. Sci. USA 115, 8511–8516 (2018).
Jiang, P. et al. Ferroelectric control of electron half-metallicity in a-type antiferromagnets and its application to nonvolatile memory devices. Phys. Rev. B 102, 245417 (2020).
Magda, G. Z. et al. Room-temperature magnetic order on zigzag edges of narrow graphene nanoribbons. Nature 514, 608–611 (2014).
Kim, K. et al. Atomically perfect torn graphene edges and their reversible reconstruction. Nat. Commun. 4, 1–6 (2013).
Sivadas, N., Okamoto, S., Xu, X., Fennie, C. J. & Xiao, D. Stacking-dependent magnetism in bilayer cri3. Nano Lett. 18, 7658–7664 (2018).
Sun, Z. et al. Giant nonreciprocal second-harmonic generation from antiferromagnetic bilayer cri 3. Nature 572, 497–501 (2019).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Errata: generalized gradient approximation made simple. Phy. Rev. Lett. 77, 3865–3868 (1996).
Dudarev, S. L., Botton, G. A., Savrasov, S. Y., Humphreys, C. J. & Sutton, A. P. Electron-energy-loss spectra and the structural stability of nickel oxide: an lsda+u study. Phys. Rev. B 57, 1505–1509 (1998).
Maassen, J., Harb, M., Michaud-Rioux, V., Zhu, Y. & Guo, H. Quantum transport modeling from first principles. Proc. IEEE 101, 518–530 (2013).
Taylor, J., Guo, H. & Wang, J. Ab initio modeling of quantum transport properties of molecular electronic devices. Phys. Rev. B 63, 245407 (2001).
Cohen-Tannoudji, C., Diu, B. & Laloe, F. Quantum Mechanics, Vol. II, 1304–1315 (Wiley, 1991).
Zhang, L. et al. Generation and transport of valley-polarized current in transition-metal dichalcogenides. Phys. Rev. B 90, 195428 (2014).
Henrickson, L. E. Nonequilibrium photocurrent modeling in resonant tunneling photodetectors. J. Appl. Phys. 91, 6273–6281 (2002).
Acknowledgements
We gratefully acknowledge financial support by the National Natural Science Foundation of China under Grant Nos. 11974355 and 61674022; and the Program of State Key Laboratory of Quantum Optics and Quantum Optics Devices under Grant No. KF201810. Calculations were performed in Center for Computational Science of CASHIPS, the ScGrid of Supercomputing Center and Computer Network Information Center of Chinese Academy of Sciences.
Author information
Authors and Affiliations
Contributions
P.J. and X.H.Z. devised to the initial idea. P.J. performed the first-principles and quantum transport calculations with the help from X.X.T., H.H., and Y.S.L. All authors discussed the results and participated in the writing and revision of the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jiang, P., Tao, X., Hao, H. et al. Two-dimensional centrosymmetrical antiferromagnets for spin photogalvanic devices. npj Quantum Inf 7, 21 (2021). https://doi.org/10.1038/s41534-021-00365-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-021-00365-7
This article is cited by
-
A Bi2C Photodetector Based on the Spin-Dependent Photogalvanic Effect
Journal of Electronic Materials (2024)