Abstract
We propose an entanglement-creation scheme in a multi-atom ensemble trapped in an optical cavity, named entanglement amplification, converting unentangled states into entangled states and amplifying less-entangled ones to maximally entangled Greenberger-Horne-Zeilinger (GHZ) states whose fidelity is logarithmically dependent on the atom number and robust against common experimental noises. The scheme starts with a multi-atom ensemble initialized in a coherent spin state. By shifting the energy of a particular Dicke state, we break the Hilbert space of the ensemble into two isolated subspaces to tear the coherent spin state into two components so that entanglement is introduced. After that, we utilize the isolated subspaces to further enhance the entanglement by coherently separating the two components. By single-particle Rabi drivings on atoms in a high-finesse optical cavity illuminated by a single-frequency light, 2000-atom GHZ states can be created with a fidelity above 80% in an experimentally achievable system, making resources of ensembles at Heisenberg limit practically available for quantum metrology.
Similar content being viewed by others
Introduction
Entanglement plays a central role in quantum mechanics. It is one of the most important topics in fields including quantum information1,2,3, quantum communication4,5, and quantum metrology6,7,8. By utilizing different classes of entangled states, one can speed up computations9,10,11, secure private communications12,13,14,15,16, and overcome the standard quantum limit17,18,19,20,21,22,23,24. Among all the classes of entangled states, the Greenberger-Horne-Zeilinger (GHZ) state25 is one of the ultimate goals for quantum information and quantum metrology26,27,28,29,30,31,32,33,34,35,36,37, for it displays the Heisenberg limit38 with the best precision guaranteed by fundamental principles of quantum mechanics.
However, it is challenging to create GHZ states in multi-particle ensembles. In the past few years, pioneering contributions have been made to realize multi-particle GHZ states at different platforms, including 14 trapped ions26,27,28,29, 18 state-of-the-art photon qubits30,31,32, and 12 superconducting qubits33,34. These outstanding works start an era in developing scalable quantum computers, advancing quantum metrology, and establishing quantum communication. Recently, there is a breakthrough where up to 20 qubits35,36,37 are entangled with a fidelity above 0.529. Nevertheless, the required precision of the control and technical difficulties increase exponentially as the number of qubits grows, making it difficult to increase the size of the GHZ state.
In this manuscript, we propose a deterministic scheme, named entanglement amplification, to convert non-entangled states into less-entangled states, and further amplify the less-entangled ones to maximally entangled GHZ states in atomic ensembles. Different from the pioneering experiments generating atomic entanglement in a cavity based on a continuous non-demolition measurement39,40, we break the Hilbert space of atomic spins into two isolated subspaces by shifting the energy of one particular angular momentum eigenstate of colletive atomic spins (Dicke state41). Any wavefunction in one of the subspaces is not allowed to leak out to or penetrate from the other. When a coherent spin state is approaching the boundary by Rabi drivings between two spins of each atom, the wavefunction coherently evolves around the boundary, being torn into two separated components, and becomes a cat state. Furthermore, by carefully choosing the boundary and the orientation of the wavefunction, one component can be frozen, while the other continues rotating under Rabi drivings, which further stretches the wavefunction separation of the cat state, until the maximally separated state (GHZ state) is obtained. Estimated with experimentally achievable parameters, a 100-atom GHZ state can be obtained with a fidelity at 0.92, and the one with 2000 atoms can be achieved with a fidelity at 0.89. Moreover, the fidelity of GHZ states obtained using entanglement amplification decreases logarithmically as the atom number increases, enabling the extension of this scheme into systems of larger atom number.
Results
Creating GHZ states in an ideal model
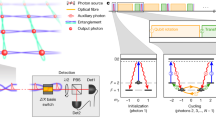
We consider N three-level atoms trapped in an optical cavity (see Fig. 1), with two ground states \(\left|\uparrow \right\rangle\) and \(\left|\downarrow \right\rangle\), and one excited state \(\left|\,\text{e}\,\right\rangle\). The cavity mode couples \(\left|\uparrow \right\rangle\) to \(\left|\,\text{e}\,\right\rangle\) with a single-photon Rabi frequency 2g and a detuning Δ, where Δ is much larger than the spontaneous-decay rate Γ of \(\left|\,\text{e}\,\right\rangle\). By adiabatically eliminating \(\left|\,\text{e}\,\right\rangle\), we obtain an effective Hamiltonian Hc42,43, describing the interaction between the cavity field and N two-level atoms:
Here, Sz is the collective angular momentum operator along z axis, ωs = g2/Δ is the coupling strength, S = N/2 is the total spin magnitude, and \({\hat{c}}^{\dagger }\) (\(\hat{c}\)) is the creation (annihilation) operator of the cavity field.
a N atoms are coupled to a high-finesse optical cavity, and the cavity is illuminated by a single-frequency light which can be turned on or off. b The atomic level diagram and the cavity transmission spectra. The Rabi drivings couple \(\left|\uparrow \right\rangle\) and \(\left|\downarrow \right\rangle\). The cavity mode couples \(\left|\uparrow \right\rangle\) to \(\left|\,\text{e}\,\right\rangle\) with a detuning Δ. Due to the strong coupling in the atom-cavity system, each atom in \(\left|\uparrow \right\rangle\) shifts the cavity resonance by an amount of ωs = g2/Δ > κ. Thus, the incident light with frequency of ω1 = ωc + ωs only shifts the energy of the Dicke state \(\left|-S+1\right\rangle\) and creates a boundary in the Hilbert space at this state. c The quasi-probability distribution (Husimi-Q function) on the Bloch sphere before, within, and after entanglement amplification process.
Each atom in the state \(\left|\uparrow \right\rangle\) shifts the cavity resonance ωc by an amount of ωs. When the cavity is illuminated by a light beam at frequency ωn = ωc + nωs, the intracavity intensity \({\langle {\hat{c}}^{\dagger }\hat{c}\rangle }_{m,n}\) is negligibly small if m ≠ n, where m is the number of atoms in \(\left|\uparrow \right\rangle\). In this case, only quantum states with n atoms in \(\left|\uparrow \right\rangle\) introduce significant intracavity intensity, and thus introduce a significant AC Stark shift \(n\hslash {\omega }_{\text{s}}{\langle {\hat{c}}^{\dagger }\hat{c}\rangle }_{n,n}\) to the Dicke state \(\left|m=-N/2+n\right\rangle\), while the light-induced energy shifts of other Dicke states are negligible. This achieves the goal of shifting one particular Dicke state away without affecting the others and thus forms a boundary separating the Hilbert space. In the following context, we choose an incident light beam at frequency ω1 = ωc + ωs to illuminate the cavity so that the boundary separating the Hilbert space is set to the Dicke state \(\left|m=-N/2+1\right\rangle\). As a result, in an ideal case, the effective Hamiltonian becomes \(H^{\prime} (\delta )=\,\text{diag}\,(0,0,\ldots ,\hslash \delta ,0)\), where each diagonal matrix element \({H}_{m,m}^{\prime}\) corresponds to the energy shift of the Dicke state \(\left|m=-N/2+n\right\rangle\), as n = N to 0 in a descending order, and \(\delta ={\omega }_{\text{s}}{\langle {\hat{c}}^{\dagger }\hat{c}\rangle }_{1,1}\).
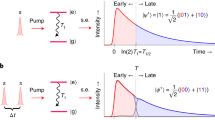
We realize entanglement amplification in the following steps. Step 1: All the atoms are initialized in \(\left|\uparrow \right\rangle\) and then rotated along x-axis by Rabi drivings approaching the Dicke state \(\left|m=-N/2+1\right\rangle\) (Fig. 2a, b). This process can be described by the rotation Hamiltonian \(\hslash\)ΩSx where Sx is the collective angular momentum operator along x-axis and Ω is the Rabi frequency of single-particle Rabi drivings. Step 2: Turn on the cavity light to introduce the energy shift at \(\left|m=-N/2+1\right\rangle\), and continue the Rabi rotation along x-axis (Fig. 2b, c). This process is described by \(\hslash {{\Omega }}{S}_{x}+H^{\prime}\). Here we require \(\sqrt{N}{{\Omega }}\,<\,| \delta |\) to guarantee the off-resonance condition. The wavefunction propagates around \(\left|m=-N/2+1\right\rangle\) and evolves into two separate components. By choosing a proper time to stop applying such Rabi drivings, the ensemble evolves into a cat state \(\left|{\psi }_{\text{cat}}\right\rangle\) where two components of the wavefunction are coherently separated on the Bloch sphere (Fig. 2c):
where t1 and t2 represent the duration time of Step 1 and Step 2, respectively.
Four steps of entanglement amplification protocol illustrated by the Husimi-Q function for a 100-atom ensemble, using the spherical coordinates (θ, ϕ) on the Bloch sphere. Each panel contains one top view (θ from 0 to π/2) and one bottom view (θ from π/2 to π) of the Bloch sphere. a A coherent spin state is initialized in \({\left|\uparrow \right\rangle }^{\otimes N}\). b After Step 1, the state is rotated close to \(\left|m=-N/2+1\right\rangle\). c After Step 2, a cat state is created by the boundary at \(\left|m=-N/2+1\right\rangle\). d After Step 3, the orientation of the cat state is re-aligned so that one component sits at the south pole of the Bloch sphere. e A GHZ state is created after Step 4 by freezing one component of the wavefunction in \(\left|m=-N/2\right\rangle\) using the boundary of \(\left|m=-N/2+1\right\rangle\).
Then, we convert the obtained cat state into a GHZ state by two additional steps. Step 3: Turn off the cavity light, apply Rabi drivings to rotate the cat state to align one component of the state into the south pole of the Bloch sphere, namely \(\left|m=-N/2\right\rangle\) (Fig. 2c, d). In this step, the separation between two components stays unchanged. Step 4: Turn on both the cavity light and the Rabi Drivings (Fig. 2d, e). The component in \(\left|m=-N/2\right\rangle\) is frozen by the boundary at \(\left|m=-N/2+1\right\rangle\), while the other component is rotated into the state \(\left|m=N/2\right\rangle\). A GHZ state \(\left|{\psi }_{\text{GHZ}}\right\rangle\) with two coherent components each on the north and south pole of the Bloch sphere is thus obtained:
where \({S}_{{\phi }_{i}}={S}_{x}\cos {\phi }_{i}+{S}_{y}\sin {\phi }_{i}\). Here, \({e}^{-\text{i}{{\Omega }}{S}_{{\phi }_{3}}{t}_{3}}\) corresponds to Step 3, the process of the orientation alignment, and \({e}^{-\text{i}\left[{{\Omega }}{S}_{{\phi }_{4}}+H^{\prime} ({\delta }_{4})/\hslash \right]{t}_{4}}\) corresponds to Step 4, the process of entanglement amplification.
With all these operations, we convert a non-entangled CSS into a less-entangled cat state, and amplify this cat state into a maximally entangled GHZ state, assuming that the cavity lines are infinitely narrow compared with the amount of cavity resonance shift introduced by one atom in \(\left|\uparrow \right\rangle\). This situation corresponds to an infinitely large cavity cooperativity η.
Considerations in a realistic system
In a realistic system with a finite cavity cooperativity, we need to consider dissipation due to spontaneous decay and effects of the finite cavity linewidth. Both processes decrease the fidelity of the obtained GHZ state. Suppose the excited state \(\left|\,\text{e}\,\right\rangle\) has a decoherence rate Γ, and a detuned coupling from \(\left|\uparrow \right\rangle\) to \(\left|\,\text{e}\,\right\rangle\) brings an AC Stark shift E↑ to the energy of \(\left|\uparrow \right\rangle\), and then introduces a spontaneous-decay rate Γ↑ = E↑ × Γ/Δ for each atom in \(\left|\uparrow \right\rangle\). The overall evolution with atomic spontaneous decay can be described by the master equations with Lindblad forms. The quantum fluctuation of the damping is smeared out by the ensemble average, which suggests the final state to be a mixed state rather than a pure state. After the four-step operations, the density matrix of the atomic ensemble can be decomposed into two parts and decribed as ρ = ρcoh + ρdecay: \({\rho }_{\text{coh}}=\left|{\psi }_{\text{GHZ}}\right\rangle \left\langle {\psi }_{\text{GHZ}}\right|\) represents the coherent-evolution part, while ρdecay corresponds to the incoherent-scattered part where the spontaneous decay introduces atom loss. Because of the fragility of the GHZ state, any atom experiencing spontaneous decay will destroy the whole state. Thus, we are only interested in the coherent-evolution part and we define the fidelity by its lower bound
where \(\left|\,\text{GHZ}\,,\phi \right\rangle =({\left|\uparrow \right\rangle }^{\otimes N}+{\text{e}}^{\text{i}\phi }{\left|\downarrow \right\rangle }^{\otimes N})/\sqrt{2}\). Here we use the phase ϕ to match the known phase difference between \({\left|\uparrow \right\rangle }^{\otimes N}\) and \({\left|\downarrow \right\rangle }^{\otimes N}\) of the generated GHZ state \(\left|{\psi }_{\text{GHZ}}\right\rangle\). We can also use the matrix elements ρm,n to describe the fidelity \({\mathcal{F}}\):
where ρm,n corresponds to the coefficients of \(\left|m\right\rangle \left\langle n\right|\) in ρcoh. This method was first used to characterize the fidelity of the GHZ state in ref. 29.
When the cavity has a finite linewidth, the cavity light at frequency ω1 introduces non-negligible AC Stark shifts to other Dicke states besides \(\left|m=-N/2+1\right\rangle\). Therefore, in a realistic system, a modified non-Hermitian Hamiltonian \({H}_{\exp }^{\prime}\) replaces the ideal \(H^{\prime}\) to describe the cavity linewidth broadening and the cavity-assisted energy shift under the dissipation of spontaneous decay (see part A in Supplementary Notes for details):
The real part of \({H}_{\exp }^{\prime}\) characterizes AC Stark shifts for different Dicke states and the imaginary part characterizes the spontaneous-decay-induced decoherence. Here, T(ξ, n) is the amplitude transmission function of the cavity43:
where n is the atom number in \(\left|\uparrow \right\rangle\), \(\eta =4{g}^{2}/\left({{\Gamma }}\kappa \right)\) is the cavity cooperativity, κ is the cavity linewidth, and ξ = ω − ωc is the light-cavity detuning.
The scalability of GHZ states
To verify the validity of our scheme, we use experimentally achievable parameters to estimate the fidelity of the obtained GHZ states. We consider rubidium-87 as the candidate atom, with two ground states \(\left|\downarrow \right\rangle\) and \(\left|\uparrow \right\rangle\) in different hyperfine manifolds of 5S1/2, and a excited state \(\left|\,\text{e}\,\right\rangle\) in 5P3/2 with a spontaneous-decay rate Γ = 2π × 6 MHz. Choosing cavity cooperativity η = 200, and Rabi frequency of single-particle Rabi drivings Ω between 2π × 0.05 MHz and 2π × 0.2 MHz (see Supplementary Table 1 for all parameters), a GHZ state with a fidelity of 0.92 is achieved in a 100-atom ensemble, and a fidelity of 0.89 is achieved in a 2000-atom ensemble.
The fidelity \({\mathcal{F}}\) of the obtained GHZ state has a favorable scaling on atom number N, as plotted in Fig. 3a. When atom number N increases, the fidelity \({\mathcal{F}}\) of the obtained GHZ state decreases due to the dissipation induced by the spontaneous decay. For the atomic population in state \(\left|m=-N/2+1\right\rangle\), which has the highest spontaneous-decay rate, the dissipation is suppressed due to little population at this boundary state resulted from off-resonant Rabi coupling. For atomic population in the other states, the spontaneous-decay rate is low because the incident light is off-resonantly suppressed by the cavity linewidth. Such dissipation is proportional to 1/n for atomic population in state \(\left|m=-N/2+n\right\rangle\) for n = 2 to N, and thus introduces an overall dissipation proportional to \(\mathrm{ln}\,N\). This weak dependence of \({\mathcal{F}}\) on N helps to extend the scheme into the regime of thousands of atoms.
a The fidelity \({\mathcal{F}}\) versus the atom number N at η = 200. b \({\mathcal{F}}\) versus the cooperativity η at N = 100. The dashed blue line shows the empirical formula in Eq. (8). c \({\mathcal{F}}\) versus \((\mathrm{ln}\,N)/\eta\). Here we plot five sets of calculated results: η = 200, N = 100–2000 (red squares); η = 200–1000, with N = 100 (gray stars), 400 (orange diamonds), 800 (green circles), 1200 (purple triangles). The blue dashed line corresponds to the empirical formula of \({\mathcal{F}}\). d The parity oscillation of 〈P〉 versus the rotating angle θ. Here we only plot two typical intervals [−0.03π, 0.03π] and [0.47π, 0.53π] while the rapid oscillation of 〈P〉 is within the whole region of θ ∈ [−π, π].
To understand the dependence of fidelity \({\mathcal{F}}\) on cavity cooperativity η, we plot fidelities of obtained GHZ states with 100 atoms at different cavity cooperativity η with corresponding optimized detuning Δ (Fig. 3b). The optimized Δ is proportional to η, and the optimized ti are the same for different η. According to Eqs. (6) and (7), we find when η increases, the coherent evolution keeps unchanged as we set η/Δ a constant, but the spontaneous-decay rate decreases inversely proportional to η (or Δ). The empirical formula for fidelity versus N and η is (see Fig. 3c and Supplementary Fig. 3 for details):
The obtained GHZ states can be verified experimentally by detecting the parity oscillation29. One could apply a rotation \({\text{e}}^{\text{i}\pi {S}_{\theta }/2}\) to the obtained GHZ state and then measure the mean value of the parity operator \(P=\mathop{\prod }\nolimits_{i = 1}^{N}{\sigma }_{\,\text{z}\,}^{(i)}\), where \({\sigma }_{\,\text{z}\,}^{(i)}\) is the Pauli z-matrix of the i-th atom. The parity \(\langle P\rangle \sim \cos \left(N\theta \right)\) oscillates versus θ (see Fig. 3d), proving the non-trivial coherence of N atoms between the states \(\left|m=-N/2\right\rangle\) and \(\left|m=N/2\right\rangle\), and thus the formation of a GHZ state.
To show that the obtained GHZ state is useful for metrological purposes, we plot its Fisher information which characterizes its metrological gain relative to that of a CSS at different cooperativity η (Fig. 4a) and different atom number N (Fig. 4b). Here, the Fisher information can be understood as phase sensitivity, and it’s inversely relative to the smallest angle which the GHZ state rotates on the Bloch Sphere so that the initial and the rotated states are distinguishable. Please refer to ref. 6 for the formula we used to estimate the Fisher information. At a given η = 200, the relative Fisher information reaches 81 for 100 atoms, 380 for 500 atoms, and 1420 for 2000 atoms. This confirms that entanglement amplification protocol strongly amplifies the metrological gain in a many-body system, approaching the Heisenberg limit at a given atom number N.
Here we plot the normalized Fisher information relative to the CSS to characterize the metrological gain. a Fisher information of generated states versus cavity cooperativity η at N = 100 (red solid circles). b Fisher information versus the atom number N at η = 200 (red solid circles). For reference, we also show the fisher information of states at the Heisenberg limit (blue dashed line) and those at the standard quantum limit (orange dot-dashed line).
Discussion
Our GHZ-state-generation protocol is robust against common experimental noises. Since the coherence time of an atomic clock with thousands of atoms could be on the order of seconds, a 2000-atom GHZ state should survive at least for milliseconds, which is long enough to finish all processes of entanglement amplification that requires a timescale on the order of 2π/Ω ≈ 10 μs. We also estimate the effects of other technical noises on the fidelity of GHZ states (See part B in Supplementary Discussion for details), including the precision of Rabi rotations, the atom-cavity inhomogeneous coupling, the photon shot noise, and the cavity frequency instability.
The technical noises decrease the fidelity in two ways. One way is to introduce errors in the rotation angles Ωti used in Eqs. (2) and (3), such as the precision limits of Rabi rotations. For a system containing N atoms, the error of each rotation angle is required to be much smaller than the angle corresponds to the standard quantum limit \(1/\sqrt{N}\), which has already been technically achieved in most of atomic clock apparatus. By assuming that the intensity fluctuation of the Rabi driving is 0.4% and the timing control error is 1 ns, the overall fidelity decreases to 0.923 (N = 100) or 0.870 (N = 2000) while the original value is 0.924 or 0.890. This confirms that the precision limits of Rabi rotations can hardly affect the performance of our scheme.
The other way is to introduce fluctuations on AC Stark shifts, such as inhomogeneous coupling, photon shot noise, and cavity instability. The inhomogeneous coupling due to the standing wave can be avoided by choosing commensurate wavelength lasers such as 1560 nm and 780 nm for trapping and probing rubidium atoms, and this problem has been solved in many experiments. The remaining inhomogeneity is mainly due to the thermal fluctuation which results in around 1% randomness for AC Stark shifts. The photon shot noise and the cavity frequency instability randomly change the intracavity light intensity, and thus bring fluctuations to AC Stark shifts. We have estimated these effects numerically and it shows only a few percent decreasing in the GHZ-state fidelity (See part B.2 and B.3 in Supplementary Discussion for details). In fact, the drifts or fluctuations of AC Stark shifts only bring significant influence on the resonant state \(\left|m=-N/2+1\right\rangle\). Since such shift is only used to decouple the Rabi driving between \(\left|m=-N/2+1\right\rangle\) and other states, the fidelity is not sensitive to the amount of the shift as long as the shift is large enough.
Taking all these potentially adverse conditions into consideration, we find the overall fidelity decreases to 0.903 (or 0.817) for N = 100 (or N = 2000), while the original value is 0.924 (or 0.890). This result further confirms the robustness of our scheme which could create GHZ states with an atom number as large as a few thousands. We list the details of numerical methods and estimations in Supplementary Information (See part B.4 in Supplementary Discussion for details).
Similar to the previous experiments39,40, the information about the atomic state may leak out through the atom-cavity system. Here our scheme is a coherent evolution that the phase shift or the dispersion has already been included in the AC Stark shift and the Hamiltonian \({H}_{\exp }^{\prime}\) in Eq. (6), and the incident photon number fluctuation has been considered into the photon shot noise. However, the spatial choices about whether the incident photons are transmitted through or reflected by the optical cavity, leak out the information of the atomic state. To obtain the average density matrix of the atomic state, a trace out of both reflection and transmission information has to be applied, and this hurts the off-diagonal terms of the density matrix, which correspond to the phase coherence, and thus further decreases the final fidelity. This kind of information leakage can be fixed by using a single-side cavity or an asymmetric cavity where the transmissions of two mirrors are quite different, similar to the idea of a quantum erasure in ref. 44. Using a cavity with finesse of 105 and two mirrors with transmission ratio of 0.09, the fidelity of the obtained GHZ state decreases by 0.05 due to information leakage. (See part C in Supplementary Discussion and Supplementary Fig. 4 for details.)
In conclusion, we propose a scheme, entanglement amplification, for creating entangled states with high metrological gain. With realistic experimental parameters, one can obtain a 2000-atom GHZ state with a fidelity above 80% and approach the Heisenberg limit. The fidelity decreases only logarithmically when the system size increases, which paves a way to generate large-size GHZ states. We believe this scheme simplifies the complexity and enhances the robustness of the creation of large-size GHZ states. It may raise a platform for designing simpler and more robust entanglement-creation schemes for quantum information and quantum metrology. Variations of this method can be generalized to artificial-atom systems such as superconducting qubits, quantum dots, and mechanical oscillators coupled to a resonator.
Methods
Evolution of GHZ states
Replacing \(H^{\prime}\) in Eqs. (2) and (3) by the experimental Hamiltonian \({H}_{\exp }^{\prime}\), we obtain the analytical expressions for every step of state evolutions.
In Step 1, the atomic ensemble is initialized in \({\left|\uparrow \right\rangle }^{\otimes N}\) and then rotated by an angle − Ωt1 along x-axis due to Rabi driving, i.e.,
In Step 2, the incident light is turned on and we continue the Rabi driving along x-axis by an angle − Ωt2. The evolution can be described by
In Step 3, we realign the orientation of the wavefunction while turning off the incident light. The evolution is
In Step 4, the incident light is turned on again but with larger light shift induced by higher light intensity, and we continue the rotation along the orientation of ϕ4 by an angle − Ωt4. Therefore, the final obtained state in Step 4 is
Overall, the whole GHZ-state-generation process can be expressed by
which can be calculated using exponential functions of N × N matrices, where N is the total atom number. The descriptions of detailed parameters can be found in Supplemental Notes.
Experimental noise estimation
To study the robustness under common experimental noises, we randomly shuffle the experimental parameters in reasonable and experimentally achievable ranges, and repeat our calculations many times with the same experimental setup. Then we perform the ensemble average to obtain the mean density matrix ρ, which corresponds to the final GHZ state under noises and use it to calculate the actual fidelity under realistic noisy experimental environment. The discussions of each noise source can be found in Supplemental Discussions.
Data availability
The data in this manuscript are available from J.H. on reasonable requests.
References
Wang, X.-B., Hiroshima, T., Tomita, A. & Hayashi, M. Quantum information with gaussian states. Phys. Rep. 448, 1–111 (2007).
Terhal, B. M. Quantum error correction for quantum memories. Rev. Mod. Phys. 87, 307–346 (2015).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Duan, L.-M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001).
Pezzè, L., Smerzi, A., Oberthaler, M. K., Schmied, R. & Treutlein, P. Quantum metrology with nonclassical states of atomic ensembles. Rev. Mod. Phys. 90, 035005 (2018).
Kitagawa, M. & Ueda, M. Squeezed spin states. Phys. Rev. A 47, 5138–5143 (1993).
Zou, Y.-Q. et al. Beating the classical precision limit with spin-1 dicke states of more than 10,000 atoms. PNAS 115, 6381–6385 (2018).
Grover, L. K. Synthesis of quantum superpositions by quantum computation. Phys. Rev. Lett. 85, 1334–1337 (2000).
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120–126 (1998).
Duan, L.-M. & Kimble, H. J. Scalable photonic quantum computation through cavity-assisted interactions. Phys. Rev. Lett. 92, 127902 (2004).
Kuzmich, A. et al. Generation of nonclassical photon pairs for scalable quantum communication with atomic ensembles. Nature 423, 731–734 (2003).
Ren, J.-G. et al. Ground-to-satellite quantum teleportation. Nature 549, 70 (2017).
Sun, Q.-C. et al. Quantum teleportation with independent sources and prior entanglement distribution over a network. Nat. Photonics 10, 671 (2016).
Liao, S.-K. Satellite-relayed intercontinental quantum network. Phys. Rev. Lett. 120, 030501 (2018).
Yin, J. et al. Satellite-to-ground entanglement-based quantum key distribution. Phys. Rev. Lett. 119, 200501 (2017).
Takano, T., Tanaka, S.-I.-R., Namiki, R. & Takahashi, Y. Manipulation of nonclassical atomic spin states. Phys. Rev. Lett. 104, 013602 (2010).
Appel, J. Mesoscopic atomic entanglement for precision measurements beyond the standard quantum limit. PNAS 106, 10960–10965 (2009).
Gross, C., Zibold, T., Nicklas, E., Estève, J. & Oberthaler, M. K. Nonlinear atom interferometer surpasses classical precision limit. Nature 464, 1165 (2010).
Riedel, M. F. Atom-chip-based generation of entanglement for quantum metrology. Nature 464, 1170 (2010).
Schleier-Smith, M. H., Leroux, I. D. & Vuletić, V. States of an ensemble of two-level atoms with reduced quantum uncertainty. Phys. Rev. Lett. 104, 073604 (2010).
Bohnet, J. G. et al. Reduced spin measurement back-action for a phase sensitivity ten times beyond the standard quantum limit. Nat. Photonics 8, 731 (2014).
Leroux, I. D., Schleier-Smith, M. H. & Vuleti c, V. Orientation-dependent entanglement lifetime in a squeezed atomic clock. Phys. Rev. Lett. 104, 250801 (2010).
Behbood, N. et al. Feedback cooling of an atomic spin ensemble. Phys. Rev. Lett. 111, 103601 (2013).
Greenberger, D. M., Horne, M. A., Shimony, A. & Zeilinger, A. Bell’s theorem without inequalities. Am. J. Phys. 58, 1131–1143 (1990).
Leibfried, D. et al. Toward heisenberg-limited spectroscopy with multiparticle entangled states. Science 304, 1476–1478 (2004).
Monz, T. et al. 14-qubit entanglement: creation and coherence. Phys. Rev. Lett. 106, 130506 (2011).
Roos, C. F. et al. Control and measurement of three-qubit entangled states. Science 304, 1478–1480 (2004).
Sackett, C. A. et al. Experimental entanglement of four particles. Nature 404, 256–259 (2000).
Lu, C.-Y. et al. Experimental entanglement of six photons in graph states. Nat. Phys. 3, 91–95 (2007).
Wang, Xi-Lin et al. 18-qubit entanglement with six photons’ three degrees of freedom. Phys. Rev. Lett. 120, 260502 (2018).
Zhong, H.-S. et al. 12-photon entanglement and scalable scattershot boson sampling with optimal entangled-photon pairs from parametric down-conversion. Phys. Rev. Lett. 121, 250505 (2018).
Gong, M. et al. Genuine 12-qubit entanglement on a superconducting quantum processor. Phys. Rev. Lett. 122, 110501 (2019).
Song, C. et al. 10-qubit entanglement and parallel logic operations with a superconducting circuit. Phys. Rev. Lett. 119, 180511 (2017).
Wei, Ken X. et al. Verifying multipartite entangled ghz states via multiple quantum coherences. arXiv http://arxiv.org/abs/1905.05720 (2019).
Song, C. et al. Generation of multicomponent atomic schrödinger cat states of up to 20 qubits. Science 365, 574–577 (2019).
Omran, A. et al. Generation and manipulation of Schrödinger cat states in Rydberg atom arrays. Science 365, 570–574 (2019).
Bollinger, J. J., Itano, W. M., Wineland, D. J. & Heinzen, D. J. Optimal frequency measurements with maximally correlated states. Phys. Rev. A 54, R4649–R4652 (1996).
Barontini, G., Hohmann, L., Haas, F., Estève, J. & Reichel, J. Deterministic generation of multiparticle entanglement by quantum zeno dynamics. Science 349, 1317–1321 (2015).
Haas, F., Volz, J., Gehr, R., Reichel, J. & Estève, J. Entangled states of more than 40 atoms in an optical fiber cavity. Science 344, 180–183 (2014).
Dicke, R. H. Coherence in spontaneous radiation processes. Phys. Rev. 93, 99–110 (1954).
Chen, W. et al. Carving complex many-atom entangled states by single-photon detection. Phys. Rev. Lett. 115, 250502 (2015).
Tanji-Suzuki, H. et al. In Advances in Atomic, Molecular, and Optical Physics, Chapter 4, Vol. 60, pp. 201–237, (eds. Arimondo, E. Berman, P. R. and Lin, C. C.) (Academic Press, 2011).
Leroux, I. D., Schleier-Smith, M. H., Zhang, H. & Vuletić, V. Unitary cavity spin squeezing by quantum erasure. Phys. Rev. A 85, 013803 (2012).
Acknowledgements
Y.Z., W.C., and J.H. acknowledge financial support from the National Natural Science Foundation of China under grant no. 11974202 and 61975092. R.Z. and X.-B.W. acknowledge financial support from Ministration of Science and Technology of China through The National Key Research and Development Program of China under grant no. 2017YFA0303901 and the National Natural Science Foundation of China under grant no. 11474182, 11774198, and U1738142.
Author information
Authors and Affiliations
Contributions
R.Z. and X.B.W. raise the original ideas. Y.Z., W.C., and J.H. further develop this model. Y.Z. performs the numerical simulations and proves the scalability. W.C. and J.H. supervise this work. All the authors contribute in discussions and writing the manuscript. Y.Z. and R.Z. contribute equally to this work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhao, Y., Zhang, R., Chen, W. et al. Creation of Greenberger-Horne-Zeilinger states with thousands of atoms by entanglement amplification. npj Quantum Inf 7, 24 (2021). https://doi.org/10.1038/s41534-021-00364-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-021-00364-8