Abstract
The recently established resource theory of quantum coherence allows for a quantitative understanding of the superposition principle, with applications reaching from quantum computing to quantum biology. While different quantifiers of coherence have been proposed in the literature, their efficient estimation in today’s experiments remains a challenge. Here, we introduce a collective measurement scheme for estimating the amount of coherence in quantum states, which requires entangled measurements on two copies of the state. As we show by numerical simulations, our scheme outperforms other estimation methods based on tomography or adaptive measurements, leading to a higher precision in a large parameter range for estimating established coherence quantifiers of qubit and qutrit states. We show that our method is accessible with today’s technology by implementing it experimentally with photons, finding a good agreement between experiment and theory.
Similar content being viewed by others
Introduction
Quantum coherence is the most distinguished feature of quantum mechanics, characterizing the superposition properties of quantum states. An operational resource theory of coherence has been established in the last years1,2,3,4,5,6,7, allowing for a systematic study of quantum coherence in quantum technology6, including quantum algorithms8,9, quantum computation10, quantum key distribution11, quantum channel discrimination12,13, and quantum metrology14,15,16. Moreover, quantum coherence is closely related to other quantum resources, such as asymmetry17,18, entanglement19,20, and other quantum correlations21; the manipulation of coherence and conversion between coherence and quantum correlations in bipartite and multipartite systems has been explored both theoretically22,23,24,25 and experimentally26,27. Highly relevant from the experimental perspective is the recent progress on coherence theory in the finite copy regime, in particular regarding single-shot coherence distillation28,29,30,31, coherence dilution32, and incoherent state conversion33. Being a fundamental property of quantum systems, coherence plays an important role in quantum thermodynamics34,35,36,37,38,39,40, nanoscale physics41, transport theory42,43, biological systems44,45,46,47,48,49, and for the study of the wave-particle duality50,51,52.
Having identified quantum coherence as a valuable feature of quantum systems, it is important to develop methods for its rigorous quantification. First attempts for resource quantification were made in the resource theory of entanglement53,54, leading to various entanglement measures based on physical or mathematical considerations. The common feature of all resource quantifiers is the postulate that they should not increase under free operations of the theory, which in entanglement theory are known as “local operations and classical communication”. In the resource theory of coherence, the free operations are incoherent operations, corresponding to quantum measurements, which cannot create coherence for individual measurement outcomes1.
While various coherence measures have been proposed6, an important issue is how to efficiently estimate them in experiments. Clearly, one possibility is to perform quantum state tomography55 and then use the derived state density matrix to estimate the amount of coherence. However, estimation of coherence measures in general does not require the complete information about the state of the system, a fact which has been exploited in various approaches for detecting and estimating coherence of unknown quantum states56,57,58,59.
In this paper, we put forward a general method to directly measure quantum coherence of an unknown quantum state using two-copy collective measurement scheme (CMS)60,61,62,63. We simulate the performance of this method for qubits and qutrits and compare the precision of CMS with other methods for coherence estimation, including tomography. The simulations show that in certain setups CMS outperforms all other schemes discussed in this work. We also report an experimental demonstration of CMS for qubit states. The collective measurements are performed on two identically prepared qubits, which are encoded in two degrees of freedom of a single photon. In this way, we experimentally obtain two widely studied coherence measures, finding a good agreement between the numerical simulations and the experimental results.
Results
Theoretical framework
We aim to estimate coherence of a quantum state ρ by performing measurements on two copies of the state. As quantifiers of coherence we use the ℓ1-norm of coherence \({C}_{{\ell }_{1}}\) and the relative entropy of coherence Cr, defined as1:
Here, \(S(\rho )=-{\rm{Tr}}[\rho \,{\mathrm{log}\,}_{2}\rho ]\) is the von Neumann entropy, \({\rho }_{{\mathrm{diag}}}={\sum }_{i}\left|i\right\rangle \left\langle i\right|\rho \left|i\right\rangle \left\langle i\right|\), and we consider coherence with respect to the computational basis \(\{\left|i\right\rangle \}\). For single-qubit states with Bloch vector r = (rx, ry, rz), both quantities can be expressed as64:
with the binary entropy \(h(x)=-x\,{\mathrm{log}\,}_{2}x-(1-x)\,{\mathrm{log}\,}_{2}(1-x)\) and the Bloch vector length \(r={({r}_{x}^{2}+{r}_{y}^{2}+{r}_{z}^{2})}^{1/2}\).
In the next step, we will express both \({C}_{{\ell }_{1}}\) and Cr in terms of the outcome probabilities of a collective measurement in the maximally entangled basis, performed on two copies ρ ⊗ ρ. We denote the corresponding outcome probabilities as \({P}_{i}={\rm{Tr}}[{M}_{i}\rho \otimes \rho ]\), where
are projectors onto maximally entangled states \(\left|{\psi }^{\pm }\right\rangle =(\left|01\right\rangle \pm \left|10\right\rangle )/\sqrt{2}\) and \(\left|{\varphi }^{\pm }\right\rangle =(\left|00\right\rangle \pm \left|11\right\rangle )/\sqrt{2}\). As we show in Method section, the outcome probabilities fulfill the relations
Thus, both coherence measures \({C}_{{\ell }_{1}}\) and Cr can be expressed as simple functions of Pi. We further note that in general CMS can be used to estimate absolute values of the Bloch vector components of a single-qubit state ρ. This implies that CMS allows to evaluate any coherence measure of single-qubit states, as any such measure is a function of the absolute values of the Bloch coordinates, see Method section for more details.
In the following, we use numerical simulation to compare the collective measurement scheme (CMS) discussed above to three alternative schemes for measuring \({C}_{{\ell }_{1}}\) for single-qubit states. The first alternative scheme is to directly measure observables σx and σy, and estimate \({C}_{{\ell }_{1}}\) via Eq. (3). The second scheme is a two-step adaptive measurement: step one is to measure observables σx and σy; based on the feedback results of the first step, step two is to choose optimal observable aσx + bσy to obtain \(| \langle 0| \rho | 1\rangle |\). The third alternative scheme is to perform state tomography and then, subject to the derived density matrix, to estimate the value of \({C}_{{\ell }_{1}}\). We further use the tomography results to estimate the relative entropy of coherence Cr via Eq. (4), and compare the performance of the estimation with CMS.
For the numerical simulation we use single-qubit states
with θ ranging from 0 to π/2. All simulations are performed on N = 1200 copies of \(\left|\Psi \right\rangle\). We further repeat each simulation 1000 times and average the numerical data overall repetitions. We are in particular interested in the error of the estimation:
where Cest and C are the estimated and the actual coherence measures, respectively. Figure 1a shows the results of numerical simulation for \({C}_{{\ell }_{1}}\), together with experimental data; the experiment will be discussed in more detail below. Each data point in the figure is the average of T = 1000 repetitions, i.e., \(\frac{1}{T}\mathop{\sum }\nolimits_{i = 1}^{T}{\varepsilon }_{i}\), where εi is the error of the ith measurement. The error bar denotes the standard deviation of εi. Figure 1b shows the corresponding comparison between CMS and tomography for estimating the relative entropy of coherence Cr.
Mean errors for estimating ℓ1-norm coherence in a and relative entropy coherence in b for a family of qubit states with different measurement schemes. The states have the form \(\left|\Psi \right\rangle =\sin \theta \left|0\right\rangle +\cos \theta \left|1\right\rangle\) with θ ranging from 0 to π/2. In a, the performances of CMS (numerical simulation and experiment); σx, σy measurement (simulation); two-step adaptive measurements (simulation); and tomography (simulation) are shown for comparison. In b, the performances of CMS (numerical simulation and experiment) and tomography (simulation) are shown for comparison. The sample size is N = 1200. Each data point is the average of 1000 repetitions, and the error bar denotes the standard deviation.
As we see from the data shown in Fig. 1a, b, there is a range of θ where CMS outperforms all other schemes, leading to the smallest error. Moreover, while the error in general depends on θ, this dependence is comparably weak for CMS. To compare the accuracy achieved by different estimation methods more intuitively and clearly, we average the mean error for all input states shown in Fig. 1a, and the average results are shown in Fig. 2. For the estimation of \({C}_{{\ell }_{1}}\) the adaptive measurement scheme outperforms CMS on average, which again outperforms all other estimation schemes presented above. In the Supplementary Information we further report theoretical and experimental results for estimating coherence of formation3,65 for qubits. Also in this case CMS outperforms all other schemes discussed in this paper in a certain range of θ.
Average results of the mean error for all input states shown in Fig. 1a. The corresponding average values of these methods from left to right: 0.0263, 0.0234, 0.0156, 0.0176, 0.0187.
While the above discussion was restricted to qubit systems, the CMS method can also be applied to estimate \({C}_{{\ell }_{1}}\) for states of higher dimensions. We consider an arbitrary quantum state \(\rho ={\sum }_{i,j}{\rho }_{ij}\left|i\right\rangle \left\langle j\right|\), where i, j = 0, 1, …, d − 1 and d is the dimension of Hilbert space. After an appropriate set of collective measurements are performed on the two-copy state ρ ⊗ ρ, we find that the absolute value of the off-diagonal element ∣ρij∣ for i ≠ j can be expressed as
where \(|{\psi }_{ij}^{\pm }\rangle =(\left|ij\right\rangle \pm \left|ji\right\rangle )/\sqrt{2}\). Therefore, the ℓ1-norm coherence can be written as
We use numerical simulation to compare the performance of the CMS method to the qutrit state tomography for the family of qutrit states
with α ranging from 0 to π/2 (see Supplementary Information for more details). The results of the simulation are shown in Fig. 3. As before, we use N = 1200 copies of the state \(\left|\Phi \right\rangle\) for both CMS and state tomography, and average over 1000 repetitions. The results show that CMS outperforms the tomography method for a large range of α. Apart from a higher accuracy, the CMS method requires only a single measurement setup, while four measurement setups are required for qutrit tomography.
Mean error for estimating \({C}_{{\ell }_{1}}\) for a family of qutrit states in Eq. (11) for CMS and qutrit state tomography (numerical simulation). The sample size is N = 1200. Each data point is the average of 1000 repetitions, and the error bars denote the standard deviation.
Experimental implementation
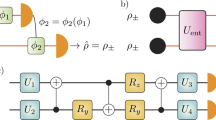
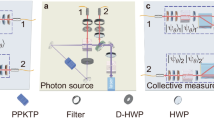
The experimental setup for realizing CMS to estimate coherence of qubit states is presented in Fig. 4. The setup is composed of three modules designed for single-photon source, two-copy state preparation, and collective measurements, respectively. In the single-photon source module, a 80-mW cw laser with a 404-nm wavelength (linewidth = 5 MHz) pumps a type-II beamlike phase-matching beta-barium-borate (BBO, 6.0 × 6.0 × 2.0 mm3, θ = 40.98∘) crystal to produce a pair of photons with wavelength λ = 808 nm. The two photons pass through two interference filters (IF) whose FWHM (full width at half maximum) is 3 nm. The photon pairs generated in spontaneous parametric down-conversion (SPDC) are coupled into single-mode fibers separately. One photon is detected by a single-photon detector acting as a trigger. The coincidence counts are ~5 × 103 per second. In the two-copy state preparation module, we first prepare copy 1 in the path degree of freedom of single photon, i.e., the first qubit encoded in positions 1 and 0 (see a in Fig. 4). After passing a half-wave plate (HWP) and a quarter-wave plate (QWP) with deviation angles H1, Q1, the photon is prepared in the desired state ρ. To encode the polarization state into the path degree of freedom, beam displacer (BD1) is used to displace the horizontal polarization (H) component into path 0, which is 4-mm away from the vertical polarization (V) component in path 1; then a HWP (H3) with deviation angle 45∘ is placed in path 0. The resulting photon is described by the state \(\rho \otimes \left|V\right\rangle \left\langle V\right|\). Then we encode the second copy of ρ into the polarization degree of freedom of single photon using a HWP and a QWP with deviation angles H2, Q2 (see b in Fig. 4). In this way, we can prepare the desired two-copy state ρ ⊗ ρ.
The setup consists of three modules designed for single-photon source, two-copy state preparation (a, b) and collective measurement, respectively. In the single-photon source module, the photon pairs generated in spontaneous parametric down-conversion are coupled into single-mode fibers separately. One photon is detected by a single-photon detector (SPD) acting as a trigger. In the two-copy state preparation module, a prepares the first copy in the path degree of freedom of the photon; b prepares the second copy in the polarization degree of freedom of the photon. In the collective measurement module, combinations of beam displacers (BDs) and half-wave plates (HWPs) with certain angular settings are used to realize collective measurement, where H4 and H5 are 22.5∘. Four SPDs M1 to M4 correspond to the four outcomes of the collective measurement. Each SPD is a silicon avalanche photodiode (Si-APD), with detection efficiency of ~60%.
The collective measurement module realizes a measurement on ρ ⊗ ρ in the maximally entangled basis, where Mi are given in Eq. (5). When estimating the ℓ1-norm coherence, only the probabilities of the outcomes M1 and M2 are used, see the discussion below Eq. (3). The probabilities of all outcomes are used for estimating the relative entropy of coherence, see Eq. (4). To verify the experimental implementation of the collective measurement, we take the conventional method of measuring the probability distributions after preparing the input states \(\left|{\psi }^{+}\right\rangle\), \(\left|{\psi }^{-}\right\rangle\), \(\left|{\varphi }^{+}\right\rangle\) and \(\left|{\varphi }^{-}\right\rangle\). These input states can be prepared by choosing proper rotation angles H1, Q1, H2, H3 as specified in the Supplementary Information. Each input state is prepared and measured 5000 times, and the probability of obtaining the outcomes M1, M2, M3, and M4 are 0.9981 ± 0.0006, 0.9973 ± 0.0007, 0.9962 ± 0.0009, and 0.9961 ± 0.0009, respectively (ideal value is 1). The theoretical values of other probability distributions for the input states are all 0, experimentally the maximum error of other probability is 0.0037 ± 0.0009.
The experimental deterministic realization of the collective measurement allows us to estimate the amount of coherence with a single measurement setup. We experimentally investigate the error achieved by CMS when the input states \(\left|\Psi \right\rangle\) have the form Eq. (7) with θ ranging from 0 to π/2. The sample size of the experiment is N = 1200 copies of \(\left|\Psi \right\rangle\); same sample size has been used in the numerical simulations reported above. As in the numerical simulation, we average over 1000 repetitions of the experiment. The experimental results for the estimation precision of \({C}_{{\ell }_{1}}\) and Cr are shown in Fig. 1a, b, respectively. The experimental data are in good agreement with the theoretical prediction. The errors in our experiment mainly come from the inaccuracy of angles of the wave plates and the imperfect interference visibility of the interferometer.
Discussion
We introduce a general method to directly measure quantum coherence of an unknown quantum state using two-copy collective measurement, focusing on two established coherence quantifiers: ℓ1-norm coherence and relative entropy coherence. As we demonstrate by numerical simulation for qubit and qutrit states, in a certain parameter region the collective measurement scheme outperforms other estimation techniques, including methods based on adaptive σx, σy measurement for qubits, and tomography-based coherence estimation for qubits and qutrits. We test our results by experimentally estimating the ℓ1-norm coherence and relative entropy coherence of qubit states by collective measurements in optical setup, finding good agreement between theory and experiment. For single-qubit states our method allows to estimate absolute values of the Bloch coordinates, implying that any coherence quantifier of a qubit can be estimated with the collective measurement scheme.
Although the precision achieved by our method is not always better than by adaptive measurement, our scheme has several advantages with respect to other techniques. In particular, our method does not need any optimization procedures or feedback, which are required for coherence estimation via adaptive measurements. Moreover, the entire experiment can be performed in a single measurement setup. Thus, our work provides a simple method to measure coherence, and highlights the application of collective measurement in quantum information processing.
Methods
Estimating general coherence measures for qubits with collective measurements
For a single-qubit state ρ with Bloch vector r = (rx, ry, rz) the probabilities \({P}_{i}={\rm{Tr}}[{M}_{i}\rho \otimes \rho ]\) are given explicitly as
It thus follows that collective measurements can be used to evaluate absolute values of the Bloch coordinates:
From these results, it is straightforward to verify Eq. (6).
In the following, C(rx, ry, rz) will denote a coherence measure for a qubit state ρ with Bloch vector r = (rx, ry, rz). As we will now show, for single-qubit states any coherence measure C depends only on the absolute values of the Bloch vector coordinates. For this, it is enough to show that
for any coherence measure C and any Bloch vector. This can be seen by noting that the vector (rx, ry, rz) can be transformed into the vector (−rx, ry, rz) via a rotation around the z-axis, which corresponds to an incoherent unitary operation. Since any coherence measure is invariant under incoherent unitaries, it follows that C(rx, ry, rz) = C(−rx, ry, rz). By similar arguments we obtain C(rx, ry, rz) = C(rx, −ry, rz). Moreover, note that σx is an incoherent unitary inducing the transformation (rx, ry, rz) → (rx, −ry, −rz), and thus it must be that C(rx, ry, rz) = C(rx, −ry, −rz). Combining these arguments completes the proof of Eq. (14).
Data availability
All data not included in the paper and its Supplementary Information are available upon reasonable request from the corresponding authors.
References
Baumgratz, T., Cramer, M. & Plenio, M. B. Quantifying coherence. Phys. Rev. Lett. 113, 140401 (2014).
Levi, F. & Mintert, F. A quantitative theory of coherent delocalization. N. J. Phys. 16, 033007 (2014).
Winter, A. & Yang, D. Operational resource theory of coherence. Phys. Rev. Lett. 116, 120404 (2016).
Yadin, B., Ma, J., Girolami, D., Gu, M. & Vedral, V. Quantum processes which do not use coherence. Phys. Rev. X 6, 041028 (2016).
BenDana, K., GarcíaDíaz, M., Mejatty, M. & Winter, A. Resource theory of coherence: Beyond states. Phys. Rev. A 95, 062327 (2017).
Streltsov, A., Adesso, G. & Plenio, M. B. Colloquium: quantum coherence as a resource. Rev. Mod. Phys. 89, 041003 (2017).
Hu, M. L. et al. Quantum coherence and geometric quantum discord. Phys. Rep. 762, 1–100 (2018).
Hillery, M. Coherence as a resource in decision problems: the Deutsch-Jozsa algorithm and a variation. Phys. Rev. A 93, 012111 (2016).
Shi, H.-L. et al. Coherence depletion in the Grover quantum search algorithm. Phys. Rev. A 95, 032307 (2017).
Matera, J. M., Egloff, D., Killoran, N. & Plenio, M. B. Coherent control of quantum systems as a resource theory. Quantum Sci. Technol. 1, 01LT01 (2016).
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002).
Napoli, C. et al. Robustness of coherence: an operational and observable measure of quantum coherence. Phys. Rev. Lett. 116, 150502 (2016).
Piani, M. et al. Robustness of asymmetry and coherence of quantum states. Phys. Rev. A 93, 042107 (2016).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum-enhanced measurements: beating the standard quantum limit. Science 306, 1330–1336 (2004).
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photonics 5, 222–229 (2011).
Giorda, P. & Allegra, M. Coherence in quantum estimation. J. Phys. A Math. Theory 51, 025302 (2018).
Gour, G. & Spekkens, R. W. The resource theory of quantum reference frames: manipulations and monotones. N. J. Phys. 10, 033023 (2008).
Marvian, I. & Spekkens, R. W. How to quantify coherence: distinguishing speakable and unspeakable notions. Phys. Rev. A 94, 052324 (2016).
Streltsov, A., Singh, U., Dhar, H. S., Bera, M. N. & Adesso, G. Measuring quantum coherence with entanglement. Phys. Rev. Lett. 115, 020403 (2015).
Chitambar, E. & Hsieh, M.-H. Relating the resource theories of entanglement and quantum coherence. Phys. Rev. Lett. 117, 020402 (2016).
Tan, K. C., Kwon, H., Park, C.-Y. & Jeong, H. Unified view of quantum correlations and quantum coherence. Phys. Rev. A 94, 022329 (2016).
Chitambar, E. et al. Assisted distillation of quantum coherence. Phys. Rev. Lett. 116, 070402 (2016).
Ma, J., Yadin, B., Girolami, D., Vedral, V. & Gu, M. Converting coherence to quantum correlations. Phys. Rev. Lett. 116, 160407 (2016).
Streltsov, A., Rana, S., Bera, M. N. & Lewenstein, M. Towards resource theory of coherence in distributed scenarios. Phys. Rev. X 7, 011024 (2017).
Streltsov, A. et al. Entanglement and coherence in quantum state merging. Phys. Rev. Lett. 116, 240405 (2016).
Wu, K.-D. et al. Experimentally obtaining maximal coherence via assisted distillation process. Optica 4, 454–459 (2017).
Wu, K.-D. et al. Experimental cyclic interconversion between coherence and quantum correlations. Phys. Rev. Lett. 121, 050401 (2018).
Regula, B., Fang, K., Wang, X. & Adesso, G. One-shot coherence distillation. Phys. Rev. Lett. 121, 010401 (2018).
Regula, B., Lami, L. & Streltsov, A. Nonasymptotic assisted distillation of quantum coherence. Phys. Rev. A 98, 052329 (2018).
Vijayan, M. K., Chitambar, E. & Hsieh, M.-H. One-shot assisted concentration of coherence. J. Phys. A. 51, 414001 (2018).
Zhao, Q., Liu, Y., Yuan, X., Chitambar, E. & Winter, A. One-shot coherence distillation: towards completing the picture. IEEE Trans. Inf. Theory 65, 6441–6453 (2019).
Zhao, Q., Liu, Y., Yuan, X., Chitambar, E. & Ma, X. One-shot coherence dilution. Phys. Rev. Lett. 120, 070403 (2018).
Wu, K.-D. et al. Quantum coherence and state conversion: theory and experiment. npj Quantum Inf. 6, 1–9 (2020).
Narasimhachar, V. & Gour, G. Low-temperature thermodynamics with quantum coherence. Nat. Commun. 6, 7689 (2015).
Åberg, J. Catalytic coherence. Phys. Rev. Lett. 113, 150402 (2014).
Lostaglio, M., Jennings, D. & Rudolph, T. Description of quantum coherence in thermodynamic processes requires constraints beyond free energy. Nat. Commun. 6, 6383 (2015).
Korzekwa, K., Lostaglio, M., Oppenheim, J. & Jennings, D. The extraction of work from quantum coherence. N. J. Phys. 18, 023045 (2016).
Lostaglio, M., Korzekwa, K., Jennings, D. & Rudolph, T. Quantum coherence, time-translation symmetry, and thermodynamics. Phys. Rev. X 5, 021001 (2015).
Ćwikliński, P., Studziński, M., Horodecki, M. & Oppenheim, J. Limitations on the evolution of quantum coherences: towards fully quantum second laws of thermodynamics. Phys. Rev. Lett. 115, 210403 (2015).
Rodríguez-Rosario, C.A., Frauenheim, T. & Aspuru-Guzik, A. Thermodynamics of quantum coherence. Preprint at http://arXiv.org/quant-ph/1308.1245 (2013).
Karlström, O., Linke, H., Karlström, G. & Wacker, A. Increasing thermoelectric performance using coherent transport. Phys. Rev. B 84, 113415 (2011).
Herranen, M., Kainulainen, K. & Rahkila, P. M. Kinetic transport theory with quantum coherence. Nucl. Phys. A 820, 203c–206c (2009).
Rebentrost, P., Mohseni, M. & Aspuru-Guzik, A. Role of quantum coherence and environmental fluctuations in chromophoric energy transport. J. Phys. Chem. B 113, 9942–9947 (2009).
Huelga, S. F. & Plenio, M. B. Vibrations, quanta and biology. Contemp. Phys. 54, 181–207 (2013).
Lloyd, S. Quantum coherence in biological systems. J. Phys. 302, 012037 (2011).
Plenio, M. B. & Huelga, S. F. Dephasing-assisted transport: quantum networks and biomolecules. N. J. Phys. 10, 113019 (2008).
Lambert, N. et al. Quantum biology. Nat. Phys. 9, 10–18 (2013).
Romero, E. et al. Quantum coherence in photosynthesis for efficient solar-energy conversion. Nat. Phys. 10, 676–682 (2014).
Huelga, S. F. & Plenio, M. B. Quantum biology: a vibrant environment. Nat. Phys. 10, 621–622 (2014).
Bera, M. N., Qureshi, T., Siddiqui, M. A. & Pati, A. K. Duality of quantum coherence and path distinguishability. Phys. Rev. A 92, 012118 (2015).
Bagan, E., Bergou, J. A., Cottrell, S. S. & Hillery, M. Relations between coherence and path information. Phys. Rev. Lett. 116, 160406 (2016).
Yuan, Y. et al. Experimental demonstration of wave-particle duality relation based on coherence measure. Opt. Express 26, 4470–4478 (2018).
Vedral, V., Plenio, M. B., Rippin, M. A. & Knight, P. L. Quantifying entanglement. Phys. Rev. Lett. 78, 2275–2279 (1997).
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009).
James, D. F. V., Kwiat, P. G., Munro, W. J. & White, A. G. Measurement of qubits. Phys. Rev. A 64, 052312 (2001).
Girolami, D. Observable measure of quantum coherence in finite dimensional systems. Phys. Rev. Lett. 113, 170401 (2014).
Wang, Y.-T. et al. Directly measuring the degree of quantum coherence using interference fringes. Phys. Rev. Lett. 118, 020403 (2017).
Zhang, D.-J., Liu, C. L., Yu, X.-D. & Tong, D. M. Estimating coherence measures from limited experimental data available. Phys. Rev. Lett. 120, 170501 (2018).
Carmeli, C., Heinosaari, T., Maniscalco, S., Schultz, J. & Toigo, A. Determining quantum coherence with minimal resources. N. J. Phys. 20, 063038 (2018).
Massar, S. & Popescu, S. Optimal extraction of information from finite quantum ensembles. Phys. Rev. Lett. 74, 1259–1263 (1995).
Tarrach, R. & Vidal, G. Universality of optimal measurements. Phys. Rev. A 60, R3339–R3342 (1999).
Bagan, E., Ballester, M. A., Gill, R. D., Muñoz-Tapia, R. & Romero-Isart, O. Separable measurement estimation of density matrices and its fidelity gap with collective protocols. Phys. Rev. Lett. 97, 130501 (2006).
Hou, Z. et al. Deterministic realization of collective measurements via photonic quantum walks. Nat. Commun. 9, 1414 (2018).
Ren, H., Lin, A., He, S. & Hu, X. Quantitative coherence witness for finite dimensional states. Ann. Phys. 387, 281–289 (2017).
Yuan, X., Zhou, H., Cao, Z. & Ma, X. Intrinsic randomness as a measure of quantum coherence. Phys. Rev. A 92, 022124 (2015).
Acknowledgements
We thank Huangjun Zhu for fruitful discussions. This work was supported by the National Natural Science Foundation of China (Grants No. 11574291 and No. 11774334), National Key Research and Development Program of China (Grants No. 2016YFA0301700 and No.2017YFA0304100), and Anhui Initiative in Quantum Information Technologies. A.S. acknowledges financial support by the ”Quantum Coherence and Entanglement for Quantum Technology” project, carried out within the First Team programme of the Foundation for Polish Science co-financed by the European Union under the European Regional Development Fund.
Author information
Authors and Affiliations
Contributions
Y.Y. and A.S. developed the theoretical approach; G.Y.X. supervised the project; Y.Y., Z.H., and G.Y.X. designed the experiment and the measurement apparatus; Y.Y. built the instruments, performed the experiment, and collected the data with assistance from Z.H., J.F.T., and G.Y.X.; Y.Y., H.Z., and G.Y.X. performed numerical simulations and analysed the experimental data with assistance from C.F.L. and G.C.G.; A.S., Y.Y., and G.Y.X. prepared and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yuan, Y., Hou, Z., Tang, JF. et al. Direct estimation of quantum coherence by collective measurements. npj Quantum Inf 6, 46 (2020). https://doi.org/10.1038/s41534-020-0280-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-020-0280-6
This article is cited by
-
Quantification of entanglement and coherence with purity detection
npj Quantum Information (2024)
-
Coherence dynamics of spin systems in critical environment with topological characterization
Quantum Information Processing (2024)
-
Approaching optimal entangling collective measurements on quantum computing platforms
Nature Physics (2023)
-
Experimental study of quantum coherence decomposition and trade-off relations in a tripartite system
npj Quantum Information (2021)