Introduction

With quantum computing technology advancing at a fast pace, noisy intermediate-scale quantum (NISQ) technology with 50–100 qubits are predicted to be realized in the near future1,2. Solid-state quantum processors in the NISQ era and beyond will be realized by mass-fabrication on wafers including 300 mm technology3,4,5. Optimization and validation approaches for quantum materials and devices are therefore required that can rely on an increasingly fast-feedback cycle. Since quantum technology operates at sub-kelvin temperatures, cryogenic solutions for fast testing will have to be developed.

The decades of advancement in classical technology following Moore’s law has been made possible by approaches dictated by Rent’s rule T = tgp, where the Rent exponent p relates the total number of control lines T and proportionality factor t with the number of internal components g6,7. This same rule has been predicted to be required for practical quantum processors8, but we also envision that this rule will determine the progress in fabrication and validation, with the Rent factor crucially determining how many devices can be tested simultaneously.

One pursuit toward scalable testing is to adapt room temperature wafer-scale probing at cryogenic temperatures. Indeed, a cryogenic wafer prober has recently been developed to establish a high-volume 300 mm test-line for quantum devices9. The measurement temperature in probe-based systems, however, is limited to a few kelvin. Furthermore, integration of magnets required for material characterization is challenging to achieve in large-size probe systems. Alternatively, cryogenic on-chip multiplexers have been developed in GaAs/AlGaAs10,11,12,13 and Si/SiGe14 heterostructures, operating at a temperature of 1.6 and 0.2 K, respectively. With this approach the number of quantum devices measured in one cooldown on a single chip is increased without the need to alter existing cryostat setups. However, the design and implementation of on-chip multiplexers is specific to the materials and device under test (DUT). Furthermore, an architecture that works at base temperature of a dilution refrigerator, high magnetic fields, and is independent of the number and type of DUT is yet to be developed.

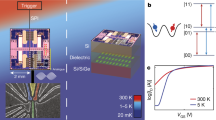
In this article, we deploy digital CMOS logic at T = 50 mK to increase the number of wires available at cryogenic temperature by an order of magnitude while keeping the overhead number of I/O wires at room temperature fixed (Fig. 1). Our cryogenic platform is based on general-purpose commercial off-the-shelf multiplexers driven by a nearby shift register, is operated under the extreme temperature and magnetic fields achieved in dilution refrigerators, and can be readily integrated in any kind of cryostat. We have specifically designed the cryo-CMOS circuit to act as a switch and allow for high-throughput quantum transport measurements. Multiple devices can be screened for relevant metrics in the same cooldown either individually or at once by time-division multiplexing (TDM) without introduction of any artifacts.

Fig. 1: Setup for accelerated cryo-testing of quantum materials and devices.
figure 1

Left panel: a number N of dies, each containing a device under test (DUT), are selected from a wafer and wire bonded onto a printed circuit board (DUT-PCB; blue circle). Middle panel: the DUT-PCB is mounted to the cold finger of a dilution refrigerator (MCK 50-400 by Leiden Cryogenics) connected by flat ribbon cables to a printed circuit board containing CMOS components (cryo-MUX PCB; blue star). The DUT-PCB and cryo-MUX PCB are operated at T = 50 mK. Right panel: schematics of the cold finger showing how the use of cryo-CMOS allows cold-wires multiplication on the DUT-PCB with a fixed overhead of wires to room temperature. Devices may be selected for single measurements or time-division multiplexing.

Full size image

To prove the value of this architecture for accelerating the fabrication-measurement cycle of quantum devices, we focus on an archetypal measurement in condensed matter physics: magnetotransport of 2DEGs in the classical and quantum Hall regime. These measurements are used to evaluate statistically key metrics of high-mobility Si/SiGe heterostructure field effect transistors (H-FETs), relevant for spin-qubits in Si15,16, currently leading the field of quantum computation with quantum dots17. We exploit the cryo-multiplexing platform to accelerate the development of 300 mm epitaxial wafers manufactured in an industrial CMOS fab and report record values of electron mobility and percolation density at sub-kelvin temperatures, relevant for large silicon spin-qubit arrays.

Results

Cryogenic multiplexer platform

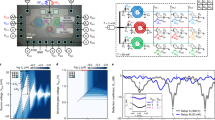
Figure 2 shows the schematics of our experimental setup. At the heart of the architecture is a printed circuit board (cryo-MUX PCB; Fig. 2c) operating at 50 mK. The cryo-MUX PCB comprises cascaded serial-input parallel-output (SIPO) shift registers, which provide N output lines, each of them controlling M output lines of multiplexer components. Few input/output (I/O) wires connect the cryo-MUX PCB to room temperature electronics (Fig. 2a) with the following purpose: (i) provide supply voltages and digital logic levels to the board components; (ii) connect the multiplexers to current/voltage supplies and equipment for performing measurements of the devices. Each of the DUT has M (S) multiplexed (shared) terminals and is bonded to a printed circuit board (DUT-PCB; Fig. 2d). The DUT-PCB, also operating at 50 mK, is connected to the multiplexers on the cryo-MUX PCB by flat ribbon I/O cables supporting more than NM + S wires.

Fig. 2: Cryo-multiplexing platform setup.
figure 2

a Electronics operated at room temperature is controlled by a computer (b) using the QCoDeS framework and supplies voltages to the components located on the cryo-MUX PCB (c). The serial-input parallel-output shift registers receive a string of bits from the room temperature electronics to control the multiplexers. Each bit corresponds to all multiplexers associated with one device under test, located on the DUT-PCB (d). The multiplexed lines of select devices can be switched either to the supply and measurement equipment or to ground.

Full size image

Table 1 presents an overview of the scaling properties of the number of lines between the different parts of the cryogenic architecture in our experimental setup. The system can be scaled by either adding more devices or by adding more lines per device, i.e increasing N or M, respectively. When devices are added, additional shift registers are required to select these devices. When the number of lines per device is increased, additional multiplexers and room temperature measurement equipment are needed. Crucially, this protocol requires a constant number of lines between room temperature and cryogenic components, regardless how large N is. This approach yields an optimal Rent exponent at room temperature pRT = 0; however, the time necessary to perform a measurement cycle through all DUT scales linearly with N.

Table 1 Number of lines between parts of the cryo-multiplexer platform.
Full size table

The whole system is controlled by sending commands to the electronics through a software environment built on QCoDeS18 (Fig. 2b), while timing is done using an internal hardware clock for increased precision. Three signals generated from custom digital to analog converters are sent to the SIPO shift registers to perform switching between DUT. All signals are produced by low-noise equipment to avoid any coupling of noise and interference to the multiplexers, since additional line filters were not present due to space constraints in our dilution refrigerator. Firstly, a sequence of data bits is sent that defines which DUT will be selected. Secondly, a clocking signal is sent while loading each bit. Thirdly, a strobe signal is supplied, indicating when the shift register is fully loaded and the outputs can be sent to the multiplexers.

To achieve switching between lines, each line in the DUT is connected to a multiplexer consisting of a CMOS analog integrated circuit configured as a single-pole/double-throw switch. The input terminal of the switch is connected to the DUT, while the output terminals are connected to room temperature equipment and ground. All switches associated with a DUT are controlled through logic inputs connected to the same shift register output. All possible 2N combinations of DUT can be selected since the multiplexers are driven by the parallel output of the shift register.

In all the experiments presented here, the cryo-MUX PCB comprises two cascaded shift registers with eight parallel outputs each (Texas Instruments 74HC4094; specifications in ref. 19), allowing, in principle to measure up to N = 16 DUT. Each of the N parallel outputs of the shift registers control M = 6 multiplexed lines, separated over two components, each containing three single-pole/double-throw switches (Maxim MAX4619; specifications in ref. 20). These components show an on-resistance of 28 Ω and an off-leakage current ≤1 fA at T ≤ 80 mK (see Supplementary Information). The shift registers and multiplexer components are powered with positive and negative supply voltages of 1.1 and −3.9 V, respectively. The same values define the digital logic levels. In total, the 16 available channels and 6 multiplexed lines result in 96 wires available at the base temperature of the dilution refrigerator. Up to 13 devices are bonded on the DUT-PCB, less than N = 16 due to the specific die-size chosen for the DUT and the limited sample space. A complete circuit diagram of the cryo-MUX PCB and DUT-PCB is provided in the Supplementary Information.

We are able to discriminate whether correct switching has occurred, and consequently whether an intended DUT has been selected, by monitoring the resistance of N control resistors, each connected to one of the M = 6 multiplexed lines. We send commands to switch more than 103 times between randomly selected control resistors at a strobe frequency fstrobe. We then verify that the measured resistance matches the expected value of the control resistors. We obtain a switching success rate of 100% at T ≤ 80 mK, while loading the shift register at a clock signal frequency of 4.4 MHz and while switching between resistors at a frequency fstrobe = 1 KHz, much larger than fstrobe = 8 Hz used in the experiments reported below. By increasing fstrobe to 8 KHz, we observe that the steady temperature of the dilution refrigerator stage has increased to 130 mK, signaling that the power dissipation in the MUX-PCB has exceeded the cooling power of our dilution refrigerator at base temperature (see Supplementary Information).

Time-division multiplexing of control resistors

Thirteen metal thin film resistors (N = 13) are bonded to the DUT-PCB in a four-probe configuration (Fig. 3a) to validate multiplexed electrical transport under different control sequences and conditions of external parameters, such as source-drain voltage applied to the resistors (VSD), magnetic field (B), and temperature (T). The four-probe setup eliminates the series resistance originating from fridge wiring and electrical contacts and is a test-bed for quantum devices characterization. At room temperature the resistances of the chosen components range from 100 Ω to 8.2 kΩ and are expected to be temperature independent, minimizing device unpredictability.

Fig. 3: Multiplexed measurements of known resistors.
figure 3

a Four-probe setup for multiplexed measurements of known resistors. b DC voltage–current characteristics of 13 resistors measured individually (dots) or all at once (lines) by time-division multiplexing. Different colors correspond to different resistors. c–e Multiplexed resistance measurements while sweeping source-drain voltage (VSD), magnetic field (B), and temperature (T). On the vertical axis, the AC resistance R = dVxx/dISD is normalized to the resistance value R0 measured at zero DC source-drain voltage, zero magnetic field, and T = 50 mK. For clarity, curves are offset by an amount 0.25j, with j being an integer from 0 (bottom curve) to 12 (top curve).

Full size image

We investigate two measurement protocols. Firstly, the cryo-MUX PCB may act as a simple DUT-selector by keeping a single device connected to the measurement equipment while sweeping the relevant parameter. This allows for a traditional single device measurement, with N devices measured one after the other. Alternatively, TDM is achieved by sequentially selecting for measurement all resistors at each point in the parameter sweep, allowing all N measurements to be completed within a single parameter sweep. In addition to benefiting from measurement speedup, this protocol allows for a better comparison between devices since differences in time-dependent factors are minimized.

In Fig. 3b we compare the DC voltage–current characteristics of the resistors obtained by sweeping the source-drain voltage VSD following the two methodologies (sequential sweeps vs. TDM). For all resistors the curves obtained with the two methodologies are matching, with fitted resistance values differing by 0.7% at most, limited by measurement resolution. Having established the validity of the TDM methodology, we further test its applicability to VSD, B, or T sweeps, to emulate typical quantum transport measurements. For these measurements we use four-terminal low-frequency lock-in techniques by applying constant AC source-drain voltages of 100 μV. As seen in Fig. 3c–e, the resistance values remain constant for all N devices while sweeping VSD, B, or T. Overall, this characterization indicates that TDM does not introduce nonlinearity in the four terminal measurements and that the whole architecture works properly under high magnetic fields and different temperature conditions.

Multiplexed quantum transport of industrial Si/SiGe field effect transistors

We now harness the power of the multiplexing platform to measure quantum transport of buried-channel semiconductor heterostructures, an archetype material platform for the fabrication of gated semiconductor quantum devices. In the Si/SiGe heterostructures a type II band alignment promotes electron confinement at the interface between a strained Si quantum well and an SiGe barrier21. Si/SiGe heterostructures fabricated in academic environments have proven a successful material platform for obtaining long-lived high-fidelity electron spin-qubits in silicon22 and demonstrating strong spin-photon coupling23,24. Furthermore, the advanced level of quantum control in these qubits allows to run quantum algorithms on two qubit processors15,16.

By investigating quantum transport in Hall-bar-shaped H-FETs25,26,27, key material metrics such as maximum mobility and percolation density are extracted. Electron mobility is a straightforward figure of merit to asses the overall quality of the 2DEG in the high density regime, where screening of impurity scattering is relevant28,29. On the other hand, the percolation density indicates the minimum density necessary to establish a metallic conduction channel and is a gauge for disorder at low density, where quantum devices operate.

In this work we take advantage of the cryo-multiplexer platform to reduce the total time required to characterize in detail multiple devices at sub-kelvin temperatures, thereby accelerating the process development for Si/SiGe heterostructures on 300 mm Si substrates in an industrial manufacturing CMOS fab. Si/SiGe H-FETs are fabricated in an academic clean room on 100 mm wafers laser-cut from the original 300 mm Si/SiGe industrial wafer (see details in “Methods” section).

Ten dies (N = 10) are randomly selected from different locations of the 100 mm wafer (Fig. 4a), bonded onto the DUT-PCB, and cooled down to 50 mK for measurements. Figure 4b, c shows a cross-section of the H-FETs and a schematic of the multiple connecting lines, respectively. Each device has eight terminals. Five ohmic contacts (O1–O3, O5, O6) are multiplexed, whereas the source contact (O4) and the gate contacts (G1, G2) are shared by all N devices (M = 5, S = 3). Using these connections we perform magnetotransport measurements on all DUT by standard low-frequency lock-in techniques (see “Methods” section).

Fig. 4: Multiplexed quantum transport in the classical Hall regime at T = 50 mK.
figure 4

a Dicing scheme of the wafer. Each die and associated measurements throughout the figure are assigned a unique color. b Cross-section schematic of the DUT, an Si/SiGe heterostructure field effect transistor and c contact schematics. d Conductivity σxx (upper panel) and density n (lower panel) as a function of gate voltage Vg. e Mobility μ (upper panel) and conductivity σxx (lower panel) as a function of density n. Statistical analysis of datasets in (d) and (e) yield box plots of f threshold voltage V0, g capacitance C, h maximum mobility μmax, and i percolation density np with mean and standard deviation (black crosses). To draw a meaningful comparison between variations in (f–i), the range of each vertical axis is chosen to equal the mean value of the plotted variable. All measurements are taken in a single cooldown.

Full size image

Figure 4d shows the conductivity (σxx) and the electron density (n) of the devices measured by time-division multiplexing as a function of gate voltage (upper and lower panel, respectively). Above a threshold voltage V0, electrons accumulate in the quantum well, current flows in the transistor channel and σxx increases monotonically with V0. Correspondingly, in all devices, the electron density increases linearly as VG sweeps more positive, consistent with a parallel-plate capacitor model where dielectric between the 2DEG and metallic top-gate comprises the Si0.7Ge0.3 barrier and the Al2O3 layer.

Figure 4e shows the density-dependent mobility (μ) and conductivity (upper and lower panel respectively). Excluding the purple and red curves, all the other devices follow a similar trend. The mobility increases steeply at small densities (n ≤ 1.4 × 1011 cm−2), before slowing down and eventually saturating at higher densities (n ≥ 2 × 1011 cm−2). This behavior is indicative of a high-quality Si/SiGe 2DEG. The mobility is limited at low density by scattering from remote charged impurities, likely at the oxide interface, whereas saturation at higher density is given by short-range scattering from impurities within or nearby the quantum well. Remarkably, four devices (black, green, yellow, brown) stand out for exhibiting overlapping mobility density curves over the entire density range, indicating a uniform disorder landscape across the wafer30. This is beneficial for the future development of large Si qubit arrays with shared control lines31.

By analyzing the datasets in Fig. 4d, e, we perform statistical analysis of key metrics of the 2DEG. Threshold voltage, capacitance (C), maximum mobility (μmax), and percolation density (np) are reported as box plots in Fig. 4f–i. The threshold voltage V0 (Fig. 4f) is extrapolated from the linear density-gate voltage dependence to zero density, whereas the capacitance (Fig. 4g) is given by the relationship \(C=\frac{{\mathrm {d}}n}{{\mathrm {d}}{V}_{{\mathrm {g}}}}e\). We observe small variations in both V0 (2.75%) and C (1.34%), indicating that the dielectric stack comprising a 30-nm-thick Si0.7Ge0.3 barrier and the Al2O3 layer are uniform across the wafer. A record high μmax (Fig. 4h) of 4.2 × 105 cm2/Vs is achieved for these industrially manufactured Si 2DEGs, with an average value of (3.9 ± 0.6) × 105 cm2/Vs, corresponding to a standard deviation below 20%. Our maximum mobility is less than the value of 6.5 × 105 cm2/Vs obtained previously in Si/SiGe32 possibly because the dielectric interface in our samples is much closer to the channel (30 nm compared to 50–60 nm in ref. 32).

As expected from the density-dependent mobility curves, the box plot of μmax reveals the outliers (purple and red), with values outside of the standard deviation. The percolation density np (Fig. 4i) is obtained by fitting the density-dependent conductivity to a 2D percolation transition model \({\sigma }_{xx} \sim {(n-{n}_{{\mathrm {p}}})}^{1.31}\)29. We obtain an average np of (6.9 ± 0.4) × 1010 cm−2, corresponding to a standard deviation below 6%. The percolation density has a minimum value of 6.4 × 1010 cm−2, on par with the best values reported in the literature26,32. Overall these results support the use of 300 mm epitaxial Si/SiGe as a promising material platform to manufacture industrial spin-qubits.

We now examine magnetotransport at high magnetic field, where quantum effects are dominant. Figure 5a shows ρxx and ρxy of the black device measured either in multiplexed or nonmultiplexed conditions. The overlap between the two curves is excellent, confirming the robustness of the setup against magnetic field sweeps. Clear Shubnikov–de Haas oscillations with zero-resistivity minima are observed in the longitudinal resistance ρxx as a function of the magnetic field B. Correspondingly, flat quantum Hall effect plateaus are visible in ρxy. The oscillations structure is typical of an Si/SiGe structure. The first oscillations at low fields correspond to integer filling factors ν = 4k due to the spin and valley degeneracy. At higher fields, opening of the Zeeman gap and increased valley splitting leads to lifting of spin and valley degeneracy and observation of the associated even (ν = 4k − 2) and odd (ν = 2k − 1) filling factors. The QHE plateau values are quantized as expected at values of h/e2v, where h is Planck’s constant and e the elementary charge.

Fig. 5: Multiplexed quantum transport in the quantum Hall regime at T = 50 mK.
figure 5

a Resistivity ρxx and Hall resistivity ρxy of an Si/SiGe heterostructure field effect transistor at T = 50 mK measured individually (red curves) or by multiplexing (black curves) through all other devices. b Multiplexed resistivity ρxx and c Hall conductivity σxy as a function of filling factor ν for eight devices. Color coding as described in Fig. 4a. d Box plot of the percentage difference between Hall density n and density nSdH, with average and standard deviation (cross), extracted by analysis of the Shubnikov–de Haas oscillation periodicity.

Full size image

Figure 5b shows the multiplexed ρxx measurements for all devices. We exclude the purple and red device because analysis of the Shubnikov–de Haas oscillations reveals for these devices the presence of a spurious conduction channel in parallel to the quantum well, possibly due to leakage from the gate. This spurious channel is likely the cause of the reduced mobility compared to the other devices at similar density. The measurements are taken at a fixed VG, corresponding to n ~ 4.3 × 1011 cm−2. For clarity, the curves are plotted against filling factor ν. All devices show clearly the spin and valley split levels; however, differences in the values of ρxx are seen, possibly due to the different Landau level broadening and/or different energy splittings across devices. Similar considerations apply to the minor difference observed in quantum Hall measurements reported in Fig. 5c. As a final statistical analysis, we show in Fig. 5d a box plot of the percentage difference between Hall density and Shubnikov–de Haas density nSdH, obtained by the periodicity of the oscillations as a function of 1/B. The discrepancy is less than 3%, indicating that population of only one high-mobility subband is achieved uniformly across the wafer.

Discussion

In conclusion, we investigate a cryo-CMOS architecture that uses general-purpose discrete components at 50 mK to increase the number of wires available at cryogenic temperature by an order of magnitude. This is obtained while keeping the overhead number of I/O wires to room temperature fixed. As a proof of principle, we develop and operate a cryo-MUX PCB with 16 selectable channels and 6 multiplexed lines, resulting in 96 wires available at the base temperature of the dilution refrigerator. This solution, implemented in a dilution refrigerator insert with a small sample space, can be further expanded and readily applied to virtually any cryostat.

We show control experiments where time-division multiplexed measurements of known resistors are performed to demonstrate robustness of the setup with respect to applied voltages, magnetic field, and temperature sweeps. We harness the power of the multiplexing architecture to measure quantum transport of numerous Si/SiGe H-FETs in one cooldown, accelerating the development of 300 mm Si/SiGe wafers fabricated in an industrial CMOS fab. We report record values of maximum mobility and percolation density and further improvements of these two metrics are expected by processing the entire gate stack in the high-volume manufacturing environment, due to the better semiconductor/oxide interface attainable with an advanced process control. Multiplexed measurements of Shubnikov–de Haas oscillations and quantum Hall effect are performed successfully. These capabilities provide scope for future high-volume measurements of valley splitting in Si 2DEGs based on thermal activation measurements in the QHE regime33.

We show a path forward for high-throughput quantum transport at cryogenic temperatures, which will help to accelerate the fabrication-measurement cycle of quantum devices in industrial settings. The cryogenic multiplexing demonstrated here may be used already to set the potential landscape of large quantum dot arrays31,34,35. Moreover, the recent demonstration of universal quantum logic above 1 K with silicon qubits36 provides avenue for switching rates exceeding MHz frequencies, thus enabling full control over quantum circuits with only a few room temperature control lines. We envisage that investigations of different components with smaller footprints, circuits, and architectures at cryogenic temperatures37, including custom fully integrated CMOS solutions, will help to satisfy the ever-growing need for scalable wiring solutions to control large quantum systems.

Methods

Si/SiGe heterostructure and device fabrication

The Si/SiGe heterostructure comprises an Si0.7Ge0.3 strained relaxed buffer obtained by step grading of the germanium content, a 10-nm-thick strained Si quantum well, a 30-nm-thick Si0.7Ge0.3 barrier and a 1-nm-thick Si cap. The fabrication process for H-FETs involves: mesa-trench for device isolation; P ion implantation and annealing at T = 750 °C for contacting the 2DEG; atomic layer deposition of a 30-nm-thick Al2O3 dielectric layer to isolate the 2DEG from the Hall-bar-shaped metallic top-gate; metallization for gate, ohmic contacts, and bonding pads.

Quantum transport measurements

We apply a source-drain bias of 0.1 mV and measure ISD, the longitudinal voltage Vxx, and the transverse Hall voltage Vxy as a function of gate voltage VG and B. These measurements are carried out by sequential selection or time-division multiplexing. As for the control resistance measurements discussed previously, the datasets obtained with the two methodologies agree within less than 1%, indicating that time-division multiplexing does not perturb the measurements. The longitudinal resistivity ρxx and transverse Hall resistivity ρxy are then calculated. The longitudinal (σxx) and transverse (σxy) conductivity are obtained via tensor inversion. The Hall electron density n is obtained from the linear dependence ρxy = B/en at low magnetic fields. The carrier mobility μ is extracted from the relationship σxx = neμ, where e is the electron charge.