Abstract
Kernel methods have a wide spectrum of applications in machine learning. Recently, a link between quantum computing and kernel theory has been formally established, opening up opportunities for quantum techniques to enhance various existing machine-learning methods. We present a distance-based quantum classifier whose kernel is based on the quantum state fidelity between training and test data. The quantum kernel can be tailored systematically with a quantum circuit to raise the kernel to an arbitrary power and to assign arbitrary weights to each training data. Given a specific input state, our protocol calculates the weighted power sum of fidelities of quantum data in quantum parallel via a swap-test circuit followed by two single-qubit measurements, requiring only a constant number of repetitions regardless of the number of data. We also show that our classifier is equivalent to measuring the expectation value of a Helstrom operator, from which the well-known optimal quantum state discrimination can be derived. We demonstrate the performance of our classifier via classical simulations with a realistic noise model and proof-of-principle experiments using the IBM quantum cloud platform.
Similar content being viewed by others
Introduction
Advances in quantum information science and machine learning have led to the natural emergence of quantum machine learning, a field that bridges the two, aiming to revolutionize information technology1,2,3,4,5. The core of its interest lies in either taking advantage of quantum effects to achieve machine learning that surpasses the classical pendant in terms of computational complexity or to entirely be able to apply such techniques on quantum data. A prominent application of machine learning is classification for predicting a category of an input data by learning from labeled data, an example of pattern recognition in big data analysis. As most techniques in classical supervised machine learning are aimed to getting the best result while using a polynomial amount of computational resources at most, an exact solution to the problem is usually out of reach. Therefore many such learning protocols have empirical scores instead of analytically calculated bounds. Even with this lack of rigorous mathematics they have been applied with great success in science and industry. In pattern analysis, the use of a kernel, i.e. a similarity measure of data that corresponds to an inner product in higher-dimensional feature space, is vital6,7. However, classical classifiers that rely on kernel methods are limited when the feature space is large and the kernel functions are computationally expensive to evaluate. Recently, a link between the kernel method with feature maps and quantum computation was formally established by proposing to use quantum Hilbert spaces as feature spaces for data8. The ability of a quantum computer to efficiently access and manipulate data in the quantum feature space offers potential quantum speedups in machine learning9.
Recent work in ref. 10 showed a minimal quantum interference circuit for realizing a distance-based supervised binary classifier. The goal of this task is, given a labelled dataset \({\mathcal{D}}=\left\{({{\bf{x}}}_{1},{y}_{1}),\ldots ,({{\bf{x}}}_{M},{y}_{M})\right\}\subset {{\mathbb{C}}}^{N}\times \{0,1\}\), to classify an unseen datapoint \(\tilde{{\bf{x}}}\in {{\mathbb{C}}}^{N}\) as best as possible. Conventional machine-learning problems usually deal with real-valued data points, which is, however, not the natural choice for quantum information problems. In particular, having quantum feature maps in mind, we generalize the dataset to be complex valued. The quantum interference circuit introduced in ref. 10 implements a distance-based classifier through a kernel based on the real part of the transition probability amplitude (state overlap) between training and test data. Once the set of classical data is encoded as a quantum state in a specific format, the classifier can be implemented by interfering the training and test data via a Hadamard gate and gathering the projective measurement statistics on a post-selected state, which has been projected to a particular subspace. For brevity, we refer to this classifier as Hadamard classifier. Since a Hadamard classifier only takes the real part of the state overlap into account it does not work for an arbitrary quantum state, which can represent classical data via a quantum feature map or be an intrinsic quantum data. Thus, designing quantum classifiers that work for an arbitrary quantum state is of fundamental importance for further developments of quantum methods for supervised learning.
In this work, we propose a distance-based quantum classifier whose kernel is based on the quantum state fidelity, thereby enabling the use of a quantum feature map to the full extent. We present a simple and systematic construction of a quantum circuit for realizing an arbitrary weighted power sum of quantum state fidelities between the training and test data as the distance measure. The argument for the introduction of non-uniform weights can also be applied to the Hadamard classifier of ref. 10. The classifier is realized by applying a swap-test11 to a quantum state that encodes the training and test data in a specific format. The quantum state fidelity can be raised to the power of n at the cost of using n copies of training and test data. We also show that the post-selection can be avoided by measuring an expectation value of a two-qubit observable. The swap-test classifier can be implemented without relying on the specific initial state by using a method based on quantum forking12,13 at the cost of increasing the number of qubits. In this case, the training data, corresponding labels, and the test data are provided on separate registers as a product state. This approach is especially useful for a number of situations: intrinsic—possibly unknown—quantum data, parallel state preparation and gate intensive routines, such as quantum feature maps. Furthermore, we show that the swap-test classifier is equivalent to measuring the expectation value of a Helstrom operator, from which the optimal projectors for the quantum state discrimination is constructed14. This motivates further investigations on the fundamental connection between the distance-based quantum classification and the Helstrom measurement. To demonstrate the feasibility of the classifier with near-term quantum devices, we perform simulations on a classical computer with a realistic error model, and realize a proof-of-principle experiment on a five-qubit quantum computer in the cloud provided by IBM15.
Results
Classification without post-selection
The Hadamard classifier requires the training and test data to be prepared in a quantum state as
where the data are encoded into the state representation \(\left|{{\bf{x}}}_{m}\right\rangle =\mathop{\sum }\nolimits_{i = 1}^{N}{x}_{m,i}\left|i\right\rangle\), \(\left|\tilde{{\bf{x}}}\right\rangle =\mathop{\sum }\nolimits_{i = 1}^{N}{\tilde{x}}_{i}\left|i\right\rangle\), the binary label is encoded in ym ∈ {0, 1}, and all inputs xm and \(\tilde{{\bf{x}}}\) have unit length10. The superscript h indicates that the state is for the Hadamard classifier. The first and the last qubits are an ancilla qubit used for interfering training and test data and index qubits for training data, respectively. In ref. 10, each subspace has an equal probability amplitude, i.e. wm = 1/M ∀ m, resulting in a uniformly weighted kernel. Here we introduce an arbitrary probability amplitude \(\sqrt{{w}_{m}}\), where ∑mwm = 1, to show that a non-uniformly weighted kernel can also be generated. The goal of the classifier is to assign a new label \(\tilde{y}\) to the test data, which predicts the true class of \(\tilde{{\bf{x}}}\) denoted by \(c(\tilde{{\bf{x}}})\) with high probability. The classifier is implemented by a quantum interference circuit consisting of a Hadamard gate and two single-qubit measurements. The state after the Hadamard gate applied to the ancilla qubit is
with \(\left|{\psi }_{\pm }\right\rangle =\left|{{\bf{x}}}_{m}\right\rangle \pm \left|\tilde{{\bf{x}}}\right\rangle\). Measuring the ancilla qubit in the computational basis and post-selecting the state \(\left|a\right\rangle\), a ∈ {0, 1}, yield the state
where \({p}_{a}=\mathop{\sum }\nolimits_{m = 1}^{M}{w}_{m}(1+{(-1)}^{a}{\rm{Re}}\left\langle {\psi }_{{{\bf{x}}}_{m}}| {\psi }_{\tilde{{\bf{x}}}}\right\rangle )/2\) is the probability to post-select a = 0 or 1, and ψ0(1) = ψ+(−). The Hadamard classifier in ref. 10 selects the measurement outcome a = 0 and proceeds with a measurement of the label register in the computational basis, resulting in the measurement probability of
where b ∈ {0, 1}. The test data are classified as \(\tilde{y}\) that is obtained with a higher probability. Since the success probability of the classification depends on p0, in ref. 10, a dataset is to be pre-processed in a way that the post-selection succeeds with a probability of around 1/2. This is done by standardizing all data xm such that they have mean 0 and standard deviation 1 and applying the transformation to the test datum \(\tilde{{\bf{x}}}\) too. Now we show that the classifier can be realized without the post-selection, thereby reducing the number of experiments by about a factor of two, and avoiding the pre-processing (see Supplementary Information).
If the classifier protocol proceeds with the ancilla qubit measurement outcome of 1, the probability to measure b on the label qubit is
Thus, when the ancilla qubit measurement outputs 1, \(\tilde{y}\) should be assigned to the label with a lower probability. This result shows that both branches of the ancilla state can be used for classification. The difference in the post-selected branch only results in different post-processing of the measurement outcomes.
The measurement and the post-processing procedure can be described more succinctly with an expectation value of a two-qubit observable, \(\langle {\sigma }_{z}^{(a)}{\sigma }_{z}^{(l)}\rangle\), where the superscript a (l) indicates that the operator is acting on the ancilla (label) qubit. The expectation value is
The last expression is obtained by using \({\rm{tr}}(\left|{\psi }_{\pm }\right\rangle \left\langle {\psi }_{\pm }\right|)=2\pm 2{\rm{Re}}\left\langle \tilde{{\bf{x}}}| {{\bf{x}}}_{m}\right\rangle\), and \({\rm{tr}}({\sigma }_{z}\left|{y}_{m}\right\rangle \left\langle {y}_{m}\right|)=1\) for ym = 0 and −1 for ym = 1. The test data are classified as 0 if \(\langle {\sigma }_{z}^{(a)}{\sigma }_{z}^{(l)}\rangle\) is positive, and 1 if negative:
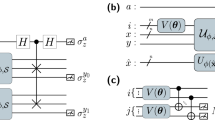
A quantum circuit for implementing a Hadamard classifier is depicted in Fig. 1.
Quantum kernel based on state fidelity
In order to take the full advantage of the quantum feature maps8,9 in the full range of machine-learning applications, it is desirable to construct a kernel based on the quantum state fidelity, rather than considering only a real part of the quantum state overlap as done in ref. 10. We propose a quantum classifier based on the quantum state fidelity by using a different initial state than described in ref. 10 and replacing the Hadamard classification with a swap-test.
The state preparation requires the training data with labels to be encoded as a specific format in the index, data and label registers. In parallel, a state preparation of the test data is done on a separate input register. Unlike in the Hadamard classifier, the ancilla qubit is not in the part of the state preparation, and it is only used in the measurement step as the control qubit for the swap-test. The controlled-swap gate exchanges the training data and the test data, and the classification is completed with the expectation value measurement of a two-qubit observable on the ancilla and the label qubits. For brevity, we refer to this classifier as swap-test classifier.
With multiple copies of training and test data, polynomial kernels can be designed16,17. With any \(n\in {\mathbb{N}}\), a swap-test on n copies of training and test data that are entangled in a specific form results in
where \(\left|{\psi }_{n\pm }\right\rangle ={\left|\tilde{{\bf{x}}}\right\rangle }^{\otimes n}{\left|{{\bf{x}}}_{m}\right\rangle }^{\otimes n}\pm {\left|{{\bf{x}}}_{m}\right\rangle }^{\otimes n}{\left|\tilde{{\bf{x}}}\right\rangle }^{\otimes n}\), and the superscript s indicates that the state is for the swap-test classifier. Using \({\rm{tr}}(\left|{\psi }_{n\pm }\right\rangle \left\langle {\psi }_{n\pm }\right|)=2\pm 2| \left\langle \tilde{{\bf{x}}}| {{\bf{x}}}_{m}\right\rangle {| }^{2n}\), the expectation value of \({\sigma }_{z}^{(a)}{\sigma }_{z}^{(l)}\) for this state is given as
The swap-test classifier also assigns a label to the test data according to Eq. (7). A quantum circuit for implementing a swap-test classifier with a kernel based on the nth power of the quantum state fidelity is depicted in Fig. 2.
The first register is the ancilla qubit (a), the second is the data qubit (d), the third is the label qubit (l), and the last one corresponds to the index qubits (m). An operator \({U}_{h}({\mathcal{D}})\) creates the input state necessary for the classification protocol. The Hadamard gate and the two-qubit measurement statistics yield the classification outcome.
The first register is the ancilla qubit (a), the second contains n copies of the test datum (\(\tilde{x}\)), the third are the data qubits (d), the fourth is the label qubit (l) and the final register corresponds to the index qubits (m). An operator \({U}_{s}({\mathcal{D}})\) creates the input state necessary for the classification protocol. The swap-test and the two-qubit measurement statistics yield the classification outcome.
Note that if the projective measurement in the computational basis followed by post-selection is performed as in ref. 10, the probability of classification can be obtained as
where \({p}_{a}=\mathop{\sum }\nolimits_{m}^{M}{w}_{m}(1+{(-1)}^{a}| \left\langle \tilde{{\bf{x}}}| {{\bf{x}}}_{m}\right\rangle {| }^{2n})/2\). Since pa here is a function of the quantum state fidelity, which is non-negative, p0 ≥ p1 and p0 ≥ 1/2. As a result, the data pre-processing used in the Hadamard classifier for ensuring a high success probability of the post-selection is not strictly required for the swap-test classifier.
We demonstrate the performance of the swap-test classifier using a simple example dataset that only consists of two training data and one test data as
For simplicity, we omit the parameter θ and write \(\tilde{{\bf{x}}}=\tilde{{\bf{x}}}(\theta )\) when the meaning is clear. The classification for this trivial example requires quantum state fidelity rather than the real component of the inner product as the distance measure, verifying the advantage of the proposed method. Since the classification relies on the distance between the training and test data in the quantum feature space, we also choose c as to compare the distance between the test datum and training data of each class. The inner products are \(\left\langle \tilde{{\bf{x}}}| {{\bf{x}}}_{1}\right\rangle =i\sin \left(\frac{\theta }{2}+\frac{\pi }{4}\right)\), and \(\left\langle \tilde{{\bf{x}}}| {{\bf{x}}}_{2}\right\rangle =i\cos \left(\frac{\theta }{2}+\frac{\pi }{4}\right)\). According to Eq. (9) the expectation value is
Thus the swap-test classifier outputs \(\tilde{y}\) that coincides with \(c(\tilde{{\bf{x}}}(\theta ))\,\forall\, \theta\). Note that although we have chosen q = 2 in this example, the swap-test classifier can correctly assign a new label \({\tilde y}\,\forall\, q\,>\,0\). In contrast, the Hadamard classifier will have the classification expectation value (see Eq. (6))
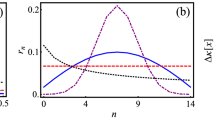
Thus in this example, for any test data parameterized by θ, the Hadamard classifier cannot find the new label \(\tilde{y}\). This dataset will be used throughout the paper for demonstrating all subsequent results. Moreover, since the non-uniform weights merely create a systematic shift of the expectation value (see Methods), without loss of generality, we use w1 = w2 = 1/2 in all examples throughout the manuscript. Using the above example dataset, we illustrate the sharpening of the classification as n increases in Fig. 3.
Theoretical results of the swap-test classifier for the example given in Eq. (11), for n = 1, 10 and 100 copies of training and test data. The test data are classified as 0 (1) if the expectation value, \(\langle {\sigma }_{z}^{(a)}{\sigma }_{z}^{(l)}\rangle\), is positive (negative). The comparison of the results for various n illustrates the polynomial sharpening which will eventually result into a Dirac δ if the number of copies approaches to the limit of ∞.
There are several interesting remarks on the result described by Eq. (9). First, since the cross-terms of the index qubit cancel out, dephasing noise acting on the index qubit does not alter the final result. The same argument also holds for the label qubit. Moreover, the same result can be obtained with the index and label qubits initialized in the classical state as \({\sum }_{m}{w}_{m}\left|{y}_{m}\right\rangle \left\langle {y}_{m}\right|\otimes \left|m\right\rangle \left\langle m\right|\), where ∑mwm = 1. In fact, since the classification is based on measuring the σz operator on ancilla and label qubits, our algorithm is robust to any error that effectively appears as Pauli error on the final state of them. It is straightforward to see that any Pauli error that commutes with \({\sigma }_{z}^{(a)}{\sigma }_{z}^{(l)}\) does not affect the measurement outcome. When a Pauli error does not commute with the measurement operator, such as a single-qubit bit flip error on the ancilla or the label qubit, the measurement outcome becomes \((1-2p)\langle {\sigma }_{z}^{(a)}{\sigma }_{z}^{(l)}\rangle\), where p is the error rate. This result is due to the fact that Pauli operators either commute or anti-commute with each other. This error can be easily circumvented since the classification only depends on the sign of the measurement outcome as shown in Eq. (7), as long as p < 1/2. The same level of the classification accuracy as that of the noiseless case can be achieved by repeating the measurement O(1/(1 − 2p)2) times. Also, any error that effectively appears at the end of the circuit on any other qubits does not affect the classification result. Second, as the number of copies of training and test data approaches a large number, we find the limit,
Therefore, as the number of data copies reaches a large number, the classifier assigns a label to the test data approximately by counting the number of training data to which the test data exactly match.
Kernel construction from a product state
The classifiers discussed thus far require the preparation of a specific initial state structure. Full state preparation algorithms are able to produce the desired state12,18,19,20,21,22,23,24,25,26,27,28,29. However, all such approaches implicitly assume knowledge of the training and testing data before preparation, and some of the procedures need classical calculation during a pre-processing step. In this section, we present the implementation of the swap-test classifier when training and test data are encoded in different qubits and provided as a product state. In this case, the classifier does not require knowledge of either training and test data. The input can be intrinsically quantum, or can be prepared from the classical data by encoding training and test data on a separate register. The label qubits can be prepared with an \({X}^{{y}_{m}}\) gate applied to \(\left|0\right\rangle\).
Given the initial product state, the quantum state required for the swap-test classification can be prepared systematically via a series of controlled-swap gates controlled by the index qubits, which is also provided on a separate register, initially uncorrelated with the reset of the system. The underlying idea is to adapt quantum forking introduced in refs. 12,13 to create an entangled state such that each subspace labeled by a basis state of the index qubits encodes a different training dataset. For brevity, we denote the controlled-swap operator by c-swap(a, b∣c) to indicate that a and b are swapped if the control is c. With this notation, the classification can be expressed with the following equations.
where \(\left|{{\rm{junk}}}_{m}\right\rangle\) is some normalized product state. Other than being entangled with the junk state, \(\left|{\Phi }_{f}^{s}\right\rangle\) in Eq. (15) is the same as \(\left|{\Psi }_{f}^{s}\right\rangle\) derived in Eq. (8). Since \({\rm{tr}}(\left|{{\rm{junk}}}_{m}\right\rangle \left\langle {{\rm{junk}}}_{m}\right|)=1\), the expectation value of an observable \({\sigma }_{z}^{(a)}{\sigma }_{z}^{(l)}\) is the same as the result shown in Eq. (9). A quantum circuit for implementing the swap-test classifier with the input data encoded as a product state is depicted in Fig. 4.
The entire quantum circuit can be implemented with Toffoli, controlled-NOT, X and Hadamard gates with additional qubits for applying multi-qubit controlled operations. Here we assume that the gate cost is dominated by Toffoli and controlled-NOT gates and focus on counting them using the gate decomposition given in ref. 30. Note that a Toffoli gate can be further decomposed to one and two-qubit gates with six controlled-NOT gates. In total, \(n(M+2)\lceil {\mathrm{log}\,}_{2}(N)\rceil +2\lceil {\mathrm{log}\,}_{2}(M)\rceil +M+1\) qubits, \(n(M+1)\lceil {\mathrm{log}\,}_{2}(N)\rceil +M\left(2\lceil {\mathrm{log}\,}_{2}(M)\rceil -1\right)\) Toffoli gates, and \(2\left(n(M+1)\lceil {\mathrm{log}\,}_{2}(N)\rceil +M\right)\) controlled-NOT gates are needed. More details on the qubit and gate count can be found in Supplementary Note II. Due to the linear dependence on M and logarithmic dependence on N in the number of gates and qubits, we expect our algorithm to be practically useful for machine-learning problems that involve a small number of training data but large feature space. As an example, for n = 1, the number of qubits, Toffoli and controlled-NOT gates needed for 16 training data with eight features are 79, 163 and 134. For 16 training data with 16 features, these numbers increase to 97, 180, and 168. For 32 training data with eight features, these numbers become 145, 387 and 262. These numbers suggest that a quantum device with an order of 100 qubits and with an error rate of a Toffoli or a controlled-NOT gate to an arbitrary set of qubits being less than about 10−3 can implement interesting quantum binary classification tasks. Due to the aforementioned robustness to some errors that effectively appear on the final state, we expect the requirement on the gate fidelity to be relaxed. To our best knowledge, currently available quantum devices do not satisfy the above technical requirement. Nevertheless, with an encouragingly fast pace of improvement in quantum hardware31,32, we expect interesting machine-learning tasks can be performed using our algorithm in the near future.
The connection to the Helstrom measurement
The swap-test classifier turns out to be an adaptation of the measurement of a Helstrom operator, which leads to the optimal detection strategy for deciding which of two density operators ρ0 or ρ1 describes a system. The quantum kernel shown in Eq. (9) is equivalent to measuring the expectation value of an observable,
on n copies of \(\left|\tilde{{\bf{x}}}\right\rangle\). This can be easily verified as follows:
The above observable can also be written as a Helstrom operator p0ρ0 − p1ρ1, where ρi represents a hypothesis under a test with the prior probability pi in the context of quantum state discrimination, by defining \({\rho }_{i}={\sum }_{m| {y}_{m} = i}({w}_{m}/{p}_{i})\left|{{\bf{x}}}_{m}\right\rangle {\left\langle {{\bf{x}}}_{m}\right|}^{\otimes n}\), where \({\sum }_{m| {y}_{m} = i}{w}_{m}/{p}_{i}=1\) and p0 + p1 = 1. In this case, measuring the expectation value of \({\mathcal{A}}\) is equivalent to measuring the expectation value of a Helstrom operator with respect to the test data. The ability to implement the swap-test classifier without knowing the training data via quantum forking leads to a remarkable result that the measurement of a Helstrom operator can also be performed without a priori information of target states.
Experimental and simulation results
To demonstrate the proof-of-principle, we applied the swap-test classifier to solve the toy problem of Eq. (11) using the IBM Q 5 Ourense (ibmq_ourense)15 quantum processor. Since n = 1 in this example, five superconducting qubits are used in the quantum circuit. The number of elementary quantum gates required for realizing the example classification is 27: 14 single-qubit gates and 13 controlled-NOT gates (see Supplementary Fig. 6), which is small enough for currently available noisy-intermediate scale quantum (NISQ) devices.
The experimental results33 are presented with triangle symbols, and compared to the theoretical values indicated by solid and dotted lines in Fig. 5. Albeit having an amplitude reduction of a factor of about 0.65 and a small phase shift in θ of about 2°, the experimental result qualitatively agrees well with the theory. We performed simulations of the experiment using the IBM quantum information science kit (qiskit)34 with realistic device parameters and a noise model in which single- and two-qubit depolarizing noise, thermal relaxation errors, and measurement errors are taken into account. The noise model provided by qiskit is detailed in Supplementary Note III. The relevant parameters used in simulations are typical data for ibmq_ourense, and are listed in Supplementary Table I. The simulation results are shown as blue squares in Fig. 5 and we find amplitude reduction of a factor of about 0.82 with a negligible phase shift. The difference between simulation and experimental results can be attributed to time-dependent noise, various cross-talk effects35, and non-Markovian noise.
The test data are classified as 0 (1) if the expectation value, \(\langle {\sigma }_{z}^{(a)}{\sigma }_{z}^{(l)}\rangle\), is positive (negative). The experimental result (red triangles) is compared to simulation with a noise model relevant to currently available quantum devices (blue squares) and to the theoretical values (black line).
Despite imperfections, the experiment demonstrates that the swap-test classifier predicts the correct class for most of the input \(\tilde{{\bf{x}}}\) (about 97% of the points sampled in this experiment) in this toy problem. Supplementary information reports experimental and simulation results obtained from various cloud quantum computers provided by IBM, repeated several times over months. In summary, all results agree qualitatively well with the theory and manifest successful classification with high probabilities.
Discussion
We presented a quantum algorithm for constructing a kernelized binary classifier with a quantum circuit as a weighted power sum of the quantum state fidelity of training and test data. The underlying idea of the classifier is to perform a swap-test on a quantum state that encodes data in a specific form. The quantum data subject to classification can be intrinsically quantum or classical information that is transformed to a quantum feature space. We also proposed a two-qubit measurement scheme for the classifier to avoid the classical pre-processing of data, which is necessary for the method proposed in ref. 10. Since our measurement uses the expectation value of a two-qubit observable for classification, it opens up a possibility to apply error mitigation techniques36,37 to improve the accuracy in the presence of noise without relying on quantum error correcting codes. We also showed an implementation of the swap-test classifier with training and test data encoded in separate registers as a product state by using the idea of quantum forking. This approach bypasses the requirement of the specific state preparation and the prior knowledge of data at the cost of increasing the number of qubits linearly with the size of the data. The downside of this approach, which may limit its applicability, is the use of many qubits which must be able to interact with each other. The exponential function of the fidelity approaches to the Dirac delta function as the number of data copies, and hence the exponent, increases to a large number. In this limit, the test data are assigned to a class, which contains a greater number of training data that is identical to the test data. An intriguing question that stems from this observation is whether such behaviour of the classifier with respect to the number of copies of quantum information is related to a consequence of the classical limit of quantum mechanics.
Our results are imperative for applications of quantum feature maps such as those discussed in refs. 8,9. In this setting, data will be mapped into the Hilbert space of a quantum system, i.e. \(\Phi :{\mathbb{R}}^{d}\to {\mathcal{H}}\). Then our classifier can be applied to construct a feature vector kernel as \({\left|\langle \Phi ({\bf{x}})| \Phi ({{\bf{x}}}_{m})\rangle \right|}^{2n}:= K({\bf{x}},{{\bf{x}}}_{m})\). Given the broad applicability of kernel methods in machine learning, the swap-test classifier developed in this work paves the way for further developments of quantum machine-learning protocols that outperform existing methods. While the Hadamard classifier developed in ref. 10 also has the ability to mimic the classical kernel efficiently, only the real part of quantum states are considered. This may limit the full exploitation of the Hilbert space as the feature space. Furthermore, quantum feature maps are suggested as a candidate for demonstrating the quantum advantage over classical counterparts. It is conjectured that kernels of certain quantum feature maps are hard to estimate up to a polynomial error classically9. If this is true, then the ability to construct a quantum kernel via quantum forking and the swap-test can be a valuable tool for solving classically hard machine-learning problems.
We also showed that the swap-test classification is equivalent to measuring the expectation value of a Helstrom operator. According to the construction of the swap-test classifier based on quantum forking, this measurement can be performed without knowing the target states under hypothesis in the original state discrimination problem by Helstrom14. The derivation of the measurement of a Helstrom operator from the swap-test classifier motivates future work to find the fundamental connection between the kernel-based quantum supervised machine learning and the well-known Helstrom measurement for quantum state discrimination. Another interesting open problem is whether the Helstrom measurement is also the optimal strategy for classification problems.
During the preparation of this manuscript, we became aware of the independent work by Sergoli et al.17, in which a quantum-inspired classical binary classifier motivated by the Helstrom measurement was introduced and was verified to solve a number of standard problems with promising accuracy. They also independently found an effect of using copies of the data and reported an improved classification performance by doing so. This again advocates the potential impact of the swap-test classifier with a kernel based on the power summation of quantum state fidelities for machine-learning problems.
Other future works include the extension of our results to constructing other types of kernels, the application to quantum support vector machines16, and designing a protocol to enhance the classification by utilizing non-uniform weights in the kernel.
Methods
The quantum circuit implementing the problem of Eq. (11) is shown by Fig. 6 where α denotes the angle to prepare the index qubit to accommodate the weights w1 and w2, and θ is the parameter of the test datum. The experiment applied θ from 0 to 2π in increments of 0.1. The experiment for each θ is executed with 8129 shots to collect measurement statistics. All experiments are performed using a publicly available IBM quantum device consisting of five superconducting qubits, and we used the IBM quantum information science kit (qiskit) framework34 for circuit design and processing.
The circuit implementing the swap-test classifier on the example dataset given in Eq. (11).
Superconducting quantum computing devices that are currently available via the cloud service, such as those used in this work, have limited coupling between qubits. The challenge of rewriting the quantum circuit to match device constraints can be easily addressed for a small number of qubits and gates. The quantum circuit layout with physical qubits of the device is shown in Supplementary information. A minor challenge to be addressed is that each quantum operation of an algorithm must be decomposed into native gates that can be realized with the IBM quantum device. This step is done by the pre-processing library of qiskit. The final circuit that is executed on the device consists of 14 single-qubit gates and 13 controlled-NOT gates and is shown in Supplementary Fig. 6. The measurement statistics are gathered by repeating the two-qubit projective measurement in the σz basis. The expectation value is calculated by \(\langle {\sigma }_{z}^{(a)}{\sigma }_{z}^{(l)}\rangle =\frac{1}{8192}\left({c}_{00}-{c}_{01}-{c}_{10}+{c}_{11}\right)\), where cal denotes the count of measurement when the ancilla is a and the label is l.
The noise model that we use for classical simulation of the experiment is provided as the basic model in qiskit and is explained in detail in Supplementary information. In brief, the device calibration data and parameters, such as T1 and T2 relaxation times, qubit frequencies, average gate error rate, read-out error rate, have been extracted from the API for ibmq_ourense with the calibration date 2019-09-29 11:48:14 UTC. The simulation also requires the gate times, which can be extracted from the device data. As mentioned above, the basic error model does not include various cross-talk effects, drift and non-Markovian noise. Supplementary information details how the device data and parameters are used in the simulation, and lists the values.
The versions—as defined by PyPi version numbers—we used for this work were 0.7.0–0.10.0.
Data availability
The datasets generated during and/or analysed during the current study are available on the GitHub repository.
Change history
17 July 2023
In this article the hyperlink provided for github repository in the Ref 33 ‘https://github.com/carstenblank/Quantum-classifier-with-tailored-quantum-kernels---Supplemental’ was incorrect. The original article has been corrected.
References
Wittek, P. Quantum Machine Learning: What Quantum Computing Means to Data Mining (Academic Press, Boston, 2014).
Schuld, M., Sinayskiy, I. & Petruccione, F. An introduction to quantum machine learning. Contemp. Phys. 56, 172–185 (2015).
Biamonte, J. et al. Quantum machine learning. Nature 549, 195 EP (2017).
Schuld, M. & Petruccione, F. Supervised Learning with Quantum Computers (Springer, Cham, Switzerland, 2018).
Dunjko, V. & Briegel, H. J. Machine learning & artificial intelligence in the quantum domain: a review of recent progress. Rep. Prog. Phys. 81, 074001 (2018).
Schölkopf, B. In Proceedings of the 13th International Conference on Neural Information Processing Systems, NIPS’00, 283–289 (MIT Press, Cambridge, 2000).
Hofmann, T., Schölkopf, B. & Smola, A. J. Kernel methods in machine learning. Ann. Stat. 36, 1171–1220 (2008).
Schuld, M. & Killoran, N. Quantum machine learning in feature Hilbert spaces. Phys. Rev. Lett. 122, 040504 (2019).
Havlícek, V. et al. Supervised learning with quantum-enhanced feature spaces. Nature 567, 209–212 (2019).
Schuld, M., Fingerhuth, M. & Petruccione, F. Implementing a distance-based classifier with a quantum interference circuit. EPL (Europhys. Lett.) 119, 60002 (2017).
Buhrman, H., Cleve, R., Watrous, J. & de Wolf, R. Quantum fingerprinting. Phys. Rev. Lett. 87, 167902 (2001).
Park, D. K., Petruccione, F. & Rhee, J.-K. K. Circuit-based quantum random access memory for classical data. Sci. Rep. 9, 3949 (2019).
Park, D. K., Sinayskiy, I., Fingerhuth, M., Petruccione, F. & Rhee, J.-K. K. Parallel quantum trajectories via forking for sampling without redundancy. N. J. Phys. 21, 083024 (2019).
Helstrom, C. W. Quantum detection and estimation theory. J. Stat. Phys. 1, 231–252 (1969).
5-qubit backend: IBM Q team. IBM Q 5 Ourense backend specification v1.0.1. https://quantum-computing.ibm.com (2019).
Rebentrost, P., Mohseni, M. & Lloyd, S. Quantum support vector machine for big data classification. Phys. Rev. Lett. 113, 130503 (2014).
Sergioli, G., Giuntini, R. & Freytes, H. A new quantum approach to binary classification. PLoS ONE 14, 1–14 (2019).
Ventura, D. & Martinez, T. Quantum associative memory. Inf. Sci. 124, 273–296 (2000).
Long, G.-L. & Sun, Y. Efficient scheme for initializing a quantum register with an arbitrary superposed state. Phys. Rev. A 64, 014303 (2001).
Grover, L. & Rudolph, T. Creating superpositions that correspond to efficiently integrable probability distributions. Preprint at https://arxiv.org/abs/quant-ph/0208112 (2002).
Kaye, P. & Mosca, M. Quantum networks for generating arbitrary quantum states. Preprint at https://arxiv.org/abs/quant-ph/0407102 (2004).
Möttönen, M., Vartiainen, J. J., Bergholm, V. & Salomaa, M. M. Transformation of quantum states using uniformly controlled rotations. Quantum Inf. Comput. 5, 467–473 (2005).
Soklakov, A. N. & Schack, R. Efficient state preparation for a register of quantum bits. Phys. Rev. A 73, 012307 (2006).
Plesch, M. & Brukner, Č. Quantum-state preparation with universal gate decompositions. Phys. Rev. A 83, 032302 (2011).
Iten, R., Colbeck, R., Kukuljan, I., Home, J. & Christandl, M. Quantum circuits for isometries. Phys. Rev. A 93, 032318 (2016).
Sieberer, L. M. & Lechner, W. Programmable superpositions of Ising configurations. Phys. Rev. A 97, 052329 (2018).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum random access memory. Phys. Rev. Lett. 100, 160501 (2008).
Giovannetti, V., Lloyd, S. & Maccone, L. Architectures for a quantum random access memory. Phys. Rev. A 78, 052310 (2008).
Hong, F.-Y., Xiang, Y., Zhu, Z.-Y., Jiang, L.-z. & Wu, L.-n. Robust quantum random access memory. Phys. Rev. A 86, 010306 (2012).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information: 10th Anniversary Edition, 10th edn. (Cambridge University Press, New York, 2011).
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Write, K. et al. Benchmarking an 11-qubit quantum computer. Nat. Commun. 10, 5464 (2019).
Blank, C. & Park, D. K. Quantum classifier with tailored quantum kernels—supplemental, GitHub repository. https://github.com/carstenblank/Quantum-classifier-with-tailored-quantum-kernels---Supplemental (2019).
Abraham, H. et al. Qiskit: an open-source framework for quantum computing. https://qiskit.org (2019).
Sarovar, M. et al. Detecting crosstalk errors in quantum information processors. Preprint at https://arxiv.org/abs/1908.09855 (2019).
Temme, K., Bravyi, S. & Gambetta, J. M. Error mitigation for short-depth quantum circuits. Phys. Rev. Lett. 119, 180509 (2017).
Endo, S., Benjamin, S. C. & Li, Y. Practical quantum error mitigation for near-future applications. Phys. Rev. X 8, 031027 (2018).
Acknowledgements
We acknowledge use of IBM Q for this work. The views expressed are those of the authors and do not reflect the official policy or position of IBM or the IBM Q team. This research is supported by the National Research Foundation of Korea (Grant No. 2019R1I1A1A01050161 and 2018K1A3A1A09078001), by the Ministry of Science and ICT, Korea, under an ITRC Program, IITP-2019-2018-0-01402, and by the South African Research Chair Initiative of the Department of Science and Technology and the National Research Foundation. We thank Spiros Kechrimparis for stimulating discussions on the Helstrom measurement. We acknowledge use of the IBM Q for this work. The views expressed are those of the authors and do not reflect the official policy or position of IBM or the IBM Q team.
Author information
Authors and Affiliations
Contributions
C.B. and D.K.P. contributed equally to this work. C.B. and D.K.P designed and analysed the model. C.B. conducted the simulations and the experiments on the IBM Q. All authors reviewed and discussed the analyses and results, and contributed towards writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Blank, C., Park, D.K., Rhee, JK.K. et al. Quantum classifier with tailored quantum kernel. npj Quantum Inf 6, 41 (2020). https://doi.org/10.1038/s41534-020-0272-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-020-0272-6
This article is cited by
-
Quantum deep generative prior with programmable quantum circuits
Communications Physics (2024)
-
Better-than-classical Grover search via quantum error detection and suppression
npj Quantum Information (2024)
-
Network intrusion detection based on variational quantum convolution neural network
The Journal of Supercomputing (2024)
-
Practical advantage of quantum machine learning in ghost imaging
Communications Physics (2023)
-
Variational quantum approximate support vector machine with inference transfer
Scientific Reports (2023)