Introduction

The discovery and utilization of purely quantum resources is an ongoing issue for basic research in quantum mechanics and quantum information processing1,2. Processes of quantum metrology3, quantum key distribution4, teleportation5, or quantum sensing6 essentially rely on the entanglement feature7,8. Unfortunately, entanglement is fragile due to the inevitable interaction between system and surrounding environment already in the initial stage of pure state preparation, making the state mixed9,10. As a result, protecting entanglement from unavoidable noises remains a main objective for quantum-enhanced technology11.

Many-body quantum networks usually employ identical quantum subsystems (e.g., qubits) as building blocks12,13,14,15,16,17,18,19. Characterizing peculiar features linked to particle indistinguishability in composite systems assumes importance from both the fundamental and technological points of view. Discriminating between indistinguishable and distinguishable particles has always been a big challenge for which different theoretical20,21,22,23 and experimental24,25,26,27,28 techniques have been suggested. Recently, particle identity and statistics have been shown to be a resource29,30,31,32,33,34 and experiments which witness its presence have been performed35. One aspect that remains unexplored is how the continuous control of the spatial configurations of one-particle wave functions, ruling the degree of indistinguishability of the particles, influences noisy entangled state preparation. Moreover, a measure of the degree of indistinguishability lacks.

Pursuing this study requires an entanglement quantifier for an arbitrary (mixed) state of the system with tunable spatial indistinguishability. It is desirable that this quantifier is defined within a suitable operational framework reproducible in the laboratory. The natural approach to this aim is the recent experimentally friendly framework based on spatially localized operations and classical communication (sLOCC), which encompasses entanglement under generic spatial overlap configurations34. This approach has been shown to also enable remote entanglement36,37 and quantum coherence38.

Here, we adopt the sLOCC framework to unveil further fundamental traits of composite quantum systems. We first define the entanglement of formation for an arbitrary state of two indistinguishable qubits (bosons or fermions). We then introduce the degree of indistinguishability as an entropic measure of information, tunable by the shapes of spatial wave functions. We finally apply these tools to a situation of experimental interest, that is noisy entangled state preparation. We find spatial indistinguishability can act as a tailored property protecting entanglement generation against noise.

Results

sLOCC-based entanglement of formation of an arbitrary state of two identical qubits

We first focus on the quantification of entanglement for an arbitrary state (pure or mixed) of identical particles. For identical particles we in general mean identical constituents of a composite system. In quantum mechanics identical particles are not individually addressable, as are instead non-identical (distinguishable) particles, so that specific approaches are needed to treat their collective properties39,40,41,42,43,44,45,46. Our goal is accomplished by straightforwardly redefining the entanglement of formation known for distinguishable particles47 to the case of indistinguishable particles, thanks to the sLOCC framework34.

The separability criterion in the standard theory of entanglement for distinguishable particles8,47 maintains its validity also for a state of indistinguishable particles once it has been projected by sLOCC onto a subspace of two separated locations \({\mathcal{L}}\) and \({\mathcal{R}}\). In fact, after the measurement, the particles are individually addressable into these regions and the criteria known for distinguishable particles can be adopted34,38.

Consider two identical qubits, with spatial wave functions ψ1 and ψ2, for which one desires to characterize the entanglement between the pseudospins between the separated operational regions. States of the system can be expressed by the elementary-state basis \(\{\left|{\psi }_{1}{\sigma }_{1},{\psi }_{2}{\sigma }_{2}\right\rangle ,{\sigma }_{1},{\sigma }_{2}=\uparrow ,\downarrow \}\), expressed in the no-label particle-based approach44,45 where fermions and bosons are treated on the same footing. The density matrix of an arbitrary state of the two identical qubits can be written as

$$\rho =\mathop{\sum }\limits_{{\sigma }_{1},{\sigma }_{2},{\sigma }_{1}^{\prime},{\sigma }_{2}^{\prime} = \downarrow ,\uparrow }{p}_{{\sigma }_{1}{\sigma }_{2}}^{{\sigma }_{1}^{\prime},{\sigma }_{2}^{\prime}}\left|{\psi }_{1}{\sigma }_{1},{\psi }_{2}{\sigma }_{2}\right\rangle \left\langle {\psi }_{1}{\sigma }_{1}^{\prime},{\psi }_{2}{\sigma }_{2}^{\prime}\right|/{\mathcal{N}},$$
(1)

where \({\mathcal{N}}\) is a normalization constant. Projecting ρ onto the (operational) subspace spanned by the computational basis \({{\mathcal{B}}}_{{\rm{LR}}}=\{\left|{\rm{L}}\uparrow ,{\rm{R}}\uparrow \right\rangle ,\left|{\rm{L}}\uparrow ,{\rm{R}}\downarrow \right\rangle ,\left|{\rm{L}}\downarrow ,{\rm{R}}\uparrow \right\rangle ,\left|{\rm{L}}\downarrow ,{\rm{R}}\downarrow \right\rangle \}\) by the projector

$${\Pi }_{{\rm{LR}}}^{(2)}=\mathop{\sum }\limits_{{\tau }_{1},{\tau }_{2} = \uparrow ,\downarrow }\left|{\rm{L}}{\tau }_{1},{\rm{R}}{\tau }_{2}\right\rangle \left\langle {\rm{L}}{\tau }_{1},{\rm{R}}{\tau }_{2}\right|,$$
(2)

one gets the distributed resource state

$${\rho }_{{\rm{LR}}}={\Pi }_{{\rm{LR}}}^{(2)}\rho {\Pi }_{{\rm{LR}}}^{(2)}/{\rm{Tr}}({\Pi }_{{\rm{LR}}}^{(2)}\rho ),$$
(3)

with probability \({P}_{{\rm{LR}}}={\rm{Tr}}({\Pi }_{{\rm{LR}}}^{(2)}\rho )\). We call PLR sLOCC probability since it is related to the post-selection procedure to find one particle in \({\mathcal{L}}\) and one particle in \({\mathcal{R}}\). The state ρLR is then exploitable for quantum information tasks by addressing the individual pseudospins in the separated regions \({\mathcal{L}}\) and \({\mathcal{R}}\), which represent the nodes of a quantum network. The state ρLR can be in fact remotely entangled in the pseudospins and constitute the distributed resource state. The trace operation is clearly performed in the LR-subspace (see Supplementary Notes 1 and 3 for details). The state ρLR, containing one particle in \({\mathcal{L}}\) and one particle in \({\mathcal{R}}\), can be diagonalized as \({\rho }_{{\rm{LR}}}={\sum }_{i}{p}_{i}\left|{\Psi }_{i}^{{\rm{LR}}}\right\rangle \left\langle {\Psi }_{i}^{{\rm{LR}}}\right|\), where pi is the weight of each pure state \(\left|{\Psi }_{i}^{{\rm{LR}}}\right\rangle\) which is in general non-separable. Entanglement of formation of ρLR is as usual48\({E}_{f}({\rho }_{{\rm{LR}}})=\min {\sum }_{i}{p}_{i}E(\left|{\Psi }_{i}^{{\rm{LR}}}\right\rangle )\), where minimization occurs over all the decompositions of ρLR and \(E({\Psi }_{i}^{{\rm{LR}}})\) is the entanglement of the pure state \(\left|{\Psi }_{i}^{{\rm{LR}}}\right\rangle\). We thus define the operational entanglement ELR(ρ) of the original state ρ obtained by sLOCC as the entanglement of formation of ρLR, that is

$${E}_{{\rm{LR}}}(\rho ):= {E}_{f}({\rho }_{{\rm{LR}}}).$$
(4)

We can conveniently quantify the entanglement of formation Ef(ρLR) by the concurrence C(ρLR), according to the well-known relation \({E}_{f}=h[(1+\sqrt{1-{C}^{2}})/2]\)47,49, where \(h(x)=-x\,{\mathrm{log}\,}_{2}x-(1-x)\;{\mathrm{log}\,}_{2}(1-x)\). The concurrence CLR(ρ) in the sLOCC framework can be easily introduced by

$${C}_{{\rm{LR}}}(\rho ):= C({\rho }_{{\rm{LR}}})=\max \left\{0,\sqrt{{\lambda }_{4}}-\sqrt{{\lambda }_{3}}-\sqrt{{\lambda }_{2}}-\sqrt{{\lambda }_{1}}\right\},$$
(5)

where λi are the eigenvalues, in decreasing order, of the non-Hermitian matrix \(R={\rho }_{{\rm{LR}}}{\widetilde{\rho }}_{{\rm{LR}}}\), being \({\widetilde{\rho }}_{{\rm{LR}}}={\sigma }_{y}^{{\rm{L}}}\otimes {\sigma }_{y}^{{\rm{R}}}{\rho }_{{\rm{LR}}}^{* }{\sigma }_{y}^{{\rm{L}}}\otimes {\sigma }_{y}^{{\rm{R}}}\) with localized Pauli matrices \({\sigma }_{y}^{{\rm{L}}}=\left|{\rm{L}}\right\rangle \left\langle {\rm{L}}\right|\otimes {\sigma }_{y}\), \({\sigma }_{y}^{{\rm{R}}}=\left|{\rm{R}}\right\rangle \left\langle {\rm{R}}\right|\otimes {\sigma }_{y}\). The entanglement quantifier of ρ so obtained contains all the information about spatial indistinguishability and statistics (bosons or fermions) of the particles.

sLOCC-based entropic measure of indistinguishability

In quantum mechanics, identical particles can be given the property of indistinguishability associated to a specific set of quantum measurements, being different from identity that is an intrinsic property of the system. With respect to the set of measurements, it seems natural to define a continuous degree of indistinguishability, which quantifies how much the measurement process can distinguish the particles. In this section, we deal with this aspect within sLOCC. For simplicity, the treatment is first presented for a two-particle pure state and then generalized to N-particle pure states. It is worth to mention that the framework is universal and also valid for mixed states.

Let us consider an elementary pure state of two identical particles \(\left|{\Psi }^{(2)}\right\rangle =\left|{\chi }_{1},{\chi }_{2}\right\rangle\), where \(\left|{\chi }_{i}\right\rangle\) is a generic one-particle state containing a set of commuting observables such as spatial wave function \(\left|{\psi }_{i}\right\rangle\) and an internal degree of freedom \(\left|{\sigma }_{i}\right\rangle\) (e.g., pseudospin with basis {↑, ↓}). The two-particle state \(\left|{\Psi }^{(2)}\right\rangle\) is thus

$$\left|{\Psi }^{(2)}\right\rangle =\left|{\chi }_{1},{\chi }_{2}\right\rangle =\left|{\psi }_{1}{\sigma }_{1},{\psi }_{2}{\sigma }_{2}\right\rangle .$$
(6)

In general, the degree of indistinguishability depends on both the quantum state and the measurement performed on the system. This means a given set of operations allows one to distinguish the particles while another set of operations does not. Let us narrow the analysis down to spatial indistinguishability within the sLOCC framework, linked to the incapability of distinguish which one of the two particles is found in each of the separated operational region. This framework thus leads to the concept of remote spatial indistinguishability of identical particles. The suitable class of measurements to this aim is represented by local counting of particles, leaving the pseudospins untouched. Inside this class, the joint projective measurement \({\Pi }_{{\rm{LR}}}^{(2)}\) defined in Eq. (2) represents the detection of one particle in \({\mathcal{L}}\) and of one particle in \({\mathcal{R}}\). We indicate with \({P}_{{\rm{X}}{\psi }_{i}}={\left|\langle {\rm{X}}| {\psi }_{i}\rangle \right|}^{2}\) (X = L, R and i = 1, 2) the probability of finding one particle in the region \({\mathcal{X}}\) (\({\mathcal{X}}={\mathcal{L}},{\mathcal{R}}\)) coming from \(\left|{\psi }_{i}\right\rangle\). We then define the joint probabilities of the two possible events when one particle is detected in each region: (i) \({{\mathcal{P}}}_{12}={P}_{{\rm{L}}{\psi }_{1}}{P}_{{\rm{R}}{\psi }_{2}}\) related to the event of finding a particle in \({\mathcal{L}}\) emerging from \(\left|{\psi }_{1}\right\rangle\) and a particle in \({\mathcal{R}}\) emerging from \(\left|{\psi }_{2}\right\rangle\), (ii) \({{\mathcal{P}}}_{21}={P}_{{\rm{L}}{\psi }_{2}}{P}_{{\rm{R}}{\psi }_{1}}\) related to the vice versa. The amount of the no-which way information emerging from the outcomes of the joint sLOCC measurement \({\Pi }_{{\rm{LR}}}^{(2)}\) is a measure of the spatial indistinguishability of the particles in the state \(\left|{\Psi }^{(2)}\right\rangle\). We thus use \({{\mathcal{Z}}}^{(2)}:= {\rm{Tr}}({\Pi }_{{\rm{LR}}}^{(2)}\left|{\Psi }^{(2)}\right\rangle \left\langle {\Psi }^{(2)}\right|)={{\mathcal{P}}}_{12}+{{\mathcal{P}}}_{21}\), that encloses the essence of this lack of information, to introduce the entropic measure of the degree of remote spatial indistinguishability

$${{\mathcal{I}}}_{{\rm{LR}}}:= -\frac{{{\mathcal{P}}}_{12}}{{\mathcal{Z}}}{\mathrm{log}\,}_{2}\frac{{{\mathcal{P}}}_{12}}{{\mathcal{Z}}}-\frac{{{\mathcal{P}}}_{21}}{{\mathcal{Z}}}{\mathrm{log}\,}_{2}\frac{{{\mathcal{P}}}_{21}}{{\mathcal{Z}}}.$$
(7)

The entropic expression above naturally arises from the requirement of quantifying the no which-way information associated to the uncertainty about the origin (spatial wave function) of the particle found in each of the operational regions. If particles do not spatially overlap in both remote regions, we have maximum information (\({{\mathcal{P}}}_{12}=1\), \({{\mathcal{P}}}_{21}=0\) or vice versa) and \({{\mathcal{I}}}_{{\rm{LR}}}=0\) (the particles can be distinguished by their spatial location). On the other hand, \({{\mathcal{I}}}_{{\rm{LR}}}=1\) when there is no information at all about each particle origin (\({{\mathcal{P}}}_{12}={{\mathcal{P}}}_{21}\)) and the particles are maximally overlapping in both regions. Notice that a given value of \({{\mathcal{I}}}_{{\rm{LR}}}\) corresponds to a class of different shapes of the single-particle spatial wave functions \(\left|{\psi }_{i}\right\rangle\). Moreover, in an experiment which reconstructs the identical particle state by standard quantum tomography, the corresponding value of \({{\mathcal{I}}}_{{\rm{LR}}}\) can be indirectly obtained50.

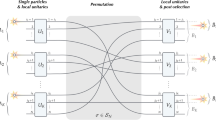
The above definition of the degree of spatial indistinguishability for two identical particles allows us to defining a more general degree of indistinguishability for N identical particles. In general, N different operational regions \({{\mathcal{R}}}_{i}\) (i = 1, …, N) are needed to quantify the indistinguishability of N identical particles (see Fig. 1). Let us consider a N-identical particle elementary pure state \(\left|{\Psi }^{(N)}\right\rangle =\left|{\chi }_{1},{\chi }_{2},...,{\chi }_{N}\right\rangle\), where \(\left|{\chi }_{i}\right\rangle\) is the ith single-particle state. Each \(\left|{\chi }_{i}\right\rangle\) is characterized by the set of values \({\chi }_{i}={\chi }_{i}^{a},{\chi }_{i}^{b},\ldots ,{\chi }_{i}^{n}\) corresponding to a complete set of commuting observables \(\hat{a},\hat{b},\ldots ,\hat{n}\). For example, if \(\hat{a}\) describes the spatial distribution of the single-particle states, \({\chi }_{i}^{a}\) is a spatial wavefunction ψi. To define a suitable class of measurements, we take the N-particle state

$${\left|\alpha \beta \right\rangle }_{N}:= \left|{\alpha }_{1}{\beta }_{1},{\alpha }_{2}{\beta }_{2},\ldots ,{\alpha }_{N}{\beta }_{N}\right\rangle ,$$
(8)

where the ith single-particle state \(\left|{\alpha }_{i}{\beta }_{i}\right\rangle\) is characterized by a subset \(\hat{a},\hat{b},\ldots ,\hat{j}\) of the \(\hat{a},\hat{b},\ldots ,\hat{n}\) commuting observables with eigenvalues \({\alpha }_{i}={\alpha }_{i}^{a},{\alpha }_{i}^{b},\ldots ,{\alpha }_{i}^{j}\), and by the remaining observables \(\hat{k},\ldots ,\hat{n}\) with eigenvalues \({\beta }_{i}={\beta }_{i}^{k},\ldots ,{\beta }_{i}^{n}\). In the first member of Eq. (8) we have set α ≔ {α1, …, αN} and β ≔ {β1, …, βN}. The N-particle projector on outcomes (α, β) of the complete set of observables is \({\Pi }_{\alpha \beta }^{(N)}={\left|\alpha \beta \right\rangle }_{N}\left\langle \alpha \beta \right|\), while the projector on outcomes α of the partial set of observables is

$${\Pi }_{\alpha }^{(N)}=\mathop{\sum }\limits_{\beta }{\Pi }_{\alpha \beta }^{(N)}.$$
(9)
Fig. 1: Projective measurements based on sLOCC.
figure 1

Illustration of different single-particle spatial wave functions ψi (i = 1, …, N) associated to N identical particles in a generic spatial configuration. The amount of spatial indistinguishability of the particles can be defined by using spatially localized single-particle measurements in N separated regions \({{\mathcal{R}}}_{i}\).

Full size image

Within the sLOCC framework, we can quantify to which extent particles in the state \(\left|{\Psi }^{(N)}\right\rangle\) can be distinguished by knowing the results α of the local measurements described by \({\Pi }_{\alpha }^{(N)}\) of Eq. (9), considering that single-particle spatial wave functions {ψi} can overlap (see Fig. 1). The (sLOCC) measurements have to satisfy the following properties: (1) the N single-particle states \(\{\left|{\alpha }_{i}{\beta }_{i}\right\rangle \}\) are peaked in separated spatial regions \(\{{{\mathcal{R}}}_{i}\}\) (see Fig. 1); (2) \(\langle {\Psi }^{(N)}| {\Pi }_{\alpha }^{(N)}| {\Psi }^{(N)}\rangle\;\ne\; 0\), i.e., the probability of obtaining the projected state must be different from zero (see Methods and Supplementary Note 1 for the general formulas).

We indicate with \({P}_{{\alpha }_{i}{\chi }_{j}}\) the single-particle probability that the result αi comes from the state \(\left|{\chi }_{j}\right\rangle\). We then define the joint probability \({P}_{\alpha {\mathcal{P}}}:= {P}_{{\alpha }_{1}{\chi }_{{p}_{1}}}{P}_{{\alpha }_{2}{\chi }_{{p}_{2}}}\cdots {P}_{{\alpha }_{N}{\chi }_{{p}_{N}}}\), where \({\mathcal{P}}=\{{p}_{1},{p}_{2},...,{p}_{N}\}\) is one of the N! permutations of the N single-particle states \(\{\left|{\chi }_{i}\right\rangle \}\). Notice that \({P}_{\alpha {\mathcal{P}}}\) can be nonzero for each of the N! permutations, since in general the outcome αi can come from any of the single-particle state \(\left|{\chi }_{j}\right\rangle\). The quantity \({\mathcal{Z}}={\sum }_{{\mathcal{P}}}{P}_{\alpha {\mathcal{P}}}\) thus accounts for this no which-way effect concerning the probabilities. The degree of indistinguishability is finally given by

$${{\mathcal{I}}}_{\alpha }:= -\mathop{\sum }\limits_{{\mathcal{P}}}\frac{{P}_{\alpha {\mathcal{P}}}}{{{\mathcal{Z}}}^{(N)}}{\mathrm{log}\,}_{2}\frac{{P}_{\alpha {\mathcal{P}}}}{{{\mathcal{Z}}}^{(N)}}.$$
(10)

This quantity depends on measurements performed on the state. If the particles are initially all spatially separated, each in a different measurement region, only one permutation remains and \({{\mathcal{I}}}_{\alpha }=0\): we have complete knowledge on the single-particle state \(\left|{\chi }_{j}\right\rangle\) which gives the outcome αi, meaning that the particles are distinguishable with respect to the measurement \({\Pi }_{\alpha }^{(N)}\). On the other hand, if for any possible permutation \({\mathcal{P}}^{\prime}\,\ne\,{\mathcal{P}}\) one has \({P}_{\alpha {\mathcal{P}}}^{\prime}={P}_{\alpha {\mathcal{P}}}\), indistinguishability is maximum and reaches the value \({{\mathcal{I}}}_{\alpha }={\mathrm{log}\,}_{2}N!\). As a specific example, when \({\chi }_{i}^{a}={\psi }_{i}\) (spatial wave functions) and \({\chi }_{i}^{b}={\sigma }_{i}\) (pseudospins), \({{\mathcal{I}}}_{\alpha }\) of Eq. (10) is the direct generalization of \({{\mathcal{I}}}_{{\rm{LR}}}\) of Eq. (7) and provides the degree of spatial indistinguishability under sLOCC for N identical particles.

Application: noisy preparation of pure entangled state

We now apply the tools above to a situation of experimental interest, namely noisy entanglement generation with identical particles.

Werner state51 \({W}_{{\rm{AB}}}^{\pm }\) for two nonidentical qubits A and B is considered as the paradigmatic example of realistic noisy preparation of a pure entangled state subject to the action of white noise. In the usual formulation, it is defined as a mixture of a pure maximally entangled (Bell) state and of the maximally mixed state (white noise). Its explicit expression, assuming to be interested in generating the Bell state \(\left|{\Psi }_{\pm }^{{\rm{AB}}}\right\rangle =(\left|{\uparrow }_{{\rm{A}}},{\downarrow }_{{\rm{B}}}\right\rangle \pm \left|{\downarrow }_{{\rm{A}}},{\uparrow }_{{\rm{B}}}\right\rangle )/\sqrt{2}\), is \({W}_{{\rm{AB}}}^{\pm }=(1-p)\left|{\Psi }_{\pm }^{{\rm{AB}}}\right\rangle \left\langle {\Psi }_{\pm }^{{\rm{AB}}}\right|+p{{\mathbb{I}}}_{{\rm{4}}}/4\), where \({{\mathbb{I}}}_{{\rm{4}}}\) is the 4 × 4 identity matrix and p is the noise probability which accounts for the amount of white noise in the system during the pure state preparation stage. The Werner state \({W}_{{\rm{AB}}}^{\pm }\) is also the product of a single-particle depolarizing channel induced by the environment applied to an initial Bell state7,8. It is known that the concurrence for such state is \(C({W}_{{\rm{AB}}}^{\pm })=1-3p/2\) when 0 ≤ p < 2/3, being zero otherwise8 (see black dot-dashed line of Fig. 3a).

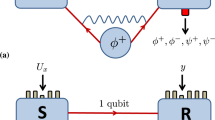
In perfect analogy, the Werner state for two identical qubits with spatial wave functions ψ1, ψ2 can be defined by

$${{\mathcal{W}}}^{\pm }=\left(1-p\right)\left|{1}\!_{\pm }\right\rangle \left\langle {1}\!_{\pm }\right|+p{{\mathcal{I}}}_{{\rm{4}}}/4,$$
(11)

where \({{\mathcal{I}}}_{{\rm{4}}}={\sum }_{i = 1,2;s = \pm }\left|{i}_{s}\right\rangle \left\langle {i}_{s}\right|\), having used the orthogonal Bell-state basis \({{\mathcal{B}}}_{\{{1}_{\pm },{2}_{\pm }\}}=\{\left|{1}_{+}\right\rangle ,\left|{1}_{-}\right\rangle ,\left|{2}_{+}\right\rangle ,\left|{2}_{-}\right\rangle \}\) with

$$\left|{1}_{\pm }\right\rangle := (\left|{\psi }_{1}\uparrow ,{\psi }_{2}\downarrow \right\rangle \pm \left|{\psi }_{1}\downarrow ,{\psi }_{2}\uparrow \right\rangle )/\sqrt{2},$$
$$\left|{2}_{\pm }\right\rangle := (\left|{\psi }_{1}\uparrow ,{\psi }_{2}\uparrow \right\rangle \pm \left|{\psi }_{1}\downarrow ,{\psi }_{2}\downarrow \right\rangle )/\sqrt{2}.$$
(12)

The Werner state of Eq. (11) is justified as a model of noisy state. In fact, it is straightforward to see that \({{\mathcal{W}}}^{\pm }\) is produced by a localized depolarizing channel acting on one of two initially separated identical qubits, followed by a quick single-particle spatial deformation procedure which makes the two identical qubits spatially overlap (see Supplementary Note 2). Hence, in Eq. (11), \(\left|{1}_{\pm }\right\rangle\) is the target pure state to be prepared and \({{\mathcal{I}}}_{4}/4\) is the noise as a mixture of the four Bell states.

Given the configuration of the spatial wave functions and using the sLOCC framework, the amount of operational entanglement contained in \({{\mathcal{W}}}^{\pm }\) can be obtained by the concurrence \({C}_{{\rm{LR}}}({{\mathcal{W}}}^{\pm })=C({{\mathcal{W}}}_{{\rm{LR}}}^{\pm })\) of Eq. (5). Notice that the state of Eq. (11) is in general not normalized, depending on the specific spatial degrees of freedom45. This is irrelevant at this stage, since the entanglement of \({{\mathcal{W}}}^{\pm }\) is calculated on the final distributed state \({{\mathcal{W}}}_{{\rm{LR}}}^{\pm }\), which is obtained from \({{\mathcal{W}}}^{\pm }\) after sLOCC and is normalized (see Eq. (3). Focusing on the observation of entanglement, a well-suited configuration for the spatial wave functions is \(\left|{\psi }_{1}\right\rangle =l\left|{\rm{L}}\right\rangle +r\left|{\rm{R}}\right\rangle\) and \(\left|{\psi }_{2}\right\rangle =l^{\prime} \left|{\rm{L}}\right\rangle +r^{\prime} {e}^{i\theta }\left|{\rm{R}}\right\rangle\), where l, r, \(l^{\prime}\), \(r^{\prime}\) are non-negative real numbers (\({l}^{2}+{r}^{2}=l{^{\prime} }^{2}+r{^{\prime} }^{2}=1\)) and θ is a phase. The wave functions are thus peaked in the two localized measurement regions \({\mathcal{L}}\) and \({\mathcal{R}}\), as depicted in Fig. 2. The degree of spatial indistinguishability \({{\mathcal{I}}}_{{\rm{LR}}}\) of Eq. (7) is tailored by adjusting the shapes of \(\left|{\psi }_{1}\right\rangle\), \(\left|{\psi }_{2}\right\rangle\), with \({P}_{{\rm{L}}{\psi }_{1}}={l}^{2}\), \({P}_{{\rm{L}}{\psi }_{2}}=l{^{\prime} }^{2}\) (implying \({P}_{{\rm{R}}{\psi }_{1}}={r}^{2}\), \({P}_{{\rm{R}}{\psi }_{2}}=r{^{\prime} }^{2}\)). The interplay between \({C}_{{\rm{LR}}}({{\mathcal{W}}}^{\pm })\) and \({{\mathcal{I}}}_{{\rm{LR}}}\) vs. noise probability p can be then investigated (see Supplementary Note 3 for some explicit expressions of \({C}_{{\rm{LR}}}({{\mathcal{W}}}^{\pm })\)).

Fig. 2: Noisy entanglement preparation with tailored spatial indistinguishability.
figure 2

Illustration of two controllable spatially overlapping wave functions ψ1, ψ2 peaked in the two localized regions of measurement \({\mathcal{L}}\) and \({\mathcal{R}}\). The two identical qubits are prepared in an entangled state under noisy conditions, giving \({{\mathcal{W}}}^{\pm }\). The degree of spatial indistinguishability can be tuned, being \(0\le {{\mathcal{I}}}_{{\rm{LR}}}\le 1\).

Full size image

Generally, the entanglement amount is conditional since the state is obtained by postselection. As a result, the entangled state ρLR is detectable if the sLOCC probability PLR is high enough to be of experimental relevance. Let us see what happens for \({{\mathcal{I}}}_{{\rm{LR}}}=1\) (\(l=l^{\prime}\)). When the target pure state in Eq. (11) is \(\left|{1}_{-}\right\rangle\), using in Eq. (12) the explicit expressions of \(\left|{\psi }_{1}\right\rangle\), \(\left|{\psi }_{2}\right\rangle\) with θ = 0 (θ = π) for fermions (bosons), from \({{\mathcal{W}}}^{-}\) we obtain by sLOCC the distributed Bell state \({{\mathcal{W}}}_{{\rm{LR}}}^{-}=\left|{1}_{-}^{{\rm{LR}}}\right\rangle \left\langle {1}_{-}^{{\rm{LR}}}\right|\), with \(\left|{1}_{-}^{{\rm{LR}}}\right\rangle =(\left|{\rm{L}}\uparrow ,{\rm{R}}\downarrow \right\rangle -\left|{\rm{L}}\downarrow ,{\rm{R}}\uparrow \right\rangle )/\sqrt{2}\), therefore (see blue solid line of Fig. 3a)

$${C}_{{\rm{LR}}}({{\mathcal{W}}}^{-})=C({{\mathcal{W}}}_{{\rm{LR}}}^{-})=1,\,{\rm{for}}\,{\rm{any}}\,{\rm{noise}}\,{\rm{probability}}\,p$$
(13)

for which the probabilities of detecting this state for fermions and bosons are, respectively

$${P}_{{\rm{LR}}}^{{\rm{(f)}}}=2{l}^{2}(1-{l}^{2}),\quad {P}_{{\rm{LR}}}^{{\rm{(b)}}}=\frac{2{l}^{2}\left(1-{l}^{2}\right)(4-3p)}{2-{\left(1-2{l}^{2}\right)}^{2}(2-3p)}.$$
(14)

Notice that the sLOCC probability for fermions, \({P}_{{\rm{LR}}}^{{\rm{(f)}}}\), is in this case independent of the noise probability. Fixing l2 = 1/2 we maximize the sLOCC probability, which is 1/2 for fermions and 1/4 for bosons in the worst scenario of maximum noise probability p = 1. Differently, targeting the pure state \(\left|{1}_{+}\right\rangle\) in Eq. (11), for fermions (bosons) with θ = π (θ = 0), one gets a p-dependent \({{\mathcal{W}}}_{{\rm{LR}}}^{+}\) by sLOCC with \({C}_{{\rm{LR}}}({{\mathcal{W}}}^{+})=C({{\mathcal{W}}}_{{\rm{LR}}}^{+})=(4-5p)/(4-p)\) when 0 ≤ p < 4/5, being zero elsewhere. The entanglement now decreases with increasing noise, remaining however larger than that for nonidentical qubits (see red dashed line of Fig. 3a). The choice of the state to generate makes a difference concerning noise protection by indistinguishability. However, we remark that identical qubits in the distributed resource state after sLOCC, \({{\mathcal{W}}}_{{\rm{LR}}}^{\pm }\), are individually addressable. Local unitary operations (rotations) in \({\mathcal{L}}\) and \({\mathcal{R}}\) can be applied to each qubit to transform the noise-free prepared \(\left|{1}_{-}^{{\rm{LR}}}\right\rangle\) into any other Bell state8. Another relevant aspect is that the phase θ in \(\left|{\psi }_{2}\right\rangle\) acts as a switch between fermionic and bosonic behavior of entanglement (see Supplementary Note 3 for details on more general instances). The result for nonidentical particles is retrieved when the qubits become distinguishable (\({{\mathcal{I}}}_{{\rm{LR}}}=0\), \(l=r^{\prime} =1\) or \(l=r^{\prime} =0\)).

Fig. 3: Prepared entanglement and indistinguishability.
figure 3

a Entanglement \({C}_{{\rm{LR}}}({{\mathcal{W}}}^{\pm })\) as a function of noise probability p for different degrees of spatial indistinguishability \({{\mathcal{I}}}_{{\rm{LR}}}\) and system parameters: blue solid line is for target state \(\left|{1}_{-}\right\rangle\), \({{\mathcal{I}}}_{{\rm{LR}}}=1\) (\(l=l^{\prime}\)), fermions (with θ = 0) or bosons (with θ = π); red dashed line is for target state \(\left|{1}_{+}\right\rangle\), \({{\mathcal{I}}}_{{\rm{LR}}}=1\) (\(l=l^{\prime}\)), fermions (with θ = π) or bosons (with θ = 0); black dot-dashed line is for distinguishable qubits (\({{\mathcal{I}}}_{{\rm{LR}}}=0\), l = 1 and \(l^{\prime} =0\) or vice versa). b Contour plot of entanglement \({C}_{{\rm{LR}}}({{\mathcal{W}}}^{-})\) versus noise probability p and spatial indistinguishability \({{\mathcal{I}}}_{{\rm{LR}}}\) for target state \(\left|{1}_{-}\right\rangle\), fermions (with θ = 0) or bosons (with θ = π), fixing \(l=r^{\prime}\).

Full size image

Since the preparation of \(\left|{1}_{-}\right\rangle\), as represented by Eq. (11), results to be noise-free for both fermions and bosons when \({{\mathcal{I}}}_{{\rm{LR}}}=1\), it is important to know what occurs for a realistic imperfect degree of spatial indistinguishability. In Fig. 3b, we display entanglement as a function of both p and \({{\mathcal{I}}}_{{\rm{LR}}}\). The plot reveals that entanglement preparation can be efficiently protected against noise also for \({{\mathcal{I}}}_{{\rm{LR}}}\;<\;1\). A crucial information in this scenario is the minimum degree of \({{\mathcal{I}}}_{{\rm{LR}}}\) that guarantees nonlocal entanglement in \({\mathcal{L}}\) and \({\mathcal{R}}\), by violating a CHSH-Bell inequality8, whatever the noise probability p. We remark that a Bell inequality violation based on sLOCC provides a faithful test of local realism52. Using the Horodecki criterion53, we find that the Bell inequality is violated for any p whenever \(0.76\,<\,{{\mathcal{I}}}_{{\rm{LR}}}\,\le\,1\), implying \(0.56<{C}_{{\rm{LR}}}({{\mathcal{W}}}^{-})\le 1\) (see Supplementary Note 4 for details). This is basically different from the case of distinguishable qubits where, as known8, \({W}_{{\rm{AB}}}^{\pm }\) violates Bell inequality only for small white noise probabilities 0 ≤ p < 0.292 (giving \(0.68<C({W}_{{\rm{AB}}}^{\pm })\le 1\)). These results show robust quantum entanglement preparation against noise through spatial indistinguishability, even partial. In fact, rather than addressing individual qubits, here one controls the shapes of their spatial wave functions \(\left|{\psi }_{1}\right\rangle\), \(\left|{\psi }_{2}\right\rangle\). Significant changes in these shapes can occur that anyway maintain \({{\mathcal{I}}}_{{\rm{LR}}}\) of Eq. (7) beyond the threshold (≈0.76) assuring noise-free generation of nonlocal entanglement. Indistinguishability here emerges as a property of composite quantum systems inherently robust to surrounding-induced disorder, protecting exploitable quantum correlations.

Discussion

In this work, we have studied the effect of spatial indistinguishability on entanglement preparation under noise, within the sLOCC framework. Firstly, thanks to the analogy with known methods for distinguishable particles, the entanglement of formation, and the related concurrence, has been defined for an arbitrary pure or mixed state of two identical qubits. Secondly, we have introduced the degree of spatial indistinguishability of identical particles by an entropic measure of information. This achievement entails a continuous quantitative identification of indistinguishability as an informational resource. Hence, one can evaluate the amount of entanglement exploitable by sLOCC into two separated operational sites under general conditions of spatial indistinguishability and state mixedness.

The Werner state \({{\mathcal{W}}}^{\pm }\) has been then chosen as a typical instance of noisy mixed state of two identical qubits, with tunable spatial overlap of their wave functions on the two remote operational regions. The tunable spatial overlap rules the indistinguishability degree. We have found that, under conditions of complete spatial indistinguishability, maximally entangled pure states between internal (spin-like) degrees of freedom can be prepared unaffected by noise. Even in the more realistic scenario of experimental errors in controlling particle spatial overlap, we have supplied a lower bound for the degree of spatial indistinguishability beyond which the generated entangled state violates the CHSH-Bell inequality independently of the amount of noise. These findings are independent of particle statistics, holding for both bosons and fermions. One reasonably may expect that also coherence can be protected by spatial indistinguishability, based on a previous work showing that the latter enables quantum coherence38. This supports the observed effects in an experiment of coherence endurance due to particle indistinguishability54.

The degree of spatial indistinguishability exhibits robustness to variations in the configuration of spatial wave functions, being then capable of shielding nonlocal entangled states against preparation noise. Therefore, indistinguishability represents a resource of quantum networks made of identical qubits enabling noise-free entanglement generation by its physical nature. Such a finding, which is promising to fault-tolerant quantum information tasks under environmental noise, adds to other known protection techniques of quantum states based on, for example, topological properties55,56,57,58,59,60,61,62, dynamical decoupling or decoherence-free subspace63,64,65,66,67. As an outlook, the effects of spatial indistinguishability on quantumness protection for different types of environmental noises will be addressed elsewhere.

Various experimental contexts can be thought for implementing the above theoretical scenario. For example, in quantum optics, spatially localized detectors can perform the required measurements while beam splitters can serve as controller of spatial wave functions of independent traveling photons (bosons) with given polarization pseudospin50. In a more sophisticated example with circular polarizations, one may employ orbital angular momentum of photons as spatial wave function and spin angular momentum as spin-like degree of freedom68,69,70. Setups using integrated quantum optics can also simulate fermionic statistics using photons71. Other suitable platforms for fermionic subsystems can be supplied either by superconducting quantum circuits with Ramsey interferometry72, or by quantum electronics with quantum point contacts as electronic beam splitters73,74,75. The results of this work are expected to stimulate further theoretical and experimental studies concerning the multiple facets of indistinguishability as a controllable fundamental quantum trait and its exploitation for quantum technologies.

Methods

Amplitudes and probabilities in the no-label approach

For calculating all the necessary probabilities and traces to obtain the results of the work, under different spatial configurations of the wave functions, we need to compute scalar products (amplitudes) between states of N identical particles.

The N-particle probability amplitude has been defined in the literature by means of the no-label particle-based approach, here adopted, to deal with systems of identical particles45. Indicating with χi, \({\chi }_{i}^{\prime}\) (i = 1, …, N) single-particle states containing all the degrees of freedom of the particle, the general expression of the N-particle probability amplitude is

$$\langle {\chi }_{1}^{\prime},{\chi }_{2}^{\prime},\ldots ,{\chi }_{n}^{\prime}| {\chi }_{1},{\chi }_{2},\ldots ,{\chi }_{n}\rangle\;:=\;\mathop{\sum }\limits_{P}{\eta }^{P}\langle {\chi }_{1}^{\prime}| {\chi }_{{P}_{1}}\rangle \langle {\chi }_{2}^{\prime}| {\chi }_{{P}_{2}}\rangle \ldots \langle {\chi }_{n}^{\prime}| {\chi }_{{P}_{n}}\rangle ,$$
(15)

where P = {P1, P2, …, Pn} in the sum runs over all the one-particle state permutations, η = ±1 for bosons and fermions, respectively, and ηP is 1 for bosons and 1 (−1) for even (odd) permutations for fermions. Notice that the explicit dependence on the particle statistics appears, as expected.

Along our manuscript, we especially need two-particle probabilities and trace operations. For N = 2, the general expression above reduces to the following two-particle probability amplitude

$$\langle {\chi }_{1}^{\prime},{\chi }_{2}^{\prime}| {\chi }_{1},{\chi }_{2}\rangle =\langle {\chi }_{1}^{\prime}| {\chi }_{1}\rangle \langle {\chi }_{2}^{\prime}| {\chi }_{2}\rangle +\eta \langle {\chi }_{1}^{\prime}| {\chi }_{2}\rangle \langle {\chi }_{2}^{\prime}| {\chi }_{1}\rangle .$$
(16)