Abstract
Entanglement is a counterintuitive feature of quantum physics that is at the heart of quantum technology. High-dimensional quantum states offer unique advantages in various quantum information tasks. Integrated photonic chips have recently emerged as a leading platform for the generation, manipulation and detection of entangled photons. Here, we report a silicon photonic chip that uses interferometric resonance-enhanced photon-pair sources, spectral demultiplexers and high-dimensional reconfigurable circuitries to generate, manipulate and analyse path-entangled three-dimensional qutrit states. By minimizing on-chip electrical and thermal cross-talk, we obtain high-quality quantum interference with visibilities above 96.5% and a maximally entangled-qutrit state with a fidelity of 95.5%. We further explore the fundamental properties of entangled qutrits to test quantum nonlocality and contextuality, and to implement quantum simulations of graphs and high-precision optical phase measurements. Our work paves the path for the development of multiphoton high-dimensional quantum technologies.
Similar content being viewed by others
Introduction
Entanglement is a central resource for quantum-enhanced technology, including quantum computation1, communication2 and metrology3. To demonstrate the advantage of quantum systems, it is necessary to generate, manipulate and detect entangled states. Quantum states span the Hilbert space with a dimensionality of dn, where d is the dimensionality of a single particle and n is the number of particles in the entangled states. Most of the widely used quantum information processing protocols are based on qubits, a quantum system with d = 2. Recently, higher-dimensional entangled states (qudits, d > 2) have gained substantial interest, owing to their distinguishing properties. For example, qudits provide larger channel capacity and better noise tolerance in quantum communication4,5,6,7, as well as higher efficiency and flexibility in quantum computing8,9 and simulations10. From the fundamental point of view, qudits also provide stronger violations of Bell inequalities11, lower bounds for closing the fair-sampling loopholes in Bell tests12 and possibilities to test contextuality13. Recent reviews on the high-dimensional entanglement can be found in refs 14,15.
High-dimensional entangled photons have been realized in various degrees of freedom (DOFs), including orbital angular momentum (OAM)11,16, frequency17,18, path19,20, temporal21,22 and hybrid time-frequency modes23. In particular, path-entangled photon pairs have been studied with a view to quantum information processing, where they are particularly attractive due to their conceptual simplicity24. However, the generation of high-dimensional path-entangled photon pairs typically requires the simultaneous operation of several coherently pumped indistinguishable photon-pair sources and several multi-path interferometers with high phase stability25. As the dimensionality increases, the phase stabilization quickly becomes a daunting task in experiments based on bulk and fibre optical elements.
Integrated photonic circuits based on silicon offer dense component integration, high optical nonlinearity and good phase stability, which are highly desirable properties for photonic quantum technology26,27,28,29,30,31. Moreover, silicon photonic devices are routinely fabricated in complementary metal oxide semiconductor (CMOS) processes. Therefore, a new field called silicon quantum photonics has recently been developed and has emerged as a promising platform for large-scale quantum information processing32. Recent advances of on-chip high-dimensional entanglement have employed frequency-encoding generated from a micro-resonator photon-pair source17 and path-encoding generated from meander waveguides photon-pair source20. Specifically, silicon waveguides with cm-length are often employed as sources to create photon-pairs9,20,28. However, the natural bandwidth of the photons generated from meander waveguides is about 30 nm20. In order to obtain high-quality photons, it is necessary to employ bandpass filters (~1 nm bandwidth in ref. 20), which unavoidably reduces the photon count rate drastically.
In this work, we employ a silicon photonic chip using an advanced resonator source embedded in Mach-Zehnder interferometers (MZIs) to generate, manipulate and characterize path-entangled qutrits (d = 3). Cavity-enhanced processes and independent tuning capabilities of the coupling coefficients of pump, signal and idler photons allow us to generate high-indistinguishable and high-brightness photons without using passive filtering. The bandwidth of the photon generated from our source is about 50 pm, about a factor of 600 narrower to that of ref. 20. This narrow-band feature not only provides high-quality single photons, but also holds the promise for direct coupling with telecom quantum memory33, which is not possible for the nanowire source due to the prohibitive low count rate after ~GHz bandwidth filtering. In particular, we perform the on-chip test of quantum contextuality with the closed compatible loophole. Furthermore, using the entangled-qutrit state, we simulate a two-vertex and three-edge graph and obtain the number of the perfect matchings of this graph, which is in the #P-complete complexity class34. Although the structure of the graph of our demonstration is simple, it can be viewed as the first step towards achieving the ambitious goal of solving #P hard problem with quantum photonic devices. We also employ our device to demonstrate the excellent phase sensitivity, exceeding both classical three-path linear interferometer and quantum second-order nonlinear interferometer limits. To be best of our knowledge, none of these three experiments have ever been realized with an integrated chip.
Results
Silicon quantum photonic chip and experimental setup
We have employed a scalable scheme for generating high-dimensional entangled states25. As shown in the conceptual scheme (Fig. 1a), entangled qutrits are generated by three coherently pumped non-degenerate spontaneous four wave mixing (SFWM) photon-pair sources, in which two pump photons generate one signal photon and one idler photon with different wavelengths (Fig. 1b, c). The signal and idler photons are separated by dichroic mirrors (DMs) and then sent through reconfigurable linear optical circuits for implementing arbitrary 3-D unitary operations via three-dimensional multiports (3D-MPs). Finally, we verify and harness the qutrit entanglement by detecting single photons at the outputs.
a Conceptual scheme of the approach for generating and manipulating two entangled qutrits. Three non-degenerate photon-pair sources, S1, S2 and S3, are coherently pumped, and three dichroic mirrors, DM1, DM2 and DM3, separate signal and idler photons into two collective paths S and I, which consist of three individual (Ind) paths 1, 3 and 5, and 2, 4 and 6, respectively. Then two three-dimensional multiport interferometers (3D-MP) perform unitary transformations to the entangled qutrits. b Diagram of a dual Mach-Zehnder interferometer micro-ring (DMZI-R) photon-pair source. This source has four ports: input, throughput, add and drop. Pump photons are sent into the input port and critically coupled into the ring resonator, where signal and idler photons are generated. By adjusting the phases of MZIs 1 and 2, we can reduce the photon leakage into the through port and increase the signal and idler photons coupling to the drop port. c Two identical pump photons (1552.1 nm) generate one signal (1545.9 nm) and one idler (1558.3 nm) photons in non-degenerate spontaneous four wave mixing. d Optical microscopy image of the DMZI-R photon-pair source, with scale bar representing 20 μm. Thermo-optical phase shifters (PSs) are shown as thick black curves. e Optical microscopy image of the whole entangled qutrit chip. Several important on-chip elements are labelled: (1) DMZI-R photon-pair source; (2) wavelength division multiplexer (WDM); (3) crossing; (4) multi-mode interferometer (MMI); (5) common ground of the electrical signals; (6) thermo-optic PS. f Schematic of the complete experimental setup. A picosecond pump pulse is filtered, polarized and coupled into the chip via a bandpass filter, a polarization controller and a grating coupler, respectively. A photon pair is created in a superposition between three coherently pumped DMZI-R sources (S1-3). By adjusting four PSs for the pump (Py1, Py2, Pz1 and Pz2), we can generate a tunable qutrit entangled state. The signal (red) and idler (blue) photons are separated by W1-3 and routed to two 3D-MPs, which are composed of 12 MMIs and 12 PSs and enable us to implement arbitrary 3D local unitary transformation. Both signal and idler photons are then coupled out from the chip, filtered and detected by six grating couplers, filters and superconducting single-photon detectors (SSPDs). Coincidence events are recorded by an FPGA-based timetag unit. All on-chip PSs are controlled with current sources.
To obtain an efficient photon-pair source, we use a dual Mach-Zehnder interferometer micro-ring (DMZI-R) photon-pair source35,36. Such a DMZI-R photon-pair source is inspired by the design of a wavelength division multiplexer (WDM) in classical optical communication37 and could circumvent the trade-off between the utilization efficiency of the pump photon and the extraction efficiency of the signal and idler photon pairs from a ring resonator38. The DMZI-R photon-pair source was first demonstrated in ref. 35, where enhanced coincidence efficiency of a single source was shown. The working principle of the DMZI-R photon source is as follows: by wrapping two pulley waveguides around a ring resonator, one can construct a four-port device, as shown in Fig. 1b. We couple each waveguide at two points to the resonator, using four directional couplers. By adjusting the relative phases of two waveguides to the resonator, we can tune the coupling between waveguides to the resonator at the pump, signal and idler wavelengths independently. In the ideal case, we would like to have the pump circulate in the ring resonator to generate photon pairs, and therefore, the critical coupling condition for the pump is preferred. On the other hand, we want to extract the signal and idler photons from the resonator as soon as they are generated to minimize the propagation loss of photon pairs in the resonator. As a consequence, it is desirable to over-couple the waveguide to the resonator at the wavelengths of signal and idler photons. These two requirements can be fulfilled simultaneously by setting the free spectral range (FSR) of the MZIs to be twice that of the ring, such that every second resonance of the ring is effectively suppressed. By doing so, we can achieve the desired distinct coupling conditions for the pump, signal and idler photons and maximally utilize the pump to efficiently extract photon pairs. The ring has a radius of 15 μm and a coupling gap of 250 μm (200 μm) at the input (output) side. The length difference of the unbalanced MZI1 (MZI2) is 47.8 μm (48 μm). Optical microscopy images of the DMZI-R photon-pair source and the whole entangled-qutrit chip are shown in Fig. 1d, e, respectively. Note that the sizes of the gaps of critical and over-critical couplings depend on the propagating loss of the photons in the ring. One should be able to obtain a higher count rate by optimizing the gap size35 (see Supplementary Information for a theoretical analysis and a detailed characterization of the DMZI-R photon source).
Following the DMZI-R photon-pair source, we use an asymmetric MZI (AMZI) as an on-chip WDM to separate the non-degenerate signal and idler photons. As shown in Fig. 1f, we repeat this combination of DMZI-R source and WDM three times, and excite these sources coherently. When the generation rate is the same for all three sources and the relative phases of the pump are all zero, we generate a maximally entangled state of two qutrits: \(\left|\Psi \right\rangle =\frac{1}{\sqrt{3}}(\left|00\right\rangle +\left|11\right\rangle +\left|22\right\rangle )\). Note that \(\left|0\right\rangle\), \(\left|1\right\rangle\) and \(\left|2\right\rangle\) are the individual path states of single photons.
Each qutrit can be locally manipulated by a 3D-MP24, which is composed of thermo-optic phase shifters (PSs) and multi-mode interferometers (MMIs). In particular, one of the essential components, formed by a single PS and a tunable beam splitter, is realized with a MZI, consisting of two balanced MMIs and a PS.These components are used to realize Rz(φz) and Ry(θy) rotations, and thus to obtain an arbitrary SU(2) operation in the two-dimensional subspace. Note that our experimental configuration is also closely related to a recent proposal on generating OAM entanglement by path identity39. The collective paths and individual paths in our work correspond to the path and OAM in ref. 40. After manipulating and characterizing the entangled qutrits with two 3D-MPs, both the signal and idler photons are coupled out from the chip, filtered to suppress residual pumping with off-chip filters, and detected with superconducting nanowire single-photon detectors (SSPDs). The single-photon detection events are recorded by a field-programmable gate array (FPGA)-based timetag unit. Then both single counts and coincidence counts CCij between path i (i = 1, 3, 5) and path j (j = 2, 4, 6) are extracted from these timetag records (see Supplementary Information for further experimental details).
From qubit entanglement to qutrit entanglement
To generate three-dimensional (3D) path-entangled photons, it is necessary to ensure that all three coherently pumped photon-pair sources are identical. This means that the emitted photon pairs from different sources should be the same in all DOFs, including polarization, spatial mode, count rate and frequency. For our chip-based system, we use single-mode waveguides, which automatically give us the same polarization states and spatial modes of photons from different sources. However, the count rate and frequency of the photons are not necessarily identical for different sources. To eliminate the count rate distinguishability, we can tune the pump power of the individual source. The last DOF is the frequency. In non-resonant broad band (~nm to tens of nm) photon-pair sources, such as silicon nanowires, one can use off-chip narrow-band filtering to post-select identical spectra of different photons9,20, which unavoidably reduces the count rate. In the resonant sources, such as our DMZI-R source, we can actively tune the resonance wavelengths of each individual source with PSs. In doing so, we obtain identical photons without sacrificing the photon count rate, which is particularly important for multiphoton high-dimensional experiments. However, aligning the frequency of the narrow-band photons generated from resonance-enhanced sources is challenging within the sub-mm foot-print of our chip. The reasons are follows: silicon has a relatively high thermo-optic coefficient. On the one hand, this feature of silicon is desirable for realizing reconfigurable photonic circuits by using thermo-optic PSs with low power consumption. On the other hand, it presents an experimental challenge to stabilize the frequency of the single photons generated from resonance-enhanced photon-pair sources under several distinct configurations of thermal PSs, due to thermal cross-talk41.
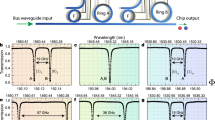
As the first step to generate 3D entanglement, we verify the identicality of two sources with time-reversed Hong-Ou-Mandel (RHOM) interference42. Highly indistinguishable photons produce the high visibility of RHOM interference. We investigate the indistinguishability between all pairs of the three sources by interfering signal-idler photon pairs generated from S1, S2 and S3 on the top 3D-MP. For instance, we set the phases Sy1 and Sy2 to be π and Sy3 to be π∕2 and scan the phase of Sz3 to obtain the RHOM interference fringe between S2 and S3. The RHOM interference fringes between S1 and S2, S1 and S3 and S2 and S3 are shown in Fig. 2a–c, respectively. The visibility of the fringe is defined as V = (CCmax − CCmin)/(CCmax + CCmin), where CCmax and CCmin are the maximum and minimum of the coincidence counts. The measured visibilities are greater than 96.49% in all cases, indicating high-quality spectral overlaps. All of our data are raw, and no background counts are subtracted. To obtain high interference visibilities, we have spent significant amount of efforts to eliminate thermal noise (see Supplementary Information for further experimental details). We believe that by using better designs of the thermal PSs such as reported in refs 43,44, the noise can be greatly mitigated. In additional to reduce cross-talks, for reaching a visibility required for the practical applications, high-fidelity quantum control is a necessity. Remarkably, previous work has shown one can achieve excellent on/off ratio (~0.5 dB), equivalent to having a Pauli-Z error rate of <10−6 45 by using cascaded MZIs. Over 100 dB pass-band to stop-band contrast filters have also been realized by cascaded microrings46 and AMZIs47, respectively. By combining these high-performance devices, we believe integrated quantum photonics is a promising route in the development of future quantum technologies and applications48.
Interference fringes of the two-photon RHOM experiments are shown in a–c for S1 and S2, S1 and S3 and S2 and S3, respectively. The measured visibilities are greater than 96.49% in all three cases, indicating high-quality indistinguishabilities between the three sources. Path-correlations of the three two-qubit subspaces for the entangled-qutrit state \(\frac{1}{\sqrt{3}}(\left|00\right\rangle +\left|11\right\rangle +\left|22\right\rangle )\) are shown in d–f for S1 and S2, S1 and S3, and S2 and S3, respectively. The signal photon is projected on to \(\frac{1}{\sqrt{2}}(\left|j\right\rangle +\left|k\right\rangle )\), and the idler photon is measured in the base \(\frac{1}{\sqrt{2}}(\left|j\right\rangle +{e}^{i\varphi }\left|k\right\rangle )\) with φ being the scanning phase and with (j,k) = (0,1), (0,2) and (1,2), respectively. The measured visibilities are greater than 94.72% in all three cases, indicating high-quality path entanglement. The points are experimental data, and the curves are fits. The uncertainties denote the standard deviations from the Poisson distribution of the raw photon counts. The real and imaginary parts of the reconstructed density matrix of the two-photon entangled-qutrit state are shown in g and h. Eighty-one measurement settings are decomposed into \(\left|{p}_{s}\right\rangle \otimes \left|{p}_{i}\right\rangle\), where \(\left|{p}_{k}\right\rangle \ =\ \left|{\psi }_{k}\right\rangle \left\langle {\psi }_{k}\right|\). \(\left|{\psi }_{k}\right\rangle\) is chosen from the following set: \(\left|0\right\rangle\), \(\left|1\right\rangle\), \(\left|2\right\rangle\), \(\frac{1}{\sqrt{2}}(\left|0\right\rangle +\left|1\right\rangle )\), \(\frac{1}{\sqrt{2}}(\left|1\right\rangle +\left|2\right\rangle )\), \(\frac{1}{\sqrt{2}}(\left|0\right\rangle +\left|2\right\rangle )\), \(\frac{1}{\sqrt{2}}(\left|0\right\rangle +i\left|1\right\rangle )\), \(\frac{1}{\sqrt{2}}(\left|1\right\rangle +i\left|2\right\rangle )\) and \(\frac{1}{\sqrt{2}}(\left|0\right\rangle +i\left|2\right\rangle )\). We obtain the quantum-state fidelity of the measured quantum states to the ideal state as 95.50% ± 0.17%. The maximum matrix element of the imaginary part is smaller than 0.015. The coloured bar graph is the experimental result and the wire grid indicates the expected values for the ideal case. The uncertainties in the fidelities extracted from these density matrices are calculated using a Monte Carlo routine, assuming Poissonian errors.
The next step is to verify the qubit entanglement of path states between three different pairs of sources. We measure the correlation of the path-entangled states in mutually unbiased bases (MUBs). We set the measurement base of the signal photon to be the coherent superpositions of the computational base, \(\frac{1}{\sqrt{2}}(\left|j\right\rangle +\left|k\right\rangle )\), where (j,k) = (0,1), (0,2), (1,2). Then, we scan the phase φ in the quantum state of the idler photon, \(\frac{1}{\sqrt{2}}(\left|j\right\rangle +{e}^{i\varphi }\left|k\right\rangle )\) and measure the coincidence counts between the signal and idler photons. The coincidence fringes are shown in Fig. 2d–f for S1 and S2, S1 and S3 and S2 and S3, respectively. The values of various visibilities range from 94.72% ± 0.50% to 97.50% ± 0.38%, indicating high-quality qubit entanglement. The phase doubling signature of RHOM fringes compared to the correlation counterparts can be seen by comparing Fig. 2a–c, and Fig. 2d–f. In the RHOM experiment, both signal and idler photons create a coherent superposition of two photons in two paths, the state that evolves under a phase shift in one of the modes then displays the phase doubling42. Note that the count rate of the path-correlation measurement is lower than that of the RHOM measurement, mainly because the design of the on-chip WDM is not optimal. Higher count rates of the correlation measurement can be achieved by optimizing the length difference between the two arms of the WDM.
Having established high-quality qubit entanglement, we proceed to characterize the qutrit entangled state with complete high-dimensional quantum-state tomography (QST). We use a set of all possible combinations of Gell-Mann matrices and apply the corresponding settings to both 3D-MPs49. The QST method takes approximately 33 mins with a typical count rate ~100 Hz per setting. Figure 2g, h displays the real and imaginary parts of the reconstructed density matrix of the state, respectively, showing good agreement between the maximally entangled and measured quantum states with a fidelity of 95.50% ± 0.17%. The maximum matrix element of the imaginary part is smaller than 0.015. From the reconstructed density matrix, we obtain an I-concurrence of 1.149 ± 0.00250. The uncertainties in the state fidelity extracted from these density matrices are calculated using a Monte Carlo routine assuming Poissonian statistics. In the context of quantum communication, a multi-dimension entanglement-based Ekert91 QKD protocol51 was initially proposed and analyzed in refs 52,53, where high-dimension mutually unbiased bases correlations between two Alice and Bob can be used to generate keys. The upper bound error rate (ER) that guarantees security against coherent attacks for device-dependent QKD in three dimensions is 15.95%. For a maximally qutrit entangled state, the fidelity (F) of the state can be used to infer the ER if Alice and Bob use the same MUB54; that is F = (3-4*ER)/3. From the fidelity we obtain, the ER is only 3.375%, which is considerably below the required bound, indicating the high quality of our qutrit state.
Tests of quantum nonlocality and contextuality with entangled qutrits
To benchmark the high-quality qutrit entanglement and high-precision quantum control, we demonstrate experimental tests of quantum nonlocality and quantum contextuality. Violations of Bell inequalities based on local realistic theories provide evidence of quantum nonlocality. It has been demonstrated that, high-dimensional correlations compatible with local realism satisfy a generalized Bell-type inequality, the Collins-Gisin-Linden-Massar-Popescu (CGLMP) inequality, with Id ≤ 2 for all d ≥ 255. Expression I3 is given by joint probabilities as
where P\(\left({A}_{{\rm{a}}}={B}_{{\rm{b}}}+k\right)\) with (a, b = 1, 2) and (k = 0, 1) represent the joint probabilities for the outcomes of Aa that differ from Bb by k. The measurement bases used to maximise the violation of Eq. (1) for the maximally entangled state \(\left|\Psi \right\rangle =\sum _{j=0}^{2}{\left|j\right\rangle }_{A}\bigotimes {\left|j\right\rangle }_{B}\) are defined as
where i = \(\sqrt{-1}\), α1 = 0, α2 = 1∕2, β1 = 1∕4 and β2 = −1∕4, K and L ∈ {0, 1, 2} denote Alice’s and Bob’s measurement outcomes respectively, and \(\left|j\right\rangle\) denotes the computational basis. These measurement bases can be implemented by configuring PSs in the 3D-MPs. For instance, we set Sz1 = 0.333π, Sy1 = 0.5π, Sz2 = 0.583π, Sy2 = 0.392π, Sz3 = 0.779π and Sy3 = 0.5π to realize setting A1. In the context of quantum computation, entanglement is the essential resource. For one-way quantum computation, ref. 23 reported the noise sensitivity of a two-photon, three-level and four-partite (two DOFs) cluster state with entanglement witness. CGLMP inequality is an entanglement criterion with higher correlation requirements comparing to entanglement witness. We witness the existence of entanglement between two qutrits in our experiment by using CGLMP inequality. The classical bound is violated by 51.46σ (I3 = 2.7307 ± 0.0142), benchmarking the resilience to errors. The experimental results for the four base settings are shown in Table 1.
Contextuality is a fundamental concept in quantum mechanics13,56,57,58 and an important resource for fault-tolerant universal quantum computation59. A single qutrit is the simplest quantum system showing the contradiction between non-contextual hidden-variable models and quantum mechanics13. However, the testability of the Kochen-Specker (KS) theorem is debated due to the finite precision in a single qutrit in practical experiments60,61. An approach based on maximally entangled-qutrit pair has been proposed62, which was recently realized with bulk optics63.
The experimental setting is as follows. A pair of maximally entangled qutrits is sent to two parties, Alice (A) and Bob (B). Alice performs projective measurements, either \({D}_{1}^{A}\) or \({T}_{0}^{A}\), \({T}_{1}^{A}\), and Bob simultaneously performs measurement \({D}_{0}^{B}\), where \({D}_{1}^{A}\) and \({D}_{0}^{B}\) are dichotomic projectors with two possible outcomes, 0 or 1, and \({T}_{0}^{A}\) and \({T}_{1}^{A}\) are trichotomic projectors with three possible outcomes, a, b or c. These four projectors are defined as \({D}_{0}^{B}=\left|i\right\rangle \left\langle i\right|,{D}_{1}^{A}=\left|f\right\rangle \left\langle f\right|,{T}_{0}^{A}=\left|{a}_{0}\right\rangle \left\langle {a}_{0}\right|\) and \({T}_{1}^{A}=\left|{a}_{1}\right\rangle \left\langle {a}_{1}\right|\), where \(\left|i\right\rangle =(\left|0\right\rangle +\left|1\right\rangle +\left|2\right\rangle )/\sqrt{3}\), \(\left|f\right\rangle =(\left|0\right\rangle -\left|1\right\rangle +\left|2\right\rangle )/\sqrt{3}\), \(\left|{a}_{0}\right\rangle =(\left|1\right\rangle -\left|2\right\rangle )/\sqrt{2}\) and \(\left|{a}_{1}\right\rangle =(\left|0\right\rangle -\left|1\right\rangle )/\sqrt{2}\). The non-compatibility loophole contextuality inequality can be expressed as62:
where \(P({D}_{1}^{A}=1| {D}_{0}^{B}=1)\) stands for the conditional probability of Alice obtaining result 1 for \({D}_{1}^{A}\) when Bob also obtains result 1 with \({D}_{0}^{B}\). \(P({T}_{0}^{A}=1| {D}_{0}^{B}=1)\) and \(P({T}_{1}^{A}=1| {D}_{0}^{B}=1)\) are defined analogously. For our experiment, we need to reconfigure two 3D-MPs according to these projectors and measure the coincidence counts to reconstruct the conditional probabilities in Eq. (4). For example, \(\left|f\right\rangle\) can be projected to port 3 by setting Sz1 = 0, Sy1 = 0.5π, Sz2 = 1.25π, Sy2 = 0.608π, Sz3 = 0 and Sy3 = π. We experimentally violate the noncontextuality inequality by 9.5 standard deviations (0.085 ± 0.009). The detailed experimental results are listed in Table 2. The no-signaling conditions, confirming the compatibility assumption between the measurements of Alice and Bob, are checked, as shown in Table 3. The results deviate slightly from 0 because of experimental imperfections.
Harnessing two-qutrit quantum correlations: quantum simulation of graphs and quantum metrology
High-order quantum correlations are unique properties of high-dimensional entangled quantum systems and are a central resource for quantum information processing. To probe the quantum correlations in the entangled-qutrit system, we measure the coincidence counts between the signal and idler photons under different MUBs by tuning both the phases of the signal/idler and pump photons. Here we use the quantum correlation between two entangled qutrits to demonstrate the quantum simulation of graphs and quantum metrology based on a quantum multi-path interferometer with third-order nonlinearity.
Quantum simulation of graphs
Graphs are mathematical structures for describing relations between objects and have been widely used in various areas, including physics, biology and information science. A graph typically consists of a set of vertices and edges connecting the vertices. A subset of the edges containing every vertex of the n-vertex graph exactly once is defined as a perfect matching of the graph. To find the number of perfect matchings of a graph is a problem that lies in the #P-complete complexity class34. To provide an algorithm to solve such a hard problem is highly desirable. Recent studies have shown that a carefully designed quantum optical experiment can be associated with an undirected graph64. In Particular, the number of coherently superimposed terms of the generated high-dimensional quantum state from a quantum optical experiment is exactly the number of perfect matchings in the corresponding graph. Each vertex stands for an optical path occupied by a single photon and every edge represents a photon-pair source. This scheme can be viewed as a quantum simulation of graphs.
As the first step towards the quantum simulation of graphs, we use entangled qutrits to experimentally demonstrate the connection between graph theory and quantum optical experiments. Figure 3a shows a conceptual scheme of our realization. Each pair of photons generated from sources propagates along their paths, denoted by black arrows, and acquires additional mode shifts due to the mode converters between the sources. As mentioned above, the path and OAM in ref. 64 are equivalent to the collective and the individual paths of our integrated quantum photonic circuit, as shown in Fig. 1a. Therefore, the mode converters can be implemented by routing the individual paths of the photon on our chip. By suitably setting up the 3D-MPs, we verify the resultant quantum state with coherent superimposed terms corresponding to the number of perfect matchings. We implement two experimental steps to realize this goal. First, we measure the coincidence counts between the signal and idler photons on the computational basis, S1I1. The experimental results are shown in Fig. 3b. It is clear that the major contributions are the 00, 11 and 22 terms. The second step is to verify the coherence between these three terms. For the entangled-qutrit pair system, each individual qutrit has four MUBs. Therefore, we have to measure the correlation coefficients in all four base combinations, i.e. S1I1, S2I2, S3I3 and S4I4, where S\({}_{k}={I}_{k}^{* }\), with (k = 1, 2, 3, 4). These MUBs, up to normalization, are defined as
where \(\omega ={e}^{i\frac{2\pi }{3}}\) and * stands for the complex conjugation.
a The optical setup corresponding to the experimental implementation on the chip and the corresponding graph. A two-fold coincidence in the experiment can be seen as a subset of edges containing each of the vertices only once, which is called a perfect matching in the graph. A coherent superposition of three perfect matchings leads therefore to the quantum state \(\left|\Psi \right\rangle =\frac{1}{\sqrt{3}}\left(\left|00\right\rangle +\left|11\right\rangle +\left|22\right\rangle \right.\). b The measured coincidence counts between the signal and idler photons on the computational basis, S1I1. Dashed empty bars are deduced results by balancing the loss for every port. c–e The balanced normalized coincidence results for S2I2, S3I3 and S4I4. f The experimental correlation coefficients are measured in all four MUBs (S1I1, S2I2, S3I3 and S4I4) for the entangled qutrits. Ideal results are shown with dashed empty bars. The uncertainties denote the standard deviations from the Poisson distribution for raw photon counts.
The normalized coincidence counts of S2I2, S3I3 and S4I4 are shown in Fig. 3c–e, respectively, by balancing the loss for every port. The experimental correlation coefficients derived from the coincidence counts in the four MUB combinations are shown in Fig. 3f. For an ideal maximally entangled-qutrit pair, the correlation coefficients should be unity. Due to the experimental imperfections, we obtain the correlation coefficients with the values of 98.17% ± 0.11%, 87.61% ± 0.27%, 91.32% ± 0.24% and 89.01 ± 0.27%, which shows correlations in all MUBs.
Quantum metrology with entangled qutrits
Accurate phase measurements are at the heart of metrological science. One figure-of-merit for evaluating the accuracy of phase measurement is sensitivity, S, which is defined as the derivative of the output photon number with respect to a phase change S ∝ 1∕N. In the experimental setting of classical interferometers, it is well known that increasing the number of paths of the interferometer can enhance the sensitivity65. On the other hand, in the field of quantum metrology, one can further enhance the sensitivity by using entanglement3. Here, we combine both traits from classical and quantum systems and employ a three-dimension-entanglement third-order-nonlinearity interferometer to demonstrate the enhanced phase sensitivity compared to the classical three-path66 and quantum second-order-nonlinearity interferometers19. We send the entangled-qutrit state \(\left|\Psi \right\rangle =\frac{1}{\sqrt{3}}\left({e}^{i2Pz1}\left|00\right\rangle +{e}^{i2Pz2}\left|11\right\rangle +\left|22\right\rangle \right.\) into two separate 3D-MPs. We then scan the relative pump phases Pz1 and Pz2 and measure the coincidence between two qutrits (outputs 1,3,5 and 2,4,6). In total, there are nine different coincidence combinations. We quantify the qutrit-qutrit correlations as functions of phase settings of Pz1, Pz2. The normalized coincidences along with the theoretical results are shown in Fig. 4a–c. It is easily understood that the phase dependence is different between the second and third-order nonlinear interactions67. In the generation of entangled photon pairs, two pump photons are involved in the third-order processes providing a double phase compared to the second-order processes with the participation of only one pump photon. The measurements confirm this difference. Specifically, if the phases are chosen such that Pz1 = −Pz2, the intensity varies from maximum to minimum as the pump phase is changed. This phase setting also gives the maximal sensitivity S. The raw data are extracted from the measured results and fitted with theoretical curves as shown in Fig. 4d. The averaged phase sensitivity \(S=\frac{1}{C{C}_{ab\,max}}| \frac{dC{C}_{ab}}{d\varphi }|\) is 1.476 ± 0.048 rad−1, more than the theoretical ideal value of 0.5 rad−1 for the two-path interferometer and 0.78 rad−1 for the ideal three-path interferometer. The reason for the increased sensitivity is that the doubled phase sensitivity of the SFWM process and the side lobes appears between the two main peaks in three-path interference patterns, which enhance the steepness of the peaks of the correlations.
a–c correspond to coincidence detection combinations of detectors (1,2) (1,4) and (1,6), respectively, with two relative pump phases Pz1 and Pz2 scanned. The normalized measured coincidences (Norm. C. C) (red dots) and simulated results without any free parameters (lines and surfaces) are shown. The data display excellent agreement with the theoretical predictions. d Diagonal cuts through the three-dimensional plots by setting Pz1 = −Pz2 in a–c reveal the typical structure of the three-path interferometer with a sensitivity of 1.476 ± 0.048, exceeding both classical three-path linear interferometer and quantum second-order nonlinear limits. The red, pink and blue points represent the experimental data extracted from a–c and are identified as white lines respectively. The curves show the theoretical results. The error bars are calculated by a Poissonian distribution.
Discussion
We have integrated three resonance-enhanced photon-pair sources embedded in interferometers, three WDMs and two 3D-MPs on a single monolithic silicon chip. We made all three sources identical without using frequency post-selection and observe high-visibility quantum interference, which allowed us to prepare, manipulate and analyse the high-quality path-entangled-qutrit state. We violated the CGLMP inequality to confirm quantum nonlocality and the KS inequality to confirm contextuality with the entangled qutrits, verifying fundamental properties of quantum theory. Furthermore, we used two-qutrit quantum correlations to simulate graphs and identify the number of perfect matchings for a small-scale graph. Finally, by using our chip for 3D entanglement, a third-order nonlinearity interferometer, we improved the phase sensitivity by a factor of 2 compared to a classical three-path interferometer.
Our demonstration of finding the number of the perfect matchings of the graph could be further extended to the multiphoton and higher-dimension experiments, which might be suitable to demonstrate the quantum advantage in the near or mid term. To reach this regime, one needs to develop high-brightness multiphoton sources. The source presented in this work is a promising candidate for such a source. Although there exist a few technical challenges towards full integrated silicon quantum chips, such as cryogenic-compatible photon manipulation and high-efficiency photon detection, heterogeneous integrated chips are a promising approach for achieving this goal68,69,70. Combined with an efficient on-chip SSPD69 and recently demonstrated cryogenic operation of Si-barium titanate70, our work could be viewed as a solid basis of future photonic quantum devices and systems for quantum information processing.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
Code availability
The codes that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Ladd, T. D. et al. Quantum computers. Nature 464, 45–53 (2010).
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145 (2002).
Giovannetti, V., Lloyd, S. & Maccone, L. Advances in quantum metrology. Nat. Photon. 5, 222–229 (2011).
D’Ambrosio, V. et al. Complete experimental toolbox for alignment-free quantum communication. Nat. Commun. 3, 961 (2012).
Graham, T. M., Bernstein, H. J., Wei, T.-C., Junge, M. & Kwiat, P. G. Superdense teleportation using hyperentangled photons. Nat. Commun. 6, 7185 (2015).
Luo, Y.-H. et al. Quantum teleportation in high dimensions. Phys. Rev. Lett. 123, 070505 (2019).
Hu, X.-M. et al. Experimental multi-level quantum teleportation. Preprint at https://arxiv.org/abs/1904.12249 (2019).
Lanyon, B. P. et al. Simplifying quantum logic using higher-dimensional Hilbert spaces. Nat. Phys. 5, 134–140 (2008).
Qiang, X. et al. Large-scale silicon quantum photonics implementing arbitrary two-qubit processing. Nat. Photon. 12, 534–539 (2018).
Neeley, M. et al. Emulation of a quantum spin with a superconducting phase qudit. Science 325, 722–725 (2009).
Dada, A. C., Leach, J., Buller, G. S., Padgett, M. J. & Andersson, E. Experimental high-dimensional two-photon entanglement and violations of generalized Bell inequalities. Nat. Phys. 7, 677–680 (2011).
Vértesi, T., Pironio, S. & Brunner, N. Closing the detection loophole in bell experiments using qudits. Phys. Rev. Lett. 104, 060401 (2010).
Lapkiewicz, R. et al. Experimental non-classicality of an indivisible quantum system. Nature 474, 490–493 (2011).
Erhard, M., Krenn, M. & Zeilinger, A. Advances in high dimensional quantum entanglement. Preprint at https://arxiv.org/abs/1911.10006 (2019).
Wang, J., Sciarrino, F., Laing, A. & Thompson, M. G. Integrated photonic quantum technologies. Nat. Photon. 1–12 (2019).
Wang, X.-L. et al. Quantum teleportation of multiple degrees of freedom of a single photon. Nature 518, 516–519 (2015).
Kues, M. et al. On-chip generation of high-dimensional entangled quantum states and their coherent control. Nature 546, 622–626 (2017).
Imany, P. et al. 50-GHz-spaced comb of high-dimensional frequency-bin entangled photons from an on-chip silicon nitride microresonator. Opt. Express 26, 1825–1840 (2018).
Schaeff, C., Polster, R., Huber, M., Ramelow, S. & Zeilinger, A. Experimental access to higher-dimensional entangled quantum systems using integrated optics. Optica 2, 523–529 (2015).
Wang, J. et al. Multidimensional quantum entanglement with large-scale integrated optics. Science 360, 285–291 (2018).
Thew, R., Acín, A., Zbinden, H. & Gisin, N. Experimental realization of entangled qutrits for quantum communication. Quantum Info. Comput. 4, 93–101 (2004).
Richart, D., Fischer, Y. & Weinfurter, H. Experimental implementation of higher dimensional time-energy entanglement. Appl. Phys. B 106, 543–550 (2012).
Reimer, C. et al. High-dimensional one-way quantum processing implemented on d-level cluster states. Nat. Phys. 15, 148–153 (2019).
Reck, M., Zeilinger, A., Bernstein, H. J. & Bertani, P. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 73, 58–61 (1994).
Schaeff, C. et al. Scalable fiber integrated source for higher-dimensional path-entangled photonic quNits. Opt. Express 20, 16145–16153 (2012).
Mower, J. & Englund, D. Efficient generation of single and entangled photons on a silicon photonic integrated chip. Phys. Rev. A 84, 052326 (2011).
Collins, M. J. et al. Integrated spatial multiplexing of heralded single-photon sources. Nat. Commun. 4, 2582 (2013).
Silverstone, J. W. et al. On-chip quantum interference between silicon photon-pair sources. Nat. Photon. 8, 104–108 (2014).
Harris, N. C. et al. Integrated source of spectrally filtered correlated photons for large-scale quantum photonic systems. Phys. Rev. X 4, 041047 (2014).
Silverstone, J. W. et al. Qubit entanglement between ring-resonator photon-pair sources on a silicon chip. Nat. Commun. 6, 7948 (2015).
Feng, L.-T. et al. On-chip coherent conversion of photonic quantum entanglement between different degrees of freedom. Nat. Commun. 7, 11985 (2016).
Silverstone, J. W., Bonneau, D., O’Brien, J. L. & Thompson, M. G. Silicon quantum photonics. IEEE J. Sel. Top. Quantum Electron. 22, 390–402 (2016).
Saglamyurek, E. et al. Quantum storage of entangled telecom-wavelength photons in an erbium-doped optical fibre. Nat. Photon. 9, 83 (2015).
Valiant, L. G. The complexity of computing the permanent. Theoret. Comput. Sci. 8, 189–201 (1979).
Tison, C. C. et al. Path to increasing the coincidence efficiency of integrated resonant photon sources. Opt. Express 25, 33088–33096 (2017).
Vernon, Z. et al. Truly unentangled photon pairs without spectral filtering. Opt. Lett. 42, 3638–3641 (2017).
Barbarossa, G., Matteo, A. M. & Armenise, M. N. Theoretical analysis of triple-coupler ring-based optical guided-wave resonator. IEEE J. Lightwave Technol. 13, 148–157 (1995).
Vernon, Z., Liscidini, M. & Sipe, J. E. No free lunch: the trade-off between heralding rate and efficiency in microresonator-based heralded single photon sources. Opt. Lett. 41, 788–791 (2016).
Krenn, M., Hochrainer, A., Lahiri, M. & Zeilinger, A. Entanglement by path identity. Phys. Rev. Lett. 118, 080401 (2017).
Kysela, J., Erhard, M., Hochrainer, A., Krenn, M. & Zeilinger, A. Experimental high-dimensional entanglement by path identity. Preprint at https://arxiv.org/abs/1904.07851 (2019).
Carolan, J. et al. Scalable feedback control of single photon sources for photonic quantum technologies. Optica 6, 335–340 (2019).
Chen, J., Lee, K. F. & Kumar, P. Deterministic quantum splitter based on time-reversed Hong-Ou-Mandel interference. Phys. Rev. A 76, 031804 (2007).
Harris, N. C. et al. Efficient, compact and low loss thermo-optic phase shifter in silicon. Opt. Express 22, 10487–10493 (2014).
Gao, S. et al. Power-efficient thermal optical tunable grating coupler based on silicon photonic platform. IEEE Photon. Technol. Lett. 31, 537–540 (2019).
Wilkes, C. M. et al. 60 db high-extinction auto-configured mach-zehnder interferometer. Opt. Lett. 41, 5318–5321 (2016).
Ong, J. R., Kumar, R. & Mookherjea, S. Ultra-high-contrast and tunable-bandwidth filter using cascaded high-order silicon microring filters. IEEE Photon. Technol. Lett. 25, 1543–1546 (2013).
Piekarek, M. et al. High-extinction ratio integrated photonic filters for silicon quantum photonics. Opt. Lett. 42, 815–818 (2017).
Rudolph, T. Why i am optimistic about the silicon-photonic route to quantum computing. APL Photonics 2, 030901 (2017).
Thew, R. T., Nemoto, K., White, A. G. & Munro, W. J. Qudit quantum-state tomography. Phys. Rev. A 66, 012303 (2002).
Fedorov, M., Volkov, P., Mikhailova, J. M., Straupe, S. & Kulik, S. Entanglement of biphoton states: qutrits and ququarts. New J. Phys. 13, 083004 (2011).
Ekert, A. K. Quantum cryptography based on bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).
Cerf, N. J., Bourennane, M., Karlsson, A. & Gisin, N. Security of quantum key distribution using d-level systems. Phys. Rev. Lett. 88, 127902 (2002).
Bruß, D. & Macchiavello, C. Optimal eavesdropping in cryptography with three-dimensional quantum states. Phys. Rev. Lett. 88, 127901 (2002).
Zhu, H. & Hayashi, M. Optimal verification and fidelity estimation of maximally entangled states. Phys. Rev. A 99, 052346 (2019).
Collins, D., Gisin, N., Linden, N., Massar, S. & Popescu, S. Bell inequalities for arbitrarily high-dimensional systems. Phys. Rev. Lett. 88, 040404 (2002).
Kochen, S. & Specker, E. P. The problem of hidden variables in quantum mechanics. J. Math. Mech. 17, 59–87 (1967).
Klyachko, A. A., Can, M. A., Binicioğlu, S. & Shumovsky, A. S. Simple test for hidden variables in spin-1 systems. Phys. Rev. A 101, 020403 (2008).
Kirchmair, G. et al. State-independent experimental test of quantum contextuality. Nature 460, 494–497 (2009).
Howard, M., Wallman, J., Veitch, V. & Emerson, J. Contextuality supplies the ‘magic’ for quantum computation. Nature 510, 351–355 (2014).
Meyer, D. A. Finite precision measurement nullifies the Kochen-Specker theorem. Phys. Rev. Lett. 83, 3751 (1999).
Kent, A. Noncontextual hidden variables and physical measurements. Phys. Rev. Lett. 83, 3755 (1999).
Cabello, A. & Cunha, M. T. Proposal of a two-qutrit contextuality test free of the finite precision and compatibility loopholes. Phys. Rev. Lett. 106, 190401 (2011).
Hu, X.-M. et al. Experimental test of compatibility-loophole-free contextuality with spatially separated entangled qutrits. Phys. Rev. Lett. 117, 170403 (2016).
Krenn, M., Gu, X. & Zeilinger, A. Quantum experiments and graphs: multiparty states as coherent superpositions of perfect matchings. Phys. Rev. Lett. 119, 240403 (2017).
Sheem, S. K. Optical fiber interferometers with [3 × 3] directional couplers: analysis. J. Appl. Phys. 52, 3865–3872 (1981).
Weihs, G., Reck, M., Weinfurter, H. & Zeilinger, A. All-fiber three-path Mach-Zehnder interferometer. Opt. Lett. 21, 302–304 (1996).
Reimer, C. et al. Generation of multiphoton entangled quantum states by means of integrated frequency combs. Science 351, 1176–1180 (2016).
He, M. et al. High-performance hybrid silicon and lithium niobate mach-zehnder modulators for 100 gbit s−1 and beyond. Nat. Photon. 13, 359 (2019).
Ferrari, S., Schuck, C. & Pernice, W. Waveguide-integrated superconducting nanowire single-photon detectors. Nanophotonics 7, 1725–1758 (2018).
Eltes, F. et al. An integrated cryogenic optical modulator. Preprint at https://arxiv.org/abs/1904.10902 (2019).
Acknowledgements
We thank M. Erhard, X. Gu, M. Krenn, A. Zeilinger and J. Wang for fruitful discussions. This research is supported by the National Key Research and Development Program of China (2017YFA0303704, 2019YFA0308704), National Natural Science Foundation of China (Grant Nos. 11674170, 11690032, 11321063, 11804153), NSFC-BRICS (No. 61961146001), NSF Jiangsu Province (No. BK20170010), the program for Innovative Talents and Entrepreneur in Jiangsu, and the Fundamental Research Funds for the Central Universities.
Author information
Authors and Affiliations
Contributions
L.L., L.X., Z.C. and X.M. designed and performed the experiment. L.C., T.Y., T.T., Y.P. and X.C. provided experimental assistance and suggestions. W.M. provided theoretical assistance. L.L., L.X. and X.M. analysed the data. L.L. and X.M. wrote the manuscript with input from all authors. Y.L., S.Z. and X.M. supervised the project. L.L, L.X. and Z.C. contributed equally to this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lu, L., Xia, L., Chen, Z. et al. Three-dimensional entanglement on a silicon chip. npj Quantum Inf 6, 30 (2020). https://doi.org/10.1038/s41534-020-0260-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-020-0260-x
This article is cited by
-
Quantum storage of entangled photons at telecom wavelengths in a crystal
Nature Communications (2023)
-
Multiphoton non-local quantum interference controlled by an undetected photon
Nature Communications (2023)
-
Integrated photonic platforms for quantum technology: a review
ISSS Journal of Micro and Smart Systems (2023)
-
Boosting the dimensionality of frequency entanglement using a reconfigurable microring resonator
Science China Physics, Mechanics & Astronomy (2023)
-
Computer-inspired quantum experiments
Nature Reviews Physics (2020)