Abstract
Quantum computing leverages the quantum resources of superposition and entanglement to efficiently solve computational problems considered intractable for classical computers. Examples include calculating molecular and nuclear structure, simulating strongly interacting electron systems, and modeling aspects of material function. While substantial theoretical advances have been made in mapping these problems to quantum algorithms, there remains a large gap between the resource requirements for solving such problems and the capabilities of currently available quantum hardware. Bridging this gap will require a co-design approach, where the expression of algorithms is developed in conjunction with the hardware itself to optimize execution. Here we describe an extensible co-design framework for solving chemistry problems on a trapped-ion quantum computer and apply it to estimating the ground-state energy of the water molecule using the variational quantum eigensolver (VQE) method. The controllability of the trapped-ion quantum computer enables robust energy estimates using the prepared VQE ansatz states. The systematic and statistical errors are comparable to the chemical accuracy, which is the target threshold necessary for predicting the rates of chemical reaction dynamics, without resorting to any error mitigation techniques based on Richardson extrapolation.
Similar content being viewed by others
Introduction
Quantum computation has attracted much attention for its potential to solve certain computational problems that are difficult to tackle with classical computers. For example, integer factorization1, unsorted database search2, and the simulation of quantum systems3 admit quantum algorithms that outperform the best-known classical algorithms given a sufficiently large problem size. However, these algorithms require substantial quantum resources to achieve a practical advantage over classical techniques, limiting their near-term utility on noisy intermediate-scale quantum (NISQ) devices4 that are severely limited in the number of gates they can perform before errors dominate the output. Any useful quantum computation on a NISQ device will require further advances in hardware performance, as well as advances in algorithmic design.
Quantum chemistry is a promising application where quantum computing might overcome the limitations of known classical algorithms, hampered by an exponential scaling of computational resource requirements. One of the most challenging tasks in quantum chemistry is to determine molecular energies to within chemical accuracy, defined to be the target accuracy necessary to estimate chemical reaction rates at room temperature and generally taken to be \(\approx\)4 kJ/mol = \(1.6\ \times 1{0}^{-3}\) Hartree (Ha)5. Achieving chemical accuracy would allow computational methods to replace costly experimental procedures in chemical and materials engineering, augmenting these fields to accelerate the pace of discovery.
Early quantum computational techniques to simulate many-body Fermi systems6 or calculate molecular energies7 have dramatically improved over the past decade8,9,10, but the resource requirements for useful chemical simulations still remain out of reach11. Hybrid approaches might relax these requirements, where a short quantum computation serves as a subroutine to calculate classically difficult quantities. The variational quantum eigensolver (VQE) method is one example, which estimates the ground state of a system by positing an ansatz state defined by a set of variational parameters and minimizing its energy. The quantum subroutine determines the energy for a particular set of ansatz parameters, and a classical optimization algorithm iteratively updates the ansatz to reduce the energy until it converges. Early demonstrations of the VQE method have been performed on different quantum architectures12,13,14,15, some of which relied on native interactions to create an ansatz state. Generalizing the hardware-efficient method into a systematic framework applicable to large systems may prove problematic. Furthermore, systematic errors in the experimental results compared to the exact, ideal circuit execution have at times far exceeded the order magnitude of chemical accuracy.
Here we provide a highly optimized, systematic VQE approach that has a potential to scale to much larger molecular systems and use it to minimize the quantum resources required to estimate the ground-state energy of the water molecule (\({{\rm{H}}}_{2}{\rm{O}}\)). We embrace co-design principles to fully optimize the quantum circuits for a trapped-ion quantum computer (QC) and experimentally compute the first three correction terms beyond the mean-field (Hartree–Fock (HF)) approximation. We achieve computational errors approaching \(1.6\) mHa (equivalent to the bound of chemical accuracy), without using any error mitigation techniques. These results establish a path for future computations on more complex systems as trapped-ion QCs continue to improve, eventually reaching beyond the capability of classical methods.
Readers are strongly encouraged to read “Methods” section before “Results” section. In “Methods” section, we describe the details of the QC hardware used to simulate the water molecule and the specifics of the molecular models used to generate the quantum simulation circuits. We heavily use the notations defined in “Methods” section throughout “Results” section.
Results
Circuit optimization and co-design
We have implemented a number of circuit optimization techniques that take advantage of the unique features available in the IonQ trapped-ion QC but are generic in the sense that they are applicable to any target molecule to be simulated. The strategies described here are executed by a full-stack, modularized software toolchain, which automatically produces optimized circuits16 for generating the ansatz state of a molecular system.
Given a general unitary coupled-cluster (UCC) ansatz state, interaction terms take the form of a two-electron interaction \({\theta }_{pqrs}{c}_{p}^{\dagger }{c}_{q}^{\dagger }{c}_{r}{c}_{s}\). Since the indices \(p,q,r,s\) vary over the complete set of molecular states (which are represented by different qubits), implementing this interaction requires entangling gates between arbitrary pairs of qubits in the system. The all-to-all connectivity of trapped-ion QCs makes this a native operation, eliminating the overhead incurred by repeated SWAP gates to reorder qubits before an entangling operation can be applied between nearest-neighbor qubits. Given that the infidelity of these SWAP operations can dominate the quality of complicated computations, eliminating them from the optimized circuit dramatically increases the accuracy of the VQE result. This circuit optimization is a direct result of co-design for a particular hardware advantage.
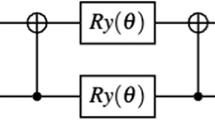
Another general optimization strategy is to represent the bosonic excitations, where two electrons remain paired, as a creation or annihilation operator on a single qubit. It is convenient to expand the spin orbital (SO) label for the operator \({c}_{p}\) to \({c}_{k\alpha }\), where \(k\) and \(\alpha\) denote the molecular orbital (MO) and spin label, respectively. Then the bosonic operators are \({d}_{k}^{\dagger }={c}_{k\alpha }^{\dagger }{c}_{k\beta }^{\dagger }\) and \({d}_{j}={c}_{j\alpha }{c}_{j\beta }\) (\(\alpha\; \ne \;\beta\)), which can be directly translated to the Pauli raising/lowering operators \({\sigma }_{\pm }^{j}\) on qubit \(j\). The UCC operator corresponding to the bosonic excitation simplifies to \(\exp [{\theta }_{jk}{\sigma }_{+}^{j}{\sigma }_{-}^{k}-h.c.]\), and a pair of arbitrary-angle XX(\(\theta\)) gates is sufficient to implement this interaction (see Fig. 1c). Thus ansatz states containing only bosonic excitations can be implemented very efficiently on our QC.
a Molecular and spin orbital diagram and an example of bosonic and non-bosonic excitations from the Hartree–Fock (HF) ground state. Energies for each orbital of the water molecule we simulate are shown for completeness. b Metrics for each circuit, labeled HF+\(N\), as up to \(N\) of the most significant interaction terms are added to the ansatz state. The bosonic terms through HF+5 can be represented as pair excitations to reduce the qubit resource requirements, while the MO selection strategy prunes the two least significant molecular states (\(1{a}_{1}\) and \(1{b}_{2}\)) to reduce the qubit count slightly at the expense of approximately mHa accuracy. Energies should be compared to the (FCI) ground-state energy, which is the exact result from diagonalizing the complete Hamiltonian in the minimal STO-3G chemical basis. c Bosonic excitation template circuit. d Non-bosonic excitation template circuit.
For all remaining terms, we must implement the two-electron interaction via the Jordan–Wigner (JW) transformation. Each of these terms looks like \(\hat{V}=\exp [{\theta }_{pqrs}{\sigma }_{+}^{p}{\sigma }_{+}^{q}{\sigma }_{-}^{r}{\sigma }_{-}^{s}\;{\otimes }\;_{k}{\sigma }_{z}^{k}-{\rm{h.c.}}]\), where the product \({\otimes }_{k}{\sigma }_{z}^{k}\) denotes the adequate JW string to reflect fermionic symmetries. A JW string with \(m\)\({\sigma }_{z}\) gates converts to \(m\) controlled NOT (CNOT) gates on either side of the subcircuit that would otherwise implement \(\hat{V}\). Properly ordering these terms in the entire circuit can eliminate most of the CNOT gates, so they represent a relatively low overhead as a function of terms in the UCC ansatz8. The main portion of the quantum circuit is an implementation of a linear combination of eight terms, each containing a product of four \({\sigma }_{x}\) and \({\sigma }_{y}\) operators (with odd number of \({\sigma }_{x}\) in each term). By optimizing the order of these eight operators and taking advantage of the all-to-all connectivity, we can implement this circuit with 13 CNOT gates (see Fig. 1d). When we concatenate several of these terms, some CNOT gates at the ends, including those that arise from a JW string, may cancel out.
Most ansatz states have both bosonic and non-bosonic excitation terms. For these situations, we start with the reduced representation where each qubit describes one MO and run the quantum circuit that corresponds to all bosonic excitation terms first. Then additional qubits (all prepared in the \(\left|0\right\rangle\) state) are introduced, and each is entangled with a qubit representing an MO using a CNOT gate. Each entangled pair can now represent the two SOs corresponding to the MO (Supplementary Information (SI) Fig. S2e).
One last optimization takes advantage of the asymmetric state preparation and measurement (SPAM) error observed in our system. Normally, we encode a filled orbital (MO or SO) with \(\left|1\right\rangle\) and an empty orbital with \(\left|0\right\rangle\), but in a molecule with mostly closed molecular shells like \({{\rm{H}}}_{2}{\rm{O}}\), the filled orbitals in the HF ground state remain mostly filled in the full configuration-interaction (FCI) ground state as well. Since our SPAM error is more than a factor of two smaller for \(\left|0\right\rangle\) compared to \(\left|1\right\rangle\), we encode the filled orbitals as \(\left|0\right\rangle\) to reduce the systematic shift associated with readout from the \(\left|1\right\rangle\) state. This encoding has the ancillary benefit of requiring fewer single-qubit gates to initialize the circuit, but the advantage diminishes as measurement errors are suppressed or become more symmetric.
Combining these strategies, we achieve the quantum circuits for preparing the ansatz state with total entangling gate counts shown in Fig. 1b. The methodology reported in this section and the resulting circuit efficiency is due to the culmination of different circuit optimization strategies applied in a carefully chosen sequence to maximize the opportunities to reduce a large number of quantum gates in an automated fashion. These methods represent a fully general, near-optimal framework that can be extended to generate UCC ansatz states for any physical system.
Experimental example
Using our trapped-ion QC, we compute the first three bosonic excitation terms of the VQE ansatz for the \({{\rm{H}}}_{2}{\rm{O}}\) molecule (see SI Fig. S2). In order to ultimately estimate the minimum energy for each circuit within chemical accuracy (fractional uncertainty of ~10−5), all systematic errors in our QC must be carefully characterized and controlled. The intrinsic decoherence of a \(^{171}\)Yb\(^{+}\) trapped-ion qubit is negligible over the timescale of our computation17, so the dominant errors arise in calibrating the angle of the XX(\(\theta\)) gate and correcting for the systematic SPAM error of our ion chain. We accurately calibrate the angle \(\theta\) using a circuit similar to that shown in Fig. 1c, where the parity varies as \(\sin\)(\(2\theta\)). Fitting the parity to this functional form (Fig. 2a) compensates for non-linearities in the acousto-optic modulator (AOM) and enables easy interpolation for arbitrary gate angles. Uncertainty in the SPAM correction can be made arbitrarily small given sufficient measurement statistics. Gate fidelity will begin to dominate as the computation length increases, but for the circuits experimentally demonstrated here we are not limited by this error and found no benefit to error mitigation techniques like Richardson extrapolation18.
a Calibration curve for the small-angle XX(\(\theta\)) gate. b Bootstrap distribution of the HF+2 energy with mean and \(1\sigma\) uncertainty indicated by the orange diamond and experimentally determined energy surfaces for HF+1 (c) and HF+2 (d). Each data point (orange diamond) represents an average of \(\gtrsim\!\!1000\) experimental runs, with the blue dash-dotted lines indicating in silico results. e Comparison of ground-state energy estimates as additional interactions are included in the UCC ansatz state (labeled HF+\(N\), for \(N\) significant determinants). The orange diamonds indicate experimental results, with error bars indicating \(1\sigma\) uncertainty from the bootstrap distribution. The remaining points are from the in silico VQE simulation as detailed in Fig. 1 and show how the ansatz states converge to the full configuration-interaction ground state, indicated by the dot-dashed blue line. Computational error equivalent to the bound for chemical accuracy (\(1.6\) mHa) is indicated by the shaded green region in all figures.
To compute the energy corresponding to a prepared ansatz state, we make a set of projective measurements in bases corresponding to the terms in the Hamiltonian, as previously described. We use a statistical bootstrapping technique19 that accounts for SPAM error to estimate uncertainties from the resulting histograms (Fig. 2b). Figures 2c, d show the experimentally determined energy surface for HF+1 and HF+2 as the ansatz parameters \(\{{\theta }_{i}\}\) are scanned about their optimum values, and the data for HF+3 (evaluated at a single point) is shown in SI Fig. S3. The optimum values of the ansatz parameters were obtained from the in silico simulations of the VQE, detailed in "Methods" section and references to appropriate SI sections therein. The experimentally determined ground-state energies for each of these three ansatz states is \(-74.977(1)\), \(-74.979(2)\), and \(-74.985(5)\) Ha, respectively, with parenthetical errors indicating \(1\sigma\) uncertainty derived from the bootstrapped distribution. The dominant experimental uncertainty arises in the SPAM correction, which can be improved with upgrades to the hardware and new tomographic methods20,21. A direct comparison to the in silico VQE simulation can be found in Fig. 2e. The match to theory is very good—both the precision and absolute accuracy (relative to the ansatz circuit) are comparable to the chemical accuracy. Achieving low computational error in experimental implementations of quantum chemistry circuits is necessary for VQE-type optimization algorithms to provide useful results.
Discussion
Dramatic improvements must be made to both QC hardware and techniques to efficiently use the available quantum resources in order to perform meaningful quantum computations on a NISQ device. The work presented here is a framework for end-to-end optimization that maps useful problems in quantum chemistry to a trapped-ion QC, fully leveraging the hardware-specific advantages. This framework yields near-optimal quantum circuits for a UCC-based approach, and we compute the post-HF ground-state energy of \({{\rm{H}}}_{2}{\rm{O}}\) on a trapped-ion QC to verify the performance of both the hardware and the optimization procedure. Without any error mitigation, the experimental results for the first three correction terms are in excellent agreement with the theoretical predictions. This demonstrates the degree of controllability offered by trapped-ion QCs, which we expect to improve with additional engineering efforts. Our UCC-based, systematic framework can thus serve as a litmus test for the quantum simulation capabilities and limitations of existing and future NISQ hardware.
While these results are specific to a particular quantum chemistry problem and the trapped-ion QC hardware, the computational methodology we develop is completely general to simulating quantum systems. We anticipate that similar advances can be applied to other optimization problems that work on variational methods, such as the quantum approximate optimization algorithm22 and various quantum machine learning applications23,24. Increased attention to co-design principles like those demonstrated here will be necessary to push the boundary of possibility in near-term quantum computation.
Methods
Trapped-ion QC
The trapped-ion system used in this study is a scalable, general-purpose programmable QC constructed at IonQ, Inc. (https://ionq.com (accessed 29 Oct 2018)) and illustrated schematically in Fig. 3a; see Supplementary Information for additional experimental details. The computer consists of a linear chain of \(^{171}\)Yb\(^{+}\) ions on a surface trap operating at room temperature, where the qubit is implemented between the \(\left|0\right\rangle \equiv \left|F=0,\ {m}_{F}=0\right\rangle\) and the \(\left|1\right\rangle \equiv \left|F=1,\ {m}_{F}=0\right\rangle\) hyperfine levels of the \(^{2}{S}_{1/2}\) ground state of each ion, split by 12.6 GHz17.
a Schematic representation of the trapped-ion QC. The qubit register is implemented in a linear chain of \(^{171}\)Yb\(^{+}\) ions residing inside an ultra-high vacuum chamber (not shown), and high-NA imaging optics enable individual addressing and readout of the ion qubits. The Raman beams (shown in red and purple) are generated from a pulsed laser at 355 nm and drive a two-photon transition between \(\left|0\right\rangle\) and \(\left|1\right\rangle\). Full control of the amplitude, frequency, and phase of the individual addressing beams enables implementations of arbitrary single- and two-qubit operators. b SPAM characterization on a three-ion chain. From top to bottom, we show the SPAM error of each three-qubit state, the per-qubit SPAM error for \(\left|0\right\rangle\) and \(\left|1\right\rangle\), and a bar plot of the full SPAM matrix where the color is log-scaled for visibility. We see no indication of measurement crosstalk between qubits. c Characterization of the small-angle XX(\(\theta\)) gate performance. The state fidelity after 50 consecutive small-angle XX gates is \(\approx 78 \%\), and we estimate the per-gate error to be \(\epsilon \lesssim \ 4\times 10^{-3}\).
The qubit register is initialized to the \(\left|0\right\rangle\) state using optical pumping and measured at the end of the computation by state-dependent fluorescence on the dipole-allowed cycling transition between \(\left|1\right\rangle\) and the \(^{2}{P}_{1/2}\) excited state20. Scattered photons from the ions during detection are collected through a high numerical aperture lens (\({\rm{NA}}\approx 0.6\)) and passed through a dichroic mirror to an array of photon detectors for simultaneous readout of the entire qubit register. SPAM errors are routinely characterized during computation, with typical data for a three-ion chain shown in Fig. 3b. Our system exhibits a small asymmetry in the SPAM error for \(\left|0\right\rangle\) versus \(\left|1\right\rangle\) (0.6% and 1.3%, respectively), which is well understood from an atomic model of the detection process25. We observe no evidence of measurement crosstalk where the state of one qubit affects the readout of neighboring qubits, which allows SPAM correction to be performed with low overhead. SPAM errors can be readily improved by increasing the collection efficiency of the detection optics20,25,26.
Quantum gates are implemented via two-photon Raman transitions driven by two laser beams from a mode-locked pulsed laser at 355 nm, where the two laser beams generate a beat note close to the qubit frequency27. One of the beams is a “global” beam, with a wide profile that uniformly illuminates all qubits in the chain. The other is an array of tightly focused beams, generated from a diffractive optical element and a multi-channel AOM, that address the ions individually. By controlling the phase, frequency, and amplitude of these beams, we can manipulate individual qubits to implement arbitrary quantum logic gates28. The AOM in our system has 32 independent channels, allowing us to scale the number of individually addressable and fully connected qubits to this number. Further scaling is possible with alternative optical set-ups or by sacrificing full connectivity and using ion-shuttling protocols29.
We drive high-fidelity single-qubit operations with a resonant Raman transition between \(\left|0\right\rangle\) and \(\left|1\right\rangle\) using a composite pulse sequence30,31. Two-qubit operations are mediated by the shared motional modes of the entire chain via an effective XX–Ising interaction using the Mølmer–Sørensen protocol32,33 and can be written in terms of Pauli X matrices on ions \(i\) and \(j\) as XX(\(\theta\)) \(=\exp \left[-i\theta {\sigma }_{x}^{i}{\sigma }_{x}^{j}/2\right]\). Since the motional modes involve every ion in the chain, we can apply the XX gate between arbitrary pairs of ions with comparable speed and fidelity28,34,35,36. This native all-to-all connectivity of two-qubit gates in the trapped-ion QC provides complete flexibility to choose qubit mappings and gate configurations that maximize circuit performance on the hardware. Under typical operating conditions for this QC, the single-qubit gate fidelity can be maintained \(\gtrsim99.9 \%\), and the state fidelity of a maximally entangling XX(\(\pi /2\)) gate is \(\gtrsim96 \%\). We estimate the fidelity of small-angle XX gates by concatenating XX(\(\pi /2n\)) gates \(n\) times to approximate a full XX(\(\pi /2\)) gate. The state fidelity \({\mathcal{F}}\) is measured, and we estimate the per-gate error to be \(\epsilon \lesssim (1-{\mathcal{F}})/n\). We show an example in Fig. 3c for \(n=50\), and calculate \(\epsilon \ \lesssim \ 4\times 1{0}^{-3}\) for the XX(\(\pi /100\)) gate. In general, small-angle XX gates have higher fidelities in a trapped-ion QC than maximally entangling XX gates. Therefore, if quantum circuits admit using small-angle XX-gates in place of a collection of maximally entangling gates, they may be used to improve the quality of a quantum computation.
Molecular modeling
We choose \({{\rm{H}}}_{2}{\rm{O}}\) as a testbed for quantum co-design principles. The structure of \({{\rm{H}}}_{2}{\rm{O}}\) is sufficiently complex to develop and test universal techniques for scalable quantum circuit synthesis, while simple enough to be accessible by currently available trapped-ion QCs. Simulations using classical hardware provide fully verified solutions to assess the performance of the quantum hardware and build intuition about successful co-design strategies. What follows is a brief summary of the VQE co-design methodology, with further details supplied in Supplementary Information.
We first write down a Hamiltonian under the Born–Oppenheimer approximation, where the atomic nuclei are fixed to their known equilibrium geometry. The Hamiltonian is represented in the second-quantized form
where \({c}_{p}^{\dagger }\) (\({c}_{p}\)) are the creation (annihilation) operators for a molecular SO \(p\). The SOs are spin-labeled MOs obtained as a linear combination of atomic orbitals from the minimal STO-3G chemical basis37 using the HF method38. The resulting 7 MOs (14 SOs) are shown schematically in Fig. 1a, and the terms \({h}_{pq}\) and \({h}_{pqrs}\) from Eq. (1) are computed classically using a standard open-source tool based on ab initio methods39. The \({c}_{p}\) and \({c}_{p}^{\dagger }\) operators can be represented as Pauli operators acting on individual qubits using the JW transformation40, and we use the UCC method to generate an ansatz state41,42,43 with the first-order Trotter formula and one Trotter step. The expectation value of the Hamiltonian is computed by measuring projections of the prepared ansatz state in the combination of Pauli bases that correspond to each term in the JW-transformed Hamiltonian. To achieve meaningful accuracy, the circuit must be sufficiently sampled in each basis to reduce statistical errors14, and systematic errors must be controlled.
For a small molecule like \({{\rm{H}}}_{2}{\rm{O}}\) in the minimal basis set, it is possible to diagonalize the Hamiltonian in Eq. (1) to compute the FCI ground-state energy (\(-75.0116\) Ha); see SI Section S2i for larger systems where FCI calculations may not necessarily be available. This energy is lower than the mean-field HF result (\(-74.9624\) Ha) by ~49.2 mHa. From the FCI diagonalization, we generate a list of two-electron interaction terms (\({c}_{p}^{\dagger }{c}_{q}^{\dagger }{c}_{r}{c}_{s}\)) that contribute to modifications in the energy during the diagonalization process, with the degree of contribution characterized by the determinant. Some of these terms correspond to a pair of spin-up and spin-down electrons from the same filled MO being simultaneously excited to an empty MO (called the bosonic excitation terms hereafter), and the rest correspond to excitations of two electrons that are not paired in this way (see examples in Fig. 1a). Each term can be included in the preparation of the UCC ansatz in the form of \(\exp [{\theta }_{pqrs}{c}_{p}^{\dagger }{c}_{q}^{\dagger }{c}_{r}{c}_{s}-c.c.]\) in the Trotter product formula, where \({\theta }_{pqrs}\) becomes the optimization parameter, \({\rm{h.c.}}\) denotes the Hermitian conjugate operator, and p, q and r, s respectively denote unoccupied and occupied orbitals. We perform a numerical simulation of the VQE process as more terms are added to the UCC ansatz and estimate the lowest energy for each ansatz state as the parameters are optimized (see SI Section S2j for detail). This in silico result serves as a reference to benchmark the computational outcome from the QC.
Figure 1b shows the quantum resource requirements for each UCC ansatz circuit optimized for the trapped-ion QC. Relevant resource metrics include the number of qubits and the number of entangling gates. We also tabulate the ground-state energy from our in silico VQE simulation, as up to 21 terms are added to the ansatz beyond the HF calculations (see SI Fig. S1). We see that the estimate of the ground-state energy approaches the FCI value as more terms are added, reaching the FCI value within chemical accuracy once ≥17 terms are included in the ansatz. Inspecting the 21 most significant determinants in the FCI energy calculation, we observe that (1) the innermost MO \(1{a}_{1}\) is always filled and therefore can be ignored for the purpose of excitation, and (2) the \(1{b}_{2}\) MO participates only once as a bosonic excitation. Ignoring \(1{a}_{1}\) and \(1{b}_{2}\) in the ansatz state preparation can reduce the qubit requirement without sacrificing much in absolute accuracy: the reduced Hamiltonian reaches within 2.1 mHa of the FCI ground state at HF+16 terms using 10 qubits and 140 entangling gates. Chemical accuracy for the full Hamiltonian is achieved at HF+17 terms with 11 qubits and 143 entangling gates, of which 89 are CNOT gates and 54 are small-angle XX(\(\theta\)) gates that feature higher fidelity. These resource requirements are realistically within the near-term performance targets of an NISQ computer based on trapped ions.
Data availability
The experimental data presented in this manuscript are available from the corresponding author upon reasonable request.
References
Shor, P. W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 41, 303–332 (1999).
Grover, L. K. Quantum mechanics helps in searching for a needle in a haystack. Phys. Rev. Lett. 79, 325 (1997).
Feynman, R. P. Simulating physics with computers. Int. J. Theor. Phys. 21, 467–488 (1982).
Preskill, J. Quantum computing in the nisq era and beyond. Quantum 2, 79 (2018).
McArdle, S., Endo, S., Aspuru-Guzik, A., Benjamin, S. & Yuan, X. Quantum computational chemistry. Preprint at https://arxiv.org/abs/1808.10402 (2018).
Abrams, D. S. & Lloyd, S. Simulation of many-body fermi systems on a universal quantum computer. Phys. Rev. Lett. 79, 2586–2589 (1997).
Aspuru-Guzik, A., Dutoi, A. D., Love, P. J. & Head-Gordon, M. Simulated quantum computation of molecular energies. Science 309, 1704–1707 (2005).
Hastings, M. B., Wecker, D., Bauer, B. & Troyer, M. Improving quantum algorithms for quantum chemistry. Quantum Inf. Comput. 15, 1–21 (2015).
Babbush, R. et al. Exponentially more precise quantum simulation of fermions in the configuration interaction representation. Quantum Sci. Technol. 3, 015006 (2017).
Berry, D. W. et al. Improved techniques for preparing eigenstates of fermionic hamiltonians. npj Quantum Inf. 4, 22 (2018).
Reiher, M., Wiebe, N., Svore, K. M., Wecker, D. & Troyer, M. Elucidating reaction mechanisms on quantum computers. Proc. Natl Acad. Sci. USA 114, 7555–7560 (2017).
Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 5, 4213 (2014).
O‘malley, P. et al. Scalable quantum simulation of molecular energies. Phys. Rev. X 6, 031007 (2016).
Kandala, A. et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242 (2017).
Hempel, C. et al. Quantum chemistry calculations on a trapped-ion quantum simulator. Phys. Rev. X 8, 031022 (2018).
Nam, Y., Ross, N. J., Su, Y., Childs, A. M. & Maslov, D. Automated optimization of large quantum circuits with continuous parameters. npj Quantum Inf. 4, 23 (2018).
Olmschenk, S. et al. Manipulation and detection of a trapped Yb\(^{+}\) hyperfine qubit. Phys. Rev. A 76, 052314 (2007).
Richardson, L. F. & Gaunt, J. A. VIII the deferred approach to the limit. Phil. Trans. R. Soc. Lond. A 226, 299–361 (1927).
Efron, B. & Tibshirani, R. J. An Introduction to the Bootstrap (CRC Press, 1994).
Noek, R. et al. High speed, high fidelity detection of an atomic hyperfine qubit. Opt. Lett. 38, 4735–4738 (2013).
Keith, A. C., Baldwin, C. H., Glancy, S. & Knill, E. Joint quantum state and measurement tomography with incomplete measurements. Phys. Rev. A 98, 042318 (2018).
Farhi, E., Goldstone, J. & Gutmann, S. A quantum approximate optimization algorithm. Preprint at https://arxiv.org/abs/1411.4028 (2014).
Gao, X., Zhang, Z.-Y. & Duan, L.-M. A quantum machine learning algorithm based on generative models. Sci. Adv. 4, eaat9004 (2018).
Zhu, D. et al. Training of quantum circuits on a hybrid quantum computer. Sci. Adv. 5, eaaw9918 (2019).
Acton, M. et al. Near-perfect simultaneous measurement of a qubit register. Quantum Inf. Comp. 6, 465 (2006).
Myerson, A. H. et al. High-fidelity readout of trapped-ion qubits. Phys. Rev. Lett. 100, 200502 (2008).
Hayes, D. et al. Entanglement of atomic qubits using an optical frequency comb. Phys. Rev. Lett. 104, 140501 (2010).
Debnath, S. et al. Demonstration of a small programmable quantum computer with atomic qubits. Nature 536, 63 (2016).
Kielpinski, D., Monroe, C. & Wineland, D. J. Architecture for a large-scale ion-trap quantum computer. Nature 417, 709–711 (2002).
Brown, K. R., Harrow, A. W. & Chuang, I. L. Arbitrarily accurate composite pulse sequences. Phys. Rev. A 70, 052318 (2004).
Mount, E. et al. Error compensation of single-qubit gates in a surface-electrode ion trap using composite pulses. Phys. Rev. A 92, 060301 (2015).
Sørensen, A. & Mølmer, K. Quantum computation with ions in thermal motion. Phys. Rev. Lett. 82, 1971–1974 (1999).
Choi, T. et al. Optimal quantum control of multimode couplings between trapped ion qubits for scalable entanglement. Phys. Rev. Lett. 112, 190502 (2014).
Zhu, S.-L., Monroe, C. & Duan, L.-M. Arbitrary-speed quantum gates within large ion crystals through minimum control of laser beams. Europhys. Lett. 73, 485–491 (2006).
Zhu, S.-L., Monroe, C. & Duan, L.-M. Trapped ion quantum computation with transverse phonon modes. Phys. Rev. Lett. 97, 050505 (2006).
Linke, N. M. et al. Experimental comparison of two quantum computing architectures. Proc. Natl Acad. Sci. USA 114, 3305–3310 (2017).
Taketa, H., Huzinaga, S. & O-ohata, K. Gaussian-expansion methods for molecular integrals. J. Phys. Soc. Jpn. 21, 2313–2324 (1966).
Szabo, A. & Ostlund, N.S. Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory (Courier Corp., 2012).
Turney, J. M. et al. Psi4: an open-source ab initio electronic structure program. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2, 556–565 (2012).
Jordan, P. & Wigner, E. Über das paulische äquivalenzverbot. Z. Phys. 47, 631–651 (1928).
Čížek, J. On the correlation problem in atomic and molecular systems. calculation of wavefunction components in ursell-type expansion using quantum-field theoretical methods. J. Chem. Phys. 45, 4256–4266 (1966).
Hoffmann, M. R. & Simons, J. A unitary multiconfigurational coupled-cluster method: theory and applications. J. Chem. Phys. 88, 993–1002 (1988).
Bartlett, R. J., Kucharski, S. A. & Noga, J. Alternative coupled-cluster ansätze II. The unitary coupled-cluster method. Chem. Phys. Lett. 155, 133–140 (1989).
Acknowledgements
The authors thank the EURIQA team at the University of Maryland and Duke University for sharing their designs and for useful conversations. The authors also thank Qingfeng Wang at the University of Maryland for pointing out a typo in one of the circuits and in one of the figures shown in an earlier version of the manuscript and Zlatko Minev at IBM for pointing out the same typo in one of the circuits shown in an earlier version of the manuscript.
Author information
Authors and Affiliations
Contributions
Experimental data collected and analyzed by N.C.P. and J.-S.C.; Y.N., C.D., D.M., K.R.B., and J.K. performed the circuit design; Y.N. performed in silico VQE simulation; the apparatus was designed and built by K.W., J.M.A., K.M.B., J.-S.C., M.C., S.D., K.M.H., J.M., N.C.P., J.D.W.-C., S.M.K., S.A., J.A., P.S., M.W., A.M.D., A.B., V.C., M.K., C.C., C.M., and J.K.; Y.N., N.C.P., J.-S.C., and J.K. prepared the manuscript, with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nam, Y., Chen, JS., Pisenti, N.C. et al. Ground-state energy estimation of the water molecule on a trapped-ion quantum computer. npj Quantum Inf 6, 33 (2020). https://doi.org/10.1038/s41534-020-0259-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-020-0259-3
This article is cited by
-
Seeking a quantum advantage with trapped-ion quantum simulations of condensed-phase chemical dynamics
Nature Reviews Chemistry (2024)
-
Quantum many-body simulations on digital quantum computers: State-of-the-art and future challenges
Nature Communications (2024)
-
A versatile single-photon-based quantum computing platform
Nature Photonics (2024)
-
Demonstration of three- and four-body interactions between trapped-ion spins
Nature Physics (2023)
-
Orbital-optimized pair-correlated electron simulations on trapped-ion quantum computers
npj Quantum Information (2023)