Abstract
Reaching high-speed, high-fidelity qubit operations requires precise control over the shape of the underlying pulses. For weakly anharmonic systems, such as superconducting transmon qubits, short gates lead to leakage to states outside of the computational subspace. Control pulses designed with open-loop optimal control may reduce such leakage. However, model inaccuracies can severely limit the usability of such pulses. We implemented a closed-loop optimization that simultaneously adapts all control parameters based on measurements of a cost function built from Clifford gates. We directly optimize the amplitude and phase of each sample point of the digitized control pulse. We thereby fully exploit the capabilities of the pulse generation electronics and create a 4.16 ns single-qubit pulse with 99.76 % fidelity and 0.044 % leakage. This is a sevenfold reduction of the leakage rate and a threefold reduction in standard errors of the best DRAG pulse we have calibrated at such short durations on the same system.
Similar content being viewed by others
Introduction
Superconducting qubits are a promising candidate to realize large-scale quantum computing systems1,2,3. The architecture is scalable4, microwave control electronics are well developed and readily available, and transmon-type qubit designs5 allow for stable operations. To accurately manipulate the quantum state of the weakly anharmonic qubit, control methods have been steadily improved to address common problems such as frequency crowding6,7,8 and cross talk9. In particular, with the powerful tools provided by open-loop optimal control theory preparing target states10,11,12 and gates13,14 can be realized with high fidelity. In these methods, numerically simulated system models are used to optimize hundreds of parameters that determine the shape of the control fields applied to the quantum system15,16. When the system model is accurate enough, the optimized control pulses can immediately be applied in experiment, yielding high performance and reliable control17,18,19. However, applying such control methods to superconducting qubits produces less accurate results in comparison to ion traps20,21 and nuclear magnetic resonance systems15,22 since models with sufficient accuracy are not available for superconducting qubits. Effects that are hard to accurately reproduce in simulation include instrument noise, transfer functions23,24,25, additional modes and coupling to unwanted quantum systems26,27,28,29. As a result, pulse shaping for superconducting qubits requires closed-loop optimal control, i.e., direct optimization on the experimental system, which limits the amount of tunable parameters defining the pulse shapes14,30.
Furthermore, optimal control can suppress leakage out of the computational subspace occurring for fast qubit gates. Fast gates are required to lower the limits on gate errors set by decoherence. Moreover, in combination with short readout times31 and fast qubit reset32,33 fast gates are useful to reduce the overall execution time of quantum algorithms, such as variational quantum eigensolvers34 that require many repetitions to gather statistics on quantum measurements35,36,37. However, fast qubit gates suffer from leakage effects and additional unitary errors caused by the large bandwidth of the short control pulse6. Reducing leakage out of the computational subspace is paramount for error correction since correcting such errors requires significantly more resources than correcting errors in the computational subspace38,39,40.
In this work, we increase the fidelity of short duration single-qubit gates. Control shapes are optimized in a closed-loop fashion to capture the full system dynamics and avoid model limitations. The resulting pulses significantly mitigate leakage effects. As optimization is limited by the experimental runtime, we investigate the time budget of the setup. We employ methods such as restless measurements41 to speed-up the optimization and use the covariance matrix adaptation-evolution strategy (CMA-ES) algorithm42 instead of, for instance, Nelder-Mead43 to handle the large number of parameters. With these improvements we experimentally optimize pulses with up to 55 parameters.
Results
Setup and system control
The system consists of two transmon-type fixed-frequency superconducting qubits44 coupled by a flux tunable coupler45,46, with an identical architecture as used in36. Experiments are carried out on one of the qubits with a transition frequency of ω01/2π = 5117.22 MHz, an anharmonicity Δ/2π = − 315.28 MHz and coherence times of 105 μs and 39 μs for T1 and T2, respectively. The qubit is controlled by microwave pulses applied via a readout resonator capacitively coupled to the qubit. Pulses consist of two control components Ωx(t) and Ωy(t), which are combined into a single drive signal Ω = Ωx + iΩy. The pulse is up-converted to the qubit frequency using a microwave vector signal generator in a single-sideband configuration.
The in-phase- and quadrature-(IQ) components in the mixing process are the real and imaginary parts of the pulse modulated at an intermediate sideband frequency \({{\Omega }}(t)\exp \{i({\omega }_{\text{ssb}}t+\phi )\}\) with ωssb/2π = 100 MHz. Synthesizing this signals by an arbitrary waveform generator (AWG) results in real-time control over phase, frequency and amplitude47.
In a frame rotating at the qubit frequency, the transmon Hamiltonian is given by
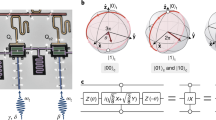
where terms rotating at twice the qubit frequency have been omitted. Here, \({\widetilde{{{\Omega }}}}_{x,y}\) are the IQ-components of the drive after the displacement due to the microwave resonator48. The ith level of the transmon is denoted by \(\left|i\right\rangle\). The operators \({\hat{\sigma }}_{j,j-1}^{x}=\sqrt{j}\left(\left|j\right\rangle \left\langle j-1\right|+\left|j-1\right\rangle \left\langle j\right|\right)\) and \({\hat{\sigma }}_{j,j-1}^{y}=i\sqrt{j}\left(\left|j\right\rangle \left\langle j-1\right|-\left|j-1\right\rangle \left\langle j\right|\right)\) couple adjacent energy levels. Therefore, Ωx-pulses at the resonance frequency ω01 drive rotations about the x − axis of the Bloch sphere spanned by \(\{\left|0\right\rangle ,\left|1\right\rangle \}\), see Fig. 1. The total area of the pulse envelope defines the rotation angle Θ. The rotation axis can be freely chosen in the xy-plane by changing the phase of the drive signal ϕ. By selecting ϕ = nπ/2 (n = 0, 1, …) and Θ = π/2, ±X/2 and ±Y/2 single-qubit operations are realized.
a The dashed lines show the analytic DRAG pulse, with Ωx in red and Ωy in blue. The solid lines show the same pulse sampled by the AWG. The optimization parameters an and bn of the piecewise-constant pulse are depicted as modifications of the sampled DRAG pulse by gray arrows and dashed lines. b Ideal Bloch sphere trajectory of the Ωx-pulse. The rotation angle Θ is given by the total area under the pulse.
Since transmons have a low anharmonicity, fast pulses with a wide frequency response lead to leakage out of the computational subspace defined by the two lowest-lying energy eigenstates. This process is suppressed by derivative removal gates (DRAG)6,49,50, designed to reduce leakage and phase errors caused by inadvertent driving of the \(\left|1\right\rangle \leftrightarrow \left|2\right\rangle\) transition. The first-order DRAG correction (Fig. 1(a); dashed lines) to a Gaussian shaped pulse \({{{\Omega }}}_{x}(t)=A\exp \left\{-{t}^{2}/(2{\sigma }^{2})\right\}\) with amplitude A and width σ, is
The correction in the imaginary component of ΩDRAG(t) with the scaling parameter β eliminates the spectral weight of the pulse at the \(\left|1\right\rangle \leftrightarrow \left|2\right\rangle\) transition.
Although being designed for fast, short gates DRAG fails to produce high fidelities when the gate duration is lower than ~ 10/Δ6. To overcome this, either higher-order correction terms or pulses with more degrees of freedom have to be employed. To find suitable pulses we use a parameterization that applies a correction δn = an + ibn at each point in time to a calibrated DRAG pulse, similar to common optimal control approaches17,51. This results in a list of piecewise-constant (PWC) control amplitudes
as shown in Fig. 1(a). The time discretization Δt is naturally given by the sampling rate of the AWG generating the pulse envelope. We use a Zurich Instruments HDAWG52 operating at a sampling rate of fs = 2.4GS/s. The optimization parameters are the amplitude corrections an and bn to the n-th sample of Ωx and Ωy, respectively, with the initial guess an = bn = 0.
Pulse parameter optimization
Since the parametrization in Eq. (3) no longer permits an individual optimization of each parameter we simultaneously optimize all of them using the CMA-ES optimization algorithm42 (see “Methods” section). It is based on generating sets of parameters \({{\mathcal{S}}}^{k}\) that describe k = 1, . . . , λ different pulse shapes as candidate solutions. The parameters in \({{\mathcal{S}}}^{k}\) are defined by the parametrization of the pulse shape. The fidelity of each candidate solution is evaluated by a cost function, which serves to generate a new set of candidate solutions. This process is repeated until convergence is reached and the best solution is found.
As a cost function we use randomized benchmarking (RB) sequences with a fixed number of m Clifford gates30 averaged over K sequence realizations, see Fig. 2(a). This corresponds to evaluating only a single-point in a standard RB measurement53,54, which reduces the runtime to evaluate the cost function. We construct the Clifford gates by composing ±X/2 and ±Y/2 pulses, each based on the pulse shape defined by \({{\mathcal{S}}}^{k}\), see Fig. 2(b). The average ground state population \({\overline{p}}_{0}(m)\) of the final qubit state defines the cost function, which is maximized by the optimizer. To estimate the fidelity of the optimized pulses we finally perform a full randomized benchmarking measurement.
a Single-qubit Clifford gate sequence of length m. b Schematic visualization of the composition of a Clifford gate from ± X/2, ± Y/2 pulses based on a specific pulse shape. The Ωx and Ωy components are displayed in red and blue, respectively. c Sketch of ideal RB curves \(\left(1+{{\mathcal{F}}}^{m}\right)/2\) with the cost function for m = 120 Clifford gates indicated as points for several fidelities \({\mathcal{F}}\). d Experimental data of a full optimization run for a 23 dimensional parameter space. Each blue point represents the cost function of each of the λ = 30 candidate pulse shapes based on a unique parameter set \({{\mathcal{S}}}^{k}\) evaluated using 20 Clifford sequences. The red points represent the average cost function at each iteration of the optimizer.
Fidelity estimates of optimized short pulses
We optimize single-qubit pulses of varying duration ranging from N = 10 to N = 26 samples per pulse, corresponding to a duration τ = N ⋅ fs ranging from 4.16 ns to 10.83 ns. We use K = 20 sequences of m = 120 Clifford gates. Each sequence is measured 1000 times using the restless measurement protocol41 at a rate of 100 kHz. We first use the CMA-ES-based optimization procedure to calibrate DRAG pulses, defined in Eq. (2). For this we choose the amplitude A, the DRAG parameter β and the sideband frequency ωssb as optimization parameters, i.e., \({\mathcal{S}}=\left\{A,\beta ,{\omega }_{{\rm{ssb}}}\right\}\). The results of our CMA-ES-based calibration are shown in Fig. 3 (blue circles). The resulting fidelities compare well with standard sequential error amplification calibration methods50. The optimized DRAG pulse then serves as initial guess for a second optimization step in which we extend \({\mathcal{S}}\) by the amplitude corrections to \({\mathcal{S}}^{\prime} =\left\{A,\beta ,{\omega }_{{\rm{ssb}}},{a}_{1},{b}_{1},...,{a}_{N},{b}_{N}\right\}\). Initializing the PWC optimization with optimal DRAG pulses reduces the number of iterations, as they already produce high fidelities (see Supplementary Notes 5).
The fidelity is measured with RB as a function of pulse length for optimized DRAG (blue circles) and piecewise-constant (PWC) pulses (red squares). Simulated fidelities are shown as lines (see Methods and Supplementary Notes 1 and 3). The simulated PWC fidelities (red solid line) reach the T1 coherence limit.
For gates longer than τ = 5 ns we find a constant fidelity of F = 99.87(1) % both for the DRAG pulse and the piecewise-constant optimized pulse, see Fig. 3. For gates shorter than 5ns we observe a decrease of fidelity for the DRAG pulses consistent with the 10/Δ limit (see the gray line in Fig. 3), while the fidelity of the piecewise-constant optimized pulses remains constant even for the shortest gate duration. Note that drive power limitations prevent us from implementing gates shorter than 4ns. The simulated DRAG pulses have higher fidelity than the experimental pulses for gates below 5ns (dashed blue line in Fig. 3). This indicates the presence of unknown error sources, such as potential non-linearities in the transfer function at high power55, and demonstrates the effectiveness of the subsequent optimization as the PWC optimized pulses overcome these unknown effects. The optimized DRAG and PWC pulses are not decoherence limited as shown by the discrepancy between the noiseless simulations (solid lines) and the measured fidelities. Possible explanations for the observed noise floor are amplitude noise, phase noise, or a combination thereof in the drive signal, which we investigate numerically (dashed lines in Fig. 3) in Supplementary Note 3.
To assess the influence of leakage on the shortest 4.16 ns pulse displayed in Fig. 4(a) and (b) we follow the leakage randomized benchmarking protocol outlined in ref. 40. The leakage RB analysis requires measuring the probabilities pj to occupy the states \(\left|j\right\rangle\) with j ∈ {0, 1, 2} after the standard RB gate sequences. The probability \({p}_{{\chi }_{1}}={p}_{0}+{p}_{1}=1-{p}_{2}\) of remaining in the computational subspace \({\chi }_{1}=\{\left|0\right\rangle ,\left|1\right\rangle \}\) is fitted using the decay model \(A+B{\lambda }_{1}^{n}\) to find the average leakage per Clifford \({L}_{1}=\left(1-A\right)\left(1-{\lambda }_{1}\right)\). Here, n is the number of Clifford gates while A, B, and λ1 are fit parameters.
a In-phase and b quadrature amplitude component of the pulse envelope before (blue) and after the piecewise-constant optimization (red), as represented in AWG memory. The dashed lines indicate the analytical DRAG pulse shapes. c Remaining population in the computational subspace χ1 for randomized benchmarking measurements using pulses based on the DRAG and optimized piecewise-constant pulses. The decay constant λ1 characterizes the population remaining in χ1. d Full leakage RB analysis characterization using a double decay with decay constants λ1 and λ2 for leakage and standard errors, respectively.
Using the extracted leakage decay \(B{\lambda }_{1}^{n}\) we fit p0(n) using the double decay model \({A}_{0}+B{\lambda }_{1}^{n}+{C}_{0}{\lambda }_{2}^{n}\) to find the average Clifford gate fidelity
The leakage rate of the optimized piecewise-constant pulses \({L}_{1}^{\,\text{PWC}\,}=0.044(25)\ \%\) is five times lower than the leakage rate of the DRAG pulse \({L}_{1}^{\,\text{DRAG}\,}=0.29(3)\ \%\), see Fig. 4(c). Additionally, we observe a reduction of standard errors from \(1-{\lambda }_{2}^{\,\text{DRAG}\,}=1.49(15)\ \%\) to \(1-{\lambda }_{2}^{\,\text{PWC}\,}=0.44(15)\ \%\), see Fig. 4(d). The resulting average fidelity per Clifford gate, computed using Eq. (4), is \({\overline{F}}_{\text{PWC}}=99.76(8)\ \%\) for the piecewise-constant pulse and \({\overline{F}}_{\text{DRAG}}=99.11(8)\ \%\) for the DRAG pulse.
Discussion
Our results show that optimal pulse shaping using a piecewise-constant basis improves the gate fidelity of short pulses, reducing leakage errors by a factor of seven and standard errors by a factor of three. Increasing the fidelity of short pulses is beneficial for quantum computers56, in particular considering that the single-qubit gates have similar length than two-qubit gates in certain systems57. Moreover, the closed-loop optimal control method we have implemented allows us to overcome leakage in short pulses benefiting low anharmonicity qubits, as discussed in more detail in Supplementary Note 2.
At longer gate durations, controlling the pulse shapes beyond analytical DRAG pulses does not improve the fidelity. All our pulses, aside from the DRAG pulses shorter than 5.5 ns, are limited to an error per gate of 0.13(1) % on average. The fidelities that we measured are, however, not limited by the T1-time, which sets an error per gate limit of 5 ⋅ 10−5, see Fig. 3. Although we show that the observed fidelity limit can be reproduced using a combination of noises on the control electronics (see Supplementary Note 3), determining the exact composition of error sources is subject of ongoing research.
The improvements with more complex pulse shapes come at the expense of long calibration times. Optimizing the longest pulse shape with N = 26 samples (i.e., 55 parameters) took up to 25 h. To understand how this time can be reduced we have measured the time taken to create the pulse sequences, initialize the control electronics, and gather the data (see “Methods” section). Creating the pulse sequences and initializing the control electronics at each iteration consumes the most time. Gathering the required data is only a small fraction of the total experimental runtime. With further improvements of the control electronics, for instance an internal generation of the 100 MHz sideband modulation, we expect further significant reductions in the overall runtime of the optimizer.
Our work demonstrates that optimizing—or calibrating—pulses with up to 55 parameters is experimentally feasible. This opens up the possibility to explore more elaborate optimal control methods on superconducting qubit platforms. We plan to extend this scheme to multi-qubit gates, where system dynamics are more complex and analytic optimal control methods are not as developed as for single-qubit gates16. While a piecewise-constant parametrization, as done for single-qubit gates, is harder due to the long duration of two-qubit gates, other analytical pulse representations, such as its spectral components, will be explored to improve on gate performance.
Methods
Multidimensional parameter calibration
To optimize all parameters of the pulse shape simultaneously on the experimental setup, we have chosen the CMA-ES optimization algorithm as a noise-resilient and time-efficient optimizer42. This algorithm optimizes a population of λ candidate solutions, which are normally distributed in the parameter space. The center and spread of the distribution are given as starting conditions and are updated by the optimizer at each iteration42. See Supplementary Notes 6 for an example optimization showing the distribution of parameters during calibration.
Generally, the choice of the population size λ is a trade-off between fast convergence speed and avoiding local optima42. However, experimentally we have to consider the time required to process the pulse sequences (i.e., the time required to compile the pulse sequences into AWG files), to initialize the hardware (including data transfer) and to measure the cost function for different population sizes λ, see Fig. 5. We benchmark these three times using a set of 20 Clifford gate sequences per candidate solution, each with 100 Clifford gates. By dividing the total time required to evaluate the entire population by λ we calculate the effective time required to asses a single candidate solution. This allow us to gauge how efficiently the hardware is being used, see Fig. 5(c). The instrument initialization introduces a constant overhead, see Fig. 5(a), which decreases the efficiency of the optimization algorithm for lower population sizes. Single-point optimizers, such as Nelder-Mead43, are thus an inefficient choice. However, when evaluating larger populations the contribution of the constant offset of the initialization is distributed over multiple measurements, leading to a convergence of the evaluation time per candidate. The data acquisition time is small due to our implementation of restless measurements41, which allows for a 100 kHz repetition rate. The data analysis time is negligible in comparison to the three main contributions and is not included in the analysis.
a Experimental runtime consisting of processing the pulse sequences (red right triangles), initializing the setup (blue circles) and measuring the cost function (gray left triangles). b Time per iteration of CMA-ES split into those three categories. In one iteration the cost function of each candidate solution in the whole population of size λ is measured. Error bars are smaller than the size of the data points. c Time per evaluation, as a function of population size. Each candidate solution in a given population requires one evaluation. As the population size increase the experimental runtime to evaluate a full iteration increases and the average time to evaluate a candidate solution decreases.
Numerical results
To obtain the numerical results (lines in Fig. 3) we model the qubit as a driven an-harmonic oscillator with a Hilbert space of dimension d = 4. See Supplementary Note 4 for a discussion on leakage to higher energy states. We simulate the quantum dynamics and perform quantum optimal control with the q-optimize package58,59. For each of the ± X/2 and ± Y/2 gates, we obtain the dynamics as superoperator60 matrices \({{\mathcal{E}}}_{\pm X/2}\) and \({{\mathcal{E}}}_{\pm Y/2}\) by solving the master equation in Lindblad form, which includes T1 and T2. Next, we compose the gates Ci in the Clifford group C from these atomic operations, for example \({C}_{6}={{\mathcal{E}}}_{-X/2}\circ {{\mathcal{E}}}_{-Y/2}\circ {{\mathcal{E}}}_{+X/2}\). The pulse parameters \({\mathcal{S}}\) are optimized using the L-BFGS gradient search61 to maximize the average Clifford gate fidelity \({F}_{C}={\left|C\right|}^{-1}{\sum }_{i}{F}_{{C}_{i}}\), where \({F}_{{C}_{i}}\) is the fidelity of each Clifford gate62. This optimizer is more efficient for numerical simulations than the CMA-ES optimizer if measurement noise is neglected and gradients can be computed. Additional details regarding the simulations are provided in Supplementary Notes 1.
Data availability
All relevant data supporting the main conclusions and figures of the document are available on request. Please refer to Max Werninghaus at maw@zurich.ibm.com.
References
Devoret, M. & Schoelkopf, R. J. Superconducting circuits for quantum information: an outlook. Science 339, 1169–1174 (2013).
Krantz, P. et al. A quantum engineeras guide to superconducting qubits. Appl. Phys. Rev. 6, 021318, https://doi.org/10.1063/1.5089550 (2019).
Wendin, G. Quantum information processing with superconducting circuits: a review. Rep. Prog. Phys. 80, 106001 (2017).
Acín, A. et al. The quantum technologies roadmap: a European community view. N. J. Phys. 20, 080201 (2018).
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).
Motzoi, F., Gambetta, J. M., Rebentrost, P. & Wilhelm, F. K. Simple pulses for elimination of leakage in weakly nonlinear qubits. Phys. Rev. Lett. 103, 110501 (2009).
Schutjens, R., Dagga, F.A., Egger, D. J., & Wilhelm, F.K. Single-qubit gates in frequency-crowded transmon systems. Phys. Rev. 88, 10502947, https://doi.org/10.1103/PhysRevA.88.052330. (2013)
Vesterinen, V., Saira, O.-P., Bruno, A., & DiCarlo, L. Mitigating information leakage in a crowded spectrum of weakly anharmonic qubits. Preprint at http://arxiv.org/abs/1405.0450 (2014).
Sheldon, S., Magesan, E., Chow, J. M. & Gambetta, J. M. Procedure for systematically tuning up cross-talk in the cross-resonance gate. Phys. Rev. A 93, 060302 (2016).
Rojan, K. et al. Arbitrary-quantum-state preparation of a harmonic oscillator via optimal control. Phys. Rev. https://doi.org/10.1103/PhysRevA.90.023824. (2014).
Reich, D. M., Gualdi, G. & Koch, C. P. Optimal strategies for estimating the average fidelity of quantum gates. Phys. Rev. Lett. 111, 200401 (2013).
Mališ, M. et al. Local control theory for superconducting qubits. Phys. Rev. A 99, 052316 (2019).
Spörl, A. et al. Optimal control of coupled josephson qubits. Phys. Rev. A 75, 012302 (2007).
Egger, D. J. & Wilhelm, F. K. Adaptive hybrid optimal quantum control for imprecisely characterized systems. Phys. Rev. Lett. 112, 240503 (2014).
Glaser, S. J. et al. Training Schrödinger’s cat: quantum optimal control Strategic report on current status, visions and goals for research in Europe. Eur. Phys. J. D. 69, 279 (2015).
Machnes, S., Assémat, E., Tannor, D. & Wilhelm, F. K. Tunable, flexible, and efficient optimization of control pulses for practical qubits. Phys. Rev. Lett. 120, 150401 (2018).
Khaneja, N., Reiss, T., Kehlet, C., Schulte-Herbrüggen, T. & Glaser, S. J. Optimal control of coupled spin dynamics: design of NMR pulse sequences by gradient ascent algorithms. J. Magn. Reson 172, 296–305 (2005).
Lapert, M., Zhang, Y., Braun, M., Glaser, S. J. & Sugny, D. Singular extremals for the time-optimal control of dissipative spin 1/2 particles. Phys. Rev. Lett. 104, 083001 (2010).
Heeres, R. W. et al. Implementing a universal gate set on a logical qubit encoded in an oscillator. Nat. Commun. 8, 94 (2017).
Timoney, N. et al. Error-resistant single-qubit gates with trapped ions. Phys. Rev. A 77, 052334 (2008).
Mount, E. et al. Error compensation of single-qubit gates in a surface-electrode ion trap using composite pulses. Phys. Rev. A 92, 060301 (2015).
Kobzar, K., Luy, B., Khaneja, N. & Glaser, S. J. Pattern pulses: design of arbitrary excitation profiles as a function of pulse amplitude and offset. J. Magn. Reson 173, 229–235 (2005).
Rol, M. A. et al. Time-domain characterization and correction of on-chip distortion of control pulses in a quantum processor. Appl. Phys. Lett. 116, 054001 (2020).
Jerger, M., Kulikov, A., Vasselin, Z. & Fedorov, A. In situ characterization of qubit control lines: A qubit as a vector network analyzer. Phys. Rev. Lett. 123, 150501 (2019).
Gustavsson, S. et al. Improving quantum gate fidelities by using a qubit to measure microwave pulse distortions. Phys. Rev. Lett. 110, 040502– (2013).
Müller, C., Lisenfeld, J., Shnirman, A. & Poletto, S. Interacting two-level defects as sources of fluctuating high-frequency noise in superconducting circuits. Phys. Rev. B 92, 035442 (2015).
Müller, C., Cole, J. H. & Lisenfeld, J. Towards understanding two-level-systems in amorphous solids: insights from quantum circuits. Rep. Prog. Phys. 82, 124501 (2019).
Schlör, S. et al. Correlating decoherence in transmon qubits: low frequency noise by single fluctuators. Phys. Rev. Lett. 123, 190502 (2019).
Burnett, J. J. et al. Decoherence benchmarking of superconducting qubits. NPJ Quantum Inf. 5, 1–8 (2019).
Kelly, J. et al. Optimal quantum control using randomized benchmarking. Phys. Rev. Lett. 112, 240504 (2014).
Heinsoo, J. et al. Rapid high-fidelity multiplexed readout of superconducting qubits. Phys. Rev. A 10, 034040 (2018).
Egger, D. et al. Pulsed reset protocol for fixed-frequency superconducting qubits. Phys. Rev. A 10, 044030 (2018).
Magnard, P. et al. Fast and unconditional all-microwave reset of a superconducting qubit. Phys. Rev. Lett. 121, 060502 (2018).
Moll, N. et al. Quantum optimization using variational algorithms on near-term quantum devices. Quantum Sci. Technol. 3, 030503 (2018).
Torlai, G., Mazzola, G., Carleo, G. & Mezzacapo, A. Precise measurement of quantum observables with neural-network estimators. Phys. Rev. Res. 2, 022060(R) (2020).
Ganzhorn, M. et al. Gate-efficient simulation of molecular eigenstates on a quantum computer. Phys. Rev. Appl. 11, 044092 (2019).
Wecker, D., Hastings, M. B. & Troyer, M. Progress towards practical quantum variational algorithms. Phys. Rev. A 92, 042303 (2015).
Fowler, A. G. Coping with qubit leakage in topological codes. Phys. Rev. A 88, 10502947, https://doi.org/10.1103/PhysRevA.88.042308 (2013).
Suchara, M., Cross, A. W. & Gambetta, J. M. Leakage suppression in the Toric code. Quantum Inf. Comput. 15, 997–1016 (2015).
Wood, C. J. & Gambetta, J. M. Quantification and characterization of leakage errors. Phys. Rev. A 97, 032306 (2018).
Rol, M. A. et al. Restless tuneup of high-fidelity qubit gates. Phys. Rev. Appl. 7, 041001 (2017).
Hansen, N. The CMA evolution strategy: a tutorial. hal-01297037 (2005).
Nelder, J. A. & Mead, R. A simplex method for function minimization. Comput. J. 7, 308–313 (1965).
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).
McKay, D. C. et al. Universal gate for fixed-frequency qubits via a tunable bus. Phys. Rev. Appl. 6, 064007 (2016).
Roth, M. et al. Analysis of a parametrically driven exchange-type gate and a two-photon excitation gate between superconducting qubits. phys. rev. A 96, 62323 (2017).
Jorgesen, D. IQ, Image Reject & Single Sideband Mixer Primer. https://www.everythingrf.com/whitepapers/details/3186-iq-image-reject-single-sideband-mixer-primer (2018).
Blais, A. et al. Quantum-information processing with circuit quantum electrodynamics. Phys. Rev. A 75, 032329 (2007).
Chen, Z. et al. Measuring and suppressing quantum state leakage in a superconducting qubit. Phys. Rev. Lett. 116, 020501 (2016).
Sheldon, S., Magesan, E., Chow, J. M. & Gambetta, J. M. Procedure for systematically tuning up cross-talk in the cross-resonance gate. Phys. Rev. A 93, 60302 (2016).
Schulte-Herbrüggen, T. et al. Control aspects of quantum computing using pure and mixed states. Philos. Trans. R. Soc. A: Math., Phys. Eng. Sci. 370, 4651–4670 (2012).
Zurich Instruments. 750 MHz Arbitrary Waveform Generator, https://www.zhinst.com/ch/en/products/hdawg-arbitrary-waveform-generator (2020).
Magesan, E., Gambetta, J. M. & Emerson, J. Characterizing quantum gates via randomized benchmarking. Phys. Rev. A 85, 42311 (2012).
Magesan, E., Gambetta, J. M. & Emerson, J. Scalable and robust randomized benchmarking of quantum processes. Phys. Rev. Lett. 106, 180504 (2011).
Kalfus, W. et al. High-fidelity control of superconducting qubits using direct microwave synthesis in higher nyquist zones. Preprint at https://arxiv.org/abs/2008.02873v1.
Wecker, D., Bauer, B., Clark, B. K., Hastings, M. B. & Troyer, M. Gate-count estimates for performing quantum chemistry on small quantum computers. Phys. Rev. A 90, 022305 (2014).
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Wittler, N. et al. An integrated tool-set for control, calibration and characterization of quantum devices applied to superconducting qubits. Preprint at https://arxiv.org/abs/2009.09866.
Wittler N. et al. Q-optimize–C3: Control, Calibrate, Characterize-Open-source software, http://q-optimize.org/ (2020).
Lidar, D. A. Lecture notes on the theory of open quantum systems. Preprint at https://arxiv.org/abs/1902.00967 (2019).
Nocedal, J. Updating quasi-newton matrices with limited storage. Math. Comput. 35, 773–773 (1980).
Magesan, E., Blume-Kohout, R. & Emerson, J. Gate fidelity fluctuations and quantum process invariants. Phys. Rev. A 84, 012309 (2011).
Acknowledgements
We thank A. Fuhrer, M. Ganzhorn, M. Mergenthaler, P. Mueller, S. Paredes, M. Pechal, and G. Salis for insightful discussions as well as R. Heller and H. Steinauer for technical support. We also acknowledge useful discussions and the provision of qubit devices with the quantum team at IBM T.J. Watson Research Center, Yorktown Heights. This work was supported by the European Commission Marie Curie ETN QuSCo (Grant Nr. 765267), the IARPA LogiQ program under contract W911NF-16-1-0114-FE and the ARO under contract W911NF-14-1-0124. S.M. and F.W. acknowledge support from the the project OpenSuperQ (Grant Nr. 820363) and project VERTICONS (BMBF, Project 13N14872)
Author information
Authors and Affiliations
Contributions
All authors developed the idea for the experiment; M.W. performed the measurements and analyzed the data; M.W. and D.E. implemented the control methods. F.R. and S.M. carried out the numerical simulations. M.W., D.E., F.R., and S.F. wrote the manuscript. All authors contributed to the discussions and interpretations of the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Werninghaus, M., Egger, D.J., Roy, F. et al. Leakage reduction in fast superconducting qubit gates via optimal control. npj Quantum Inf 7, 14 (2021). https://doi.org/10.1038/s41534-020-00346-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-020-00346-2
This article is cited by
-
Markovian noise modelling and parameter extraction framework for quantum devices
Scientific Reports (2024)
-
A long lifetime floating on neon
Nature Physics (2024)
-
Direct manipulation of a superconducting spin qubit strongly coupled to a transmon qubit
Nature Physics (2023)
-
Real-time quantum error correction beyond break-even
Nature (2023)
-
Error rate reduction of single-qubit gates via noise-aware decomposition into native gates
Scientific Reports (2022)