Abstract
The development of efficient network nodes is a key element for the realization of quantum networks which promise great capabilities as distributed quantum computing or provable secure communication. We report the realization of a quantum network node using a trapped ion inside a fiber-based Fabry–Perot cavity. We show the generation of deterministic entanglement at a high fidelity of 90.1(17)% between a trapped Yb ion and a photon emitted into the resonator mode. We achieve a success probability for generation and detection of entanglement for a single shot of 2.5 × 10−3 resulting in 62 Hz entanglement rate.
Similar content being viewed by others
Introduction
The communication between different quantum nodes is central to many branches of quantum technology, such as quantum computation1, quantum metrology2, and secure communication3,4. Quantum nodes consist of an interface between a stationary qubit and a traveling qubit, which usually is a photon in order to bridge large distances. Therefore, the development of light–matter interfaces operating at the quantum limit and providing control of the quantum states of both the traveling qubits and the quantum network node itself is of great importance. However, applications of light–matter interfaces as quantum network nodes face several challenges. First, nodes have to exhibit long coherence times, scaling with the characteristic distances of the targeted network. Second, the stationary qubits at the network nodes must be efficiently coupled to traveling qubits which carry quantum information across the network application. Third, the stationary qubits should be accessible to high-fidelity initialization, manipulation, and readout.
There have been several approaches toward the experimental realization of quantum network nodes, for example, using trapped ions5,6,7,8, neutral atoms9,10, NV-centers11 or SV-centers12 in diamond, and semiconductor quantum dots13,14. For both the photon collection and the readout of the network node, experimental approaches have ranged from collecting light with high numerical aperture objectives7,11,15,16,17 to embedding emitters in optical cavities in order to enhance the light–matter coupling strength6,9,18,19.
In order to distribute quantum information in networks or to deliver it to frequency-conversion units, it is desirable to couple traveling photonic qubits into optical fibers. A particularly elegant approach toward this goal are fiber-based Fabry–Perot resonators20. This device composes of a pair of optical fibers with micromachined endfacets with a highly-reflective optical coating. They combine the best of two worlds: on the one hand, they are optical microresonators with small mode volume and on the other hand the cavity mode is directly fiber-coupled. Cavities with small mode volumes offer large coupling between light and matter and therefore can enhance the efficiency of the light–matter interface. Moreover, they have the conceptual advantages of overcoming difficulties of orthogonality of polarizations in light collection with high numerical aperture objectives due to their small solid angle and increasing the bandwidth of the emitted photons. The integration of fiber Fabry–Perot cavities into quantum network nodes is considered to be a promising route for quantum communication21. However, even though neutral atoms22,23, trapped ions19,24,25,26,27, NV centers28, and semiconductor quantum dots29 have been coupled to fiber Fabry–Perot resonators, the entanglement between light and matter in such an experimental setting has not yet been demonstrated.
In this work, we realize a quantum network node of a trapped 171Yb+ ion coupled to a fiber Fabry–Perot cavity and demonstrate the generation and verification of a maximally entangled atom-photon state with a fidelity of F = (90.1 ± 1.7)%. The entanglement is realized between the spin state of the trapped ion and the polarization degree of freedom of the emitted photon. We have measured a single-shot success probability of 2.5 × 10−3 for the generation and detection of entangled states resulting in a rate of 62 s−1.
Results
Preparation sequence and photon generation
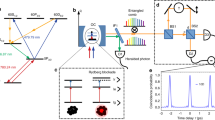
Our quantum network node consists of a single trapped 171Yb+ ion in a radiofrequency (Paul) needle trap embedded into a fiber Fabry–Perot cavity, conceptually similar to our previous work19,24,30, see Fig. 1a. The ion is confined with trap frequencies of ωx,y = 2π × 1.5 MHz and ωz = 2π × 2.5 MHz and Doppler-cooled by a near-resonant laser at 370 nm wavelength. The fiber Fabry–Perot cavity has a length of 261 μm and a finesse of F = 4700 ± 700 at 370 nm and serves as a light–matter interface on the principal 2S1/2 ↔ 2P1/2 dipole transition of the ion. The cavity linewidth is \(\kappa =2\pi \cdot \left(58\pm 9\right)\) MHz and together with the Purcell–enhanced excited state lifetime of the 2P1/2 manifold of \(\tau =1/{\Gamma }^{\prime}=7.4(2)\,{\rm{ns}}\), the photons emitted by the ion and leaving the cavity exhibit a minimum duration of 9.9(7) ns (FWHM). The lifetime arising from the natural linewidth of the transition is 8.12(2) ns31.
a We collect the single emitted photons along the quantization axis with a fiber Fabry–Perot cavity and analyze them using a projective measurement of polarization. b Selected energy levels of 171Yb+ including the relevant optical transitions. After pulsed excitation from the \(\left|0\right\rangle\) to the \(\left|e\right\rangle\) state, the ion decays in a superposition of decay channels emitting a σ± polarized photon. Subsequent manipulation of the atomic qubit is done via microwave pulses. c Experimental sequence for creating and verifying atom-photon entanglement including decision branching, see main text for explanation. d Readout of the hyperfine qubit using discrimination between dark and bright hyperfine states. In σz ⊗ σz basis we achieve a readout fidelity of 98.2(6)% using the dashed line as bright/dark threshold for a readout window length of 400 μs (see, methods for details). Error bars show the standard error.
For the generation of entanglement, we initialize the ion in the hyperfine ground state \(\left|0\right\rangle ={\left.\right|}^{2}{S}_{1/2},F=0,{m}_{F}=0\left.\right\rangle\) within 10 μs with more than 99% fidelity using optical pumping with continuous-wave laser light. Subsequently, we excite the ion to the electronically excited state \(\left|e\right\rangle ={\left.\right|}^{2}{P}_{1/2},F^{\prime} =1,{m}_{F}=0\left.\right\rangle\) using a laser pulse derived from a frequency-doubled mode-locked Ti:sapphire laser of duration tpulse = (134 ± 1) ps, see Fig. 1b. The pulse duration is much shorter than the Purcell–enhanced lifetime of the 2P1/2 state. The laser pulse intensity is calibrated by driving Rabi oscillations on the S ↔ P transition and we observe a fidelity of the preparation of the \(\left|e\right\rangle\) state in excess of 95% which is limited by polarization purity of the excitation pulse. Following the excitation, the ion decays in a superposition of decay channels into the \(\left|{g}^{+}\right\rangle ={\left.\right|}^{2}{S}_{1/2},F=1,{m}_{F}=-1\left.\right\rangle\) and \(\left|{g}^{-}\right\rangle ={\left.\right|}^{2}{S}_{1/2},F=1,{m}_{F}=1\left.\right\rangle\) states by emission of a single photon. We apply an external magnetic field of 603.6(7) mG along the cavity axis in order to suppress emission into the cavity mode with a change of magnetic quantum number of ΔmF = 0, see Fig. 1a. Hence, only circularly polarized photons are emitted into the cavity mode. The success probability of an emission into the cavity mode is (10.1 ± 1.9)% which together with the extraction, path, and detector efficiencies, sets the detection success probability per shot, see Methods for details. The external magnetic field leads to a level shift between the \(\left|{g}^{\pm }\right\rangle\) states, however, the resulting frequency difference between the two polarization modes \(\left|{\sigma }^{\pm }\right\rangle\) of the emitted photon is much smaller than the atomic and the cavity linewidth which preserves the capability of the ion–cavity system to decay in a superposition of channels, see Fig. 1b and Methods for details to cavity polarization modes. Hence, for a photon emitted into the cavity mode the ideal maximal entangled atom-photon state reads \(\left|{\Psi }_{{\rm{atom}}-{\rm{photon}}}\right\rangle =\frac{1}{\sqrt{2}}\left(\left|{\sigma }^{+}\right\rangle \left|{g}^{+}\right\rangle -\left|{\sigma }^{-}\right\rangle \left|{g}^{-}\right\rangle \right)\).
State detection
The collected photons leave the cavity into a single-mode optical fiber. After ~1.5 m of fiber we detect the quantum state of the photons by a projective measurement on a polarizing beam splitter (PBS) and two single photon counters (SPCs), one on each exit path of the PBS. The photonic readout basis is defined by a set of waveplates which rotate the polarization qubit into an arbitrary basis (see Methods and Fig. 4). After the polarization rotation, we end up with the transformed state
in which \(\left|H\right\rangle\) and \(\left|V\right\rangle\) denote the horizontal and vertical polarizations, respectively.
After excitation of the ion and subsequent emission of the photon, we wait for a count on the single-photon counters. If no photon is detected within 1 μs after the excitation, the experimental sequence continues with new initialization and excitation of the ion qubit (see Fig. 1c). In contrast, if a photon has been detected, we read out the atomic state in order to conduct a correlation analysis between photon polarization and atomic spin state. The first stage of detection is the mapping from the Zeeman qubit states \(\left|{g}^{\pm }\right\rangle\) to the hyperfine states \(\left|{g}^{+}\right\rangle\) and \(\left|0\right\rangle\) which usually is done with more than 97% transfer fidelity. To this end, we employ a microwave π-pulse from the \(\left|{g}^{-}\right\rangle\) to the \(\left|0\right\rangle\) state at a frequency near 12.6 GHz. Considering the ion as a two-level system, we refer to this atomic basis as the σz–basis. Due to the external magnetic field, the degeneracy of the \(\left|{g}^{\pm }\right\rangle\) states is much higher than the microwave transition linewidth which is typically around 20 kHz. This allows for precise selection of the driving transition. The microwave π–pulse is then followed by hyperfine-state selective fluorescence detection. We are able to discriminate between the hyperfine qubit states within a few 100 μs by using fluorescence detection on the \({\left.\right|}^{2}{S}_{1/2},F=1\left.\right\rangle \leftrightarrow {\left.\right|}^{2}{P}_{1/2},F^{\prime} =0\left.\right\rangle\) transition. For detection of the photons emitted into free space we use an objective with a numerical aperture of NA = 0.48. The distribution of photon numbers for a dark and bright ion are shown in Fig. 1d for 400 μs readout time. We define the discrimination fidelity as the average detection fidelity of each qubit state \((\left|{g}^{+}\right\rangle /\left|0\right\rangle )\). In total, we achieve a discrimination fidelity between a dark and a bright ion of 98.2(6)% which is on par with the values achieved previously on the 171Yb+ hyperfine qubit32,33 and mainly limited by off-resonant scattering of photons on the \({\left.\right|}^{2}{P}_{1/2},F^{\prime} =1\left.\right\rangle\) level.
In Fig. 2a we show the results of correlations between photons in the polarization states \(\left|{\sigma }^{\pm }\right\rangle\) and the atomic states \(\left|{g}^{+}\right\rangle\) and \(\left|0\right\rangle\). We observe correlations with (90.7 ± 3.9)% contrast which is mainly limited by the atomic readout process (7.8(14)%) including state discrimination and transfer π–pulse.
a Correlations for the σz ⊗ σz basis are shown with time-binned arrival times of the photons for this measurement as inset. We measure a FWHM of 9.9(7) ns for the photon duration. From the atomic decay constant the light–matter coupling rate can be estimated (see Methods for details). The gray shaded areas represent the post-selection boundaries (10ns width) for photons accepted for analysis (see main text for details). b) The parity oscillations for a photon readout in σx and σy bases are shown. The relative phase difference Δϕ = ϕ1 − ϕ2 of the microwave pulses sets the readout basis of the atomic qubit in the equatorial plane of the Bloch sphere. Red crosses: P(0∣Hx) ⋅ P(Hx) + P(g+∣Vx) ⋅ P(Vx) correlations. Blue dots: P(0∣Hy) ⋅ P(Hy) + P(g+∣Vy) ⋅ P(Vy) correlations. Error bars show the standard error.
In contrast to a statistical mixture of states, the entangled state of two qubits exhibits a definite phase relation between them, and quantum correlations between atom and photon states are visible in any two-qubit basis σi ⊗ σi. In order to verify the entanglement in different bases orthogonal to σz, we rotate both qubits into the equatorial plane of the Bloch sphere. For the photonic qubit we adjust the waveplate angles as described in Methods. For the atomic basis we apply a π/2–pulse with a phase difference of Δϕ = ϕ1 − ϕ2 with respect to the first π–pulse. The relative phase difference Δϕ of the pulses sets the exact readout basis of the atomic qubit, which is especially important to select a specific basis such as σx ⊗ σx and σy ⊗ σy. For these rotated bases also the Larmor precession of superposition spin states comes into play. The magnetic field lifts the degeneracy between the \(\left|{g}^{-}\right\rangle\) and \(\left|{g}^{+}\right\rangle\) states which results in a precession of the atomic and photonic superposition states in the laboratory frame with Larmor-frequency \({\omega }_{L}=2.8\frac{{\rm{MHz}}}{{\rm{Gauss}}}\cdot (603.6\pm 0.7){\rm{mG}}=1.690(2){\rm{MHz}}\). The photonic modes do not exhibit additional splitting due to the cavity modes because a potential birefringence of the mirrors usually occurs for linearly polarized light, see Methods. For the photon, the precession requires a stable optical path length with a fixed time between generation and detection such that the projective measurement always happens to the same basis. For the atom, the phases of the microwave pulses must have defined starting times relative to the flying qubit emission such that the microwave pulses arrive always at the same phase of the Larmorprecession of the stationary qubit. Due to the near-instant excitation of the ion, the arrival time of the excitation pulse determines the emission time of a photon to a uncertainty of τ = 7.4(2) ns. We fix the starting time of the microwave pulses with respect to the arrival time of the excitation pulse to less than 400 ps by synchronizing them to the cavity round-trip time of the Ti:sapphire laser. Both pulses originate from an arbitrary waveform generator and are mixed to a carrier signal red detuned by ~8 MHz from the center of the two microwave transition frequencies. Mixing to the same carrier preserves the relative phase Δϕ between the pulses. Since the experimental sequence is not synchronized to the microwave carrier phase, the first π-pulse starts with a random phase with respect to the Larmor precession of the atomic qubit. The following π/2 pulse acting on the \(\left|0\right\rangle\)/\(\left|{g}^{+}\right\rangle\) qubit rotates around an axis with a fixed relative orientation to the phase of the \(\left|0\right\rangle\)/\(\left|{g}^{+}\right\rangle\) superposition. The relative orientation of this rotation axis is determined by the phase difference Δϕ. In total, both pulses rotate the ion qubit around a fixed axis regardless of the phase of the first pulse. We end up in total with a defined atomic basis for readout by considering a fixed timing of the pulses in the laboratory frame with respect to the Larmor precession. Using this technique we are able to precisely select any basis orthogonal to σz for the atomic qubit.
In Fig. 2b, we show the oscillation of correlations between a photon readout in the basis σx/σy and a varying atomic readout basis determined by Δϕ, also referred to as parity oscillations. We observe correlations with (81 ± 16)% contrast for σx ⊗ σx and (87.0 ± 2.6)% for σy ⊗ σy. The contrast in the rotated bases is limited by decoherence due to magnetic field noise (<1%), timing jitter of the microwave pulses (<1%), and mainly an increased error in atomic state discrimination due to the formation of coherent dark states in the readout transition (~11%) (see Methods).
Fidelity
Following5 we calculate the lower bound of the detection fidelity for the maximally entangled atom-photon state to be F≥(89.8 ± 2.2)% from the correlation measurements in z-basis and in the orthogonal bases (see Methods for details). This value is a measure for the quality of the whole setup and not only of the generated entangled state, as it includes all experimental noise and errors like SPCs dark counts, polarization mixing effects, qubit manipulations, the atomic readout, and the dephasing of the atomic qubit due to magnetic field noise. To estimate the quality of the generation of entanglement, we investigate the contribution of each error source to the fidelity starting with correction for the dark counts on the SPCs resulting in ~1% increase of the measured entanglement fidelity. The small error due to detector dark counts originates from the short temporal shape of our photon wave function, which enables a short acceptance window of 10 ns for post-analysis. This lowers the contribution of false–positives detection events.
Further, we determine the full density matrix of the two-qubit state and use a maximum likelihood estimation34 to ensure the density matrix ρ to be physical, see Fig. 3a. We use this matrix to determine the contribution of unwanted unitary rotations on the atom and photon bases to be ≲1%. This confirms our statement of having precise control over both qubit bases. Subsequently, we compute the state fidelity to:
We estimate the contribution of noise to the detection fidelity of the entangled state by adapting the methods described in7,35 to a 4 × 4 density matrix. We compute an upper bound for the entanglement fidelity \({F}_{\max }=\frac{1}{2}\left(1+\sqrt{\frac{4P-1}{3}}\right)=(94.0\pm 1.0) \%\) from the purity \(P={\rm{Tr}}\left({\rho }^{2}\right)=(83.0\pm 3.0) \%\) of the state. The maximal state fidelity \({F}_{\max }\) is limited by noise contributions, as for example qubit dephasing and state preparation. Specifically, we have studied the influence of the external magnetic field noise on the performance of our quantum network node. The external magnetic field has two main effects: (1) for the successful detection of correlations, both atomic and photonic channels have to be stable with respect to the Larmor precession, since this is the dominant rate of the phase evolution of the entangled state (see Methods). The spontaneous decay time τ = 7.4(2) ns of the excited state \(\left|e\right\rangle\) introduces the main timing uncertainty from emission of the single-photon until detection of the atomic qubit state. (2) On the other hand, magnetic field fluctuations directly modulate the Larmor frequency ωL resulting in additional phase noise. The fluctuations reduce the coherence time of the qubit of which the \(\left|{g}^{\pm }\right\rangle\) states are magnetic-field sensitive. We have measured the coherence time of both the \(\left|{g}^{\pm }\right\rangle\) and the \(\left|{g}^{+}\right\rangle /\left|0\right\rangle\) qubits using a Ramsey sequence with variable hold time. For each hold time we obtain the remaining coherence fraction by the contrast of a full scan of the relative phase between the pulses. The results are shown in Fig. 3b, and we observe a coherence time of (496 ± 42) μs and (1022 ± 121) μs for the \(\left|{g}^{\pm }\right\rangle\) and the \(\left|{g}^{+}\right\rangle /\left|0\right\rangle\) qubits, respectively. For the duration of the atomic basis manipulation we determine a reduction in contrast of <1%.
a Absolute values of the density matrix ρ obtained from a full quantum state tomography followed by a maximum likelihood estimation as described in methods. Errors are denoted with gray bars. b The experimental data show the visibility of a Ramsey like sequence for different evolution times between the two π/2 pulses. The visibility for each evolution time is determined by scanning the relative phase between the pulses (inset). Blue circles: The Zeeman qubit \(\left|{g}^{\pm }\right\rangle\) exhibits a coherence time of (496 ± 42) μs. Yellow triangles: The hyperfine qubit \(\left|{g}^{+}\right\rangle /\left|0\right\rangle\) exhibits a coherence time of (1022 ± 121) μs. The times are extracted from fits (solid lines) with the function \(\exp \left(-\left(t/\tau \right)\right)\). Error bars show the standard error.
Discussion
The presented system is well suitable as a node in quantum networks. The small size of the fiber Fabry–Perot cavity enables very good optical access to the trapped ion allowing for precise control and manipulation of the long-lived stationary qubit. We have achieved a deterministic entanglement at a high fidelity of F = (90.1 ± 1.7)%. Effects reducing the fidelity are error in state detection of the atomic qubit (manipulation and state discrimination), imperfect excitation of the \(\left|e\right\rangle\) state (~1.8%), dark counts on the SPCs (~1%), dephasing of the atomic qubit due to magnetic field noise (<1%) and timing of the readout (<1%). The atomic transition linewidth of 2π ⋅ 19.4 MHz allows for high generation rate of entanglement supported by fast extraction of photons out of the cavity of 1.3(2) ns which are intrinsically fiber coupled allowing for easy distribution to further elements of the network where the short temporal profile of the photons is beneficial for impedance matching36. Compared to previous cavity-based atom-photon entanglements, we achieved to our knowledge the yet shortest temporal shape of photons of 9.9(7) ns extracted through the cavity by more than one order of magnitude. At the same time we maintained a high success rate of generating atom-photon entanglement per shot 2.5 × 10−3 which is one magnitude below the success rate of15 who reported the yet highest measurement rate of atom-photon entanglement. We suffer from an imperfect length stabilization of the fiber cavity due to strong mechanical resonances and an imperfect ion localization which reduces the achievable cooperativity of C0 = 1.9(4) to an effective value of C0,eff = 0.056(13) (see Methods).
In the future, we expect to increase the detection rate of entanglements of 62 s−1 by an order of magnitude when approaching the maximum repetition rate allowed for by the ion initialization time of 3.25 μs, since we did not optimize the experimental sequence for speed yet. Further improvements to ion localization and locking quality of the cavity could yield another factor of five which we calculate by assuming the theoretical achievable cooperativity of C0 = 1.9(4) ns. Furthermore, the coherence time could be enhanced by shifting the atomic qubit to the clock transition of 171Yb+ using additional microwave pulses32. A logical next step in the realization of a quantum network node would be the inclusion of a frequency conversion to telecom wavelength, which has been demonstrated recently for Ca+ ions7,18 and single Rubidium atoms37. The principle of a conversion between 370 nm and 1314 nm with 10.5% efficiency38 or 1580.3 nm with 9% efficiency39 has been demonstrated already for weak laser fields. Also, conversion pathways for matching the trapped ion qubit to semiconductor quantum dots36 or other emitters can be explored.
Methods
Fiber Fabry–Perot cavity
The fiber Fabry–Perot cavity composes of two single-mode optical fibers, each having a concave mirror structure on its front facet with radii of curvature of \({R}_{1}=\left(255\pm 16\right)\) μm and \({R}_{2}=\left(304\pm 34\right)\) μm and reflectivities of T1 = 500 ppm and T2 = 100 ppm, respectively. From the measured finesse of F = 4700 ± 700 we estimate the losses of the mirrors to be L = (350 ± 100) ppm, in agreement with the manufacturer’s expectation. Similar to our previous work on ultraviolet cavities40, the losses have remained constant over time even under ultrahigh vacuum conditions. With a cavity length of (261 ± 1) μm we calculate a mode waist (1/e2 intensity radius) of ωcavity = 4.1(2) μm. Using the cavity waist we compute a theoretical cooperativity of \({C}_{0,{\rm{theo}}}=\frac{\sigma }{A}\cdot \frac{F}{\pi }=1.9(4)\) with \(\sigma =\frac{3{\lambda }^{2}}{2\pi }\) beeing the cross-section of the ion and \(A=\pi {{\omega }_{0}}^{2}\) the area of the cavity mode at its smallest waist.
Due to their slightly elliptic shape, our fiber mirrors usually exhibits birefringence which manifests itself in a frequency splitting νΔHV of the linear polarization modes H/V within the resonator. For the cavity we choose a set of fibers which radii of curvature results in νΔHV being smaller than the cavity linewidth \(\kappa =2\pi \cdot \left(58\pm 9\right)\) MHz which in fact could be still much higher than the Larmor precision ωL = 1.690(2) MHz such that the photonic modes exhibit additional splitting due to the cavity modes. However, for emission of a circularly polarized photon into the cavity the equal superposition of linear polarization modes cancel out in phase evolution and we observe that the important timescale of the correlation measurements in the rotated bases is the energy splitting of the stationary qubit levels \(\left|{g}^{\pm }\right\rangle\). The emission probability of circularly polarized photons into the cavity mode depends on the spectral overlap of the H– and V–polarized resonator modes which can reduce the rate of generated entanglements.
We stabilize the cavity length using a side-of-fringe locking technique using an auxiliary laser detuned by one free spectral range from the resonance of the atom. In order to avoid charging of the dielectric mirror surfaces due to ultraviolet light41 coupled into the cavity, we conduct the lock at ultralow light levels of less than 50 pW.
Pulsed excitation
We derive the excitation pulse from a mode-locked frequency-doubled Ti:sapphire laser running at 54 MHz intracavity repetition rate. This results in 18.5 ns uncertainty of the pulse arrival time at the ion position. We synchronize parts of the experimental sequence to a trigger signal sent out with 50 ps jitter simultaneously to the outcoupling of a laser pulse. The pulses exhibit a spectral linewidth of ~90 GHz which we filter using a cavity resonant to the ion excitation transition with linewidth of 2π ⋅ 1.19(1) GHz. This not only reduces unwanted excitations of the ion but also suppresses the scattering of stray photons into the fiber-cavity detuned by 12.6 GHz from the pulsed excitation frequency.
Detection efficiency
We estimate the effective light–matter coupling rate \({g}_{{\rm{eff}}}=\sqrt{{C}_{0,{\rm{eff}}}\cdot 2\cdot \kappa \cdot \gamma }=2\pi \cdot \left(7.9\pm 1.0\right)\) MHz from the Purcell-enhanced spontaneous decay of the ion into a single mode of the resonator. The cavity linewidth κ dictates the decay constant of the intra-cavity electric field of τcavity = 1.3(2) ns, which we take into account for the decay time of the ion’s excited state using two convolved exponential decays. Due to an excitation pulse length of ~134 ps the population transfer to the ion’s excited state can be seen as instantly. The resulting photon timeshape is shown in Fig. 2a where the cavity decay time rounds the otherwise sharp rising edge. With the Purcell-enhanced linewidth \({\Gamma }^{\prime}=\Gamma \left(1+2{C}_{0,{\rm{eff}}}\right)=2\pi \cdot 21.6(5)\) MHz and the atomic linewidth of 2γ = Γ = 2π ⋅ 19.4 MHz we calculate the effective cooperativity C0,eff = 0.056(12). The effective value includes the effects of an imperfect locking of the cavity onto the atomic resonance wavelength and the imperfect localization of the ion due to residual (micro–)motion. From the effective cooperativity we calculate the probability of a photon emitted into the cavity mode \({P}_{{\rm{c,eff}}}=\frac{2{C}_{0,{\rm{eff}}}}{2{C}_{0,{\rm{eff}}}+1}=(10.1\pm 1.9) \%\). We determine the efficiency of detecting the photon on one of the single-photon counting modules to be Pd,eff = Pc,eff × ηext × ϵ × ηpath × ηDetector = 3.2(9) × 10−3. Here, we use the probability of the photon to be extracted through the desired low-reflectivity cavity mirror \({\eta }_{{\rm{ext}}}=\frac{{T}_{2}}{{T}_{1}+{T}_{2}+{L}_{1+2}}=0.53(6)\), the mode-matching efficiency into the single-mode optical fiber ϵ = 0.44(3), the quantum efficiency of the single-photon counters of ηDetector = 0.215, and path efficiency ηpath = 0.65(11) due to optical fibers and further optical elements. The calculated value agrees with the measured detection efficiency of Pd,measured = 2.5 × 10−3.
Lower bound of fidelity and correlation contrast
The lower bound of the entanglement fidelity can be estimated using the formula5,42
With \(\left|\uparrow \right\rangle \equiv \left|{g}^{+}\right\rangle\) and \(\left|\downarrow \right\rangle \equiv \left|0\right\rangle\) the terms ρσλ,σλ = P(σ∣λ) × P(λ) are expressed in terms of measured probabilities. Here λ = {H, V} are the photon states and σ = {↑, ↓} the atom states. For the z–basis the ρσλ,σλ can be directly extracted from Fig. 2a whereas for the rotated basis the \({\tilde{\rho }}_{\sigma \lambda ,\sigma \lambda }\) from Fig. 2b. When corrected for the false readouts per sequence originating from dark counts of the cavity SPCs of 1.7(5) × 10−6 {6.6(9) × 10−6} for H {V} we achieve a lower bound on the generated atom-photon state fidelity of F ≥ 90.7 ± 1.5%. We subtract half of the expected dark–counts on the bright and dark correlation side of the atom, since we expect an equal probability for a dark or bright ion.
Using the conditional probabilities as defined above, we compute the correlation contrast C as:
Full quantum state tomography
We reconstruct the density matrix from the joint expectation values Si,j for 16 different combinations of Pauli basis σi ⊗ σj with σi/j ∈ {1, σx, σy, σz}. We make use of the symmetry of the off-diagonal elements for the x−, y− and z− bases Sm,n = Sn,m for m/n ∈ {x, y, z} and m ≠ n. We extract the values from the measurements shown in Fig. 2 to compute:
Subsequently, we apply unitary transformations on the basis of each qubit in order to post-hoc maximize the overlap with the Bell state \(\frac{1}{\sqrt{2}}\left(\left|V\right\rangle \left|{g}^{+}\right\rangle -\left|H\right\rangle \left|{g}^{-}\right\rangle \right)\). Following34, we perform a maximum likelihood estimation to ensure the density matrix ρ to be physical with the previously obtained matrix as a starting point. We use this matrix to estimate the contribution of unwanted unitary rotations on the atom and photon basis and to compute an upper bound of the fidelity.
Upper bound of fidelity
The following calculations were made in35 for a 2 × 2 density matrix. We adapt the methods for a 4 × 4 density matrix. The contribution of experimental noise to the state fidelity can be calculated using the state purity P which becomes 1 for a noise-free pure entangled state whereas for increasing noise it approaches 1/2. A pure state \(\left|\psi \right\rangle\) mixed to a probability (1 − V) with white noise can be written as:
where \({\mathbb{I}}\) is the 4 × 4 identity matrix. With fidelity F = (1 + V)/2 we obtain for the purity
and subsequently for the fidelity \({F}_{\max }\) limited by white noise:
Magnetic field stability
Our magnetic field noise is estimated to be smaller than 0.7 mG with main noise contributions at 50 Hz and 150 Hz. We measure the magnetic field noise using a fluxgate sensor placed 10 cm away from the ion’s position but outside the stainless steel vacuum chamber. In order to reduce magnetic field noise the chamber is surrounded on 5 out of 6 sides with 3 layers of cobalt foil (MCL61).
Dark state repumping
For magnetic fields lower than 1 G (≈3 MHz splitting) we observe a drastic decrease of the ion fluorescence resulting from the formation of coherent dark states of the 2S1/2, F = 1 hyperfine levels43,44. Decreasing the magnetic field into this range reduces the Larmor frequency and therefore improve timing synchronization. We are able to partly recover the fluorescence (~50%) by using a second cooling laser with different polarization through a different beam path destroying the dark states. For the ion state readout based on free-space fluorescence detection, this second laser beam results in an increase of dark counts while at the same time the bright counts are reduced by a factor of two by dark states. Both effects reduce the contrast of the fluorescence-based atomic readout by ≲10%.
Photonic basis
The photonic readout basis is defined by a half- and a quarter-wave plate (HWP & QWP) which rotate the basis of the polarization qubit. A projective measurement is achieved by a polarizing beam splitter (PBS) and two single-photon counters (SPCs) on each exit path of the PBS respectively, detecting horizontal (H) or vertical (V) polarized photons (see Fig. 1a). The two waveplates can select any basis of the photons extracted through the fiber-cavity to be projected as (H/V) on the two SPCs. For a defined selection of a basis, knowledge about the influence of the fiber on the polarization is required. We characterize the photon path using a weak laser (~50 pW) coupled through the PBS into the fiber. Since the laser frequency is off-resonant by a few GHz with respect to the cavity, it gets reflected on the first fiber mirror and we detect the reflected light on the V-SPC. Repeating the measurement for different waveplate rotation angles leads to a heat map, as shown in Fig. 4. Using the Jones–formalism we are able to do a best fit to the acquired data and find the polarization retardation of the fiber as well as the rotation offset of the fast axis of our waveplates. As an example, for selecting the σz–basis, fiber, QWP, and HWP should act in total as a quarter-wave plate mapping a circularly polarized photon to a linearly polarized (and vice versa). For the reflection of the initial H-polarized reference light this results in maximal counts on the V-SPC. When selecting bases orthogonal to σz we found that defining the σx/y–basis as \({\sigma }_{k}=\{\frac{1}{\sqrt{2}}\left(\left|{\sigma }^{+}\right\rangle +{e}^{i{\phi }_{k}}\left|{\sigma }^{-}\right\rangle \right),\frac{1}{\sqrt{2}}\left(\left|{\sigma }^{+}\right\rangle +{e}^{i{\phi }_{k}+\pi }\left|{\sigma }^{-}\right\rangle \right)\},k\in (x,y)\) with ϕx = π/4 and ϕy = − π/4 (same holds then for the ion basis) results in easily accessible waveplate angles as shown in Fig. 4.
a Characterisation of the photon detection setup using a reference laser as shown in Fig. 1. The normalized count rate of reflected photons on the V-detector for different waveplate angles is shown (top). Fit of the data assuming the fiber to be an arbitrary polarization element (bottom). b Calculated correlation heat-map for different atomic qubit basis using fiber parameters determined from the fit in a). The optimal waveplate settings of the photon readout basis σi used for the measurements in Fig. 2 are labeled accordingly with lower indices Hi/Vi; i ∈ (x, y, z).
Data availability
The data and code that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The data and code that support the findings of this study are available from the corresponding author upon reasonable request.
References
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Degen, C. L., Reinhard, F. & Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 89, 035002 (2017).
Wootters, W. K. & Zurek, W. H. A single quantum cannot be cloned. Nature 299, 802–803 (1982).
Shor, P. W. & Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 85, 441–444 (2000).
Blinov, B. B., Moehring, D. L., Duan, L.-M. & Monroe, C. Observation of entanglement between a single trapped atom and a single photon. Nature 428, 153–157 (2004).
Stute, A. et al. Tunable ion-photon entanglement in an optical cavity. Nature 485, 482–485 (2012).
Bock, M. et al. High-fidelity entanglement between a trapped ion and a telecom photon via quantum frequency conversion. Nat. Commun. 9, 1998 (2018).
Stute, A. et al. Quantum-state transfer from an ion to a photon. Nat. Photonics 7, 219–222 (2013).
Wilk, T., Webster, S. C., Kuhn, A. & Rempe, G. Single-atom single-photon quantum interface. Science 317, 488–490 (2007).
Volz, J. et al. Observation of entanglement of a single photon with a trapped atom. Phys. Rev. Lett. 96, 030404 (2006).
Togan, E. et al. Quantum entanglement between an optical photon and a solid-state spin qubit. Nature 466, 730–4 (2010).
Nguyen, C. T. et al. Quantum network nodes based on diamond qubits with an efficient nanophotonic interface. Phys. Rev. Lett. 123, 183602 (2019).
De Greve, K. et al. Quantum-dot spin-photon entanglement via frequency downconversion to telecom wavelength. Nature 491, 421–425 (2012).
Gao, W. B., Fallahi, P., Togan, E., Miguel-Sanchez, J. & Imamoglu, A. Observation of entanglement between a quantum dot spin and a single photon. Nature 491, 426–430 (2012).
Stephenson, L. J. et al. High-rate, high-fidelity entanglement of qubits across an elementary quantum network. Phys. Rev. Lett. 124, 110501 (2020).
Almendros, M. et al. Bandwidth-tunable single-photon source in an ion-trap quantum network. Phys. Rev. Lett. 103, 213601 (2009).
Gerber, S. et al. Quantum interference from remotely trapped ions. N. J. Phys. 11, 013032 (2009).
Krutyanskiy, V. et al. Light-matter entanglement over 50 km of optical fibre. npj Quantum Inf. 5, 72 (2019).
Steiner, M., Meyer, H. M., Deutsch, C., Reichel, J. & Köhl, M. Single ion coupled to an optical fiber cavity. Phys. Rev. Lett. 110, 043003 (2013).
Hunger, D. et al. A fiber Fabry–Perot cavity with high finesse. N. J. Phys. 12, 065038 (2010).
Northup, T. E. & Blatt, R. Quantum information transfer using photons. Nat. Photonics 8, 356–363 (2014).
Gallego, J. et al. Strong Purcell effect on a neutral atom trapped in an open fiber cavity. Phys. Rev. Lett. 121, 173603 (2018).
Colombe, Y. et al. Strong atom-field coupling for Bose-Einstein condensates in an optical cavity on a chip. Nature 450, 272–276 (2007).
Steiner, M., Meyer, H. M., Reichel, J. & Köhl, M. Photon emission and absorption of a single ion coupled to an optical-fiber cavity. Phys. Rev. Lett. 113, 263003 (2014).
Takahashi, H., Kassa, E., Christoforou, C. & Keller, M. Cavity-induced anticorrelated photon-emission rates of a single ion. Phys. Rev. A 96, 023824 (2017).
Brandstätter, B. et al. Integrated fiber-mirror ion trap for strong ion-cavity coupling. Rev. Sci. Instrum. 84, 123104 (2013).
Takahashi, H., Kassa, E., Christoforou, C. & Keller, M. Strong coupling of a single ion to an optical cavity. Phys. Rev. Lett. 124, 013602 (2020).
Albrecht, R., Bommer, A., Deutsch, C., Reichel, J. & Becher, C. Coupling of a single nitrogen-vacancy center in diamond to a fiber-based microcavity. Phys. Rev. Lett. 110, 243602 (2013).
Muller, A., Flagg, E. B., Metcalfe, M., Lawall, J. & Solomon, G. S. Coupling an epitaxial quantum dot to a fiber-based external-mirror microcavity. Appl. Phys. Lett. 95, 173101 (2009).
Ballance, T. G. et al. Cavity-induced back-action in purcell-enhanced photoemission of a single ion in an ultraviolet fiber-cavity. Phys. Rev. A 95, 033812 (2017).
Olmschenk, S. et al. Measurement of the lifetime of the \(6{p}^{2}{P}_{1/2}^{o}\) level of Yb+. Phys. Rev. A 80, 022502 (2009).
Olmschenk, S. et al. Manipulation and detection of a trapped Yb+ hyperfine qubit. Phys. Rev. A 76, 052314 (2007).
Ejtemaee, S., Thomas, R. & Haljan, P. C. Optimization of Yb+ fluorescence and hyperfine-qubit detection. Phys. Rev. A 82, 063419 (2010).
James, D. F. V., Kwiat, P. G., Munro, W. J. & White, A. G. Measurement of qubits. Phys. Rev. A 64, 052312 (2001).
Bussières, F. et al. Quantum teleportation from a telecom-wavelength photon to a solid-state quantum memory. Nat. Photonics 8, 775–778 (2014).
Meyer, H. M. et al. Direct photonic coupling of a semiconductor quantum dot and a trapped ion. Phys. Rev. Lett. 114, 123001 (2015).
Ikuta, R. et al. Polarization insensitive frequency conversion for an atom-photon entanglement distribution via a telecom network. Nat. Commun. 9, 1997 (2018).
Rütz, H., Luo, K.-H., Suche, H. & Silberhorn, C. Quantum frequency conversion between infrared and ultraviolet. Phys. Rev. Appl. 7, 024021 (2017).
Kasture, S. et al. Frequency conversion between UV and telecom wavelengths in a lithium niobate waveguide for quantum communication with yb+ trapped ions. J. Opt. 18, 104007 (2016).
Schmitz, J., Meyer, H. M. & Köhl, M. Ultraviolet Fabry-Perot cavity with stable finesse under ultrahigh vacuum conditions. Rev. Sci. Instrum. 90, 063102 (2019).
Harlander, M., Brownnutt, M., Hänsel, W. & Blatt, R. Trapped-ion probing of light-induced charging effects on dielectrics. N. J. Phys. 12, 093035 (2010).
Vasconcelos, R. et al. Scalable spin-photon entanglement by time-to-polarization conversion. npj Quantum Inf. 6, 9 (2020).
Berkeland, D. J. & Boshier, M. G. Destabilization of dark states and optical spectroscopy in Zeeman-degenerate atomic systems. Phys. Rev. A 65, 033413 (2002).
Milner, V. & Prior, Y. Multilevel dark states: coherent population trapping with elliptically polarized incoherent light. Phys. Rev. Lett. 80, 940–943 (1998).
Acknowledgements
We thank T.G. Ballance, K. Kluge, and H.M. Meyer for early contributions to this work and R. Berner for experimental assistance. This work has been funded by the Alexander-von-Humboldt Stiftung, DFG (SFB/TR 185 project A2), BMBF (FaResQ and Q.Link.X), and the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy—Cluster of Excellence Matter and Light for Quantum Computing (ML4Q) EXC 2004/1—390534769.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
All authors contributed to the design, development, and characterization of the experiment. P.K. conducted the measurements and the data analysis, M.B. manufactured and characterized the fiber cavity setup. P.K. and M.K. wrote the paper. The project was conceived and supervised by M.K.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kobel, P., Breyer, M. & Köhl, M. Deterministic spin-photon entanglement from a trapped ion in a fiber Fabry–Perot cavity. npj Quantum Inf 7, 6 (2021). https://doi.org/10.1038/s41534-020-00338-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-020-00338-2