Abstract
Preparing and observing quantum states of nanoscale particles is a challenging task with great relevance for quantum technologies and tests of fundamental physics. In contrast to atomic systems with discrete transitions, nanoparticles exhibit a practically continuous absorption spectrum and thus their quantum dynamics cannot be easily manipulated. Here, we demonstrate that charged nanoscale dielectrics can be artificially endowed with a discrete level structure by coherently interfacing their rotational and translational motion with a superconducting qubit. We propose a pulsed scheme for the generation and read-out of motional quantum superpositions and entanglement between several levitated nanoparticles, providing an all-electric platform for networked hybrid quantum devices.
Similar content being viewed by others
Introduction
Opto- and electromechanical systems are at the cutting edge of modern quantum devices1,2,3, with great potential for technological application and fundamental tests4,5,6. Levitating nanoscale objects almost perfectly isolates them from their surroundings, enabling superior force sensitivity and coherence times7. Optically levitated nanoparticles have been successfully cooled into their motional quantum groundstate8, opening the door to free-fall center-of-mass9,10,11 and rotational12,13 quantum superposition tests.
Quantum experiments with trapped nanoparticles7 require schemes to control their rotational and translational quantum states. Continuous-wave optical techniques are limited by the detrimental impact of photon scattering decoherence14 and by internal heating due to photon absorption15,16. In addition, the fact that nanoscale particles lack the discrete internal spectrum of atoms or other microscopic quantum systems makes it difficult to address them coherently with laser pulses.
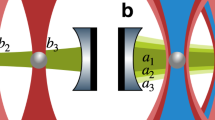
Here, we demonstrate that the states of a superconducting qubit can be used to manipulate and read out the quantum dynamics of a charged nanoparticle levitated in a Paul trap (see Fig. 1). While this has been achieved with clamped oscillators2,17,18,19, for levitated nanoparticles it requires decoupling their rotations from their center-of-mass motion. We argue that this task can be realistically achieved in the all-electrical setup proposed here. Electrically levitated nanorotors are thus ideally suited for trapped superposition experiments with a wide variety of particle geometries and charge distributions, and present a versatile alternative to other nanoparticle-qubit setups20,21,22,23.
The rotational and translational motion of a charged nanoparticle (blue) levitated in a Paul trap induces an electrical current between the superconducting endcap electrodes. The latter can be coherently interfaced with a charge qubit formed by a superconducting island (red). This Cooper-pair box can be used to generate and read-out spatial superpositions of the nanoparticle. The system constitutes the basic element for networking levitated nanoparticles into hybrid quantum devices based on superconducting circuitry.
Quadrupole ion traps provide exceptionally stable confinement for charged nanoparticles24. Moreover, the particle motion induces an electric current in the endcap electrodes25,26,27. We propose to use this current for first cooling the nanoparticle to milliKelvin temperatures and then interfacing its motion with a superconducting circuit. The resulting coupling between superconductor and particle scales as charge over square root mass28,29 and can thus be as strong as for a single atomic ion for realistic charge distributions.
We show that the proposed all-electrical platform enables cooling and interference experiments with levitated nanorotors, making it well suited for generating and reading-out entanglement between several particles and superconducting qubits, thus forming a building block of a larger quantum network. The motional quantum state can be prepared and observed by qubit manipulations with an ultra-fast pulsed scheme, operating on a timescale much shorter than the mechanical period and within the coherence time of the charge qubit. This pulse scheme allows to speed-up the observation of nanoscale quantum interference in a variety of opto- and electromechanical setups20,21,30,31.
Results
Ro-translational macromotion
A charged nanoparticle is suspended in a hyperbolic Paul trap of endcap distance 2z0 and radius \(\sqrt{2}{z}_{0}\), where the ring electrode is put to the time-dependent potential \({U}_{{\rm{PT}}}(t)={U}_{{\rm{dc}}}+{U}_{{\rm{ac}}}\cos ({\Omega }_{{\rm{ac}}}t)\) with respect to the floating endcaps (see Fig. 1). Due to the quadrupole symmetry of the electric field, the rotational and translational particle motion is fully determined by its total charge q, orientation-dependent dipole vector p(Ω), and quadrupole tensor \({\mathsf{Q}}\left(\Omega \right)\). Here, Ω denotes the orientational degrees of freedom of the particle, e.g. parametrized by Euler angles; its center-of-mass position is r.
In general, the resulting time-dependent force and torque will lead to complicated and unstable dynamics of the nanoparticle. However, if the trap is driven sufficiently fast, its micromotion can be separated, and one obtains a time-independent effective trapping potential for the macromotion (see “Methods”)
Here, M is the particle mass and the Paul trap symmetry axis is aligned with ez, such that \({\mathsf{A}}\) = \({\mathbb{1}}\) − 3ez ⊗ ez. The Ii denote the moments of inertia with ni the associated directions of the rotor principal axes. We dropped the orientation dependence of p, \({\mathsf{Q}}\), and ni for compactness.
The effective potential (1) describes the coupled rotational and translational macromotion of an arbitrarily charged and shaped nanoparticle in a quadrupole ion trap, and is thus pertinent for ongoing nanoparticle experiments24,31,32. It shows that stable trapping can be achieved for sufficiently small bias voltages Udc (with frequencies \({\omega }_{z}=q{U}_{{\rm{ac}}}/\sqrt{2}M{\Omega }_{{\rm{ac}}}{z}_{0}^{2}\) and ωx,y = ωz/2). In addition, the rotational and translational motion decouple for particles with vanishing dipole moment. Note that if the particle has a finite quadrupole moment its rotation dynamics can still be strongly affected by the trapping field. This may provide means to manipulate the rotation dynamics of nanoscale particles, a challenging task due to the nonlinearity of rotations32,33,34,35,36.
Particle-circuit coupling
The rotational and translational motion of the particle induces mirror charges in the endcap electrodes. The latter can be quantified by extending the Shockley−Ramo theorem to arbitrary charge distributions (see “Methods”), yielding the capacitor charge Qind = −kez ⋅ (qr + p)/z0 + CV, given the endcap capacitance C and voltage drop V. The geometry factor k, with values of 0 < k ≲ 1/2 for realistic electrode geometries, determines the approximately homogeneous field −kV/z0ez close to the trap center in the absence of the particle. (A perfect plate capacitor corresponds to k = 1/2).
The induced capacitor charge only depends on the total motional dipole moment qr + p along the Paul trap axis, and is thus independent of the particle quadrupole moment. A circuit connecting the electrodes picks up the ro-translational motion of the particle via the current I = dQind/dt. At the same time, the particle feels a voltage-dependent electrostatic force and torque depending on the circuit state. This can be used for resistive cooling and for coherently interfacing the particle with a superconducting qubit.
Nanoparticle resistive cooling can be achieved by joining the endcaps with a resistance R. The dissipation of the induced current in the resistor leads to thermalization of the particle motion at the circuit temperature. The timescale of this resistive cooling can be tuned by adding an inductance in series to the circuit29. In the adiabatic limit, it reacts almost instantaneously to the particle motion. Thus, the circuit degrees of freedom can be expanded to first order in the particle velocity and rotation speed, yielding the effective total cooling rate
This quantifies how fast an initially occupied phase-space volume contracts, predicting the timescale of rotational and translational thermalization with the circuit. The rate (2) is always positive and exhibits a q2/M-scaling, indicating that charged nanoparticles can be cooled as efficiently as atomic ions.
Interfacing nanoparticle and charge qubit
The levitated nanoparticle can be coherently coupled to a superconducting Cooper-pair box37 by attaching the latter to the endcap electrodes (see Fig. 1), as also proposed for atomic ions28,38. The nanoparticle motion towards the endcaps modifies the voltage drop over the Cooper-pair box, whose charge state determines the force and torque acting on the particle. Preparing the Cooper-pair box in a superposition of charge states37 thus entangles the nanoparticle motion with the circuit. This can be used to generate and verify nanoscale motional superposition states.
The combined nanoparticle-Cooper-pair box Hamiltonian can be derived in a lengthy calculation from Kirchhoff’s circuit laws (see “Methods”). Operating the Cooper-pair box in the charge qubit regime37 of N and N + 1 Cooper pairs yields the nanorotor-qubit coupling
where CΣ is the effective capacitance of the circuit and the qubit raising and lowering operators are denoted by σ+, σ−. This interaction couples the charge eigenstates of the box to the motional dipole moment of an arbitrarily shaped and charged nanorotor, implying that qubit charge states are conserved by the interaction and that rotations of the quadrupole or higher multipole moments of the nanoparticle are not coupled by the qubit.
In the experimentally realistic situation that the nanoparticle is almost homogeneously charged and inversion symmetric, its dipole moment is negligibly small (see “Methods”). The rotational and translational macromotion in the Paul trap (1) then decouple even for large quadrupole moments. The center-of-mass motion along the Paul trap axis further decouples from the transverse degrees of freedom, since only the motion towards the electrode is affected by the Cooper-pair box. The particle trapping potential in z-direction is slightly shifted and stiffened due to the charge qubit (with N ≠ 0), yielding the effective Hamiltonian
with charge energy Ec and coupling strength \(\kappa =2ekq/{C}_{\Sigma }{z}_{0}\sqrt{2M\hslash \omega }\), where the nanoparticle oscillation with frequency \({\omega }^{2}={\omega }_{z}^{2}+{q}^{2}{k}^{2}/{C}_{\Sigma }M{z}_{0}^{2}\) is described by the ladder operators a, a† (see “Methods”).
The Hamiltonian (4) demonstrates the important fact that the qubit can be used to generate quantum states as if the nanoparticle were non-rotating18,20,21,30. The absence of discrete internal transitions can thus be compensated by the nonlinearity provided by a superconducting circuit. The nanoparticle-qubit coupling strength is proportional to charge over square root mass, yielding appreciable coupling for highly charged nanoscale objects (see “Methods”).
Note that a finite bias voltage Udc applied to the ring electrode will not affect the Cooper-pair box, but produce an additional, approximately linear potential at the shifted trap center zs. It adds the term −Vext (a + a†) to (4), with \({V}_{{\rm{ext}}}=q{U}_{{\rm{dc}}}{z}_{s}\sqrt{\hslash /2M\omega {z}_{0}^{4}}\). This term will be used below to control the relative phase of the nanoparticle superposition state. The linear approximation is valid as long as the thermal width \(\sqrt{2{k}_{{\rm{B}}}T/M{\omega }^{2}}\) is much smaller than zs.
Generating and observing superpositions
Quantum interference of the nanoparticle motion on short timescales can now be performed by a rapid sequence of qubit rotations and measurements. At the beginning of the interference scheme, the charge qubit is prepared in its groundstate \(\left|N\right\rangle\), while the nanoparticle is cooled to temperature T, \({\rho }_{0}=\left|N\right\rangle \left\langle N\right|\otimes \exp (-\hslash \omega {a}^{\dagger }a/{k}_{{\rm{B}}}T)/Z\). After this initial state preparation Vext is switched to a constant value. The free dynamics governed by (4) with the external potential is then intersected by σx-rotations of the qubit at four different times:
-
(i)
a π/2-pulse at t = 0, which prepares the qubit in a superposition of charge states,
-
(ii)
a π-pulse at t = t1, which flips the qubit state,
-
(iii)
another π-pulse at t = t2, and
-
(iv)
a π/2-pulse at t = t3 with subsequent measurement of the qubit occupation σ+σ−.
With a symmetric pulse scheme, i.e. t1 = t3 − t2 = τ, it is always possible to find a Δτ ≡ t2 − t1 such that the nanoparticle state evolves into a superposition and then recombines with maximal overlap (see “Methods”). The corresponding phase-space trajectories are illustrated in Fig. 2. In this case, the particle motion is first entangled with the qubit, generating a motional quantum superposition. This superposition is then reversed by steps (ii) and (iii), and finally recombined, undoing the entanglement. Through this sequence, the phase imprinted on the nanoparticle motion through the external voltage Vext is transferred onto the qubit state and read-out via its population,
Varying Vext and observing the corresponding modulation of the qubit population can thus be used to verify that the nanoparticle existed in a spatial superposition state. The final population also oscillates as a function of the pulse time τ.
An initial π/2-pulse on the Cooper-pair box generates a charge superposition in the endcap electrodes, so that the charged nanoparticle feels a superposition of a spatially shifted and an unshifted harmonic potential. The time evolution (4) gives rise to two wave packets traveling on separate position and momentum trajectories. The corresponding classical trajectories are shown here. To verify this motional superposition state, the wave packets must be reunited. This can be achieved by applying two π-pulses, each interchanging the potentials felt by the two branches, in such a way that the trajectories finally coincide in position and momentum. (a) In the simplest case all pulses are separated by one sixth of the harmonic oscillation period and the particle is initially at rest. The π/2-pulse then leaves one branch unaffected (red dashed line), while the other one is accelerated (blue line). The first π-pulse accelerates the resting branch and decelerates the moving one to a standstill at the time of the second π-pulse. After that, the blue trajectory remains at rest while the red one is decelerated until it reaches the blue one with zero velocity. (b) Even for arbitrary pulse times τ the separation Δτ between the π-pulses can be chosen such that the corresponding paths in phase space coalesce for all initial states at 2τ + Δτ. (c) The scheme works for time durations much shorter than the oscillation period, which makes it particularly suitable for limited coherence times. In this short time limit the accelerations are essentially constant and Δτ = 2τ.
This pulse scheme enables the generation and observation of nanoscale quantum superpositions in harmonic potentials with pulse separations τ much shorter than the particle oscillation period. It is therefore applicable to various opto- and electromechanical systems20,30,31. The required accuracy of the pulse times, determined by the qubit frequency and the particle temperature T, must ensure that the phase κVext(2τ − Δτ)/\(\hbar\)ω is measurable.
To illustrate that nano- to microsecond motional superpositions can be realistically prepared and observed on the coherence timescale of a charge qubit39, we show in Fig. 3 the expected interference signal of a 106 amu particle at T = 1 mK. The nanoparticle is assumed to be cylindrically shaped, with a homogeneous surface charge of q = 200e and a realistic dipole moment (see “Methods”). It is stably levitated inside a sub-millimeter Paul trap, its motion well approximated by a harmonic oscillation with ω = 138 kHz. We find that the resulting strong coupling to the Cooper-pair box of κ = 16.8 MHz renders the nanoparticle particle sensitive to the presence or absence of a single Cooper-pair. A voltage of Udc = 25 V then suffices to imprint a relative phase on the motional superposition that shifts the interference pattern by a full fringe.
The Cooper-pair box occupation (24) shows a pronounced interference signal for experimentally realistic parameters if π-pulses are applied at t1 = 21.7 ns and t2 = 65.1 ns. The interfering trajectories then coalesce at 86.9 ns. (a) The envelope of the interference pattern is determined by the overlap of the two associated nanoparticle wave packets. Its width decreases with increasing temperature. Even at 1 mK, corresponding a mean phonon number of 945, more than a thousand fringes can be expected. We assume a qubit dephasing time of 1/γd = 100 ns, dominating all other decoherence mechanisms on the timescale of the experiment (see “Methods”). (b) The frequency of the interference signal is mainly determined by the charge energy Ec of the qubit. A bias voltage Udc = 5 V applied on the ring electrode imprints a phase on the nanoparticle, which shifts the interference pattern by about 2π/5 (dashed line).
Networking levitated nanoparticles
The proposed interference protocol can be extended to transfer qubit entanglement to nanoparticles. Levitated objects may thus be coherently integrated into superconducting quantum networks, e.g. for sensing and metrology applications. Here we illustrate how to entangle the nanoparticle with a second, separated charge qubit, or with another nanoparticle levitating in a distant Paul trap.
Entanglement of the nanoparticle with a second qubit is achieved by replacing the initial π/2-pulse with an operation that prepares a maximally entangled two-qubit state40,41. To verify the involvement of the particle in the nonlocal dynamics, one carries out the above interference protocol by performing all pulses on both qubits. During the pulse sequence one qubit is coupled to the nanoparticle, while the other qubit is isolated and can in principle be located at large distances. The occupation of the separated qubit, conditioned on having found the directly coupled one in the groundstate, is then given by
with χ = κ2/ω + 2κVext/\(\hbar\)ω − (Ec1 − Ec2)/\(\hbar\). This assumes that the qubits were initially prepared in the singlet state \(\left|{\Psi }^{-}\right\rangle\). The external potential Vext, acting only on the nanoparticle, thus serves to fully control the measurement outcome of the distant qubit. Having established that the coherent dynamics extends from the particle to the distant qubit, entangled states of these two systems can be produced by carrying out step (iv) and the subsequent measurement of the directly coupled qubit at t3 < 2τ + Δτ, i.e. before the particle wave packets overlap.
An all-electrical protocol to entangle two distant levitated nanoparticles works along the same lines: We consider two distant nanoparticle-qubit setups of identical frequency ω, where the qubits are again initially in the state \(\left|{\Psi }^{-}\right\rangle\). To verify the involvement of both particles in the nonlocal dynamics, one carries out the protocol on each nanoparticle-qubit setup until the time t3 = 2τ + Δτ of wave packet overlap. The occupation of the second qubit, conditioned on having found the first one in the groundstate, is then given by (6), with χ = χ1 − χ2, where \({\chi }_{i}={\kappa }_{i}^{2}/\omega +2{\kappa }_{i}{V}_{i}/\hslash \omega -{E}_{{\rm{c}}i}/\hslash\). The interference pattern thus depends on the difference of the local nanoparticle phases. By measuring both qubits before the wave packets overlap, e.g. at τ + Δτ < t3 < 2τ + Δτ the two oscillators can be projected onto an entangled motional state (see “Methods”).
Discussion
The coherent control of charged nanoparticles by superconducting qubits offers a new avenue for quantum superposition experiments with massive objects. The nanoparticle superposition state is generated and read-out by pulsed qubit rotations and measurements, enabling interference experiments on ultra-short time scales. All-electric trapping, cooling, and manipulation avoids photon scattering and absorption, the dominant decoherence sources in laser fields. In addition, the nanoparticle rotations decouple from the center-of-mass motion for realistic particle shapes and charge distributions, rendering this setup widely applicable. It holds the potential of bridging the mass gap in quantum superposition tests from current experiments with massive molecules42 to future guided interferometers with superconducting microscale particles43. Moreover, these hybrid quantum devices can serve as building blocks for larger networks connected by superconducting circuitry, distributing entanglement between multiple nanoparticles.
The presented qubit-nanoparticle coupling scheme is feasible with available technology for realistic particles. Beyond that, if it were possible to achieve qubit coherence times on the order of the oscillator period, the generation of more complex mechanical superposition states might become possible44. Similarly, combining qubit rotations with variable interaction times might enable implementing nonlinear phase gates acting on the nanoparticle state45. In addition, the degree of quantum control can be enhanced by fabricating particles with tailored dipole and quadrupole moments and by combining electric with optical techniques46,47,48,49. This may give rise to the observation of coherent effects between the rotational and translational nanoparticle degrees of freedom, and provide a platform for studying charge-induced decoherence in an unprecedented mass and complexity regime.
Methods
Ro-translational macromotion in a Paul trap
An arbitrarily charged nanoparticle moving and revolving at position R and orientation Ω in a hyperbolic Paul trap is subject to the time-dependent potential
with \({\mathsf{A}}\) = \({\mathbb{1}}\) − 3ez ⊗ ez. Here, the dipole moment p and the quadrupole tensor \({\mathsf{Q}}\) depend on the principal axes Ni of the nanoparticle with the associated moments of inertia Ii. The effective potential for the macromotion is obtained by setting R = r + ϵ, and Ni = ni + δ × ni, serving to separate the center-of-mass macromotion r from the much faster micromotion ∣ϵ∣ ≪ ∣r∣ varying with zero mean. Similarly, the rotational micromotion ∣δ∣ ≪ 1 varies much faster than ni. The center-of-mass and angular momentum obey
and
Taking macromotion to be approximately constant on the time scale of the micromotion and neglecting all small terms yields
and
The dipole and quadrupole moments here only include the macromotion, i.e. p = ∑pini and Q = ∑Qijni ⊗ nj, in contrast to (8A and 8B). The Mathieu parameter \({U}_{{\rm{ac}}}q/2M{\Omega }_{{\rm{ac}}}^{2}{z}_{0}^{2}\) and its rotational analogs \({U}_{{\rm{ac}}}| {\boldsymbol{p}}| /2M{\Omega }_{{\rm{ac}}}^{2}{z}_{0}^{2}{l}_{{\rm{cm}}}\), \({U}_{{\rm{ac}}}| {Q}_{\ell m}| /2{I}_{i}{\Omega }_{{\rm{ac}}}^{2}{z}_{0}^{2}\) and \({U}_{{\rm{ac}}}| {\boldsymbol{p}}| {l}_{{\rm{cm}}}/2{I}_{i}{\Omega }_{{\rm{ac}}}^{2}{z}_{0}^{2}\) in (8C and 8D) determine when the micromotion ϵ and δ is small. Here lcm is the length scale of the center-of-mass motion.
The effective force and torque of the macromotion can be obtained by inserting (8C and 8D) into (8A and 8B) and averaging over one micromotion cycle. A lengthy but straightforward calculation demonstrates that they can be expressed through the time-independent effective potential (1). We remark that the same potential (1) can also be derived quantum mechanically by adapting the method outlined in ref. 50 for the combined rotational and translational motion of the nanoparticle.
Generalized Shockley−Ramo theorem
To calculate the current induced by an arbitrary, rigidly bound charge distribution moving and rotating between the endcap electrodes we use Green’s reciprocity theorem,
It relates the particle charge density ρ, the electrode surface charge density σ and the electrostatic potential ϕ to those of a reference system. Choosing the reference system to have no particle in the trap volume \({\mathcal{V}}\), a vanishing potential on the ring electrode, and opposite potentials on the endcaps leads to an approximately linear potential ϕref near the trap center. This results in
where Q1 and Q2 are the total charges on the top and bottom endcap and x originates from the trap center. The remaining integration yields the capacitance charge Qind= (Q1 − Q2)/2 = −kez ⋅ (qr + p)/z0 + CV, and its time derivative the induced current.
Cooper-pair box-nanoparticle Hamiltonian
Figure 4 shows how the Paul trap is connected with the circuit. The latter consists of a superconducting loop with two Josephson junctions modeled as a capacitance CJ and a tunneling junction in parallel. The loop of vanishing inductance encloses an external magnetic flux Φ.
The tunable Cooper-pair box is coupled to the particle via the trap capacitor. The dashed line indicates the superconducting island from which Cooper pairs can tunnel onto the endcap electrode. The arrows indicate the direction of increasing electrostatic potential for positive U’s and of the electron flow for positive I’s.
The quantum state of the circuit is described by a macroscopic wave function whose phase jumps φ1, φ2 at the Josephson junctions satisfy φ2 − φ1 + 2πΦ/\(\hbar\) = 2πm with m an integer. Josephson’s equations \({I}_{{\rm{J}}i}={I}_{{\rm{c}}}\sin {\varphi }_{i}\) and \({U}_{{\rm{J}}i}=\frac{\hslash }{2e}\dot{{\varphi }_{i}}\) relate them to the tunneling current and the voltage drop in each junction i = 1, 2. The loop is coupled capacitatively to the endcaps via Cc, and can be controlled with the external voltage U, applied via the gate capacitance Cg. The circuit equations of motion can be obtained starting from Kirchhoff’s laws,
Inserting the capacitance charge (10) into (11A), differentiating with respect to time and using that Uci = Qci/Cc and that \(I=\dot{Q}_{\rm ind}={\dot{Q}}_{{\rm{c}}i}\) yields
with the effective capacitance Ceff = CCc/(Cc + 2C). In addition, (11B) and (11C) yield the relations
Inserting (12) and (13) into (14), using flux quantization, and defining φ = φ1 − eΦ/\(\hbar\) finally yields the circuit equation of motion,
with CΣ = Ceff + Cg + 2CJ.
The ro-translational motion of the particle is driven by the endcap voltage V via the force F = −kVqez/z0 and the torque N = kVez × p/z0, in addition to the Paul trap force and torque. In the relevant limit of large Cc the Hamiltonian generating the coupled dynamics of circuit and particle takes the form
where the canonical momentum Π conjugate to φ quantifies the number of Cooper pairs on the island and Hrb is the free rigid body Hamiltonian for the center-of-mass motion and rotation. Equation (16) involves the voltage-induced number of Cooper pairs \({n}_{{\rm{g}}}={C}_{{\rm{g}}}U/2e+\left(C+{C}_{{\rm{g}}}\right)\dot{\Phi }/4e\), and the Josephson energy \({E}_{{\rm{J}}}=\hslash {I}_{{\rm{c}}}\cos \left(e\Phi /\hslash \right)/e\).
We choose the flux Φ and applied voltage U so that the Cooper-pair box can be treated as an effective two-level system51 with N or N + 1 Cooper pairs on the island, Π = \(\hbar\)(N + σ+σ−). Tuning ng, EJ, and \(\dot{\Phi }\) to zero yields the Hamiltonian
which leaves the charge eigenstates of the box unaffected. The charge-dependent potential shift given by the second term yields the nanorotor-qubit coupling (3) and will drive the particle into a ro-translational superposition if the charge states are superposed.
Neglecting the dipole moment and separating the nanoparticle transverse motion and rotations finally yields (4) with the potential minimum shifted to zs = 2ekNq/CΣz0Mω2 and the charge energy Ec = 2e2(1 + 2N − kqzs/ez0)/CΣ.
Time evolution and measurement outcome
The time evolution generated by (4) with external potential Vext can be written, up to a global phase, as a combination of a qubit-dependent phase, qubit-dependent particle displacements and the free time evolution of the harmonic oscillator,
The qubit is initially prepared in its groundstate while the nanoparticle is in a thermal state of temperature T. A π/2-pulse rotates the qubit into the superposition \(\left(\left|N\right\rangle +i\left|N+1\right\rangle \right)/\sqrt{2}\), so that the system after time t is given by \({\rho }_{t}=\mathop{\sum }\nolimits_{n = 0}^{\infty }\exp \left(-\hslash \omega n/{k}_{{\rm{B}}}T\right)\left|{\Psi }_{n}\right\rangle \left\langle {\Psi }_{n}\right|/Z\) with \(\left|{\Psi }_{n}\right\rangle =\left(\left|N\right\rangle {U}_{{\rm{g}}}(t)+i\left|N+1\right\rangle {U}_{{\rm{e}}}(t)\right)\left|n\right\rangle /\sqrt{2}\). This involves particle time-evolution operators associated with the ground and the excited state of the qubit,
and
where \({\mathsf{D}}(\alpha)=\exp \left(\alpha {{\mathsf{a}}}^{\dagger }-{\alpha }^{* }{\mathsf{a}}\right)\) is the displacement operator. The scheme with π-pulses at times t1 and t2 then results in \(\left|{\Psi }_{n}\right\rangle =\left(\left|N\right\rangle {{\mathsf{U}}}_{+}+i\left|N+1\right\rangle {{\mathsf{U}}}_{-}\right)\left|n\right\rangle /\sqrt{2}\) at time t3, where
The charge occupation of the box after a final π/2-pulse is thus given by
Noting that \({{\mathsf{U}}}_{+}^{\dagger }{{\mathsf{U}}}_{-}\) displaces the particle state in phase space and using
one obtains
where \(d({t}_{1},{t}_{2},{t}_{3})=2{e}^{i\omega {t}_{1}}-2{e}^{i\omega {t}_{2}}+{e}^{i\omega {t}_{3}}-1\). Qubit dephasing is the dominant decoherence mechanism in Fig. 3 and is modeled by taking ng in (16) to be a random number with Lorentzian distribution of width γdCΣ\(\hbar\)/(2e)2. This effectively modifies the charge energy and thus the qubit oscillation frequency between the pulses, resulting in an exponential factor \(\exp (-{\gamma }_{{\rm{d}}}{t}_{3})\) multiplied to the second term in (24).
Equation (24) shows that the envelope of the qubit occupation assumes its maximum at d(t1, t2, t3) = 0 and that the particle temperature determines the width of the peak. Operating the interference protocol at the point of maximal envelope (corresponding to a maximal overlap in the particle state of both superposition branches) can be achieved with the symmetric choice t1 = τ, t2 = τ + Δτ and t3 = 2τ + Δτ, where
and τ < π/ω. Evaluating (24) for these times finally yields (5).
Generation of nanoparticle entanglement
The time evolution involving two nanoparticles can be described by means of the respective particle operators
where the Di are phase-space displacement operators acting on nanoparticle i.
To entangle the particles one prepares the qubits in a Bell state and performs the trapped interference scheme on both subsystems. Measuring both qubits before the wave packets overlap, e.g. at τ + Δτ < t3 < 2τ + Δτ projects the two oscillators onto the outcome-conditioned state
where
The amplitudes αi, βi and the phase \(\phi ={\phi }_{-}^{(1)}+{\phi }_{+}^{(2)}-{\phi }_{+}^{(1)}-{\phi }_{-}^{(2)}\) depend on the pulse times, whereas the sign in (28) is fixed by the outcome of the qubit measurements. The values of αi and βi determine the amount of entanglement of the state (27), as quantified by a suitable entanglement measure.
Experimental parameters
For calculating the interference pattern in Fig. 3 we consider a cylindrically shaped silicon nanoparticle (diameter of 4.7 nm, length of 42 nm, homogeneously and positively charged with q = 200 e 52. A 106 amu particle with this charge exhibits the same coupling strength as a doubly charged strontium ion. The proposed interference scheme works also for other particle shapes with appropriately adjusted trap and circuit parameters.
We assume a dipole moment of ∣p∣ = 200 eÅ, motivated by randomly distributing charges on the cylinder surface and accounting for the opposed internal polarization field induced by the charges. This dipole moment is well within the regime where rotations are negligible (see below), and exceeds reported values of a few 10 eÅ for neutral particles of the same size53,54,55,56.
The Paul trap, with an endcap distance of 2z0 = 0.5 mm and geometry factor k = 0.4 29,57, is driven by an AC voltage of Uac = 1 kV with frequency Ω = 2π × 250 MHz 58.
The empty Cooper-pair box has a capacitance of CΣ = 4.4 fF, yielding a charge energy of 2e2/CΣ ≈ 72 μeV. A relatively high occupation N = 10 shifts the potential minimum by the distance zs = 1.17 μm from the trap center. The fast box oscillations then require a measurement time resolution on the ps-scale51. The total duration of the experiment of 87 ns is on the expected coherence time scale of a charge qubit39. Specifically, qubit dephasing with timescale 1/γd = 100 ns decreases the visibility by 60% (see Fig. 3). Other decoherence sources such as gas collisions, black-body scattering, or thermal emission can be neglected on the short time scale of the experiment (see Supplementary Note II). For instance, on average only 0.016 gas collisions occur during the pulse sequence in a room-temperature nitrogen gas at 10−4 mbar.
An initial motional temperature of the particle of T = 1 mK can be achieved via resistive cooling29,59,60 (and potentially by electric feedback cooling29,46,47 or optical techniques8). Assuming a resistance of R = 100 MΩ, the adiabatic cooling rate is 163 Hz, corresponding to 1.54 × 105 quanta per second in thermal equilibrium. Surface noise61 for the present system with endcap electrodes at 77 K would yield a particle heating rate of 170 \(\hbar\)ω/s, which does not noticeably raise the temperature or lead to decoherence on the time scale of the experiment.
Impact of dipole moments
In the effective potential (1) the initial thermal state shows no correlations between rotations and center-of-mass motion at mK temperatures, because even a dipole moment of 2000 eÅ suppresses all coupling terms. In addition, these rotational and translational coupling terms can also be neglected compared to the direct rotation-qubit interaction with rate κrot = ek∣p∣/\(\hbar\)z0CΣ; see Eq. (3). Approximating the cylinder as a linear rotor and ignoring the kinetic terms due to the large moment of inertia yields that the rotations affect the measurement outcome by (i) adding a phase to the cosine function in (24), which is negligible since q2/M ≫ ∣p∣2/I, and by (ii) reducing the contrast of the interference signal, which can be conservatively estimated as sinc[2κrot(2t1 − 2t2 + t3)]. This reduction is negligibly small for the proposed setup (see Supplementary Note I).
References
Rossi, M., Mason, D., Chen, J., Tsaturyan, Y. & Schliesser, A. Measurement-based quantum control of mechanical motion. Nature 563, 53 (2018).
Ockeloen-Korppi, C. et al. Stabilized entanglement of massive mechanical oscillators. Nature 556, 478 (2018).
Riedinger, R. et al. Remote quantum entanglement between two micromechanical oscillators. Nature 556, 473 (2018).
Pikovski, I., Vanner, M. R., Aspelmeyer, M., Kim, M. & Brukner, Č. Probing Planck-scale physics with quantum optics. Nat. Phys. 8, 393 (2012).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
Khosla, K. E., Vanner, M. R., Ares, N. & Laird, E. A. Displacemon electromechanics: how to detect quantum interference in a nanomechanical resonator. Phys. Rev. X 8, 021052 (2018).
Millen, J., Monteiro, T. S., Pettit, R. & Vamivakas, A. N. Optomechanics with levitated particles. Rep. Prog. Phys. 83, 026401 (2020).
Delić, U. et al. Cooling of a levitated nanoparticle to the motional quantum ground state. Science 367, 892–895 (2020).
Romero-Isart, O. et al. Large quantum superpositions and interference of massive nanometer-sized objects. Phys. Rev. Lett. 107, 020405 (2011).
Bateman, J., Nimmrichter, S., Hornberger, K. & Ulbricht, H. Near-field interferometry of a free-falling nanoparticle from a point-like source. Nat. Commun. 5, 4788 (2014).
Wan, C. et al. Free nano-object Ramsey interferometry for large quantum superpositions. Phys. Rev. Lett. 117, 143003 (2016).
Stickler, B. A. et al. Probing macroscopic quantum superpositions with nanorotors. New J. Phys. 20, 122001 (2018).
Ma, Y., Khosla, K. E., Stickler, B. A. & Kim, M. Quantum persistent tennis racket dynamics of nanorotors. Phys. Rev. Lett. 125, 053604 (2020).
Romero-Isart, O. et al. Optically levitating dielectrics in the quantum regime: theory and protocols. Phys. Rev. A 83, 013803 (2011).
Millen, J., Deesuwan, T., Barker, P. & Anders, J. Nanoscale temperature measurements using non-equilibrium brownian dynamics of a levitated nanosphere. Nat. Nanotechnol. 9, 425 (2014).
Hebestreit, E., Reimann, R., Frimmer, M. & Novotny, L. Measuring the internal temperature of a levitated nanoparticle in high vacuum. Phys. Rev. A 97, 043803 (2018).
Reed, A. et al. Faithful conversion of propagating quantum information to mechanical motion. Nat. Phys. 13, 1163–1167 (2017).
LaHaye, M., Suh, J., Echternach, P., Schwab, K. C. & Roukes, M. L. Nanomechanical measurements of a superconducting qubit. Nature 459, 960–964 (2009).
O’Connell, A. D. et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 464, 697 (2010).
Scala, M., Kim, M., Morley, G., Barker, P. & Bose, S. Matter-wave interferometry of a levitated thermal nano-oscillator induced and probed by a spin. Phys. Rev. Lett. 111, 180403 (2013).
Yin, Z.-q, Li, T., Zhang, X. & Duan, L. Large quantum superpositions of a levitated nanodiamond through spin-optomechanical coupling. Phys. Rev. A 88, 033614 (2013).
Pflanzer, A. C., Romero-Isart, O. & Cirac, J. I. Optomechanics assisted by a qubit: from dissipative state preparation to many-partite systems. Phys. Rev. A 88, 033804 (2013).
Pedernales, J. S., Morley, G. W. & Plenio, M. B. Motional dynamical decoupling for interferometry with macroscopic particles. Phys. Rev. Lett. 125, 023602 (2020).
Millen, J., Fonseca, P., Mavrogordatos, T., Monteiro, T. & Barker, P. Cavity cooling a single charged levitated nanosphere. Phys. Rev. Lett. 114, 123602 (2015).
Shockley, W. Currents to conductors induced by a moving point charge. J. Appl. Phys. 9, 635–636 (1938).
Dehmelt, H. & Walls, F. “Bolometric” technique for the rf spectroscopy of stored ions. Phys. Rev. Lett. 21, 127 (1968).
Cornell, E. A. et al. Single-ion cyclotron resonance measurement of M(CO+)/M(N2+). Phys. Rev. Lett. 63, 1674 (1989).
Tian, L., Rabl, P., Blatt, R. & Zoller, P. Interfacing quantum-optical and solid-state qubits. Phys. Rev. Lett. 92, 247902 (2004).
Goldwater, D. et al. Levitated electromechanics: all-electrical cooling of charged nano-and micro-particles. Quantum Sci. Technol. 4, 024003 (2018).
Armour, A., Blencowe, M. & Schwab, K. C. Entanglement and decoherence of a micromechanical resonator via coupling to a cooper-pair box. Phys. Rev. Lett. 88, 148301 (2002).
Delord, T. et al. Ramsey interferences and spin echoes from electron spins inside a levitating macroscopic particle. Phys. Rev. Lett. 121, 053602 (2018).
Delord, T., Huillery, P., Nicolas, L. & Hétet, G. Spin-cooling of the motion of a trapped diamond. Nature 580, 56–59 (2020).
Kuhn, S. et al. Optically driven ultra-stable nanomechanical rotor. Nat. Commun. 8, 1670 (2017).
Ahn, J. et al. Optically levitated nanodumbbell torsion balance and GHz nanomechanical rotor. Phys.Rev. Lett. 121, 033603 (2018).
Reimann, R. et al. GHz rotation of an optically trapped nanoparticle in vacuum. Phys. Rev. Lett. 121, 033602 (2018).
Bang, J. et al. Five-dimensional cooling and nonlinear dynamics of an optically levitated nanodumbbell. Phys. Rev. Res. 2, 043054 (2020).
Makhlin, Y., Schön, G. & Shnirman, A. Quantum-state engineering with Josephson-junction devices. Rev. Mod. Phys. 73, 357 (2001).
Xiang, Z.-L., Ashhab, S., You, J. & Nori, F. Hybrid quantum circuits: superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 85, 623 (2013).
Houck, A. A., Koch, J., Devoret, M. H., Girvin, S. M. & Schoelkopf, R. J. Life after charge noise: recent results with transmon qubits. Quantum Inf. Process. 8, 105–115 (2009).
Yamamoto, T., Pashkin, Y. A., Astafiev, O., Nakamura, Y. & Tsai, J.-S. Demonstration of conditional gate operation using superconducting charge qubits. Nature 425, 941 (2003).
Rodrigues, D., Jarvis, C., Györffy, B., Spiller, T. & Annett, J. Entanglement of superconducting charge qubits by homodyne measurement. J. Phys.: Cond. Mat. 20, 075211 (2008).
Fein, Y. Y. et al. Quantum superposition of molecules beyond 25 kDa. Nat. Phys. 15, 1242–1245 (2019).
Pino, H., Prat-Camps, J., Sinha, K., Venkatesh, B. P. & Romero-Isart, O. On-chip quantum interference of a superconducting microsphere. Quantum Sci. Technol. 3, 025001 (2018).
Flühmann, C. et al. Encoding a qubit in a trapped-ion mechanical oscillator. Nature 566, 513–517 (2019).
Park, K., Marek, P. & Filip, R. Deterministic nonlinear phase gates induced by a single qubit. New J. Phys. 20, 053022 (2018).
Tebbenjohanns, F., Frimmer, M., Militaru, A., Jain, V. & Novotny, L. Cold damping of an optically levitated nanoparticle to microkelvin temperatures. Phys. Rev. Lett. 122, 223601 (2019).
Conangla, G. P. et al. Optimal feedback cooling of a charged levitated nanoparticle with adaptive control. Phys. Rev. Lett. 122, 223602 (2019).
Dania, L., Bykov, D. S., Knoll, M., Mestres, P. & Northup, T. E. Optical and electrical feedback cooling of a silica nanoparticle in a Paul trap. Preprint at https://arxiv.org/abs/2007.04434 (2020).
Bullier, N., Pontin, A. & Barker, P. Characterisation of a charged particle levitated nano-oscillator. J. Phys. D Appl. Phys. 53, 175302 (2020).
Cook, R. J., Shankland, D. G. & Wells, A. L. Quantum theory of particle motion in a rapidly oscillating field. Phys. Rev. A 31, 564 (1985).
Nakamura, Y., Pashkin, Y. A. & Tsai, J. Coherent control of macroscopic quantum states in a single-Cooper-pair box. Nature 398, 786 (1999).
Draine, B. & Sutin, B. Collisional charging of interstellar grains. Astrophys. J. 320, 803–817 (1987).
Li, L.-s. & Alivisatos, A. P. Origin and scaling of the permanent dipole moment in CdSe nanorods. Phys. Rev. Lett. 90, 097402 (2003).
Shanbhag, S. & Kotov, N. A. On the origin of a permanent dipole moment in nanocrystals with a cubic crystal lattice: effects of truncation, stabilizers, and medium for CdS tetrahedral homologues. J. Phys. Chem. B 110, 12211–12217 (2006).
Shim, M. & Guyot-Sionnest, P. Permanent dipole moment and charges in colloidal semiconductor quantum dots. J. Chem. Phys. 111, 6955–6964 (1999).
Yan, W., Li, S., Zhang, Y., Yao, Q. & Tse, S. D. Effects of dipole moment and temperature on the interaction dynamics of titania nanoparticles during agglomeration. J. Phys. Chem. C 114, 10755–10760 (2010).
Itano, W. M., Bergquist, J. C., Bollinger, J. J. & Wineland, D. J. Cooling methods in ion traps. Phys. Scr. 1995, 106 (1995).
Jefferts, S. R., Monroe, C., Bell, E. & Wineland, D. J. Coaxial-resonator-driven rf (Paul) trap for strong confinement. Phys. Rev. A 51, 3112 (1995).
Clark, A., Schwarzwälder, K., Bandi, T., Maradan, D. & Zumbühl, D. Method for cooling nanostructures to microkelvin temperatures. Rev. Sci. Instrum. 81, 103904 (2010).
Iftikhar, Z. et al. Primary thermometry triad at 6 mK in mesoscopic circuits. Nat. Commun. 7, 12908 (2016).
Lakhmanskiy, K. et al. Observation of superconductivity and surface noise using a single trapped ion as a field probe. Phys. Rev. A 99, 023405 (2019).
Acknowledgements
L.M., K.H., and B.A.S. acknowledge funding from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—411042854. B.A.S. acknowledges funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodovska-Curie grant agreement no. 841040. M.S.K. thanks the Royal Society, the UK EPSRC (EP/R044082/1) and KIST Open Research Program. J.M. is supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement no. 803277), and by EPSRC New Investigator Award EP/S004777/1.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
All authors contributed conceptually to the proposal. L.M., K.H., and B.A.S. performed the analytic calculations and wrote the manuscript with input from J.M. and M.S.K.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Martinetz, L., Hornberger, K., Millen, J. et al. Quantum electromechanics with levitated nanoparticles. npj Quantum Inf 6, 101 (2020). https://doi.org/10.1038/s41534-020-00333-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-020-00333-7
This article is cited by
-
Stroboscopic high-order nonlinearity for quantum optomechanics
npj Quantum Information (2021)
-
Quantum rotations of nanoparticles
Nature Reviews Physics (2021)