Abstract
Two-dimensional nuclear magnetic resonance (NMR) is indispensable to molecule structure determination. Nitrogen-vacancy center in diamond has been proposed and developed as an outstanding quantum sensor to realize NMR in nanoscale or even single molecule. However, like conventional multi-dimensional NMR, a more efficient data accumulation and processing method is necessary to realize applicable two-dimensional (2D) nanoscale NMR with a high spatial resolution nitrogen-vacancy sensor. Deep learning is an artificial algorithm, which mimics the network of neurons of human brain, has been demonstrated superb capability in pattern identifying and noise canceling. Here we report a method, combining deep learning and sparse matrix completion, to speed up 2D nanoscale NMR spectroscopy. The signal-to-noise ratio is enhanced by 5.7 ± 1.3 dB in 10% sampling coverage by an artificial intelligence protocol on 2D nanoscale NMR of a single nuclear spin cluster. The artificial intelligence algorithm enhanced 2D nanoscale NMR protocol intrinsically suppresses the observation noise and thus improves sensitivity.
Similar content being viewed by others
Introduction
Molecular structure analysis is the cornerstone of biology, chemistry, and medicine. Among three vastly used techniques for structure analysis, X-ray, electron microscopy, and nuclear magnetic resonance (NMR), NMR is the most promising technique to reveal the structure information with nondestructive detection in the room temperature under living condition. However, the conventional NMR relies on a large scale of molecule ensembles to obtain sufficient signal-to-noise ratio (SNR), which loses some individual information of single molecule. Thus, there is an urgent need for single molecular structure analysis by a more sensitive, non-label, and living-condition-compatible NMR method. Thank to high sensitive atomical-scale nitrogen-vacancy (NV) centers1,2, nanoscale magnetic resonance spectroscopy has been developed rapidly over the past years. Single spin sensitivity NMR3, single-molecule magnetic resonance4,5, and microscopic 2D NMR6 have been realized with NV centers. While these works on nanoscale NMR make it possible to provide an insight into molecule structure, 2D nanoscale NMR7,8 is a crucial step. Although 2D NMR reveals much more information of the spectrum, the measuring times of the two-dimensional NMR increase quadratically with sampling numbers.
Thus, there is a compelling need to speed up 2D nanoscale NMR. Both compressive sensing and sparse approximation has been used in conventional9,10,11,12 and nanoscale3,13,14 magnetic resonance. However, compressive sensing is based on the prior knowledge of additional information to effectively recover the measured data13. And the sparse approximation, which is used to accelerate 2D NMR spectroscopy13, may not well handle the case with very low sampling coverage15, has limited speed-up capacity.
Deep learning (DL), using multi-layered artificial neural networks, which mimics the network of neurons of the human brain, has been demonstrated superb capability in super-resolution imaging16, imaging denoising17, inpainting, and completion18. Recently, deep learning has also been applied in the physics field, e.g. mitigating effects of noise in nano-NMR14 and characterizing states and charge configurations of semiconductor quantum dot arrays19. The success of DL stems from its capability of learning complex non-linear models from a large training dataset, which enables it to learn superhuman proficiency to recognize special patterns in the two-dimensional spectrum. For 2D NV spectrum map reconstruction, this means a large amount of full-resolution spectra from experiments should be provided.
However, data acquisition is highly time-consuming for now, which hinders training deep neural networks on real experimental data. Due to the lack of experimental training data, to leverage the power of DL for 2D NV spectrum map reconstruction, we have to turn to an alternative: using simulation data for DL network training. This yet may generally introduce the domain shift problem20, i.e. the distribution of the simulated data could be different from that of real experimental data, causing reduced quality of the reconstructed NV spectrum map. In addition, the DL network may not be able to well capture the global low-rank feature of the NV spectrum map.
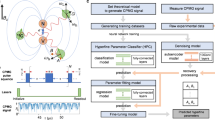
Inspired by unobserved entries fill strategy21,22 and matrix completion based domain adaptation23,24,25, we propose to combine the deep learning network with the matrix completion algorithm15 to develop our DLMC method for efficient NV spectrum map reconstruction. DL can learn very complex non-linear mapping from a partially filled spectrum map to its full-resolution map, with the DL network trained with simulation data; while the traditional matrix completion (MC) method is used for post-processing the DL output map to keep its low-rank property, thus further alleviate the domain shift problem. In our experiment, we adopt this method to recover the missing entries from a partially sampled 2D NV spectrum map (Fig. 1a), which largely enhances the experiment efficiency. Compared with the MC method and the barely DL method, our speed-up protocol can reconstruct the experiment data with very low sampling ratio and no domain shift (Fig. 1b).
a NV center is a state-of-art quantum NMR spectrometer. A single NV center (red) is fabricated underneath several nanometers from diamond surface while a target molecule is placed on the surface. 2D NMR method can help to reveal the molecule structure in nanoscale. Artificial intelligence is able to recover full spectrum from sparse sampled experiment data. b Illustration of the proposed DLMC method and the MC method when the sampling ratio is low. Here we use the topological isomorphism as a metaphor indicating whether there exist possible legitimate mappings between different data manifolds. The combined deep-learning-matrix-completion (DLMC) method is immune from both drawbacks.
Here we present the proposed DLMC method for 2D NV spectrum map reconstruction based on deep learning (DL) and the classical matrix completion method (MC).
Results
Deep learning network construction
The deep learning network is a trained convolutional neural network (CNN) for the 2D NMR map reconstruction, including the CNN architecture, training data generation and network training. The DLNet is trained with simulated 2D NMR spectra (see “Methods” for detail).
A deep learning encoder-decoder convolutional neural network (DLNet) was utilized for the 2D NV spectrum map reconstruction, which is demonstrated in Fig. 2a. The encoder (the left half part) consists of a sequence of six groups of convolutional layers for image feature extraction. The first group contains one convolutional layer with 32 kernels. The next four groups have a similar architecture, each of which contains a residual (Res) block followed by a learnable pooling layer. Each Res block consists of a stack of one convolution layer, a rectified linear unit (ReLU) layer, followed by another convolution layer, an element-wise sum layer, and a ReLU layer. The pooling layer in each group reduces the size of the feature image output by the group, enabling more global views of the NV spectrum map. On the other hand, this pooling operations cause the loss of resolution. The number of kernels used in each convolutional layer in the second group is 32. To compensate for the resolution loss, from the 3rd to 4th group, the number of kernels used in the convolutional layers is doubled from the previous group. The 6th group contains a Res block with 512 kernels used in each convolution layer.
The experiment was performed on the time domain. a DLNet architecture. One encoder-decoder convolutional neural network (CNN) was chosen here. In the encoder (left half) part, a sequence of hierarchical filters was utilized to recognize the image features, enabling to encode the global structure of the correlation maps in the neural network. In the decoder (right half) part, contrary operations were performed. The network was trained by simulated data. b The schematic configuration for building blocks. Details for each building blocks can be found in “Methods” and Fig. 8. c The DLNet is trained on the simulated data. The dotted line denotes the back propagation.
The output feature images of the encoder then flow into the decoder (the right half part in Fig. 2a), which consists of 5 sequential groups of convolutional layers. Except for the last group, which contains a single convolution layer, each group contains a transposed convolution layer (Trans conv) followed by a Res block. The serial of transposed convolution operations helps recover the solution of the NV spectrum map. With the resolution recovered, the number of kernels used in convolution layers of the groups is reduced by half from one group to the next, as shown in Fig. 2a.
In addition, to preserve detailed image information and to alleviate the gradient vanishing problem, horizontal skipping connections (Skipping conn) are added between the corresponding layers of the same resolution between the encoder and the decoder (Fig. 2a). All convolution layers have the same kernel size of 3 × 3 with a stride of 1 and padding of 1. All the pooling layers and transposed convolution layers have the same kernel size of 2 × 2 with a stride of 2. The output of the decoder is the reconstructed 2D NV spectrum map.
The building blocks for our proposed DLNet, convolution layers, pooling layers, ReLU activation layers, and transposed convolution layers compose a deep learning convolutional neuron network (DLNet). The tremendous success of CNNs is due to its capacity of learning rich multi-resolutional features from training data, accomplished through recipes of combining convolutions and poolings. Our proposed DLNet learns a variety of kernels (shape templates) of different patterns and different sizes. Those templates allow DLNet encode an NV spectrum map into a rich set of multi-resolutional feature responses, which represent spatial and hierarchical distribution of various patterns in the spectrum map, providing highly predictive visual cues for sparse reconstruction. Illustrations of each building blocks can be found in Fig. 2b.
The proposed DLNet was trained on the simulated data. The process of training is illustrated in Fig. 2c. The original simulated NV spectrum map is of size 50 × 50. For simplicity, we padded the map to have a size of 64 × 64. We also normalized all map entries to the range of [0, 1], and manually added Gaussian noise with zero mean and 0.1 standard deviation. The sparsely sampled normalized map \({{\mathcal{M}}}_{{\rm{sim}}}\) and its corresponding sampling matrix were concatenated in channel dimension and fed into the proposed DLNet. At the output end, a reconstructed spectrum map \({\rm{DL}}({{\mathcal{M}}}_{{\rm{sim}}})\) with a full resolution is generated. For training, we utilized an L1 loss for back propagation. The Adam optimizer with a learning rate 5 × 10−4 was chosen. The training process ran for 500 epochs.
Combination of DL and MC
However, the output of DLNet may be biased to training data. Specially, we propose to utilize traditional MC method to post-process the output of DLNet. In this way, helpful information provided by DLNet can be used, and also domain shift problem can be relieved. The proposed DLMC algorithm for the 2D NV spectrum map reconstruction with low data sampling coverage consists of two steps, as shown in the Fig. 3. The first step is to utilize the trained DLNet to reconstruct a full-resolution spectrum map, denote by \({\rm{DL}}({\mathcal{M}})\), from an input partially sampled map \({\mathcal{M}}\in {{\mathbb{R}}}^{n\times n}\). The pipeline is illustrated in Fig. 4. As DLNet is trained on simulated NV spectra, the output full-resolution spectrum map \({\rm{DL}}({\mathcal{M}})\) is subject to the data distribution of the simulated data, which could be subtly different from that of the experimental spectrum maps. In addition, our experiments show that DLNet did not well capture the low rank property of the NV spectrum map. Thus, as the second step of our DLMC method, we make use of the traditional MC algorithm to post-process the output spectrum map \({\rm{DL}}({\mathcal{M}})\) of DLNet to enhance the low-rank of \({\rm{DL}}({\mathcal{M}})\), further improving the domain adaptation.
The trained DLNet is utilized to generate the reconstruction, followed by the classical matrix completion algorithm (MC) for post-processing of the reconstructed spectrum map to produce the final prediction. For clarity, the reconstructions of experiment data are demonstrated in the frequency domain.
The singular value thresholding (SVT) algorithm15, which is one of the classical MC methods, is utilized as a post processing to realize the low-rank property of the reconstructed map. Due to its efficiency, simplicity of implementation, and guaranteed convergence, SVT has been widely used for matrix completion. The while loop in Fig. 3 presents the major steps of the SVT algorithm, in which τ is a user defined singular value threshold and σ is the step size. Note that \({\mathcal{M}}\) is the input partially sampled matrix (an NV spectrum map), whose sampled locations are denoted by Ω, that is, for any (i, j) ∉ Ω, \({{\mathcal{M}}}_{ij}\) is unknown. The reconstruction error for the known entries in \({\mathcal{M}}\) is defined as \(| | {{\mathcal{P}}}_{\Omega }({\mathcal{M}}-X)| {| }_{\text{F}}/| | {{\mathcal{P}}}_{\Omega }({\mathcal{M}})| {| }_{\text{F}}\), where \({{\mathcal{P}}}_{\Omega }(A)\) is equal to Aij if (i, j) ∈ Ω and null otherwise, and ∣∣ ⋅ ∣∣F is Frobenius norm. ϵ is a user defined tolerance of the reconstruction error. The loop starts from singular value decomposition of \({\rm{DL}}({\mathcal{M}})\), and then thresholds the singular matrix in step 6, followed by the generation of a new reconstruction X(k). Step 7 is used to compensate the changes of the sample entries induced by the SVT computation.
Experiment with AI enhancement
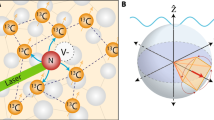
The nanoscale 2D NMR spectroscopy is performed on a coupled nuclear cluster probed by quantum NV sensor7. The system is controlled by the COSY protocol (Fig. 5a) to reveal the coupling between two nuclear spins. The system is a coupled nuclear spin dimer and the NV sensor inside a diamond. The external magnetic field is 158 mT along the main axis of NV sensor. The evolution of the coupled nuclear spin dimer is readout by the correlation sequence on the NV sensor. The nuclear spins are firstly initialized to the x–y plane of Bloch sphere. Secondly, the system evolves freely for time t1. Then a half π is performed on the nuclear spin. In our experiment, the half π pulse is carried on through coherent control of NV sensor. However, it can be realized by RF pulse without loss of generality of our nanoscale 2D NMR method. After a second free evolution time t2, the final result is then readout by NV sensor. Both time parameters t1 and t2 are swept from 4 μs to 0.9 ms to get 2D NMR spectrum, the spectrum matrix is shown in Fig. 5c. Each entry of the spectrum matrix is an average of the 1.5 × 105 measurement readouts. The artificial intelligence DLMC algorithm is utilized here to improve data acquisition efficiency. The intrinsic bias problem of the deep learning algorithm is alleviated while combined with the matrix completion method. As shown in Fig. 5d, the result obtained by the DLMC algorithm on the 40% sampled data shows less noise and resonant peaks in the upper-right corner compared to the MC-only method. For the 10% sampled data (Fig. 5e), the MC-only method fails to recover the spectrum while DLMC is still able to recover the spectrum. From the residual analysis, the spectrum processed by DLMC on the 10% sampled data has fewer residuals compared to the spectrum recovered by the MC-only method from the 40% sampled data. Thus, the performance of DLMC on the 10% sampled data is better than that of the MC-only method on the 40% sampled data. The sampled data was generated by a randomly generated mask for each sampling coverage.
a Control protocols for 2D nanoscale NMR spectrum, it is in analog to the conventional COSY sequence. The nuclear spin evolution on Bloch sphere is also shown here. b The spatial configuration of the NV sensor (red) and nuclear spins (green). c The 2D nanoscale spectrum in time domain. The data is adopted from ref. 7. d The spectrum reconstructed by DLMC and MC method from 40% sampled data. Both can recover the 2D spectrum. e The spectrum reconstructed by DLMC and MC method from 10% sampled data. DLMC succeeds to recover 2D spectrum while MC-only fails.
Discussion
To evaluate the performance of our method, we calculate the signal to noise ratio (SNR) and root mean square error (RMSE) in frequency domain to analyze both relative and absolute noise. In order to calculate the SNR we take the maximal signal of [21.9, 21.9] kHz, [23.5, 21.9] kHz, [21.9, 23.5] kHz, [23.5, 23.5] kHz peaks and compare them with the mean amplitude of a blank region which doesn’t contain peaks. Due to the long acquisition time, we only acquire 80% of the 50 × 50 spectrum matrix in the time domain. Each experimental spectrum in the time domain is normalized to the range of [0, 1], as in the DLNet training. The proposed DLMC method is compared to the MC method15, the DL alone method (with no MC post-processing), and the trivial method of recovering the missing entries with the mean of their observed neighbors (which is denoted by orig).
The calculated results are demonstrated in Fig. 6. In order to quantify the signal to noise ratio (SNR), the maximum of the peaks and standard deviation of other spectrum region are calculated. As seen from the result, the DLMC method has the best SNR for most cases. Compared to the FFT result of the original data, the SNR is enhanced by 5.7 ± 1.3 dB, while the MC method enhance only 3.2 ± 3.1 dB. However, DLMC worked similarly to DL-only and outperformed the other two methods because here SNR neglecting the noise of the concerned peak regions. With the analysis of RMSE (Fig. 6b), which evaluates the overall fidelity between the original and reconstruction spectrum, our DLMC method has the best performance. The results show clearly that even for a spectrum matrix with a sampling coverage of only 10%, our DLMC method has the capability to reconstruct from sparse data with higher SNR and lower RMSE compared to the MC-only method while applying on a spectrum matrix with a sampling coverage of 40%. As the DLMC method maintains the SNR and RMSE while the sampling coverage decrease from 80% to 10%, the bond length sensitivity would be enhanced from 0.8 nm/\(\sqrt{{\rm{Hz}}}\)7 to 0.3 nm/\(\sqrt{{\rm{Hz}}}\).
Although our DLMC method has the best performance in SNR and to eliminate distortions compare with other methods (Figs. 5d, e, 6, and 10), there’re still visible artifacts and amplitude distortion in the reconstruction spectrum, especially in low sampling coverage case. However, incorporation of some other metrics like structural similarity index measure (SSIM)26 in the loss function to train the DLNet using the training datasets, it’s possible to further reduce signal distortions in the reconstructed spectrum maps. Furthermore, the proposed DLNet can be trained with a simulated dataset7 consisting of instances with different peaks. This arms the trained DLNet with the capacity of reconstructing NV spectrum maps with different number of peaks. The postprocessing MC algorithm can naturally deal with arbitrary peaks. Thus, our DLMC method is well feasible to scale to multiple peaks. Moreover, special sampling schemes27,28,29,30 can jointly optimize the sampling pattern and the proposed DLNet to further improve the NV spectrum map reconstruction. Overall, in the future, combined with conventional signal processing method like filtering function, special sampling schemes and GFT10, it’s possible for our DLMC method to handle more complicated and high-dimensional nanoscale NMR spectroscopy experiments.
In conclusion, the artificial intelligence enhanced nanoscale 2D NMR spectrum by NV quantum sensor is demonstrated. With deep learning, the full 2D spectrum can be recovered from 10% of the data, thus the experimental time is shortened by an order of magnitude, where the compression ratio may be improved with more training. Together with previous work on nanoscale NMR spectroscopy, the speed up nanoscale 2D NMR can yield valuable structural information as opposed to bulk NMR, where such interactions typically hamper the structure analysis. And without loss of generality, the DLMC method can also be applied to other magnetic resonance and imaging experiments. In the future, it is possible to construct the whole three-dimensional structure of the molecule from enough information of the lengths and angles of chemical bonds obtained by the high-speed 2D NMR.
Methods
Nanoscale 2D NMR experiments
The details for the experiment are shown in Fig. 7.
Sample and setup
A single NV center in a CVD-grown diamond with natural abundance (1.1%) of 13C nuclear spins is used in experiment. External 1580 Gauss magnetic field is applied here. Thus the Larmor frequency of 13C nuclear spin is ωL = 1.69 MHz. A NV electron spin and 13C nuclear-spin pair system is studied in our work.
Initialization
The initialization of nuclear spin is shown in Fig. 7a. Firstly, a 1.5 μs laser pulse is applied to initialize the electron spin to ms = 0 state. Secondly, a half π pulse transform the electron spin to x–y plane. Then a train of periodical π pulses \({(\frac{\tau }{2}-\pi -\frac{\tau }{2})}^{\text{N}}\) is applied to the NV sensor. τ is set as τ = 7/(2ωnuc) to be resonant with the nuclear spin. τ = 2045 ns, N = 40 in our experiment. Then, end is another π/2 pulse with 90° in the microwave pulse. The procedure is not actually the initialization of the nuclear spin, but to correlate the nuclear spin state with the electron spin state31.
π/2 pulse
The π/2 pulse on nuclear spin is realized by a periodical π pulses on NV sensor32. The time interval is set to be τ = 292 ns.
Correlation read
The last readout protocol is similar with initialization process. The microwave control pulses are the same. But the laser pulse is added in the end to readout the change of the correlation of the nuclear spin and the NV sensor.
2D NMR procedure
A two-dimensional protocol is performed in analog to the COSY spectroscopy in conventional NMR. The Hamiltonian is \(H=D{S}_{z}^{2}+{\gamma }_{e}{\bf{B}}\cdot {\bf{S}}+{\gamma }_{c}{\bf{B}}\cdot \left({{\bf{I}}}_{1}+{{\bf{I}}}_{2}\right)+{\bf{S}}\cdot \left({{\bf{A}}}_{1}\cdot {{\bf{I}}}_{1}+{{\bf{A}}}_{2}\cdot {{\bf{I}}}_{{\bf{2}}}\right)+{{\bf{I}}}_{1}\cdot {\bf{J}}\cdot {{\bf{I}}}_{2}\), where S, Sz denotes the NV electron spin, Iα denotes the αth nuclear spin, Aα denotes the hyperfine coupling tensor between NV and nuclear, J denotes dipolar coupling interaction between two nuclear spins. Then target nuclear spins are then evolve under [initialization − free evolution t1 − π/2 pulse − free evolution t2 − correlation read] as shown in Fig. 5a. During the first interval of 0 to t1, the two nuclear spins I1 and I2 interact and a phase ϕ1 = (ωL + a1,∥Sz + Jzzm2)m1t1 is accumulated in the first nuclear spin, where a1,∥ is the parallel component of the hyperfine interaction of the NV sensor with I1, and Jzz is the zz component of the coupling between nuclear spin I1 and I2. The second free evolution comes after the π/2 pulse. Another phase ϕ2 = (ωL + a1,∥Sz + Jzzm2)m1t2 accumulates. In the end, correlation read pulse read out the transverse component of the nuclear spin.
Data acquirement
Sweeping the duration time t1 and t2 from 4 μs to 0.9 ms with 18 μs step, a 50 × 50 size data is collected. However, due to large experiment time cost, only 80% data are collected. The data correspond to nuclear spin transverse component, which are collected by NV sensor through optical detected magnetic resonance technique. The correlation spectroscopy map in time domain is shown in Fig. 5c.
Data simulation
For supervised learning, enough amount of data with ground truth should be provided. In our scenario, the pairs of partially sampled NV spectrum map and the corresponding one with a full resolution is necessary. For 2D NV NMR, data acquisition is highly time-consuming, which hinders to train deep neural networks on real experimental data. Therefore we propose to utilize simulation to generate the training data. The simulation is performed under Schrödinger equation with the NV-13C system. The Hamiltonian is
where Sz is the NV electron spin, Im,α is the m-th nuclear spin, Am,αβ is the hyperfine coupling between NV and nuclear, J is dipolar coupling interaction between two nuclear spins.
The initial state is
where ρn is the maximum mixed state of nuclear spin system as the initial state for them. Then the NV-nuclear spins interacting system evolves under dynamical decoupling sequences: π/2∣x − (τ/2 − π − τ − π − τ/2)N/2 − π/2∣y − t1 − π/2∣RF − t2 − π/2∣y − (τ/2 − π − τ − π − τ/2)N/2 − π/2∣x. In the end we extract the population in ms = 0 state as results.
Convolution layers, ReLU activation layers, and pooling layers
Convolution layers
Given a convolution kernel κ and an input matrix f, the output of a convolution layer is gm,n ≡ (f*κ)[m, n] = ∑i∑jκi,jfm−i,n−j, where m and n are the row and column indices of the matrix, respectively. Intuitively, CNNs attempt to learn a variety of kernels or “shape templates”. These kernels are slid over the matrix f to each position [m, n], and computes a weighted sum of f around the position [m, n]. The weighting is given by the kernel κ: if the values of f around the position [m, n] have a similar pattern with the kernel template κ, the convolutional response f*κ at the position [m, n] will be high, otherwise it will not. By the design philosophy of CNNs (local connectionism), the kernel is of small size, i.e. the convolution response f*κ at the position [m, n] is only related to the small region around the position [m, n] of the input matrix f, called receptive field (Fig. 8a).
ReLU activation layers
In CNNs, it is common to apply a certain threshold to the convolutional response f*κ via the means of an activation function and a bias term. One popular choice in many CNN architectures is the ReLU, defined as \(\sigma (z)=\max (0,z)\). Combined with a bias term b, the ReLU activation layer extracts only the “meaningful" convolutional responses that are above the threshold b, via \(\max (0,(f* \kappa )[m,n]+b)\). The filtered convolutional response \(a(m,n;\kappa,b)=\max (0,(f* \kappa )[m,n]+b)\) forms an activation map a. In a convolution layer, multiple activation maps a1, ⋯ , ad corresponding to different kernels κ1, ⋯ , κd and biases b1, ⋯ , bd constitute “channels" of the output. In other words, a convolution layer utilizes different kernels (shape templates) to codify the input image into a stack of activation maps a = [ai]. The stack of activation maps form essentially a 2D image with d channels and, therefore, convolutions can be applied back to back. This enables to develop a pyramid of features. With consecutive convolutions, the area of receptive fields are expanded. Hence, the convolutions in later (deeper) layers are promoted to capture patterns in a broader context, while the convolutions in earlier (shallower) layers focus on smaller primitives (Fig. 8d).
Pooling layers
The process of constructing the pyramid of features can be made more aggressive by introducing a down-sampling layer called pooling. It partitions the input image into a set of non-overlapping rectangles and, for each of such sub-regions, outputs the maximum or the values computed by convolving with learned kernels using a step size bigger than 1. The latter is utilized in the proposed DLNet, as it can make the network to learn the pooling pattern. It should be sufficient to note that pooling is an operation for reducing the resolution of activation maps into a substantially lower resolution such that the size of the receptive fields increases more aggressively (Fig. 8b).
Robustness of different sampling matrices
We also conducted an analysis to test the robustness of the proposed DLMC method for different sampling schemes. We randomly generated five sampled spectrum matrices from the experimental ground truth one, with a fixed sampling coverage of 10%. Each compared method was applied to each of those five spectrum matrices to reconstruct the spectrum in a full resolution. The average RMSE and its standard deviation, and the average SNR and its standard deviation, were computed and recorded. The results are shown in Fig. 9a, b. Compared to the MC-only method, it can be found that DLMC and DL-only have smaller variances of RMSE and smaller variance of SNR in the frequency domain, which indicates that DLMC is more robust than the MC-only method.
Evaluation for the effect of artifacts
In addition to SNR and RMSE, we further introduced the structural similarity index measure (SSIM)26 to quantify the performance of the spectrum reconstruction. Previous study has shown that both SNR and RMSE can well assess the quality of noisy images. D. C. Peters et. al. also demonstrated that a similar metric to RMSE can be used to qualify the artifacts in a 2D image33. However, neither SNR nor RMSE may be able to measure the similarity of structural contents between images. We thus proposed to additionally utilize the SSIM metric for quality assessment based on the degradation and distortion of structural information. The SSIM metric is defined as,
where x and y are two spectra data, μx and μy are their respective averages, \({\sigma }_{x}^{2}\) and \({\sigma }_{y}^{2}\) are the variances, σxy is their correlation coefficient, and c1 and c2 are small numbers to stabilize the division. A value of 0 indicates no structural similarity and value 1 is only reachable in the case of two identical images and therefore indicates perfect structural similarity. As shown in Fig. 10, the proposed DLMC method improved the SSIM values (Eq. 3) for different sampling coverages comparing to those of the original under-sampled spectrum maps. In the future, we plan to include the SSIM metric (Eq. 3) in the loss function to train the DLNet using the training data with simulated distortions to further reduce distortions in the reconstructed spectrum maps.
Deep-learning algorithm on multiple nuclear spins
Calculations on multiple nuclear spin systems are carried out to shown the speed up ability of our method on general multiple nuclear spin systems. The training data is generated by simulation on two-dimensional spectra of 5 13C nuclear spins of two isotopic labeled amino acids in a single avian pancreatic polypeptide molecule adjacent to the NV center with a 1500G external field along NV axis. The positions and orientations of molecule are randomly chosen. 0.85 MHz sampling rate and 500 points scale are chosen considering the physical system and limited computing resources.
The training data is a set of calculation outputs with random spatial parameters. The algorithm is tested with another set of random spatial simulations. The coordinates of two different nuclear spin system are shown in Fig. 11a, d. The simulated full sampled spectra and reconstructed 10% sampled spectra are shown in Fig. 11b, e and 11c, f, respectively. The RMSE of the reconstructed spectra is 0.018 ± 0.002. The RMSE is much smaller than previous because the simulated data has no experimental error and the simulated spectra amplitude here is normalized.
a NV and 5 coupled 13C system, red dots are NV centers, and blue dots are 13C nuclei. The relative position of each 13C pair is determined, the molecule position are randomly chosen in a plane 0.8 nm above the NV center, the molecule orientation is randomly chosen. b Spectra of original simulated spectra with parameters in a, experimental errors are not considered in the simulation. c Spectra reconstructed by the AI algorithm with 10% randomly sampled data from original simulation outputs. d–f Anther nuclear configuration, corresponding simulated full sampled spectra and reconstructed 10% sampled spectra.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
Code availability
The code written for the DLMC algorithm and numerical simulation within this paper are available from the corresponding author upon reasonable request.
References
Balasubramanian, G. et al. Nanoscale imaging magnetometry with diamond spins under ambient conditions. Nature 455, 648–651 (2008).
Maze, J. R. et al. Nanoscale magnetic sensing with an individual electronic spin in diamond. Nature 455, 644–647 (2008).
Müller, C. et al. Nuclear magnetic resonance spectroscopy with single spin sensitivity. Nat. Commun. 5, 4703 (2014).
Shi, F. et al. Single-protein spin resonance spectroscopy under ambient conditions. Science 347, 1135–1138 (2015).
Lovchinsky, I. et al. Nuclear magnetic resonance detection and spectroscopy of single proteins using quantum logic. Science 351, 836–841 (2016).
Smits, J. et al. Two-dimensional nuclear magnetic resonance spectroscopy with a microfluidic diamond quantum sensor. Sci. Adv. 5, eaaw7895 (2019).
Yang, Z. et al. Structural analysis of nuclear spin clusters via two-dimensional nanoscale nuclear magnetic resonance spectroscopy. Adv. Quantum Technol. https://doi.org/10.1002/qute.201900136 (2020).
Abobeih, M. H. et al. Atomic-scale imaging of a 27-nuclear-spin cluster using a quantum sensor. Nature 576, 411–415 (2019).
Barna, J., Laue, E., Mayger, M., Skilling, J. & Worrall, S. Exponential sampling, an alternative method for sampling in two-dimensional NMR experiments. J. Magn. Reson. 73, 69–77 (1987).
Kim, S. & Szyperski, T. GFT NMR, a new approach to rapidly obtain precise high-dimensional NMR spectral information. J. Am. Chem. Soc. 125, 1385–1393 (2003).
Rovnyak, D. et al. Accelerated acquisition of high resolution triple-resonance spectra using non-uniform sampling and maximum entropy reconstruction. J. Magn. Reson. 170, 15–21 (2004).
Ma, D. et al. Magnetic resonance fingerprinting. Nature 495, 187–192 (2013).
Scheuer, J. et al. Accelerated 2d magnetic resonance spectroscopy of single spins using matrix completion. Sci. Rep. 5, 17728 (2015).
Aharon, N. et al. NV center based nano-NMR enhanced by deep learning. Sci. Rep. 9, 17802 (2019).
Cai, J.-F., Candés, E. J. & Shen, Z. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 20, 1956–1982 (2010).
Dong, C., Loy, C. C., He, K. & Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 38, 295–307 (2016).
Zhang, K., Zuo, W., Chen, Y., Meng, D. & Zhang, L. Beyond a Gaussian denoiser: residual learning of deep CNN for image denoising. IEEE Trans. Image Process. 26, 3142–3155 (2017).
Yang, C. et al. High-Resolution Image Inpainting Using Multi-scale Neural Patch Synthesis. in Proc. IEEE Conference on Computer Vision and Pattern Recognition, 4076–4084 (IEEE, 2017).
Kalantre, S. S. et al. Machine learning techniques for state recognition and auto-tuning in quantum dots. npj Quantum Inf. 5, 6 (2019).
Ben-David, S. et al. A theory of learning from different domains. Mach. Learn. 79, 151–175 (2010).
Cho, J., Kim, D. & Rohe, K. Asymptotic theory for estimating the singular vectors and values of a partially-observed low rank matrix with noise. Statistica Sin. 27, 1921–1948 (2017).
Cho, J., Kim, D. & Rohe, K. Intelligent initialization and adaptive thresholding for iterative matrix completion; some statistical and algorithmic theory for adaptive-impute. J. Comput. Graph. Stat. 28, 1–26 (2018).
Xiao, M. & Guo, Y. A novel two-step method for cross language representation learning. in Advances in Neural Information Processing Systems 26, (eds. Burges, C. J. C., Bottou, L., Welling, M., Ghahramani, Z. & Weinberger, K. Q) 1259–1267 (Curran Associates, Inc., 2013).
Zhou, J. T., Pan, S. J., Tsang, I. W. & Ho, S-S. Transfer learning for cross-language text categorization through active correspondences construction. in Proc. Thirtieth AAAI Conference on Artificial Intelligence, AAAI’16, 2400–2406 (AAAI Press, 2016).
Li, H., Pan, S. J., Wang, S. & Kot, A. C. Heterogeneous domain adaptation via nonlinear matrix factorization. IEEE Trans. Neural Netw. Learn. Syst. 31, 1–13 (2019).
Wang, Z., Bovik, A., Sheikh, H. & Simoncelli, E. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13, 600–612 (2004).
Wang, Z. & Arce, G. R. Variable density compressed image sampling. IEEE Trans. Image Process. 19, 264–270 (2010).
Barranca, V. J., Kovačič, G., Zhou, D. & Cai, D. Improved compressive sensing of natural scenes using localized random sampling. Sci. Rep. 6, 1–17 (2016).
Sherry, F. et al. Learning the sampling pattern for mri. arXiv:1906.08754 (2019).
Aggarwal, H. K. & Jacob, M. J-MoDL: joint model-based deep learning for optimized sampling and reconstruction. IEEE J. Sel. Top. Signal Process. 1–1, https://ieeexplore.ieee.org/document/9122388 (2020).
Boss, J. et al. One- and two-dimensional nuclear magnetic resonance spectroscopy with a diamond quantum sensor. Phys. Rev. Lett. 116, 197601 (2016).
Taminiau, T. H. et al. Detection and control of individual nuclear spins using a weakly coupled electron spin. Phys. Rev. Lett. 109, 137602 (2012).
Peters, D. C. et al. Characterizing radial undersampling artifacts for cardiac applications. Magn. Reson. Med. 55, 396–403 (2006).
Acknowledgements
We thank Fedor Jelezko for helpful discussions. This work was supported by the National Key Research and Development Program of China (grant nos. 2018YFA0306600, 2016YFA0502400), the National Natural Science Foundation of China (grant nos. 81788101, 91636217, 11722544, and 11761131011), the CAS (grant nos. GJJSTD20170001, QYZDY-SSW-SLH004, and YIPA2015370), the Anhui Initiative in Quantum Information Technologies (grant no. AHY050000), the CEBioM, the national youth talent support program, the Fundamental Research Funds for the Central Universities.
Author information
Authors and Affiliations
Contributions
J.D. supervised the entire project. J.D., F.S., and X.K. designed the experimental scheme. L.Z. and X.W. programmed and trained the AI algorithm. X.K., Z.L., Z.Y., and F.S. prepared the setup and implemented the experiments. X.K. and Z.L. carried out the simulations. X.K., L.Z., and B.Q. analyze the performance of the AI algorithm. X.K., L.Z., Z.Y., X.W., and F.S. wrote the paper. All authors discussed the results and commented on the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kong, X., Zhou, L., Li, Z. et al. Artificial intelligence enhanced two-dimensional nanoscale nuclear magnetic resonance spectroscopy. npj Quantum Inf 6, 79 (2020). https://doi.org/10.1038/s41534-020-00311-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-020-00311-z
This article is cited by
-
Navigating with chemometrics and machine learning in chemistry
Artificial Intelligence Review (2023)
-
Parallel detection and spatial mapping of large nuclear spin clusters
Nature Communications (2022)
-
Deep learning enhanced individual nuclear-spin detection
npj Quantum Information (2021)