Abstract
Quantum thermodynamics aims at investigating both the emergence and the limits of the laws of thermodynamics from a quantum mechanical microscopic approach. In this scenario, thermodynamic processes with no heat exchange, namely, adiabatic transformations, can be implemented through quantum evolutions in closed systems, even though the notion of a closed system is always an idealization and approximation. Here, we begin by theoretically discussing thermodynamic adiabatic processes in open quantum systems, which evolve non-unitarily under decoherence due to its interaction with its surrounding environment. From a general approach for adiabatic non-unitary evolution, we establish heat and work in terms of the underlying Liouville superoperator governing the quantum dynamics. As a consequence, we derive the conditions that an adiabatic open-system quantum dynamics implies in the absence of heat exchange, providing a connection between quantum and thermal adiabaticity. Moreover, we determine families of decohering systems exhibiting the same maximal heat exchange, which imply in classes of thermodynamic adiabaticity in open systems. We then approach the problem experimentally using a hyperfine energy-level quantum bit of an Ytterbium 171Yb+ trapped ion, which provides a work substance for thermodynamic processes, allowing for the analysis of heat and internal energy throughout a controllable engineered dynamics.
Similar content being viewed by others
Introduction
The notion of adiabaticity is a fundamental concept in a number of different areas in physics, including quantum information processing1,2,3,4 and quantum thermodynamics5,6,7. In the context of closed quantum systems, adiabaticity is understood as the phenomenon in which the Hilbert space of the system can be (quasi-)perfectly decomposed into decoupled Schrodinger-eigenspaces, composed by the eigenvectors of the Hamiltonian with distinct non-crossing instantaneous energies8,9,10. Then, by initially preparing a quantum system in an energy eigenstate, the system undergoes a decoupled evolution to the corresponding energy eigenstate at later times. However, the concept of a closed system is always an idealization and approximation. Indeed, real quantum systems are always coupled to a surrounding environment. In open quantum systems described by time-local master equations, the definition of adiabaticity can be naturally extended to the decomposition of the Hilbert-Schmidt space into Lindblad-Jordan eigenspaces associated with distinct eigenvalues of the generator of the dynamics11,12,13,14,15,16,17.
In thermodynamics, adiabaticity is associated to a process with no heat exchange between the system and its reservoir. In general, it is not possible to associate an observable for the thermodynamic definition of heat and of work18. Then, the starting point widely used to define such physical quantities in quantum systems is from the definition of internal energy given as U(t) = 〈H(t)〉5,19. From this definition, we obtain the work (dW) and exchanged heat (dQ) between the reservoir and system as
respectively. As originally introduced in Ref. 19, these quantities are defined in the weak coupling limit between system and reservoir (see also Refs. 20,21 for recent attempts to examine strongly coupled quantum systems and Refs. 22,23 for separation of internal energy variation in terms of entropy changes). Notice also that dW and dQ are exact differential forms when at least one of them vanishes, thus the non-vanishing quantity can be identified with the internal energy variation ΔU(t) during the entire process. For example, for a unitary transformation associated with a closed quantum system, we necessarily have dQclosed = 0, so that any variation ΔU(t) is due some work performed on/by the system5,24. Eq. (1) can be directly employed to analyze quantum thermodynamical cycles, as an efficient way of assuring that no heat is exchanged in intermediate steps25,26,27 or to minimize quantum friction in a non-equilibrium setup28,29,30.
Here, we theoretically and experimentally discuss thermodynamical adiabatic processes in real (open) quantum systems evolving under decoherence. To this end, we address the problem from a general approach for adiabatic dynamics in decohering systems. In contrast with closed systems, heat may be exchanged in the case of non-unitary evolution. In particular, we will establish a sufficient condition to ensure that an adiabatic open-system dynamics (associated with Lindblad-Jordan decoupled eigenspaces) leads to an adiabatic thermodynamical process (associated with no heat exchange). Moreover, for thermodynamically non-adiabatic processes, we evaluate the von Neumann entropy, discussing its relation with heat for arbitrary evolution time. Our results are then experimentally implemented by using a hyperfine energy-level quantum bit (qubit) of an Ytterbium 171Yb+ trapped ion, where reservoir engineering is performed to achieve a controllable adiabatic dynamics. Due to requirements of the usual definitions of heat and work, the investigation of thermodynamic quantities in adiabatic dynamics is achieved with time-dependent decoherence effects. To this end, we introduce an efficient control to a Gaussian noise with time-dependent amplitude, which is then used to simulate a dephasing channel with a time-dependent decoherece rate γ(t).
Results
Work and heat in the adiabatic dynamics of open systems
We start by introducing heat and work in a general formalism for adiabaticity in open quantum systems, namely, the superoperator formalism11. In this work, we will consider a discrete quantum systems \({\mathcal{S}}\) defined over a d-dimensional Hilbert space. The system \({\mathcal{S}}\) interacts with its surrounding environment \({\mathcal{A}}\). The dynamics is assumed to be described by a time-local master equation \(\dot{\rho }(t)={{\mathcal{L}}}_{t}[\rho (t)]\), where ρ(t) is the density operator associated with \({\mathcal{S}}\) and \({{\mathcal{L}}}_{t}[\bullet ]\) is a time-dependent Liouville operator. The Liouville operator takes the form \({{\mathcal{L}}}_{t}[\rho (t)]={{\mathcal{H}}}_{t}[\rho (t)]+{{\mathcal{R}}}_{t}[\rho (t)]\), where \({{\mathcal{H}}}_{t}[\bullet ]=(1/i\hslash )[H(t),\bullet ]\) is the unitary part of the dynamics and \({{\mathcal{R}}}_{t}[\bullet ]\) describes the decohering effects of \({\mathcal{A}}\) over \({\mathcal{S}}\).
In the superoperator formalism, the open-system dynamics can be provided from a Schrödinger-like equation \(\left.\left|\dot{\rho }(t)\right\rangle \right\rangle ={\mathbb{L}}(t)\left.\left|\rho (t)\right\rangle \right\rangle\), where \({\mathbb{L}}(t)\) is termed the Lindblad superoperator and the density operator \(\left.\left|\rho (t)\right\rangle \right\rangle\) is represented by a D2-dimensional vector (hence the double ket notation), whose components ϱk(t) can be suitably expanded in terms of tensor products of the Pauli basis { 1, σ1, σ2, σ3}11. For instance, for the case of a single qubit (D = 2), we have \(\rho (t)=\frac{1}{2}\mathop{\sum }\nolimits_{k = 0}^{3}{\varrho }_{k}(t){\sigma }_{k}\) and \({\varrho }_{k}(t)={\rm{Tr}}\{\rho (t){\sigma }_{k}\}\), with σk denoting an element of the Pauli basis. Moreover, \({\mathbb{L}}(t)={\mathbb{H}}(t)+{\mathbb{R}}(t)\), where \({\mathbb{H}}(t)\) and \({\mathbb{R}}(t)\) are (D2 × D2)-dimensional super-matrices, whose elements are \({{\mathbb{H}}}_{ki}(t)=(1/D){\rm{Tr}}\{{\sigma }_{k}^{\dagger }{{\mathcal{H}}}_{t}[{\sigma }_{i}]\}\) and \({{\mathbb{R}}}_{ki}(t)=(1/D){\rm{Tr}}\{{\sigma }_{k}^{\dagger }{\mathcal{R}}[{\sigma }_{i}]\}\), respectively. The thermodynamic quantities defined in Eq. (1) are then rewritten as (see Methods section)
with the components hk(t) of \(\left\langle \left\langle h(t)\right|\right.\) defined by \({h}_{k}(t)={\rm{Tr}}\{H(t){\sigma }_{k}\}\). In this notation, the inner product of vectors \(\left.\left|u\right\rangle \right\rangle\) and \(\left.\left|v\right\rangle \right\rangle\) associated with operators u and v, respectively, is defined as 〈〈u∣v〉〉 = (1/D)Tr(u†v).
Because \({\mathbb{L}}(t)\) is non-Hermitian, it cannot always be diagonalized. Then, the definition of adiabaticity in this scenario is subtler than in the case of closed systems. For open systems, the adiabatic dynamics can be defined in terms of the Jordan decomposition of \({\mathbb{L}}(t)\)11. More specifically, adiabaticity is associated with a completely positive trace-preserving dynamics that can be decomposed into decoupled Lindblad-Jordan eigenspaces associated with distinct non-crossing instantaneous eigenvalues λi(t) of \({\mathbb{L}}(t)\). We notice here that some care is required in order to find a basis for describing the density operator. The standard technique is to start from the instantaneous right and left eigenstates of \({\mathbb{L}}(t)\), completing these eigensets in order to compose right \(\{|{{\mathcal{D}}}_{i}^{({k}_{i})}(t)\rangle \rangle \}\) and left \(\{\langle \langle {{\mathcal{E}}}_{i}^{({k}_{i})}(t)| \}\) vector bases, where \(|{{\mathcal{D}}}_{i}^{({k}_{i})}(t)\rangle \rangle\) and \(\langle \langle {{\mathcal{E}}}_{i}^{({k}_{i})}(t)|\) are the ki-th right and left vectors, respectively, associated with the eigenspace with eigenvalue λi(t) in the Jordan decomposition of \({\mathbb{L}}(t)\). These Jordan left and right bases can always be built such that they satisfy a bi-orthonormal relationship \(\langle \langle {{\mathcal{E}}}_{i}^{(\alpha )}(t)| {{\mathcal{D}}}_{j}^{(\beta )}(t)\rangle \rangle ={\delta }_{ij}{\delta }^{\alpha \beta }\). Assuming an open-system adiabatic dynamics, we can analytically derive work, heat, and entropy variation. Indeed, by taking the initial density operator as \(|\rho (0)\rangle \rangle ={\sum }_{i,{k}_{i}}{c}_{i}^{({k}_{i})}|{{\mathcal{D}}}_{i}^{({k}_{i})}(0)\rangle \rangle\), we obtain that work and heat are provided by
with dWad (dQad) being identified to the amount of work (heat) performed on/by the system.
The validity of Eqs. (3) and (4) is shown in the Methods section. As long as we are in the weak coupling regime and the system is driven by a time-local master equation, Eqs. (3) and (4) provide expressions for work and heat for the adiabatic decohering dynamics. Notice also that the adiabatic dynamics will require a slowly varying Liouville superoperator \({\mathbb{L}}(t)\)11. Starting from Eq. (2), we are allowed to evaluate the density operator \(\left.\left|\rho (t)\right\rangle \right\rangle\) through an arbitrary strategy. For instance, we could apply a piecewise deterministic process approach via Feynman-Vernon path integral for the corresponding propagator31. Alternatively, we could implement a numerical simulation via a Monte Carlo wave function method (see, e.g., Ref. 32 and references therein). In all these cases, from Eqs. (3) and (4), we can obtain a sufficient condition for avoiding heat exchange in a quantum mechanical adiabatic evolution. More specifically, if the initial state ρ(0) of the system can be written as a superposition of the eigenstate set \(\{|{{\mathcal{D}}}_{i}^{({k}_{i})}(0)\rangle \rangle \}\) with eigenvalue λi(t) = 0, for every t ∈ [0, τ], the adiabatic dynamics implies in no heat exchange. Therefore, we can establish that an adiabatic dynamics in quantum mechanics is not in general associated with an adiabatic process in quantum thermodynamics, with a sufficient condition for thermal adiabaticity being the evolution within an eigenstate set with vanishing eigenvalue of \({\mathbb{L}}(t)\). This condition is satisfied by a quantum system that adiabatically evolves under a steady state trajectory, since such dynamics can be described by an eigenstate (or a superposition of eigenstates) of \({\mathbb{L}}(t)\) with eigenvalue zero14. As an example, Ref. 33 has considered the adiabatic evolution of 2D topological insulators, where the system evolves through its steady state trajectory. For this system, the evolved state \(\left.\left|{\rho }_{{\rm{s}}s}(t)\right\rangle \right\rangle\), associated with the steady state of the system ρss(t), satisfies \({\mathbb{L}}(t)\left.\left|{\rho }_{{\rm{s}}s}(t)\right\rangle \right\rangle =0\), ∀ t. This means that \(\left.\left|{\rho }_{{\rm{s}}s}(t)\right\rangle \right\rangle\) is an instantaneous eigenstate of \({\mathbb{L}}(t)\) with eigenvalue λ(t) = 0.
Thermal adiabaticity for a qubit adiabatic dynamics
As a further illustration, let us consider a two-level system initialized in a thermal equilibrium state ρth(0) for the Hamiltonian H(0) at inverse temperature β = 1/kBT, where kB and T are the Boltzmann’s constant and the absolute temperature, respectively. Let the system be governed by a Lindblad equation, where the environment acts as a dephasing channel in the energy eigenstate basis \(\{\left|{E}_{n}(t)\right\rangle \}\) of H(t). Thus, we describe the coupling between the system and its reservoir through \({{\mathcal{R}}}_{t}^{{\rm{dp}}}[\bullet ]=\gamma (t)[{\Gamma }^{{\rm{dp}}}(t)\bullet {\Gamma }^{{\rm{dp}}}(t)-\bullet ]\), where \({\Gamma }^{{\rm{dp}}}(t)=\left|{E}_{0}(t)\right\rangle \left\langle {E}_{0}(t)\right|-\left|{E}_{1}(t)\right\rangle \left\langle {E}_{1}(t)\right|\). In this case, the set of eigenvectors of \({\mathbb{L}}(t)\) can be obtained from set of operators \({P}_{nm}(t)=\left|{E}_{n}(t)\right\rangle \left\langle {E}_{m}(t)\right|\), where the components \({{\mathcal{D}}}_{nm}^{(i)}(t)\) of \(\left.\left|{{\mathcal{D}}}_{nm}(t)\right\rangle \right\rangle\) are given by \({{\mathcal{D}}}_{nm}^{(i)}(t)={\rm{Tr}}\{{P}_{nm}(t){\sigma }_{i}\}\). Moreover, the eigenvalue equation for \({\mathbb{L}}(t)\) can be written as \({\mathbb{L}}(t)\left.\left|{{\mathcal{D}}}_{nm}(t)\right\rangle \right\rangle ={\lambda }_{nm}(t)\left.\left|{{\mathcal{D}}}_{nm}(t)\right\rangle \right\rangle\), where λnm(t) = En(t) − Em(t) − 2(1 − δnm)γ(t). In the superoperator formalism, the initial state ρth(0) is written as \(\left.\left|{\rho }_{{\rm{t}}h}(0)\right\rangle \right\rangle ={{\mathcal{Z}}}^{-1}(0){\sum }_{n}{e}^{-\beta {E}_{n}(0)}\left.\left|{{\mathcal{D}}}_{nn}(0)\right\rangle \right\rangle\), where \({\mathcal{Z}}(t)={\rm{Tr}}\{{e}^{-\beta H(t)}\}\) is the partition function of the system. Therefore, since \(\left.\left|{\rho }_{{\rm{t}}h}(0)\right\rangle \right\rangle\) is given by a superposition of eigenvectors of \({\mathbb{L}}(t)\) with eigenvalue λnn(t) = 0, we obtain from Eq. (4) that dQad = 0. Therefore, thermal adiabaticity is achieved for an arbitrary open-system adiabatic dynamics subject to dephasing in the energy eigenbasis. Hence, any internal energy variation for this situation should be identified as work.
Heat exchange for a qubit adiabatic dynamics
In contrast, we can use a similar qubit system to find a process in which heat can be exchanged, i.e., dQad ≠ 0. To this end, let us consider dephasing in the computational basis, with the coupling between the system and its reservoir through \({{\mathcal{R}}}_{t}^{{\rm{z}}}[\bullet ]=\gamma (t)\left[{\sigma }_{z}\bullet {\sigma }_{z}-\bullet \right]\). In order to guarantee that any internal energy variation is associated to heat exchange, we consider a constant Hamiltonian during the entire non-unitary evolution (so that dWad = 0). Since \({{\mathcal{R}}}_{t}^{{\rm{z}}}[\bullet ]\) must not be written in the eigenbasis of the Hamiltonian, we assume a Hamiltonian Hx = ħωσx, where the system is initialized in the typical initial state of a thermal machine, namely, the thermal state of the Hamiltonian Hx at some arbitrary temperature β. By letting the system undergo a non-unitary adiabatic dynamics under dephasing, the evolved state is (see Methods section)
From Eq. (4) we then compute the amount of exchanged heat during an infinitesimal time interval dt as \(d{Q}^{{\rm{ad}}}(t)=2\hslash \tanh (\beta \hslash \omega )\omega \gamma (t){e}^{-2\mathop{\int}\nolimits_{\!\!{0}}^{t}\gamma (\xi )d\xi }dt\). The negative argument in the exponential shows that the higher the mean-value of γ(t) the faster the heat exchange ends (see Methods section). Thus, if we define the amount of exchanged heat during the entire evolution as \(\Delta Q({\tau }_{{\rm{dec}}})=\mathop{\int}\nolimits_{\!{0}}^{{\tau }_{{\rm{dec}}}}[d{Q}^{{\rm{ad}}}(t)/dt]dt\), where τdec is the total evolution time of the nonunitary dynamics, we get
where \(\bar{\gamma }=(1/{\tau }_{{\rm{dec}}})\mathop{\int}\nolimits_{\!{0}}^{{\tau }_{{\rm{dec}}}}\gamma (\xi )d\xi\) is the average dephasing rate during τdec. Notice that ΔQ(τdec) > 0 for any value of \(\bar{\gamma }\). Therefore, the dephasing channel considered here works as an artificial thermal reservoir at inverse temperature \(\tilde{\beta }={\beta }_{{\rm{deph}}}\, < \, \beta\), with \({\beta }_{{\rm{deph}}}=(1/\hslash \omega ){\rm{arctanh}}[{e}^{-2\bar{\gamma }{\tau }_{{\rm{dec}}}}\tanh (\beta \hslash \omega )]\) (see Methods section). We can further compute the maximum exchanged heat from Eq. (6) as a quantity independent of the environment parameters and given by \(\Delta {Q}_{\max }=\hslash \omega \tanh (\beta \hslash \omega )\). It would be worth to highlight that, for quantum thermal machines weakly coupled to thermal reservoirs at different temperatures19, the maximum heat \(\Delta {Q}_{\max }\) is obtained with high-temperature hot reservoirs25,34,35.
Despite we have provided a specific open-system adiabatic evolution, we can determine infinite classes of system-environment interactions exhibiting the same amount of heat exchange dQ. In particular, there are infinite engineered environments that are able to extract a maximum heat amount \(\Delta {Q}_{\max }\). A detailed proof of this result can be found in Methods section.
Experimental realization
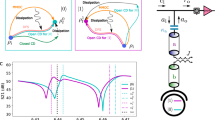
We now discuss an experimental realization to test the thermodynamics of adiabatic processes in an open-system evolution. This is implemented using the hyperfine energy levels of an Ytterbium ion 171Yb+ confined by a six-needles Paul trap, with a qubit encoded into the 2S1/2 ground state, \(\left|0\right\rangle \equiv {\left.\right|}^{2}{S}_{1/2};\ F=0,{m}_{F}=0\left.\right\rangle\) and \(\left|1\right\rangle \equiv \ {\left.\right|}^{2}{S}_{1/2};\ F=1,{m}_{F}=0\left.\right\rangle\), as shown in Fig. 1a36. The qubit initialization is obtained from the standard Rabi Oscillation sequence36, where we first implement the Doppler cooling for 1 ms, after we apply a standard optical pumping process for 0.01 ms to initialize the qubit into the \(\left|0\right\rangle\) state, and then we use microwave to implement the desired dynamics. The target Hamiltonian Hx can be realized using a resonant microwave with Rabi frequency adjusted to ω. To this end, the channel 1 (CH1) waveform of a programmable two-channel arbitrary waveform generator (AWG) is used, which has been programmed to the angular frequency 2π × 200 MHz. As depicted in Fig. 1(b), to implement the dephasing channel we use the Gaussian noise frequency modulation (FM) microwave technique, which has been developed in a recent previous work and shows high controllability37. Since we need to implement a time-dependent decohering quantum channel, we use the channel 2 (CH2) waveform as amplitude modulation (AM) source to achieve high control of the Gaussian noise amplitude, consequently, to optimally control of the dephasing rate γ(t). The dephasing rates are calibrated by fitting the Rabi oscillation curve with exponential decay. Since the heat flux depend on the non-unitary process induced by the system-reservoir coupling, then by using a different kind of noise (other than the Gaussian form) we may obtain a different heat exchange behavior. See Methods section for a detailed description of the experimental setup, including the implementation of the quantum channel and the quantum process tomography (see Methods section).
a Schematic diagram of the six-needle Paul trap and relevant levels of the 171Yb+ ion. b Experimental microwave instrument for generating the field to drive the two level system. The AWG is programmed to implement the target Hamiltonian and control the amplitude of the Gaussian noise which is used as a dephasing channel.
As a further development, we analyze in Fig. 2 the experimental results for the heat exchange ΔQ(τdec) as a function of τdec, where we have chosen γ(t) = γ0(1 + t/τdec), where τdec is experimentally controlled through the time interval associated to the action of our decohering quantum channel. The solid curves in Fig. 2 are computed from Eq. (6), while the experimental points are computed through the variation of internal energy as ΔQ(τdec) = Ufin − Uini, where \({U}_{{\rm{fin(ini)}}}={\rm{Tr}}\{{\rho }_{{\rm{fin(ini)}}}H(\tau )\}\). The computation of Ufin(ini) is directly obtained from quantum state tomography of ρfin(ini) for each value of τdec. Although the maximum exchanged heat is independent of γ0, the initial dephasing rate γ0 affects the power for which the system exchanges heat with the reservoir for a given evolution time τdec (See Methods section). Thus, since we have an adiabatic path in open system (see Methods section), the curves in Fig. 2 represent the heat exchanged during the adiabatic dynamics. It is worth highlighting here that we can have different noise sources in the trapped ion system in addition to dephasing. However, the coherence timescale of the Ytterbium hyperfine qubit is around 200 ms37. Therefore, it is much larger than the timescale of the experimental implementation. Indeed, the dephasing rates implemented in our realization are simulated by the experimental setup.
We use ħω = 82.662 peV and β−1 = 17.238 peV, with the physical constants ħ ≈ 6.578 × 10−16 eV ⋅ s and kB ≈ 8.619 × 10−5 eV/K38.
As previously mentioned, since the Hamiltonian is time-independent, any internal energy variation is identified as heat. In order to provide a more detailed view of this heat exchange, we analyze the von Neumann entropy \(S(\rho )=-{\rm{t}}r\ (\rho \mathrm{log}\,\rho )\) during the evolution. To this end, by adopting the superoperator formalism as before, the entropy variation for an infinitesimal time interval dt reads \(dS=-(1/D)\left\langle \left\langle {\rho }_{\mathrm{log}\,}(t)\right|\right.{\mathbb{L}}(t)\left.\left|\rho (t)\right\rangle \right\rangle\), where \(\left\langle \left\langle {\rho }_{\mathrm{log}\,}(t)\right|\right.\) is a supervector with components given by \({\varrho }_{n}^{\mathrm{log}\,}(t)={\rm{Tr}}\left\{{\sigma }_{n}\mathrm{log}\,\rho (t)\right\}\) (see Methods section). Thus, for an adiabatic evolution in an open system we find that (see Methods section)
where \({\Gamma }_{i,{k}_{i}}(t)=\langle \langle {\rho }_{\mathrm{log}\,}^{{\rm{ad}}}(t)| {{\mathcal{D}}}_{i}^{({k}_{i}-1)}(t)\rangle \rangle +{\lambda }_{i}(t)\langle \langle {\rho }_{\mathrm{log}\,}^{{\rm{ad}}}(t)| {{\mathcal{D}}}_{i}^{({k}_{i})}(t)\rangle \rangle\), with \(\langle \langle {\rho }_{\mathrm{log}\,}^{{\rm{ad}}}(t)|\) defined here as a supervector with components \({\varrho }_{\mathrm{log}\,}^{{\rm{ad}}}(t)={\rm{Tr}}\{{\sigma }_{n}\mathrm{log}\,{\rho }_{\mathrm{log}\,}^{{\rm{ad}}}(t)\}\). For the adiabatic dynamics considered in Fig. 2 the infinitesimal von Neumann entropy variation dS in interval dt is given by
where we define \(g(t)={e}^{-2\mathop{\int}\nolimits_{\!\!{0}}^{t}\gamma (\xi )d\xi }\tanh (\beta \hslash \omega )\). Notice that the relation between heat and entropy can be obtained by rewriting the exchanged heat dQ in the interval dt as dQad(t) = 2\(\hslash\)ωγ(t)g(t)dt. In conclusion, the energy variation can indeed be identified as heat exchanged along the adiabatic dynamics. Indeed, by computing the thermodynamic relation between dS(t) and dQad(t) we get dS(t) = βdephdQad(t), where βdeph is the inverse temperature of the simulated thermal bath.
Discussion
From a general approach for adiabaticity in open quantum systems driven by time-local master equations, we provided a relationship between adiabaticity in quantum mechanics and in quantum thermodynamics in the weak coupling regime between system and reservoir. In particular, we derived a sufficient condition for which the adiabatic dynamics in open quantum systems leads to adiabatic processes in thermodynamics. By using a particular example of a single qubit undergoing an open-system adiabatic evolution path, we have illustrated the existence of both adiabatic and diabatic regimes in quantum thermodynamics, computing the associated heat fluxes in the processes. As a further result, we also proved the existence of an infinite family of decohering systems exhibiting the same maximum heat exchange. From the experimental side, we have realized adiabatic open-system evolutions using an Ytterbium trapped ion, with its hyperfine energy level encoding a qubit (work substance). In turn, we have experimentally shown that heat exchange can be directly provided along the adiabatic path in terms of the decoherence rates as a function of the total evolution time. In particular, the relationship between heat and entropy is naturally derived in terms of a simulated thermal bath. Our implementation exhibits high controllability, opening perspectives for analyzing thermal machines (or refrigerators) in open quantum systems under adiabatic evolutions. Moreover, a further point to be explored is the speed up of the adiabatic path through the transitionless quantum driving (TQD) method for open systems39. Indeed, TQD can be incorporated in the formalism for adiabatic thermodynamics we introduced in this work. The starting point is the generalization of Eqs. (3) and (4) through the introduction of the superadiabatic Lindbladian superoperator \({{\mathbb{L}}}_{{\rm{TQD}}}(t)\) governing the open system evolution39. Notice that \({{\mathbb{L}}}_{{\rm{TQD}}}(t)\) will include counter-diabatic contributions generally obtained by reservoir engineering. Suppression of heat may be possibly obtained by constraining the evolution inside the Jordan block of \({{\mathbb{L}}}_{{\rm{TQD}}}(t)\) with vanishing eigenvalue. Naturally, the requirements of weak coupling and time-local master equations are still to be kept. The associated effects of the engineered reservoirs on the thermal efficiencies and TQD dynamics are left for future research.
Methods
Thermodynamics in the superoperator formalism
Let us consider the heat exchange as
where we have used the equation \(\dot{\rho }(t)={\mathcal{L}}[\rho (t)]\). To derive the corresponding expression in the superoperator formalism we first define the basis of operators given by {σi}, i = 0, ⋯, D2 − 1, where \({\rm{Tr}}\{{\sigma }_{i}^{\dagger }{\sigma }_{j}\}=D{\delta }_{ij}\). In this basis, we can write ρ(t) and H(t) generically as
where we have \({h}_{n}(t)={\rm{Tr}}\{H(t){\sigma }_{n}\}\) and \({\varrho }_{n}(t)={\rm{Tr}}\{\rho (t){\sigma }_{n}^{\dagger }\}\). Then, we get
Now, we use the definition of the matrix elements of the superoperator \({\mathbb{L}}(t)\), associated with \({\mathcal{L}}[\bullet ]\), which reads \({{\mathbb{L}}}_{mn}=(1/D){\rm{Tr}}\{{\sigma }_{m}^{\dagger }{\mathcal{L}}[{\sigma }_{n}]\}\), so that we write
In conclusion, by defining the vector elements
we can rewrite Eq. (12), yielding
Equivalently,
where we have used Eq. (10) to write \(\dot{H}(t)=(1/D)\mathop{\sum }\nolimits_{n = 0}^{{D}^{2}-1}{\dot{h}}_{n}(t){\sigma }_{n}^{\dagger }\) and, consequently,
so that we use the definition of the coefficients ϱn(t) to get
By using Eqs. (13) and (14) into Eq. (18), we conclude that
In thermodynamics, heat exchange is accompanied of an entropy variation. Then, in order to provide a complete thermodynamic study from this formalism, we now compute the instantaneous variation of the von Neumann entropy \(S(t)=-{\rm{Tr}}\{\rho (t)\mathrm{log}\,[\rho (t)]\}\), which reads
By using that \({\rm{Tr}}\{\rho (t)\}=1\), we get \({\rm{Tr}}\{\dot{\rho }(t)\}=0\). Therefore
where we also used that \(\dot{\rho }(t)={{\mathcal{L}}}_{t}[\rho (t)]\). Now, let us to write
so that we can define the vectors \(\left\langle \left\langle {\rho }_{\mathrm{log}\,}(t)\right|\right.\) associated to \(\mathrm{log}\,\rho (t)\) with components \({\varrho }_{n}^{\mathrm{log}\,}(t)\) obtained as \({\varrho }_{n}^{\mathrm{log}\,}(t)={\rm{Tr}}\{{\sigma }_{n}\mathrm{log}\,\rho (t)\}\). Thus, we get
In the superoperator formalism, we then have
Alternatively, it is possible to get a similar result for the entropy variation in an interval Δt = t − t0 as
where we can use Eq. (10) to write
so that we can identify \({\varrho }_{n}^{\mathrm{log}\,}(t)={\rm{Tr}}\left\{{\sigma }_{n}\mathrm{log}\,\rho (t)\right\}\) and we finally write
Adiabatic quantum thermodynamics
Let us start by briefly reviewing the adiabatic dynamics in the context of open systems. To this end, let us consider the local master equation (in the superoperator formalism)
which describes a general time-local physical process in open systems. The dynamical generator \({\mathcal{L}}[\bullet ]\) is requested to be a linear operation, namely,
for any complex numbers α1,2 and matrices ρ1,2(t), with α1 + α2 = 1, because we need to satisfy \({\rm{Tr}}\left\{{\alpha }_{1}{\rho }_{1}(t)+{\alpha }_{2}{\rho }_{2}(t)\right\}=1\). Thus, by using this property of the operator \({\mathcal{L}}[\bullet ]\), it is possible to rewrite Eq. (27) as11
where \({\mathbb{L}}(t)\) and \(\left.\left|\rho (t)\right\rangle \right\rangle\) have been already previously defined. In general, due to the non-Hermiticity of \({\mathbb{L}}(t)\), there are situations in which \({\mathbb{L}}(t)\) cannot be diagonalized, but it is always possible to write a block-diagonal form for \({\mathbb{L}}(t)\) via the Jordan block diagonalization approach40. Hence, it is possible to define a set of right and left quasi-eigenstates of \({\mathbb{L}}(t)\), respectively, as
From the above equations, we can write the Jordan form of \({\mathbb{L}}(t)\) as
where N is the sum of the geometric multiplicities of all the distinct eigenvalues λα(t) and each block Jα(t) is given by
In the adiabatic dynamics of closed systems, the decoupled evolution of the set of eigenvectors \(\left|{E}_{n}^{{k}_{n}}(t)\right\rangle\) of the Hamiltonian associated with an eigenvalue En(t), where kn denotes individual eigenstates, characterizes what we call Schrödinger-preserving eigenbasis. In an analogous way, the set of right and left quasi-eigenstates of \({\mathbb{L}}(t)\) associated with the Jordan block Jα(t) characterizes the Jordan-preserving left and right bases. Here, we will restrict our analysis to a particular case where each block Jα(t) is one-dimensional, so that the set of quasi-eigenstates given in Eq. (30) becomes a genuine eigenstate equation given by
In this case, we can expand the matrix density \(\left.\left|\rho (t)\right\rangle \right\rangle\) in basis \(\left.\left|{{\mathcal{D}}}_{\alpha }(t)\right\rangle \right\rangle\) as
with rβ(t) being parameters to be determined. By using the Eq. (29), one gets the dynamical equation for each rβ(t) as
Now, we can define a new parameter pβ(t) as
so that one finds an equation for pβ(t) given by
with the first term in right-hand-side being the responsible for coupling distinct Jordan-Lindblad eigenspaces during the evolution. If we are able to apply some strategy to minimize the effects of such a term in the above equation, we can approximate the dynamics to
Then, the adiabatic solution rβ(t) for the dynamics can be immediately obtained from Eq. (36), which reads
where we already used pβ(t0) = rβ(t0). In conclusion, if the system undergoes an adiabatic dynamics along a non-unitary process, the evolved state can be written as
with \({\tilde{\lambda }}_{\alpha }(t)={\lambda }_{\alpha }(t)-\langle \langle {{\mathcal{E}}}_{\alpha }(t)| {\dot{{\mathcal{D}}}}_{\alpha }(t)\rangle \rangle\) being the generalized adiabatic phase accompanying the dynamics of the n-th eigenvector. The same mathematical procedure can be applied for multi-dimensional blocks11. In this scenario, let \(|\rho (0)\rangle \rangle ={\sum }_{i,{k}_{i}}{c}_{i}^{({k}_{i})}|{{\mathcal{D}}}_{i}^{({k}_{i})}(0)\rangle \rangle\) be the initial state of the system associated with the initial matrix density ρ(0). By considering a general adiabatic evolution, the state at a later time t will be given by11
with \({\tilde{\lambda }}_{i,{k}_{i}}(t)={\lambda }_{i}(t)-\langle \langle {{\mathcal{E}}}_{i}^{({k}_{i})}(t)| {\dot{{\mathcal{D}}}}_{i}^{({k}_{i})}(t)\rangle \rangle\), where \(\{\langle \langle {{\mathcal{E}}}_{i}^{({k}_{i})}(t)|\}\) and \(\{|{{\mathcal{D}}}_{i}^{({k}_{i})}(t)\rangle \rangle \}\) denote the instantaneous Jordan-preserving left and right bases of \({\mathbb{L}}(t)\), respectively11. Therefore, from Eq. (2), we can write the work dWop for an adiabatic dynamics as
On the other hand, when no work is realized, we can obtain the heat dQop for an adiabatic dynamics as
so that dQad represents the exchanged heat if no work is performed during such dynamics. Moreover, from Eq. (24), we can write the von Neumann entropy variation as
so that we can use the Eq. (30) to write
where \({\Gamma }_{i,{k}_{i}}(t)=\langle \langle {\rho }_{\mathrm{log}\,}^{{\rm{ad}}}(t)| {{\mathcal{D}}}_{i}^{({k}_{i}-1)}(t)\rangle \rangle +{\lambda }_{i}(t)\langle \langle {\rho }_{\mathrm{log}\,}^{{\rm{ad}}}(t)| {{\mathcal{D}}}_{i}^{({k}_{i})}(t)\rangle \rangle\), with \(\langle \langle {\rho }_{\mathrm{log}\,}^{{\rm{ad}}}(t)|\) standing for the adiabatic evolved state associated with \(\left\langle \left\langle {\rho }_{\mathrm{log}\,}(t)\right|\right.\).
Heat in adiabatic quantum processes
We will discuss how to determine infinite classes of systems exhibiting the same amount of heat exchange dQ. This is provided in Theorem 1 below.
Theorem 1
Let \({\mathcal{S}}\)be an open quantum system governed by a time-local master equation in the form \(\dot{\rho }(t)={\mathcal{H}}[\rho (t)]+{{\mathcal{R}}}_{t}[\rho (t)]\), where \({\mathcal{H}}[\bullet ]=(1/i\hslash )[H,\bullet ]\)and \({{\mathcal{R}}}_{t}[\bullet ]={\sum }_{n}{\gamma }_{n}(t)[{\Gamma }_{n}(t)\bullet {\Gamma }_{n}^{\dagger }(t)-(1/2)\{{\Gamma }_{n}^{\dagger }(t){\Gamma }_{n}(t),\bullet \}]\). The Hamiltonian H is taken as a constant operator so that no work is realized by/on the system. Assume that the heat exchange between \({\mathcal{S}}\)and its reservoir during the quantum evolution is given by dQ. Then, any unitarily related adiabatic dynamics driven by \({\dot{\rho }}^{\prime}(t)={{\mathcal{H}}}^{\prime}[{\rho }^{\prime}(t)]+{{\mathcal{R}}}_{t}^{\prime}[{\rho }^{\prime}(t)]\), where \({\dot{\rho }}^{\prime}(t)=U\dot{\rho }(t){U}^{\dagger }\), \({{\mathcal{H}}}^{\prime}[\bullet ]=U{\mathcal{H}}[\bullet ]{U}^{\dagger }\) and \({{\mathcal{R}}}_{t}^{\prime}[\bullet ]=U{{\mathcal{R}}}_{t}[\bullet ]{U}^{\dagger }\), for some constant unitary U, implies in an equivalent heat exchange \(d{Q}^{\prime}=dQ\).□
Proof
Let us consider that ρ(t) is solution of
so, by multiplying both sides of the above equation by U (on the left-hand-side) and U† (on the right-hand-side), we get
thus, by using the relations [UAU†, UBU†] = U[A, B]U† and {UAU†, UBU†} = U{A, B}U†, we find
where \({\Gamma }^{\prime}(t)=U{\Gamma }_{n}(t){U}^{\dagger }\). In conclusion, we get that \({\rho }^{\prime}(t)=U\rho (t){U}^{\dagger }\) is a solution of
where
Now, by taking into account that the Hamiltonian H is a constant operator, we have that no work is realized by/on the system. Then, by computing the amount of heat extracted from the system in the prime dynamics during an interval t ∈ [0, τ], we obtain
where, by definition, we can use \({\rho }^{\prime}(t)=U\rho (t){U}^{\dagger }\), ∀ t ∈ [0, τ]. Hence
where we have used the cyclical property of the trace and that \(\Delta Q={\rm{Tr}}\{H\rho (\tau )\}-{\rm{Tr}}\{H\rho (0)\}\). ■
As an example of application of the above theorem, let us consider a system-reservoir interaction governed by \({{\mathcal{R}}}_{t}^{{\rm{x}}}[\bullet ]=\gamma (t)\left[{\sigma }_{x}\bullet {\sigma }_{x}-\bullet \right]\) (bit-flip channel). We can then show that the results previously obtained for dephasing can be reproduced if the quantum system is initially prepared in thermal state of \({H}_{{\rm{y}}}^{0}=\omega {\sigma }_{y}\). Such a result is clear if we choose U = Rx(π/2)Rz(π/2). Then, it follows that \({{\mathcal{R}}}_{t}^{{\rm{x}}}[\bullet ]=U{{\mathcal{R}}}_{t}^{{\rm{z}}}[\bullet ]{U}^{\dagger }\) and \({{\mathcal{H}}}^{\prime}[\bullet ]=U{\mathcal{H}}[\bullet ]{U}^{\dagger }\), where Rz(x)(θ) are rotation matrices with angle θ around z(x)-axes for the case of a single qubit. Thus, the above theorem assures that the maximum exchanged heat will be \(\Delta {Q}_{\max }=\hslash \tilde{\omega }\tanh [\beta \hslash \omega ]\).
Let us discuss now the adiabatic dynamics under dephasing and heat exchange. Consider the Hamiltonian Hx = \(\hslash\)ωσx, where the system is initialized in the thermal of Hx at inverse temperature β. In this case, the initial state can be written as
If we rewrite the above state in superoperator formalism as the state \(\left.\left|{\rho }^{{\rm{x}}}(0)\right\rangle \right\rangle\), we can compute the components \({\rho }_{n}^{{\rm{x}}}(0)\) of \(\left.\left|{\rho }^{{\rm{x}}}(0)\right\rangle \right\rangle\) from \({\rho }_{n}^{{\rm{x}}}(0)={\rm{Tr}}\{\rho (0){\sigma }_{n}\}\), where σn = {\({\mathbb{1}}\), σx, σy, σz}. Thus we get
where we define the basis \(\left.\left|k\right\rangle \right\rangle ={[\begin{array}{cccc}{\delta }_{k1}&{\delta }_{kx}&{\delta }_{ky}&{\delta }_{kz}\end{array}]}^{t}\). If we drive the system under the master equation
the superoperator \({\mathbb{L}}(t)\) associated with the generator \({\mathcal{L}}[\bullet ]\) reads
Thus, it is possible to show that the set \(\{\left.\left|1\right\rangle \right\rangle ,\left.\left|x\right\rangle \right\rangle \}\) satisfies the eigenvalue equation for \({\mathbb{L}}(t)\) as
It can be shown that this eigenstates are nondegenerate. Therefore, if the dynamics is adiabatic, we can write the evolved state as \(\left.\left|{\rho }^{{\rm{x}}}(t)\right\rangle \right\rangle ={c}_{1}(t)\left.\left|1\right\rangle \right\rangle +{c}_{x}(t)\left.\left|x\right\rangle \right\rangle\), where cy(t) = cy(0) = 0 and cz(t) = cz(0) = 0 because the coefficients evolve independently form each other. Thus, from the adiabatic solution in open quantum system given in Eq. (41), we obtain c1(t) = 1 and \({c}_{x}(0)=-\tanh [\beta \hslash \omega ]\), so that we can use \({\tilde{\lambda }}_{1}=0\) and \({\tilde{\lambda }}_{x}=-2\gamma (t)\) to obtain
Notice that Eq. (7) in the main text directly follows by rewriting Eq. (58) in the standard operator formalism. Moreover, by using this formalism, it is also possible to show that the dephasing channel can be used as a thermalization process if we suitably choose the parameter γ(t) and the total evolution time τdec. In fact, we can define a new inverse temperature βdeph so that Eq. (58) behaves as thermal state, namely,
where we immediately identify
In particular, by using the mean value theorem, there is a value \(\bar{\gamma }\) so that \(\bar{\gamma }=(1/{\tau }_{{\rm{dec}}})\mathop{\int}\nolimits_{0}^{{\tau }_{{\rm{dec}}}}\gamma (t)dt\). Then, the above equation becomes
In addition, heat can be computed from Eq. (43) as
where we already used ci = 0, for i = y, z. Now, we can use that the vector \(\left\langle \left\langle h(t)\right|\right.\) has components hn(t) given by \({h}_{n}(t)={\rm{Tr}}\{\rho (0)H(t)\}\), in which H(t) is the Hamiltonian that acts on the system during the non-unitary dynamics. In conclusion, by using this result and Eq. (57), we get
Now, let us to use the mean-value theorem for real functions to write \(\bar{\gamma }=(1/\Delta t)\mathop{\int}\nolimits_{\!{0}}^{t}\gamma (\xi )d\xi\) within the interval Δt, so that we get \({e}^{-2\mathop{\int}\nolimits_{\!{0}}^{t}\gamma (\xi )d\xi }={e}^{-2\bar{\gamma }\Delta t}\). It shows that the higher the mean-value of γ(t) the faster the heat exchange ends. Now, by integrating the above result
To solve the above equation, we need to solve
where we can note that
Therefore, we can write the Eq. (65) as
where we used the mean-value theorem in the last step. Therefore, by using this result in Eq. (64), we find
In order to study the the average power for extracting/introducing the amount ∣ΔQ(τdec)∣, we define the quantity \(\bar{{\mathcal{P}}}({\tau }_{{\rm{dec}}})=| \Delta Q({\tau }_{{\rm{dec}}})| /{\tau }_{{\rm{dec}}}\), where τdec is the time interval necessary to extract/introduce the amount of heat ∣Q(τdec)∣. Thus, from the above equation we obtain
with \(\Delta {Q}_{\max }=\hslash \omega \tanh [\beta \hslash \omega ]\) and \(\eta ({\tau }_{{\rm{dec}}},\bar{\gamma })=(1-{e}^{-2\bar{\gamma }{\tau }_{{\rm{dec}}}})/{\tau }_{{\rm{dec}}}\). This result is illustrated in Fig. 3, where we have plotted \(\bar{{\mathcal{P}}}({\tau }_{{\rm{dec}}})\) during the entire heat exchange (within the interval τdec) as a function of τdec. Notice that, as in the case of ΔQ(τdec), the asymptotic behavior of the average power is independent of γ0.
Here we use ħω = 82.662 peV and β−1 = 17.238 peV, with the physical constants ħ ≈ 6.578 × 10−16 eV and kB ≈ 8.619 × 10−5 eV38.
For our dynamics, the entropy variation is obtained from Eq. (44) for a one-dimensional block Jordan decomposition. Thus, by computing \(\langle \langle {\rho }_{\mathrm{log}\,}^{{\rm{Ad}}}(t)|\), where we find
with \(g(t)={e}^{-2\mathop{\int}\nolimits_{\!{0}}^{t}\gamma (\xi )d\xi }\tanh (\beta \hslash \omega )\). Then, from Eq. (44) we get
where \({\Gamma }_{i}(t)={\lambda }_{i}(t)\langle \langle {\rho }_{\mathrm{log}\,}^{{\rm{ad}}}(t)| {{\mathcal{D}}}_{i}(t)\rangle \rangle\). Hence, from the set of adopted values for our parameters and the spectrum of the Lindbladian, we get
Trapped-ion experimental setup
We encode a qubit into hyperfine energy levels of a trapped Ytterbium ion 171Yb+, denoting its associated states by \(\left|0\right\rangle \equiv {\left.\right|}^{2}{S}_{1/2};F=0,m=0\left.\right\rangle\) and \(\left|1\right\rangle \equiv {\left.\right|}^{2}{S}_{1/2};F=1,m=0\left.\right\rangle\). By using an arbitrary waveform generator (AWG) we can drive the qubit through either a unitary or a non-unitary dynamics (via a frequency mixing scheme). The detection of the ion state is obtained from use of a “readout” laser with wavelength 369.526 nm.
Applying a static magnetic field with intensity 6.40 G, we get a frequency transition between the qubit states given by ωhf = 2π × 12.642825 GHz. Therefore, by denoting the states \(\left|0\right\rangle\) and \(\left|1\right\rangle\) as ground and excited states, respectively, the inner system Hamiltonian is given by
where \({\sigma }_{z}=\left|1\right\rangle \left\langle 1\right|-\left|0\right\rangle \left\langle 0\right|\). Therefore, to unitarily drive the system through coherent population inversions within the subspace \(\{\left|0\right\rangle ,\left|1\right\rangle \}\), we use a microwave at frequency ωmw whose magnetic field
interacts with the electron magnetic dipole moment \(\hat{\mu }={\mu }_{M}\hat{S}\), with μM a constant and \(\hat{S}\) is the electronic spin. Then, the system Hamiltonian reads
Thus, by defining the Rabi frequency \(\hslash {\Omega }_{{\rm{R}}}\equiv -{\mu }_{M}| {\overrightarrow{B}}_{0}| /4\)41, we obtain that the effective Hamiltonian that drives the qubit is (in interaction picture)
where ω = ωhf − ωmw and \({\sigma }_{x}=\left|1\right\rangle \left\langle 0\right|+\left|0\right\rangle \left\langle 1\right|\). By using the AWG we can efficiently control the parameters ω and ΩR. In particular, in our experiment to implement the Hamiltonian \({\tilde{H}}_{{\rm{x}}}\), we have used a resonant (ωmw = ωhf) microwave with Rabi frequency \({\Omega }_{{\rm{R}}}=\tilde{\omega }\), while the frequency ωhf has been adjusted around 2π × 12.642 GHz, with \(\tilde{\omega }\) modulated by using the channel 1 (CH1) of the AWG.
After the experimental qubit operation, we use the state-dependent florescence detection method to implement the quantum state binary measurement. We can observe on average 13 photons for the bright state \(\left|1\right\rangle\) and zero photon for the dark state \(\left|0\right\rangle\) in the 500 μs detection time interval, as shown in Fig. 4. These scattered photons at 396.526 nm are collected by an objective lens with numerical aperture NA = 0.4. After the capture of these photons, they go through an optical bandpass filter and a pinhole, after which they are finally detected by a photomultiplier tube (PMT) with 20% quantum efficiency. By using this procedure, the measurement fidelity is measured to be 99.4%.
Due to the long coherence time of the hyperfine qubit, the decoherence effects can be neglected in our experimental timescale. However, since we are interested in a nontrivial non-unitary evolution, we need to perform environment engineering. This task can be achieved by using a Gaussian noise source to mix the carrier microwave \({\overrightarrow{B}}_{{\rm{un}}}(t)\) by a frequency modulation (FM) method. Thus, by considering the noise source encoded in the function η(t) = Ag(t), where A is average amplitude of the noise and g(t) is a random analog voltage signal, the driving magnetic field will be in form
where \(| {\overrightarrow{B}}_{0}|\) is field intensity and C is the modulation depth supported by the commercial microwave generator E8257D. If C is a fixed parameter (for example, C = 96.00 KHz/V), the dephasing rate γ(t) associated with Lindblad equation
is controlled from the average amplitude of the Gaussian noise function η(t). To see that η(t) is a Gaussian function in the frequency domain, we show its spectrum in Fig. 5.
In order to certify that the decoherence channel is indeed a σz channel (dephasing channel) in our experiment, we employed quantum process tomography. A general quantum evolution can be typically described by the operator-sum representation associated to a trace-preserving map ε. For an arbitrary input state ρ, the output state ε(ρ) can be written as42
where Am are basis elements (usually a fixed reference basis) that span the state space associated with ρ and χmn is the matrix element of the so-called process matrix χ, which can be measured by quantum state tomography. In a single qubit system, we take A0 = I, A1 = σx, A2 = σy, A3 = σz. The quantum process tomography is carried out for the quantum process described by the Lindblad equation given by Eq. (78), where H(t) = ωσx, with ω = 5.0 × 2π KHz and γ = 2.5 KHz. We fixed the total evolution time as 0.24 ms (here, the noise amplitude is 1.62 V and the modulation depth is 96.00 KHz). The resulting estimated process matrix is shown in Fig. 6. We can calculate the fidelity between the experimental process matrix χexp and the theoretical process matrix χid
We measured several process with different evolution times. For example, when the amplitude of the noise is set to 1.54V, the process fidelities are measured as \({{\mathcal{F}}}_{{t}_{1}}=99.27 \%\), \({{\mathcal{F}}}_{{t}_{2}}=99.50 \%\), \({{\mathcal{F}}}_{{t}_{3}}=99.72 \%\), \({{\mathcal{F}}}_{{t}_{4}}=99.86 \%\) and \({{\mathcal{F}}}_{{t}_{5}}=99.87 \%\), at times t1 = 0.08 ms, t2 = 0.16 ms, t3 = 0.24 ms, t4 = 0.32 ms and t5 = 0.40 ms, respectively. Thus, the dephasing channel can be precisely controlled as desired and it can support the scheme to implement the time-dependent dephsing in experiment.
The function η(t) depends on an amplitude parameter A, which is used to control γ(t). As shown in Fig. 7, we experimentally measured the relation between A and γ(t) for a situation where γ(t) is a time-independent value γ0. As result, we find a linear relation between \(\sqrt{{\gamma }_{0}}\) and A, which reads
For the case A = 0, we get the natural dephasing rate γnd = 1.742 Hz of the physical system. Thus, we can see that, if we change the parameter A, which we can do with high controllability, the quantity \(\sqrt{{\gamma }_{0}}\) can be efficiently controlled. On the other hand, if we need a time-dependent rate γ(t), we just need to consider a way to vary A as a function A(t). To this end, we use a second channel (CH2) of the AWG to perform amplitude modulation (AM) of the Gaussian noise. The temporal dependence of A(t) is achieved by programming the channel (CH2) to change during the evolution time.
a Rabi oscillations between states \(\left|0\right\rangle\) and \(\left|1\right\rangle\) under different noise intensities. From top to bottom, the noise amplitude is set to 0.4 V, 0.8 V, 1.2 V, 1.6 V and 2.0 V, with the corresponding damping rates 182 Hz, 650 Hz, 1426 Hz, 2469 Hz and 3846 Hz, respectively. b Dephasing rate as a function of the noise amplitude. Points are measured data. A linear fit is obtained. Without driving noise (noise amplitude is zero), the dephasing rate of the qubit is fitted as 3.03 Hz, which is caused by the magnetic fluctuation in the laboratory.
In order to guarantee that the dynamics of the system is really adiabatic11 we compute the fidelity \({\mathcal{F}}({\tau }_{{\rm{dec}}})\) of finding the system in a path given by Eq. (5), where \({\mathcal{F}}(t)={\rm{Tr}}\left\{{\left[{\rho }_{{\rm{exp}}}^{1/2}(t){\rho }_{{\rm{ad}}}(t){\rho }_{{\rm{exp}}}^{1/2}(t)\right]}^{1/2}\right\}\), with ρad(t) the density matrix provided Eq. (5) and ρexp(t) the experimental density matrix obtained from quantum tomography. In Table 1 we show the minimum experimental fidelity \({{\mathcal{F}}}_{{\rm{min}}}=\mathop{\min }\nolimits_{{\tau }_{{\rm{dec}}}}{\mathcal{F}}({\tau }_{{\rm{dec}}})\) for several choices of the parameter γ0. This result shows that the system indeed evolves as predicted by the adiabatic solution for every γ0 and τdec with excellent experimental agreement.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
Code availability
The code that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Farhi, E. et al. A quantum adiabatic evolution algorithm applied to random instances of an np-complete problem. Science 292, 472–475 (2001).
Bacon, D. & Flammia, S. T. Adiabatic gate teleportation. Phys. Rev. Lett. 103, 120504 (2009).
Bacon, D., Flammia, S. T. & Crosswhite, G. M. Adiabatic quantum transistors. Phys. Rev. X 3, 021015 (2013).
Albash, T. & Lidar, D. A. Adiabatic quantum computation. Rev. Mod. Phys. 90, 015002 (2018).
Kieu, T. D. The second law, maxwell’s demon, and work derivable from quantum heat engines. Phys. Rev. Lett. 93, 140403 (2004).
Maruyama, K., Nori, F. & Vedral, V. Colloquium: The physics of maxwell’s demon and information. Rev. Mod. Phys. 81, 1–23 (2009).
Abah, O. & Lutz, E. Energy efficient quantum machines. Europhys. Lett. 118, 40005 (2017).
Born, M. & Fock, V. Beweis des adiabatensatzes. Z. f.ür. Phys. A Hadrons Nucl. 51, 165 (1928).
Kato, T. On the adiabatic theorem of quantum mechanics. J. Phys. Soc. Jpn. 5, 435–439 (1950).
Messiah, A. Quantum Mechanics (North-Holland Publishing Company, 1962).
Sarandy, M. S. & Lidar, D. A. Adiabatic approximation in open quantum systems. Phys. Rev. A 71, 012331 (2005).
Sarandy, M. S. & Lidar, D. A. Adiabatic quantum computation in open systems. Phys. Rev. Lett. 95, 250503 (2005).
Sarandy, M. S., Wu, L.-A. & Lidar, D. A. Consistency of the adiabatic theorem. Quantum Inf. Process. 3, 331–349 (2004).
Venuti, L. C., Albash, T., Lidar, D. A. & Zanardi, P. Adiabaticity in open quantum systems. Phys. Rev. A 93, 032118 (2016).
Oreshkov, O. & Calsamiglia, J. Adiabatic markovian dynamics. Phys. Rev. Lett. 105, 050503 (2010).
Thunström, P., Åberg, J. & Sjöqvist, E. Adiabatic approximation for weakly open systems. Phys. Rev. A 72, 022328 (2005).
Albash, T., Boixo, S., Lidar, D. A. & Zanardi, P. Corrigendum: quantum adiabatic markovian master equations (2012 new j. phys. 14 123016). New J. Phys. 17, 129501 (2015).
Talkner, P., Lutz, E. & Hänggi, P. Fluctuation theorems: Work is not an observable. Phys. Rev. E 75, 050102 (2007).
Alicki, R. The quantum open system as a model of the heat engine. J. Phys. A: Math. Gen. 12, L103 (1979).
Rivas, A. Strong coupling thermodynamics of open quantum systems. Phys. Rev. Lett. 124, 160601 (2020).
Guarnieri, G., Morrone, D., Cakmak, B., Plastina, F. & Campbell, S. Non-equilibrium steady-states of memoryless quantum collision models. Phys. Lett. A 384, 126576 (2020).
Alipour, S., Rezakhani, A. T., Chenu, A., del Campo, A. & Ala-Nissila, T., Unambiguous formulation for heat and work in arbitrary quantum evolution. Preprint at https://arxiv.org/abs/1912.01939 (2019).
Ahmadi, B., Salimi, S. & Khorashad, A. S., Refined definitions of heat and work in quantum thermodynamics. Preprint at https://arxiv.org/abs/1912.01983 (2019).
Anders, J. & Giovannetti, V. Thermodynamics of discrete quantum processes. New J. Phys. 15, 033022 (2013).
Geva, E. & Kosloff, R. A quantum-mechanical heat engine operating in finite time. a model consisting of spin-1/2 systems as the working fluid. J. Chem. Phys. 96, 3054–3067 (1992).
Zhang, T., Cai, L.-F., Chen, P.-X. & Li, C.-Z. The second law of thermodynamics in a quantum heat engine model. Commun. Theor. Phys. 45, 417 (2006).
Quan, H., Liu, Y.-X., Sun, C. & Nori, F. Quantum thermodynamic cycles and quantum heat engines. Phys. Rev. E 76, 031105 (2007).
Esposito, M. & Van den Broeck, C. Three detailed fluctuation theorems. Phys. Rev. Lett. 104, 090601 (2010).
Deffner, S. & Lutz, E. Generalized clausius inequality for nonequilibrium quantum processes. Phys. Rev. Lett. 105, 170402 (2010).
Plastina, F. et al. Irreversible work and inner friction in quantum thermodynamic processes. Phys. Rev. Lett. 113, 260601 (2014).
Breuer, H.-P. & Petruccione, F. The Theory of Open Quantum Systems. (Cambridge University Press, Oxford University Press, Oxford, UK, 2007).
Plenio, M. B. & Knight, P. L. The quantum-jump approach to dissipative dynamics in quantum optics. Rev. Mod. Phys. 70, 101–144 (1998).
Li, D., Wu, S., Shen, H. & Yi, X. Adiabatic evolution of an open quantum system in its instantaneous steady state. Int. J. Theor. Phys. 56, 3562–3571 (2017).
Henrich, M. J., Rempp, F. & Mahler, G. Quantum thermodynamic otto machines: a spin-system approach. Eur. Phys. J. Spec. Top. 151, 157–165 (2007).
Roßnagel, J. et al. A single-atom heat engine. Science 352, 325–329 (2016).
Olmschenk, S. et al. Manipulation and detection of a trapped yb+ hyperfine qubit. Phys. Rev. A 76, 052314 (2007).
Hu, C.-K. et al. Experimental implementation of generalized transitionless quantum driving. Opt. Lett. 43, 3136–3139 (2018).
Mohr, P. J., Newell, D. B. & Taylor, B. N. Codata recommended values of the fundamental physical constants: 2014. Rev. Mod. Phys. 88, 035009 (2016).
Vacanti, G. et al. Transitionless quantum driving in open quantum systems. New J. Phys. 16, 053017 (2014).
Horn, R. A. & Johnson, C. R. Matrix analysis. 2nd edn (Cambridge University Press, Cambridge, 2012).
Wineland, D. J. et al. Experimental issues in coherent quantum-state manipulation of trapped atomic ions. J. Res. Natl Inst. Stan. 103, 259 (1998).
Nielsen, M. A. & Chuang, I. L. Quantum computation and quantum information: 10th anniversary edition (Cambridge University Press, New York, NY, USA, 2011).
Acknowledgements
We thank Yuan-Yuan Zhao, Zhibo Hou, Jun-Feng Tang, and Yue-xin Huang for valuable discussion. This work was supported by the National Key Research and Development Program of China (No. 2017YFA0304100), National Natural Science Foundation of China (Nos. 11734015, 11774335), Anhui Initiative in Quantum Information Technologies (AHY070000, AHY020100), Anhui Provincial Natural Science Foundation (No. 1608085QA22), Key Research Program of Frontier Sciences, CAS (No. QYZDY-SSWSLH003), the Fundamental Research Funds for the Central Universities (WK2470000026, WK2470000027, WK2470000028), and the China Postdoctoral Science Foundation (Grant No. 2020M671861). A.C.S. is supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq-Brazil). M.S.S. is supported by CNPq-Brazil (No. 303070/2016-1) and Fundação Carlos Chagas Filho de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ) (No. 203036/2016). D.O.S.P is supported by Brazilian funding agencies CNPq (Grants No. 142350/2017-6 and 305201/2016-6), and FAPESP (Grant No. 2017/03727-0). A.C.S., D. O. S.-P. and M.S.S. also acknowledge financial support in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) (Finance Code 001) and by the Brazilian National Institute for Science and Technology of Quantum Information [CNPq INCT-IQ (465469/2014-0)]. A.C.S., D. O. S.-P. and M.S.S. would like to thank F. Brito and J. G. Filgueiras for fruitful comments.
Author information
Authors and Affiliations
Contributions
A.C.S., D.O.S.-P. and M.S.S. developed and performed the theoretical analysis. C.-K.H., J.-M.C., Y.-F.H. and C.-F.L. designed the experiment. C.-K.H., J.-M.C. and Y.-F.H. performed the experiment. C.-K.H., Y.-F.H., A.C.S., D.O.S.-P. and M.S.S. wrote the manuscript. C.-F.L. and G.-C.G. supervised the project. All authors discussed and contributed to the analysis of the experimental data.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hu, CK., Santos, A.C., Cui, JM. et al. Quantum thermodynamics in adiabatic open systems and its trapped-ion experimental realization. npj Quantum Inf 6, 73 (2020). https://doi.org/10.1038/s41534-020-00300-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-020-00300-2
This article is cited by
-
Quantum control operations with fuzzy evolution trajectories based on polyharmonic magnetic fields
Scientific Reports (2020)