Abstract
Hybrid architectures combining complementary quantum systems will be largely used in quantum technologies and the integration of different components is one of the key issues. Thanks to their long coherence times and the easy manipulation with microwave pulses, electron spins hold a potential for the realization of quantum memories. Here, we test diluted oxovanadium tetraphenyl porphyrin (VO(TPP)) as a prototypical molecular spin system for the Storage/Retrieval of microwave pulses when embedded into planar superconducting microwave resonators. We first investigate the efficiency of several pulse sequences in addressing the spins. The Carr-Purcell and the Uhrig Dynamical Decoupling enhance the memory time up to three times with three π pulses. We then successfully store and retrieve trains of up to 5 small pulses by using a single recovery pulse. These results demonstrate the memory capabilities of molecular spin ensembles when embedded into quantum circuits.
Similar content being viewed by others
Introduction
Quantum memories are fundamental components in quantum hardware like quantum computers, sensors or repeaters. To perform Storage/Retrieval operations the physical system must fulfill two conditions: (i) having a phase memory time Tm (this one being the characteristic lifetime the hardware can sustain coherent dynamics) long enough to allow for the survival of the information during operation and (ii) allow for the possibility of codifying a pulse sequence into the memory through a suitable protocol1. Nuclear spin ensembles have been demonstrated to work as efficient quantum memories operating at radio frequencies2,3,4. Spin states of magnetic impurities and color centers in silicon or diamond with long Tm3,5,6 can be individually or collectively addressed by combining microwave (MW) excitations with their photoluminescent properties. In the perspective of scalable platforms however, hybrid architectures working with a single frequency mode allows for a simplification of the design of the platforms. Avoiding multiple frequency conversion is also highly desirable. Electronic spin degrees of freedom provided by ensembles have been efficiently exploited into circuit quantum electrodynamics (cQED) architectures including superconducting devices and resonators7,8,9 fully operating at microwave frequency. Although the use of individual (natural or artificial) spins is the ultimate goal10 collective excitations in spin ensembles may preserve and coherently exchange electromagnetic excitations, and eventually quantum information, under optimal conditions8,9,11,12. In this context, molecular spins have recently emerged as a new class of quantum systems whose electronic and nuclear spin states and their relative quantum features (including g-factor13,14, coherence time15,16,17, “atomic-clock” transitions13,18,19) can be extensively tailored synthetically. Different strategies for encoding quantum information protocols into molecular ensembles20,21 or single molecules in a spin transistor geometry22,23 have been developed and experimentally proven. The magnetic coupling and the integration of molecular spins into planar resonant geometries has been extensively investigated24,25,26,27. Moreover, the coherent coupling with MW photons has been recently achieved using transition metal-based oxovanadium(IV) complexes28,29, as well as organic radicals29,30,31 embedded into planar resonant geometries, paving the way for the integration of molecular spin ensembles into microwave quantum architectures. However, optimal experimental conditions and protocols (i.e., pulse sequences) to address the spins and to correct intrinsic (related to the ensemble) or extrinsic factors (such as inhomogeneities of resonant geometry) that may limit Tm still need to be discovered in order to efficiently encode and exchange states of qubits between spins and superconducting circuits.
In this work we test an oxovanadium(IV) complex, VO(TPP) (where TPP is the tetraphenylporphyrin)32 as a prototypical molecular spin system embedded into a planar superconducting microwave resonator by addressing it with several MW pulse sequences. Previous Pulsed Wave (PW) Electron Spin Resonance (ESR) study performed with a commercial spectrometer gave a (Hahn echo) Tm ≈ 1 μs at 4 K, with essentially no temperature dependence between 4 and 30 K32. Rabi oscillations were observed up to room temperature, consistent with that reported for similar oxovanadium(IV) complexes33,34,35. We first measure the phase memory time of diluted single crystal samples with the Hahn echo sequence and we then test two dynamical decoupling sequences: the Carr-Purcell-Meiboom-Gill (hereafter CP) sequence and the Uhrig Dynamical Decoupling (hereafter DD) sequence. These protocols are widely used to dynamically decouple the spins from environmental sources of decoherence and, hence, are expected to enhance Tm36,37,38,39. Although the efficiency of CP and DD sequences has been previously investigated on spin impurities in inorganic matrices40,41,42 and in organic molecules43,44,45 (including radicals39,46) coupled to conventional (3-dimensional) ESR cavities, their efficiency still needs to be tested on molecular spins in working conditions1,21. Here we report, for the first time to the best of our knowledge, an extensive study concerning the PW manipulation of molecular spins embedded into planar resonators. We finally demonstrate the use of VO(TPP) spin ensembles as storage memories for trains of weak MW excitations, in which their individual and selective control9,47,48,49 is achieved.
Results
Experimental details
We use VO(TPP) molecular spin ensembles 2% diluted in a diamagnetic isostructural analogue, oxotitanium tetraphenylporphyrin (TiO(TPP)), both as a single crystal and as a polycrystalline powder. The d1 electronic configuration and the square pyramidal coordination of V(IV) provide an orbitally non-degenerate S = 1/2 ground state that is split by the hyperfine interaction with the I = 7/2 nuclear spin of the 51V ion32 (natural abundance 99.95%, see Supplementary Section 2.2 for further details).
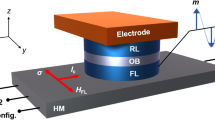
Transmission spectroscopy is done by placing our samples on a superconducting coplanar resonator (ν0 ≈ 6.85 GHz) made from superconducting YBa2Cu3O7 (YBCO) films on a Sapphire substrate28,50, as depicted in Fig. 1.a. Here, the static magnetic field B0 is applied along the direction of the longitudinal axis of the resonator (red arrow), while the sample couples to the magnetic component of the resonant MW mode (B1), which oscillates in the plane perpendicular to B0. The MW excitation is injected and collected through two feed antennas placed in proximity of the resonant strip (yellow cylinders with green arrows, see “Methods” section and Supplementary Sections 1.2 and 1.3). The generation of the MW pulses and the time domain acquisition is done with a home-made heterodyne spectrometer, which is based on an Arbitrary Waveform Generator (see “Methods” section and Supplementary Section 1.4). A commercial Quantum Design Physical Properties Measurement System (QD PPMS) is used to cool-down the sample and to apply the external static magnetic field (see Supplementary Section 1.3).
a Pictorial sketch of the coplanar resonator with a VO(TPP) crystal on it. Green arrows represent the direction of the MW signal while the red arrow represents the applied static magnetic field B0. Yellow cylinders are the tunable coupling antennas. b Comparison between the CW spectra for the VO(TPP) crystal sample (red) measured at 2 K and its corresponding EasySpin51 simulation (blue). c Echo-Detected Field-sweep (EDFS) spectrum acquired for a single crystal at 2 K. The rescaled CW spectrum (gray dashed line, with offset) is added for comparison.
Continuous wave transmission spectroscopy
The normalized Continuous Wave (CW) transmission spectrum for the 2% single crystal is reported in Fig. 1.b. The spectrum shows eight lines, as expected by the presence of the hyperfine split of the VO2+ moiety. Their spacing is consistent with the orientation of the static field perpendicular to the V=O double bond. The latter coincides with the z molecular axis and the c crystallographic axis of the tetragonal VOTPP crystal, as evidenced by the simulation performed with the EasySpin software51 (blue line). Here, the spectrum is modeled assuming a Gaussian strain of the hyperfine tensor \({}^{{\rm{V}}}\widehat{{\bf{A}}}\) acting on a Voigtian lineshape (see “Methods” section and Supplementary Section 2.2). We additionally test the 2% polycrystalline sample at 2 K and found that the spectrum shows lines arising from microcrystals oriented parallel and perpendicular to the static magnetic field, consistent with that previously reported in refs 28,33 and observed by conventional ESR spectroscopy32 (see Supplementary Fig. 9).
In the following we focus on the line at ∣B0∣ = 0.24 T of the crystal spectrum. The intrinsic homogeneous linewidth of the ensemble, γhom, is related to the spin-spin (T2) and to the spin-lattice (T1) relaxation rates according to the relation:
where γe is the electronic gyromagnetic ratio and B1 is the MW magnetic field52. At our working temperatures (2 K) γhom is dominated by T232. As for conventional ESR spectroscopy, T2 is bound by the phase memory time, Tm ≤ T253, which is the one effectively measured by ESR. In turns, this gives an upper limit γhom ≤ 1/Tm ≈ 1/(1 μs) = 1 MHz (taking the values in ref. 32 and assuming no line saturation), which is well below our measured CW linewidth (see Supplementary Section 2.1 and Supplementary Fig. 6). The upper limit of γhom evidences that the main line broadening contribution in the CW spectrum is inhomogeneous, and related to both intrinsic (sample) and extrinsic (resonator) features (see ref. 28 for a discussion under similar experimental conditions). The main intrinsic sources of broadening are the dipolar spin-spin interaction, the hyperfine interaction and its strain, and the presence of an additional unresolved super-hyperfine interaction with Nitrogen (see Supplementary Fig. 10 and ref. 28). In the experiments carried out with superconducting planar resonators, we expect the magnetic field distributions to be the main extrinsic source of broadening. In particular, a non negligible static magnetic field gradient (≈0.5 T ⋅ m−1) develops along the longitudinal axis of our resonator28,30, thus giving rise to an inhomogeneous magnetic field around the externally applied field B0. This implies the presence of a distribution of spin precession frequencies, resulting in a CW line broadening and fast spin dephasing after each single MW pulse. The inhomogeneity of B1 also contributes to broadening: since the spins are not excited in the same way during the application of the MW excitation, their precession is smeared around the direction given by the nominal pulse angle54,55.
Hahn echo sequence and Rabi oscillations
We first test standard ESR manipulations on our samples, starting from the Hahn Echo sequence52,56 (see Supplementary Section 1.5). Fig. 1c shows the Echo-Detected Field-Sweep (EDFS) spectrum for the 2% VO(TPP) crystal (the rescaled CW transmission intensity is also plotted for comparison). The EDFS shows at a glance that pulses can address all the molecular transitions through the planar resonator. Each of them gives an echo, thus eight resonance lines are visible at their corresponding magnetic field values. In a similar way, the echo is found also for the polycrystalline sample (see Supplementary Fig. 11a). We measure the decay of the Hahn echo for different inter-pulse delays, tdelay, and we fit it with the equation:
In Eq. (2) Tm is the memory time, while x is a stretching exponent. I(t) is the echo integral, t0 is the initial sequence time, and t = ∑#delaytdelay + ∑#pulsetpulse is the total sequence time (being tpulse the duration of each pulse).
For the 2% diluted crystal the fitted memory time is Tm = 0.97 ± 0.10 μs (with x = 1.2 ± 0.1), which is close to the one measured for the 2% polycrystalline sample (Tm = 1.04 ± 0.10 μs). The latter is also consistent with the one reported in ref. 32 from conventional X-band ESR (for similar temperatures). The agreement with conventional ESR indicates that the Hahn echo sequence efficiently overcomes the Free Induction Decay (FID) limit and lead us to conclude that the measured memory time essentially results from the spin dynamics (i.e., only from intrinsic effects of the sample)47,48. In other words, the Hahn sequence is correcting the inhomogeneities of the static magnetic field B048. The observation of the Rabi oscillations on both crystal and polycrystalline samples, together with their characteristic linear frequency dependence on the MW magnetic field intensity (see Supplementary Section 2.5), further corroborates the capability to coherently manipulate the spin ensemble with the pulsed MW field B1 delivered through our superconducting resonator.
Dynamical decoupling sequences
Thanks to the successful manipulation achieved with the Hahn Echo, we now extend our pulse sequences by considering two dynamical decoupling protocols. Each sequence will be identified as CPN (Carr-Purcell-Meiboom-Gill) or DDN (Uhrig Dynamical Decoupling), with N the number of π pulses sent. The pulse patterns of the two sequences are sketched in Figs. 2a and b for the case N = 3.
Carr-Purcell-Meiboom-Gill (CP) and Uhrig Dynamical Decoupling (DD) sequences for different numbers N of π pulses (CPN or DDN). a, b Sketches of the pulse patterns for N = 3. The relevant delays (\(\tau ,\ {t}^{\prime}\)) used in this work are reported (continuous or dashed black arrows, not in scale) and only the echoes of interest are shown (see Supplementary Section 1.5). Green dashed line in a shows the decay of the echo train. c, d Echo integral as a function of time t − t0 for the decoupling sequences (CP and DD, respectively) on the 2% VO(TPP) crystal at 2 K and ∣B0∣ = 0.24 T. Dashed lines are fits based on Eq. (2). e Comparison between the memory times obtained from the fits of the curves in c and d as a function of the number of π pulses.
The decay of the echo integral as a function of time for the crystal at 2 K and for both CP and DD is shown in Figs. 2c and d, respectively. In both cases the phase memory time clearly increases with N. We fit the data of Fig. 2 with Eq. (2) (dashed lines), leaving Tm and x as free parameters. For the CP sequences a stretch parameter x ≈ 1.2, independent of the number of applied pulses, is obtained as best fit parameter57,58. For the DD sequences, the stretch exponent is found to be x ≈ 1 for all the data set. All the obtained Tm’s are summarized in Fig. 2.e. Both sequences progressively enhance Tm up to 3 μs, that is ≈3 times longer with respect to the one found with the Hahn echo sequence. The increasing trend suggests that further enhancement of Tm can be expected in both sequences by applying a larger number of pulses, even if the small echo intensity found in our experimental conditions limits us to N = 3 (DD) or N = 4 pulses (CP). Although similar enhancement is observed, a larger number of π pulses (N = 4) is needed for CP with respect to DD (N = 3) to obtain similar Tm values, suggesting that the latter control sequences are more efficient in decoupling the spins from the environment36,37,59.
Our results show that both CP and DD protocols can address and correct the dephasing effects and, since a single π pulse (i.e. the Hahn sequence) essentially corrects inhomogeneities of the static magnetic field (see above), we can ultimately attribute the observed phenomenology (Fig. 2e) to the intrinsic spin dynamics of the sample. We might also argue that the different efficiency of CP and DD sequences is due to the fact they address different spectral portions of the environmental noise distribution36,38,42. However, a more detailed analysis of this latter point would require a dedicated work. Although polycrystalline samples provide larger echo signals than single crystal ones, thus allowing the application of longer sequences (up to N = 5), we find both the DD and the CP protocols to be no more progressively efficient with increasing N than the single crystal (see Supplementary Section 2.6 and Supplementary Fig. 13).
Storage and retrieval of MW excitations
To test the viability of the VO(TPP) ensembles as storage memories, we send a train of weak MW pulses followed by a π pulse at 2 K and ∣B0∣ = 0.24 T, as depicted in Fig. 3a (see Supplementary Section 1.5). An increasing number of output echos is found as the number of input pulses is increased (Fig. 3b), and up to 3 well resolved echoes, corresponding to 3 weak input pulses, can be detected with the single crystal under our experimental conditions. Similar results are found also for the powder sample, for which the larger echo signal allows the storage and retrieval of up to 5 pulses (Fig. 4a). These observations reflect the memory effect of the spin ensemble in the precession of the spins9,47,48: once the MW excitations are sent (stored) into the ensemble, the spins dephase until the refocusing π pulse is applied. At this point the excitations are retrieved as an echo train. In other words, the ensemble has kept trace of the initial excitations9,47,48,60.
a Sketch of the pulse pattern used and of the echo train for the case of 3 weak excitations. The delays and the amplitudes are not in scale. b Echo trains measured for increasing number of input pulses on 2% VO(TPP) crystal at 2 K and at ∣B0∣ = 0.24 T. Vertical dashed lines help in recognizing the echo positions.
a Echo trains measured for increasing number of input pulses. b Selective on/off of the input MW excitations for the case of 5 input pulses. The labels show which input pulses are on (1) or off (0). Vertical dashed lines help in recognizing the echo positions. Data in a and b are taken at 2 K and on the main line of the powder sample.
It is worth noting that the duration of the free spin precession after all the excitations have been stored is tprec ≥ 2τ = 2.2 μs >Tm, being τ = 1.1 μs the inter-pulse delay of Fig. 3a (the shortest value between the one used for powder and crystal was used here). Note also that the decay time of the echo train is consistent with the intrinsic Hahn echo Tm, corroborating the fact that the Storage/Retrieval is essentially limited by dephasing processes within the sample and not by the resonator (see Supplementary Fig. 16).
The larger echo signals observed on the powder sample allow us to manipulate sequences of five pulses. For instance we selectively turn on (1) and off (0) the second, the third and the fourth input pulse with respect to the others and then the second and the fourth together, as in Fig. 4b. As a consequence the number of the output echoes changes, depending on which pulses are switched on/off. Interestingly, this allows us to verify that the order of the output echoes is reversed with respect to the input excitations, as expected by the time reversal (refocusing) of the π pulse. Similar selectivity and control on the output echoes is observed also for the single crystal and even when the magnetization of the ensemble is firstly rotated by an arbitrary rotation angle (Supplementary Figs 15 and 17).
Discussion
Overall, our results show viable paths for the integration of molecular spin ensembles into hybrid quantum circuits. More specifically we successfully apply protocols to store and retrieve sequences of MW pulses into the molecular ensembles. Further analysis of our results indicates that with regard to true quantum memories there are large margins of improvement, as we are going to discuss in the following section.
Firstly, it should be kept in mind that our experiments are performed at 2 K, with relatively high photon numbers (nph ≈ 1011 for π/2, π pulses and nph ≈ 109 for the weak ones, see Supplementary Table 3 and Supplementary Section 2.7) and with effective numbers of spins ≈ 1015−1016 ≫ nph (see Supplementary Section 2.1). While these working conditions can be suitable for some applications, they are still far from the typical ones required by quantum circuits. In fact, these operate at much lower temperatures (mK, that is two order of magnitude below) and make use of spin excitations with much lower photon numbers (nph ≈ 1 − 100, that is several orders of magnitude lower)9,48. Note that the limit set by our working conditions is rather technological than fundamental and it can be overcome with the currently available MW and cryogenic instrumentation and techniques. For instance, lowering the temperature (down to ≈ tens-a hundred of mK) will help in increasing the spin polarization. Moreover, an increased dilution of the spins might lead to a further increase in Tm. Finally, since the decay of the echo train is dominated by Tm, one might wonder whether it is possible to extend the memory capability (i.e., the number of storable echoes, see below) by combining the Storage/Retrieval protocol with a dynamical decoupling sequence. Based on our results on a single crystal, this can be achieved on ordered arrays of (molecular) spins by using a proper optimization of the pulse sequences and by increasing the sensitivity of the set-up61. These latter improvements would also help in applying sequences with larger number of pulses.
It is also interesting to consider two figures of merit of our molecular spin memory and to compare them with the ones obtained in similar Storage/Retrieval experiments performed on alternative platforms based on e.g., Nitrogen Vacancy (NV) centers8,48 or Er3+ ions-doped inorganic crystals9. The first one is the memory capability, i.e., the maximum number of pulses which can be stored. This is defined as \(\#M={T}_{{\rm{m}}}/{T}_{{\rm{m}}}^{* }\)47,48, where \({T}_{{\rm{m}}}^{* }\) is the FID limit of the ensemble. By taking Tm ≈ 1 μs and \({T}_{{\rm{m}}}^{* }\approx 120\) ns (the typical decay time of the Rabi Oscillations for the crystal, see Supplementary Section 2.5) we get an upper limit #M ≈ 8, which is larger than the number of echoes found in our experiments. This is due to the weak signals measured under our experimental conditions. Further optimization of the pick up element61 and additional echo signal amplification would allow for implementation and use of longer pulse sequences. The second figure of merit is the echo efficiency, which is defined as the ratio between the energy radiated during the echo and the energy of the incoming pulse48. An estimate for our samples gives E ≈ 4.5 ⋅ 10−5 (see Supplementary Section 2.7). With these values in mind, it is instructive to directly compare our results with similar experiments reported in the literature. In refs 8,48 NV center spin ensembles embedded into planar superconducting resonant geometries (ν0 ≈ 2.88 GHz) at much lower temperature (T = 100–400 mK) are used. In these cases the Storage/Retrieval protocol is demonstrated by using 6 input pulses and by retrieving their 6 corresponding output echoes, which is close to our measured number of 5 echoes. In addition, a laser for the reset of the magnetization, not needed in our case, is also used to reduce the repetition time of the experiments. The efficiency is E = 2 ⋅ 10−4 (only one order of magnitude larger, despite the different working conditions described above). In ref. 9 the storage and retrieval protocol is demonstrated with an ensemble of Er3+ ions-doped inorganic crystal coupled to a copper coplanar resonator (ν0 ≈ 3.75 GHz) at a temperature of 25–50 mK. Up to 16 pulses (but with #M = 56) are retrieved and the efficiency achieved is E = 10−4.
In summary we performed pulsed ESR manipulation of a VO(TPP) molecular spin ensembles embedded into a planar superconducting geometry to test their potential viability as quantum memories. We first demonstrate that the ensemble can be efficiently addressed through the most common sequences of ESR spectroscopy, such as Hahn Echo, Echo-Detected Field-Sweep and Rabi Oscillations. We then test the efficiency of two different dynamical decoupling sequences in preserving the memory time of the molecular ensembles. This is found to progressively increase on the single crystal with both CP and DD, becoming 3 times longer (with only N = 3 or N = 4 applied pulses) with respect to the Hahn echo sequence (N = 1). The results also suggest that further margins for improvement are possible on single crystal samples. Finally in a proof-of-concept experiment we demonstrate that the ensembles can be used to successfully store and retrieve trains of up to 5 input pulses (excitations). Here, the typical figure of merit defined for a spin memory compares well to the values reported in the literature, despite the more limiting experimental conditions. The individual control achievable on the excitations further corroborates the possibility to codify information inside the ensemble. After the acceptance of this work, we learnt about two preprints concerning the implementation of quantum memories on the clock-transition provided by ensembles of bismuth donors in silicon coupled to planar superconducting resonators62,63.
Methods
VO(TPP) samples
The details about the synthesis of the samples, their crystal structure and their preliminary characterization are given in ref. 32 and in the Supplementary Section 1.1. We report here that TiO(TPP):VO(TPP) crystals assume the shape of an octahedron with well developed (±1, ±1, ±1) faces and dimensions of ≈1 × 1 × 1 mm3. The long axis of the octaedron corresponds to the direction of the V=O bond32. This gives some hints in recognizing the orientation of the crystals on the resonator, since the crystals are mounted to have the z axis of the molecular framework perpendicular to the surface of the resonator (i.e., the V=O direction perpendicular to the applied magnetic field B0). The polycrystalline sample is compressed in pellets with diameter of ≈5 mm and thickness of ≈1−2 mm.
Coplanar resonator
The resonant strip is 8 mm long and 600 μm wide, while the gap between the strip and the ground planes on two sides is 800 μm. These dimensions give a fundamental quasi-TEM (Transverse Electromagnetic) mode at ν0 ≈ 6.85 GHz, with the MW field B1 almost entirely in the plane perpendicular to the direction of the longitudinal axis of axis of the resonator (Fig. 1.a and Supplementary Figs 1 and 2). The maximum for the MW magnetic component is located in the middle of the resonant strip, at the position where the sample is placed (Fig. 1.a). Additional details are reported in Supplementary Section 1.2.
Pulsed-wave heterodyne spectrometer
The generation of the MW pulses is based on an Arbitrary Waveform Generator (AT ARB Rider AWG-4022 by Active Technologies, hereafter AWG). The pulsed pattern designed with the AWG at radiofrequency (νRF = 90 MHz) is first up-converted to the resonant MW frequency ν0 by mixing it with the carrier frequency generated by a CW MW source (blue side-band generation, see Supplementary Fig. 4). The signal is then amplified and routed into the cryostat and to the resonator through the input MW coaxial line. The transmitted signal from the resonator goes first through the output MW coaxial line, it is amplified and then down-converted back to radiofrequency with another IQ mixer. The time domain acquisition of the signal is performed by using an oscilloscope (Supplementary Fig. 4). The oscilloscope traces are then integrated via software after data acquisition. The typical length of our π/2 pulses is tπ/2 = 120–150 ns, while the MW magnetic field strength is ∣B1∣ ≈ 10−5 T (see Supplementary Section 2.5). The details of the experimental set-up and of the pulse sequences are reported in Supplementary Sections 1.4 and 1.5, respectively.
EasySpin simulation of VO(TPP) transmission spectra
We simulate the CW spectra of Fig. 1.b with Eq. (3), using the values reported in ref. 32 and assuming Voigtian lineshapes (see Supplementary Section 2.2).
The superconducting nature of the resonator is taken into account by introducing in Eq. (3) an effective static magnetic field Beff = B0 + Bmeiss. Here, B0 is the externally applied static magnetic field and Bmeiss is an additional screening contribution arising from the superconducting material of the resonator (see Supplementary Section 2.2). The angle between B0 and the molecular z axis was considered to be θ = 90∘ ± α, with α an adjustable tilt angle parameter taking into account the visual misalignment of the crystal (see Supplementary Section 1.1). The best agreement with the experimental spectrum was found for α = 8∘ (Fig. 1). The simulation of the CW spectrum for the crystal sample reproduces both the eight main transitions and the formally forbidden ones that are visible in the lower field region (Fig. 1). The presence of such low intensity transitions between states with different mI is due to the non-negligible admixing of the ∣mS, mI > states at the applied magnetic field value (see Supplementary Section 2.2). The simulation of the EDFS spectrum is carried out by adding to Eq. (3) an additional super-hyperfine contribution given by the nitrogen atoms coordinate to V in the plane perpendicular to V=O (see Supplementary Section 2.2).
Supplementary information
Supplementary information on experimental methods, as well as additional data and discussion are reported in the on-line Supplementary Information file.
Data availability
The data reported in this work and in the Supplementary Information are available from the corresponding author upon reasonable request.
References
Heshami, H. et al. Quantum memories: emerging applications and recent advances. J. Mod. Opt. 63, 2005–2028 (2016).
Chen, C., Sun, W. K. C., Saha, S., Jaskula, J.-C. & Cappellaro, P. Protecting solid-state spins from a strongly coupled environment. N. J. Phys. 20, 063011 (2018).
Metsch, M. H. et al. Initialization and readout of nuclear spins via a negatively charged silicon-vacancy center in diamond. Phys. Rev. Lett. 122, 190503 (2019).
Morton, J. J. L. et al. Solid-state quantum memory using the 31P nuclear spin. Nature 455, 1085–1088 (2008).
Abe, E. & Sasaki, K. Tutorial: magnetic resonance with nitrogen-vacancy centers in diamond microwave engineering, materials science, and magnetometry. J. Appl. Phys. 123, 161101 (2018).
Siyushev, P. et al. Coherent properties of single rare-earth spin qubits. Nat. Commun. 5, 3895 (2014).
Kurizki, G. et al. Quantum technologies with hybrid systems. PNAS 112, 3866–3873 (2015).
Grezes, C. et al. Towards a spin-ensemble quantum memory for superconducting qubits. C. R. Phys. 17, 693–704 (2016).
Probst, S., Rotzinger, H., Ustinov, A. V. & Bushev, P. A. Microwave multimode memory with an erbium spin ensemble. Phys. Rev. B 92, 014421 (2015).
Bradley, C. E. et al. A ten-qubit solid-state spin register with quantum memory up to one minute. Phys. Rev. X 9, 031045 (2019).
Morton, J. J. & Bertet, P. Storing quantum information in spins and high-sensitivity ESR. J. Magn. Reson. 287, 128–139 (2018).
Afzelius, M., Sangouard, N., Johansson, G., Staudt, M. U. & Wilson, C. M. Proposal for a coherent quantum memory for propagating microwave photons. N. J. Phys. 15, 065008 (2013).
Gaita-Ariño, A., Luis, F., Hill, S. & Coronado, E. Molecular spins for quantum computation. Nat. Chem. 11, 301–309 (2019).
Troiani, F. & Affronte, M. Molecular spins for quantum information technologies. Chem. Soc. Rev. 40, 3119–3129 (2011).
Bader, K., Winkler, M. & van Slageren, J. Tuning of molecular qubits: very long coherence and spin-lattice relaxation times. Chem. Commun. 52, 3623–3626 (2016).
Bader, K. et al. Room temperature quantum coherence in a potential molecular qubit. Nat. Commun. 5, 5304 (2014).
Warner, M. et al. Potential for spin-based information processing in a thin-film molecular semiconductor. Nature 503, 504–508 (2013).
Shiddiq, M. et al. Enhancing coherence in molecular spin qubits via atomic clock transitions. Nature 531, 348–351 (2016).
Giménez-Santamarina, S., Cardona-Serra, S., Clemente-Juan, J., M.Gaita-Ariño, A. & Coronado, E. Exploiting clock transitions for the chemical design of resilient molecular spin qubits. Chem. Sci. https://doi.org/10.1039/D0SC01187H (2020).
Ferrando-Soria, J. et al. A modular design of molecular qubits to implement universal quantum gates. Nat. Commun. 7, 11377 (2016).
Rabl, P. et al. Hybrid quantum processors: molecular ensembles as quantum memory for solid state circuits. Phys. Rev. Lett. 97, 033003 (2006).
Thiele, S. et al. Electrically driven nuclear spin resonance in single-molecule magnets. Science 344, 1135–1138 (2014).
Godfrin, C. et al. Generalized Ramsey interferometry explored with a single nuclear spin qudit. Npj Quantum Inf. 4, 53 (2018).
Jenkins, M. et al. Coupling single-molecule magnets to quantum circuits. N. J. Phys. 15, 095007 (2013).
Bonizzoni, C. et al. Coupling molecular spin centers to microwave planar resonators: towards integration of molecular qubits in quantum circuits. Dalton Trans. 45, 16596–16603 (2016).
Urtizberea, A. et al. Vanadyl spin qubit 2D arrays and their integration on superconducting resonators. Mater. Horiz. 7, 885–897 (2020).
Gimeno, I. et al. Enhanced molecular spin-photon coupling at superconducting nanoconstrictions. ACS Nano. https://doi.org/10.1021/acsnano.0c03167 (2020).
Bonizzoni, C. et al. Coherent coupling between Vanadyl Phthalocyanine spin ensemble and microwave photons: towards integration of molecular spin qubits into quantum circuits. Sci. Rep. 7, 13096 (2017).
Bonizzoni, C., Ghirri, A. & Affronte, M. Coherent coupling of molecular spins with microwave photons in planar superconducting resonators. Adv. Phys. X 3, 1435305 (2018).
Ghirri, A. et al. Coherently coupling distinct spin ensembles through a high-Tc superconducting resonator. Phys. Rev. A 93, 063855 (2016).
Mergenthaler, M. et al. Strong coupling of microwave photons to antiferromagnetic fluctuations in an organic magnet. Phys. Rev. Lett. 119, 147701 (2017).
Yamabayashi, T. et al. Scaling up electronic spin qubits into a three-dimensional metal organic framework. J. Am. Chem. Soc. 140, 12090–12101 (2018).
Atzori, M. et al. Room-temperature quantum coherence and rabi oscillations in vanadyl phthalocyanine: toward multifunctional molecular spin qubits. J. Am. Chem. Soc. 138, 2154–2157 (2016).
Atzori, M. et al. Quantum coherence times enhancement in vanadium(IV)-based potential molecular qubits: the key role of the vanadyl moiety. J. Am. Chem. Soc. 138, 11234–11244 (2016).
Zadrozny, J. M., Niklas, J., Poluektov, O. G. & Freedman, D. E. Multiple quantum coherences from hyperfine transitions in a vanadium(IV) complex. J. Am. Chem. Soc. 136, 15841–15844 (2014).
Souza, M. A., lvarez, G. A. & Suter, D. Robust dynamical decoupling. Philos. Trans. R. Soc. A 370, 4748–4769 (2012).
Uhrig, G. S. Keeping a quantum bit alive by optimized π-pulse sequences. Phys. Rev. Lett. 98, 100504 (2007).
Pasini, S. & Uhrig, G. S. Optimized dynamical decoupling for power-law noise spectra. Phys. Rev. A 81, 012309 (2010).
Soetbeer, J., Húlsmann, M., Godt, A., Polyhach, Y. & Jeschke, G. Dynamical decoupling of nitroxides in o-terphenyl: a study of temperature, deuteration and concentration effects. Phys. Chem. Chem. Phys. 20, 1615–1628 (2018).
De Lange, G., Wang, Z. H., Ristè, D., Dobrovitski, V. V. & Hanson, R. Universal dynamical decoupling of a single solid-state spin from a spin bath. Science 330, 60–63 (2010).
Witzel, W. M. & Sarma, S. D. Multiple-pulse coherence enhancement of solid state spin qubits. Phys. Rev. Lett. 98, 077601 (2007).
Lim, H.-J., Welinski, S., Ferrier, A., Goldner, P. & Morton, J. J. L. Coherent spin dynamics of ytterbium ions in yttrium orthosilicate. Phys. Rev. B 97, 064409 (2018).
Shukla, A. & Mahesh, T. S. Dynamical decoupling of spin-clusters using solid state NMR. Preprint at: https://arxiv.org/abs/1110.1473v1 (2011).
Roy, S. S., Mahesh, T. S. & Agarwal, G. S. Storing entanglement of nuclear spins via Uhrig dynamical decoupling. Phys. Rev. A 83, 062326 (2011).
Harbridge, J. R., Eaton, S. S. & Eaton, G. R. Comparison of electron spin relaxation times measured by Carr Purcell Meiboom Gill and two-pulse spin-echo sequences. J. Magn. Reson. 164, 44–53 (2003).
Du, J. et al. Preserving electron spin coherence in solids by optimal dynamical decoupling. Nature 461, 1265 (2009).
Wu, H. et al. Storage of multiple coherent microwave excitations in an electron spin ensemble. Phys. Rev. Lett. 105, 140503 (2010).
Grezes, C. et al. Multimode storage and retrieval of microwave fields in a spin ensemble. Phys. Rev. X 4, 021049 (2014).
Julsgaard, B., Grezes, C., Bertet, P. & Mølmer, K. Quantum memory for microwave photons in an inhomogeneously broadened spin ensemble. Phys. Rev. Lett. 110, 250503 (2013).
Ghirri, A. et al. YBa2Cu3O7 microwave resonators for strong collective coupling with spin ensembles. Appl. Phys. Lett. 106, 184101 (2015).
Stoll, S. & Schweiger, A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 178, 42–55 (2006).
Abragam, A. & Bleaney, B. Electron Paramagnetic Resonance of Transition Ions (Oxford Classics Texts in the Physical Sciences, 2012).
Eaton, G. R. & Eaton, S. S. Multifrequency electron spin‐relaxation times. In Multifrequency Electron Paramagnetic Resonance, S. K. Misra (Ed.) (2011). https://doi.org/10.1002/9783527633531.ch17.
Sigillito, A. J. et al. Fast, low-power manipulation of spin ensembles in superconducting microresonators. Appl. Phys. Lett. 104, 222407 (2014).
Malissa, H., Schuster, D. I., Tyryshkin, A. M., Houck, A. A. & Lyon, S. A. Superconducting coplanar waveguide resonators for low temperature pulsed electron spin resonance spectroscopy. Rev. Sci. Instrum. 84, 025116 (2013).
Hahn, E. L. Spin echoes. Phys. Rev. 80, 580–594 (1950).
Yu, S. et al. Suppressing phase decoherence of a single atom qubit with Carr-Purcell-Meiboom-Gill sequence. Opt. Express 21, 32130–32140 (2013).
Pham, L. M. et al. Enhanced solid-state multispin metrology using dynamical decoupling. Phys. Rev. B 86, 045214 (2012).
Yang, W. & Liu, R.-B. Universality of Uhrig dynamical decoupling for suppressing qubit pure dephasing and relaxation. Phys. Rev. Lett. 101, 180403 (2008).
Yap, Y. S., Tabuchi, Y., Negoro, M., Kagawa, A. & Kitagawa, M. A Ku band pulsed electron paramagnetic resonance spectrometer using an arbitrary waveform generator for quantum control experiments at millikelvin temperatures. Rev. Sci. Instrum. 86, 063110 (2015).
Narkowicz, R., Suter, D. & Niemeyer, I. Scaling of sensitivity and efficiency in planar microresonators for electron spin resonance. Rev. Sci. Instrum. 79, 084702 (2008).
O’Sullivan, J. et al. Spin resonance linewidths of bismuth donors in silicon coupled to planar microresonators. Preprint at: https://arxiv.org/abs/2007.07600v1 (2020).
Ranjan, V. et al. Multimode storage of quantum microwave fields in electron spins over 100 ms. Preprint at: https://arxiv.org/abs/2005.09275v1 (2020).
Acknowledgements
We thank Prof. Mario Chiesa (University of Turin, Italy) and Dr. Enrico Salvadori (University of Turin, Italy) for useful discussion and complementary ESR characterization. Dr. Filippo Troiani (Istituto Nanoscienze CNR, section S3 of Modena) and Prof. Stefano Carretta (University of Parma, Italy) are acknowledged for useful discussions. We thank Prof. Oscar Moze (University of Modena and Reggio-Emilia) for the careful proof reading of our manuscript. This work was partially funded by the Italian Ministry of Education and Research (MIUR) through PRIN Project (contract no 2015HYFSRT), by the Air Force Office of Scientific Research grant (contract no FA2386-17-1-4040) and by the University of Modena and Reggio Emilia through the FAR Research Project 2018 Junior category (Decreto n. 161/18, Prot. no 61656/18 of april 3rd 2018 and Prot. 178151 of october 31st 2018).
Author information
Authors and Affiliations
Contributions
C.B. carried out all the measurements and data analysis and the design and the fabrication of the resonator. The home-made pulsed-microwave spectrometer, as well as all the pulse sequences used in this work has been designed, realized, tested, and implemented by C.B. F.S. prepared the crystal samples and part of the polycrystalline sample, M.At. prepared part the polycrystalline samples and contributed to their preliminary ESR and magnetic characterization. The EasySpin simulations of the spectra were carried out by F.S. and L.S. C.B., A.G. and M.Af. conceive the experiment. The manuscript was written by C.B., A.G., and M.Af. with contributions from all the authors. The manuscript has been revised by all authors before submission.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bonizzoni, C., Ghirri, A., Santanni, F. et al. Storage and retrieval of microwave pulses with molecular spin ensembles. npj Quantum Inf 6, 68 (2020). https://doi.org/10.1038/s41534-020-00296-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-020-00296-9
This article is cited by
-
Quantum sensing of magnetic fields with molecular spins
npj Quantum Information (2024)
-
Coupling Sub-nanoliter BDPA Organic Radical Spin Ensembles with YBCO Inverse Anapole Resonators
Applied Magnetic Resonance (2023)
-
Single organic molecules for photonic quantum technologies
Nature Materials (2021)