Abstract
Reliable single-photon emission is crucial for realizing efficient spin-photon entanglement and scalable quantum information systems. The silicon vacancy (\({V}_{{\rm{Si}}}\)) in 4H-SiC is a promising single-photon emitter exhibiting millisecond spin coherence times, but suffers from low photon counts, and only one charge state retains the desired spin and optical properties. Here, we demonstrate that emission from \({V}_{{\rm{Si}}}\) defect ensembles can be enhanced by an order of magnitude via fabrication of Schottky barrier diodes, and sequentially modulated by almost \(50 \%\) via application of external bias. Furthermore, we identify charge state transitions of \({V}_{{\rm{Si}}}\) by correlating optical and electrical measurements, and realize selective population of the bright state. Finally, we reveal a pronounced Stark shift of 55 GHz for the V1′ emission line state of \({V}_{{\rm{Si}}}\) at larger electric fields, providing a means to modify the single-photon emission. The approach presented herein paves the way towards obtaining complete control of, and drastically enhanced emission from, \({V}_{{\rm{Si}}}\) defect ensembles in 4H-SiC highly suitable for quantum applications.
Similar content being viewed by others
Introduction
Solid-state single-photon emitters (SPEs) and optically addressable spin centers are an emerging technology ideally suited for quantum computing, sensing, and information processing applications.1,2 Efficient room-temperature single-photon sources naturally fulfill key requirements for enabling secure communication via quantum key distribution,3,4 and offer a platform for optical quantum computing5 and communication.6 Moreover, single-photon emission from a bound and individually addressable paramagnetic state enables optical manipulation of the spin state and entanglement between quantum systems,7 culminating in the feasibility of quantum networks.8
The nitrogen-vacancy center in diamond1 has become a benchmark for implementing semiconductor point defects in quantum technologies, but is suffering from the immaturity of the material and device fabrication. More recently, point defects in silicon carbide (4H-SiC) have gained attention as a more device-friendly alternative, offering a platform to merge existing semiconductor processing capabilities with the quantum technology of the future.9,10 Recent testaments to the viability of 4H-SiC as a quantum host include single-photon emission from, and coherent control of, the silicon vacancy (\({V}_{{\rm{Si}}}\)),11,12,13 carbon antisite-vacancy pair (\({{\rm{C}}}_{{\rm{Si}}}{V}_{{\rm{C}}}\)),14 transition metal15 and silicon-carbon divacancy (\({V}_{{\rm{Si}}}{V}_{{\rm{C}}}\))16 spins at room temperature, as well as observations of millisecond spin coherence times for \({V}_{{\rm{Si}}}\)17 and \({V}_{{\rm{Si}}}{V}_{{\rm{C}}}\)18 at cryogenic temperatures.
Hitherto, the desired quantum properties of defects in 4H-SiC have been established for specific charge states only, with the remainder being dark and exhibiting no identified spin signals. In the case of \({V}_{{\rm{Si}}}\), the negative charge state (\({V}_{{\rm{Si}}}^{-}\)) exhibits both a high-spin ground state of \(S=3/2\) and two single-photon radiative channels, as observed by photoluminescence (PL), and labeled V1 and V2.19 Recently, robustness towards detrimental effects such as electron–phonon interactions and fast spin dephasing was established for \({V}_{{\rm{Si}}}^{-}\),20 and a large fraction (\(40 \%\)) of optical emission was found in the zero-phonon line (ZPL),21 cementing the position of \({V}_{{\rm{Si}}}^{-}\) as a promising qubit candidate. However, the overall low photon count rates plague emission from \({V}_{{\rm{Si}}}\) in SiC, and optical signals from isolated defects are challenging to detect without resorting to nanofabricated waveguides,11,22,23 or implementation into photonic crystal cavities.24
Charge state conversion between the different \({V}_{{\rm{Si}}}\) and \({V}_{{\rm{Si}}}{V}_{{\rm{C}}}\) states in 4H-SiC9,25 has been demonstrated by applying electric fields26,27,28 or via laser excitation.29,30,31 Unfortunately, the dark charge states under scrutiny remain largely unknown, and selective charge state population of \({V}_{{\rm{Si}}}^{-}\) accompanied by reliable switching between known bright and dark states has not been achieved so far.
In the present work, we enhance the V1 emission from ensembles of negatively charged silicon vacancies via the built-in field generated by Schottky barrier diodes (SBDs), and manipulate the bright state by an external bias. Our findings are discussed in terms of band bending at the SBD/semiconductor interface and the resulting selective charge state population of \({V}_{{\rm{Si}}}^{-}\). The charge state transitions \({V}_{{\rm{Si}}}\)(\(-/2-\)) and \({V}_{{\rm{Si}}}\)(\(2\!-\!/3-\)) are then identified by combining deep level transient spectroscopy (DLTS), PL spectroscopy, and hybrid density functional theory calculations. The correlation between optical and electrical characterization is rarely seen for qubit candidates, and to the best of our knowledge unique in silicon carbide. Finally, we reveal a Stark shift for \({V}_{{\rm{Si}}}^{-}\)-related emission with a quadratic field dependency, illuminating the nature of the \({V}_{{\rm{Si}}}^{-}\) ground and excited states and providing a means of tuning the emission energy. Our findings prove that selective and controlled charge state population and switching is possible for a solid-state quantum bit, and we therefore propose the SBD platform to control the charge state, spin state and luminescence from isolated qubits (or ensembles thereof) in 4H-SiC.
Results
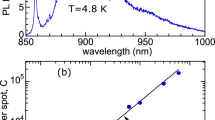
The silicon monovacancy (\({V}_{{\rm{Si}}}\)) remains one of the most extensively studied quantum emitters in 4H-SiC. Two ZPLs observed in the near-infrared region of PL spectra from n-type 4H-SiC exhibit single-photon emission characteristics and have been attributed to internal transitions of the negatively charged \({V}_{{\rm{Si}}}\),11,19 namely V1 at 1.44 eV and V2 at 1.35 eV.32 An exemplar PL spectrum of proton-irradiated n-type 4H-SiC, with the V1 and V2 lines highlighted, is shown in Fig. 1a (see Supplementary Notes 1 for further details). Recently, the V1 and V2 emission lines were attributed to the inequivalent hexagonal (\(h\)) and pseudo-cubic (\(k\)) \({V}_{{\rm{Si}}}^{-}\) defect configurations, respectively,20,33 in contrast to what was previously suggested.32 Figure 1b illustrates the ground state defect configuration, partial charge density and spin state for \({V}_{{\rm{Si}}}^{-}\)(\(h\)) and \({V}_{{\rm{Si}}}^{-}\)(\(k\)), respectively. In addition, \({V}_{{\rm{Si}}}^{-}\) manifests single-photon emission, from one excited state accessible for \({V}_{{\rm{Si}}}^{-}\)(\(k\)) (the V2 transition) and two for \({V}_{{\rm{Si}}}^{-}\)(\(h\)) (the V1 and V1′ transitions). The presence of V1′, a ZPL closely related to V1, but assigned to a second excited state of \({V}_{{\rm{Si}}}^{-}\) that is slightly higher in energy,19,21,24,33 marks the V1/V1′ defect center as dichroic. Here, we will focus on the V1/V1′ defect, firstly to avoid interference from the broad luminescence band overlapping with V2, and secondly because of the large Debye–Waller factor of the V1 line (\(>40 \%\)21). With a large portion of photons channeled into the V1 ZPL, we are more likely to observe any electrically induced modulation of the V1/V1′ emission intensity.
Internal transitions of \({V}_{{\rm{Si}}}\) in 4H-SiC. a Representative PL spectrum highlighting the V1 and V2 silicon vacancy-related emission lines. b Ground state (GS) atomic and electronic structures of the negatively charged \({V}_{{\rm{Si}}}\) in both the \(h\) and \(k\) configurations, with the available internal transitions V1, V1′, and V2 highlighted, and showing the partial charge densities of \({a}_{1}\) states.
Effect of built-in field on silicon vacancy-related emission
The influence of the SBD-induced built-in field on the V1 emission originating from \({V}_{{\rm{Si}}}^{-}\) is investigated using an experimental setup as illustrated in Fig. 2a. We study n-type 4H-SiC samples having 10 µm epitaxial layers topped by circular nickel SBDs of 1 mm diameter. The defects are optically addressed at temperatures ranging from 10 to 100 K, and defect-related PL is analyzed using backside imaging geometry, where both laser excitation and PL acquisition are from the substrate side (see Fig. 2a). The dopant concentration in the epitaxial layer was \(1\,\times 1{0}^{15}\) cm\({}^{-3}\), as determined by capacitance–voltage measurements, with substrate doping being estimated at several orders of magnitude higher (see Supplementary Notes 2 for further information about the samples and SBDs). The silicon vacancies were formed using 1.8 MeV proton irradiation to varying fluences, having a projected range located \(\sim\!27\,\mu {\rm{m}}\) into the sample, which was calculated using collision Monte Carlo models as implemented in the SRIM code34 (see Supplementary Methods 1). At room temperature, the space charge region (SCR, see Fig. 2a) spans approximately 1.5 µm and 4 µm into the sample for zero (0 V) and reverse bias (\(-10\) V), respectively. Consequently, the \({V}_{{\rm{Si}}}\) concentration is assumed constant throughout the probed region, as illustrated by the \({V}_{{\rm{Si}}}\) concentration versus depth profile in Fig. 2c.
Experimental considerations and electrical field effects on V1 emission. a Micro-imaging PL spectroscopy setup in back-illumination/detection geometry: laser excitation (EXC) beam passing through substrate (SUB) and epilayer (EPI) is reflected at Schottky contact outwards; the confocal approach, ensured by microscope objective (OBJ) and narrow slit (SL) of imaging spectrometer (IS), maximizes pickup of PL signal from the focal plane in the space charge region (SCR) of Schottky barrier diode (SBD). b PL spectra obtained at 10 K from SCR or depletion region within SBD, and from nearby area outside SBD perimeter, demonstrating a significant enhancement of V1-related emission by the built-in field of unbiased SBD. c Representative depth profile of the 1.8 MeV proton irradiation-induced \({V}_{{\rm{Si}}}\) concentration in the 4H-SiC epilayer/substrate structure. Note that \({V}_{{\rm{Si}}}\) concentration is nearly constant throughout the depletion region and entire epilayer. d Electrical modulation of V1′ emission for a proton fluence of \(2\,\times 1{0}^{12}\) cm\({}^{-2}\): by applying an external forward bias the V1′ emission is seen to diminish by over \(40 \%\) at 10 K for \(\sim\!\! 100\) W cm\({}^{-2}\) excitation intensity (laser power 25 mW). At 80 K and \(\sim\!\! 1\) kW cm\({}^{-2}\) excitation (laser power 250 mW), the modulation is \(\sim\!\! 25 \%\), as shown in the Inset. The reproducibility is verified by consecutive PL acquisitions as specified in the legend, with solid/dotted lines representing the initial and repeated measurements, respectively. e Selective switching of \({V}_{{\rm{Si}}}\) luminescence intensity is demonstrated for forward and reverse biased SBD for a proton fluence of \(1\,\times 1{0}^{12}\) cm\({}^{-2}\). For each acquisition cycle, the intensity level on the plot represents an averaged value over 201 measurements, resulting in minimal standard deviation (within the marker size).
The effect of the built-in field induced by the SBD on the V1/V1′ emission intensity is displayed in Fig. 2b, where PL spectra obtained at 10 K from the SCR within the SBD and from the nearby area outside the SBD perimeter are put alongside for comparison. One can observe significant, more than by an order of magnitude, enhancement of V1-related emission once collected from the SCR of the SBD (further examples are shown in Supplementary Notes 3). Importantly, this drastic increase is larger than could be expected from purely geometrical considerations that include reflection/scattering from the semiconductor–metal interface along with possible contributions from double-pass excitation and retroflection. In our opinion, such a significant enhancement can only be adequately explained by assuming that the band-bending induced by the Schottky barrier is affecting the charge state of the silicon vacancies being illuminated, with a larger portion of \({V}_{{\rm{Si}}}\) in the negative charge state inside compared to outside of the space charge region. It is worth noting at this point that the V1-related emission peak is clearly visible up to 150 K, although a significant line broadening occurs at higher temperatures (see Supplementary Notes 1). Moreover, the identity of the two peaks around 867 nm in Fig. 2b are at the present time unknown.
Intriguingly, which excited state \({V}_{{\rm{Si}}}^{-}\) prefers upon illumination seems to depend on the presence of the SBD. When no SBD is present, both the V1 and V1′ lines (with typically reported values of 861.3 nm and 858.7 nm, respectively) are observed, with the V1:V1′ ratio depending on factors such as the \({V}_{{\rm{Si}}}\) concentration, the incident laser intensity and polarization, and the temperature. The built-in field of the SBD, however, seems to promote excitation to the higher-lying V1′ excited state as shown in Fig. 2b; the lower energy V1 emission line was not detected for any of the tested SBDs. Thus, the promotion of \({V}_{{\rm{Si}}}^{-}\) to the V1′ excited state (see Fig. 1b) appears to be connected to the SBD-induced field. Fortunately, as optical spin manipulation can be improved by selectively exciting the V1′ state due to the reduced intersystem crossing rates,20 the straightforward process of depositing a nickel SBD on the sample surface promises both enhanced optical emission and now also augmented control over spin dynamics. Therefore, for the remainder of this manuscript, we have opted to refer to the collected \({V}_{{\rm{Si}}}^{-}\) emission as V1′.
Intensity modulation
To verify the influence of the SBD-induced built-in field on V1′ emission, and to provide a means of tuning the bright state of \({V}_{{\rm{Si}}}\), we apply external (i) forward and (ii) reverse bias to the SBD and study the resulting V1′ PL intensity. Figure 2d showcases representative PL spectra of the proton-irradiated samples with SBD (here for a fluence of \(2\,\times 1{0}^{12}\) cm\({}^{-3}\)) during sequential zero (black) and forward (red) bias conditions. Solid lines denote first acquisition of a given voltage, and dashed lines the second acquisition (acquisitions with time occurred in the order of the legend). Indeed, an intensity modulation is observed when modifying the electric field via biasing of SBD, confirming the influence of the band bending and charge state manipulation of the bright \({V}_{{\rm{Si}}}^{-}\) state: emission from the V1′ defect can be selectively switched off (lower intensity) and on (higher intensity) by manipulating the electric field at the interface of the Schottky contact and 4H-SiC. While some variation between diodes and applied voltages exists (see also Supplementary Notes 3), unambiguous evidence of V1′ emission intensity manipulation via the applied voltage is found. The general trend is clear; for a larger (\(>\pm\, 1.5\) V) forward or reverse bias, the intensity of V1′ is reduced compared to that without applied bias. For low forward bias conditions up to \(\sim\!\! 1\) V, however, the V1′ intensity can be manipulated to increase compared to the 0 V conditions (we will return to this in a moment). The reproducible electrical modulation of the V1′ intensity is further confirmed in Fig. 2e, showing a series of cyclic acquisitions for two relevant biasing conditions, forward (top panel) and reverse (bottom panel), obtained for a different proton fluence than that of Fig. 2d. Here, it should be noted that only low to moderate electric fields are required. Once the applied bias exceeds approximately \(\pm 5\) V, the electrically induced modulation of the V1′ emission intensity, demonstrated in Fig. 2d, e, ceases to be predictable and reproducible, with intensities changing in a more random manner. While the exact reasons for this remain unclear, among the most likely are charging effects of defects localized at the interface with the Schottky contact. It is also important to point out that both the enhancement and modulation are observed also at higher temperatures, e.g. 80 and 100 K, although the line width of the V1′ peak increases.
Finally, Fig. 2d, e also demonstrate the defect concentration dependency of our SBD-centered technique. The sample used to create Fig. 2d was irradiated to a proton fluence twice that of the sample shown in Fig. 2e, which is visualized in the enhanced modulation depth of over \(45 \%\) in 2d as compared to a \(15 \%\) modulation in Fig. 2e.
Identifying charge state transitions of the silicon vacancy
To explain the switching demonstrated above, the accessible \({V}_{{\rm{Si}}}\) charge states must be established, including the energy level transitions. Figure 3 displays the formation energy diagram for \({V}_{{\rm{Si}}}\) as calculated using hybrid density functional theory, where the red and blue lines represent hexagonal and pseudo-cubic \({V}_{{\rm{Si}}}\) configurations, respectively. Evidently, \({V}_{{\rm{Si}}}\) is electrically active, with thermodynamic (\(0/-\)) transition levels located close to mid-gap for both \({V}_{{\rm{Si}}}\) configurations, (\(-/2-\)) at \({E}_{{\rm{c}}}-0.6\) eV for both \({V}_{{\rm{Si}}}\)(\(k\)) and \({V}_{{\rm{Si}}}\)(\(h\)), and (\(2-/3-\)) at \({E}_{{\rm{c}}}-0.4\) eV for \({V}_{{\rm{Si}}}\)(\(k\)) and \({E}_{{\rm{c}}}-0.3\) eV for \({V}_{{\rm{Si}}}\)(\(h\)). Note the predicted stability of the triply negative charge state for both the \(h\) and \(k\) configurations, \({V}_{{\rm{Si}}}^{3-}\), the presence of which has previously been subject to some controversy.9,25 The calculations presented in Fig. 3 indicate that \(q=0\), \(2-\) and \(3-\) are likely candidates for the so-called dark states accessed during the electrical modulation of \({V}_{{\rm{Si}}}^{-}\) emission demonstrated above (Fig. 2), and provide upper and lower bounds for the stability region of the negative silicon vacancy.
Charge states of the silicon vacancy. Formation energy diagram for the \(h\) and \(k\) \({V}_{{\rm{Si}}}\) as a function of the Fermi-level position relative to the VBM under Si rich conditions, with the thermodynamic (\(-/2-\)) and (\(2\!-\!/3-\)) charge state transitions highlighted. The inset shows the 4H-SiC crystal structure with alternating \(h\) and \(k\) lattice sites (C atoms are red, and Si blue).
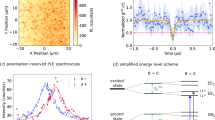
Deep level transient spectroscopy (DLTS) is a capacitance spectroscopy technique enabling both direct observation of defect charge state transitions as well as extraction of their energetic positions within the band gap. Unfortunately, the quantum-compatible defects in 4H-SiC (\({V}_{{\rm{Si}}}\), \({V}_{{\rm{Si}}}{V}_{{\rm{C}}}\), \({{\rm{C}}}_{{\rm{Si}}}{V}_{{\rm{C}}}\)) lack reliable identification of their thermodynamic charge transition levels, rendering the dark states generated during both electrical and optical charge state control experiments uncertain. DLTS spectra of irradiated n-type 4H-SiC samples are presented in Fig. 4a and show two main carrier traps in the vicinity of the conduction band edge: the Z\({}_{1/2}\) double acceptor level arising from the (\(0/2-\)) charge state transition of the carbon vacancy (\({V}_{{\rm{C}}}\)),35 and the S-center consisting of two contributions (S1 and S2) located at 0.4 and 0.7 eV below the conduction band minimum (CBM), respectively. S1 and S2 arise from different charge state transitions of the same defect, and have been tentatively attributed to \({V}_{{\rm{Si}}}\) following theoretical calculations.25 DLTS measurements occur under conditions where the defect can relax fully to its equilibrium configuration after the charge state transition. For this reason, the activation energy for carrier emission from a defect extracted from DLTS should be compared with thermodynamic charge state transition levels,36 i.e., those indicated in Fig. 3. However, the activation energies obtained by DLTS may also include a capture barrier, which can be sizable in some cases. An upper estimate for this barrier can be obtained by constructing a one-dimensional configuration coordinate diagram for the transition, as explained in refs. 37,38, i.e., the activation energies for \({V}_{{\rm{Si}}}\) observed by DLTS are predicted to occur within the highlighted ranges in Fig. 3. Here, we observe excellent overlap between the DLTS-deduced activation energies for the S-center (Fig. 4a) and the \({V}_{{\rm{Si}}}\)(\(-/2-\)) and \({V}_{{\rm{Si}}}\)(\(2\!-/3-\)) charge state transitions obtained from Fig. 3, and attempt to prove that the S-center indeed arises from \({V}_{{\rm{Si}}}\).
Experimental characterization of \({V}_{{\rm{Si}}}\)charge state transitions. a DLTS spectra of proton-irradiated n-type 4H-SiC samples, evidencing an increase in S1, Z\({}_{1/2}\) and S2 intensities with proton fluence. b Temperature-dependent Laplace-DLTS measurements of the S1 peak, demonstrating that S1 contains contributions from two defect centers, likely \({V}_{{\rm{Si}}}\)(\(h\)) and \({V}_{{\rm{Si}}}\)(\(k\)). c Arrhenius behavior of the two contributions to S1 revealed by the Laplace-DLTS measurements. The confidence intervals for the activation energies are approximately \(\pm\! 0.01\) eV for E\({}_{{\rm{t}}}\)(P1), and \(\pm\! 0.02\) eV for E\({}_{{\rm{t}}}\)(P2).
Interestingly, the S1 DLTS peak accommodates contributions from two distinct defect centers,39 as revealed by the Laplace-DLTS spectra (see Supplementary Methods 2 for details) in Fig. 4b. Recently, Z\({}_{1/2}\) was also found to contain two distinct signals, which were assigned to the \(h\) and \(k\) configurations of the carbon vacancy.40 Similarly, we infer from Fig. 3 that the \(h\) and \(k\) \({V}_{{\rm{Si}}}\)(\(2\!-/3-\)) charge state transitions likely have an energy level position difference of up to 0.1 eV. The temperature-dependent Laplace-DLTS signal in Fig. 4b of the S1 peak, and the Arrhenius plot in Fig. 4c, evidence that the two individual S1 contributors are separated in energy by 0.04 eV. Accordingly, we assign the two defect centers encompassed by S1 to \({V}_{{\rm{Si}}}\)(\(h\)) and \({V}_{{\rm{Si}}}\)(\(k\)), and make a tentative assignment of S1(peak 1) and S1(peak 2) to the (\(2\!-/3-\)) transitions of \({V}_{{\rm{Si}}}\)(\(k\)) and \({V}_{{\rm{Si}}}\)(\(h\)), respectively. In contrast to what is often found for Z\({}_{1/2}\),40 the two contributions to the S1 defect center have approximately equal integrated intensities. This is as expected for proton-irradiated material, with the \(h\) and \(k\) \({V}_{{\rm{Si}}}\) configurations formed by displacement caused by the nuclear energy deposition.
Comparing the expected behavior of \({V}_{{\rm{Si}}}\) and S-center, we find a striking similarity (see also Supplementary Discussion 1); the S-center only appears in irradiated n-type material, and anneals out between 400 and 600 °C.41,42 Coincidentally, the \({V}_{{\rm{Si}}}\) is a metastable defect in 4H-SiC, transforming into \({{\rm{C}}}_{{\rm{Si}}}{V}_{{\rm{C}}}\) within the same temperature range in n-type material.14 The calculated barrier for \({V}_{{\rm{Si}}}\) transforming into \({{\rm{C}}}_{{\rm{Si}}}{V}_{{\rm{C}}}\) is 1.8 eV,43 which is identical to the experimentally deduced barrier for S-center annealing.44 At these temperatures, self-interstitials should already have annealed out,45 while the carbon vacancy remains present and becomes mobile at significantly higher temperatures,46 eliminating these defects as contenders for the S-center source. Furthermore, the absence of the Poole–Frenkel effect for S1 indicates an acceptor-like behavior, and the difference of more than an order of magnitude between the capture cross-sections for S1 and S2 is well explained by the large electron repulsion associated with \({V}_{{\rm{Si}}}^{2-}\) capturing an additional electron.44 In conclusion, the excellent agreement between calculated and experimental \({V}_{{\rm{Si}}}\) and S-center properties provide compelling evidence for the assignation of the \({V}_{{\rm{Si}}}\)(\(-/2-\)) and \({V}_{{\rm{Si}}}\)(\(2\!-/3-\)) charge state transitions to generate the S2 and S1 signals, respectively, and indicate these transitions as accomplices in reducing the single-photon count from \({V}_{{\rm{Si}}}\).
Proton fluence dependence of the S-center
To unambiguously attribute the DLTS S-center to \({V}_{{\rm{Si}}}\), and thereby provide experimental verification of the upper boundary for the Fermi level where \({V}_{{\rm{Si}}}^{-}\) and hence single-photon emission prevails, we relate the DLTS S-center to PL emission from the V1 center. Figure 5a demonstrates a linear dependence of S-center concentration41 in blue (and \({V}_{{\rm{C}}}\) in pink) on proton irradiation fluence, as expected for primary point defects. Note that the proton fluence range reflects the detection limits of the DLTS technique, where the defect concentration cannot exceed \(20 \%\) of net carriers. All defect concentrations were estimated assuming uniform defect concentration profiles within the depletion region as justified by Fig. 2c, and simulated due to overlapping peaks in the 4H-SiC DLTS spectrum (see Supplementary Discussion 2 for details). The slight difference between S1 and S2 concentrations is attributed to the overlap between the S2 and Z\({}_{1/2}\) peaks (see Fig. 4a). Figure 5a also compares experimentally deduced S-center concentrations to those estimated using SRIM simulations (using displacement energies of 20 eV and 30 eV for C and Si, respectively), with simulated concentrations depicted as red open squares for \({V}_{{\rm{C}}}\) and black open triangles for \({V}_{{\rm{Si}}}\). An excellent agreement is found between the experimentally deduced S-center concentration and that estimated for \({V}_{{\rm{Si}}}\) using the SRIM code, using the well known and ever-present \({V}_{{\rm{C}}}\) as a benchmark.
Correlating the S and V1 centers
Figure 5b correlates the proton fluence dependence of the S-center concentration (fit to experimental data in blue extended from Fig. 5a) and V1/V1′ emission intensity (green). The V1/V1′ intensities were determined after baseline subtraction, and the deviation from a linear fit for the largest fluences is partly attributed to the strong compensation resulting in a substantial shift in the Fermi level. The match in slope between the S1/S2 and V1/V1′ linear fits is excellent, and provides strong support for the optical V1/V1′ signals and the electrical S1/S2 signals having the same origin: the silicon vacancy.
To summarize, we combine DFT calculations with DLTS and PL measurements to assign the S1 and S2 DLTS peaks to the (\(-/2-\)) and (\(2\!-/3-\)) charge state transitions of the silicon vacancy in 4H-SiC, respectively. Hopefully, the newfound electrical degree of freedom provided by the DLTS technique will yield enhanced control over both \({V}_{{\rm{Si}}}\) formation and placement, and the relation between bright and dark charge states. Indeed, we have identified two new accessible charge states for \({V}_{{\rm{Si}}}\) in 4H-SiC: the doubly and triply negative, and thus experimentally provided an upper bound for the bright \({V}_{{\rm{Si}}}^{-}\).
Field effect on band bending
The strong enhancement of the V1′ signal under the SBD indicates that emission arises from the depletion region of the junction, and is related to the electric field or the current provided by the junction. However, no electroluminescence has so far been observed, and the strong enhancement also occurs without applied bias. Thus, one can rule out enhancement of the emission by impact excitation47 as the only cause for the increased V1′ emission, i.e. that charge carriers are accelerated in the electric field and cause excitation resulting in V1′ emission when interacting with \({V}_{{\rm{Si}}}\). Hence, the manipulation of the charge states by the depletion region appears as an important factor for the enhanced emission of V1.
Combining the optical and electrical observations above, we can consider the field-induced switching of \({V}_{{\rm{Si}}}^{-}\) luminescence shown in Fig. 2 with respect to the charge state transitions: \({V}_{{\rm{Si}}}\)(\(-/2-\)) at \({E}_{{\rm{C}}}-0.7\) eV, and \({V}_{{\rm{Si}}}\)(\(2\!-/3-\)) at \({E}_{{\rm{C}}}-0.4\) eV. First, consider the band diagram at temperatures above the freeze-out of the main dopant, so that thermally excited charge carriers are still available, i.e., above \(\sim\!\! 50\) K in nitrogen doped 4H-SiC. As illustrated in Fig. 6a for a temperature of 100 K, the Fermi level in n-type 4H-SiC, having carrier concentrations in the \(\sim\!\! 1{0}^{15}\) cm\({}^{-3}\) range or above, is situated \(\lesssim\! 0.1\) eV below the conduction band edge, or lower. Therefore, at 80 K or above, \({V}_{{\rm{Si}}}\) predominantly inhabits the triply negative charge state, with the doubly and singly negative charge states mainly being available through illumination.
Applying a SBD causes band bending in the near surface region, as illustrated in the technology computer-aided design (TCAD) simulation shown in Fig. 6b (further details on the temperature- and voltage dependence can be found in Supplementary Methods 3). The blue colored region in Fig. 6b indicates where \({V}_{{\rm{Si}}}^{-}\) is predominantly populated. Importantly, at room temperature and zero bias, the depletion region provides conditions where \({V}_{{\rm{Si}}}^{-}\) is the prevailing charge state, and likely explains the enhancement of the V1′ emission demonstrated in Fig. 2b.
Although not directly transferable to the non-equilibrium situation of carrier injection established by external bias and illumination, the conceptual band model presented in Fig. 6 hints at which charge state transitions are occurring during the electrically induced V1′ modulation of Figs. 2d, e. Under forward biasing, we approach flat-band conditions. The resulting lowering of the V1′ intensity demonstrated in Fig. 2d likely results from transitions between the singly negative and the \(2-\) and \(3-\) charge states of \({V}_{{\rm{Si}}}\), occurring from the deep end of the depletion region. Furthermore, we speculate that the enhancement of V1′ PL intensity shown in Fig. 2e may be explained by a transition from neutral to negative \({V}_{{\rm{Si}}}\) in the near surface region when increasing the voltage slightly. The \({V}_{{\rm{Si}}}\)(\(0/-\)) transition is expected at 1.3–1.5 eV above the valence band edge (Fig. 3), but this has not been experimentally verified.
Stark shift of the V1′ line
The SBDs also provide opportunities to study the \({V}_{{\rm{Si}}}\) emission under larger electric fields. Although the intensity modulation of the V1′ PL peak is no longer accurately predicted for applied voltages \(>\pm\! 5\) V in our samples, we observe a significant shift in the energy positioning of the V1′ ZPL for reverse biasing \(>10\) V. Figure 7a demonstrates the effect of large electric fields on V1′ emission for a sample irradiated to a proton fluence of \(1\times 1{0}^{12}\) cm\({}^{-3}\). Interestingly, the full width half maximum (FWHM) of the V1′ peak is consistent as the field increases, although shifted. Thus, one can conclude that a majority of the emitting \({V}_{{\rm{Si}}}\) centers is affected by the electric field, confirming that V1′ emission mainly arises from defects within the depletion region of the SBD. Electrically induced shifting or splitting of spectral lines is a phenomenon commonly known as the Stark effect,48 and would explain the observed continuous red-shift of the V1′ line with increasingly negative applied bias. Forward biasing the sample did not affect the V1′ peak position. The extent of the red-shift exhibits a clear dose dependence, and was also influenced by both the carrier concentration and the depth of the depletion region. Indeed, a stronger Stark effect can be attributed to the individual \({V}_{{\rm{Si}}}\) defects experiencing stronger local field (see Supplementary Notes 2 for a discussion on how the electric field strength was estimated from the reverse bias and the SBD characteristics).
Electrically induced shift of the V1′ line. a The Stark effect is clearly observed for the V1′ emission line in proton-irradiated 4H-SiC, here demonstrated for a fluence of \(1\,\times 1{0}^{12}\) cm\({}^{-3}\) at 50 K and a laser intensity of 250 mW, where the vertical lines indicate the peak position. b The V1′ Stark shift versus electric field (left and bottom axis) and the V1′ peak energy vs. square of the electric field (right and upper axis) demonstrate a quadratic Stark effect for the \({V}_{{\rm{Si}}}^{-}\) energy levels. The error bars for the peak positions are within the marker size, and the applied bias voltages range up to \(-60\) V.
The shift in V1′ peak position exhibits both quadratic and linear dependences on the applied electric field, as shown in Fig. 7b, regardless of \({V}_{{\rm{Si}}}\) concentration and carrier concentration. Defects in 4H-SiC, \({V}_{{\rm{Si}}}\) included, are non-centrosymmetric, and for such defects both linear and quadratic Stark effects take place.49 The \({V}_{{\rm{Si}}}^{-}\) has C\({}_{3\nu }\) ground state symmetry, and the V1′ transition is between the \({}^{4}{\rm{E}}\) excited and \({}^{4}{{\rm{A}}}_{2}\) ground states.19 This transition is analogous to that of the negatively charged NV center in diamond, for which the quadratic Stark effect was previously demonstrated.50 At the moment, the reason for the quadratic Stark shift of the V1′ ZPL remains an open question.
Stark tuning has previously been demonstrated for the divacancy in 4H-SiC,26,28 but not for the the silicon vacancy. Consequently, we herein provide a means of tuning the \({V}_{{\rm{Si}}}\)-related emission energy, while simultaneously establishing that the V1′ excited state of \({V}_{{\rm{Si}}}\)(\(h\)) seems to be more robust towards stray electric fields than, e.g., the \(hh\) configuration of the divacancy.28
Discussion
In summary, we characterize the electric field response of optical emission from \({V}_{{\rm{Si}}}\) ensembles, and find that both a substantial intensity increase as well as controlled modulation of V1′ emission are obtainable using highly accessible techniques and voltages. By correlating the PL and DLTS responses of \({V}_{{\rm{Si}}}\) and identifying the DLTS S-center, we identify thermodynamic transition levels of a solid-state qubit candidate, and provide an additional means of detecting and controlling the \({V}_{{\rm{Si}}}\) in 4H-SiC. Having established upper and lower bounds for the Fermi levels ensuring optimal \({V}_{{\rm{Si}}}^{-}\) charge state populations, our work promises greater ease of ensuring that all silicon vacancies inhabit the bright state. The results presented herein for charge state modulation of \({V}_{{\rm{Si}}}\) in n-type 4H-SiC apply to a defect ensemble, and we are therefore unable to completely switch the \({V}_{{\rm{Si}}}^{-}\) luminescence ON and OFF by manipulating the defect charge state. However, in the event of a single \({V}_{{\rm{Si}}}\) defect being situated at a suitable distance from a Schottky contact, applying external bias is a promising approach to selectively alter the \({V}_{{\rm{Si}}}\) charge state and effectively switching the quantum-compatible state ON and OFF. In that event, the challenge becomes placing a \({V}_{{\rm{Si}}}\) within a highly localized and easily identifiable depletion region, which can be solved by, e.g, depositing a SBD on top of a nanopillar containing only one or two silicon vacancies.22
Recently, electric field-dependent manipulation of single silicon vacancies was demonstrated using the intrinsic region of 4H-SiC p-i-n diodes.51 In the intrinsic region, the Fermi level is close to the middle of the band gap, and switching may occur between the neutral and single negative charge state. In n-type material, on the other hand, the Fermi level is close to the conduction band with \({V}_{{\rm{Si}}}\) predominantly in the \(2-\) or \(3-\) charge states. Hence, the charge states affected by the depletion region will be closer to the metal–semiconductor interface compared to that of the p-i-n diode.
Finally, we reinforce the robustness of the V1 defect center ZPL with respect to stray electric fields by demonstrating a Stark shift that is much smaller than the splitting between the V1 and V1′ excited states. Although electric fields above \(2\,\times 1{0}^{4}\) V\(/\)cm are needed to shift the V1′ peak position, voltages below \(\pm\! 5\) V can subdue or enhance the intensity by over \(40 \%\). Combined with the strong sensitivity of the \({V}_{{\rm{Si}}}\) electron spin to magnetic fields,52 we cement the position of \({V}_{{\rm{Si}}}^{-}\) in 4H-SiC as a promising quantum sensor with nanoscale resolution, employing V1′ intensity for low-field and V1′ peak position for high-field applications. Combined with nanofabrication, the SBD approach presents a powerful tool and paves the way towards obtaining complete control of, and drastically enhanced emission from, \({V}_{{\rm{Si}}}\) defect ensembles in 4H-SiC highly suitable for quantum applications.
Methods
Computational details
First-principles calculations were performed within density functional theory, as implemented in the Vienna ab-initio simulation package (VASP),53,54,55,56 using the HSE06 hybrid functional57 to accurately describe the electronic structure and the Projector-Augmented Wave (PAW) method to consider valence electrons only.58 The calculated 4H-SiC 0 K band-gap of 3.17 eV is close to the experimental value of 3.27 eV,59 lending support to the calculated charge state transitions. The \({V}_{{\rm{Si}}}\) was created by removing a Si(\(h\)) or Si(\(k\)) atom from a 96-atom cubic 4H-SiC supercell. The electronic self-consistent energy was minimized to a numerical accuracy of \(1{0}^{-6}\) eV, while atomic coordinates were optimized until forces were below \(0.02\,{\rm{eV}}/\AA\). A \(2\,\times 2\,\times 2\) Monkhorst-Pack type k-mesh and a 420 eV plane-wave energy cut-off were deemed sufficient for capturing defect energetics accurately. Defect formation energies and thermodynamic charge state transition levels were calculated by using the established formalism described in ref. 36 For charged defects, the extended60 Freysoldt, Neugebauer, and Van de Walle correction scheme60,61,62 was employed.
Sample preparation
The \({V}_{{\rm{Si}}}\) was studied experimentally using (\(0001\)) 4H-SiC samples purchased from Cree, Inc. holding \(10\ \mu {\rm{m}}\) thick epitaxial layers with net doping concentrations of \({N}_{{\rm{D}}} \sim 1\times 1{0}^{15}{{\rm{cm}}}^{-3}\), as determined from capacitance-voltage measurements. The substrates are n-doped with a nominal concentration of \(8\,\times 1{0}^{18}\) cm\({}^{-3}\). To selectively form the \({V}_{{\rm{Si}}}\) defects, the samples were irradiated at room temperature with 1.8 MeV protons, having a projected range of \(\sim\!\! 27\ \mu {\rm{m}}\) calculated using collision Monte Carlo models as manifested in the SRIM code,34 while being tilted \(\sim {8}^{\circ }\) off with respect to the surface normal to reduce channeling effects. Proton irradiation was performed to fluences ranging from \(1\,\times 1{0}^{11}\) to \(8\,\times 1{0}^{13}\ {{\rm{cm}}}^{-2}\) to enable detection using both DLTS (with an upper defect concentration limit of \(0.2{N}_{{\rm{D}}}\)) and PL spectroscopy (our setup has a lower \({V}_{{\rm{Si}}}\) detection limit in the \(1{0}^{13}\ {{\rm{cm}}}^{-3}\) range). Following irradiation, circular nickel (Ni) contacts having 1 mm diameter and 150 nm thickness were deposited on the epitaxial-layer surface using an electron-beam evaporator to form SBDs. To alleviate implantation damage and reduce the concentration of metastable peaks appearing in the temperature region relevant for DLTS measurements,63,64 all samples were annealed at 300 °C in air for 30 min using a conventional tube furnace.
PL spectroscopy and field-dependent intensity modulation
For the PL spectroscopy the samples were placed inside a close-cycled He refrigerator system (CCS-450 Janis Research, Inc.), and the samples were measured at temperatures ranging from 10 to 300 K. Sample excitation was employed using a pulsed Ti sapphire tunable laser operating in a femtosecond mode-locked mode and utilizing an excitation wavelength of \(740\ {\rm{nm}}\). The emission was analyzed by a fiber-optic (Ocean Optics, HR4000) and imaging spectrometer systems (Horiba iHR320 coupled to Andor iXon888 EMCCD), with a spectral resolution below 0.2 nm in both cases. Positive and negative bias was applied to the SBD being addressed by individual wires attached to the Ni contact by conductive glue, and the luminescence modulation was investigated at temperatures ranging from 10 to 100 K and with laser intensities of 25 and 250 mW, which correspond to \(\sim\!\! 100\) W/cm2 and \(\sim\!\! 1\) kW/cm2 intensities for a given diameter of the excitation beam spot on the sample of \(\sim\!\! 200\mu\)m.
Defect identification
Electrical characterization in the form of DLTS was performed in the 77–370 K temperature range to encompass both the S1 and S2 peaks, with the scans starting at low temperature. The reverse bias was kept at \(-10\) V using a 10 V filling pulse. Rate windows in the range 20–640 \({\rm{ms}}\) and a standard lock-in weighting function were used to extract the DLTS signal. Optical characterization to obtain correlation with DLTS measurements was performed at 10 K using the PL setup described above with a 25 mW excitation intensity and a wavelength of \(740\ {\rm{nm}}\).
SRIM simulations were performed to provide an estimate for the \({V}_{{\rm{Si}}}\) concentration by comparing to that known for \({V}_{{\rm{C}}}\). For the simulations, we used 20 eV (30 eV) for the C (Si) displacement energy, and for the post-processing we estimated that \(3 \%\) of all vacancies (both silicon and carbon) survive dynamic annealing during ion implantation and the 300 \({}^{\circ }\)C post-irradiation anneal.
Device simulations
Based on TCAD simulations using Sentaurus Device from Synopsys, the Schottky diode was investigated regarding its electrical behavior. A simplified structure including the most important physical models for 4H-SiC was used to replicate the diode’s response to various conditions such as the external bias. The simulations were performed for \(T=100\) K and \(T=300\) K.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The code used to analyze the results presented in this paper will be made available from the corresponding author upon reasonable request.
References
Doherty, M. W. et al. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 528, 1–45 (2013).
Castelletto, S., Rosa, L.& Johnson, B. C. in Silicon Carbide Devices and Processing (InTech, 2015).
Santori, C., Fattal, D.& Yamamoto, Y. Single-photon Devices and Applications (Wiley, 2010).
Lo, H.-K., Curty, M. & Tamaki, K. Secure quantum key distribution. Nat. Photonics 8, 595–604 (2014).
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).
Xu, F. et al. Experimental quantum fingerprinting with weak coherent pulses. Nat. Commun. 6, 8735 (2015).
Togan, E. et al. Quantum entanglement between an optical photon and a solid-state spin qubit. Nature 466, 730–734 (2010).
Humphreys, P. C. et al. Deterministic delivery of remote entanglement on a quantum network. Nature 558, 268–273 (2018).
Weber, J. R. et al. Quantum computing with defects. Proc. Natl Acad. Sci. 107, 8513–8518 (2010).
Lohrmann, A., Johnson, B. C., McCallum, J. C. & Castelletto, S. A review on single photon sources in silicon carbide. Rep. Prog. Phys. 80, 034502 (2017).
Widmann, M. et al. Coherent control of single spins in silicon carbide at room temperature. Nat. Mater. 14, 164–168 (2014).
Kraus, H. et al. Room-temperature quantum microwave emitters based on spin defects in silicon carbide. Nat. Phys. 10, 157–162 (2014).
Niethammer, M.et al. Coherent electrical readout of defect spins in 4H-SiC by photo-ionization at ambient conditions. Preprint at arXiv:1903.12236 (2019).
Castelletto, S. et al. A silicon carbide room-temperature single-photon source. Nat. Mater. 13, 151–156 (2014).
Bosma, T. et al. Identification and tunable optical coherent control of transition-metal spins in silicon carbide. npj Quantum Inf. 4, 48 (2018).
Koehl, W. F., Buckley, B. B., Heremans, F. J., Calusine, G. & Awschalom, D. D. Room temperature coherent control of defect spin qubits in silicon carbide. Nature 479, 84–88 (2011).
Simin, D. et al. Locking of electron spin coherence above 20 ms in natural silicon carbide. Phys. Rev. B. 95, 161201(R) (2017).
Christle, D. J. et al. Isolated electron spins in silicon carbide with millisecond coherence times. Nat. Mater. 14, 160–163 (2015).
Janzén, E. et al. The silicon vacancy in SiC. Phys. B: Condens. Matter 404, 4354–4358 (2009).
Nagy, R. et al. High-fidelity spin and optical control of single silicon-vacancy centres in silicon carbide. Nat. Commun. 10, 1054 (2019).
Nagy, R. et al. Quantum properties of dichroic silicon vacancies in silicon carbide. Phys. Rev. Appl. 9, 034022 (2018).
Radulaski, M. et al. Scalable quantum photonics with single color centers in silicon carbide. Nano Lett. 17, 1782–1786 (2017).
Wang, J. et al. Efficient generation of an array of single silicon-vacancy defects in silicon carbide. Phys. Rev. Appl. 7, 064021 (2017).
Bracher, D. O., Zhang, X. & Hu, E. L. Selective Purcell enhancement of two closely linked zero-phonon transitions of a silicon carbide color center. Proc. Natl Acad. Sci. USA 114, 4060 (2017).
Hornos, T., Gali, A. & Svensson, B. G. Large-scale electronic structure calculations of vacancies in 4H-SiC using the Heyd-Scuseria-Ernzerhof screened hybrid density functional. Mater. Sci. Forum 679-680, 261–264 (2011).
de la Casas, C. F., Christle, D. J., Hassan, J. U., Son, T. O. O. T. & Awschalom, D. D. Stark tuning and electrical charge state control of single divacancies in silicon carbide. Appl. Phys. Lett. 111, 262403 (2017).
ichiro Sato, S. et al. Room temperature electrical control of single photon sources at 4H-SiC surface. ACS Photonics 5, 3159–3165 (2018).
Anderson, C. P.et al. Electrical and optical control of single spins integrated in scalable semiconductor devices. Preprint at arXiv:1906.08328 (2019).
Golter, D. A. & Lai, C. W. Optical switching of defect charge states in 4H-SiC. Sci. Rep. 7, 13406 (2017).
Wolfowicz, G. et al. Optical charge state control of spin defects in 4H-SiC. Nat. Commun. 8, 1876 (2017).
Wolfowicz, G., Whiteley, S. J. & Awschalom, D. D. Electrometry by optical charge conversion of deep defects in 4H-SiC. Proc. Natl Acad. Sci. 115, 7879–7883 (2018).
Wagner, M. et al. Electronic structure of the neutral silicon vacancy in 4H and 6H SiC. Phys. Rev. B. 62, 16555 (2000).
Ivády, V. et al. Identification of Si-vacancy related room-temperature qubits in 4H silicon carbide. Phy. Rev. B. 96, 161114(R) (2017).
Ziegler, J. F., Ziegler, M. & Biersack, J. SRIM—the stopping and range of ions in matter (2010). Nucl. Instrum. Methods Phys. Res. B: Beam Interactions Mater. Atoms 268, 1818–1823 (2010).
Son, N. T. et al. Negative-U system of carbon vacancy in 4H-SiC. Phys. Rev. Lett. 109, 187603 (2012).
Freysoldt, C., Grabowski, B., Hickel, T. & Neugebauer, J. First-principles calculations for point defects in solids. Rev. Mod. Phys. 86, 253–305 (2014).
Wickramaratne, D. et al. Defect identification based on first-principles calculations for deep level transient spectroscopy. Appl. Phys. Lett. 113, 192106 (2018).
Frodason, Y. K., Johansen, K. M., Alkauskas, A. & Vines, L. Negative-U and polaronic behavior of the Zn–O divacancy in ZnO. Phys. Rev. B. 99, 174106 (2019).
Omotoso, E., Mayer, W. E., Auret, F. D., Paradzah, A. T. & Legodi, M. J. Electrical characterization of deep levels created by bombarding nitrogen-doped 4H-SiC with alpha-particle irradiation. Nucl. Instrum. Methods Phys. Res. B. 371, 312–316 (2016).
Capan, I. et al. Double negatively charged carbon vacancy at the h- and k-sites in 4H-SiC: Combined laplace-DLTS and DFT study. J. Appl. Phys. 123, 161597 (2018).
Storasta, L., Bergman, J. P., Janzén, E., Henry, A. & Lu, J. Deep levels created by low energy electron irradiation in 4H-SiC. J. Appl. Phys. 96, 4909–4915 (2004).
Alfieri, G., Monakhov, E. V., Svensson, B. G. & Linnarsson, M. K. Annealing behavior between room temperature and 2000 C of deep level defects in electron-irradiated n-type 4H silicon carbide. J. Appl. Phys. 98, 043518 (2005).
Rauls, E. et al. Metastability of the neutral silicon vacancy in 4H-SiC. Phys. Status Solidi B. 217, R1 (2000).
David, M. L. et al. Electrically active defects in irradiated 4H-SiC. J. Appl. Phys. 95, 4728–4733 (2004).
Iwamoto, N.& Svensson, B. G. in Defects in Semiconductors vol. 91 of Semiconductors and Semimetals (eds Romano, L., Privitera, V. & Jagadish, C.) 369–407 (Elsevier, 2015).
Bathen, M. E. et al. Diffusion of the carbon vacancy in a-cut and c-cut n-type 4H-sic. Mater. Science Forum 924, 200–203 (2018).
Bringuier, E. Impact excitation in ZnS-type electroluminescence. J. Appl. Phys. 70, 4505–4512 (1991).
Stark, J. Beobachtungen über den effekt des elektrischen feldes auf spektrallinien i. quereffekt. Ann. Physik 50, 489 (1914).
Stoneham, A. M.Theory of Defects in Solids: Electronic Structure of Defects in Insulators and Semiconductors (Clarendon Press, 2001).
Tamarat, P. et al. Stark shift control of single optical centers in diamond. Phys. Rev. Lett. 97, 083002 (2006).
Widmann, M. et al. Electrical charge state manipulation of single silicon vacancies in a silicon carbide quantum optoelectronic device. Nano Lett. 19, 7173–7180 (2019).
Niethammer, M. et al. Vector magnetometry using silicon vacancies in 4H-SiC under ambient conditions. Phys. Rev. Appl. 6, 034001 (2016).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B. 47, 558–561 (1993).
Kresse, G. & Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B. 49, 14251–14269 (1994).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B. 54, 11169–11186 (1996).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B. 50, 17953–17979 (1994).
Grivickas, P., Grivickas, V., Linnros, J. & Galeckas, A. Fundamental band edge absorption in nominally undoped and doped 4H-SiC. J. Appl. Phys. 101, 123521 (2007).
Kumagai, Y. & Oba, F. Electrostatics-based finite-size corrections for first-principles point defect calculations. Phys. Rev. B. 89, 195205 (2014).
Freysoldt, C., Neugebauer, J. & de Walle, C. G. V. Fully Ab Initio Finite-size corrections for charged-defect supercell calculations. Phys. Rev. Lett. 102, 016402 (2009).
Komsa, H.-P., Rantala, T. T. & Pasquarello, A. Finite-size supercell correction schemes for charged defect calculations. Phys. Rev. B. 86, 045112 (2012).
Nielsen, H., Martin, D., Lévêque, P., Hallén, A. & Svensson, B. Annealing study of a bistable defect in proton-implanted n-type 4H-SiC. Phys. B: Condens. Matter 340-342, 743–747 (2003).
Alfieri, G., Monakhov, E. V., Svensson, B. G. & Hallén, A. Defect energy levels in hydrogen-implanted and electron-irradiated n-type 4H silicon carbide. J. Appl. Phys. 98, 113524 (2005).
Acknowledgements
The authors would like to sincerely thank the late Professor Bengt G. Svensson for all the enlightening discussion and support, and for initiating the work presented herein. Financial support was kindly provided by the Research Council of Norway and the University of Oslo through the frontier research project FUNDAMeNT (no. 251131, FriPro ToppForsk-program), and the Norwegian Micro- and Nanofabrication Facility (NorFAB 245963). The computations were performed on resources provided by UNINETT Sigma2—the National Infrastructure for High Performance Computing and Data Storage in Norway. J.C. thanks the Fundação para a Ciência e a Tecnologia (FCT) for support under project UID/CTM/50025/2019, co-funded by FEDER funds through the COMPETE 2020 Program. J.C. also acknowledges support by the NATO SPS programme (Project No. 985215).
Author information
Authors and Affiliations
Contributions
M.E.B. and Y.K.F. performed the calculations. M.E.B, L.V., A.G., and B.G.S. designed the experiments; M.E.B., A.G., and H.M.A performed the experiments. J.M. and U.G. performed the device simulations. All authors analyzed the data and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bathen, M.E., Galeckas, A., Müting, J. et al. Electrical charge state identification and control for the silicon vacancy in 4H-SiC. npj Quantum Inf 5, 111 (2019). https://doi.org/10.1038/s41534-019-0227-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-019-0227-y
This article is cited by
-
Analysis, recent challenges and capabilities of spin-photon interfaces in Silicon carbide-on-insulator
npj Nanophotonics (2024)
-
Fabrication and polarization modulation of waveguides in 4H-SiC crystals by femtosecond laser direct writing
Applied Physics A (2022)
-
Spin-controlled generation of indistinguishable and distinguishable photons from silicon vacancy centres in silicon carbide
Nature Communications (2020)