Abstract
Spin-based quantum processors in silicon quantum dots offer high-fidelity single and two-qubit operation. Recently multi-qubit devices have been realized; however, many-qubit demonstrations remain elusive, partly due to the limited qubit-to-qubit connectivity. These problems can be overcome by using SWAP gates, which are challenging to implement in devices having large magnetic field gradients. Here we use a primitive SWAP gate to transfer spin eigenstates in 100 ns with a fidelity of \({\bar{F}}_{{\rm{SWAP}}}^{{\rm{(p)}}}=98 \%\). By swapping eigenstates we are able to demonstrate a technique for reading out and initializing the state of a double quantum dot without shuttling charges through the quantum dot. We then show that the SWAP gate can transfer arbitrary two-qubit product states in 300 ns with a fidelity of \({\bar{F}}_{{\rm{SWAP}}}^{{\rm{(c)}}}=84 \%\). This work sets the stage for many-qubit experiments in silicon quantum dots.
Similar content being viewed by others
Introduction
Solid state quantum processors based on spins in silicon quantum dots are emerging as a powerful platform for quantum information processing.1,2 High-fidelity single- and two-qubit gates have recently been demonstrated2,3,4,5,6 and large extendable qubit arrays are now routinely fabricated.7 However, two-qubit gates are mediated through nearest-neighbor exchange interactions,1,8 which require direct wavefunction overlap. This limits the overall connectivity of these devices and is a major hurdle to realizing error correction,9 quantum random access memory,10 and multi-qubit quantum algorithms.11 To extend the connectivity, qubits can be shuttled around a device using quantum SWAP gates, but phase coherent SWAPs have not yet been realized in silicon quantum dot devices.2,3,4,5,6
Here, we demonstrate a single-step resonant SWAP gate. We first use the gate to efficiently initialize and readout our double quantum dot. We then show that the gate can move spin eigenstates in 100 ns with average fidelity \({\bar{F}}_{{\rm{SWAP}}}^{{\rm{(p)}}}=98 \%\). Finally, the transfer of arbitrary two-qubit product states is benchmarked using state tomography and Clifford randomized benchmarking,5,6,12 yielding an average fidelity of \({\bar{F}}_{{\rm{SWAP}}}^{{\rm{(c)}}}=84 \%\) for gate operation times of ~300 ns. Through coherent spin transport, our resonant SWAP gate enables the coupling of non-adjacent qubits, thus paving the way to large scale experiments using silicon spin qubits.
Results
Device architecture
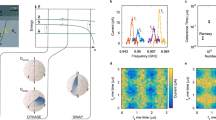
In this work, we use two sites of a quadruple quantum dot fabricated on a 28Si/SiGe heterostructure (inset of Fig. 1a).13 Electric dipole spin resonance14,15 enables single-spin control and an on-chip micromagnet detunes the frequency of each spin to enable site-selective control.13,16 For demonstration purposes, we use two dots in the device with qubits accumulated under plunger gates \({P}_{3}\) and \({P}_{4}\). We hereafter refer to the two qubits as \({Q}_{3}\) and \({Q}_{4}\), respectively. This naming is consistent with our previous work where operation of the device was first demonstrated.13 The charge stability diagram of this DQD is shown in Fig. 1a and quantum control is performed in the \(({N}_{3},{N}_{4})=(1,1)\) charge configuration, where \({N}_{i}\) denotes the number of electrons on dot \(i\). We measure the state of \({Q}_{4}\) through spin-selective tunneling to a drain reservoir accumulated beneath gate \({D}_{3}\).17 State initialization is also performed through spin-selective tunneling and the loading fidelity is limited to 95% by the 110 mK electron temperature.
Procedure for SWAP-based readout and initialization. a Charge stability map for a DQD formed using sites 3 and 4 in the quadruple dot array (inset). Quantum control is performed near the center of the (1,1) charge stability region as denoted by the green circle. Readout of dot 4 is performed at the (1,0)–(1,1) charge transition denoted by the blue triangle. The scale bar for the inset corresponds to 300 nm. b The typical measurement cycle is shown for controlling and reading out two quantum dots. In panel A, the qubits are manipulated and in panel B \({Q}_{4}\) is read out through spin-selective tunneling—leaving the qubit in the \(\left|\downarrow \right\rangle\) state. In panel C, the exchange interaction \({J}_{34}\) between \({Q}_{3}\) and \({Q}_{4}\) is modulated (through modulation of the barrier) to induce a SWAP operation, thus mapping the state of \({Q}_{3}\) onto \({Q}_{4}\). \({Q}_{4}\) is then read out once more to determine the state of \({Q}_{3}\).
Two-qubit Interactions
There are two modes of operation for the resonant SWAP gate demonstrated in this article. First, a projection-SWAP can be used to transfer spin eigenstates between quantum dots. The projection-SWAP enables rapid initialization and readout of inner sites in an array that are not directly connected to the leads—meaning they cannot be directly initialized or measured. Secondly, a coherent-SWAP can be used to transfer arbitrary quantum states between quantum dots, thus allowing the rearrangement of qubits in the array. A coherent-SWAP is important for performing multi-qubit algorithms or error correction in devices with limited qubit-to-qubit connectivity.18 The coherent- and projection-SWAP gates are realized using the same resonant SWAP gate; however, the coherent-SWAP requires more stringent calibration.
In our device architecture, two-qubit gates are mediated through the exchange interaction \({J}_{i,i+1}({V}_{{\rm{B}}i+1})\), which is proportional to the wavefunction overlap between the two adjacent qubits \(i\) and \(i+1\). This wavefunction overlap, and thus the exchange interaction, is controlled by adjusting the barrier gate voltage \({V}_{Bi+1}\). Here, we realize our SWAP gate through a resonant drive on that barrier at a frequency \({f}_{{\rm{SWAP}}}\) according to the formula \({V}_{{{B}}i+1}(t)={V}_{{{B}}i+1}^{({\rm{dc}})}+{V}_{{{B}}i+1}^{({\rm{ac}})}\cos (2\pi {f}_{{\rm{SWAP}}}t+\phi )\) where \({V}_{{{B}}i+1}^{({\rm{ac}})}\) is the amplitude of the drive and \({V}_{{{B}}i+1}^{({\rm{dc}})}\) is a static offset voltage. We note that the exchange interaction and the gate can also be modulated by varying the double quantum dot detuning.8
In the absence of a magnetic field gradient, when \({J}_{i,i+1}\gg {\gamma }_{\mathrm e}| {B}_{i}^{{\rm{tot}}}-{B}_{i+1}^{{\rm{tot}}}|\), where \({\gamma }_{\mathrm e}\) is the electronic gyromagnetic ratio and \({B}_{i}^{{\rm{tot}}}\) is the magnetic field at dot \(i\), the two qubits directly undergo SWAP oscillations.8,19,20,21 However, many spin qubit devices rely on large magnetic field gradients2,4,6,13 and our device has \({\gamma }_{\mathrm e}{B}_{3}^{{\rm{tot}}}\) = 16.949 GHz and \({\gamma }_{\mathrm e}{B}_{4}^{{\rm{tot}}}\) = 17.089 GHz at an external magnetic field of 410 mT. In this regime, the exchange interaction leads to a CPHASE-like evolution.2,22,23 To recover the two-qubit SWAP oscillations in the presence of such large magnetic field gradients, we effectively rotate out the gradient by applying an exchange pulse that is resonant with the difference frequency of the two qubits (\(2\pi {f}_{{\rm{SWAP}}}={\gamma }_{\mathrm e}| {B}_{i}^{{\rm{tot}}}-{B}_{i+1}^{{\rm{tot}}}|\)).24,25 This can be qualitatively understood as stroboscopically applying exchange whenever the evolution due to the magnetic field gradient returns to its initial state.
Resonant modulation of \({V}_{{{B}}i+1}\) at the difference frequency of the two qubits will drive Rabi rotations in the \(\left|{\phi }_{3},{\phi }_{4}\right\rangle \in \{\left|\uparrow \downarrow \right\rangle ,\left|\downarrow \uparrow \right\rangle \}\) subspace, while leaving the fully spin-polarized states unaffected. A \(\pi\)-pulse in this subspace is a SWAP gate up to additional phases on the state of each qubit. These phases do not affect the operation of the projection-SWAP, but will affect the coherent-SWAP. The theory describing these phase shifts and a procedure for calibrating them out is outlined in Supplementary Discussions I–III (see Supplemental Material at https://doi.org/10.1038/s41534-019-0225-0 for additional gate tuneup data and theory). Our resonant SWAP gate is therefore efficiently realized through a single RF burst on the barrier gate between qubits \(i\) and \(i+1\).
Projection-SWAP
We first describe how the projection-SWAP gate can be used for readout of an interior site in our device using the protocol outlined in Fig. 1b. In a typical measurement cycle, after quantum control is performed at (1,1), \({Q}_{4}\) is read out through spin-selective tunneling to the leads [blue triangle in Fig. 1a]. If \({Q}_{4}\) is in the \(\left|\uparrow \right\rangle\) state, the electron has enough energy to tunnel off of the dot and is replaced by a lower-energy electron in the \(\left|\downarrow \right\rangle\) state. However, if \({Q}_{4}\) is in the \(\left|\downarrow \right\rangle\) state, no tunneling occurs.17 Any charge hops are detected by monitoring the current through an adjacent charge sensor [\({I}_{{\rm{S}}2}\) in Fig. 1a]. If a charge hopping event is detected, we record the spin state as \(\left|\uparrow \right\rangle\). Regardless of its initial state, \({Q}_{4}\) is left in the \(\left|\downarrow \right\rangle\) state after measurement to within initialization errors. We next tune the device back into the (1,1) charge configuration and apply the resonant SWAP gate. In this process, \({Q}_{3}\)’s state is mapped on to \({Q}_{4}\) and \({Q}_{3}\) is left in the \(\left|\downarrow \right\rangle\) state. We once again measure \({Q}_{4}\) to infer \({Q}_{3}\)’s original state. This measurement protocol leaves the DQD in the \(\left|\downarrow \downarrow \right\rangle\) state.
To calibrate the SWAP gate, the system is initialized in the \(\left|{\phi }_{3},{\phi }_{4}\right\rangle =\left|\downarrow \downarrow \right\rangle\) state through spin-dependent tunneling from a Fermi reservoir into Q4 (ref. 4) is then flipped using an \(X\) gate. The SWAP is implemented by driving gate \({B}_{4}\) with an RF burst at frequency \({f}_{{\rm{SWAP}}}\) and duration 600 ns. Figure 2a shows the spin-up probability of \({Q}_{4}\), \({P}_{4,\uparrow }\) as a function of \({f}_{{\rm{SWAP}}}\) and \({V}_{{\rm{B}}4}^{({\rm{ac}})}\). For small \({V}_{{\rm{B}}4}^{({\rm{ac}})}\), there are no measureable SWAP oscillations. At around \({V}_{B4}^{({\rm{ac}})}\) = 10 mV, coherent-SWAP oscillations in \({P}_{4,\uparrow }\) appear. The pattern is symmetric about \({f}_{{\rm{SWAP}}}\) = 140 MHz. For a 600 ns burst at 140 MHz, a SWAP is achieved with \({V}_{B4}^{{\rm{ac}}}\) = 10 mV. To minimize the SWAP time, we fix \({f}_{{\rm{SWAP}}}\) = 140 MHz and vary \({V}_{{\rm{B}}4}^{({\rm{ac}})}\) and the drive time (\({t}_{{\rm{SWAP}}}\)) in Fig. 2b. Each alternating bright fringe corresponds to an even number of SWAPs. The minimum SWAP time shown here is 23 ns and is limited by the dynamic range of our control electronics. The coherence times \({T}_{2}^{* }\) are approximately 10 μs for both dots,13 which is long relative to these gate operation times.
Coherent exchange oscillations and SWAP-based readout. a SWAP oscillations measured on \({Q}_{4}\), where \({P}_{4,\uparrow }\) is the probability of measuring \({Q}_{4}\) in the spin-up state. The pulse length (\({t}_{{\rm{SWAP}}}\)) is fixed at 600 ns, whereas the amplitude of the drive (\({V}_{B4}^{({\rm{ac}})}\)) and the frequency of the modulation (\({f}_{{\rm{SWAP}}}\)) are varied to map out the ideal SWAP gate parameters. b SWAP oscillations are shown for varying \({V}_{B4}^{({\rm{ac}})}\) keeping \({f}_{{\rm{SWAP}}}\) = 140 MHz. c SWAP-based readout is demonstrated for \({Q}_{3}\) and \({Q}_{4}\), where we simultaneously drive Rabi oscillations on both qubits and then read them out in series. Here, each dot is read out for 3 ms. The higher frequency Rabi oscillations observed for \({Q}_{3}\) are attributed to a larger transverse field gradient at Q3.13
We now demonstrate simultaneous quantum control, initialization, and readout of both dots using spin-to-charge conversion of only \({Q}_{4}\). Starting in the \(\left|\downarrow \downarrow \right\rangle\) state, we apply a microwave burst with duration \({\tau }_{{\rm{p}}}\) and frequency \(f\). We measure \({Q}_{4}\) through spin-selective tunneling to \({D}_{3}\), leaving \({Q}_{4}\) in the \(\left|\downarrow \right\rangle\) state. We then apply a projection-SWAP to the qubits, mapping the state of \({Q}_{3}\) onto \({Q}_{4}\), and leaving \({Q}_{3}\) in the \(\left|\downarrow \right\rangle\) state. \({Q}_{4}\) is then measured so that we can infer the state of \({Q}_{3}\). Once \({Q}_{4}\) is measured, the qubits are left in the \(\left|\downarrow \right\rangle\) state, and the DQD is prepared for the next experiment. The spin-up probability for both qubits is plotted as a function of \({\tau }_{{\rm{p}}}\) and \(f\) in Fig. 2c. The fringes observed are Rabi oscillations, whose spacing is largest when the qubits are on resonance. These data reveal a qubit difference frequency of 140 MHz, which is consistent with the two-qubit spectroscopy in Fig. 2a. These data show that we can initialize, control, and readout our DQD even though readout only occurs on \({Q}_{4}\).
To quantitatively study the projection-SWAP gate for readout purposes, we designed an experiment to be insensitive to state preparation and measurement (SPAM) errors. We prepare the qubits in one of the four spin eigenstates \({\left|{\phi }_{3},{\phi }_{4}\right\rangle }_{{\rm{in}}}=\left|\downarrow \downarrow \right\rangle\), \(\left|\downarrow \uparrow \right\rangle\), \(\left|\uparrow \downarrow \right\rangle\), and \(\left|\uparrow \uparrow \right\rangle\) before applying the SWAP gate to the qubits \(N\) times as shown in Fig. 3. We expect the spin-polarized states to decay towards a mixed state with \({P}_{3,\uparrow }\) and \({P}_{4,\uparrow }\) = 0.5 for large \(N\). The antiparallel spin input states should flip-flop between the \(\left|\downarrow \uparrow \right\rangle\) and \(\left|\uparrow \downarrow \right\rangle\) states for each additional SWAP we apply. \({P}_{3,\uparrow }\) and \({P}_{4,\uparrow }\) will then converge to 0.5 in the large \(N\) limit. The decay envelope is given by \({F}_{{s}_{3}{s}_{4}}^{({\rm{p}})N}\), where \({F}_{{s}_{3}{s}_{4}}^{({\rm{p}})}\) is the fidelity of the projection-SWAP on spin states \({s}_{3}\) and \({s}_{4}\) between \({Q}_{3}\) and \({Q}_{4}\). Fitting these curves we find an average fidelity of \({F}_{\downarrow \uparrow }^{({\rm{p}})}={F}_{\uparrow \downarrow }^{({\rm{p}})}=96.5 \%\) for \({\left|{\phi }_{3},{\phi }_{4}\right\rangle }_{{\rm{in}}}=\left|\downarrow \uparrow \right\rangle\) or \(\left|\uparrow \downarrow \right\rangle\). In cases where both qubits have the same initial state \({\left|{\phi }_{3},{\phi }_{4}\right\rangle }_{{\rm{in}}}=\left|\downarrow \downarrow \right\rangle\) or \(\left|\uparrow \uparrow \right\rangle\), we achieve fidelities of \({F}_{\downarrow \downarrow }^{({\rm{p}})}=99.6 \%\) and \({F}_{\uparrow \uparrow }^{({\rm{p}})}=99.2 \%\) respectively. Thus, we find an average fidelity for the projection-SWAP of \({\bar{F}}_{{\rm{SWAP}}}^{({\rm{p}})}=98 \%\). The spin-polarized input states are insensitive to errors due to noise in the drive field and pulse miscalibrations, but should be sensitive to spin relaxation. The 96.5% fidelity for antiparallel spin input states is, therefore, not likely limited by relaxation. This is expected, since \({T}_{1}\) is 134 ms (52 ms) for \({Q}_{3}\) (\({Q}_{4}\)), which gives an upper bound of 99.97% fidelity for implementing 60 SWAPs, each padded with a 100 ns idle. The likely source of errors for antiparallel spin states arises from time-dependent fluctuations in the magnetic field gradients or exchange interaction, which lead to miscalibrations in the projection-SWAP gate.
Projection-SWAP fidelity. The probability of measuring a spin-up \({P}_{i,\uparrow }\) on \({Q}_{i}\) is plotted for \({Q}_{4}\) (a) and \({Q}_{3}\) (b) after the two-qubit system undergoes \(N\) SWAP operations. The input states are denoted by color and the dashed lines are fits to the data (see Supplemental Material at https://doi.org/10.1038/s41534-019-0225-0 for additional gate tuneup data and theory). The extracted fidelity \({F}_{{s}_{3}{s}_{4}}^{({\rm{p}})}\) from each fit is shown in the table.
The high-fidelity of our projection-SWAP gates implies that this SPAM technique can be useful for much larger arrays than the DQD configuration studied here. Our current fidelity suggests we could shuttle a spin projection across a nine-dot array26 with a fidelity of 85%. It is notable that while the SWAP gate leads to spin transport between adjacent dots, the electron wavefunctions remain localized on the dots and there is no charge transport. This is in contrast to typical spin-shuttle experiments27 that physically move electrons, a process which can be complicated by low-lying valley states,28 spin–orbit coupling,29 or spin-relaxation hotspots.2 Because spin transport can be controlled using only barrier gates, no fast plunger gate control is necessary, which should enable the operation of devices having fixed charge configurations. This could be of particular interest in two-dimensional arrays where for even small numbers of qubits, charge state control and readout of interior sites becomes unmanageable. Finally, the projection-SWAP is compatible with singlet-triplet readout8,21,30 and cavity-based dispersive readout.31,32
Coherent-SWAP
With the projection-SWAP, we have shown that it is possible to transfer spin eigenstates oriented along the magnetic field axis. More generally, the ability to transfer arbitrary quantum information is crucial to operating multi-qubit devices with limited connectivity. Therefore, having achieved a high-fidelity projection-SWAP, we turn our attention to transferring product states oriented along arbitrary directions with the coherent-SWAP, e.g.,\(({\alpha }_{1}\left|\uparrow \right\rangle +{\beta }_{1}\left|\downarrow \right\rangle )\otimes ({\alpha }_{2}\left|\uparrow \right\rangle +{\beta }_{2}\left|\downarrow \right\rangle )\to ({\alpha }_{2}\left|\uparrow \right\rangle +{\beta }_{2}\left|\downarrow \right\rangle )\otimes ({\alpha }_{1}\left|\uparrow \right\rangle +{\beta }_{1}\left|\downarrow \right\rangle )\). The coherent-SWAP has additional calibration requirements outlined in the Methods section. These tuning requirements are also sufficient for performing SWAP gates on entangled states (see Supplemental Material at https://doi.org/10.1038/s41534-019-0225-0 for additional gate tuneup data and theory). Here we realize a coherent-SWAP in 302 ns, which can be made faster by superimposing a dc exchange pulse as shown in Supplementary Fig. 2 (see Supplemental Material at https://doi.org/10.1038/s41534-019-0225-0 for additional gate tuneup data and theory).
To verify our calibration, we prepared \({Q}_{3}\) in a superposition state, and performed state tomography before and after applying a coherent-SWAP. By measuring the \(x\), \(y\), and \(z\) spin projections, we are able to reconstruct the single-spin density matrices \({\rho }_{i}\) as plotted in Fig. 4a. The imaginary components of \({\rho }_{i}\) are shown in Supplementary Fig. 5 (see Supplemental Material at https://doi.org/10.1038/s41534-019-0225-0 for additional gate tuneup data and theory). From these data, we can estimate the SWAP fidelity \(F(\rho )\) by comparing the output state to the targeted state \({\psi }_{{\rm{ideal}}}\) using \(F(\rho )=\left\langle {\psi }_{{\rm{ideal}}}\right|\rho \left|{\psi }_{{\rm{ideal}}}\right\rangle\) and \(\rho ={\rho }_{3}\otimes {\rho }_{4}\).33 When constructing the two-qubit density matrices, SPAM errors are subtracted out (see Supplemental Material at https://doi.org/10.1038/s41534-019-0225-0 for additional gate tuneup data and theory).2,4 This analysis gives a state fidelity of \(F(\rho )=89 \%\). Because this technique only measures the fidelity of swapping one pair of input states, obtaining an average gate fidelity requires repeating the experiment for each possible input.
Coherent-SWAP fidelity. a Real part of the density matrix \({\rho }_{i}\) for \({Q}_{i}\) obtained via state tomography on \({Q}_{3}\) and \({Q}_{4}\) before (left) and after (right) applying a 302 ns SWAP gate. \({Q}_{3}\) was prepared in a superposition state by applying a \(\pi\)/2 pulse and \({Q}_{4}\) is prepared in the down state. After applying the SWAP gate, we find that the density matrices are transferred between the two qubits. The density matrices are corrected for SPAM errors.2\({Q}_{3}\) was measured using the projection-SWAP protocol outlined in this article. From these data we estimate a SWAP fidelity of 89%. b Single qubit randomized benchmarking was performed simultaneously on \({Q}_{3}\) and \({Q}_{4}\) and the probability of measuring \(\left|\uparrow \uparrow \right\rangle\) (corrected for SPAM errors) is shown in black as a function of the number of Clifford gates (\(N\)). The experiment is repeated interleaving SWAP gates with each pair of Clifford gates and the decay is shown in red. Each point consists of 40 random sequences and 500 averages. Error bars denote the standard error of the mean. The extracted SWAP fidelity is \({\bar{F}}_{{\rm{SWAP}}}^{({\rm{c}})}=84 \%\).
To measure the average SWAP fidelity, we turn to Clifford randomized benchmarking, which is insensitive to SPAM errors.5,6,12,34 In Clifford randomized benchmarking, quantum circuits consisting of \(N\) randomly chosen Clifford gates are applied to a qubit, and at the end of the sequence, the qubit is rotated into a known state. Any gate infidelity throughout the sequence leads to errors in the final state. The qubit is measured and the experiment is repeated varying \(N\). As \(N\) increases, integrated errors cause the qubit state to become mixed and the probability of measuring \({P}_{i,\uparrow }\) approaches 50%.
To avoid the extensive overhead associated with full two-qubit randomized benchmarking, which requires calibration of an entangling two-qubit gate in addition to the SWAP gate, we use a technique pioneered by Chen et al.35 to benchmark two-qubit gates using interleaved randomized benchmarking.6,12 We note that while there are no entangled states generated by our single qubit Clifford gates, entanglement generation exists as a decay channel. We first perform single qubit Clifford randomized benchmarking on \({Q}_{3}\) and \({Q}_{4}\) by measuring the spin-up probability \({P}_{\left|\uparrow \uparrow \right\rangle }\) as a function of sequence length \(N\). These data, shown in black in Fig. 4b, are acquired with \({Q}_{3}\) and \({Q}_{4}\) single qubit rotations implemented in parallel. We next repeat the randomized benchmarking experiment, this time interleaving \(coherent\)-SWAP gates after each set of parallel single qubit Clifford gates on \({Q}_{3}\) and \({Q}_{4}\). These results are plotted in red in Fig. 4b. The decays are fit to \({P}_{\left|\uparrow \uparrow \right\rangle }={A}_{0}{p}_{c}^{m}+C\) where \({A}_{0}\) is the measurement visibility, \(C\) is the dark count, and \({p}_{c}\) is a decay parameter.12 This fit yields a decay parameter \({p}_{c}\) = 0.843 for the reference curve and \({\bar{p}}_{c}\) = 0.665 for the interleaved curve. By comparing these decay parameters we can extract an average coherent-SWAP fidelity of \({\bar{F}}_{{\rm{SWAP}}}^{({\rm{c}})}=1-3/4(1-\bar{{p}_{c}}/{p}_{c})=84 \%\), which is in good agreement with our estimate from state tomography.12
Discussion
In conclusion, we have demonstrated a resonant SWAP gate that can be used for coherent spin transport and high-fidelity state preparation and readout in an array of quantum dot spin qubits. We measure an average projection-SWAP gate fidelity of \({\bar{F}}_{{\rm{SWAP}}}^{({\rm{p}})}=98 \%\) when transferring eigenstates with a 100 ns gate time. We further show that a coherent-SWAP gate can be used to transfer arbitrary two-qubit states between spins with an average fidelity of \({\bar{F}}_{{\rm{SWAP}}}^{({\rm{c}})}=84 \%\) in ~300 ns as measured using interleaved randomized benchmarking. By implementing automatic calibration and feedback,5 we should be able to significantly improve this fidelity. SWAP gates are an important building block in any quantum processor with limited qubit-to-qubit connectivity and are necessary to unlock the full capabilities of the multi-qubit devices currently being fabricated in Si/SiGe.13,26 This robust implementation of a resonant SWAP gate promises to enable beyond nearest-neighbor operation in quantum dot arrays, which is necessary for quantum information processing with more than two qubits.
Methods
Beyond the calibration required for the projection-SWAP, there are three additional constraints that must be satisfied to achieve high-fidelity coherent-SWAP gates. First, the resonant SWAP pulse must remain phase coherent with the qubits in their doubly rotating reference frame between calibrations (i.e. for hours). Second, because of the constraint that the exchange interaction is always positive, the time-averaged exchange pulse necessarily has some static component, which leads to evolution under an Ising interaction as discussed in Supplementary Discussions I–III (see Supplemental Material at https://doi.org/10.1038/s41534-019-0225-0 for additional gate tuneup data and theory). These Ising phases must be calibrated out. Finally, voltage pulses on any gate generally displace both electrons by some small amount. This movement induces phase shifts in both qubits, since they are located in a large magnetic field gradient. These phase shifts must be compensated for.
To satisfy these additional tuning requirements, we first ensure that our RF exchange pulse remains phase coherent. Each qubit’s reference frame is defined by the microwave signal generator controlling it, so by mixing together the local oscillators of these signal generators, we obtain a beat frequency that is phase locked to the doubly rotating two-qubit reference frame. We then amplitude modulate this signal to generate our exchange pulses. A detailed schematic is shown in Supplementary Fig. 6 (see Supplemental Material at https://doi.org/10.1038/s41534-019-0225-0 for additional gate tuneup data and theory).
To calibrate for the single and two-qubit Ising phases, we use state tomography on both qubits before and after applying a SWAP gate. In these measurements, we vary the input states to distinguish between errors caused by two-qubit Ising phases, and the single qubit phase shifts. We choose a SWAP time and amplitude such that the Ising phases cancel out, which for this particular configuration occurs for a 302 ns SWAP gate. The single qubit phase shifts were measured to be 180° for \({Q}_{3}\) and 140° for \({Q}_{4}\). By superimposing the SWAP pulse with a dc exchange pulse, one can compensate for the Ising phases at arbitrary SWAP lengths, leading to faster operation (see Supplemental Material at https://doi.org/10.1038/s41534-019-0225-0 for additional gate tuneup data and theory).
Data availability
The data supporting the findings of this study are available within the paper and its Supplementary Information (see Supplemental Material at https://doi.org/10.1038/s41534-019-0225-0 for additional gate tuneup data and theory). The data are also available from the authors upon reasonable request.
References
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120 (1998).
Watson, T. F. et al. A programmable two-qubit quantum processor in silicon. Nature 555, 633 (2018).
Veldhorst, M. et al. A two-qubit logic gate in silicon. Nature 526, 410 (2015).
Zajac, D. M. et al. Resonantly driven CNOT gate for electron spins. Science 359, 439 (2018).
Huang, W. et al. Fidelity benchmarks for two-qubit gates in silicon. Nature 569, 532 (2019).
Xue, X. et al. Benchmarking gate fidelities in a \({\rm{Si}}/{\rm{SiGe}}\) two-qubit device. Phys. Rev. X 9, 021011 (2019).
Zajac, D. M., Hazard, T. M., Mi, X., Nielsen, E. & Petta, J. R. Scalable gate architecture for a one-dimensional array of semiconductor spin qubits. Phys. Rev. Appl. 6, 054013 (2016).
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180 (2005).
Fowler, A. G., Hill, C. D. & Hollenberg, L. C. L. Quantum-error correction on linear-nearest-neighbor qubit arrays. Phys. Rev. A 69, 042314 (2004).
Giovannetti, V., Lloyd, S. & Maccone, L. Architectures for a quantum random access memory. Phys. Rev. A 78, 052310 (2008).
Farhi, E., Goldstone, J. & Gutmann, S. A quantum approximate optimization algorithm. Preprint at https://arxiv.org/abs/1411.4028 (2014).
Magesan, E. et al. Efficient measurement of quantum gate error by interleaved randomized benchmarking. Phys. Rev. Lett. 109, 080505 (2012).
Sigillito, A. J. et al. Site-selective quantum control in an isotopically enriched 28Si/SiGe quadruple quantum dot. Phys. Rev. Appl. 11, 061006 (2019).
Pioro-Ladriere, M. et al. Electrically driven single-electron spin resonance in a slanting Zeeman field. Nat. Phys. 4, 776 (2008).
Tokura, Y., van der Wiel, W. G., Obata, T. & Tarucha, S. Coherent single electron spin control in a slanting Zeeman field. Phys. Rev. Lett. 96, 047202 (2006).
Yoneda, J. et al. Robust micromagnet design for fast electrical manipulations of single spins in quantum dots. Appl. Phys. Express. 8, 084401 (2015).
Elzerman, J. et al. Single-shot read-out of an individual electron spin in a quantum dot. Nature 430, 431 (2004).
Linke, N. et al. Experimental comparison of two quantum computing architectures. Proc. Natl. Acad. Sci. USA 114, 3305 (2017).
Nowack, K. C. et al. Single-shot correlations and two-qubit gate of solid-state spins. Science 333, 1269 (2011).
Maune, B. et al. Coherent singlet-triplet oscillations in a silicon-based double quantum dot. Nature 481, 344 (2012).
Kandel, Y. et al. Coherent spin-state transfer via Heisenberg exchange. Nature 573, 553 (2019).
Meunier, T., Calado, V. E. & Vandersypen, L. M. K. Efficient controlled-phase gate for single-spin qubits in quantum dots. Phys. Rev. B 83, 121403 (2011).
Russ, M. et al. High-fidelity quantum gates in Si/SiGe double quantum dots. Phys. Rev. B 97, 085421 (2018).
Nichol, J. et al. High-fidelity entangling gate for double-quantum-dot spin qubits. npj Quantum Inf. 3, 3 (2017).
Harvey-Collard, P. et al. All-electrical universal control of a double quantum dot qubit in silicon MOS. In 2017 IEEE International Electron Devices Meeting (IEDM), 36.5.1 (San Francisco, CA, 2017).
Mills, A. R. et al. Shuttling a single charge across a one-dimensional array of silicon quantum dots. Nat. Commun. 10, 1063 (2019).
Baart, T. et al. Single-spin CCD. Nat. Nanotechnol. 11, 330 (2016).
Zwaneburg, F. et al. Silicon quantum electronics. Rev. Mod. Phys. 85, 961 (2013).
Tyryshkin, A. M., Lyon, S. A., Jantsch, W. & Schäffler, F. Spin manipulation of free two-dimensional electrons in \({\rm{Si}}/{\rm{SiGe}}\) quantum wells. Phys. Rev. Lett. 94, 126802 (2005).
Harvey-Collard, P. et al. High-fidelity single-shot readout for a spin qubit via an enhanced latching mechanism. Phys. Rev. X 8, 021046 (2018).
Zheng, G. et al. Rapid high-fidelity gate-based spin read-out in silicon. Nat. Nanotechnol. 14, 742–746 (2019).
Petersson, K. D. et al. Circuit quantum electrodynamics with a spin qubit. Nature 490, 380 (2012).
Uhlmann, A. Fidelity and concurrence of conjugated states. Phys. Rev. A 62, 032307 (2000).
Knill, E. et al. Randomized benchmarking of quantum gates. Phys. Rev. A 77, 012307 (2008).
Chen, Y. et al. Qubit architecture with high coherence and fast tunable coupling. Phys. Rev. Lett. 113, 220502 (2014).
Acknowledgements
Funded by Army Research Office grant no. W911NF-15-1-0149, DARPA grant no. D18AC0025, and the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant GBMF4535. Devices were fabricated in the Princeton University Quantum Device Nanofabrication Laboratory. The authors acknowledge the use of the Princeton University Imaging and Analysis Center, which is partially supported by the Princeton Center for Complex Materials, a National Science Foundation MRSEC program (DMR-1420541).
Author information
Authors and Affiliations
Contributions
A.J.S., M.J.G., and J.R.P. designed and planned the experiments, A.J.S. fabricated the device and performed the measurements, M.J.G. provided theory support, L.F.E. and M.B. provided the isotopically enriched heterostructure. A.J.S., M.J.G., and J.R.P. wrote the manuscript with input from all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sigillito, A.J., Gullans, M.J., Edge, L.F. et al. Coherent transfer of quantum information in a silicon double quantum dot using resonant SWAP gates. npj Quantum Inf 5, 110 (2019). https://doi.org/10.1038/s41534-019-0225-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-019-0225-0
This article is cited by
-
Pipeline quantum processor architecture for silicon spin qubits
npj Quantum Information (2024)
-
Fast universal quantum gate above the fault-tolerance threshold in silicon
Nature (2022)
-
Phase flip code with semiconductor spin qubits
npj Quantum Information (2022)
-
Impact of the valley orbit coupling on exchange gate for spin qubits in silicon
npj Quantum Information (2022)
-
Review of performance metrics of spin qubits in gated semiconducting nanostructures
Nature Reviews Physics (2022)