Abstract
Quantum algorithms have the potential to outperform their classical counterparts in a variety of tasks. The realization of the advantage often requires the ability to load classical data efficiently into quantum states. However, the best known methods require \({\mathcal{O}}\left({2}^{n}\right)\) gates to load an exact representation of a generic data structure into an \(n\)-qubit state. This scaling can easily predominate the complexity of a quantum algorithm and, thereby, impair potential quantum advantage. Our work presents a hybrid quantum-classical algorithm for efficient, approximate quantum state loading. More precisely, we use quantum Generative Adversarial Networks (qGANs) to facilitate efficient learning and loading of generic probability distributions - implicitly given by data samples - into quantum states. Through the interplay of a quantum channel, such as a variational quantum circuit, and a classical neural network, the qGAN can learn a representation of the probability distribution underlying the data samples and load it into a quantum state. The loading requires \({\mathcal{O}}\left(poly\left(n\right)\right)\) gates and can thus enable the use of potentially advantageous quantum algorithms, such as Quantum Amplitude Estimation. We implement the qGAN distribution learning and loading method with Qiskit and test it using a quantum simulation as well as actual quantum processors provided by the IBM Q Experience. Furthermore, we employ quantum simulation to demonstrate the use of the trained quantum channel in a quantum finance application.
Similar content being viewed by others
Introduction
The realization of many promising quantum algorithms is impeded by the assumption that data can be efficiently loaded into a quantum state.1,2,3,4 However, this may only be achieved for particular but not for generic data structures. In fact, data loading can easily dominate the complexity of an otherwise advantageous quantum algorithm.5 In general, data loading relies on the availability of a quantum state preparing channel. But, the exact preparation of a generic state in \(n\) qubits requires \({\mathcal{O}}\left({2}^{n}\right)\) gates.6,7,8,9 In many cases, this complexity diminishes a potential quantum advantage.
This work discusses the training of an approximate, efficient data loading channel with Quantum Machine Learning for particular data structures. More specifically, we present a feasible learning and loading scheme for generic probability distributions based on a generative model. The scheme utilizes a hybrid quantum-classical implementation of a Generative Adversarial Network (GAN)10,11 to train a quantum channel such that it reflects a probability distribution implicitly given by data samples.
In classical machine learning, GANs have proven useful for generative modeling. These algorithms employ two competing neural networks - a generator and a discriminator - which are trained alternately. Replacing either the generator, the discriminator, or both with quantum systems translates the framework to the quantum computing context.12
The first theoretical discussion of quantum GANs (qGANs) was followed by demonstrations of qGAN implementations. Some focused on quantum state estimation,13 i.e., finding a quantum channel whose output is an estimate to a given quantum state.14,15,16 Others exploited qGANs to generate classical data samples in accordance with the training data’s underlying distribution.17,18,19
In contrast, our qGAN implementation learns and loads probability distributions into quantum states. More specificially, the aim of the qGAN is not to produce classical samples in accordance with given classical training data but to train the quantum generator to create a quantum state which represents the data’s underlying probability distribution. The resulting quantum channel, given by the quantum generator, enables efficient loading of an approximated probability distribution into a quantum state. It can be easily prepared and reused as often as needed. Now, applying this qGAN scheme for data loading can facilitate quantum advantage in combination with other algorithms such as Quantum Amplitude Estimation (QAE)4 or the HHL-algorithm.1 Notably, QAE and HHL - given a well-conditioned matrix and a suitable classical right-hand-side5 - are both compatible with approximate state preparation as these algorithms are stable to small errors in the input state, i.e., small deviations in the input only lead to small deviations in the result.
The remainder of this paper is structured as follows. First, we explain classical GANs. Then, the qGAN-based distribution learning and loading scheme is introduced and analyzed on different test cases. Next, we discuss the exploitation of qGANs to facilitate quantum advantage in financial derivative pricing. More explicitly, we discuss the training of the qGAN with data samples drawn from a log-normal distribution and present the results obtained with a quantum simulator and the IBM Q Boeblingen superconducting quantum computer with 20 qubits, both accessible via the IBM Q Experience.20 Furthermore, the resulting quantum channel is used in combination with QAE to price a European call option. Finally, the conclusions and a discussion on open questions and additional possible applications of the scheme are presented.
Results
Generative Adversarial Networks
The generative models considered in this work, GANs,10,11 employ two neural networks - a generator and a discriminator - to learn random distributions that are implicitly given by training data samples. Originally, GANs were used in the context of image generation and modification. In contrast to previously used generative models, such as Variational Auto Encoders (VAEs),21,22 GANs managed to generate sharp images and consequently gained popularity in the machine learning community.23 VAEs and other generative models relying on log-likelihood optimization are prone to generating blurry images. Particularly for multi-modal data, log-likelihood optimization tends to spread the mass of a learned distribution over all modes. GANs, on the other hand, tend to focus the mass on each mode.10,24
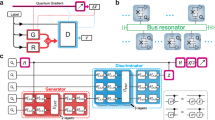
Suppose a classical training data set \(X=\{{{\boldsymbol{x}}}^{0},\ldots ,{{\boldsymbol{x}}}^{s-1}\}\subset {{\mathbb{R}}}^{{k}_{{\rm{out}}}}\) sampled from an unknown probability distribution \({p}_{{\rm{real}}}\). Let \({G}_{{\boldsymbol{\theta }}}:{{\mathbb{R}}}^{{k}_{{\rm{in}}}}\to {{\mathbb{R}}}^{{k}_{{\rm{out}}}}\) and \({D}_{{\boldsymbol{\phi }}}:{{\mathbb{R}}}^{{k}_{{\mathrm{out}}}}\to \{0,1\}\) denote the generator and the discriminator networks, respectively. The corresponding network parameters are given by \({\boldsymbol{\theta }}\in {{\mathbb{R}}}^{{k}_{{\rm{g}}}}\) and \({\boldsymbol{\phi }}\in {{\mathbb{R}}}^{{k}_{{\rm{d}}}}\). The generator \({G}_{{\boldsymbol{\theta }}}\) translates samples from a fixed prior distribution \({p}_{{\rm{prior}}}\) in \({{\mathbb{R}}}^{{k}_{{\rm{in}}}}\) into samples which are indistinguishable from samples of the real distribution \({p}_{{\rm{real}}}\) in \({{\mathbb{R}}}^{{k}_{{\rm{out}}}}\). The discriminator \({D}_{{\boldsymbol{\phi }}}\), on the other hand, tries to distinguish between data from the generator and from the training set. The training process is illustrated in Fig. 1.
The optimization objective of classical GANs may be defined in various ways. In this work, we consider the non-saturating loss25 which is also used in the code of the original GAN paper.10 The generator’s loss function
aims at maximizing the likelihood that the generator creates samples that are labeled as real data samples. On the other hand, the discriminator’s loss function
aims at maximizing the likelihood that the discriminator labels training data samples as training data samples and generated data samples as generated data samples. In practice, the expected values are approximated by batches of size \(m\)
for \({{\boldsymbol{x}}}^{l}\in X\) and \({{\boldsymbol{z}}}^{l} \sim {p}_{{\rm{prior}}}\). Training the GAN is equivalent to searching for a Nash-equilibrium of a two-player game:
Typically, the optimization of Eqs. (5) and (6) employs alternating update steps for the generator and the discriminator. These alternating steps lead to non-stationary objective functions, i.e., an update of the generator’s (discriminator’s) network parameters also changes the discriminator’s (generator’s) loss function. Common choices to perform the update steps are ADAM26 and AMSGRAD,27 which are adaptive-learning-rate, gradient-based optimizers that use an exponentially decaying average of previous gradients, and are well suited for solving non-stationary objective functions.26
qGAN distribution learning
Our qGAN implementation uses a quantum generator and a classical discriminator to capture the probability distribution of classical training samples. Notably, the aim of this approach is to train a data loading quantum channel for generic probability distributions. As discussed before, GAN-based learning is explicitly suitable for capturing not only uni-modal but also multi-modal distributions, as we will demonstrate later in this section.
In this setting, a parametrized quantum channel, i.e., the quantum generator, is trained to transform a given \(n\)-qubit input state \(\left|{\psi }_{{\rm{in}}}\right\rangle\) to an \(n\)-qubit output state
where \({p}_{{\boldsymbol{\theta }}}^{j}\) describe the resulting occurrence probabilities of the basis states \(\left|j\right\rangle\).
For simplicity, we now assume that the domain of \(X\) is \(\{0,...,{2}^{n}-1\}\), and thus the existence of a natural mapping between the sample space of the training data and the states that can be represented by the generator. This assumption can be easily relaxed, for instance, by introducing an affine mapping between \(\{0,...,{2}^{n}-1\}\) and an equidistant grid suitable for \(X\). In this case, it might be necessary to map points in \(X\) to the closest grid point to allow for an efficient training. The number of qubits \(n\) determines the distribution loading scheme’s resolution, i.e., the number of discrete values \({2}^{n}\) that can be represented. During the training, this affine mapping can be applied classically after measuring the quantum state. However, when the resulting quantum channel is used within another quantum algorithm the mapping must be executed as part of the quantum circuit. As was discussed in ref., 28 such an affine mapping can be implemented in a gate-based quantum circuit with linearly many gates.
The quantum generator is implemented by a variational form,29 i.e., a parametrized quantum circuit. We consider variational forms consisting of alternating layers of parametrized single-qubit rotations, here Pauli-Y-rotations \(\left({R}_{Y}\right)\),3 and blocks of two-qubit gates, here controlled-\(Z\)-gates \(\left(CZ\right)\),3 called entanglement blocks \({U}_{{\rm{ent}}}\). The circuit consists of a first layer of \({R}_{Y}\) gates, and then \(k\) alternating repetitions of \({U}_{{\rm{ent}}}\) and further layers of \({R}_{Y}\) gates. The rotation acting on the \({i}{{\rm{th}}}\) qubit in the \({j}{{\rm{th}}}\) layer is parametrized by \({\theta }^{i,j}\). Moreover, the parameter \(k\) is called the depth of the variational circuit. If such a variational circuit acts on \(n\) qubits it uses in total \((k+1)n\) parametrized single-qubit gates and \(kn\) two-qubit gates, see Fig. 2 for an illustration. Similarly to increasing the number of layers in deep neural networks,30 increasing the depth \(k\) enables the circuit to represent more complex structures and increases the number of parameters. Another possibility of increasing the quantum generator’s ability to represent complex correlations is adding ancilla qubits, as this facilitates an isometric instead of a unitary mapping,3 see Supplementary Notes A for more details.
Quantum generator. The variational form, depicted in (a), with depth \(k\) acts on \(n\) qubits. It is composed of \(k+1\) layers of single-qubit Pauli-\(Y\)-rotations and \(k\) entangling blocks \({U}_{{\rm{ent}}}\). As illustrated in (b), each entangling block applies \(CZ\) gates from qubit \(i\) to qubit \(\left(i+1\right)\,{\mathrm{mod}}\,\ n,\ i\in \{0,\ldots ,n-1\}\) to create entanglement between the different qubits.
The rationale behind choosing a variational form with \({R}_{Y}\) and \(CZ\) gates, e.g., in contrast to other Pauli rotations and two-qubit gates, is that for \({\theta }^{i,j}=0\) the variational form does not have any effect on the state amplitudes but only flips the phases. These phase flips do not perturb the modeled probability distribution which solely depends on the state amplitudes. Thus, if a suitable \(\left|{\psi }_{{\rm{in}}}\right\rangle\) can be loaded efficiently, the variational form allows its exploitation.
To train the qGAN, samples are drawn by measuring the output state \(\left|{g}_{{\boldsymbol{\theta }}}\right\rangle\) in the computational basis, where the set of possible measurement outcomes is \(\left|j\right\rangle ,\ j\in \{0,\ldots ,{2}^{n}-1\}\). Unlike in the classical case, the sampling does not require a stochastic input but is based on the inherent stochasticity of quantum measurements. Notably, the measurements return classical information, i.e., \({p}_{j}\) being defined as the measurement frequency of \(\left|j\right\rangle\). The scheme can be easily extended to \(d\)-dimensional distributions by choosing \(d\) qubit registers with \({n}_{i}\) qubits each, for \(i=1,\ldots ,d\), and constructing a multi-dimensional grid, see Supplementary Notes B for an explicit example of a qGAN trained on multivariate data.
A carefully chosen input state \(\left|{\psi }_{{\rm{in}}}\right\rangle\) can help to reduce the complexity of the quantum generator and the number of training epochs as well as avoid local optima in the quantum circuit training. Since the preparation of \(\left|{\psi }_{{\rm{in}}}\right\rangle\) should not dominate the overall gate complexity, the input state must be loadable with \({\mathcal{O}}\left(poly\left(n\right)\right)\) gates. This is feasible, e.g., for efficiently integrable probability distributions, such as log-concave distributions.31 In practice, statistical analysis of the training data can guide the choice for a suitable \(\left|{\psi }_{{\rm{in}}}\right\rangle\) from the family of efficiently loadable distributions, e.g., by matching expected value and variance. Later in this section, we present a broad simulation study that analyzes the impact of \(\left|{\psi }_{{\rm{in}}}\right\rangle\) as well as the circuit depth \(k\).
The classical discriminator, a standard neural network consisting of several layers that apply non-linear activation functions, processes the data samples and labels them either as being real or generated. Notably, the topology of the networks, i.e., number of nodes and layers, needs to be carefully chosen to ensure that the discriminator does not overpower the generator and vice versa.
Given \(m\) data samples \({{\boldsymbol{g}}}^{l}\) from the quantum generator and \(m\) randomly chosen training data samples \({x}^{l}\), where \(l=1,\ldots ,m\), the loss functions of the qGAN are
for the generator, and
for the discriminator, respectively. As in the classical case, see Eqs. (5) and (6), the loss functions are optimized alternately with respect to the generator’s parameters \({\boldsymbol{\theta }}\) and the discriminator’s parameters \({\boldsymbol{\phi }}\).
Next, we present the results of a broad simulation study on training qGANs with different settings for different target distributions. The quantum generator is implemented with Qiskit32 which enables quantum circuit execution with quantum simulators as well as quantum hardware provided by the IBM Q Experience.20 We consider a quantum generator acting on \(n=3\) qubits, which can represent \({2}^{3}=8\) values, namely \(\{0,1,\ldots ,7\}\). The method is applied for \(20,\!000\) samples of, first, a log-normal distribution with \(\mu =1\) and \(\sigma =1\), second, a triangular distribution with lower limit \(l=0\), upper limit \(u=7\) and mode \(m=2\), and last, a bimodal distribution consisting of two superimposed Gaussian distributions with \({\mu }_{1}=0.5\), \({\sigma }_{1}=1\) and \({\mu }_{2}=3.5\), \({\sigma }_{2}=0.5\), respectively. All distributions are truncated to \(\left[0,7\right]\) and the samples were rounded to integer values.
The generator’s input state \(\left|{\psi }_{{\rm{in}}}\right\rangle\) is prepared according to a discrete uniform distribution, a truncated and discretized normal distribution with \(\mu\) and \(\sigma\) being empirical estimates of mean and standard deviation of the training data samples, or a randomly chosen initial distribution. Preparing a uniform distribution on \(3\) qubits requires the application of \(3\) Hadamard gates, i.e., one per qubit.3 Loading a normal distribution involves more advanced techniques, see Supplementary Methods A for further details. For both cases, we sample the generator parameters from a uniform distribution on \([-\delta ,+\delta ]\), for \(\delta =1{0}^{-1}\). By construction of the variational form, the resulting distribution is close to \(\left|{\psi }_{{\rm{in}}}\right\rangle\) but slightly perturbed. Adding small random perturbations helps to break symmetries and can, thus, help to improve the training performance.33,34,35 To create a randomly chosen distribution, we set \(\left|{\psi }_{{\rm{in}}}\right\rangle ={\left|0\right\rangle }^{\otimes 3}\) and initialize the parameters of the variational form following a uniform distribution on \([-\pi ,\pi ]\). From now on, we refer to these three cases as uniform, normal, and random initialization. Furthermore, we test quantum generators with depths \(k\in \{1,2,3\}\).
The discriminator, a classical neural network, is implemented with PyTorch.36 The neural network consists of a \(50\)-node input layer, a \(20\)-node hidden layer and a single-node output layer. First, the input and the hidden layer apply linear transformations followed by Leaky ReLU functions.10,37,38 Then, the output layer implements another linear transformation and applies a sigmoid function. The network should neither be too weak nor too powerful to ensure that neither the generator nor the discriminator overpowers the other network during the training. The choice for the discriminator topology is based on empirical tests.
The qGAN is trained using AMSGRAD27 with the initial learning rate being \(1{0}^{-4}\). Due to the utilization of first and second momentum terms, this is a robust optimization technique for non-stationary objective functions as well as for noisy gradients,26 which makes it particularly suitable for running the algorithm on real quantum hardware. Methods for the analytic computation of the quantum generator loss function’s gradients are discussed in Supplementary Methods B. The training stability is improved further by applying a gradient penalty on the discriminator’s loss function.39,40
In each training epoch, the training data is shuffled and split into batches of size 2000. The generated data samples are created by preparing and measuring the quantum generator 2000 times. Then, the batches are used to update the parameters of the discriminator and the generator in an alternating fashion. After the updates are completed for all batches, a new epoch starts.
According to the classical GAN literature, the loss functions do not neccessarily reflect whether the method converges.41 In the context of training a quantum representation of some training data’s underlying random distribution, the Kolmogorov–Smirnov statistic as well as the relative entropy represent suitable measures to evaluate the training performance. Given the null-hypothesis that the probability distribution from \(\left|{g}_{{\boldsymbol{\theta }}}\right\rangle\) is equivalent to the probability distribution underlying \(X\), the Kolmogorov–Smirnov statistic \({D}_{{\rm{KS}}}\) determines whether the null-hypothesis is accepted or rejected with a certain confidence level, here set to \(95 \%\). The relative entropy quantifies the difference between two probability distributions. In the following, we analyze the results using these two statistical measures, which are formally introduced in Supplementary Methods C.
For each setting, we repeat the training \(10\) times to get a better understanding of the robustness of the results. Table 1 shows aggregated results over all 10 runs and presents the mean \({\mu }_{{\rm{KS}}}\), the standard deviation \({\sigma }_{{\rm{KS}}}\) and the number of accepted runs \({n}_{\le b}\) according to the Kolmogorov–Smirnov statistic as well as the mean \({\mu }_{{\rm{RE}}}\) and standard deviation \({\sigma }_{{\rm{RE}}}\) of the relative entropy outcomes between the generator output and the corresponding target distribution. The data shows that increasing the quantum generator depth \(k\) usually improves the training outcomes. Furthermore, the table illustrates that a carefully chosen initialization can have favorable effects, as can be seen especially well for the bimodal target distribution with normal initialization. Since the standard deviations are relatively small and the number of accepted results is usually close to 10, at least for depth \(k\ge 2\), we conclude that the presented approach is quite robust and also applicable to more complicated distributions. Figure 3 illustrates the results for one example of each target distribution.
Benchmarking results for qGAN training. Log-normal target distribution with normal initialization and a depth \(2\) generator (a, b), triangular target distribution with random initialization and a depth \(2\) generator (c, d), and bimodal target distribution with uniform initialization and a depth \(3\) generator (e, f). The presented probability density functions correspond to the trained \(\left|{g}_{{\boldsymbol{\theta }}}\right\rangle\) (a, c, e) and the loss function progress is illustrated for the generator as well as for the discriminator (b, d, f).
Application in quantum finance
Now, we demonstrate that training a data loading unitary with qGANs can facilitate financial derivative pricing. More precisely, we employ qGANs to learn and load a model for the spot price of an asset underlying a European call option. We perform the training for different initial states with a quantum simulator, and also execute the learning and loading method for a random initialization on an actual quantum computer, the IBM Q Boeblingen 20 qubit chip. Then, the fair price of the option is estimated by sampling from the resulting distribution, as well as with a QAE algorithm4,28 that uses the quantum generator trained with IBM Q Boeblingen for data loading. A detailed description of the QAE algorithm is given in Supplementary Methods D.
The owner of a European call option is permitted, but not obliged, to buy an underlying asset for a given strike price \(K\) at a predefined future maturity date \(T\), where the asset’s spot price at maturity \({S}_{T}\) is assumed to be uncertain. If \({S}_{T}\le K\), i.e., the spot price is below the strike price, it is unreasonable to exercise the option and there is no payoff. However, if \({S}_{T}>K\), exercising the option to buy the asset for price \(K\) and immediately selling it again for \({S}_{T}\) can realize a payoff \({S}_{T}-K\). Thus, the payoff of the option is defined as \(\max \{{S}_{T}-K,0\}\). Now, the goal is to evaluate the expected payoff \({\mathbb{E}}\left[\max \{{S}_{T}-K,0\}\right]\), whereby \({S}_{T}\) is assumed to follow a particular random distribution. This corresponds to the fair option price before discounting.42 Here, the discounting is neglected to simplify the problem.
To demonstrate and verify the applicability of the suggested training method, we implement a small illustrative example that is based on the analytically computable standard model for European option pricing, the Black-Scholes model.42 The qGAN algorithm is used to train a corresponding data loading unitary which enables the evaluation of characteristics of this model, such as the expected payoff, with QAE.
It should be noted that the Black-Scholes model often over-simplifies the real circumstances. In more realistic and complex cases, where the spot price follows a more generic stochastic process or where the payoff function has a more complicated structure, options are usually evaluated with Monte Carlo simulations.43 A Monte Carlo simulation uses \(N\) random samples drawn from the respective distribution to evaluate an estimate for a characteristic of the distribution, e.g., the expected payoff. The estimation error of this technique behaves like \(\epsilon ={\mathcal{O}}(1/\sqrt{N})\). When using \(n\) evaluation qubits to run a QAE, this induces the evaluation of \(N={2}^{n}\) quantum samples to estimate the respective distribution charactersitic. Now, this quantum algorithm achieves a Grover-type error scaling for option pricing, i.e., \(\epsilon ={\mathcal{O}}(1/N)\).4,28,44 To evaluate an option’s expected payoff with QAE, the problem must be encoded into a quantum operator that loads the respective probability distribution and implements the payoff function. In this work, we demonstrate that this distribution can be loaded approximately by training a qGAN algorithm.
In the remainder of this section, we first illustrate the training of a qGAN using classical quantum simulation. Then, the results from running a qGAN training on actual quantum hardware are presented. Finally, we employ the generator trained with a real quantum computer to conduct QAE-based option pricing.
According to the Black-Scholes model,42 the spot price at maturity \({S}_{T}\) for a European call option is log-normally distributed. Thus, we assume that \({p}_{{\rm{real}}}\), which is typically unknown, is given by a log-normal distribution and generates the training data \(X\) by randomly sampling from a log-normal distribution.
As for the simulation study, the training data set \(X\) is constructed by drawing \(20,\!000\) samples from a log-normal distribution with mean \(\mu =1\) and standard deviation \(\sigma =1\) truncated to \(\left[0,7\right]\), and then by rounding the sampled values to integers, i.e., to the grid that can be natively represented by the generator. We discuss a detailed analysis of training a model for this distribution with a depth \(k=1\) quantum generator, which is sufficient for this small example, with different initializations, namely uniform, normal, and random. The discriminator and generator network architectures as well as the optimization method are chosen equivalently to the ones described in the context of the simulation study.
First, we present results from running the qGAN training with a quantum simulator. The training procedure involves 2000 epochs. Figure 4 shows the PDFs corresponding to the trained \(\left|{g}_{{\boldsymbol{\theta }}}\right\rangle\) and the target PDF. The figures visualize that both uniform and normal initialization perform better than the random initialization.
Simulation training. The figure illustrates the PDFs corresponding to \(\left|{g}_{{\boldsymbol{\theta }}}\right\rangle\) trained on samples from a log-normal distribution using a uniformly (a), randomly (b), and normally (c) initialized quantum generator. Furthermore, the convergence of the relative entropy for the various initializations over 2000 training epochs is presented (d).
Moreover, Fig. 4 shows the progress of the relative entropy and, thereby, illustrates how the generated distributions converge toward the training data’s underlying distribution. This also shows that the generator model which is initialized randomly performs worst. Notably, the initial relative entropy for the normal distribution is already small. We conclude that a carefully chosen initialization clearly improves the training, although all three approaches eventually lead to reasonable results.
Table 2 presents the Kolmogorov–Smirnov statistics of the experiments. The results also confirm that initialization impacts the training performance. The statistics for the normal initialization are better than for the uniform initialization, which itself outperforms random initialization. It should be noted that the null-hypothesis is accepted for all settings.
Next, we present the results of the qGAN training run on an actual quantum processor, more precisely, the IBM Q Boeblingen chip.20 We use the same training data, quantum generator and discriminator as before. To improve the robustness of the training against the noise introduced by the quantum hardware, we set the optimizer’s learning rate to \(1{0}^{-3}\). The initialization is chosen according to the random setting because it requires the least gates. Due to the increased learning rate, it is sufficient to run the training for \(200\) optimization epochs. For more details on efficient implementation of the generator on IBM Q Boeblingen, see Supplementary Methods E.
Equivalent to the simulation, in each epoch, the training data is shuffled and split into batches of size 2000. The generated data samples are created by preparing and measuring the quantum generator 2000 times. To compute the analytic gradients for the update of \({\boldsymbol{\theta }}\), we use 8000 measurements to achieve suitably accurate gradients.
Figure 5 presents the PDF corresponding to \(\left|{g}_{{\boldsymbol{\theta }}}\right\rangle\) trained with IBM Q Boeblingen, respectively, with a classical quantum simulation that models the quantum chip’s noise. To evaluate the training performance, we evaluate again the relative entropy and the Kolmogorov–Smirnov statistic. A comparison of the progress of the loss functions and the relative entropy for a training run with the IBM Q Boeblingen chip and with the noisy quantum simulation is shown in Fig. 5. The plot illustrates that the relative entropy for both, the simulation and the real quantum hardware, converge to values close to zero and, thus, that in both cases \(\left|{g}_{{\boldsymbol{\theta }}}\right\rangle\) evolves toward the random distribution underlying the training data samples.
Quantum hardware training with a randomly initialized qGAN. The shown PDFs correspond to \(\left|{g}_{{\boldsymbol{\theta }}}\right\rangle\) trained on (a) the IBM Q Boeblingen and (c) a quantum simulation employing a noise model. Moreover, the progress in the (b) loss functions and the (d) relative entropy during the training of the qGAN with the IBM Q Boeblingen quantum computer and a noisy quantum simulation are presented.
Again, the Kolmogorov–Smirnov statistic \({D}_{{\rm{KS}}}\) determines whether the null-hypothesis is accepted or rejected with a confidence level of \(95 \%\). The results presented in Table 3 confirm that we were able to train an appropriate model on the actual quantum hardware.
Notably, some of the more prominent fluctuations might be due to the fact that the IBM Q Boeblingen chip is recalibrated on a daily basis which is, due to the queuing, circuit preparation, and network communication overhead, shorter than the overall training time of the qGAN.
In the following, we demonstrate that the qGAN-based data loading scheme enables the exploitation of the potential quantum advantage of algorithms such as QAE by using a generator trained with actual quantum hardware to facilitate European call option pricing. The resulting quantum generator loads a random distribution that approximates the spot price at maturity \({S}_{T}\). More specifically, we integrate the distribution loading quantum channel into a quantum algorithm based on QAE to evaluate the expected payoff \({\mathbb{E}}\left[\max \left\{{S}_{T}-K,0\right\}\right]\) for \(K=\$2\), illustrated in Fig. 6. Given this efficient, approximate data loading, the algorithm can achieve a quadratic improvement in the error scaling compared with classical Monte Carlo simulation. We refer to ref. 28 and to Supplementary Methods D for a detailed discussion of derivative pricing with QAE.
The results for estimating \({\mathbb{E}}\left[\max \left\{{S}_{T}-K,0\right\}\right]\) are given in Table 4, where we compare
an analytic evaluation with the exact (truncated and discretized) log-normal distribution \({p}_{{\rm{real}}}\),
a Monte Carlo simulation utilizing \(\left|{g}_{{\boldsymbol{\theta }}}\right\rangle\) trained and generated with the quantum hardware (IBM Q Boeblingen), i.e., 1024 random samples of \({S}_{T}\) are drawn by measuring \(\left|{g}_{{\boldsymbol{\theta }}}\right\rangle\) and used to estimate the expected payoff, and
a classically simulated QAE-based evaluation using \(m=8\) evaluation qubits, i.e., \({2}^{8}=256\) quantum samples, where the probability distribution \(\left|{g}_{{\boldsymbol{\theta }}}\right\rangle\) is trained with IBM Q Boeblingen chip.
The resulting confidence intervals (CI) are shown for a confidence level of \(95 \%\) for the Monte Carlo simulation as well as the QAE. The CIs are of comparable size, although, because of better scaling, QAE requires only a fourth of the samples. Since the distribution is approximated, both CIs are close to the exact value but do not actually contain it. Note that the estimates and the CIs of the MC and the QAE evaluation are not subject to the same level of noise effects. This is because the QAE evaluation uses the generator parameters trained with IBM Q Boeblingen but is run with a quantum simulator, whereas the Monte Carlo simulation is solely run on actual quantum hardware. To be able to run QAE on a quantum computer, further improvements are required, e.g., longer coherence times and higher gate fidelities.
Discussion
We demonstrated the application of an efficient, approximate probability distribution learning and loading scheme based on qGANs that requires \({\mathcal{O}}\left(poly\left(n\right)\right)\) many gates. In contrast to this, current state-of-the-art techniques for exact loading of generic random distributions into an \(n\)-qubit state necessitate \({\mathcal{O}}\left({2}^{n}\right)\) gates which can easily predominate a quantum algorithm’s complexity.
The respective quantum channel is implemented by a gate-based quantum algorithm and can, therefore, be directly integrated into other gate-based quantum algorithms. This is explicitly shown by the learning and loading of a model for European call option pricing which is evaluated with a QAE-based algorithm that can achieve a quadratic improvement compared with classical Monte Carlo simulation. The model is flexible because it can be fitted to the complexity of the underlying data and the loading scheme’s resolution can be traded off against the complexity of the training data by varying the number of used qubits \(n\) and the circuit depth \(k\). Moreover, qGANs are compatible with online or incremental learning, i.e., the model can be updated if new training data samples become available. This can lead to a significant reduction of the training time in real-world learning scenarios.
Some questions remain open and may be subject to future research, for example, an analysis of optimal quantum generator and discriminator structures as well as training strategies. Like in classical machine learning, it is neither apriori clear what model structure is the most suitable for a given problem nor what training strategy may achieve the best results.
Furthermore, although barren plateaus45 were not observed in our experiments, the possible occurrence of this effect, as well as counteracting methods, should be investigated. Classical ML already offers a wide variety of potential solutions, e.g., the inclusion of noise and momentum terms in the optimization procedure, the simplification of the function landscape by increase of the model size46 or the computation of higher order gradients. Moreover, schemes that were developed in the context of VQE algorithms, such as adaptive initialization,47 could help to circumvent this issue.
Another interesting topic worth investigating considers the representation capabilities of qGANs with other data types. Encoding data into qubit basis states naturally induces a discrete and equidistantly distributed set of represented data values. However, it might be interesting to look into the compatibility of qGANs with continuous or non-equidistantly distributed values.
Data availability
The data that support the findings of this study are available from the corresponding author upon justified request.
Code availability
The code for the qGAN algorithm is publicly available as part of Qiskit.32 The algorithms as well as tutorials explaining the training and the application in the context of QAE can be found at https://github.com/Qiskit.
References
Harrow, A. W., Hassidim, A. & Lloyd, S. Quantum algorithm for linear systems of equations. Phys. Rev. Lett. 15, 150502 (2009).
Lloyd, S., Mohseni, M. & Rebentrost, P. Quantum principal component analysis. Nat. Phys. 10, 631 (2013).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge University Press, 2010).
Brassard, G., Hoyer, P., Mosca, M. & Tapp, A. Quantum amplitude amplification and estimation. Contemp. Math. 305, 53–74 (2002).
Aaronson, S. Read the fine print. Nat. Phys. 11, 291–293 (2015).
Grover, L. K. Synthesis of quantum superpositions by quantum computation. Phys. Rev. Lett. 85, 1334–1337 (2000).
Sanders, Y., Low, G. H., Scherer, A. & Berry, D. W. Black-box quantum state preparation without arithmetic. Phys. Rev. Lett. 122, 020502 (2019).
Plesch, M. & Brukner, Č. Quantum-state preparation with universal gate decompositions. Phys. Rev. A 83, 032302 (2010).
Shende, V. V., Bullock, S. S. & Markov, I. L. Synthesis of quantum logic circuits. In Proceedings of the 2005 Asia and South Pacific Design Automation Conference, 272–275 (ACM, New York, NY, USA, 2005).
Goodfellow, I. et al. in Advances in Neural Information Processing Systems 27, 2672–2680 (Curran Associates, Inc., 2014).
Kurach, K., Lucic, M., Zhai, X., Michalski, M. & Gelly, S. The gan landscape: losses, architectures, regularization, and normalization. Preprint at https://arxiv.org/pdf/1807.04720v1.pdf (2018).
Lloyd, S. & Weedbrook, C. Quantum generative adversarial learning. Phys. Rev. Lett. 121, 040502 (2018).
Paris, M. & Rehacek, J. in Lecture Notes in Physics 1st edn (Springer Publishing Company, Incorporated, 2010).
Dallaire-Demers, P.-L. & Killoran, N. Quantum generative adversarial networks. Phys. Rev. A 98, 012324 (2018).
Benedetti, M., Grant, E., Wossnig, L. & Severini, S. Adversarial quantum circuit learning for pure state approximation. New J. Phys. 21, 043023 (2019).
Hu, L. et al. Quantum generative adversarial learning in a superconducting quantum circuit. Sci. Adv. 5, eaav2761 (2019).
Situ, H., He, Z., Li, L. & Zheng, S. Quantum generative adversarial network for generating discrete data. Preprint at https://arxiv.org/pdf/1807.01235.pdf (2018).
Romero, J. & Aspuru-Guzik, A. Variational quantum generators: Generative adversarial quantum machine learning for continuous distributions. Preprint at https://arxiv.org/pdf/1901.00848.pdf (2019).
Zeng, J., Wu, Y., Liu, J.-G., Wang, L. & Hu, J. Learning and inference on generative adversarial quantum circuits. Phys. Rev. A 99, 052306 (2019).
IBM Q Experience. https://quantumexperience.ng.bluemix.net/qx/experience.
Kingma, D. P. & Welling, M. Auto-encoding variational bayes. In Proceedings of the International Conference on Learning Representations (2014).
Burda, Y., Grosse, R. B. & Salakhutdinov, R. Importance weighted autoencoders. In Proceedings of the International Conference on Learning Representations (ICLR) (2016).
Dumoulin, V. et al. Adversarially learned inference. in Proceedings of the International Conference on Learning Representations (2017).
Metz, L., Poole, B., Pfau, D. & Sohl-Dickstein, J. Unrolled generative adversarial networks. In Proceedings of the International Conference on Learning Representations (ICLR) (2017).
Fedus, W. et al. Many paths to equilibrium: GANs do not need to decrease a divergence at every step. In Proceedings of the International Conference on Learning Representations (2018).
Kingma, D. & Ba, J. Adam: a method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR) (2014).
Reddi, S.J., Kale, S. & Kumar, S. On the convergence of adam and beyond. In Proceedings of the International Conference on Learning Representations (ICLR) (2018).
Woerner, S. & Egger, D. J. Quantum risk analysis. npj Quant. Inf. 5, 15 (2019).
McClean, J., Romero, J., Babbush, R. & Aspuru-Guzik, A. The theory of variational hybrid quantum-classical algorithms. New J. Phys. 18, 023023 (2015).
Goodfellow, I., Bengio, Y. & Courville, A. Deep Learning (MIT Press, 2016).
Grover, L. & Rudolph, T. Creating superpositions that correspond to efficiently integrable probability distributions. Preprint at https://arxiv.org/pdf/quant-ph/0208112.pdf (2002).
Abraham, H. et al. Qiskit: an open-source framework for quantum computing. https://github.com/Qiskit/qiskit.
Lehtokangas, M. & Saarinen, J. Weight initialization with reference patterns. Neurocomputing 20, 265–278 (1998).
Thimm, G. & Fiesler, E. High-order and multilayer perceptron initialization. IEEE Trans. Neural Netw. 8, 349–359 (1997).
Chen, Y., Chi, Y., Fan, J. & Ma, C. Gradient descent with random initialization: fast global convergence for nonconvex phase retrieval. Math. Programming 176, 5–37 (2019).
Pytorch. https://pytorch.org.
Pedamonti, D. Comparison of non-linear activation functions for deep neural networks on mnist classification task. Preprint at https://arxiv.org/pdf/1804.02763.pdf (2018).
He, K., Zhang, X., Ren, S. & Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. IEEE International Conference on Computer Vision (ICCV 2015) 1502 (2015).
Kodali, N., Abernethy, J. D., Hays, J. & Kira, Z. On convergence and stability of gans. Preprint at https://arxiv.org/pdf/1705.07215.pdf (2017).
Roth, K., Lucchi, A., Nowozin, S. & Hofmann, T., Stabilizing training of generative adversarial networks through regularization. in Advances in Neural Information Processing Systems 30, 2018–2028 (Curran Associates, Inc., 2017).
Grnarova, P. et al. Evaluating gans via duality. Preprint at https://arxiv.org/abs/1811.05512 (2018).
Black, F. & Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 81, 637–654 (1973).
Glasserman, P. Monte Carlo Methods in Financial Engineering. (Springer-Verlag, New York, 2003).
Rebentrost, P., Gupt, B. & Bromley, T. R. Quantum computational finance: Monte Carlo pricing of financial derivatives. Phys. Rev. A 98, 022321 (2018).
McClean, J., Boixo, S., N. Smelyanskiy, V., Babbush, R. & Neven, H. Barren plateaus in quantum neural network training landscapes. Nat. Commun. 9, 4812 (2018).
Stanford, J., Giardina, K., Gerhardt, G., Fukumizu, K. & Amari, S.-i. Local minima and plateaus in hierarchical structures of multilayer perceptrons. Neural Networks 13, 317–327 (2000).
Grimsley, H., Economou, S., Barnes, E. & Mayhall, N. An adaptive variational algorithm for exact molecular simulations on a quantum computer. Nat. Commun. 10, 3007 (2019).
Acknowledgements
We would like to thank Giovanni Mariani, Almudena Carrera Vazquez, PauIine Ollitrault, Guglielmo Mazzola, Panagiotis Barkoutsos, Igor Sokolov, and Ivano Tavernelli for sharing their knowledge in helpful discussions. Furthermore, we are grateful to Stephen Wood and Sarah Sheldon for their support on the code implementation and the experiments, respectively. IBM and IBM Q are trademarks of International Business Machines Corporation, registered in many jurisdictions worldwide. Other product or service names may be trademarks or service marks of IBM or other companies.
Author information
Authors and Affiliations
Contributions
All authors researched, collated, and wrote this paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zoufal, C., Lucchi, A. & Woerner, S. Quantum Generative Adversarial Networks for learning and loading random distributions. npj Quantum Inf 5, 103 (2019). https://doi.org/10.1038/s41534-019-0223-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-019-0223-2
This article is cited by
-
A framework for demonstrating practical quantum advantage: comparing quantum against classical generative models
Communications Physics (2024)
-
Quantum state preparation of normal distributions using matrix product states
npj Quantum Information (2024)
-
Quantum deep generative prior with programmable quantum circuits
Communications Physics (2024)
-
Scalable parameterized quantum circuits classifier
Scientific Reports (2024)
-
Hyperparameter importance and optimization of quantum neural networks across small datasets
Machine Learning (2024)