Introduction

The ability to control massive mechanical objects at the quantum level constitutes a very interesting task for many technological applications, ranging from microwave-to-optical conversion to quantum memories, as well as fundamental studies regarding the quantum-classical divide.1,2,3,4,5,6,7,8,9,10 The rapid development of cavity optomechanics over the last decade has enabled the exploration of mechanical resonators in regimes where quantum effects become prominent. One approach relies on resonant coupling of acoustic phonons to microwave excitations via piezoelectric materials,11,12 however, the amplitude of the lattice vibrations in these systems is very small, limiting their applications. On the other hand, in typical opto- and electromechanical setups, low-frequency mechanical resonators are controlled via parametric coupling to an optical or microwave cavity.13,14,15,16,17 The mechanical elements in these systems are usually realised with metal drumheads or beams, which are characterised by large quality factors and large mass, making them also prime candidates for experimental tests of gravity-induced wavefunction collapse theories.1,2,3,4

Following the pioneering work on acoustic resonators,11 recently, quantum superpositions of the ground and first excited state were for the first time generated in a parametrically coupled mechanical resonator.18 In this approach, a superconducting qubit is used to create the excitation, which decays into a microwave resonator on a different chip and subsequently transferred to the mechanical element via an effective linearised interaction. It is recognised, however, that this method has severe limitations as it relies on strong driving, which is challenging with qubits, and suffers from unavoidable losses during the state transfer between different chips, limiting the fidelity of the prepared state.19 A different scheme, implemented in the optical domain, uses entanglement and post-selective measurements to generate single-photon states,20 although the non-deterministic nature of the protocol in combination with low count rates limits the types of states that can be prepared.

A promising route towards high-fidelity mechanical quantum control is the ability to operate in the single-photon strong-coupling regime, where interaction times are faster than dissipation processes, which however still remains an experimental challenge for far-detuned parametrically coupled mechanical resonators.19,21 Operating in this regime is predicted to give rise to non-classical photon correlations22 and non-Gaussian states,23,24 as well as macroscopic mechanical superpositions.25 Moreover, using the radiation-pressure coupling to qubits can lead to the creation of mechanical Schrödinger cat states.26,27 Generating Fock states in this regime could also be enabled using an additional microwave resonator to create an effective tripartite coupling, as predicted in ref. 27, although this approach is limited to low state preparation fidelities mainly due to the limitations of capacitive coupling and stray qubit–resonator interaction. In spite of the experimental and theoretical advances in the field, high-fidelity quantum state preparation of mechanical systems appears to be limited to a small class of engineerable states which are, to a large degree, architecture-dependent.

Here, we analyse a new scheme for synthesizing generic mechanical states by employing tuneable three-body interactions between two superconducting qubits and a mechanical resonator in the single-photon strong-coupling regime. The coupling relies on embedding a suspended micrometer-long beam in one of the arms of a superconducting quantum interference device (SQUID) in combination with an externally applied magnetic field.28,29,30,31 We find that, by connecting two superconducting transmon qubits32 directly via this mechanical SQUID, a tuneable three-body interaction arises as the qubit-qubit flux-mediated coupling is modulated by the mechanical displacement. Importantly, the detrimental exchange-type interaction between the two qubits can be suppressed by adding a capacitor in parallel to the SQUID, as realised in ref. 33. Using state-of-the-art parameters, reported in recent experiments,31 we numerically demonstrate the possibility of high-fidelity coherent quantum control of the beam, from ground-state cooling to fast and high-fidelity preparation of mechanical Fock states, as well as maximally entangled states of qubits and phonons. Finally, we devise a protocol consisting of qubit flux-pulsing and post-selective measurements for synthesizing multi-phonon superposition states, extending the quantum control toolbox and the plurality of engineerable quantum states in radio-frequency mechanical resonators.

Results

Motion-dependent qubit–qubit interaction

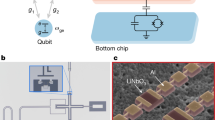
The proposed circuit, shown in Fig. 1a, comprises two transmon qubits coupled directly via a superconducting quantum interference device (SQUID) shunted by a capacitor, \({C}_{{\rm{c}}}\). This tuneable coupling scheme has recently been realised in circuit QED setups using transmons33 and LC resonators.34 The coupling is controlled by tuning the Josephson energy of the SQUID, \({E}_{{\rm{J}}}^{{\rm{c}}}({\Phi }_{{\rm{b}}})={E}_{{\rm{J}},\Sigma }^{{\rm{c}}}| \cos (\pi {\Phi }_{{\rm{b}}}/{\Phi }_{0})| \), with an out-of-plane flux bias, \({\Phi }_{{\rm{b}}}\), where \({\Phi }_{0}=h/2e\) is the magnetic flux quantum and \({E}_{{\rm{J}},\Sigma }^{{\rm{c}}}\) is the sum of the two junction Josephson energies in the SQUID. The mechanical part of the circuit consists of a beam of length \(l\) that is embedded in one of the arms of the SQUID loop and can oscillate out of plane. By applying an in-plane external magnetic field \(B\), the loop can pick up an additional flux \({\beta }_{0}BlX\) due to the beam displacement \(X\), resulting in a flux-tuneable and motion-dependent Josephson energy \({E}_{{\rm{J}}}^{{\rm{c}}}={E}_{{\rm{J}},\Sigma }^{{\rm{c}}}| \cos (\pi {\Phi }_{{\rm{b}}}/{\Phi }_{0}+\alpha X)| \), where \(\alpha =\pi {\beta }_{0}Bl/{\Phi }_{0}\) and \({\beta }_{0}\) is a geometric factor depending on the mode shape (for the first mechanical mode, considered here, \({\beta }_{0}\simeq 1\)).30,31,35

Fig. 1
figure 1

Tripartite coupling architecture. a Circuit diagram of the electromechanical system comprising two transmon qubits directly coupled via a SQUID coupler with an embedded beam that can oscillate out of plane. Tuning the coupler to its filter frequency, where linear currents through the capacitor and the SQUID cancel out, and applying an in-plane magnetic field \(B\), results in a dominant tripartite coupling as the beam oscillations modulate the qubit–qubit interaction. b Flux-mediated couplings as a function of flux bias \({\Phi }_{{\rm{b}}}\) for in-plane magnetic field \(B=10\) mT and circuit parameters used in this work. The red curve represents the tripartite coupling strength, while the solid/dashed blue curves correspond to the radiation-pressure coupling of the beam with each qubit.

Full size image

The Hamiltonian describing the circuit in Fig. 1a is

$$\begin{array}{ll}H\,=\,&\frac{{P}^{2}}{2m}+\frac{m{\omega }_{{\rm{m}}}^{2}{X}^{2}}{2}+\sum _{i=1}^{2}\left[\frac{{Q}_{i}^{2}}{2{\widetilde{C}}_{i}}-{E}_{{{\rm{J}}}_{i}}\cos \left(\frac{{\phi }_{i}}{{\phi }_{0}}\right)\right]\\ &+\frac{{C}_{\rm{c}}}{{C}_{1}{C}_{2}}{Q}_{1}{Q}_{2}-{E}_{{\rm{J}}}^{{\rm{c}}}(X)\cos \left(\frac{{\phi }_{1}-{\phi }_{2}}{{\phi }_{0}}\right),\end{array}$$
(1)

where \(\{X,\,P\}\) and \(\{{\phi }_{i},\,{Q}_{i}\}\) are conjugate variable pairs describing the mechanical and the electrical degrees of freedom at circuit node \(i\), and \({\phi }_{0}={\Phi }_{0}/(2\pi )\) is the reduced flux quantum. The first four terms describe the uncoupled system of the mechanical resonator and two transmon qubits, where \(m,\,{\omega }_{{\rm{m}}}\) denote the mass and frequency of the beam and \({E}_{{{\rm{J}}}_{i}}\), \({\widetilde{C}}_{i}\) represent the Josephson energy and loaded capacitance of each transmon, respectively (see Supplementary Sec. S1). The last two terms describe the qubit–qubit interaction via their charge and flux degrees of freedom, \({Q}_{i}\) and \({\phi }_{i}\).

The core of this proposal relies on the fact that the dynamical displacement of the beam results in a modulation of the superconducting current through the coupling SQUID and its Josephson energy, which mediates the qubit–qubit interaction. Taking into account the finite asymmetry of the SQUID loop, which is present in any realistic scenario, this results in a motion-dependent Josephson energy,

$${E}_{{\rm{J}}}^{{\rm{c}}}(X)={E}_{{\rm{J}},\Sigma }^{{\rm{c}}}\left[{c}_{{\rm{J}}}\cos (\pi {\Phi }_{{\rm{b}}}/{\Phi }_{0})-{s}_{{\rm{J}}}\sin (\pi {\Phi }_{{\rm{b}}}/{\Phi }_{0})\alpha X\right],$$
(2)

where \({c}_{{\rm{J}}}=\sqrt{1+{a}_{{\rm{J}}}^{2}| \tan (\pi {\Phi }_{{\rm{b}}}/{\Phi }_{0})| }\) and \({s}_{{\rm{J}}}=(1-{a}_{{\rm{J}}}^{2})/{c}_{{\rm{J}}}\) are correction factors due to the SQUID asymmetry \({a}_{{\rm{J}}}\). Note that the above expression is valid for \(\pi {\Phi }_{{\rm{b}}}/{\Phi }_{0}\gg \alpha X\) and relies on the assumption that \(\alpha X\ll 1\) (for a full derivation see Supplementary Sec. S1). For the parameters considered here, which are compatible with values reported in recent experiments using micrometer-long Al beams and sub-Tesla magnetic fields,31 we have \(\alpha X \sim 1{0}^{-5}-1{0}^{-6}\), therefore this is a valid assumption.

Electromechanical system dynamics

The Hamiltonian of the system can be expressed in second quantisation form, as

$$\hat{H}\,=\,{\hat{H}}_{0}+{\hat{H}}_{{\rm{int}}},$$
(3)
$${\hat{H}}_{0}\,=\,\hslash {\omega }_{{\rm{m}}}{\hat{b}}^{\dagger }\hat{b}+\sum _{i=1}^{2}\hslash {\omega }_{i}{\hat{c}}_{i}^{\dagger }{\hat{c}}_{i}-\frac{{E}_{{{\rm{C}}}_{i}}}{2}{\hat{c}}_{i}^{\dagger }{\hat{c}}_{i}^{\dagger }{\hat{c}}_{i}{\hat{c}}_{i},$$
(4)
$$\begin{array}{l}{\hat{H}}_{{\rm{int}}}=\hslash g({\hat{c}}_{1}^{\dagger }{\hat{c}}_{2}+{\hat{c}}_{1}{\hat{c}}_{2}^{\dagger })(\hat{b}+{\hat{b}}^{\dagger })\\ -{\sum \limits_{i=1}^{2}}\hslash {g}_{i}{\hat{c}}_{i}^{\dagger }{\hat{c}}_{i}(\hat{b}+{\hat{b}}^{\dagger })+{\hat{H}}_{12}^{{\prime} },\end{array}$$
(5)

where \({\hat{b}}^{(\dagger )}\) and \({\hat{c}}_{i}^{(\dagger )}\) are bosonic operators describing the annihilation (creation) of phonons and qubit excitations, respectively (see Supplementary Sec. S2). The effective electromechanical frequencies are \({\omega }_{{\rm{m}}}\) and \({\omega }_{i}=\frac{1}{\hslash }(\sqrt{8{\widetilde{E}}_{{{\rm{J}}}_{i}}{E}_{{{\rm{C}}}_{i}}}-{E}_{{{\rm{C}}}_{i}})\), where \({\widetilde{E}}_{{{\rm{J}}}_{i}}\) is the modified transmon Josephson energy due to the coupler. The full quantum mechanical treatment of the circuit, including higher-order nonlinear interaction terms, is presented in the Supplementary Material.

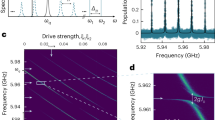
The first term in Eq. (5) describes a three-body interaction involving hopping of qubit excitations together with mechanical displacements of the beam. The coupling strength is given by

$$g\,=\,\frac{\alpha \sqrt{{Z}_{1}{Z}_{2}}}{2{\phi }_{0}^{2}}{s}_{{\rm{J}}}{E}_{{\rm{J}},\Sigma }^{{\rm{c}}}\sin (\pi {\Phi }_{{\rm{b}}}/{\Phi }_{0}){X}_{{\rm{ZPF}}},$$
(6)

where \({Z}_{i}=\frac{\hslash }{{e}^{2}}\sqrt{{E}_{{{\rm{C}}}_{i}}/(2{\widetilde{E}}_{{{\rm{J}}}_{i}})}\) denote the transmon impedances, and \({X}_{{\rm{ZPF}}}\,=\,\sqrt{\hslash /(2m{\omega }_{{\rm{m}}})}\) is the zero-point motion of the mechanical resonator. The next interaction term describes the radiation-pressure coupling of each qubit with the beam at a rate \({g}_{1(2)}\,=\,g\sqrt{{Z}_{1(2)}/{Z}_{2(1)}}\). The electromechanical coupling strengths are plotted in Fig. 1b as a function of the out-of-plane flux bias \({\Phi }_{\rm{b}}\). Close to a half-integer flux quantum, \({E}_{{\rm{J}}}^{{\rm{c}}}(X)\) is maximally susceptible to mechanical motion which maximises the electromechanical coupling. Note that all couplings become zero exactly at a half-integer flux quantum due to the finite SQUID asymmetry \({a}_{{\rm{J}}}\). In our calculations an asymmetry of \(0.01\) is included, reflecting a \(2 \% \) spread in junction fabrication targeting.

The last term in Eq. (5) describes the qubit–qubit interaction

$${\hat{H}}_{12}^{{\prime} }\,=\,\hslash ({J}_{{\rm{C}}}-{J}_{{\rm{L}}})({\hat{c}}_{1}^{\dagger }{\hat{c}}_{2}+{\hat{c}}_{1}{\hat{c}}_{2}^{\dagger })+\hslash V{\hat{c}}_{1}^{\dagger }{\hat{c}}_{1}{\hat{c}}_{2}^{\dagger }{\hat{c}}_{2},$$
(7)

where \({J}_{{\rm{C}}}\), \({J}_{{\rm{L}}}\) are exchange-type coupling strengths arising from the coupling capacitor and SQUID, respectively, and \(V\) is the cross-Kerr coupling strength, which is minimised at \({\Phi }_{\rm{b}}\simeq {\Phi }_{0}/2\) (see Supplementary Eq. S(33)). A significant advantage of this architecture for realising tripartite interactions, compared to relying exclusively on capacitive coupling,27 is that any stray linear coupling between the qubits can be suppressed with the right choice of coupling capacitance \({C}_{{\rm{c}}}\).33,34 This makes the three-body interaction dominant and ensures the ability to manipulate the state of each qubit individually by local driving, which is crucial for the state engineering protocols discussed below.

Ground-state cooling

Mechanical resonators realised using vibrating beams and drumheads lie in the radio-frequency regime (\(\sim\!\! 10\) MHz), where thermal fluctuations are dominant even at millikelvin temperatures, achieved with conventional cryogenic techniques. An essential element of control is, therefore, the ability to cool these systems to their quantum ground state before manipulating them further. Typically, electromechanical experiments employ a “cold” microwave cavity (\(\sim\!\!10\) GHz), which is coupled to the mechanical element via an effective linearised interaction in the many-photon regime, and cooling is enabled by red-sideband driving.14 However, in a system comprised of qubits, cooling the mechanical resonator via sideband driving can be a challenging task, requiring multiple tones and eventually limited by the critical number of photons in the Josephson junction.36,37

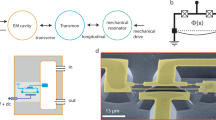
Here, we show that it is possible to overcome the challenges of sideband cooling with qubits by employing a time-domain protocol to cool the mechanical resonator to its quantum ground state, using the three-body interaction. The scheme, depicted in Fig. 2a, consists of a sequence of single-qubit operations which, combined with the tripartite interaction, enable the transfer of the thermal phonons to the environment in a stroboscopic fashion, as described below. At first, we bring one qubit (\({q}_{1}\)) to its excited state and then tune its frequency such that \({\omega }_{1}={\omega }_{2}-{\omega }_{{\rm{m}}}\). Since \(g\ll {\omega }_{{\rm{m}}}\) the interaction \(({\hat{c}}_{1}\hat{b}{\hat{c}}_{2}^{\dagger }+{\rm{H.c.}})\) is resonant at this condition, such that a phonon combined with the excitation in \({q}_{1}\) can be transferred to the other qubit (\({q}_{2}\)) after variable time \(\Delta {t}_{{\rm{cool}}}\). The cycle is then completed by reinitialising both qubits using active reset protocols.38,39,40 A similar scheme has also been realised recently for detecting microwave photons in a superconducting resonator, using tripartite interactions with a transmon qubit and a dissipative mode.41

Fig. 2
figure 2

Ground-state cooling. a Schematic of the time-domain protocol to cool the mechanical resonator to its ground state using the three-body interaction. In each cycle, qubit 1 is excited with a microwave pulse, then its frequency is tuned at \({\omega }_{1}={\omega }_{2}-{\omega }_{{\rm{m}}}\) for a variable time \(\Delta {t}_{{\rm{cool}}}\) followed by a reset on both qubits. b Numerical results after \(\sim\!\!100\) cycles demonstrating cooling to a 0.05 phonon occupancy for a 10 MHz resonator at \(T=10\) mK (\({n}_{{\rm{th}}}\simeq 20\)) using the system parameters presented in Table 1.

Full size image

In Fig. 2b we plot the average number of phonons and qubit excitations as a function of time after \(\sim\!\!100\) cooling cycles, for a mechanical beam oscillating at \({\omega }_{{\rm{m}}}/(2\pi )=10\) MHz and a tripartite coupling strength \(g/(2\pi )\simeq 0.3\) MHz. At the end of the protocol the mechanical resonator is cooled down to the ground state with a phonon occupancy of 0.05, assuming an environment temperature of \(T=10\) mK (\({n}_{{\rm{th}}}\simeq 20\)). The qubit (\({\omega }_{1}/(2\pi )=7\) GHz) is excited with a 200 ns Gaussian pulse, while the reset and cooling times are set to \(\Delta {t}_{{\rm{reset}}}=\Delta {t}_{{\rm{cool}}}=200\) ns. The cooling time would be best optimised by choosing a short time for large thermal occupation and then increase the time as the resonator cools, since phonons swap faster for higher occupations. For simplicity, here, we considered a fixed time and found that for these parameters, a 200 ns time is sufficient. Furthermore, we have assumed an in-plane magnetic field \(B=10\) mT which is well-below the critical field for thin Al beams42 and does not compromise the qubit coherence.43 All system parameters used in the simulations are listed in Table 1.

Table 1 Parameter set used in the numerical simulations.
Full size table

Mechanical Fock states and qubit-phonon entanglement

Following ground-state preparation, we present a protocol which employs the tripartite coupling to deterministically generate mechanical Fock states and maximally entangled states. As schematically depicted in the inset of Fig. 3a, it consists of preparing \({q}_{2}\) in the excited state and tuning it to \({\omega }_{2}={\omega }_{1}+{\omega }_{{\rm{m}}}\), such that the interaction \(({\hat{c}}_{1}^{\dagger }{\hat{b}}^{\dagger }{\hat{c}}_{2}+{\rm{H.c.}})\) is resonant. Ideally, assuming unitary evolution \(U(t)\) under the tripartite interaction, the state would evolve as

$$U(t)\left|{0}_{1}{0}_{{\rm{m}}}{1}_{2}\right\rangle =\cos (gt)\left|{0}_{1}{0}_{{\rm{m}}}{1}_{2}\right\rangle -i\sin (gt)\left|{1}_{1}{1}_{{\rm{m}}}{0}_{2}\right\rangle .$$
(8)

The evolution of the average number of phonons and qubit excitations, starting from an attainable mechanical state of 0.05 thermal phonons and including system dissipation (see Methods) is plotted in Fig. 3a. We consider the full interaction Hamiltonian presented in Eq. (5), including next-to-leading order non-linear corrections (see Supplementary Sec. S2), for the simulation parameters shown in Table 1. In Fig. 3b we plot the Wigner function of the final state in the mechanical resonator, after time \(t=\pi /(2g)\), revealing a single-phonon Fock state with \(97 \% \) (\(99 \% \)) fidelity, starting from an attainable (ideal) ground state. Higher phonon states could also be prepared by resetting and repeating the protocol with modified transfer times \({t}_{n}={n}_{{\rm{m}}}^{-1/2}\pi /(2g)\).

Fig. 3
figure 3

Protocol for Fock-state preparation and maximally entangled states of phonons and qubit excitations. a Time evolution after exciting qubit 2 and tuning into the operating point \({\omega }_{2}={\omega }_{1}+{\omega }_{{\rm{m}}}\) (schematically presented in the inset) such that the interaction (\({\hat{c}}_{1}b{\hat{c}}_{2}^{\dagger }\,+\,\)H.c) is resonant. Starting from a phonon occupancy of 0.05, a mechanical Fock state is generated with \(97 \% \) fidelity after time \(t=\pi /(2g)\). b Wigner function of the resulting mechanical state. c Density matrix of a Greenberger–Horne–Zeilinger state that is generated in the middle of the protocol, at \(t=\pi /(4g)\). The notation \(({0}_{1}{0}_{{\rm{m}}}{1}_{2})\) is used in labelling and only matrix elements with a magnitude larger than 0.005 are shown. d Resulting density matrix after repeating the same protocol with qubit 2 initialised in the superposition state \(\frac{1}{\sqrt{2}}(\left|{0}_{2}\right\rangle +\left|{1}_{2}\right\rangle )\), leading to a Bell state with \(96 \% \) fidelity.

Full size image

The quantum state preparation scheme described above, can also be used to generate bipartite and tripartite maximally entangled states between the mechanical resonator and the qubits. In particular, in the middle of the above protocol, at \(t=\pi /(4g)\), the system is in a Greenberger–Horne–Zeilinger (GHZ) state

$${\left|\psi \right\rangle }_{{\rm{f}}}=\frac{1}{\sqrt{2}}\left(\left|{0}_{1}{0}_{{\rm{m}}}{1}_{2}\right\rangle -i\left|{1}_{1}{1}_{{\rm{m}}}{0}_{2}\right\rangle \right),$$
(9)

with \(98\, \% \) fidelity, with the corresponding density matrix shown in Fig. 3c. Such states are particularly interesting for applications in quantum information44,45 and fundamental tests of quantum theory.46 Using the same protocol for \({q}_{2}\) in a superposition state \(\frac{1}{\sqrt{2}}(\left|{0}_{2}\right\rangle +\left|{1}_{2}\right\rangle )\), the Bell state

$${\left|\psi \right\rangle }_{{\rm{f}}}=\left(\frac{1}{\sqrt{2}}(\left|{0}_{1}{0}_{{\rm{m}}}\right\rangle +\left|{1}_{1}{1}_{{\rm{m}}}\right\rangle )\right)\left|{0}_{2}\right\rangle ,$$
(10)

is generated after time \(\pi /(2g)\) with \(96 \% \) fidelity (\(98 \% \) for ideal ground state), as depicted in Fig. 3d. The prepared state is a maximally entangled pair of a phonon and a qubit excitation, which could be utilised as a testbed for checking the validity of quantum mechanics at macroscopic scales without requiring tomography of the mechanical state.47,48 Such states might also be suitable for integrating transmon qubits into other platforms such as spins, cold atoms, or even optical photons, with the mechanical resonator mediating the coupling.49,50,51,52 They could also provide possibilities for entangling the mechanical resonator with other physical systems via the transmon.

Multi-phonon quantum superpositions

We now extend the protocol described above to create multi-phonon quantum superposition states in the mechanical resonator, simply by flux-pulsing the qubits. In the protocols discussed previously, the qubit frequencies are tuned at \({\omega }_{2}={\omega }_{1}+{\omega }_{{\rm{m}}}\) such that the states \(\left|{0}_{1}{n}_{{\rm{m}}}{1}_{2}\right\rangle \) and \(\left|{1}_{1}{(n+1)}_{{\rm{m}}}{0}_{2}\right\rangle \) are coupled. However, when tuned at \({\omega }_{2}={\omega }_{1}-{\omega }_{{\rm{m}}}\) the interaction term \(({\hat{c}}_{1}{\hat{b}}^{\dagger }{\hat{c}}_{2}^{\dagger }+{\rm{H.c.}})\) becomes resonant, which couples \(\left|{0}_{1}{(n+1)}_{{\rm{m}}}{1}_{2}\right\rangle \) and \(\left|{1}_{1}{n}_{{\rm{m}}}{0}_{2}\right\rangle \). Therefore, by interchanging the qubit frequencies with flux-tuning pulses during each cycle it could be possible to create higher phonon Fock states and multi-phonon quantum superposition states, as depicted schematically in Fig. 4a.

Fig. 4
figure 4

Synthesizing multi-phonon quantum superposition states. a Level diagram of the system indicating the resonant three-body interactions when the qubits are tuned such that \({\omega }_{2}^{\pm }\,=\,{\omega }_{1}\pm {\omega }_{{\rm{m}}}\). b, d Evolution of phonon and qubit populations after exciting qubit 2 and alternating the qubit frequencies to \({\omega }_{2}^{\pm }\), where the dashed vertical lines denote the application of a square tuning flux pulse. An attainable mechanical state of 0.05 phonons is taken initially. c, e Wigner functions of the resulting states \(\frac{1}{2}(\left|0\right\rangle +\sqrt{2}\left|2\right\rangle +\left|4\right\rangle )\) and \(\frac{1}{\sqrt{2}}(\left|0\right\rangle +\left|4\right\rangle )\) with preparation fidelities \(98 \% \) and \(97 \% \) (following post-selection on \(\left|{0}_{1}{1}_{2}\right\rangle \)), respectively.

Full size image

As a proof-of-concept, using the same simulation parameters as above (Table 1), we demonstrate the creation of superposition states \({\left|{\psi }_{{\rm{m}}}\right\rangle }^{^{\prime} }=\frac{1}{2}(\left|0\right\rangle +\sqrt{2}\left|2\right\rangle +\left|4\right\rangle )\) and \({\left|{\psi }_{{\rm{m}}}\right\rangle }^{^{\prime\prime} }=\frac{1}{\sqrt{2}}(\left|0\right\rangle +\left|4\right\rangle )\), after exciting qubit 2 and applying three flux pulses that interchange the qubit frequencies at variable times \({t}_{1},{t}_{2}\) and \({t}_{3}\). Figure 4b, d show the evolution of the qubit and resonator occupancy, starting from an attainable mechanical state of 0.05 phonons. The dashed lines indicate the times that a flux-tuning pulse is applied. The corresponding Wigner functions at the end of each protocol, following post-selection on \(\left|{0}_{1}{1}_{2}\right\rangle \), are shown in Fig. 4c, e, with preparation fidelities \(98\, \% \) and \(97\, \% \), respectively. After preparation, the states evolve naturally as \(U(t){\left|{\psi }_{{\rm{m}}}\right\rangle }^{^{\prime} }=(\alpha \left|0\right\rangle +\beta {e}^{-in{\omega }_{{\rm{m}}}t}\left|n\right\rangle +\gamma {e}^{-im{\omega }_{{\rm{m}}}t}\left|m\right\rangle )\) including dissipation, which is however not a limiting factor because of the long lifetimes of these mechanical resonators.31 Readout of the prepared states including Wigner tomography could be performed using similar techniques to the ones developed in ref. 53.

The scheme described above enables the generation of interesting classes of multi-phonon superposition states, such as the ones shown in Fig. 4, requiring only flux-tuning pulses and a projective measurement at the end. As we show in Supplementary Sec. S3, by including a projective measurement after each step of the protocol, it is possible to generate states with arbitrary phonon number probability distributions, although constrained in the relative phases of the superpositions. Furthermore, we find that quantum superpositions with arbitrary complex coefficients can also be generated with this platform by additionally employing the qubit–qubit interaction in a controllable fashion to perform exchange-type and C-Phase gates between the two qubits (see Supplementary Sec. S3). This would enable the creation of truly arbitrary states, similar to those produced in resonantly coupled qubit-resonator systems,53,54 with the trade-off of increased complexity in the protocol. Alternatively, using the radiation-pressure coupling with one qubit in combination with a sequence of driving pulses, could enable the creation of mechanical Schrödinger cat states as discussed in ref. 27.

Discussion

A reconciliation of quantum mechanics and general relativity remains elusive at a theoretical level, however, there exist several proposals for testing the quantum-classical boundary with mechanical resonators offering an ideal testbed. More specifically, it has been theorised that a massive object in quantum superposition results in two coexisting space-time geometries, leading to issues with the unitary evolution, which eventually causes it to collapse.1,3 Importantly, this relies on the zero-point motion \({X}_{{\rm{ZPF}}}\) being much larger than the approximate size of the nucleus (\(\sim\!\! 1\) fm), which is the case in our system (\({X}_{{\rm{ZPF}}}=33\) fm). The collapse timescale \({t}_{{\rm{G}}}\) is inversely proportional to the mass of the object, resulting in \({t}_{{\rm{G}}} \sim 1\!-\!10\) s for the parameters considered here (\(m \sim 1\) pg), therefore the resonator coherence time should be larger than that. Recent advances in strain engineering techniques can enable the enhancement of beam quality factors up to \({Q}_{{\rm{m}}} \sim 1{0}^{9}\),55 leading to relaxation times of hundreds of seconds, which would be sufficient for observing gravitational effects. Moreover, the ability to prepare a large variety of superposition states could offer an additional tool in testing such theories. The proposed architecture provides a very versatile platform in this regard, enabling not only generic quantum state preparation, but also with high fidelity, which has so far been a very challenging task.

Our approach combines the best of both worlds of two very versatile systems, namely the exquisite level of quantum control of qubits in circuit quantum electrodynamics56 with the long lifetimes and flexibility of mechanical elements in coupling to electromagnetic radiation. The high-fidelity generation of hybrid entangled states of phonons and qubit excitations, which have no classical analogue, may provide alternative routes for testing the limits of quantum theory at macroscopic scales.46,47,48 Additionally, such states are of particular importance in enabling quantum technologies with hybrid quantum systems, from quantum simulation to quantum computing and communication,57 and could also be used for coupling qubit excitations with other systems such as optical photons, cold atoms, or spin systems.49,50,51,52

Furthermore, we have tested the robustness of our proposal against several imperfections that may occur in a realistic experimental scenario (see Supplementary Sec. S4). The most important limitation would be the presence of a considerable amount of flux noise, resulting in stray qubit-qubit coupling; for example, adding a fluctuation of \(\delta {\Phi }_{{\rm{b}}}=1\!-\!10\,\mu {\Phi }_{0}\) results in \(0.1\!-\!1\) MHz added qubit-qubit coupling \(J\), respectively. We find that for \(J\ <\ 1\) MHz the fidelity of the cooling and quantum state preparation protocols is not compromised (Supplementary Fig. S4), therefore \(\delta {\Phi }_{{\rm{b}}}\ <\ 10\,\mu {\Phi }_{0}\) is required, which is compatible with observations in similar devices.58,59 We note that despite the steep slope of the tripartite coupling \(g\) versus flux bias for \({\Phi }_{{\rm{b}}}/{\Phi }_{0}\ >\ 0.495\) (Fig. 1b), the tripartite coupling never changes by more than \(1 \% \) for \(\delta {\Phi }_{{\rm{b}}}\ <\ 10\,\mu {\Phi }_{0}\). Another possible experimental limitation is the deviation from the target qubit frequencies due to imperfect flux tuning pulses. We have studied the effect of this imperfection and find that targeting the qubit frequencies within 100 kHz is sufficient for high-fidelity quantum state preparation (see Supplementary Fig. S5). Additionally, we have studied the robustness of the protocol against qubit coherence and find that high-fidelity quantum state preparation can be obtained for relaxation and dephasing times \({T}_{1,2}\gtrsim 10\,\mu \)s, which are typical in the superconducting qubit community and compatible with 10 mT magnetic fields.43

In conclusion, we have analysed a hybrid circuit architecture featuring strong and tuneable flux-mediated electromechanical interactions between a mechanical resonator and two superconducting transmon qubits. Using state-of-the-art parameters, we find that the coupled system can operate in the single-photon strong-coupling regime, which has been a long-standing goal in the field of optomechanics. We have proposed and numerically demonstrated several protocols for achieving ground-state cooling and preparing multi-phonon quantum superposition states as well as hybrid entanglement with high fidelities, which has been a tremendous challenge so far. Moreover, the proposed schemes for quantum manipulation are applicable to a wider range of tripartite quantum systems where a lower frequency mode, that is not directly accessible, is within the tuning range of the two other controllable modes. Our work significantly extends the quantum control toolbox of parametrically coupled radio-frequency mechanical resonators and provides a versatile on-chip interface with transmon-based processors, offering rich opportunities for technological applications as well as fundamental tests of quantum mechanics.

Methods

Numerical modelling

We model the dynamical evolution of the system, including environmental dissipation, with the Lindblad master equation

$$\begin{array}{l}\dot{\rho }\,=\,\displaystyle\frac{i}{\hslash }[\rho ,\hat{H}]+({n}_{{\rm{th}}}+1){\gamma }_{m}{\mathcal{L}}[\hat{b}]\rho +{n}_{{\rm{th}}}{\gamma }_{m}{\mathcal{L}}[{\hat{b}}^{\dagger }]\rho \\ +\,{\sum \limits_{i=1}^{2}}\displaystyle\frac{1}{{T}_{1}}{\mathcal{L}}[{\hat{c}}_{i}]\rho +\frac{1}{{T}_{2}}{\mathcal{L}}[{\hat{c}}_{i}^{\dagger }{\hat{c}}_{i}]\rho ,\end{array}$$
(11)

which is numerically solved using QuTiP.60 Here, \({\mathcal{L}}[\hat{o}]\rho \,\doteq\, (2\hat{o}\rho {\hat{o}}^{\dagger }-{\hat{o}}^{\dagger }\hat{o}\rho -\rho {\hat{o}}^{\dagger }\hat{o})/2\) are superoperators describing each dissipation process, and \({n}_{{\rm{th}}}\,=\,1/[\exp (\hslash {\omega }_{m}/({k}_{{\rm{B}}}T))-1]\) is the thermal phonon number at temperature \(T\). More specifically, we consider qubit decay and dephasing times \({T}_{1}={T}_{2}=30\,\mu\)s, which are consistent with measured values in a similar tuneable coupling transmon architecture.33 The coupling of the mechanical mode to the environment is determined by \({\gamma }_{m}={\omega }_{m}/Q\), where the quality factor \(Q=1{0}^{6}\) is chosen in agreement with experimental observations in recently fabricated SQUID-embedded beams.31 For completeness, we additionally include \({\mathcal{O}}({\phi }^{4}X)\) terms in the interaction Hamiltonian (see Supplementary Sec S2), which nevertheless cause insubstantial corrections to the system dynamics. We model the mechanical resonator using forty levels and each transmon as a three-level system (including an anharmonicity of \({E}_{{{\rm{C}}}_{i}}/h\simeq 320\) MHz). The same parameters, shown in Table 1, were considered in all the simulations.