Abstract
A quantum heat engine (QHE) based on the interaction driving of a many-particle working medium is introduced. The cycle alternates isochoric heating and cooling strokes with both interaction-driven processes that are simultaneously isochoric and isentropic. When the working substance is confined in a tight waveguide, the efficiency of the cycle becomes universal at low temperatures and governed by the ratio of velocities of a Luttinger liquid. We demonstrate the performance of the engine with an interacting Bose gas as a working medium and show that the average work per particle is maximum at criticality. We further discuss a work outcoupling mechanism based on the dependence of the interaction strength on the external spin degrees of freedom.
Similar content being viewed by others
Introduction
Universality plays a crucial role in thermodynamics, as emphasized by the description of engines, that transform heat and other resources into work. The working substance can often be described as an ideal gas and the control of interparticle interactions or the equation of state is generally beyond reach. As a result, the role of the working substance and the presence of many-particle effects are secondary in paradigmatic cycles (Carnot, Otto, etc.).1
In the quantum domain, this state of affairs should be revisited as suggested by recent works on many-particle quantum thermodynamics. The quantum statistics of the working substance can substantially affect the performance of a quantum engine.2 The need to consider a many-particle thermodynamic cycle arises naturally in an effort to scale-up thermodynamic devices3,4,5,6 and has prompted the identification of optimal confining potentials7 as well as the design of superadiabatic protocols,8,9,10,11 first proposed in a single-particle setting.12,13,14 The realization of superadiabatic strokes with ultracold atoms using a Fermi gas as a working substance has been reported.10,11,15 Intrinsically many-particle effects in the working substance, such as the divergence of energy fluctuations near a second-order phase transition16 and many-body localization,17 can prove advantageous. Many-particle thermodynamics can lead to a quantum-enhanced behavior, whereby a single many-particle cycle can outperform an ensemble of independent single-particle machines.8,18
Quantum technologies have also uncovered avenues to design thermodynamic cycles. Traditionally, interactions between particles are generally considered to be “fixed by Nature” in condensed matter. However, a variety of techniques makes possible to modify interparticle interactions in different quantum platforms. A paradigmatic example is the use of Feschbach and confinement-induced resonances in ultracold atoms.19 The engineering of interparticle interactions is similarly at reach in digital quantum simulation in trapped ions, Rydberg atoms, and superconducting qubits.20
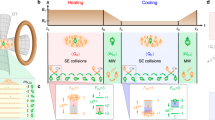
We introduce a thermodynamic cycle that exploits the many-particle nature of the working substance and thus have no single-particle counterpart. It consists of four isochoric strokes, alternating heating and cooling with a modulation of the interparticle interactions. Using Luttinger liquid theory, the efficiency of the cycle is shown to be universal in the low-temperature regime of a one-dimensional (1D) working substance, i.e. solely depending on the sound velocities at the states A and B (Fig. 1). The universal efficiency of the cycle is also shown to characterize the regime of strong interactions in the working substance, in which the spectrum is approximately scale invariant. When an interacting Bose gas is used as such, the average work output per particle is maximum at criticality.
Interaction-driven quantum cycle. The working substance is driven through four sequential isochoric strokes alternating heating and cooling processes at different temperature \(T\) with isentropes in which the interparticle interaction strength \(c\) is ramped up and down. The color coding indicates the mean energy across the \(T-c\) plane. The dashed lines correspond to the thermal entropy calculated from the thermodynamic Bethe ansatz equation of the Lieb-Liniger gas.21,22,23,24 The effective temperature assigned along the isentropes results from scale invariance in the energy spectrum, that holds for strong coupling and the Luttinger liquid region; see Section “Universal efficiency at low temperature” and the Supplementary Information Section I
Results
Interaction-driven thermodynamic cycle
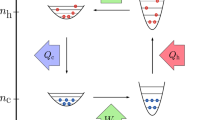
Consider a quantum heat engine (QHE) with a working substance consisting of a low-dimensional ultracold gas tightly confined in a waveguide.25,26 Ultracold gases have previously been explored in quantum cycles where work is done via expansion and compression processes, both in the non-interacting7,27 and interacting regimes.8,28,29,30,31,32 We propose the implementation of a quantum cycle consisting of four isochoric strokes, in which heating and cooling strokes are alternated with isentropic interaction-driven processes. In the latter, work is done onto and by the working substance by increasing and decreasing the interatomic interaction strength, respectively. This work can be transferred to other degrees of freedom as we shall discuss below. The working substance consists of \(N\) particles with interparticle interactions parameterized by the interaction strength \(c\). Both the particle number \(N\) and the system size \(L\) are kept constant throughout the cycle and any equilibrium point is parameterized by a point \((c,T)\) indexed by the temperature \(T\) and the interaction strength \(c\). Specifically the interaction-driven quantum cycle, shown in Fig. 1 for the 1D Lieb-Linger gas,21,22 involves the following strokes:
(1) Interaction ramp-up isentrope (A \(\to\) B): The working substance is initially in the thermal state \(A\) parameterized by \(({c}_{{\rm{A}}},{T}_{{\rm{A}}})\) and decoupled from any heat reservoir. Under unitary evolution, the interaction strength is enhanced to the value \({c}_{{\rm{B}}}\) and the final state is non-thermal. (2) Hot isochore (B \(\to\) C): Keeping \({c}_{{\rm{B}}}\) constant, the working substance is put in contact with the hot reservoir at temperature \({T}_{{\rm{C}}}\) and reaches the equilibrium state \(({c}_{{\rm{B}}},{T}_{{\rm{C}}})\). (3) Interaction ramp-down isentrope (C \(\to\) D): The working substance is decoupled from the hot reservoir and performs work adiabatically while the interaction strength decreases from \({c}_{{\rm{B}}}\) to \({c}_{{\rm{A}}}\), reaching a non-thermal state. (4) Cold isochore (D \(\to\) A): The working substance is put in contact with the cold reservoir with temperature \({T}_{{\rm{A}}}\) keeping the interaction strength constant until it reaches the thermal state \(({c}_{{\rm{A}}},{T}_{{\rm{A}}})\). The work extracted from the heat engine is given by \(W={W}_{3}-{W}_{1}={Q}_{2}-{Q}_{4}\) while the efficiency of the heat engine reads
Interacting Bose gas as a working substance
Consider as a working substance an ultracold interacting Bose gas tightly confined in a waveguide,33,34 as realized in the laboratory.35,36,37 The effective Hamiltonian for \(N\) particles is that of the Lieb-Liniger model:21,22
where \({x}_{j\ell }={x}_{j}-{x}_{\ell }\), with \(2m=\hslash =1\). The spectral properties of the Hamiltonian of Eq. 2 can be found using coordinate Bethe ansatz.21,22 We consider a box-like trap38,39 where any energy eigenvalue can be written as \(E={\sum }_{i}{k}_{i}^{2}\) in terms of the ordered quasimomenta \(0<{k}_{1}<{k}_{2}<\cdots <{k}_{N}\). The latter are the (Bethe) roots \(\{{k}_{i}\}\) of the coupled algebraic equations
determined by the sequence of quantum numbers \(\{{I}_{i}\}\) with \(i=1,\ 2,\ \cdots \ ,\ N\). As a function of \(c\) and \(T\), the 1D Bose gas exhibits a rich phase diagram. We first consider the regime of strong interactions and use a Taylor series expansion in \(1/c\). For a given set of quantum numbers \({{\mathcal{I}}}_{n}=\{{I}_{i}^{(n)}\}\), the corresponding energy eigenvalue takes the form
where the interaction-dependent factor \({\lambda }_{c}\) reads
The spectrum of a strongly interacting Bose gas is thus characterized by eigenvalues with scale-invariant behavior, i.e., \({\epsilon }_{n}(c)/{\epsilon }_{n}(c^{\prime} )={\lambda }_{c}/\lambda_{c} ^{\prime}\). This scale invariance in the spectrum allows us to assign an effective temperature along the isentropes; see Supplementary Information Section I. In this regime, the work output is thus set by \(W={Q}_{2}-{Q}_{4}=[1-({\lambda }_{{c}_{{\rm{A}}}}/{\lambda }_{{c}_{{\rm{B}}}})]{Q}_{2}\) and the efficiency
becomes independent of temperature of the heat reservoirs, as we show in Supplementary Information. Being the spectrum scale-invariant, the efficiency can be expressed in terms of the scaling factor.40 This feature is as well shared by the well-known harmonic Otto cycle.41 This is a consequence of the fact that both the cycles involve the driving of an isolated quantum system with a scale-invariant energy spectrum. However, the interaction-driven cycle generally involves a change of density of states which can be regarded as the change of the generalized exclusion statistics in an ideal gas;42 also see Supplementary Information Sections II and III. Moreover, the scale invariant character of the energy spectrum in the strongly interacting regime is also present for multicomponent Bose and Fermi gases, preserving the universal efficiency given by Eq. 6.
For weaker interactions, we resort to a numerically-exact solution of Eqs. 3 for finite particle number \(N\). We enumerate all the possible sets \({{\mathcal{I}}}_{n}\) of quantum numbers for low-energy states and solve Eqs. 3 numerically for given \(c\). With the resulting quasi-momenta \(\{{k}_{n,1},{k}_{n,2},\cdots \ \}\), and the corresponding energy eigenvalues \({\epsilon }_{n}={\sum }_{i}{k}_{n,i}^{2}\), the probability that the Bose gas at temperature \(T\) is found with energy \({\epsilon }_{n}\) is set by the Boltzmann weights \({p}_{n}={e}^{-{\epsilon }_{n}/T}/{\sum }_{m}{e}^{-{\epsilon }_{m}/T}\) (with \({k}_{{\rm{B}}}=1\)). The equilibrium energy of the states \(A\) and \(C\) is set by thermal averages of the form \(\langle E\rangle ={\sum }_{n}{p}_{n}{\epsilon }_{n}\) that in turn yield the expressions for \({Q}_{2}\) and \({Q}_{4}\). Here, a proper cutoff of the possible sets \(\{{{\mathcal{I}}}_{n}\}\) can be determined by \({p}_{n}/{p}_{{\rm{G}}}\ll 1\), where \({p}_{{\rm{G}}}\) is the probability for the working substance to be in the ground state. The numerical results for the efficiency \(\eta\) and output work \(W\) are shown in Fig. 2 as a function of the interaction strength. For fixed values of \({T}_{{\rm{C}}}\) and \({T}_{{\rm{A}}}\), the maximum work is studied as a function of \({c}_{{\rm{A}}}\) while keeping \({c}_{{\rm{B}}}\) constant (Fig. 2). The efficiency is well reproduced by Eq. 6 at strong coupling, that captures the monotonic decay with increasing interaction strength. The efficiency is found to be essentially independent of the temperature in the strong interaction regime, whereas the work output is governed by the temperature and interaction strength.
Work and efficiency as functions of the interaction strength \({c}_{{\rm{A}}}\). a Dependence of the work output \(W\) on \({c}_{{\rm{A}}}\) for different \({T}_{{\rm{A}}}\). b The efficiency \(\eta\) obtained by numerical calculation (solid lines), is compared with the analytical result (black dashed line) in Eq. 6. Here, \(N=5\), \(L=1\), \({T}_{{\rm{C}}}=150\), and \({c}_{{\rm{B}}}=200\)
Universal efficiency at low temperature
In the thermodynamic limit (where \(N\) and \(L\to \infty\) with \(n=N/L\) being kept constant), the equilibrium state of the 1D Bose gas is determined by the Yang-Yang thermodynamics23,24,42,43,44 (see “Methods”). At low energy, excitations are phonons and the behavior is described by the Tomonaga-Luttinger liquid (TLL) theory,45,46,47,48,49 in which the free energy density reads
where \({{\mathcal{E}}}_{0}\) is the energy density of the ground state, \({v}_{{\rm{s}}}\) is the sound velocity which depends on particle density \(n\) and interaction \(c\). The entropy density \(s\) can be obtained as the derivative of free energy, \(s=-\partial {\mathcal{F}}/\partial T=\pi T/3{v}_{{\rm{s}}}\). The expression for the heat absorbed and released are respectively given by energy differences
where \({s}_{i}=\pi {T}_{i}/3{v}_{s}^{i}\) and \({v}_{{\rm{s}}}^{i}\) with \({v}_{{\rm{s}}}^{{\rm{B}}}={v}_{{\rm{s}}}^{{\rm{C}}}\) and \({v}_{{\rm{s}}}^{{\rm{A}}}={v}_{{\rm{s}}}^{{\rm{D}}}\) denote the entropy density and the sound velocity of the state \(i\), respectively. Using the fact that the strokes (1) and (3) are isentropes, it follows that
where \({T}_{{\rm{B}}}\) and \({T}_{{\rm{D}}}\) are the temperatures at states B and D, respectively. As a result, the efficiency and work output are given by
where \(\kappa ={T}_{{\rm{A}}}/{T}_{{\rm{C}}}\). Since \({T}_{{\rm{A}}}\;<\;{T}_{{\rm{B}}}\;<\;{T}_{{\rm{C}}}\), we have \(0\;<\;\kappa \;<\;\xi \;<\;1\). This efficiency (11) is universal regardless the microscopic physics of the working substance with a low-energy TLL description. The work output for fixed \({T}_{{\rm{A}}}\) and \({T}_{{\rm{C}}}\) is maximized at \(\xi ={\xi }_{{\rm{c}}}\) as shown in Supplementary Information Section IV,
As the TLL theory describes the universal low-energy behavior of 1D many-body systems, Eqs. 11–13 provide a universal description of the efficiency and work of QHE with a 1D interacting working substance at low temperatures, which are applicable to any cycle in which work and heat exchange occurs in different strokes. In particular, in the strongly interacting regime, the sound velocity of 1D Bose gases is given by \({v}_{{\rm{s}}}\simeq 2\pi n(1-4n{c}^{-1}+12{n}^{2}{c}^{-2})\).24 In this regime, the result 11 thus reduces to Eq. 6. On the other hand, in the weak interaction regime, \({v}_{{\rm{s}}}\simeq 2n\sqrt{\frac{c}{n}-\frac{1}{2\pi }{\left(\frac{c}{n}\right)}^{\frac{3}{2}}}\),24 and thus the efficiency reaches the asymptotic value
indicating an enhancement of the performance with respect to the strongly interacting case.
Quantum critical region
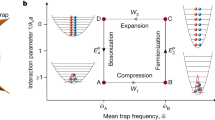
We next focus on the performance of an interaction-driven QHE across the phase diagram of the 1D Bose gas and characterized the role of quantum criticality.50 The 1D Bose gas displays a rich critical behavior as a function of the temperature \(T\) and chemical potential \(\mu\) (Fig. 3). In the region of \(\mu /T\ll 0\), i.e. the mean distance between atoms is much larger than the thermal wave length \({\lambda }_{{\rm{th}}}=\sqrt{2\pi {\hslash }^{2}/(m{k}_{{\rm{B}}}T)}\), and the system behaves as a classical gas (CG). A quantum critical region (QC) emerges between two critical temperatures (see the white dashed lines in Fig. 3c) fanning out from the critical point \({\mu }_{{\rm{c}}}=0\). In this region, the energy gap closes universally as \(\Delta \sim | \mu -{\mu }_{{\rm{c}}}{| }^{z\nu }\), in terms of the correlation length and dynamic critical exponents \(\nu =1/2\) and \(z=2\). The TLL region characterized by a phononic spectrum is found with \(\mu >0\) and \(T\) below the right critical temperature.
Performance across the phase diagram. a Efficiency \(\eta\) as a function of the density \(n\). b Average work output \(W/N\) as a function of density \(n\). c Phase diagram of a Bose gas given by a contour plot of the specific heat. The three different polygons delineate interaction-driven thermodynamic cycles in different regimes of the phase diagram corresponding to the three dashed lines in the other panels. The equilibrium states A and C are chosen with fixed \(c\) and \(T\) for the different cycles. The efficiency saturates at \(0.42\) given by Eq. 14 in the TLL regime. (d) The energy derivative \(\partial E/\partial c\) per particle as a function of the interaction strength \(c\). The areas of these three polygons correspond to the works per particle \(W/N\) for the three cycles in figure (c), respectively
For fixed cycle parameters (\({c}_{{\rm{A}}}\), \({c}_{{\rm{B}}}\), \({T}_{{\rm{A}}}\), and \({T}_{{\rm{C}}}\)), we study the performance of the engine across the QC region by changing \(n\). We numerically calculate the efficiency \(\eta\) and average work \(W/N\) by using the TBA equation 16, and show that near the QC region \(W/N\) has a maximum value; see Fig. 3. We set \({c}_{{\rm{A}}}=1\), \({c}_{{\rm{B}}}=3\), \({T}_{{\rm{A}}}=1\), and \({T}_{{\rm{C}}}=5\) for the heat engine and let the density \(n\) increase from \(0.1\) to \(23\). The red, green, and blue dashed lines in Fig. 3 correspond to the densities \(n\simeq 0.3\), \(1.4\), and \(3.0\), respectively. In order to understand the maximum of \(W/N\), we also plot these three engine cycles (A \(\to\) B \(\to\) C \(\to\) D \(\to\) A) in the phase diagram of specific heat in the \(T-\mu\) plane; see Fig. 3 (c). The performance of the cycle is optimal at the critical region (green dashed line). Specifically, when the stroke A \(\to\) B is near the TLL boundary and the stroke C \(\to\) D is in the critical region, the average work output per particle is maximized. In this scenario, the two adiabatic processes (A \(\to\) B and C \(\to\) D) pass through zones in which the change in the energy dispersion is maximized, as shown in Fig. 3c. Qualitatively, the process A \(\to\) B passes though the region where the specific heat is maximum, whereas the C \(\to\) D evolves through the region with lowest specific heat. In the adiabatic process, the particle number \(N\) and entropy \(S\) are all fixed. Figure 3d shows the work for the different cycles, where the work for each adiabatic process is given by \(W={\int }_{{c}_{{\rm{initial}}}}^{{c}_{{\rm{final}}}}\left(\partial E/\partial c\right)dc\). Even if the process is not rigorously adiabatic,51 this maximum work output still holds, as further discussed in Supplementary Information Section IV.
Discussion
The modulation of the interaction strength \(c\) is associated with the performance of work, that has recently been investigated for different working substances.52,53,54 An experimentally-realizable work outcoupling mechanism can be engineered when the coupling strength depends on the configuration of other degrees of freedom. This is analogous to the standard Carnot or Otto cycles where the working substance is confined, e.g., in a box-like trap.41 The latter is endowed with a dynamical degree of freedom that is assumed to be slow (massive) so that in the spirit of the Born-Oppenheimer approximation it can be replaced by a parameter. Similarly, the modulation of the coupling strength in an interaction-driven cycle can be associated with the coupling to external degrees of freedom.
As an instance, consider the choice of an interacting SU(2) 1D spinor Fermi gas in a tight waveguide as a working substance. The Hamiltonian can be effectively mapped to the Lieb-Liniger model (see ref. 55 and Supplementary Information Section V), with a coupling strength \(c=c(\langle {\hat{{\bf{S}}}}_{j}\cdot {\hat{{\bf{S}}}}_{\ell }\rangle )\) that depends on the spinor degrees of freedom,55,56 an approximation corroborated by the exact solution in a broad range of parameters.57 Another example relies on the use of confinement-induced resonances19,58 that govern the scattering properties of a quasi-1D working substance in a waveguide. The transverse frequency \({\omega }_{\perp }\) of the latter directly determines the interaction strength \(c\), i.e., \(c=c({\omega }_{\perp })\), and the role of \({\omega }_{\perp }\) parallels that of the trap parameters in the conventional Carnot and Otto cycles. The possibility of extracting work from quench dynamics was recently studied.59,60
Finally, we note that an interaction-driven cycle can also be used to describe QHEs in which the interaction-driven strokes are substituted by processes involving the transmutation of the particle quantum exchange statistics, e.g., a change of the statistical parameter of the working substance. The Hamiltonian of Eq. 2 can be used to describe 1D anyons with pair-wise contact interactions with coupling strength \(\tilde{c}\) and statistical parameter \(\theta\) characterizing the exchange statistics, smoothly interpolating between bosons and fermions.61,62 The spectral properties of this Lieb-Liniger anyons can be mapped to a bosonic Lieb-Liniger model given by Eq. 2 with coupling strength \(c=\tilde{c}/\cos (\theta /2)\).61,62 The modulation of \(c\) can be achieved by the control of the particle statistics, tuning \(\theta\) as proposed in ref. 63
In summary, we have proposed an experimental realization of an interaction-driven QHE that has no single-particle counterpart: it alternates heating and cooling strokes with processes that are both isochoric and isentropic and in which work is done onto or by the working substance by changing in the interatomic interaction strength. This cycle can be realized with a Bose gas in a tight waveguide as a working substance. Using Luttinger liquid theory, the engine efficiency has been shown to be universal in the low temperature limit, and set by the ratio of the sound velocities in the interaction-driven strokes. The optimal work can be achieved by changing the ratio of the sound velocity, e.g., by tuning the interaction strength. An analysis of the engine performance across the phase diagram of the Bose gas indicates that quantum criticality maximizes the efficiency of the cycle.
Our proposal can be extended to Carnot-like interaction-driven cycles in which work and heat are simultaneously exchanged in each stroke. Exploiting effects beyond adiabatic limit may lead to a quantum-enhanced performance.8,18 The use of non-thermal reservoirs64,65,66 and quantum measurements67,68 constitutes another interesting prospect. Our results identify confined Bose gases as an ideal platform for the engineering of scalable many-particle quantum thermodynamic devices.
Methods
In the Yang-Yang thermodynamics of the 1D Bose gas, the pressure is given by
where the “dressed energy” \(\varepsilon (k)\) is determined by thermodynamic Bethe Anstatz (TBA) equation
The particle density \(n\) and the entropy density \(s\) can be derived from the thermodynamic relations
in terms of which the internal energy density reads \({\mathcal{E}}=-p+\mu n+Ts\). Both interaction-driven strokes are considered to be adiabatic. As a result, the heat absorbed during the hot isochore stroke (B \(\to\) C) is given by \({Q}_{2}=L[{\mathcal{E}}({c}_{{\rm{B}}},{T}_{{\rm{C}}})-{\mathcal{E}}({c}_{{\rm{B}}},{T}_{{\rm{B}}})]\), while the heat released during the cold isochore (D \(\to\) A) equals \({Q}_{4}=L[{\mathcal{E}}({c}_{{\rm{A}}},{T}_{{\rm{D}}})-{\mathcal{E}}({c}_{{\rm{A}}},{T}_{{\rm{A}}})]\). Here \({T}_{{\rm{B}}}\) and \({T}_{{\rm{D}}}\) can be determined in terms of the isentropic strokes, in which \(s({c}_{{\rm{A}}},{T}_{{\rm{A}}})=s({c}_{{\rm{B}}},{T}_{{\rm{B}}})\) and \(s({c}_{{\rm{B}}},{T}_{{\rm{C}}})=s({c}_{{\rm{A}}},{T}_{{\rm{D}}})\), where \({T}_{{\rm{A}}}\) and \({T}_{{\rm{C}}}\) are the temperature of the cold and hot reservoir, respectively. The efficiency and work can then be obtained by numerically solving the TBA equation. This article was previously published as a preprint.69
Data availability
All data generated during this study are included in the supplementary information files.
References
Zemansky, M. W. & Dittman, R. H. Heat and Thermodynamics. Am. J. Phys. 66, 164 (1998).
Kim, S. W., Sagawa, T., DeLiberato, S. & Ueda, M. Quantum Szilard Engine. Phys. Rev. Lett. 106, 070401 (2011).
Roßnagel, J. et al. A single-atom heat engine. Science 352, 325–329 (2016).
Maslennikov, G. et al. Quantum absorption refrigerator with trapped ions. Nat. Commun. 10, 202 (2019).
Peterson, J. P. S. Experimental characterization of a spin quantum heat engine, https://arxiv.org/abs/1803.06021 (2019).
vonLindenfels, D. et al. Spin heat engine coupled to a harmonic-oscillator flywheel. Phys. Rev. Lett. 123, 080602 (2019).
Zheng, Y. & Poletti, D. Quantum statistics and the performance of engine cycles. Phys. Rev. E 92, 012110 (2015).
Jaramillo, J., Beau, M. & DelCampo, A. Quantum supremacy of many-particle thermal machines. New J. Phys. 18, 075019 (2016).
Funo, K. et al. Universal work fluctuations during shortcuts to adiabaticity by counterdiabatic driving. Phys. Rev. Lett. 118, 100602 (2017).
Deng, S., Diao, P., Yu, Q., Del Campo, A. & Wu, H. Shortcuts to adiabaticity in the strongly coupled regime: nonadiabatic control of a unitary Fermi gas. Phys. Rev. A 97, 013628 (2018).
Deng, S. et al. Superadiabatic quantum friction suppression in finite-time thermodynamics. Sci. Adv. 4, eaar5909 (2018).
Deng, J., Wang, Q., Liu, Z., Hänggi, P. & Gong, J. Boosting work characteristics and overall heat-engine performance via shortcuts to adiabaticity: quantum and classical systems. Phys. Rev. E 88, 062122 (2013).
Del Campo, A., Goold, J. & Paternostro, M. More bang for your buck: super-adiabatic quantum engines. Sci. Rep. 4, 6208 (2014).
Van Horne, N. et al. Single atom energy-conversion device with a quantum load, https://arxiv.org/abs/1812.01303 (2018).
Diao, P. et al. Shortcuts to adiabaticity in Fermi gases. New J. Phys. 20, 105004 (2018).
Campisi, M. & Fazio, R. The power of a critical heat engine. Nat. Commun. 7, 11895 (2016).
Halpern, N. Y., White, C. D., Gopalakrishnan, S. & Refael, G. Quantum engine based on many-body localization. Phys. Rev. B 99, 024203 (2019).
Bengtsson, J. Quantum szilard engine with attractively interacting bosons. Phys. Rev. Lett. 120, 100601 (2018).
Girardeau, M. D., Nguyen, H. & Olshanii, M. Effective interactions, Fermi-Bose duality, and ground states of ultracold atomic vapors in tight de Broglie waveguides. Opt. Commun. 243, 3 (2004).
Georgescu, I. M., Ashhab, S. & Nori, F. Quantum simulation. Rev. Mod. Phys. 86, 153 (2014).
Lieb, E. H. & Liniger, W. Exact analysis of an interacting Bose gas. I. The general solution and the ground state. Phys. Rev. 130, 1605 (1963).
Lieb, E. H. Exact analysis of an interacting Bose gas. II. The excitation spectrum. Phys. Rev. 130, 1616 (1963).
Yang, C. N. & Yang, C. P. Thermodynamics of a one-dimensional system of Bosons with repulsive delta-function interaction. J. Math. Phys. 10, 1115 (1969).
Jiang, Y.-Z., Chen, Y.-Y. & Guan, X.-W. Understanding many-body physics in one dimension from the Lieb-Liniger model. Chinese Physics B 24, 050311 (2015).
Rauer, B. et al. Cooling of a one-dimensional Bose gas. Phys. Rev. Lett. 116, 030402 (2016).
Bouchoule, I., Van Druten, N. & Westbrook, C. I. Atom chips and one-dimensional Bose gases. https://arxiv.org/abs/0901.3303 (2009).
Şişman, A. & Saygin, H. Re-optimisation of Otto power cycles working with ideal quantum gases. Phys. Scr. 64, 108 (2001).
Fialko, O. & Hallwood, D. W. Isolated quantum heat engine. Phys. Rev. Lett. 108, 085303 (2012).
Beau, M., Jaramillo, J. & DelCampo, A. Scaling-up quantum heat engines efficiently via shortcuts to adiabaticity. Entropy 18, 168 (2016).
Li, J., Fogarty, T., Campbell, S., Chen, X. & Busch, T. An efficient nonlinear Feshbach engine. New J. of Phys. 20, 015005 (2018).
Chen, J., Dong, H. & Sun, C.-P. Bose-Fermi duality in a quantum Otto heat engine with trapped repulsive bosons. Phys. Rev. E 98, 062119 (2018).
Ma, Y.-H., Su, S.-H. & Sun, C.-P. Quantum thermodynamic cycle with quantum phase transition. Phys. Rev. E 96, 022143 (2017).
Olshanii, M. Atomic scattering in the presence of an external confinement and a gas of impenetrable Bosons. Phys. Rev. Lett. 81, 938 (1998).
Lieb, E. H., Seiringer, R. & Yngvason, J. One-dimensional bosons in three-dimensional traps. Phys. Rev. Lett. 91, 150401 (2003).
Paredes, B. et al. Tonks-Girardeau gas of ultracold atoms in an optical lattice. Nature 429, 277 (2004).
Hofferberth, S. et al. Probing quantum and thermal noise in an interacting many-body system. Nat. Phys. 4, 489 (2008).
Gring, M. et al. Relaxation and prethermalization in an isolated quantum system. Science 337, 1318 (2012).
Gaudin, M. Boundary energy of a Bose gas in one dimension. Phys. Rev. A 4, 386 (1971).
Batchelor, M. T., Guan, X. W., Oelkers, N. & Lee, C. The 1D interacting Bose gas in a hard wall box. J. Phys. A: Math. General 38, 7787 (2005).
Gemmer, J., Michel, M. & Mahler, G. Quantum thermodynamics: emergence of thermodynamic behavior within composite quantum systems, 784 (Springer, 2009).
Kosloff, R. & Rezek, Y. The Quantum Harmonic Otto Cycle. Entropy 19, 136 (2017).
Batchelor, M. T. & Guan, X.-W. Fermionization and fractional statistics in the strongly interacting one-dimensional Bose gas. Laser Phys. Lett. 4, 77 (2007).
Korepin, V. E., Bogoliubov, N. M. & Izergin, A. G. Quantum Inverse Scattering Method and Correlation Functions (Cambridge Univ. Press, 1993).
Takahashi, M. Thermodynamics of One-Dimensional Solvable Models (Cambridge Univ. Press, 1999).
Luttinger, J. M. An exactly soluble model of a many-fermion system. J. Math. Phys. 4, 1154 (1963).
Mattis, D. C. & Lieb, E. H. Exact solution of a many-fermion system and its associated boson field. J. Math. Phys. 6, 304 (1965).
Haldane, F. D. M. General relation of correlation exponents and spectral properties of one-dimensional Fermi systems: application to the anisotropic \(S=\frac{1}{2}\) Heisenberg chain. Phys. Rev. Lett. 45, 1358 (1980).
Haldane, F. D. M. Effective harmonic-fluid approach to low-energy properties of one-dimensional quantum fluids. Phys. Rev. Lett. 47, 1840 (1981).
Cazalilla, M. A. Bosonizing one-dimensional cold atomic gases. J. Phys. B 37, S1 (2004).
Yang, B. et al. Quantum criticality and the Tomonaga-Luttinger liquid in one-dimensional Bose gases. Phys. Rev. Lett. 119, 165701 (2017).
Xiao, G. & Gong, J. Construction and optimization of a quantum analog of the Carnot cycle. Phys. Rev. E 92, 012118 (2015).
Chenu, A., Molina-Vilaplana, J. & DelCampo, A. Quantum work statistics, Loschmidt echo and information scrambling. Sci. Rep. 8, 12634 (2018).
Chenu, A., Egusquiza, I. L., Molina-Vilaplana, J. & DelCampo, A. Work Statistics, Loschmidt Echo and Information Scrambling in Chaotic Quantum Systems. Quantum 3, 127 (2019).
Rylands, C. & Andrei, N. Loschmidt Amplitude and Work Distribution in Quenches of the Sine-Gordon Model. Phys. Rev. B 99, 085133 (2019).
Girardeau, M. D. Ground and Excited States of Spinor Fermi Gases in Tight Waveguides and the Lieb-Liniger-Heisenberg Model. Phys. Rev. Lett. 97, 210401 (2006).
DelCampo, A., Muga, J. G. & Girardeau, M. D. Stability of spinor Fermi gases in tight waveguides. Phys. Rev. A 76, 013615 (2007).
Guan, L., Chen, S., Wang, Y. & Ma, Z.-Q. Exact solution for infinitely strongly interacting Fermi gases in tight waveguides. Phys. Rev. Lett. 102, 160402 (2009).
Haller, E. et al. Confinement-induced resonances in low-dimensional quantum systems. Phys. Rev. Lett. 104, 153203 (2010).
Rylands, C. & Andrei, N. Phys. Rev. B 100, 064308 (2019).
Mechael Wiedmann, J. T. S. & Joachin, A. Out-of-equilibrium operation of a quantum heat engine. https://arxiv.org/abs/1903.11368 (2019).
Kundu, A. Exact solution of double \(\delta\) function Bose gas through an interacting anyon gas. Phys. Rev. Lett. 83, 1275 (1999).
Batchelor, M. T., Guan, X.-W. & Oelkers, N. One-dimensional interacting anyon gas: low-energy properties and Haldane exclusion statistics. Phys. Rev. Lett. 96, 210402 (2006).
Keilmann, T., Lanzmich, S., McCulloch, I. & Roncaglia, M. Statistically induced phase transitions and anyons in 1D optical lattices. Nat. Commun. 2, 361 (2011).
Scully, M. O., Zubairy, M. S., Agarwal, G. S. & Walther, H. Extracting work from a single heat bath via vanishing quantum coherence. Science 299, 862 (2003).
Kieu, T. D. The second law, Maxwell’s demon, and work derivable from quantum heat engines. Phys. Rev. Lett. 93, 140403 (2004).
Roßnagel, J., Abah, O., Schmidt-Kaler, F., Singer, K. & Lutz, E. Nanoscale heat engine beyond the Carnot limit. Phys. Rev. Lett. 112, 030602 (2014).
Watanabe, G., Venkatesh, B. P., Talkner, P. & DelCampo, A. Quantum performance of thermal machines over many cycles. Phys. Rev. Lett. 118, 050601 (2017).
Elouard, C., Herrera-Martí, S. A., Clusel, M. & Auffe`ves, A. The role of quantum measurement in stochastic thermodynamics. npj Quantum Inf. 3, 9 (2017).
Chen, Y.-Y., Watanabe, G., Yu, Y.-C., Guan, X.-W. & Del Campo, A. An interaction-driven many-particle quantum heat engine: universal behavior. https://arxiv.org/abs/1812.09327 (2018).
Acknowledgements
We thank F. J. Gómez-Ruiz and Zhenyu Xu for comments on the manuscript. Funding support from the John Templeton Foundation, the National Key R&D Program of China No. 2017YFA0304500 and the key NSFC grant No. 11534014 and NSFC grant No. 11874393, is further acknowledged. G.W. was supported by the Zhejiang Provincial Natural Science Foundation Key Project (Grant No. LZ19A050001), by NSF of China (Grant No. 11674283), by the Fundamental Research Funds for the Central Universities (2017QNA3005, 2018QNA3004), by the Zhejiang University 100 Plan, and by the Thousand Young Talents Program of China. Y.-Y.C. was supported by the China Postdoctoral Science Foundation Grant (No. 2019M650145).
Author information
Authors and Affiliations
Contributions
D.C. conceived the project. Y.-Y.C. and X.-W.G. led its theoretical development. Y.-Y.C. and Y.-C.Y. performed the numerical analysis. All authors contributing to completing the development of the project, analyzing the results, and writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, YY., Watanabe, G., Yu, YC. et al. An interaction-driven many-particle quantum heat engine and its universal behavior. npj Quantum Inf 5, 88 (2019). https://doi.org/10.1038/s41534-019-0204-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-019-0204-5
This article is cited by
-
Power-law scalings in weakly-interacting Bose gases at quantum criticality
Frontiers of Physics (2022)
-
An interaction-driven many-particle quantum heat engine and its universal behavior
npj Quantum Information (2019)