Abstract
To guarantee the security of quantum key distribution (QKD), security proofs of QKD protocols have assumptions on the devices. Commonly used assumptions are, for example, each random bit information chosen by a sender to be precisely encoded on an optical emitted pulse and the photon-number probability distribution of the pulse to be exactly known. These typical assumptions imposed on light sources such as the above two are rather strong and would be hard to verify in practical QKD systems. The goal of the paper is to replace those strong assumptions on the light sources with weaker ones. In this paper, we adopt the differential-phase-shift (DPS) QKD protocol and drastically mitigate the requirements on light sources, while for the measurement unit, trusted and photon-number-resolving detectors are assumed. Specifically, we only assume the independence among emitted pulses, the independence of the vacuum emission probability from a chosen bit, and upper bounds on the tail distribution function of the total photon number in a single block of pulses for single, two and three photons. Remarkably, no other detailed characterizations, such as the amount of phase modulation, are required. Our security proof significantly relaxes demands for light sources, which paves a route to guarantee implementation security with simple verification of the devices.
Similar content being viewed by others
Introduction
Quantum key distribution (QKD) holds promise for information-theoretically secure communication between two distant parties, Alice and Bob.1 Since QKD is a physical cryptography in which security is based on a mathematical model of the devices, several assumptions on Alice’s light source and Bob’s measurement unit have to be satisfied to guarantee the security. Any discrepancies between the device model and properties of the actual devices could be exploited to hack the implemented QKD systems. In fact, several experiments to crack implementation of QKD systems have been reported,2,3,4,5,6 which is a crucial threat for security of QKD, and therefore it is important to close the gap between theory and practice.
So far, tremendous efforts have been made to relax the demands for light sources (see e.g., a review article7). Possible approaches to close the gap are to use device independent (DI) QKD (see, e.g.,8 and references therein) or entanglement based QKD with trusted detectors.9 On the other hand, as for the device-dependent QKD, the BB84 protocol10 is one of the most investigated protocols, and its security assuming an ideal single-photon source11,12,13 and an ideal phase randomized coherent-light source14 with the decoy-state method15,16,17 were proved. The security proofs were generalized to accommodate dominant imperfections of the devices. For example, perfect phase randomization is relaxed to discrete phase randomization,18 inter-pulse intensity correlations between neighboring pulses have been accommodated,19 and a perfectly symmetric encoding of random bit information is relaxed to asymmetric encoding with the loss-tolerant protocol.20,21 Another promising protocol is the round-robin differential phase shift (RRDPS) protocol.22 Its implementation security proof has been studied,23 which shows that the RRDPS protocol is robust against source flaws. However, the variable-delay interferometer used in this protocol is an obstacle to simple implementation.
In this paper, we adopt the differential-phase-shift (DPS) protocol24 and drastically mitigate the demands for light sources, which is useful for simple characterization of the devices with quantified security. Our characterizations of light sources are based on the photon-number statistics of emitted pulses. Specifically, we suppose that the vacuum emission probability of each pulse is independent of a chosen bit, and an upper bound qn (for n ∈ {1, 2, 3}) on the probability that each block of pulses contains n or more photons. Here, these probabilities are the ones that would be obtained if we performed a photon number measurement, and we do not assume that the state is a classical mixture of Fock states. Remarkably, detailed characterizations of the source devices that were needed in previous security proofs of DPS protocol25,26 and the original DPS protocol,24 such as the precise control of phase modulations, complete knowledge of the photon-number probability distribution, block-wise phase randomization, and a single-mode assumption on the emitted pulse are not necessary. At the end of this section, we remark the meaning of characterized sources in our title in comparison with the previous work in ref. 27 whose title implies that secure QKD can be realized with an uncharacterized source. An important note here is that the uncharacterized source in ref. 27 does not mean no assumptions on light sources. Indeed, this proof assumes that the state emitted by the source, averaged over the values of Alice’s key bit, is basis-independent. Therefore, both our proof and the proof in ref. 27 have some characterizations on the emitted pulses, but just the ways are different.
Results
Assumptions on the devices
Before describing the protocol, we summarize the assumptions we make on the source and the receiver. First, we list up the assumptions on Alice’s source as follows. In this paper, for simplicity of the security analysis, we consider the case where Alice employs three pulses contained in a single-block. Note that experimental implementations remain the same with and without assuming blocks. But if blocks are employed, classical post-processing needs to be modified such that at most one-bit key is extracted from a single-block.
-
(A1)
Alice chooses a random three-bit sequence \(\vec b_A: = b_1^Ab_2^Ab_3^A \in \{ 0,1\} ^3\), and \(b_i^A\) is encoded only on the ith pulse in system Si. Depending on the chosen \(\vec b_A\), Alice prepares a following three-pulse state in system S := S1S2S3:
$$\hat \rho _S^{\vec b_A}: = \mathop { \bigotimes }\limits_{i = 1}^3 \hat \rho _{S_i}^{b_i^A}.$$(1)Here, \(\hat \rho _{S_i}^{b_i^A}\) denotes a density operator of the ith pulse when \(b_i^A\) is chosen. We suppose that each system Ri that purifies each of the state \(\hat \rho _{S_i}^{b_i^A}\) is possessed by Alice, and Eve does not have access to system Ri.
-
(A2)
The vacuum emission probability of the ith pulse is independent of the chosen bit \(b_i^A\). That is, we require that the following equality holds for any i:
$${\mathrm{tr}}\hat \rho _{S_i}^0|{\mathrm{vac}}\rangle \langle {\mathrm{vac}}| = {\mathrm{tr}}\hat \rho _{S_i}^1|{\mathrm{vac}}\rangle \langle {\mathrm{vac}}|,$$(2)where |vac〉 is the vacuum state.
-
(A3)
For any chosen bit sequence \(\vec b_A\), the probability that a single-block of pulses contains n (with n ∈ {1, 2, 3}) or more photons is upper-bounded by qn. That is,
$${\mathrm{Pr}}\{ n_{{\mathrm{block}}} \ge n\} \le q_n,$$(3)where nblock denotes the number of photons contained in a single-block. Note that nblock is the sum of the number of photons in all the optical modes. By using a calibration method based on a conventional Hanbury-Brown-Twiss setup with threshold photon detectors,28 Alice can verify \(\{ q_n\} _{n = 1}^3\) before running the protocol. If \(\{ q_n\} _{n = 1}^3\) are estimated from such an off-line test, we need to assume that these bounds do not change during the on-line experiment.
We note that our security proof does not cover a situation where there is a Trojan horse attack.29 This is because one cannot verify whether or not Eve has an ancillary system of the injected light, and hence the last requirement of assumption (A1) is not satisfied. However, unless there are side-channel attacks, our security proof has following practical advantages to source imperfections. We emphasize that for the security proof, we do not make any assumptions on phase modulations. That is, the precise control over the phase modulation and its characterization are not needed. We also emphasize that we do not make the single-mode assumption on the pulses, and the optical mode of the emitted pulse can depend on the bit \(b_i^A\). This includes, for example, the case where the state of the pulse when \(b_i^A\) = 0 (1) is horizontal (vertical) polarization state. Our framework covers the original DPS protocol24 using coherent states {|α〉, |−α〉}. In this case, qn in Eq. (3) is obtained through a priori Poissonian assumption. We note that the previous security proofs25,26 of the DPS protocol have assumed ideally phase modulated single-mode coherent states {|α〉, |−α〉} with block-wise phase randomization, which is removed in our analysis.
Next, we list up the assumptions on Bob’s measurement as follows. Note that to fulfill the last requirement of (B2), one may need to adopt proper countermeasures against attacks on the detectors such as blinding attack5 or time-shift attacks.4
-
(B1)
Bob uses a one-bit delay Mach–Zehnder interferometer with two 50:50 beam splitters (BSs) and with its delay being equal to the interval of the neighboring emitted pulses.
-
(B2)
After the interferometer, the pulses are detected by two photon-number-resolving (PNR) detectors, which can discriminate the vacuum, a single-photon, and two or more photons of a specific optical mode. A click event of each detector corresponds to bit values of 0 and 1, respectively. We suppose that the quantum efficiencies and dark countings are the same for both detectors.
In Bob’s measurement, the jth (1 ≤ j ≤ 2) time slot is defined as an expected detection time at Bob’s detectors from the superposition of the jth and (j + 1)th incoming pulses. Also, the 0th (3rd) time slot is defined as an expected detection time at Bob’s detectors from the superposition of the 1st (3rd) incoming pulse and the 3rd incoming pulse in the previous block (1st incoming pulse in the next block).
Protocol
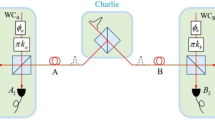
Before presenting our DPS protocol, we summarize in Table 1 the differences in our DPS protocol from the original one.24 The protocol runs as follows. In its description, |κ| denotes the length of a bit sequence κ. Figure 1 depicts a protocol with a coherent laser source, which is one possible implementation within our security framework.
-
(P1)
Alice chooses a random three-bit sequence \(\vec b_A\) and sends three pulses in a state \(\hat \rho _S^{\vec b_A}\) to Bob via a quantum channel.
-
(P2)
Bob receives an incoming three pulses and puts them into the Mach-Zehnder interferometer followed by photon detection by using the PNR detectors. We call the event detected if Bob detects exactly one photon in total among the 1st and 2nd time slots. The detection event at the jth (1 ≤ j ≤ 2) time slot determines the raw key bit kB ∈ {0, 1}. If Bob does not obtain the detected event, Alice and Bob skip steps (P3) and (P4) below.
-
(P3)
Bob announces the detected time slot j over an authenticated public channel.
-
(P4)
Alice calculates her raw key bit \(k_A = b_j^A \oplus b_{j + 1}^A\).
-
(P5)
Alice and Bob repeat (P1)–(P4) Nem times.
-
(P6)
Alice randomly selects a small portion of her raw key for random sampling. Over the authenticated public channel, Alice and Bob compare the bit values for random sampling and obtain the bit error rate ebit among the sampled bits. This gives the estimate of the bit error rate in the remaining portion.
-
(P7)
Alice and Bob respectively define their sifted keys κA and κB by concatenating their remaining raw keys.
-
(P8)
Bob corrects the bit errors in κB to make it coincide with κA by sacrificing |κA|fEC bits of encrypted public communication from Alice by consuming the same length of a pre-shared secret key.
-
(P9)
Alice and Bob conduct privacy amplification by shortening their keys by |κA|fPA to obtain the final keys.
In this paper, we only consider the secret key rate in the asymptotic limit of an infinite sifted key length. We consider the limit of Nem → ∞ while the following observed parameters are fixed:
One possible implementation of the protocol within our security framework. At Alice’s site, coherent laser pulse trains are generated by a conventional laser source followed by the phase modulator (PM) that randomly modulates a phase 0 or π. At Bob’s site, each pulse train is fed to a one-bit delay Mach–Zehnder interferometer with two 50:50 beam splitters (BSs). The pulse trains leaving the interferometer are measured by two photon-number-resolving (PNR) detectors corresponding to bit values “0” and “1”. A successful detection event occurs if Bob detects a single-photon in total among the 1st and 2nd time slots. We emphasize that the use of a coherent laser source and precise control over PM are one of the examples of the implementations, and we can use any source as long as it satisfies assumptions (A1)–(A3)
Security proof
Here, we summarize the security proof of the actual protocol described above and determine the fraction of privacy amplification fPA in the asymptotic limit. The proof is detailed in Methods section. Our proof is based on the security proof26 of the DPS protocol with block-wise phase randomization that employs complementarity.30 A major difference between our proof and the previous proof26 is that we do not assume block-wise phase randomization. If block-wise phase randomization is performed, the state of each single-block can be seen as a classical mixture of the total photon number state. This phase randomization simplifies the security proof because the amount of privacy amplification |κA|fPA can be estimated separately for each photon number emission. However, under our assumptions (A1)–(A3), a phase coherence generally exists among blocks, and the state of each single-block cannot be regarded as a classical mixture of photon number states. Therefore, we need to take into account this phase coherence in proving the security. In our security proof, the central task is to derive the information increase due to this phase coherence among the blocks.
For the security proof with complementarity, we consider alternative procedures for Alice’s state preparation in step (P1) and the calculation of her raw key bit kA in step (P4). We can employ these alternative procedures to prove the security of the actual protocol because Alice’s procedure of sending optical pulses, and producing the final key is identical to the actual protocol. Also, Bob’s procedure of receiving the pulses and making his public announcement j (for each round) in the actual protocol is identical to the corresponding procedure in the alternative protocol.
As for Alice’s state preparation in step (P1), she alternatively prepares three auxiliary qubits in system A1A2A3, which remain at Alice’s site during the whole protocol, and the three pulses (system S) to be sent, in the following state:
Here, \(\hat H: = 1/\sqrt 2 \mathop {\sum}\nolimits_{x,y = 0,1} {( - 1)^{xy}} |x\rangle \langle y|\) is the Hadamard operator, and \(|{\psi _{b_i^A}}\rangle _{S_iR_i}\) is a purification of \(\hat \rho _{S_i}^{b_i^A}\), namely, \({\mathrm{tr}}_{R_i}| {\psi _{b_i^A}}\rangle \langle {\psi _{b_i^A}} |_{S_iR_i} = \hat \rho _{S_i}^{b_i^A}\). Note from the assumption (A1) that system Ri is assumed to be possessed by Alice.
As for the calculation of the raw key bit kA in step (P4), this bit can be alternatively extracted by applying the controlled-not (CNOT) gate on the jth and (j + 1)th auxiliary qubits with the jth one being the control and the (j + 1)th one being the target followed by measuring the jth auxiliary qubit in the X-basis. Here, we define the Z-basis states for the jth auxiliary qubit as \(\{ {\left| 0 \right\rangle _{A_j},\left| 1 \right\rangle _{A_j}}\}\), and the CNOT gate \(\hat U_{{\mathrm{CNOT}}}^{(j)}\) is defined on this basis by \(\hat U_{{\mathrm{CNOT}}}^{(j)}\left| x \right\rangle _{A_j}\left| y \right\rangle _{A_{j + 1}} = \left| x \right\rangle _{A_j}\left| {x + y\,{\mathrm{mod}}2} \right\rangle _{A_{j + 1}}\) with x, y ∈ {0, 1}. Also, the X-basis states are defined as {|+〉A_j, |−〉A_j} with \(\left| \pm \right\rangle _{A_j} =( {\left| 0 \right\rangle _{A_j} \pm \left| 1 \right\rangle _{A_j}} )/\sqrt 2\).
In order to discuss the security of the key κA, we consider a virtual scenario of how well Alice can predict the outcome of the measurement complementary to the one to obtain kA. In particular, we take the Z-basis measurement as the complementary basis, and we need to quantify how well Alice can predict its outcome zj ∈ {0, 1} on the jth auxiliary qubit. To enhance the accuracy of her estimation, Alice measures the (j + 1)th auxiliary qubit in the Z-basis after performing \(\hat U_{{\mathrm{CNOT}}}^{(j)}\) on the jth and (j + 1)th auxiliary qubits. As for Bob, instead of aiming at learning κA, he tries to guess the complementary observable zj to help Alice’s prediction. More specifically, Bob performs a virual measurement to learn which of the jth or (j + 1)th half pulse has a single-photon, whose information is sent to Alice. We define the occurrence of phase error to be the case where Alice fails her prediction of the complementary measurement outcome zj (see Eq. (21) for the explicit formula of the POVM element of obtaining a phase error). Let Nph denote the number of phase errors, namely, the number of wrong predictions of zj among |κA| trials. Suppose that the upper bound f(ωobs) on the number of phase errors is estimated as a function of ωobs which denotes all the experimentally available parameters Q, ebit in Eq. (4) and \(\{ q_n\} _{n = 1}^3\) in Eq. (3). In the asymptotic limit considered here, a sufficient amount of privacy amplification is given by30
where h(x) is defined as \(h(x) = - x\log _2x - (1 - x)\log _2(1 - x)\) for 0 ≤ x ≤ 0.5 and h(x) = 1 for x > 0.5. Then, the secret key rate (per pulse) is given by
The quantity \(e_{{\mathrm{ph}}}^{\mathrm{U}}: = f(\omega _{{\mathrm{obs}}})/|{\boldsymbol{\kappa }}_A|\) in Eq. (7) is the upper bound on the phase error rate eph := Nph/|κA|. Our main result, Theorem 1, derives \(e_{{\mathrm{ph}}}^{\mathrm{U}}\) with experimentally available parameters Q, ebit and \(\{ q_n\} _{n = 1}^3\) (see Methods section for the proof).
Theorem 1
In the asymptotic limit of large key length |κA|, the upper bound on the phase error rate is given by
with \(\lambda = 3 + \sqrt 5\).
From this theorem and Eq. (7), the scaling of the key rate R with respect to the channel transmission η is estimated. If the protocol is implemented by a weak coherent laser pulse as a light source with its mean photon number μ, the detection rate Q is in the order of O(μη) and both \(\sqrt {q_1q_3}\) and q2 are in the order of O(μ2). To obtain a positive secret key rate, the upper bound on the phase error rate must be smaller than 0.5:
To maximize the key rate under this constraint, μ is decreased in proportion to η. Therefore, we find that the scaling of the key rate is in the order of R = O(μη) = O(η2).
Simulation of secure key rates
We show the simulation results of asymptotic key rate R per pulse given by Eq. (7) as a function of the overall channel transmission η (including detector efficiency). For simplicity of the simulation, we assume that each emitted pulse is a coherent pulse from a conventional laser with mean photon number μ. In this setting, qn in Eq. (3) is given by
We adopt fEC = h(ebit) and suppose the detection rate as Q = 2ημe−2ημ, where in the simulation we omit the cost of random sampling as its cost is negligible in the asymptotic limit. In Fig. 2, we plot the key rates for ebit = 0.01, ebit = 0.02 and ebit = 0.03 (from top to bottom). The key rates are optimized over μ for each value of η. The optimized values of μ when ebit = 0.02 is about 7 × 10−5 (with η = 10−2) and about 7 × 10−3 (with η = 1). From these lines, we see that all the key rates are proportional to η2. If we consider the overall channel transmission as \(\eta = 0.1 \times 10^{ - 0.2\ell /10}\) (with \(\ell\) denoting the distance between Alice and Bob) and laser diodes operating at 1 GHz repetition rate, we can generate a secure key at a rate of 170 bits s−1 for a channel length of 50 km and a bit error rate of 1%. Note that in Fig. 2, we assumed that the bit error rate is independent of channel transmission η. An η-dependence of the bit error stems from, for instance, the dark count of detectors. When dark count rate (Pdark) becomes compatible with Q, no key can be generated. For example, if Pdark = 10−7, Pdark becomes compatible with Q at η = 10−2, which can be found by substituting a typical value μ = 10−5 at η = 10−2.
Discussion
In this paper, we have provided the information-theoretic security proof of the DPS protocol based on simple source characterizations. Once one admits the commonly used assumption (A1) to be physically reasonable, our proof only requires the independence of the vacuum emission probability from a chosen bit, and the upper bounds \(\{ q_n\} _{n = 1}^3\) on the probabilities that a single-block contains at least n (n ∈ {1, 2, 3}) photons. Even with these experimentally simple assumptions, we demonstrated that we can generate a secret key at the rate of about 100 bits s−1 for inner-city QKD (\(\ell \sim 50\) km) given realistic bit error rate of 1–3%. Compared with the decoy-BB84 and the RRDPS protocols, the key rate and the achievable distance of our DPS protocol are limited. This is because the key-rate scaling of our protocol is in the order of O(η2), while the decoy-BB84 and the RRDPS protocols can achieve scaling of O(η).
We end with some open questions.
-
1.
As we have only provided the security analysis in the case of three pulses in a single-block, we leave the question about the optimal number of pulses contained in a single-block.
-
2.
In a practical perspective, it is important to refine our proof to achieve an improved key rate. The DPS protocol has no limitations on surpassing the key rate scaling of O(η2). Indeed, the DPS protocol with block-wise phase randomization25,26 can achieve the order of \(O(\eta ^{\frac{3}{2}})\) in a low bit error rate regime when the block size is larger than three. It is an interesting question whether the minimal assumptions adopted in this paper is enough or we need to make additional assumptions to achieve the same improved scaling.
-
3.
It is an interesting problem to construct a secure coherent-state-based DPS protocol combined with measurement-device-independent setting.31
-
4.
As for Alice’s side, it is interesting to extend our security proof by relaxing the assumption (A2) to the case where the vacuum emission probability is different \({\mathrm{tr}}\hat \rho _{S_i}^0|{\mathrm{vac}}\rangle \langle {\mathrm{vac}}|\, \ne\, {\mathrm{tr}}\hat \rho _{S_i}^1|{\mathrm{vac}}\rangle \langle {\mathrm{vac}}|\), and Alice only knows the bounds on \({\mathrm{tr}}\hat \rho _{S_i}^0|{\mathrm{vac}}\rangle \langle {\mathrm{vac}}|\) and \({\mathrm{tr}}\hat \rho _{S_i}^1|{\mathrm{vac}}\rangle \langle {\mathrm{vac}}|\).
-
5.
As for Bob’s measurement unit, it is important to relax the assumption (B2) to allow the use of threshold detectors. One can extend our proof to the use of threshold detectors by following the same argument done in the paper.32 To extend our proof with these detectors, we need to upper-bound the rate of detection events where two or more photons are received by Bob. This can be done by monitoring the number of double-click events occurring in a single-block of pulses. To estimate this quantity, an optical shutter needs to be placed in a long arm of the Mach–Zehnder interferometer.
Methods
Outline
Here we prove our main result, Theorem 1. First, we introduce notations that we use in the following discussions. Second, we introduce the POVM (positive operator valued measure) elements corresponding to a bit and phase error. Third, we explain the relation between the Z-basis measurement outcome (zj) on the auxiliary qubit system Aj and the number of photons contained in the jth emitted pulse. Finally, we prove Theorem 1 by using two lemmas, Lemmas 1 and 2. We leave the proofs of Lemmas 1 and 2 to Sections I and II in the Supplementary Information, respectively.
Notations
We first summarize the notations that we use in the following discussions:
for a vector |ψ〉 that is not necessarily normalized, and the Kronecker delta
Furthermore, we introduce the Z-basis states of Alice’s auxiliary qubit system A as
with z = z1z2z3 and zi ∈ {0, 1}, and wt(z) denotes the Hamming weight of a bit string z:
Let us define the projectors \(\hat P_a\) (with 0 ≤ a ≤ 3), \(\hat P_{{\mathrm{even}}}\) and \(\hat P_{{\mathrm{odd}}}\) as
POVM element for a detected event
We introduce POVM elements for Bob’s procedure of determining the detected time slot j and the bit value kB. Based on the following procedure, Bob can determine whether the event is detected or not prior to determining j and kB. Bob sends the first pulse to the first BS in Fig. 1, and after the first pulse is split, one of the pulses goes to the long arm of the Mach–Zehnder interferometer, and we call it first half pulse. Bob keeps the second pulse as it is, and sends the third pulse to the first BS. After the third pulse is split at the first BS, one of the pulses goes to the short arm of the Mach–Zehnder interferometer (we call it the third half pulse). Bob then performs the quantum nondemolition (QND) measurement of the total photon number among the first half pulse, the third half pulse and the second pulse. The detected event is equivalent to an event where the QND measurement reveals exactly one photon. If the detected event occurs, the state of the three pulses after the QND measurement is in the subspace spanned by the orthonormal basis \(\left\{ {\left| {i_B} \right\rangle } \right\}_{i = 1}^3\) with i representing the position of the single-photon (at the half pulse when i = 1, 3 and at the original pulse when i = 2). Given the detection, the POVM elements \(\left\{ {\hat {\Pi}_{j,k_B}} \right\}_{j,k_B}\) for detecting the bit kB at the jth time slot (1 ≤ j ≤ 2) is given by
with
where w1 = w3 = 1 and w2 = 1/2.
Bit- and phase-error POVM elements
Here, we construct the bit- and phase-error POVM elements \(\hat e_{{\mathrm{bit}}}\) and \(\hat e_{{\mathrm{ph}}}\), respectively. Alice and Bob measure their systems A and B just after the QND measurement reveals exactly one photon to learn whether a bit error or phase error exists. Importantly, these POVM elements are defined only on Alice’s auxiliary qubit system A and Bob’s system B, and the assumptions on the encoded states in system S do not come into their description. Therefore, even if the assumptions on Alice’s emitted states are different from those in the security proof26 of the DPS protocol with block-wise phase randomization, the same formulas of the bit- and phase-error POVM elements in26 can be used. Here, we only provide brief explanations of how to construct \(\hat e_{{\mathrm{bit}}}\) and \(\hat e_{{\mathrm{ph}}}\), and refer details to ref. 26
First, we introduce the POVM element \(\hat e_{{\mathrm{bit}}}^{\,j}\) corresponding to announcing the jth time slot and the occurrence of a bit error. As a bit error occurs when kA (Alice’s X-basis measurement outcome of the jth auxiliary qubit after performing \(\hat U_{{\mathrm{CNOT}}}^{(j)}\) on the jth and (j + 1)th ones) and Bob’s measurement outcome kB are different, \(\hat e_{{\mathrm{bit}}}^{\,j}\) is given by
Here and henceforth, we omit identity operators on subsystems, such as those for Alice’s irrelevant auxiliary qubits in the above equation. Equation (18) is re-expressed as
This equation shows that there are no cross terms between even parity terms (\(\left| {z_jz_{j + 1}} \right\rangle _{A_jA_{j + 1}}\) with zj + zj+1 is even) and odd parity terms (\(\left| {z_jz_{j + 1}} \right\rangle _{A_jA_{j + 1}}\) with zj + zj+1 is odd). Therefore, we have
This equation can be derived more intuitively. The parity of wt(z) can be determined by measuring the auxiliary qubits in the Z-basis except for the jth one after performing \(\hat U_{{\mathrm{CNOT}}}^{(j)}\) on the jth and (j + 1)th qubits. This implies that the measurement \(\{ \hat P_{{\mathrm{even}}},\hat P_{{\mathrm{odd}}}\}\) and \(\hat e_{{\mathrm{bit}}}^{\,j}\) commute, and hence we obtain Eq. (20). Equation (20) plays an important role in proving Theorem 1.
Second, we introduce the POVM element \(\hat e_{{\mathrm{ph}}}^{\,j}\) corresponding to announcing the jth time slot and the occurrence of a phase error. A phase error event is defined as an event where Alice fails her prediction of the Z-basis measurement outcome zj on the jth auxiliary qubit. To enhance the accuracy of her estimation, she measures the (j + 1)th auxiliary qubit in the Z basis (with zj+1 denoting its result) after performing \(\hat U_{{\mathrm{CNOT}}}^{(j)}\), and Bob measures system B to learn which of the jth or (j + 1)th pulse has a single-photon. With the help of information of zj+1 and Bob’s information, Alice adopts the following strategy for predicting zj. As for the case of zj+1 = 1, if Bob reveals that the jth [(j + 1)th] pulse has a single-photon, Alice predicts zj = 1 [zj = 0]. On the other hand, if zj+1 = 0, Alice predicts zj = 0 regardless of Bob’s information. The phase error event is defined as an instance of a wrong prediction of zj, and the POVM element corresponding to announcing the jth time slot and the occurrence of a phase error is represented by
Since \(\hat e_{{\mathrm{ph}}}^{\,j}\) is diagonal in the basis |z〉A, we have
Then, by taking the sum over all the time slots, we obtain the bit and phase error operators as
It follows that the probability of having a bit error is given by \({\mathrm{tr}}\hat \sigma \hat e_{{\mathrm{bit}}}\), and the one of having a phase error is \({\mathrm{tr}}\hat \sigma \hat e_{{\mathrm{ph}}}\). Here, \(\hat \sigma\) denotes a state of Alice and Bob’s systems A and B just after the QND measurement reveals exactly one photon.
Relation between wt(z) and n block
Here, we derive the relation between wt(z) and nblock. For this, we first derive the number of photons (nj) contained in system Sj when zj = 1. Recall that the assumption (A2) guarantees that \({\mathrm{tr}}\hat \rho _{S_j}^0|{\mathrm{vac}}\rangle \langle {\mathrm{vac}}| = {\mathrm{tr}}\hat \rho _{S_j}^1|{\mathrm{vac}}\rangle \langle {\mathrm{vac}}| = :P_j^{{\mathrm{vac}}}\). From this assumption, by expanding the orthonormal basis of Sj with the photon number states, \(\left| {\psi _0} \right\rangle _{S_jR_j}\) (a purification of \(\hat \rho _{S_j}^0\)) and \(\left| {\psi _1^\prime } \right\rangle _{S_jR_j}\) (a purification of \(\hat \rho _{S_j}^1\)) can be written as
Here, |u0〉, |u1〉, |v0〉 and |v1〉 are normalized vectors of system Rj, and \(P_{j,b_j^A}^1: = {\mathrm{tr}}\hat \rho _{S_j}^{b_j^A}|1\rangle \langle 1|\). Since a purification has a freedom of choosing a unitary operator \(\hat U\) on system Rj, the following state \(\left| {\psi _1} \right\rangle _{S_jR_j}\) is also a purification of \(\hat \rho _{S_j}^1\):
In the following discussions, \(\hat U\) is chosen such that \(\hat U|v_0\rangle = |u_0\rangle\) holds. Note from Eq. (5) that if zj = 1, the jth state can be written as \(\left| {{\mathrm{\Phi }}_ - } \right\rangle _{S_jR_j}: = \left( {\left| {\psi _0} \right\rangle _{S_jR_j} - \left| {\psi _1} \right\rangle _{S_jR_j}} \right)/{\mathcal{N}}\), where \({\mathcal{N}}\) is an appropriate normalization constant. Using Eqs. (24) and (26) gives the vacuum emission probability of \(\left| {{\mathrm{\Phi }}_ - } \right\rangle _{S_jR_j}\) as
This equation means that if zj = 1, the state in system Sj contains at least one photon. That is,
Therefore, we obtain
and from Eq. (3), the following inequality holds
Proof of Theorem 1
Here, we prove Theorem 1 in the main text. For this, we first find an upper-bound on the phase error probability \({\mathrm{tr}}\hat e_{{\mathrm{ph}}}\hat \sigma\) in terms of the bit error probability \({\mathrm{tr}}\hat e_{{\mathrm{bit}}}\hat \sigma\), which holds for any state \(\hat \sigma\). According to Eq. (21), since \(\hat e_{{\mathrm{ph}}}\) is diagonalized in the basis |z〉A and \(\hat P_0\hat e_{{\mathrm{ph}}}\hat P_0 = 0\), we have
To upper-bound \({\mathrm{tr}}\hat P_1\hat e_{{\mathrm{ph}}}\hat P_1\hat \sigma\) with experimentally available data, we employ the following Lemmas 1 and 2 (see Sections I and II in the Supplementary Information for their proofs).
Lemma 1
with \(\lambda : = 3 + \sqrt 5\).
Lemma 2
For any density operator \(\hat \sigma\),
Applying Lemmas 1 and 2 to Eq. (31) leads to
With the relation between the bit and phase error probabilities, the next step is to derive an upper bound on the number of phase errors with experimentally available data. For this, we use Azuma’s inequality33 to achieve this goal. Suppose that there are Ndet detected systems AB, and Alice and Bob sequentially measure each detected state in order. Let us consider the following specific way for choosing the sampled bits among the detected events; Alice probabilistically associates each detected event with a sample pair with probability 1 − t or a code pair with probability t, where 0 < t < 1. The sample pairs are employed for random sampling to obtain ebit whereas the code pairs are for distilling secret key. For each code (sample) pair, Alice and Bob measure their systems to learn whether a phase (bit) error occurs or not. If a code (sample) pair entails a phase (bit) error, we call such an event “ph” (“bit”), otherwise we call “\(\overline {{\mathrm{ph}}}\)” (“\(\overline {{\mathrm{bit}}}\)”). Also, for each code pair, Alice measures her system A in the Z-basis to obtain the outcome wt(z) = a ∈ {0, 1, 2, 3}. Such simulataneous measurements are allowed because \([\hat e_{{\mathrm{ph}}},\hat P_a] = 0\) holds for any a (0 ≤ a ≤ 3). In this stochastic trial, the set of the measurement outcomes for each detected event is given by \({\mathcal{S}}: = \{ {\mathrm{bit}},\overline {{\mathrm{bit}}} \} \cup (\mathop {\bigcup}\nolimits_{a = 0}^3 {\{ {\mathrm{ph}} \wedge a\} } ) \cup (\mathop {\bigcup}\nolimits_{a = 0}^3 {\{ \overline {{\mathrm{ph}}} \wedge a\} } )\), and let \(\xi ^i \in {\mathcal{S}}\) denote the ith measurement outcome with 1 ≤ i ≤ Ndet.
Next, let us introduce various parameters that are needed in later discussions. The phase error rate in the code pair and the bit error rate in the sample pair are defined as
where Ncode and Nsample respectively denote the number of code and sample pairs. We define the number \(N_\Omega ^l\) of events that take \({\mathrm{\Omega }} \in {\mathcal{S}}\) among l trials as
and the sum \(P_{\mathrm{\Omega }}^l\) of probabilities of obtaining Ω at the ith trial conditioned on the previous outcomes \(\left\{ {\xi ^k} \right\}_{k = 0}^{i - 1}\) with ξ0 being constant as
We can show that the sequence of random variables \(\{ X_\gamma ^0, \ldots ,X_\gamma ^{N_{\mathrm{det}}}\}\) (with γ ∈ {ph, bit, a}), which are defined as
and \(X_\gamma ^0: = 0\), satisfies the Martingale condition with respect to random variables \(\{ \xi ^0,\xi ^1,...,\xi ^{N_{\mathrm{det}}}\}\), that is ∀l, \(E[X_\gamma ^l|\{ \xi ^k\} _{k = 0}^{l - 1}] = X_\gamma ^{l - 1}\). Here, E[X|Y] denotes the expectation of X conditioned on Y. Also, \(\{ X_\gamma ^0,...,X_\gamma ^{N_{\mathrm{det}}}\}\) satisfies a bounded difference condition, namely, ∀l, \(|X_\gamma ^l - X_\gamma ^{l - 1}| \le 1\). Once Martingale and the bounded difference conditions are satisfied, we can apply Azuma’s inequality; it follows that ∀ζ > 0 and ∀Ndet > 0
Since Eq. (34) holds for any \(\hat \sigma\), by using Cauchy–Schwarz inequality: \(\mathop {\sum}\nolimits_{i = 1}^m {x_iy_i} \le \sqrt {\left( {\mathop {\sum}\nolimits_{i = 1}^m {x_i^2} } \right)\left( {\mathop {\sum}\nolimits_{i = 1}^m {y_i^2} } \right)}\), we have
where \(\tilde P_{{\mathrm{ph}}}^{N_{{\mathrm{det}}}}: = \mathop {\sum}\nolimits_{a = 0}^3 {P_{{\mathrm{ph}} \wedge a}^{N_{{\mathrm{det}}}}}\) and \(\tilde P_a^{N_{{\mathrm{det}}}}: = P_{{\mathrm{ph}} \wedge a}^{N_{{\mathrm{det}}}} + P_{\overline {{\mathrm{ph}}} \wedge a}^{N_{{\mathrm{det}}}}\).
By employing the consequence of Azuma’s inequality in Eq. (41) to each of all the five sums of conditional probabilities in Eq. (42), we obtain
where \(\tilde N_{{\mathrm{ph}}}^{N_{{\mathrm{det}}}}: = \mathop {\sum}\nolimits_{a = 0}^3 {N_{{\mathrm{ph}} \wedge a}^{N_{{\mathrm{det}}}}}\) and \(\tilde N_a^{N_{{\mathrm{det}}}}: = N_{{\mathrm{ph}} \wedge a}^{N_{{\mathrm{det}}}} + N_{\overline {{\mathrm{ph}}} \wedge a}^{N_{{\mathrm{det}}}}\). When Ndet gets larger with any fixed ζ > 0, the probability of violating Eq. (43) decreases exponentially. Here and henceforth, we consider the limit of large Ndet and neglect ζ. In this asymptotic limit, as Ncode → tNdet and Nsample → (1 − t)Ndet in Eq. (35), we obtain
The last task for deriving the upper bound on eph is to upper-bound \(\tilde N_{a \ge n}^{N_{{\mathrm{det}}}}\) with experimentally available data. In so doing, in addition to the detected instances, we assume that Alice and Bob randomly associate each of the non-detected instances with a code instance with probability t or a sample instance with probability 1 − t. Then, we have that the the number \(\tilde N_{a \ge n}^{N_{{\mathrm{det}}}}\) of obtaining the outcome a ≥ n among the detected instances can never be larger than the one \(M_{a \ge n}^{N_{{\mathrm{em}}}}\) among the emitted code blocks. Since the probability of obtaining a code pair and the outcome a ≥ n when Alice emits the ith block is upper-bounded by qn according to Eq. (30), we can imagine independent trials with probability qn. Therefore, we can use Chernoff bound and obtain
When the number Nem of emitted blocks gets larger for any fixed χ > 0, the probability of violating this inequality decreases exponentially. In the condition of asymptotic limit of Nem, we neglect χ in the following discussions. By substituting Eq. (45) to (44), we finally obtain
This ends the proof of Theorem 1.
Data availability
No datasets were generated or analyzed during the current study.
References
Lo, H.-K., Curty, M. & Tamaki, K. Secure quantum key distribution. Nat. Photonics 8, 595 (2014).
Sajeed, S. et al. Attacks exploiting deviation of mean photon number in quantum key distribution and coin tossing. Phys. Rev. A 91, 032326 (2015).
Sun, S.-H. et al. Effect of source tampering in the security of quantum cryptography. Phys. Rev. A 92, 022304 (2015).
Zhao, Y., Fung, C.-H. F., Qi, B., Chen, C. & Lo, H.-K. Quantum hacking: experimental demonstration of time-shift attack against practical quantum-key-distribution systems. Phys. Rev. A 78, 042333 (2008).
Lydersen, L. et al. Hacking commercial quantum cryptography systems by tailored bright illumination. Nat. Photonics 4, 686 (2010).
Gerhardt, I. et al. Full-field implementation of a perfect eavesdropper on a quantum cryptography system. Nat. Commun. 2, 349 (2011).
Diamanti, E., Lo, H.-K., Qi, B. & Yuan, Z. Practical challenges in quantum key distribution. npj Quantum Inf. 2, 16025 (2016).
Arnon-Friedman, R., Dupuis, F., Fawzi, O., Renner, R. & Vidick, T. Practical device-independent quantum cryptography via entropy accumulation. Nat. Commun. 9, 459 (2018).
Bennett, C. H., Brassard, G. & Mermin, N. D. Quantum cryptography without Bell’s theorem. Phys. Rev. Lett. 68, 557 (1992).
Bennett, C. H. & Brassard, G. Quantum cryptography: public-key distribution and coin tossing. Proc. IEEE Int. Conference on Computers, Systems, and Signal Processing pp. 175–179. (IEEE, NY, Bangalore, India, 1984).
Shor, P. W. & Preskill, J. Simple Proof of Security of the BB84 Quantum Key Distribution Protocol. Phys. Rev. Lett. 85, 441 (2000).
Tomamichel, M., Lim, C. C. W., Gisin, N. & Renner, R. Tight finite-key analysis for quantum cryptography. Nat. Commun. 3, 634 (2012).
Tomamichel, M. & Leverrier, A. A largely self-contained and complete security proof for quantum key distribution. Quantum 1, 14 (2017).
Lim, C. C. W., Curty, M., Walenta, N., Xu, F. & Zbinden, H. Concise security bounds for practical decoy-state quantum key distribution. Phys. Rev. A 89, 022307 (2014).
Hwang, W.-Y. Quantum key distribution with high loss: toward global secure communication. Phys. Rev. Lett. 91, 057901 (2003).
Wang, X.-B. Beating the photon-number-splitting attack in practical quantum cryptography. Phys. Rev. Lett. 94, 230503 (2005).
Lo, H.-K., Ma, X.-F. & Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 94, 230504 (2005).
Cao, Z., Zhang, Z., Lo, H.-K. & Ma, X. Discrete-phase-randomized coherent state source and its application in quantum key distribution. New J. Phys. 17, 053014 (2015).
Yoshino, K. et al. Quantum key distribution with an efficient countermeasure against correlated intensity fluctuations in optical pulses. npj Quantum Inf. 4, 8 (2018).
Tamaki, K., Curty, M., Kato, G., Lo, H.-K. & Azuma, K. Loss-tolerant quantum cryptography with imperfect sources. Phys. Rev. A 90, 052314 (2014).
Mizutani, A. et al. Quantum key distribution with setting-choice-independently correlated light sources. npj Quantum Inf. 5, 8 (2019).
Sasaki, T., Yamamoto, Y. & Koashi, M. Practical quantum key distribution protocol without monitoring signal disturbance. Nature 509, 475 (2014).
Mizutani, A., Imoto, N. & Tamaki, K. Robustness of the round-robin differential-phase-shift quantum-key-distribution protocol against source flaws. Phys. Rev. A 92, 060303 (2015).
Inoue, K., Waks, E. & Yamamoto, Y. Differential-phase-shift quantum key distribution using coherent light. Phys. Rev. A 68, 022317 (2003).
Tamaki, K., Kato, G. & Koashi, M. Unconditional security of coherent-state-based differential phase shift quantum key distribution protocol with block-wise phase randomization. arXiv:1208.1995v1 (2012).
Mizutani, A., Sasaki, T., Kato, G., Takeuchi, Y. & Tamaki, K. Information-theoretic security proof of differential-phase-shift quantum key distribution protocol based on complementarity. Quantum Sci. Technol. 3, 014003 (2017).
Koashi, M. & Preskill, J. Secure quantum key distribution with an uncharacterized source. Phys. Rev. Lett. 90, 057902 (2003).
Kumazawa, M., Sasaki, T. & Koashi, M. Rigorous characterization method for photon-number statistics. Opt. Express 27, 5297 (2019).
Gisin, N., Fasel, S., Kraus, B., Zbinden, H. & Ribordy, G. Trojan-horse attacks on quantum-key-distribution systems. Phys. Rev. A 73, 022320 (2006).
Koashi, M. Simple security proof of quantum key distribution based on complementarity. New J. Phys. 11, 045018 (2009).
Lo, H.-K., Curty, M. & Qi, B. Measurement-device-independent quantum key distribution. Phys. Rev. Lett. 108, 130503 (2012).
Sasaki, T. & Koashi, M. A security proof of the round-robin differential phase shift quantum key distribution protocol based on the signal disturbance. Quantum Sci. Technol. 2, 024006 (2017).
Azuma, K. Weighted sums of certain dependent random variables. Tohoku Math. J. 19, 357 (1967).
Acknowledgements
T.S. thanks the support from JSPS KAKENHI Grant Number JP18K13469. K.T. thanks the support from JSPS KAKENHI Grant Numbers JP18H05237 and JST-CREST JPMJCR 1671. This work was in part supported by Cross-ministerial Strategic Innovation Promotion Program (SIP) (Council for Science, Technology and Innovation (CSTI)).
Author information
Authors and Affiliations
Contributions
A.M., T.S., Y.T., K.T., and M.K. contributed to the initial conception of the ideas, to the working out the details, and to the writing up the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mizutani, A., Sasaki, T., Takeuchi, Y. et al. Quantum key distribution with simply characterized light sources. npj Quantum Inf 5, 87 (2019). https://doi.org/10.1038/s41534-019-0194-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-019-0194-3