Abstract
Traditional ghost imaging requires correlated but spatially separated photons and has been observed in many physical situations, spanning both the quantum and classical regimes. Here we observe ghost imaging in a new system—a system based on entanglement swapping, the key feature of a quantum network. We detail how the exact form of quantum interference between independent photons dictates the precise nature of the ghost imaging, for example, for an anti-symmetric projection, the recorded image is the contrast-reversed version of the object—where the object is bright, the image is dark, and vice versa. The results highlight the importance of state projection in this ghost-imaging process and provide a pathway for the teleportation of two-dimensional spatial states across a quantum network. Our results also indicate that ghost images with new image properties could be achieved in conventional settings through a variety of new signal processing procedures.
Similar content being viewed by others
Introduction
Information protocols based on photonic states of light are of significant interest in quantum and classical science. The multiple degrees of freedom, for example, spatial, frequency, polarization and the high-dimensional nature of light provide access to a large alphabet in which to encode information.1,2,3 The increased information capacity provides the ability to communicate at high data rates and provides mechanisms to test quantum fundamentals.4 However, an ongoing challenge is the exact generation, precise manipulation and efficient detection of such states of light.
In the context of quantum networks bases on photonic states of light, the challenge is to distribute quantum information over large distances in an efficient manner. At the core of a quantum network is a process known as entanglement swapping, which relies on a Bell-state measurement. Entanglement swapping5 generates correlations between systems that have not interacted and has been observed in many degrees of freedom, for example, polarisation6 and orbital angular momentum,7 and can also be used for quantum teleportation of multiple degrees of freedom.8 One protocol that requires correlations is ghost imaging, and while it is now known that ghost imaging only requires correlations in one basis, the implications of entanglement swapping on such a process remain unknown.
The term “ghost imaging” arose only in 1995 in the context of studying EPR correlations in position and momentum.9 It was noted that the position correlations of an entangled photon pair generated by means of spontaneous parametric down-conversion (SPDC) could be used in an imaging experiment, as shown in Fig. 1a. In a conventional ghost-imaging experiment, the photon in the object arm is detected with a “bucket” detector with no spatial resolution so that the object information is erased, while the photon in the other arm, which has never interacted with the object, is collected with a spatially resolved detector (camera or scanning system). Consequently, when the photons are measured in coincidence, the spatial correlations allow image reconstruction. Since this seminal work, many manifestations of the above have been realised, including the use of thermal light,10,11,12 momentum correlated ghost imaging,13 spiral ghost imaging with orbital angular momentum,14,15 time domain ghost imaging,16 computational and compressive ghost imaging,17,18 and the use of non-degenerate SPDC for dual wavelength ghost imaging.19,20
Two- and four-photon ghost imaging, using entangled photon pairs. a Two-photon ghost imaging using photon pairs generated by parametric down-conversion. b Four-photon ghost imaging showing contrast inversion. In the four-photon case, two pairs of photons are generated in two independent parametric down-conversion processes. The state of the photons A and D becomes entangled when photons B and C undergo a Bell-state measurement. Contrast reversal of the object is observed when photons B and C are projected onto the anti-symmetric state
In this work we combine the essential tools of quantum networking with high-dimensional quantum states of light and the core principles of ghost imaging. We provide a full theoretical analysis and experimental evidence of ghost imaging using two pairs of entangled photons. We demonstrate that the spatial state of non-interacting photons that were initially independent, that is, photons that have never interacted and start with no position or momentum correlations, can be used for ghost imaging. We employ entanglement swapping to establish the correlations needed to reconstruct a ghost image of an object.
We provide the first full theoretical analysis of this phenomenon and find that the Bell projection required for entanglement swapping plays a crucial role in the ghost-imaging outcome: projection onto the set of anti-symmetric states results in contrast inversion, whereas a projection onto the set of symmetric states results in conventional ghost imaging, that is, no contrast inversion. As a consequence, a projection onto all sets simultaneously, symmetric and anti-symmetric, results in no image at all. This is due to the inability to establish any spatial correlations between the two independent sources. Our work highlights a new form of ghost imaging using entanglement swapping and paves the way for long-distance image transfer across a quantum network.
Results
Consider the four-photon entanglement-swapped ghost-imaging set-up as shown schematically in Fig. 1b. This consists of two independent parametric down-conversion processes that generate two EPR states.13 Photon pairs A/B and C/D are initially entangled in their spatial degrees of freedom, so that the initial four-photon state in the position basis, |r〉, of dimension d is given by
Here the subscripts i and j denote positions at the two crystals, that is, ri is the position vector at the SPDC source for photons A/B and similarly for rj.
We now consider the state of photons in paths B and C, which are incident on a beamsplitter (BS). A coincidence in the two output paths of the BS projects onto the anti-symmetric states; the absence of a coincidence in the two output paths of the BS projects onto the symmetric states.21 In high dimensions (d > 2), there are a number of different orthogonal bases in which we can represent the state. The states that we consider are the Bell-like states \(\left\{ {\left| {{\mathrm{\Psi }}_{nm}^ \pm } \right\rangle _{{\mathrm{BC}}}} \right\}\) and {|Φn〉BC} defined below. The anti-symmetric states are
and the symmetric states are
with 1 ≤ n < m ≤ d. We do not consider the Bell-like states \(\left| {{\mathrm{\Phi }}_{n,m}^ \pm } \right\rangle _{{\mathrm{BC}}} = \frac{1}{{\sqrt 2 }}\left[ {|r_n\rangle _{\mathrm{B}}|r_n\rangle _{\mathrm{C}} \pm |r_m\rangle _{\mathrm{B}}|r_m\rangle _{\mathrm{C}}} \right]\) as they are not orthogonal to each other for d > 2, for example, \(\langle {\mathrm{\Phi }}_{1,2}^ + |{\mathrm{\Phi }}_{1,3}^ + \,\rangle\,\ne\, 0\). The probability to project the photons in path B and C onto an anti-symmetric state is (d − 1)/2d, whereas the probability to project the photons onto a symmetric state is (d + 1)/2d (see the Supplementary Information Theory for more details). Importantly, the projection onto the set of states \(\left\{ {\left| {{\mathrm{\Psi }}_{nm}^ \pm } \right\rangle _{{\mathrm{BC}}}} \right\}\) or {|Φn〉BC} leaves the photons in paths A and D in a mixture of all possible two-qubit entangled subspaces.7 It is only when one considers a single two-dimensional subspace that the state of the photons in paths A and D is pure.
The object corresponds to a transmission mask in path A, where the transmission O(i) at pixel position i is equal to either 1 or 0. The values {O(i)} contain all the information about the object. The impact of this mask is to modify the state of photon A such that \(\hat O|r_i\rangle _{\mathrm{A}} \to O(i)|r_i\rangle _{\mathrm{A}}\), and the total number of pixels in the mask with transmission equal to 1 is \(\mathop {\sum}\limits_i O (i) = \mathop {\sum}\limits_i {O^2(i)} = {\cal{B}}\).
The detection of a photon after the mask in path A combined with the different projections for the two photons in paths B and C can herald different states for photon D. This is the key to this ghost-imaging system: provided that a photon is detected at A, the state of photon D exhibits contrast reversal or not depending on the choice of projection in paths B and C.
We define our ghost images as the set of intensities \(\{ I_{\Psi ^ - }(i)\} ,\{ I_{\Psi ^ + }(i)\} ,\{ I_\Phi (i)\} ,\{ I_{{\mathrm{AS}}}(i)\}\) and {IS(i)}, where each I(i) corresponds to the probability of detecting the light at location i in path D for the different projections at B and C (AS = anti-symmetric, S = symmetric). We only make use of the position basis in the formation and detection of the object, and we disregard the phase information between the pixels. Therefore, at this stage, the information contained in the object can be treated classically. We could, however, choose to use the spatial light modulator (SLM) and single-mode fibre (SMF) for remote state preparation and then herald a qubit in path B, and the implications of this for quantum teleportation are discussed later.
Each I(i) can be measured by placing a transmission mask that lets light through at pixel i and blocks all other pixels. The intensities of the pixels of the images are given by
We see here that the contrast of the image formed from projections onto |Ψ−〉 and |Ψ+〉 is reversed with respect to that of the object, that is, bright pixels of the object will be measured as dark pixels in the image, and dark pixels of the object will be measured as bright pixels of the image. Note that a projection onto |Ψ−〉 is equivalent to the projection onto the anti-symmetric state. Using Eqs. (5)–(7), this gives a contrast of the images with respect to the initial object of
We see here that the contrasts of the images for the set of Ψ− and Ψ+ projections are reversed with respect to the original image, whereas the image for the set of Φ projections has the same contrast as the original. Note that the image contrast for the Φ projections is constant as the dimensionality increases, and the factor \(1/{\cal{B}}\) is present as we chose to measure the contrasts normalised with respect to the initial image. The factor \(1/{\cal{B}}\) is not present if we chose to normalise with respect the ghost image rather than the initial image, and the contrast is then equal to unity.
As the contrasts for the anti-symmetric and symmetric images are of opposite signs, if the two images are added together, a uniform intensity is a observed with zero contrast. This equivalent to performing no projection onto any particular state at BC and then measuring the ghost image. In this case, as one would expect, no image is observed as the independent photons AD will exhibit no correlations.
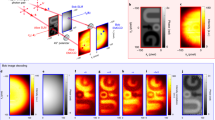
Figure 2 shows theoretically predicted ghost images for each of the different possible projections for the case of d = 100 and \({\cal{B}} = 20\). The image associated with the anti-symmetric projection (\(I_{\mathrm{AS}} = I_{{\mathrm{\Psi }}^ - }\)) exhibits contrast reversal with respect to the object. Note also that the sum of the images for the anti-symmetric and symmetric images is equal to a flat, constant value that contains no information. This is as expected from Eq. (10), as summing the anti-symmetric and symmetric projections at B and C corresponds to performing no particular projection, leaving no correlation between photons in paths A and D. Detailed analysis (see Supplementary Information Theory) shows that the sum of the conditional states ρAS and ρS in path D is proportional to the identity matrix and contains no information about the object in path A.
Predicted ghost images for different projections in path BC. a Three-dimensional representation of an object in a d = 100 dimension space with \({\cal{B}} = 20\). The transmission of each pixel is equal to zero or one. b–f Three-dimensional representations of the theoretically predicted images. The height of each pixel represents the probability of the signal. The anti-symmetric image (e) is equal to the image for the projection onto {|Ψ−〉BC} (b); the symmetric image (f) is equal to the sum of the images for the (c) {|Ψ+〉BC} and (d) {|Φ〉BC} projections
In our experiment realisation, we establish a four-photon experiment for entanglement swapping, using two BBO (β-barium borate) crystals to produce two pairs of entangled photons. We choose to project the photons in paths B and C onto the anti-symmetric state and, therefore, measure the images predicted by Eq. (5) and/or (7). We examine the behaviour of the system with a simple two-pixel (d = 2) image. We relay the crystal planes, which exhibit strong position correlations, onto two spatial light modulators (SLMs). We display an image on SLM A with one half “on” and one half “off”. On SLM D we display either the same image or the contrast-reversed image. We then measure the number of four-fold coincidences as we vary the path length difference between photons B and C. We see a Hong–Ou–Mandel (HOM) dip in the case where both SLMs have the same pattern on them, while the coincidences stay constant in the case where the SLMs have opposite patterns, (see Supplementary Information Results). This confirms contrast reversal for the anti-symmetric projection. The corresponding four-photon ghost-imaging results are shown in Fig. 3a–c, where we compare the object, theoretically predicted image and the experimentally observed image. It is clear that the image is contrast reversed with respect to the object. Positive and negative images have been observed algorithmically using thermal light,22,23 in a quantum interference experiment,24 and simulated by using thermal fermions.25
Contrast-reversed image measured in four-fold coincidence with an anti-symmetric projection. a–c d = 2 data and d–f d = 4 data. These images are normalised such that the sum of all the pixels in the image is unity. The total four-way counts for the d = 2 image were {45,175} counts in 90 min. The total four-way counts for the d = 4 image were {{168,191}, {98,227}} counts in 800 min
We also examine the case of a four-pixel image (d = 4), with the bottom left quarter of SLM A “on” and the remainder “off”. On SLM D we scan through one pixel at a time to obtain four measurements, which are then combined to determine the total image observed in photon D. As shown in Fig. 3d–f, we obtain a contrast-reversed image in photon D, albeit with a lower contrast than the d = 2 case.
The experimentally recorded images, Fig. 3c, f, clearly indicate contrast reversal of the image associated with the anti-symmetric projection in paths B and C. We choose \({\cal{B}} = 1\) in our experiment as this maximises the contrast in the image. Only in the case that \({\cal{B}} = 1\) is the corresponding pixel in the image theoretically equal to zero. The measured contrasts for these images are compared to the corresponding predictions in Fig. 4. We measure a contrast for the d = 2 case of −0.59 ± 0.13 and a contrast for the d = 4 case of −0.19 ± 0.15, which compare favourably to predicted contrast of −1.0 and −0.33, respectively. The errors are calculated assuming Poisson statistics on the measured count rates. Note that the data used in Fig. 3 is the raw data without any background subtraction applied, and any correction applied to the data will only serve to decrease the measured contrast and therefore increase the agreement between the measured and predicted values. With data processing and subtracting the anticipated four-way counts based on accidentals, the measured contrasts become −0.66 ± 0.13 and −0.26 ± 0.14 for the d = 2 and d = 4 cases respectively, in good agreement to the theory. The high contrast achieved in our experiment (Fig. 3) is because we use one pixel in the object as “on”. In higher dimensions and with more pixels used for the object, the contrast would be reduced, in line with Eq. (10).
Contrast as a function of dimension d for anti-symmetric projection. The data points correspond to the measured contrasts for the data in Fig. 3; the solid line is the theoretical prediction according to Eq. (10), considering \({\cal{B}} = 1\). The error bars are calculated assuming Poisson noise on the data. The blue points show the contrast calculated using the raw data; the red points show the contrast calculated with the background-subtracted data
Experimental set-up used to observe four-photon ghost imaging. The focal lengths of the lenses are marked in millimetres, that is, L100 corresponds to a lens of focal length 100 mm. BBO0: 0.5-mm-thick β-barium borate (BBO) crystal; BF1: two consecutive bandpass filters at 405 ± 5 nm; SF: 100-μm circular aperture; BBO1: 1-mm-thick BBO crystal; DM: dichroic mirror; BBO2: 1-mm-thick BBO crystal; LF: longpass filter, cutoff wavelength 750 nm; SLM: spatial light modulator; BF2: bandpass filter at 808 ± 1.5 nm; BF3: bandpass filter at 810 ± 10 nm; TS: translation stage; BS: non-polarising beamsplitter; SMF: single-mode fibre; MMF: multi-mode fibre; SPAD: single-photon avalanche diode
Discussion
In our experiment, we make use of quantum correlations and quantum interference between the independent photons. While we use the quantum nature of light to generate the correlations, we encode information and perform measurements in only one basis, namely, the position basis. It is well known that classical correlations are sufficient to perform ghost imaging,11,12 and therefore the traditional “classical vs. quantum” ghost-imaging question can be applied to our experiment.
Indeed, a classical analogue of our experiment would be possible and of significant interest. Such a realisation requires two independently correlated sources of light and a means to classically correlate two independent modes. The method in which the two modes are classically correlated results in a variety of possible ghost images, for example, images that are inverted, rotated and shifted. The precise form of these classically correlated images and their relative contrasts with respect to the initial object is an area of research that we are actively pursuing. One should note, however, that the method we use in this work to correlate the two modes is quantum in nature, and there is no obvious direct analogue to the projection onto anti-symmetric/symmetric states. Correlating bright modes in classical manner is possible, but very different to using quantum interference.
While a form of ghost imaging would be possible with a classical analogue of our experiment, the quantum teleportation of spatial states of light is one protocol that is only possible with our system. No classical ghost-imaging system would be able to perform quantum teleportation. The implications of our experiment for quantum teleportation are of significant interest due to the high-dimensional nature of spatial states and the corresponding restrictions of Bell-state measurements.26 To simplify our discussion, we first consider the implications for qubit teleportation and then consider the implications for qudits.
Quantum teleportation is defined as teleporting an unknown quantum state to a new location. An implementation of quantum teleportation only requires three photons, but it is conventional to start with a four-photon system such as the one outlined in our experiment. In the teleportation protocol, we use arm A to herald a single photon in arm B that we wish to teleport the state of to arm D. Depending on the outcome of the Bell-state measurement, a unitary operation is then required on the photon in path D in order to recover the teleported state.
A significant difference between the ghost-imaging and teleportation protocols is the SLM that was used to define the classical “object” in the ghost-imaging protocol is now used in combination with the SMF to remotely prepare a qubit: a quantum state given by |ψ〉 = α|0〉 + β|1〉. Here α and β are the complex coefficients of the pixel basis states, and they can be set by the parameters of the SLM. Detection of a particular photon mode in path A heralds the presence of the qubit to be teleported in path B.
Figure 3a–c shows the data for the ghost-imaging protocol. These data, however are also consistent with the result of a quantum teleportation protocol, where the SLM and SMF in path A are used to remotely prepare a quantum state in path B. Although we only perform the measurements in the pixel basis and further measurements mutually unbiased bases, momentum basis, for example would be required to unequivocally demonstrate quantum teleportation. Our results are nevertheless consistent with qubit teleportation for a spatial state of light. Full quantum teleportation of a spatial state qubit would be possible with a simple modification to our existing system. Such a system would use a complete Bell-state measurement rather than a single projection onto |Ψ−〉, and the efficiency of the scheme would be limited to 1/2 using linear optics.27 We have already demonstrated such state teleportation in prior work,7 while the emphasis of this work is on full-field quantum imaging between initially independent photons and the impact of state symmetry on the resulting image/object relation.
We now consider the implications of our system for high-dimensional teleportation. The work of Calsamiglia26 precludes perfect high-dimensional Bell-state measurements using linear optics. High-dimensional image teleportation can only be achieved by using multiple photons in an extended version of our experimental set-up,8,28 or by implementing non-linear optical imaging methods, such as those outlined in Barreto-Lemos.24 Currently in our system, when photons in BC are projected onto {|Ψ〉±} or {|Φ〉}, the photons in A and D are left in the mixed state of all possible two-photon two-dimensional anti-symmetric states. This is analogous to the simultaneous two-dimensional entanglement swapping observed in ref. 7 The state AD is a mixed state, and knowledge of the state in A does not give precise knowledge of the state in D. A consequence of this for imaging is the reduced contrast in high dimensions.
To conclude, this experiment constitutes the first implementation of ghost imaging using non-interacting photons that were initially independent, and the first observed ghost imaging using entanglement swapping. We have also outlined the implications of this experiment for quantum teleportation of spatial states of light. Our system enables teleportation exactly in two dimensions, but it is a more complex scenario in higher dimensions. We reveal the underlying physics of quantum imaging with non-interacting photons, showing the importance of state symmetry and dimension on the resultant quantum image. These findings, which we observe in a quantum setting, point to new considerations for traditional classical ghost imaging, where new signal processing methods could be developed to enhance and alter the observed images.
Methods
Our experiment, as depicted in detail in Fig. 5, consists of a Ti:sapphire laser at a wavelength of 808 nm and a repetition rate of 80 MHz. We pump a 0.5-mm-thick BBO crystal to produce 360 mW of upconverted light at 404 nm. This light then pumps two BBO crystals, each 1 mm thick, to produce downconverted entangled photons, labelled A and B from crystal 1 and C and D from crystal 2. We filter the down-conversion immediately after the crystal using 20-nm bandpass filters centred at 810 nm. Additionally, we later filter photons B and C with 3-nm bandpass filters centred at 808 nm to ensure a good HOM dip visibility.
In order to produce correlations between photons A and D, we interfere photons B and C on a beamsplitter. Using a translation stage in the path of photon B, we can match the path lengths of photons B and C so that they undergo HOM intereference. This projects their joint state into one of the four two-dimensional Bell states, from which the anti-symmetric state can be selected by postselecting on four-fold coincidences. We place an object in arm A, experimentally realised using a SLM; we then use a second SLM in arm D to make measurements.
The light is collected using SMFs in arms A and D as this results in very few background counts. However, we use multi-mode fibres in arms B and C to ensure that we are collecting as many spatial modes as possible after the interference. The light is detected using single-photon avalanche diodes (Excelitas SPCM-800-14-FC), and time tagging and coincidence counting is performed using a Picoquant HydraHarp. The data that support this work are available from https://doi.org/10.17861/eff58313-703e-474f-a139-43c582f47b8f.
Data availability
The data for this paper are available and can be accessed at the following digital object identifier: https://doi.org/10.17861/eff58313-703e-474f-a139-43c582f47b8f.
References
Wang, J. et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 6, 488EP (2012).
Mafu, M. et al. Higher-dimensional orbital-angular-momentum-based quantum key distribution with mutually unbiased bases. Phys. Rev. A 88, 032305 (2013).
Mirhosseini, M. et al. High-dimensional quantum cryptography with twisted light. N. J. Phys. 17, 033033 (2015).
Dada, A. C., Leach, J., Buller, G. S., Padgett, M. J. & Andersson, E. Experimental high-dimensional two-photon entanglement and violations of generalized Bell inequalities. Nat. Phys. 7, 677 (2011).
Żukowski, M. Z., Zeilinger, A., Horne, M. A. & Ekert, A. K. ‘Event-ready-detectors’’ Bell experiment via entanglement swapping. Phys. Rev. Lett. 71, 4287 (1993).
Pan, J.-W., Bouwmeester, D., Weinfurter, H. & Zeilinger, A. Experimental entanglement swapping: entangling photons that never interacted. Phys. Rev. Lett. 80, 3891 (1998).
Zhang, Y. et al. Simultaneous entanglement swapping of multiple orbital angular momentum states of light. Nat. Commun. 8, 632 (2017).
Wang, X.-L. et al. Quantum teleportation of multiple degrees of freedom of a single photon. Nature 518, 516 EP (2015).
Pittman, T., Shih, Y., Strekalov, D. & Sergienko, A. Optical imaging by means of two-photon quantum entanglement. Phys. Rev. A 52, R3429 (1995).
Bennink, R. S., Bentley, S. J. & Boyd, R. W. “Two-photon” coincidence imaging with a classical source. Phys. Rev. Lett. 89, 113601 (2002).
Bennink, R. S., Bentley, S. J., Boyd, R. W. & Howell, J. C. Quantum and classical coincidence imaging. Phys. Rev. Lett. 92, 033601 (2004).
Valencia, A., Scarcelli, G., D’Angelo, M. & Shih, Y. Two-photon imaging with thermal light. Phys. Rev. Lett. 94, 063601 (2005).
Howell, J. C., Bennink, R. S., Bentley, S. J. & Boyd, R. Realization of the Einstein–Podolsky–Rosen paradox using momentum- and position-entangled photons from spontaneous parametric down conversion. Phys. Rev. Lett. 92, 210403 (2004).
Jack, B. et al. Holographic ghost imaging and the violation of a Bell inequality. Phys. Rev. Lett. 103, 083602 (2009).
Chen, L., Lei, J. & Romero, J. Quantum digital spiral imaging. Light Sci. Appl. 3, e153 (2014).
Ryczkowski, P., Barbier, M., Friberg, A. T., Dudley, J. M. & Genty, G. Ghost imaging in the time domain. Nat. Photonics 10, 167 (2016).
Shapiro, J. H. Computational ghost imaging. Phys. Rev. A 78, 061802 (2008).
Katz, O., Bromberg, Y. & Silberberg, Y. Compressive ghost imaging. Appl. Phys. Lett. 95, 131110 (2009).
Chan, K. W. C., O’Sullivan, M. N. & Boyd, R. W. Two-color ghost imaging. Phys. Rev. A 79, 033808 (2009).
Karmakar, S. & Shih, Y. Two-color ghost imaging with enhanced angular resolving power. Phys. Rev. A 81, 033845 (2010).
Zhang, Y. et al. Engineering two-photon high-dimensional states through quantum interference. Sci. Adv. 2, e1501165 (2016).
Kai-Hong, L., Bo-Qiang, H., Wei-Mou, Z. & Ling-An, W. Nonlocal imaging by conditional averaging of random reference measurements. Chin. Phys. Lett. 29, 074216 (2012).
Wen, J. Forming positive-negative images using conditioned partial measurements from reference arm in ghost imaging. J. Opt. Soc. Am. A 29, 1906 (2012).
Barreto-Lemos, G. et al. Quantum imaging with undetected photons. Nature (London) 512, 409 (2014).
Liu, J. et al. Studying fermionic ghost imaging with independent photons. Opt. Express 24, 29226 (2016).
Calsamiglia, J. Generalized measurements by linear elements. Phys. Rev. A 65, 030301 (2002).
Calsamiglia, J. & Lütkenhaus, N. Maximum efficiency of a linear-optical Bell-state analyzer. Appl. Phys. B 72, 67 (2001).
Goyal, S. K., Boukama-Dzoussi, P. E., Ghosh, S., Roux, F. S. & Konrad, T. Qudit-teleportation for photons with linear optics. Sci. Rep. 4, 4543 (2014).
Acknowledgements
We thank Prof. Daniele Faccio and Dr. Yingwen Zhang for helpful discussions. A.V. was supported by the Claude Leon Foundation; N.B. was supported by the DST-CSIR; A.F. was supported by NRF; J.L. was supported by the Engineering and Physical Sciences Research Council through the Quantum Hub in Quantum Enhanced Imaging (EP/M01326X/1).
Author information
Authors and Affiliations
Contributions
The experiment was performed by M.A. and J.L., the theory was developed by N.B., M.A. and F.Z., the data analysis was performed by J.L. and A.V. and the experiment was conceived by A.F. and J.L. All authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bornman, N., Agnew, M., Zhu, F. et al. Ghost imaging using entanglement-swapped photons. npj Quantum Inf 5, 63 (2019). https://doi.org/10.1038/s41534-019-0176-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-019-0176-5
This article is cited by
-
Popper’s conjecture with angular slits and twisted light
Scientific Reports (2023)
-
Remote transport of high-dimensional orbital angular momentum states and ghost images via spatial-mode-engineered frequency conversion
Nature Communications (2023)
-
Quantum microscopy based on Hong–Ou–Mandel interference
Nature Photonics (2022)
-
Towards higher-dimensional structured light
Light: Science & Applications (2022)
-
Super-resolved quantum ghost imaging
Scientific Reports (2022)