Abstract
The Sachdev-Ye-Kitaev (SYK) model incorporates rich physics, ranging from exotic non-Fermi liquid states without quasiparticle excitations, to holographic duality and quantum chaos. However, its experimental realization remains a daunting challenge due to various unnatural ingredients of the SYK Hamiltonian such as its strong randomness and fully nonlocal fermion interaction. At present, constructing such a nonlocal Hamiltonian and exploring its dynamics is best through digital quantum simulation, where state-of-the-art techniques can already handle a moderate number of qubits. Here, we demonstrate a first step towards simulation of the SYK model on a nuclear-spin-chain simulator. We observed the fermion paring instability of the non-Fermi liquid state and the chaotic-nonchaotic transition at simulated temperatures, as was predicted by previous theories. As the realization of the SYK model in practice, our experiment opens a new avenue towards investigating the key features of non-Fermi liquid states, as well as the quantum chaotic systems and the AdS/CFT duality.
Similar content being viewed by others
Introduction
The Sachdev-Ye-Kitaev (SYK) model describes a strongly interacting quantum system with random all-to-all couplings among N Majorana fermions.1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26 At large N, this model is exactly solvable and exhibits an explicit non-Fermi liquid (NFL) behavior with nonzero entropy density at vanishing temperature. In condensed matter physics, the most well-known (yet poorly understood) NFL is the “strange metal” phase at optimal doping of the cuprates high-temperature superconductors, where the resistivity scales linearly with temperature for a very large range in the phase diagram,27,28,29,30 as shown in Fig. 1. The strange metal phase can be viewed as the parent state of high Tc superconductors, in contrast to the role of Fermi liquid in ordinary BCS superconductors. Very recently a number of works have constructed non-fermi liquid states based on SYK physics, with potential applications to condensed matter systems.31,32,33,34 The SYK model and its generalized SYKq models with a q-fermion interaction also attract tremendous interests in the quantum information and string theory community. For example, the maximal chaotic behavior for q > 2 grant the model a holographic dual to the (1 + 1)d Einstein gravity with a bulk black hole.3,4,5,35,36,37,38,39,40
Schematic phase diagram of a the generalized SYK model in Eq. (1) with pair condensation instability on the μ > 0 side, and b the standard non-Fermi liquid (NFL) behavior in the proximity of a quantum critical point covered by a superconducting (SC) dome at low temperature
Beyond the rich physics incorporated in the SYK model, the rarity of solvable, strongly interacting chaotic systems in quantum mechanics further highlight its significance. Hence, experimental realization of the SYK model is worth pursuing. The lack of experimental quantum simulations of the SYK model nowadays can be mainly attributed to two facts: it is extremely difficult to simulate the Hamiltonian with strong randomness and fully nonlocal fermion interactions, and remains unclear that how to initialize the simulated system into specific states at different temperatures and measure the concerned dynamical properties. A quantum simulator with individual and high-fidelity controllability will be the key, while the simulation process should be “digital”.41,42,43,44,45,46 As digital quantum simulation often requires error-prone Trotter-Suzuki decompositions repeatedly, relevant experiments were still performed on a few qubits.47,48,49,50 This is indeed a poignant contrast to current analog quantum simulation experiments that have already involved about 50 particles,51 but it should be understandable that the two approaches are radically different. Moreover, it is yet impossible to carry out the SYK simulation on the cloud quantum computing service launched by IBM, as that service is based on a sequential implementation of elementary quantum gates rather than dynamical evolution of given Hamiltonians.
The best route to simulate the SYK model and explore its fascinating properties at present is via fully controllable quantum systems, where nuclear magnetic resonance (NMR) is one of the most suitable systems. The goal of this work is to experimentally investigate the SYK model, in particular the fermion-pair instability of the SYK NFL and the chaotic-nonchaotic transition predicted recently.52 We realized the (0 + 1)d generalized SYK model with N = 8 Majorana fermions using a four-qubit NMR quantum simulator, and measured the boson correlation functions at different simulated temperatures and perturbations. The early-time and late-time decay behaviors of fermion-pair correlations reflect the fact that there exist two different phases of the generalized SYK model, i.e., maximally chaotic NFL phase and perturbatively weak chaotic fermion-pair condensate phase. The results reveal their competition under different perturbations, and also the thermal behavior at different simulated temperatures.
Results
Generalized SYK model
The Hamiltonian of (0 + 1)d generalized SYK model we considered is given by
where χi,j,k,l are Majorana fermion operators with indices i, j, k, l = 1, …, N, and both Jijkl and Cij are antisymmetric random tensors drawn from a Gaussian distribution: \(\overline {J_{ijkl}} = 0,\overline {J_{ijkl}^2} = 3!J_4^2/N^3\) and \(\overline {C_{ij}} = 0,\overline {C_{ij}C_{kl}} = J^2/N^2(\delta _{ik}\delta _{jl} - \delta _{il}\delta _{jk})\). Note that J4 has the dimension of energy, while J has the dimension of (energy)1/2. Its phase diagram is shown in Fig. 1a. At μ = 0, the Hamiltonian describes the pure SYK model, whose low-temperature state in the limit N ≫ J/T ≫ 0 is a maximally chaotic NFL. As pointed out in ref. 52, the SYK fixed point could be unstable towards fermion-pair condensate and spontaneous symmetry breaking, i.e., an analog of BCS instability. For instance, a positive μ term in the Hamiltonian (1) is a (marginally) relevant perturbation that drives the spontaneous breaking of the time-reversal symmetry \({\cal{T}}:\chi _i \to \chi _i,i \to - i\). In the \({\cal{T}}\)-breaking phase, the following bosonic fermion-pair operator
develops a persistent correlation 〈b(t)b(0)〉 ~ constant that does not decay in time t. We will use this long-time boson correlation as an experimental signature for the \({\cal{T}}\)-breaking phase. The ordering of b actually has a simple mean-field understanding, since the μ term can also be written as −μb2/2, which favors 〈b〉 ≠ 0 when μ > 0. This can be viewed as a (0 + 1)d analog of the Cooper instability of a NFL at low temperature. In the presence of 〈b〉 ≠ 0, the pairing term −iμ〈b〉Cijχiχj in the mean-field Hamiltonian is most relevant at low-energy, which leads to a nonchaotic ground state in the infrared limit, plus perturbatively irrelevant interaction that causes weak chaos. On the other hand, if μ is negative (μ < 0), the spontaneous symmetry breaking will not be favored and the system will remain in the maximally chaotic non-Fermi liquid phase.
Physical system
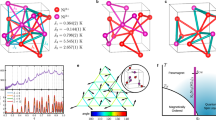
In experiment, we use four spins to simulate N = 8 Majorana fermions, as illustrated in Fig. 2a. The Hamiltonian can be encoded into the spin-1/2 operators via the Jordan Wigner transformation:
Here, σx,y,z stand for Pauli matrices. There are 70 Jijkl’s, 28 Cij’s and four types of spin interactions (i.e., 1-, 2-, 3-, and 4-body interactions) in the case of N = 8. The physical system we used has four nuclear spins (C1, C2, C3, and C4) in the sample of trans-crotonic acid dissolved in d6-acetone. Its molecular structure is shown in Fig. 2b. The natural Hamiltonian of this system in rotating frame is
where ωi represents the chemical shift of spin i and Jij the coupling constant between spins i and j. The relevant Hamiltonian parameters can be seen in Supplementary Information. The experiment was carried out on a Bruker DRX-700 spectrometer at room temperature (T = 298 K). The experiment is divided into three steps: preparation of initial states, simulation of generalized SYK model and measurement of boson correlation functions, as illustrated in Fig. 2c.
Scheme for experimentally simulating generalized SYK model and measuring the boson correlation function. a The generalized SYK model with eight Majorana fermions is mapped onto a four spin model. The curved lines denote the Majorana fermion-fermion or spin–spin interactions. b Molecular structure of 13C-labeled trans-crotonic acid, where nuclear spins of C1, C2, C3, and C4 are used as a four-qubit quantum simulator. All protons are decoupled throughout the experiments. c Quantum circuit for measuring the boson correlation function. V is the basis transformation from the computational basis to the eigenvectors of initial states ρi. M represents five readout pulses for observing b operator
Preparation of initial states
Under high-temperature approximation, the natural system is originally in the thermal equilibrium state \(\rho _{{\mathrm{eq}}} \approx ({\Bbb I} + \epsilon \mathop {\sum}\nolimits_{i = 1}^4 {\sigma _i^z} )/2^4\), where \({\Bbb I}\) is the identity and \(\epsilon \sim 10^{ - 5}\) is the polarization. During our quantum computation, the evolution preserves the unit operator \({\Bbb I}\), so we omit it and rewrite \(\rho _{eq} = \epsilon \mathop {\sum}\nolimits_{i = 1}^4 {\sigma _i^z}\). Hereinafter we used the deviation density matrices as ‘states’’.53 Starting from ρeq, the system was prepared into the initial ‘states’’: \(\rho _i^{{\mathrm{Real}}} = (\rho _{{\mathrm{eq}}}^Hb + b\rho _{{\mathrm{eq}}}^H)/2\) and \(\rho _i^{{\mathrm{Imag}}} = - i(\rho _{{\mathrm{eq}}}^Hb - b\rho _{{\mathrm{eq}}}^H)/2\), where \(\rho _{{\mathrm{eq}}}^H = e^{ - \beta H}/{\mathrm{Tr}}(e^{ - \beta H})\). These initial states can be implemented, as shown in Fig. 2c. The network with single-qubit rotations and free evolutions of the natural Hamiltonian allow us to get the states (before the first z-direction gradient field), whose diagonal elements equal to the eigenvalues of ρi. The rotation angles θj’s for different β and H were given in the Supplementary Information. The CNOT gates were applied to remove zero quantum coherence that cannot be averaged out by the z-direction gradient fields. The states after the third z-direction gradient field are thus the diagonal density matrices, i.e., \(\rho _i^d = V^\dagger \rho _iV\), where V is the basis transformation between computational basis and eigenvectors of ρi. When performing the V transformation, we can obtain the initial states ρi.
Simulation of generalized SYK model
The evolution of generalized SYK model can be simulated with a controllable NMR system effciently, as pointed out originally by Feynman.54,55 We rewrite the Hamiltonian (1) as the sum of spin interactions, i.e.,
according to Eq. (3), where subscripts α = {0, x, y, z} label the corresponding Pauli matrices, and \(\sigma_0={\Bbb I}\). All random coefficients \(a_{ijkl}^s\) are shown in Supplementary Information. Using the Trotter-Suzuki formula, its exact time evolution operator can be decomposed into,56
where \(|a| = \left( {\overline {|a_{ijkl}^s|^2} } \right)^{ - 1/2} \approx 0.64\) for μ = ±5, and ≈0.27 for μ = 0 (Here, \(J = \sqrt {J_4} = 1\) were chosen in experiments). Obtaining this exact time evolution is a difficult problem to deal with a quantum simulation, but it is possible to handle the first-order product operator \(\left( {\mathop {\prod}\nolimits_{s = 1}^{70} {e^{ - iH_s\tau /n}} } \right)^n\). The approximate simulation of \(e^{ - i{\cal{H}}\tau } \approx \left( {\mathop {\prod}\nolimits_{s = 1}^{70} {e^{ - iH_s\tau /n}} } \right)^n\) can take place to within a desired accuracy by choosing sufficiently large n. In particular, if [Hs, Hs′] = 0, there is a boost in accuracy. The fidelity between e−iHτ and \(\left( {\mathop {\prod}\nolimits_{s = 1}^{70} {e^{ - iH_s\tau /n}} } \right)^n\) as a function of τ and n is shown in Fig. 3a. For example, when ln(τ) = 2 and log(n) = 1.55, the fidelity is over 0.99.
Fidelity of the Trotter-Suzuki decomposition and pulse sequence for implementing a k-body interaction. In a the fidelities are calculated between \(e^{ - i{\cal{H}}\tau }\) and its decomposition \(\left( {\mathop {\prod}\nolimits_{s = 1}^{70} {e^{ - i{\cal{H}}_s\tau /n}} } \right)^n\) as a function of τ and n. In b to simulate a k-body interaction, the pulse sequence includes 5(k−2) 1-body interactions and 2(k − 2) 2-body interactions. θ1 = π/2 and θ2 = π
For simulating the \(\left( {\mathop {\prod}\nolimits_{s = 1}^{70} {e^{ - iH_s\tau /n}} } \right)^n\), we evolve the system forward locally over small, discrete time slices, i.e., \(e^{ - iH_1\tau /n},e^{ - iH_2\tau /n}\), and so on, up to \(e^{ - iH_{70}\tau /n}\), and repeat n times. Each local many-body spin interaction of \(H_s = a_{ijkl}^s\sigma _{\alpha _i}^1\sigma _{\alpha _j}^2\sigma _{\alpha _k}^3\sigma _{\alpha _l}^4\) can be effectively created by the means of coherent control acting on the physical system of nuclear spins.46,50,57,58,59,60 The task in coherent control is to design a pulse sequence for finding the appropriate amplitudes and phases of radio-frequency (RF) fields. To improve the control performance in our experiment, we employed the gradient ascent pulse engineering (GRAPE) algorithm61 to optimize the field parameters of a shaped pulse. The shaped pulse with the duration of 100 ms and the slices of 4000 was designed to have theoretical fidelity over 0.99, and be robust against the 5% inhomogeneity of RF fields. The detail of experimental simulation and the shaped pulse can be seen in Supplementary Information.
It is necessary to note that the quantum simulation algorithm is efficient. As shown in Fig. 3b, a k-body spin interaction with the form of \(\sigma _z^1\sigma _z^2 \cdots \sigma _z^k\) can be decomposed as a (k − 1)-body interaction by the following iteration,
where \(P_1 = e^{ - i\pi \sigma _x^2/4}e^{ - i\pi \sigma _z^1\sigma _z^2/4}e^{ - i\pi \sigma _y^2/4}\), and \(P_2 = e^{ - i\pi \sigma _y^2/4}e^{ - i\pi \sigma _z^1\sigma _z^2/4}e^{i\pi /2\sigma _y^2}e^{i\pi \sigma _x^2/4}\). For a k-body (k > 2) interaction, it requires 5(k − 2) 1-body interactions and 2(k − 2) 2-body interactions. Given an accuracy \(\epsilon\), the total number of gates is \(n\mathop {\sum}\nolimits_{i = 1}^m l (k)\), where \(n \propto |a|^2\tau ^2/\epsilon\), \(m = \left( \begin{array}{c}N\\ 4\end{array} \right)\) is the number of spin interactions, and l(k) = 7(k − 2) counts the number of gates in implementing a k-body (k ≤ N/2) spin interaction. Therefore, the total number of gates \(\propto |a|^2\tau ^2N^5/\epsilon\) grows polynomially with the number of Majorana fermions N, indicating that digital quantum simulation of the generalized SYK model is efficient.
Measurement of boson correlation function
Finally, we measure the boson correlation function to probe the instability of the SYK non-fermi-liquid ground state towards spontaneous symmetry breaking at different values of β and μ. The boson correlation function is defined as
To remove its initial value fluctuation from sample to sample (here a sample means that we randomly generate a different Hamiltonian), we average the normalized correlation function over random samples,
where the normalization is applied to avoid the unphysical phase interference among different samples. In experiment, we randomly generated eight samples or Hamiltonians, as shown in Supplementary Information.
Starting from initial states \(\rho _i^{{\mathrm{Real}}}\) and \(\rho _i^{{\mathrm{Imag}}}\), the real and imaginary parts of 〈b(τ)b(0)〉β can be obtained by measuring the bosonic fermion-pair operator b, namely, \({\mathrm{Re}}(\langle b(\tau )b(0)\rangle _\beta ) = {\mathrm{Tr}}(e^{ - iH\tau }\rho _i^{{\mathrm{Real}}}e^{iH\tau }b)\), and \({\mathrm{Im}}(\langle b(\tau )b(0)\rangle _\beta ) = {\mathrm{Tr}}(e^{ - iH\tau }\rho _i^{{\mathrm{Imag}}}e^{iH\tau }b)\). In NMR, the measured signal via quadrature detection is given by,62
where \(\rho _f = e^{ - iH\tau }\rho _i^{{\mathrm{Real}}}e^{iH\tau }\) or \(e^{ - iH\tau }\rho _i^{{\mathrm{Imag}}}e^{iH\tau }\) is the output density matrix, and M represents a series of readout operators. We can see that the NMR signal consists of both real and imaginary parts, and is the average of transverse magnetization without any readout pulse. The bosonic fermion-pair operator b including 28 spin operators can be obtained by designing a specific set of readout pulses. To get all spin operators of b, i.e., Tr[ρfb] completely, we used five readout pulses in experiments. The readout pulses and their corresponding readout spin operators are listed in Table 1.
Experimental results
The main experimental results are shown in Fig. 4, which were obtained by averaging over eight random samples. The data for each random sample is available in Supplementary Information. The error bars mainly come from the fitting procedure (about 1%) and fluctuation of random samples, which is <2% when ln(τ) ≤ 1 and around 15% when ln(τ) > 1. After normalization of the correlation function to compensate for the effect of decoherence, the experimental result is in good agreement with theoretical predictions.
Boson correlation functions for different β and μ. Solid lines are simulation results. Points are experimental data obtained by averaging over eight random samples. In a there is no significant difference of boson correlation functions between the μ = ±5 cases. However, this difference grows as the temperature (T = 1/β) goes down, as shown in b. At low temperature of c, the decay behavior of boson correlations for μ = −5 becomes similar with the case of μ = 0. For μ = 0, the pure SYK model at low temperature describes a maximally chaotic NFL phase with the fastest decay rate of boson correlation. While for μ = 5, the boson correlation decays much slower and saturates to a relatively large value, which corresponds to a spontaneous \({\cal{T}}\)-breaking phase
Let us first look at the low temperature result (β = 20) in Fig. 4c. The boson correlation was measured for three different values of μ. For both μ = 0 and μ = −5, the boson correlations decay quickly following the similar manner, which means that they are relevant chaotic phases. As the low-temperature state at μ = 0 described by the pure SYK model is a maximally chaotic NFL phase. While for μ = 5, the boson correlation decays much slower and saturates to a relatively large value. This difference indicates the long-time order of μ > 0 is the spontaneous \({\cal{T}}\)-breaking phase. In contrast, for μ < 0, there is no such instability towards symmetry breaking. So by changing the sign of μ, the system goes through a continuous chaotic-nonchaotic transition, whose critical properties are analogous to that of the Kosterlitz-Thouless transition.52
The fact that boson correlation still saturates to some finite value in the NFL phase for μ ≤ 0 is due to the finite size of our system. Theoretically, in the NFL phase (μ ≤ 0), the saturate value of boson correlation decays towards zero with the growth of the system size. In the symmetry breaking phase (μ > 0), the saturate value scales towards a finite value in the thermodynamic limit. Numerical simulations of this scaling behavior is provided in Supplementary Information. In spite of the finite size, different phases of the generalized SYK model are indeed demonstrated by different behaviors of the boson correlation in our experiment.
As we raise the temperature to β = 1 in Fig. 4b, the boson condensation is destroyed by the thermal fluctuation and the long-time correlation is suppressed. In the thermodynamic limit, the transition temperature scales as \(T_c\sim {\mathrm{exp}}( - \sqrt \pi J_4/2J^2\mu )\)52 illustrated in Fig. 1a. At infinite temperature (β = 0) in Fig. 4a, the μ = ±5 curves coincide, since the boson correlation D(τ) = Tr(eiHτbe−iHτb) in this scenario is invariant under the transformation H → −H. We observe the slightly different behaviors of boson correlations between the μ ≠ 0 and μ = 0 cases. The correlation decays fastest and to the lowest saturation value at μ = 0, which is consistent with the fact that the pure SYK model is maximally chaotic scrambling the order parameter most thoroughly.
Discussion
In summary, we report the experimental realization of the SYK model and its generalization. The measurements of fermion-pair correlation functions in our experiment exhibit the instability of the maximally chaotic NFL phase of the SYK model against certain types of four-fermion perturbations, which drives the system into a less chaotic fermion-pair condensed phase with spontaneous \({\cal{T}}\)-breaking. These successful experimental demonstrations rely heavily on the fully controllability of our NMR quantum simulator. The NMR system has the advantages of well characterized qubits, long decoherence time, and fine control of nuclear spins through RF fields, which enable us to simulate the dynamics of generalized SYK model. Our experiment demonstrates the first step towards quantum simulation of non-Fermi-liquid states in strongly interacting systems. The methods used here can also be adapted in other quantum platforms, and may provide a new path towards exploring the holographic duality. It will also be interesting to further test non-equilibrium dynamic and the scrambling of information by measuring the out-of-time-order correlation, which has been proposed as a identification of chaos in quantum systems.
One major concern is about the scalability of the control techniques adopted in the experiment, as it is supposed to be the largest obstacle when performing higher-dimensional digital quantum simulations. In fact, the gradient-based optimal control is the bottleneck that limits future experimental size. Despite its extraordinary performance in small number of qubits, this technique does not posses well scalability in principle. Recently, an alternative method that utilizes the power of quantum processor together with machine learning techniques to enhance quantum control was reported.63,64 This method is also efficient, i.e., requires polynomial time for optimization with the number of qubits. Improvement of control fidelities was solidly demonstrated on a 12-qubit system.64 Compared to the results here, this technique leads to similar control accuracies according to our numerical simulation. As this new optimization method can be scaled up to many qubits, we anticipate it to underpin future quantum simulation tasks of more complex SYK, as well as other models. For instance, one of most exciting prospects is to mimic the black holes and thus experimentally test the quantum gravitation ideas in the laboratory.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Change history
02 August 2019
An amendment to this paper has been published and can be accessed via a link at the top of the paper.
References
Sachdev, S. & Ye, J. Gapless spin-fluid ground state in a random quantum Heisenberg magnet. Phys. Rev. Lett. 70, 3339–3342 (1993).
Kitaev, A. A Simple Model of Quantum Holography. Talk at Kavli Institute for Theoretical Physics, University of California, Santa Barbara, CA, U.S.A., May 7, 2015 and May 27, 2015 (2015).
Sachdev, S. Bekenstein-Hawking entropy and strange. Met. Phys. Rev. X 5, 041025 (2015).
Polchinski, J. & Rosenhaus, V. The spectrum in the Sachdev-Ye-Kitaev model. J. High. Energy Phys. 4, 1 (2016).
Maldacena, J. & Stanford, D. Remarks on the Sachdev-Ye-Kitaev model. Phys. Rev. D. 94, 106002 (2016).
Witten, E. An SYK-like model without disorder. https://arxiv.org/abs/1610.09758 (2016).
Klebanov, I. R. & Tarnopolsky, G. Uncolored random tensors, melon diagrams, and the sachdev-ye-kitaev models. Phys. Rev. D. 95, 046004 (2017).
Gross, D. J. & Rosenhaus, V. A generalization of Sachdev-Ye-Kitaev. J. High. Energy Phys. 2, 93 (2017).
Fu, W. & Sachdev, S. Numerical study of fermion and boson models with infinite-range random interactions. Phys. Rev. B 94, 035135 (2016).
Krishnan, C., Sanyal, S. & Subramanian, P. N. B. Quantum chaos and holographic tensor models. J. High. Energy Phys. 2017, 56 (2017).
You, Y. -Z., Ludwig, A. W. W. & Xu, C. Sachdev-ye-kitaev model and thermalization on the boundary of many-body localized fermionic symmetry-protected topological states. Phys. Rev. B 95, 115150 (2017).
Banerjee, S. & Altman, E. Solvable model for a dynamical quantum phase transition from fast to slow scrambling. Phys. Rev. B 95, 134302 (2017).
Fu, W., Gaiotto, D., Maldacena, J. & Sachdev, S. Supersymmetric sachdev-ye-kitaev models. Phys. Rev. D. 95, 026009 (2017).
Gu, Y., Qi, X. -L. & Stanford, D. Local criticality, diffusion and chaos in generalized Sachdev-Ye-Kitaev models. J. High. Energy Phys. 5, 125 (2017).
Gu, Y., Lucas, A. & Qi, X. -L. Energy diffusion and the butterfly effect in inhomogeneous Sachdev-Ye-Kitaev chains. SciPost Phys. 2, 018 (2017).
Chen, Y., Zhai, H. & Zhang, P. Tunable quantum chaos in the sachdev-ye-kitaev model coupled to a thermal bath. J. High Energy Phys. 2017, 150 (2017).
Murugan, J., Stanford, D. & Witten, E. More on supersymmetric and 2d analogs of the syk model. J. High Energy Phys. 2017, 146 (2017).
Narayan, P. & Yoon, J. Syk-like tensor models on the lattice. J. High Energy Phys. 2017, 83 (2017).
Chew, A., Essin, A. & Alicea, J. Approximating the sachdev-ye-kitaev model with majorana wires. Phys. Rev. B 96, 121119 (2017).
Jian, S. -K., Xian, Z. -Y. & Yao, H. Quantum criticality and duality in the SYK/AdS_2 chain. Phys. Rev. B 97, 205141, arXiv 1709.02810 (2018).
Peng, C., Spradlin, M. & Volovich, A. Correlators in the N = 2 supersymmetric syk model. J. High Energy Phys. 2017, 202 (2017).
Yoon, J. Syk models and syk-like tensor models with global symmetry. J. High Energy Phys. 2017, 183 (2017).
Chen, X., Fan, R., Chen, Y., Zhai, H. & Zhang, P. Competition between chaotic and nonchaotic phases in a quadratically coupled sachdev-ye-kitaev model. Phys. Rev. Lett. 119, 207603 (2017).
Jian, S. -K. & Yao, H. Solvable sachdev-ye-kitaev models in higher dimensions: From diffusion to many-body localization. Phys. Rev. Lett. 119, 206602 (2017).
Zhang, P. Dispersive sachdev-ye-kitaev model: Band structure and quantum chaos. Phys. Rev. B 96, 205138 (2017).
Narayan, P. & Yoon, J. Supersymmetric S. Y. K. model with global symmetry. J. High Energy Phys. 8, 159, arXiv 1712.02647 (2018).
Gurvitch, M. & Fiory, A. T. Resistivity of la1.825sr0.175cuo4 and yba2cu3o7 to 1100 k: Absence of saturation and its implications. Phys. Rev. Lett. 59, 1337–1340 (1987).
Tozer, S. W., Kleinsasser, A. W., Penney, T., Kaiser, D. & Holtzberg, F. Measurement of anisotropic resistivity and hall constant for single-crystal yba2cu3o7−x. Phys. Rev. Lett. 59, 1768–1771 (1987).
Martin, S., Fiory, A. T., Fleming, R. M., Schneemeyer, L. F. & Waszczak, J. V. Temperature dependence of the resistivity tensor in superconducting bi2sr2.2ca0.8 cu2o8 crystals. Phys. Rev. Lett. 60, 2194–2197 (1988).
Varma, C. M., Littlewood, P. B., Schmitt-Rink, S., Abrahams, E. & Ruckenstein, A. E. Phenomenology of the normal state of cu-o high-temperature superconductors. Phys. Rev. Lett. 63, 1996–1999 (1989).
Song, X. -Y., Jian, C. -M. & Balents, L. Strongly correlated metal built from sachdev-ye-kitaev models. Phys. Rev. Lett. 119, 216601 (2017).
Patel, A. A., McGreevy, J., Arovas, D. P. & Sachdev, S. Magnetotransport in a model of a disordered strange metal. Phys. Rev. X 8, 021049 (2018).
Chowdhury, D., Werman, Y., Berg, E. & Senthil, T. Translationally invariant non-Fermi liquid metals with critical Fermi-surfaces: Solvable models. Phys. Rev. X 8, 031024, arXiv 1801.06178 (2018).
Wu, X., Chen, X., Jian, C.-M., You, Y.-Z. & Xu, C. A candidate theory for the “Strange Metal” phase at finite energy window. Phys. Rev. B 98, 165117, arXiv 1802.04293 (2018).
Sachdev, S. Holographic metals and the fractionalized fermi liquid. Phys. Rev. Lett. 105, 151602 (2010).
Jensen, K. Chaos in ads2 holography. Phys. Rev. Lett. 117, 111601 (2016).
Engelsöy, J., Mertens, T. G. & Verlinde, H. An investigation of ads2 backreaction and holography. J. High Energy Phys. 2016, 139 (2016).
Maldacena, J., Stanford, D. & Yang, Z. Conformal symmetry and its breaking in two dimensional Nearly Anti-de-Sitter space. Prog. Theor. Exp. Phys. 2016, 12C104, arXiv 1606.01857 (2016).
Gross, D. J. & Rosenhaus, V. The bulk dual of SYK: cubic couplings. J. High Energy Phys. 5, 92 (2017).
Franz, M. & Rozali, M. Mimicking black hole event horizons in atomic and solid-state systems. Nat. Rev. Mater. 3, 491–501 (2018).
Georgescu, I., Ashhab, S. & Nori, F. Quantum simulation. Rev. Mod. Phys. 86, 153 (2014).
Kim, K. et al. Quantum simulation of frustrated ising spins with trapped ions. Nature 465, 590 (2010).
Luo, Z. et al. Experimental observation of topological transitions in interacting multispin systems. Phys. Rev. A 93, 052116 (2016).
Du, J. et al. Nmr implementation of a molecular hydrogen quantum simulation with adiabatic state preparation. Phys. Rev. Lett. 104, 030502 (2010).
Kong, F. et al. Direct measurement of topological numbers with spins in diamond. Phys. Rev. Lett. 117, 060503 (2016).
Peng, X., Zhang, J., Du, J. & Suter, D. Quantum simulation of a system with competing two-and three-body interactions. Phys. Rev. Lett. 103, 140501 (2009).
Luo, Z. et al. Experimentally probing topological order and its breakdown through modular matrices. Nat. Phys. 14, 160 (2018).
Kandala, A. et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242 (2017).
Lv, D. et al. Quantum simulation of the quantum rabi model in a trapped ion. Phys. Rev. X 8, 021027 (2018).
Li, J. et al. Measuring out-of-time-order correlators on a nuclear magnetic resonance quantum simulator. Phys. Rev. X 7, 031011 (2017).
Bernien, H. et al. Probing many-body dynamics on a 51-atom quantum simulator. Nature 551, 579 (2017).
Bi, Z., Jian, C. -M., You, Y. -Z., Pawlak, K. A. & Xu, C. Instability of the non-fermi-liquid state of the sachdev-ye-kitaev model. Phys. Rev. B 95, 205105 (2017).
Chuang, I. L., Gershenfeld, N., Kubinec, M. G. & Leung, D. W. Bulk quantum computation with nuclear magnetic resonance: Theory and experiment. Proc. R. Soc. Lond. A 454, 447–467 (1998).
Feynman, R. P. Simulating physics with computers. Int. J. Theor. Phys. 21, 467–488 (1982).
Garca-Álvarez, L. et al. Digital quantum simulation of minimal ads/cft. Phys. Rev. Lett. 119, 040501 (2017).
Lloyd, S. Universal quantum simulators. Science 273, 1073–1078 (1996).
Tseng, C. et al. Quantum simulation of a three-body-interaction hamiltonian on an nmr quantum computer. Phys. Rev. A 61, 012302 (1999).
Negrevergne, C., Somma, R., Ortiz, G., Knill, E. & Laflamme, R. Liquid-state nmr simulations of quantum many-body problems. Phys. Rev. A 71, 032344 (2005).
Luo, Z. et al. Experimental preparation of topologically ordered states via adiabatic evolution. Sci. China Phys., Mech. Astron. 62, 980311 (2019).
Liu, W., Zhang, J., Deng, Z. & Long, G. Simulation of general three-body interactions in a nuclear magnetic resonance ensemble quantum computer. Sci. China Ser. G: Phys., Mech. Astron. 51, 1089 (2008).
Khaneja, N., Reiss, T., Kehlet, C., Schulte-Herbrüggen, T. & Glaser, S. J. Optimal control of coupled spin dynamics: design of nmr pulse sequences by gradient ascent algorithms. J. Magn. Reson. 172, 296–305 (2005).
Lee, J. -S. The quantum state tomography on an nmr system. Phys. Lett. A 305, 349–353 (2002).
Li, J., Yang, X., Peng, X. & Sun, C. -P. Hybrid quantum-classical approach to quantum optimal control. Phys. Rev. Lett. 118, 150503 (2017).
Lu, D. et al. Enhancing quantum control by bootstrapping a quantum processor of 12 qubits. NPJ Quantum Inf. 3, 45 (2017).
Acknowledgements
We thank X. Peng, L. Hung, and J. Mei for helpful discussion. This work was supported by CIFAR, NSERC and Industry of Canada. Z.L. acknowledge the support from the National Natural Science Foundation of China (Grants No. 11805008, No. 11734002, and No. 11374032). C.X. is supported by the David and Lucile Packard Foundation and NSF Grant No. DMR-1151208. C.J. is partly supported by the Gordon and Betty Moore Foundations EPiQS Initiative through Grant GBMF4304. D.L. are supported by the National Natural Science Foundation of China (Grants No. 11605005, No. 11875159, and No. U1801661), Science, Technology and Innovation Commission of Shenzhen Municipality (Grants No. ZDSYS20170303165926217 and No. JCYJ20170412152620376), Guangdong Innovative and Entrepreneurial Research Team Program (Grant No. 2016ZT06D348).
Author information
Authors and Affiliations
Contributions
Z.L. designed and performed the experiment. Y.Y., C.X. and C.J. developed the theory. D.L., J.L., B.Z. and R.L. supervised the project. Z.L., Y.Y., D.L. and C.X. wrote the draft. All authors contributed to discussing the results and writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Luo, Z., You, YZ., Li, J. et al. Quantum simulation of the non-fermi-liquid state of Sachdev-Ye-Kitaev model. npj Quantum Inf 5, 53 (2019). https://doi.org/10.1038/s41534-019-0166-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-019-0166-7
This article is cited by
-
A model of randomly-coupled Pauli spins
Journal of High Energy Physics (2024)
-
Fidelity of wormhole teleportation in finite-qubit systems
Journal of High Energy Physics (2024)
-
Absence of operator growth for average equal-time observables in charge-conserved sectors of the Sachdev-Ye-Kitaev model
Journal of High Energy Physics (2023)
-
Observation of information flow in the anti-𝒫𝒯-symmetric system with nuclear spins
npj Quantum Information (2020)