Abstract
The preparation of initial superposition states of discrete-time quantum walks (DTQWs) is necessary for the study and applications of DTQWs. Based on an encoding method, here, we propose a DTQW protocol in linear optics, which enables the preparation of arbitrary initial superposition states of the walker and the coin and enables to obtain the states of the DTQW in addition to the probability distribution of the walker. With this protocol, we experimentally demonstrate the DTQW in the polarization space with both the walker and the coin initially in superposition states, by using only passive linear-optical elements. The effects of the walker’s different initial superposition states on the spread speed of the DTQW and on the entanglement between the coin and the walker are also experimentally investigated, which have not been reported before. When the walker starts with superposition states, we show that the properties of DTQWs are very different from those of DTQWs starting with a single position. Our findings reveal different properties of DTQWs and pave an avenue to study DTQWs with arbitrary initial states. Moreover, this encoding method enables one to encode an arbitrary high-dimensional quantum state, using a single physical qubit, and may be adopted to implement other quantum information tasks.
Similar content being viewed by others
Introduction
Quantum walks (QWs)1 are extensions of the classical random walk and have wide applications in quantum algorithms,2,3,4 quantum simulations,5,6,7,8,9,10 quantum computation,11,12,13 and so on.14,15 In standard one-dimensional (1D) discrete-time quantum walks (DTQWs),16,17 the walker’s position can be denoted as |x〉 (x is an integer) and the coin can be described with the basis states |0〉c and |1〉c. The evolutions of the walker and the coin are usually characterized by a time-independent unitary operator U = TSc(ψ). In each step, the coin is tossed by
with ψ ∈ (0°, 90°), and the walker is shifted by \(T =\mathop {\sum}\nolimits_x |x + 1\rangle \langle x| \otimes |1\rangle _{\mathrm {c}}\langle 1| + \mathop {\sum}\nolimits_x |x - 1\rangle \langle x| \otimes |0\rangle _{\mathrm {c}}\langle 0|\). In general, the result of the DTQW with a finite number of steps is determined by the initial states of the coin and the walker, as well as the operator U. The systematic investigation of DTQW properties and the effect of the initial states on DTQW is important and necessary for applications of DTQWs.
It is worth noting that DTQW with the walker initially in a superposition state has rarely been demonstrated in experiments,18 though there were several theoretical works.19,20,21,22,23,24,25 DTQWs have been experimentally realized in several systems, such as linear optics,4,5,6,26,27,28 ion traps,29,30 cavity quantum electrodynamics,31 and neutral atom traps.32 In most DTQW experiments, the walker starts from the original position |0〉 and it is difficult to prepare an arbitrary initial quantum superposition state of the walker. Moreover, initial superposition states are usually required for applications of DTQWs. For example, an initial uniform superposition state of the walker’s position is required in the Grover walk.2 DTQWs with initial superposition states of the walker are quite different from the standard DTQW (i.e., the walker starts from a single position |x〉), because the final state of the former is a coherent superposition of the final states of the standard DTQW starting from different single positions and thus contains more quantum interference.
Note that the effects of the coin’s initial state on DTQW have been well studied,16,17,26,27,28,33 but the effects of the walker’s initial superposition states on DTQW have rarely been investigated before in experiments. In previous linear-optical DTQW implementations,34,35,36 the coin was always encoded in the two-dimensional polarization space and the position of the walker must be encoded in high-dimensional spaces. In ref. 34 the coin was encoded using the polarization state and the walker’s positions were encoded using the paths of the photons, in which an additional calcite beam displacer was needed in each step to perform the conditional shift of the walker, and DTQWs with up to six steps were measured in experiments. In ref. 18 the coin was encoded using the polarization state and the walker’s positions were encoded using the orbital angular momentum of light, in which the whole process develops in a single light beam and optical resources scaling linearly with the number of steps are required. In ref. 35 the coin was also encoded using the polarization state, and the walker’s positions were encoded using the temporal information of single photons, in which the coin operator was adjustable and five-step DTQWs were studied experimentally. In linear optics, the preparation of arbitrary initial superposition states of the coin is not difficult, because it is easy to obtain arbitrary polarization states using half-wave plates (HWPs) and quarter-wave plates (QWPs). Each DTQW implementation scheme has advantages and limitations, but the preparation of arbitrary initial superposition states of the walker is difficult in most DTQW schemes.
To our knowledge, how to encode the walker’s position using the polarization state has not been reported in both theory and experiment. It is difficult to encode a high-dimensional state using the two-dimensional state. Moreover, the higher the dimension of a quantum state is, it becomes more complex to measure the state or the corresponding density matrix. In DTQW experiments, the measured quantity is always the probability distribution of the walker. In optical experiments, the probability distribution of each position is measured one by one, i.e., a multi-step DTQW should be performed and measured many times, unless all the walker’s positions can be separated and measured simultaneously, which is challenging in most experiments. If the walker’s position can be encoded using the polarization state, arbitrary superposition states of the walker can be easily prepared and measured in linear-optical experiments.
In this work, we propose an encoding method to encode and read out high-dimensional states using only a 2D physical qubit. With this method, we report a DTQW protocol with the walker’s position encoded in the polarization space of single photons. The main advantages of this protocol are as follows: (i) the DTQW protocol together with the design of a linear-optical setup, in which the coin is encoded by two paths, allows us to arbitrarily set the input state of the walker and coin; (ii) the whole state of the multi-step DTQW can be obtained, rather than the probability distribution, which can help to study deep properties of DTQWs and extend the possible applications of DTQWs; (iii) the devices needed are simple and common, optical resources do not increase when increasing DTQW steps; (iv) the mature technique for operations of polarization of photons makes the implementation of this protocol easy and efficient. Then we demonstrate the experimental implementation of DTQW with the walker initially in superposition states. In this case, the effect of the walker’s different initial superposition states on the spread speed of the walker and on the entanglement between the coin and the walker (i.e., the entropy of the reduced density matrix of the coin) are also studied experimentally, which has not been studied in experiments before.
Results
DTQW protocol in linear optics
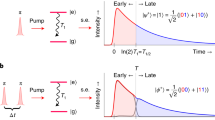
To implement DTQWs in polarization space, we propose an encoding method in the “Methods” section. Here, we make the specific choice of encoding the walker’s positions using non-orthogonal states \(|k\rangle _p = {\mathrm{cos}}{\kern 1pt} \theta _k|H\rangle + e^{i\phi _k}{\mathrm{sin}}{\kern 1pt} \theta _k|V\rangle\) (with integer k) in the polarization space of single photons, by setting θk = kΔθ and ϕk = 0. The coin is encoded by two paths |0〉 and |1〉 of the single photons. As shown in Fig. 1a, the operator for the conditional translation of |k〉p should be expressed as
a Encoding of the walker’s position and the implementation of conditional translation Tp in the polarization space. |H〉 (|V〉) is the horizontal (vertical) polarization state. b Optical realization of the time-independent evolution operator U = TpSc for a DTQW, in which the coin is tossed by the beam splitter (BS) and the conditional transition of the walker’s positions |k〉p is implemented by two half-wave plates (HWPs) oriented at Δθ/2 (for the coin state |0〉) and −Δθ/2 (for the coin state |1〉) and two 0° HWPs
In this case, the coin operator Sc can be implemented by a cos2 ψ/sin2 ψ beam splitter (BS) and the operator Tp can be implemented via two HWPs oriented at 0° and two HWPs oriented at Δθ/2 (step forward) and −Δθ/2 (step back), as shown in Fig. 1b. Note that each of the HWPs oriented at 0° can be replaced by a mirror.
In each step of a DTQW in polarization space, the state of the system can be expressed as |Ψ0〉p|0〉 + |Ψ1〉p|1〉, with
where \(a^{\prime}_k = a_k/C_a\), \(b^{\prime}_k = b_k/C_b\), \(C_a = \sqrt {{\sum} |a_k|^2}\), \(C_b = \sqrt {{\sum} |b_k|^2}\), Na = Np/Ca, Nb = Np/Cb, and Np is the normalization coefficient, which guarantees \(\mathop {\sum}\nolimits_k |a_k|^2 + \mathop {\sum}\nolimits_k |b_k|^2 = 1\). If one derives all values of ak and bk, the probability distribution of the DTQW can be obtained as \(|a_k|^2 + |b_k^2|\).
The values of ak (bk) can be obtained by using \(a_k = C_{a}{a_{k}^\prime}\) (\(b_k = C_{b}{b_{k}^\prime}\)). Note that |Ψ0〉p (|Ψ1〉p) has the same form as that of |Ψ〉q in Eq. (4) and the condition \(\mathop {\sum}\nolimits_k |a^{\prime}_k|^2 = 1\) \(\left(\mathop {\sum}\nolimits_k |b^{\prime}_k|^2 = 1\right)\) is satisfied. By using the encoding method introduced in the “Methods” section, \(a^{\prime}_k\) and \(b^{\prime}_k\) can be obtained one at a time by implementing the DTQW with different angles Δθ and measuring |Ψ0〉p and |Ψ1〉p in path |0〉 and path |1〉, respectively. Next, Ca and Cb can be obtained by solving two equations
where \(r = |\mathop {\sum}\nolimits_k a_k{\mathrm{cos}}(k\theta )|^2/|\mathop {\sum}\nolimits_k b_k{\mathrm{sin}}(k\theta )|^2\) is the ratio between the number of photons counted in path |0〉 and those counted in path |1〉 at the same time period for an arbitrary θ ≠ 0. With this protocol, DTQWs with the walker initially in an arbitrary superposition state can be easily implemented and the entire DTQW state can be obtained rather than just the probability distribution. It seems that DTQWs must be performed for at least N times, to obtain an N-dimensional state of the walker. Actually, in other DTQW experiments, the probability of each walker position is measured one by one, i.e., the DTQW also needs to be performed and measured for at least N times to obtain the probability distribution of N positions of the walker, unless the walker state is encoded by the paths of photons and multiple detectors are used simultaneously.
Experimental demonstrations
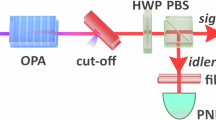
A feasible linear-optical setup for a DTQW in the photon polarization space is shown in Fig. 2. A pair of photons are generated by the type-I spontaneous parametric downconversion in a 3-mm-thick nonlinear beta-barium borate (BBO) crystal pumped by a 100-mW diode laser (centered at 405.8 nm). One photon is directly detected by detector D0 as the trigger and the other photon is adopted to make a DTQW. Then an arbitrary coin state can be initialized by a combination of one polarizing beam splitter (PBS), two QWPs, and one HWP. An arbitrary state of the walker’s position is represented as a polarization state, which can be easily initialized by using two HWPs on the two paths of the DTQW photon after the PBS.
Schematic of the experimental setup for a quantum walk in the polarization space, in which D0 is a single-photon detector and D1 (D2) represents the standard polarization analysis detector. A pair of photons are generated in the BBO crystal. One photon is detected directly by D0 as the trigger and another photon is adopted to make the DTQW. The initial states of the coin and the walker are prepared in the light-yellow block. The DTQW is realized with two optical loops. The photons experience different steps of the DTQW and can be distinguished by their arrival times at D1 or D2 after a trigger event. PBS polarizing beam splitter
In Fig. 3, we show the results of the 1D Hadamard (i.e., setting ψ = π/4) DTQW with an initial state of (0.8|−1〉p + 0.6|1〉p)|0〉. Besides the probability distribution of the walker’s position |ak|2 + |bk|2, the coefficients ak and bk of the states |Ψ0〉p and |Ψ1〉p for a two-step DTQW, a four-step DTQW, and a six-step DTQW are obtained and compared with the theoretical results. Note that the error bars only indicate statistical uncertainty, which are obtained by numerical simulations. Our results indicate that the protocol introduced here is realizable in experiments, and DTQW with small errors can be implemented by using the setup shown in Fig. 2.
Theoretical and experimental amplitudes ak, bk, and the probability |ak|2 + |bk|2 of the 1D Hadamard DTQW after two, four, and six steps, with an initial state of (0.8|−1〉p + 0.6|1〉p)|0〉. The green (blue) bars represent the experimental (theoretical) results. The red error bars represent statistical errors
Since the walker is initially in a superposition state of positions |−1〉p and |1〉p, the outermost positions of the walker after an n-step DTQW are denoted by |− n− 1〉p and |n + 1〉p. To simplify the calculation of ak and bk, we have used an+1 = 0 and b−n−1 = 0 for this type of DTQW. In this case, only n different Δθ are needed to obtain ak and bk for an n-step DTQW.
The initial state of the walker’s position can be easily prepared by rotating the angles of the HWPs in our experiment. We have also experimentally studied the DTQW with the initial state \((0.6| - 2\rangle _p + |0\rangle _p + 0.8|2\rangle _p)|0\rangle /\sqrt 2\). The results of the reconstructed ak, bk, and |ak|2 + |bk|2 after a six-step DTQW are shown in Fig. 4, which also fit well with the theoretical results.
Theoretical and experimental amplitudes ak, bk and the probability |ak|2 + |bk|2 for a six-step DTQW with an initial state of \((0.6| - 2\rangle _p + |0\rangle _p + 0.8|2\rangle _p)|0\rangle /\sqrt 2\). The green (blue) bars show the experimental (theoretical) results. The red error bars represent statistical errors
By means of this DTQW experiment, we also study the relation between the spread speed s and the initial state of the walker’s position. The spread speed s is defined as s(n) = [σ(n) − σ(0)]/n, where σ(n) is the variance of the position for an n-step DTQW. The results for a four-step DTQW are obtained and plotted in Fig. 5a, in which the initial state is set as \(|{\mathrm{\Phi }}_0\rangle = \left( {\alpha | - 1\rangle _p + \sqrt {1 - \alpha ^2} |1\rangle _p} \right)\left( {|0\rangle + i|1\rangle } \right)/\sqrt 2\), with α ∈ (−1, 1). It is shown that different initial states of the walker’s position will lead to different spread speeds of DTQW. Especially, for the DTQWs with α and −α (α ≠ 0), they have different σ(n) and s(n) (n > 0) though starting with the same σ(0), which is quite different from the classical random walk as shown in Fig. 5a, because of the quantum interference. In Fig. 5a, we also give the simulated relation of s ~ α for a DTQW with n = 16 and n → ∞. It is shown that the properties of the DTQW starting from superposition states of the walker are very different from that starting from a single position of the walker. For example, the parameter s for α ≠ 0 approaches a constant more slowly than that for α = 0, as the number of DTQW steps increases.
a Relation between the spread speed s and the initial state of the walker’s position for DTQWs with the number of steps n = 4 (red), n = 16 (blue), and n → ∞ (green). The thin solid curves are from the corresponding classical random walks for 4, 16, and 50 steps, which have a symmetry on the two sides of α = 0. b Relation between the entropy E and the initial state of the walker’s position for DTQWs with the number of steps n = 4 (red), n = 16 (blue), and n → ∞ (green). The initial state of the DTQW is assumed to be \((\alpha | - 1\rangle _p + \sqrt {1 - \alpha ^2} |1\rangle _p)(|0\rangle + i|1\rangle )/\sqrt 2\). The curves are from our theoretical calculations. The red dots show the experimental data and the red error bars represent statistical errors
A significant advantage of our DTQW protocol is that the whole final state of the coin and the walker’s position can be obtained, rather than the position distributions only in other DTQW experimental schemes. In this case, we can investigate the entanglement between the coin and the walker in experiments by calculating the entropy of the reduced density matrix of the coin. The entropy is defined as E = −Tr(ρclog2ρc), where ρc = Trx(ρcx) is obtained by tracing out the walker’s position.
The E ~ α relation of DTQW with n = 4 from the experiment and of a DTQW with n = 4, n = 16, and n → ∞ from the theory is plotted in Fig. 5b. The properties of entanglement (entropy) of a DTQW with nonlocal initial states have been studied theoretically in refs. 19,25 As the number of DTQW steps increases, the entropy E with the initial state |Φ0〉 will start from 0, then oscillate, and approach to the asymptotic entanglement19,37
As shown in Fig. 5b, the E ~ α relation for n = 4, n = 16, and n → ∞ have very similar forms, so most properties of the entanglement can be obtained by a DTQW with a low step, such as a DTQW with four steps. It indicates that different initial states of the walker will lead to different behaviors of entanglement E. The maximum (minimum) E is obtained for \(\alpha \sim - \sqrt 2 /2\) (\(\alpha \sim \sqrt 2 /2\)). This also indicates that the rate at which the asymptotic value for entanglement is approached is faster for higher entanglement, which fits with the result in ref. 19 For a local initial state (i.e., α = 0, ±1), E with n = 16 is close to the asymptotic \(\bar E\), while E with n = 4 is not. For the nonlocal initial state with \(\alpha = - \sqrt 2 /2\) (\(\alpha = \sqrt 2 /2\)), E with both n = 16 and n = 4 are (are not) close to the asymptotic \(\bar E\). Comparing Fig. 5a with Fig. 5b, it is clear that in general, a larger spread speed of the DTQW corresponds to a larger entanglement between the coin and the walker.
Discussion
To implement DTQWs for larger steps, the errors of the experiment should be analyzed and improved. The errors are related to the following factors:
-
(i)
The number of coincidence counts: Because of the leakage of photons at BS 1, the number of coincidence counts will decrease rapidly with increasing the DTQW steps. The ratio of reflection to transmission of all BSs adopted in our experiment is 50:50. The loss of detected photons after every two steps of DTQW is about 70%. It is an advantage of two optical loops adopted in the setup: photons are leaked and detected after every two steps rather than after each step.
The errors in the experiment can be reduced by increasing the number of coincident counts. One method is to replace the 50:50 coupler (i.e., BS 1) by a coupler with better ratios. The other method is to increase the number of input photons. This can be achieved in several ways. For example, the BBO can be replaced by a high-efficiency periodically poled KTiOPO4 (PPKTP), the power of the laser can be improved, or weak laser pulses can be directly used as the input photons of DTQW.
-
(ii)
The quality of the interference in the optical loops: QWs are different from classical random walks because of quantum interference. There are two optical loops in the setup. To guarantee good interference of DTQW, anticlockwise and clockwise optical paths must be adjusted to be the same in each loop, and two loops must be adjusted to match each other. In general, the quality of the interference will become worse when increasing the walk steps. An important factor leading to interference degradation is the imperfections of devices, such as the reflection dependence of the polarization and nonplanar optical surfaces.34,35
To show the scalability of this DTQW protocol and the setup, we estimate the maximum number of steps that are in principle achievable. We assume the use of perfect devices (including detectors). In addition, we assume that the loss of detected photons after every two steps of a DTQW is 70%. By replacing the 50:50 coupler with a 99:1 coupler and replacing the input single photons with laser pulses of 1.4-W power (5 MHz), there should be ~10,000 photons detected in 1 second after 150 steps, provided that the signal-to-noise ratio can be improved by adding an active switch to couple the photons out of the loops.
In summary, we have experimentally demonstrated a 1D DTQW with the walker moving in the polarization space of single photons. This work differs from previous works in that the walker is initially in a superposition state and the walker’s position is encoded using the photon polarization state. The ability to operate with arbitrary initial superposition states of DTQWs and to implement DTQWs in a low-dimensional space opens an avenue not only for discovering more properties of DTQWs but also more DTQW applications. This DTQW protocol is quite general and can be applied to other quantum systems (e.g., cavity or circuit QED systems). This work may be extended to realize multi-dimensional DTQWs, which are of importance for large-scale quantum computing based on QWs. Moreover, the proposed encoding method enables one to encode an arbitrary high-dimensional quantum state, using a single physical qubit, and may be adopted to implement other quantum information tasks.
Methods
The encoding method
Suppose there is an n-dimensional state
where |k〉 (k = 1, 2, …, n) are orthogonal states. In the following, we propose a method to encode this state with a two-dimensional qubit and to read out all ak from the qubit by measurement. The obtained ak can be used to reconstruct the n-dimensional state |Ψ〉 of Eq. (3).
The state |Ψ〉 can be encoded by using n non-orthogonal states \(|k\rangle _q = {\mathrm{cos}}\theta _k|0\rangle + {\mathrm {e}}^{i\phi _k}{\mathrm{sin}}\theta _k|1\rangle\) (k = 1, 2, …, n) of a qubit, which correspond to n different points in the Bloch sphere of the qubit. With |k〉 replaced by |k〉q, the state of the qubit in the encoded state can be expressed as
where \(C_0 = \mathop {\sum}\nolimits_{k = 1}^n a_k{\mathrm{cos}}\theta _k\), \(C_1 = \mathop {\sum}\nolimits_{k = 1}^n a_ke^{i\phi _k}{\mathrm{sin}}\theta _k\), and \(N_q = \sqrt {|C_0|^2 + |C_1|^2}\). Note that the same state |Ψ〉q can be constructed by performing suitable operations on an initial state of the qubit, which is just the case considered in the DTQW protocol above.
We now show how to read out ak from |Ψ〉q. The density matrix of the encoded state |Ψ〉q can be expressed as
which can be easily obtained by using tomographic measurement on the qubit. Then one homogeneous equation of ak can be obtained as
where R = C0/C1 is obtained from the measured ρq as
In this way, (n − 1) homogeneous equations for ak can be obtained by repeatedly encoding the state |Ψ〉 onto a qubit with (n − 1) different sets \(\left\{ {|1\rangle _q^j,|2\rangle _q^j, \ldots ,|n\rangle _q^j} \right\}\) (where j = 1, 2, …, n − 1, and \(|k\rangle _q^j = {\mathrm{cos}}\theta _k^j|0\rangle + {\mathrm {e}}^{i\phi _k^j}{\mathrm{sin}}\theta _k^j|1\rangle\)), and by measuring the corresponding Rj one at a time. Then ak (k = 1, …, n) can be solved from the (n − 1) homogeneous equations
and the normalization condition \(\mathop {\sum}\nolimits_{k = 1}^n {\kern 1pt} |a_k|^2 = 1\). Now the n-dimensional encoded state is reconstructed. Note that the n-dimensional state is actually encoded in (n − 1) qubits rather than one qubit, and all information is reconstructed from the (n − 1) qubits. Of course, one can adopt only one physical qubit which will be repeatedly used.
To study the generality and scalability of this encoding method, we calculated the fidelity between random 50-dimensional encoded states and their reconstructed states from numerical simulations of the encoding process, in which random errors of measured Rj were assumed to be within ±10% and a specific choice of the non-orthogonal states
was used (i.e., \(\theta _k^j = jk{\mathrm{\Delta }}\theta\) and \(\phi _k^j = k{\mathrm{\Delta }}\phi\)). The averaged fidelity over 1000 random simulations was obtained and its dependence on Δθ and Δϕ is plotted in Fig. 6a. The averaged fidelity is larger than 90% in the ~41% area of Δθ ∈ (0, 180°) and Δφ ∈ (0, 360°). It is not hard to find suitable θk and ϕk to implement the encoding method, and high fidelity can be achieved for encoding large-dimensional states if measurement errors are not very large.
Moreover, we experimentally demonstrated the encoding and reading of a 16-dimensional state in a linear optics system. At first, we encode a uniform state \({\mathrm{\Phi }}_{16} = \frac{1}{4}\mathop {\sum}\nolimits_{k = 1}^{16} |k\rangle\) in the two-dimensional polarization space of single photons by using Δθ = 22° and Δϕ = 12° in Eq. (9). This encoding can be easily implemented by injecting photons into an adjusted setup consisting of two QWPs and one HWP, which can be used to construct an arbitrary one-qubit gate in the polarization space. Then density matrices of the encoding photons can be measured and the initial uniform state can be reconstructed. The experimental result of the reconstructed state is shown in Fig. 6b, and a high fidelity of 99.1% is achieved.
The encoding method introduced here is feasible for the present technology of linear optics and can be easily applied to other quantum systems. One key advantage for the use of this encoding method is the simplicity of the setup, because only one physical qubit is needed.
The implementation of a DTQW
With the setup shown in Fig. 2, the steps of a DTQW are as follows:
-
(i)
Preparation of the initial states of the coin and the walker: An arbitrary coin state can be initialized by a combination of one PBS, two QWPs, and one HWP. An arbitrary state of the walker’s position is represented as a polarization state, which can be easily initialized by using two HWPs on the two paths of the DTQW photon after the PBS. Note that the lengths of the two paths from the PBS to BS 2 should be the same by adjusting the prism.
-
(ii)
Steps for implementing the DTQW: The DTQW starts as the photon enters BS 2 for the first time and is implemented in loop 1 and loop 2. In each loop, the anticlockwise and clockwise photon paths are adjusted to overlap with each other and the loop length is designed to be ~30 cm. Here, the loop’s interference visibility is measured as ~98.5%. The steps for the DTQW realization are described below:
Step 1: As the photon passes through BS 2, the coin state is tossed by the operator Sc. The photon after BS 2 will rotate anticlockwise (or clockwise) in loop 2, and the walker achieves a rotation of Δθ (or −Δθ) in the polarization space via HWP 2, just like that shown in Fig. 1a.
Step 2: Then the photon goes through BS 2 a second time and the coin is tossed once again. After BS 2, one possibility is that the photon will rotate anticlockwise (or clockwise) in loop 1 and the walker’s state achieves a rotation of Δθ (or −Δθ) in the polarization space via HWP 1. The photon will enter BS 2 one more time, and the next step of the DTQW will start. The other possibility is that the photon goes through BS 1 and then is detected by D1 (D2) to get ak (bk) for a two-step DTQW.
-
(iii)
Extracting the final state of a 2n-step DTQW: The final state of a 2n-step DTQW can be obtained by measuring the photons which are detected after repeating steps 1 and 2 for n times. Because the total length of loop 1 and loop 2 is about 60 cm, the time gap between the photon detection after a (2n−2)-step DTQW and the photon detection after a 2n-step DTQW is ~2 ns. In this case, the time window of the coincidence detections between D0 and D1 (D2) is set as 0.49 ns.
Data availability
All data supporting the findings of this study are available within the article or from the corresponding author upon reasonable request.
References
Aharonov, Y., Davidovich, L. & Zagury, N. Quantum random walks. Phy. Rev. A 48, 1687 (1993).
Shenvi, N., Kempe, J. & Whaley, B. K. Quantum random-walk search algorithm. Phys. Rev. A 67, 052307 (2003).
Franco, C. D., McGettrick, M. & Busch, T. Mimicking the probability distribution of a two-dimensional Grover walk with a single-qubit coin. Phys. Rev. Lett. 106, 080502 (2011).
Jeong, Y.-C., Franco, C. D., Lim, H.-T., Kim, M. S. & Kim, Y.-H. Experimental realization of a delayed-choice quantum walk. Nat. Commun. 4, 2471 (2013).
Crespi, A. et al. Anderson localization of entangled photons in an integrated quantum walk. Nat. Photon. 7, 322–328 (2013).
Zhan, X. et al. Detecting topological invariants in nonunitary discrete-time quantum walks. Phys. Rev. Lett. 119, 130501 (2017).
Peruzzo, A. et al. Quantum walks of correlated photons. Science 329, 1500–1503 (2010).
Kitagawa, T., Rudner, M. S., Berg, E. & Demler, E. Exploring topological phases with quantum walks. Phys. Rev. A 82, 033429 (2010).
Buluta, I. & Nori, F. Quantum simulators. Science 326, 108–111 (2009).
Georgescu, I. M., Ashhab, S. & Nori, F. Quantum simulation. Rev. Mod. Phys. 86, 153 (2014).
Childs, A. M. Universal computation by quantum walk. Phys. Rev. Lett. 102, 180501 (2009).
Underwood, M. S. & Feder, D. L. Universal quantum computation by discontinuous quantum walk. Phys. Rev. A 82, 042304 (2010).
Childs, A. M., Gosset, D. & Webb, Z. Universal computation by multiparticle quantum walk. Science 339, 791–794 (2013).
Kurzynski, P. & Wojcik, A. Quantum walk as a generalized measuring device. Phys. Rev. Lett. 110, 200404 (2013).
Lambert, N. et al. Quantum biology. Nat. Phys. 9, 10–18 (2013).
Kempe, J. Quantum random walks: an introductory overview. Conte Phys. 44, 307–327 (2003).
Venegas-Andraca, S. E. Quantum walks: a comprehensive review. Quantum Inf. Process. 11, 1015–1106 (2012).
Cardano, F. et al. Quantum walks and wavepacket dynamics on a lattice with twisted photons. Sci. Adv. 1, e1500087 (2015).
Abal, G., Siri, R., Romanelli, A. & Donangelo, R. Quantum walk on the line: entanglement and nonlocal initial conditions. Phys. Rev. A 73, 042302 (2006).
Strauch, F. W. Relativistic quantum walks. Phys. Rev. A 73, 054302 (2006).
Chandrashekar, C. M. & Laflamme, R. Quantum phase transition using quantum walks in an optical lattice. Phys. Rev. A 78, 022314 (2008).
Romanelli, A. Distribution of chirality in the quantum walk: Markov process and entanglement. Phys. Rev. A 81, 062349 (2010).
Valcrcel, G. J., Roldn, E. & Romanelli, A. Tailoring discrete quantum walk dynamics via extended initial conditions. New J. Phys. 12, 123022 (2010).
Zhang, W. W., Goyal, S. K., Gao, F., Sanders, B. C. & Simon, C. Creating cat states in one-dimensional quantum walks using delocalized initial states. New J. Phys. 18, 093025 (2016).
Orthey, A. C. & Amorim, E. P. M. Asymptotic entanglement in quantum walks from delocalized initial states. Quantum Inf. Process. 16, 224 (2017).
Xue, P. et al. Experimental quantum-walk revival with a time-dependent coin. Phys. Rev. Lett. 114, 140502 (2015).
Do, B. et al. Experimental realization of a quantum quincunx by use of linear optical elements. Opt. Soc. Am. B 22, 020499 (2005).
Sansoni, L. et al. Two-particle bosonic-fermionic quantum walk via integrated photonics. Phys. Rev. Lett. 108, 010502 (2012).
Schmitz, H. et al. Quantum walk of a trapped ion in phase space. Phys. Rev. Lett. 103, 090504 (2009).
Zahringer, F. et al. Realization of a quantum walk with one and two trapped ions. Phys. Rev. Lett. 104, 100503 (2010).
Flurin, E. et al. Observing topological invariants using quantum walks in superconducting circuits. Phys. Rev. X 7, 031023 (2017).
Karski, M. et al. Quantum walk in position space with single optically trapped atoms. Science 325, 174–177 (2009).
Xue, P. & Sanders, B. C. Two quantum walkers sharing coins. Phys. Rev. A 85, 022307 (2012).
Broome, M. A. et al. Discrete single-photon quantum walks with tunable decoherence. Phys. Rev. Lett. 104, 153602 (2010).
Schreiber, A. et al. Photons walking the line: a quantum walk with adjustable coin operations. Phys. Rev. Lett. 104, 050502 (2010).
Bouwmeester, D., Marzoli, I., Karman, G. P., Schleich, W. & Woerdman, J. P. Optical Galton board. Phys. Rev. A 61, 013410 (1999).
Carneiro, I. et al. Entanglement in coined quantum walks on regular graphs. New J. Phys. 7, 156 (2005).
Acknowledgements
This work is supported in part by the NKRDP of China (Grant No. 2016YFA0301802) and the National Natural Science Foundation of China under Grant Nos. [11504075, 11374083, 11774076, 11375003, and 11775065]. This work is partially supported by MURI Center for Dynamic Magneto-Optics via the Air Force Office of Scientific Research (AFOSR) (FA9550-14-1-0040), Army Research Office (ARO) (Grant No. W911NF-18-1-0358), Asian Office of Aerospace Research and Development (AOARD) (Grant No. FA2386-18-1-4045), Japan Science and Technology Agency (JST) (via the Q-LEAP program, the ImPACT program, and the CREST Grant No. JPMJCR1676), Japan Society for the Promotion of Science (JSPS) (JSPS-RFBR Grant No. 17-52-50023 and JSPS-FWO Grant No. VS.059.18N), the RIKEN-AIST Challenge Research Fund, and the John Templeton Foundation.
Author information
Authors and Affiliations
Contributions
Q.-P.S. devised various aspects of the project and designed the experimental methodology. Q.-P.S., Y.Z., J.-Q.Z. and S.-J.X. carried out the experiment and analyzed the data. Q.-P.S., L.Y., C.-P.Y., J.-S.J. and X.-Q.X. developed the theoretical aspects. Q.-P.S., C.-P.Y. and F.N. wrote the paper, with contributions from K.F.C., Z.S. and Q.J.X. All authors discussed the results and contributed to refining the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Su, QP., Zhang, Y., Yu, L. et al. Experimental demonstration of quantum walks with initial superposition states. npj Quantum Inf 5, 40 (2019). https://doi.org/10.1038/s41534-019-0155-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-019-0155-x
This article is cited by
-
High-fidelity state transfer via quantum walks from delocalized states
Quantum Information Processing (2024)
-
Transport properties in directed quantum walks on the line
Quantum Information Processing (2023)
-
Negative correlations can play a positive role in disordered quantum walks
Scientific Reports (2021)
-
Topological quantum walks in cavity-based quantum networks
Quantum Information Processing (2020)