Abstract
A device being a pinnacle of development of an optical quantum memory should combine the capabilities of storage, inter-communication, and processing of stored information. In particular, the ability to capture a train of optical pulses, interfere them in an arbitrary way and finally, perform on-demand release could realize arbitrary optical computation. Here we demonstrate the operation of a coherent optical memory being able to store optical pulses in the form of collective spin-wave excitations in a two-dimensional wavevector space. During storage, we perform complex beamsplitter operations and demonstrate a variety of protocols implemented at the processing stage, including real-time controlled interference of a pair of spin-wave modes with 95% visibility. The highly multimode structure of the presented memory lends itself to enhancing classical optical telecommunication, as well as parallel processing of optical qubits at the single-photon level.
Similar content being viewed by others
Introduction
As optical quantum memory technologies mature, the range of their applications increases. Basic memories operating in a single temporal and spatial mode can store only a single optical pulse, which may interfere with another incoming pulse. This operation can only be performed in the presence of the coupling light.1 Such memories, based either on Raman scattering or electromagnetically induced transparency (EIT), can achieve high efficiencies,2 but offer very limited capacity as multiplexing is limited by the number of atomic magnetic sublevels employed.2,3,4 While a single atomic ensemble may be split into an array to offer parallel storage of light,5 such a scheme hinders manipulations within the memory as communication between memory cells must be inherently light-based. It is thus highly desirable to independently store many optical pulses within the same group of atoms. Such a multiplexing scheme may utilize either the spatial6,7 or temporal degree of freedom.8,9,10 In the latter case, considered in the context of the atomic-ensemble based quantum memories, the Gradient Echo Memory (GEM)11,12,13,14,15 scheme stands out as an efficient way to engineer the phase-matching at readout stage to achieve mode-selective storage and retrieval. A similar feature is inherently offered by the atomic frequency comb (AFC) memories based on ensembles of ions in solids8,9,16 thanks to their large inhomogeneous broadening. In the spatial degree of freedom atomic ensembles allow storage of light in many angular-emission modes through spin-wave wavevector multiplexing.6,17 These schemes allow storage of hundreds of optical modes, also when used with non-classical states of light.
Manipulation of stored optical pulses, however, remains a substantial challenge, both from technical and fundamental points of view. The AFC memory has been demonstrated to allow pre-programmed interference of two stored pulses with a single output port.18,19 Most recently similar beamsplitter operations in the AFC memory have also been implemented in a multi-dimensional Hilbert space.20 Within the GEM scheme a beamsplitter operation between pre-selected, stored pulses and an input pulse has been realized.21,22 Remarkably, these schemes allow basic spectral and temporal manipulations of stored light. More work is needed however to reach the regime of efficient and arbitrary manipulations. In particular, the ac-Stark shift caused by an additional light field has been studies in optical-lattice based quantum memories,23 as well as used and proposed as a versatile way to realize the GEM scheme24 and to control photon-echoes.25 Recent theoretical proposals went beyond the simple gradient shape and suggested engineering the stored spin-wave shape to realize Kapitsa–Dirac diffraction26 or a quantum memory protected with a disordered password.27 These schemes stand out in relation to an established all-optical technique of manipulating stationary light28—since control light is not present during the manipulation process, decoherence is significantly reduced. Finally, a recent experiment used the ac-Stark shift to realize a spin-wave beamsplitter at the single-excitation level demonstrating Hong–Ou–Mandel interference for stored light.29
Here we present the realization of the ac-Stark-based spin-wave multiport interferometric processor (SMIP) and join the advantages of the transverse wavevector and temporal multiplexing to realize a variety of operations on the stored coherent states of light. The previously untackled regime of complex light patterns used to engineer spin waves is explored, which allows us to tap into the full three-dimensional potential of the wavevector-multiplexed coherent optical memory. We show that thanks to the engineering of the spatial profile of ac-Stark modulation the stored pulses may be processed, interfered, and conditionally retrieved. The scheme features both reprogrammable reordering and interference of pulses within the multiple-input, multiple-output paradigm, essential to realize true unitary operations. In the paper, we first introduce the protocol by deriving its theoretical principles and realizing a scheme reminiscent of the Gradient Echo Memory.12 Next, we realize a series of programmable beamsplitting experiments in spatial and temporal degrees of freedom. High-visibility interference of a pair of modes is demonstrated. Finally, we propose potential further applications and give technical details of the experiment and light-atom propagation simulations involved.
Results
Operation of the light-atom interface
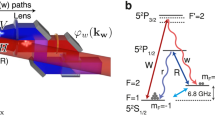
The coherent atomic optical memory based on an elongated (σx × σy × σz ≈ 0.15 × 0.15 × 2.5 mm3) ensemble of Rb-87 atoms employs a strong control field \({\cal E}_C\) to map a weak signal field \({\cal E}_{in}\) onto the atomic coherence ρhg between the two meta-stable ground states, for which we take |g〉 → F = 1, mF = −1, and |h〉 → F = 2, mF = 1 (see Fig. 1c for the atomic level scheme). In the experiment the atoms are first optically pumped to the |g〉 state and control and signal fields (both λ = 780 nm) operate with opposite circular polarizations. Typically we use 300 ns long pulses for storage and retrieval of atomic coherence. While the interaction is well characterized by a set of coupled Maxwell-Bloch equations (see Methods), first we rather choose to describe the atom-light coupling qualitatively. In particular, Fig. 1b illustrates the geometry in which the coupling and signal fields co-propagate through an elongated atomic ensemble. Assuming that the coupling beam diameter is significantly larger than the transverse size of the ensemble, we may actually solve the coupled equations within the first order in the coupling strength and obtain a simple result by which a signal \({\cal E}(k_x,k_y)\) couples to an atomic coherence
where \(K_{z0} = \sqrt {\omega ^2{\mathrm{/}}c^2 - k_x^2 - k_y^2} - \omega _C{\mathrm{/}}c\), δ is a Dirac delta function and ω and ωC are frequencies of signal and coupling fields, respectively, and c is the speed of light. For kx = ky = 0 the longitudinal wavevector simplifies to a constant component Kz0 = Δ0/c ≈ 0.14 rad mm−1, where Δ0 ≈ 2π × 6.8 GHz is the nominal frequency splitting between levels |g〉 and |h〉. To exclude these trivial dependencies from further consideration we will define the stored spin-wave excitation as
where \({\cal F}\) stands for the Fourier transform in the spatial domain, N(x, y, z) is the atom number density and \({\ast}\) denotes convolution (here in the wavevector space). Importantly, after mapping the optical field we obtain a spin-wave excitation at Kz = 0 in terms of S.
Spin-wave processing with ac-Stark modulation. a Simplified simulation of exemplary protocol implemented on SMIP, presenting the light and spin-wave domain transformations. By manipulating the spin wave using spatially varying ac-Stark (acS) shift three pulses are stored, processed and released in reversed order. In the three-dimensional plot, the colored blobs correspond to a spin-wave density exceeding a critical value. The coloring is selected to correspond to a light pulse from which the spin wave originates. b Pulses are sent to SMIP in different time-space modes, then ac-Stark manipulation is applied and at the end pulses are released. Released pulses can be detected either on Avalanche Photodiode (APD) or sCMOS camera situated in the far field (ff) for temporal or angular resolution, respectively. c Rubidium-87 energy level configuration utilized for storing and processing coherent light pulses. d Projection of the b on perpendicular plane exposing 2-d (x, z) ac-Stark modulation capabilities using Spatial-Light Modulator (SLM)
The process of reverse mapping or retrieval driven by the same coupling field occurs in a symmetric way. Essentially, an atomic spin-wave excitation will be mapped onto an optical field proportional to S in terms of the transverse wavevector dependence only if Kz = 0. This requirement arises due to the phase-matching condition. In particular, the allowed spread along Kz is inversely proportional to the atomic cloud length σz and most importantly spin waves with large Kz component (Kzσz ≫ 1) will remain stored in the memory. This remains true unless we change the frame of reference significantly by selecting much different Kx, Ky and change them substantially by δKx, δKy, as the actual phase matching is satisfied on a Kz = 0 plane only for original (unmodified) spin waves. When we modify the transverse wavevector component the plane tilts and for large Kx (Ky) the spin wave becomes phase-mismatched. However, for small Kx (Ky) and δKx (δKy) the phase-mismatch \({\mathrm{\Delta }}K_z \approx \frac{\lambda }{{4\pi }}\left( {\left( {K_x + \delta K_x} \right)^2 - K_x^2} \right)\) is small and thus we may use the phase-matching planar approximation to learn which spin waves are retrievable.
Spin-wave manipulation with the ac-Stark effect
As discussed above, only a limited space, or more precisely a thin three-dimensional volume around Kz = 0 plane in the wavevector space may be populated by spin waves by means of Raman interaction. To manipulate the spin waves within and beyond this volume we use an additional far off-resonant beam (marked in Fig. 1c as acS) that induces an additional differential ac-Stark shift between levels |g〉 and |h〉 of ΔacS that adds to Δ0. The ac-Stark beam propagating along the y-direction is z-polarized and red-detuned by ~1 GHz from the |h〉 → |e〉 transition induces ΔacS ~ 1 MHz ac-Stark shift with ~100 mW beam power. This shift causes the atomic coherence ρhg, and thus the spin wave, to accumulate an additional phase φacS = ΔacST over the interaction time T. Typically we use ac-Stark pulses of approx. T ~ 2 μs duration. By spatially shaping the ac-Stark beam intensity IacS(x, z) (see Methods and refs. 29,30 for details) we induce a spatially-dependent phase shift φacS(x, z) ∝ IacS(x, z), which due to the geometry of the experiment is limited to two dimensions (see Fig. 1b). Any spin wave is then reshaped as:
A basic example is an ac-Stark analog of the GEM, in which a phase shift linear in z (φacS = βz) shifts the spin wave in the Kz direction by β.
Here we work with nearly plane-wave optical modes characterized by small wavevector (angular) spread and therefore the spin waves are well-localized in the wavevector space. Discrete mode transformation in such a space are most conveniently performed by a spatially periodic ac-Stark modulation. Taking a spatial period 2π/kacS of the modulation in the form \(\varphi _{{\mathrm{acS}}}(x,z) = \varphi _{{\mathrm{acS}}}^{{\mathrm{periodic}}}({\bf{k}}_{{\mathrm{acS}}} \cdot (x,z))\) we may rewrite the spin-wave transformation (3) using Fourier series as:
with Fourier coefficients cn defined as:
Figure 1a presents a simplified simulation (assuming perfect write-in and read-out) of a protocol operation within this paradigm. In this exemplary protocol three pulses \({\cal E}_0\), \({\cal E}_{ - k}\), \({\cal E}_k\) with transverse optical wavevector component kx equal 0, −k and k, respectively, are stored, processed and released from the memory. When the first pulse is mapped to the ensemble, the created spin wave is phase-modulated using a sawtooth-shaped (saw) (periodic) modulation \(\varphi _{{\mathrm{acS}}}(x,z) = \varphi _{{\mathrm{acS}}}^{{\mathrm{saw}}}(k_{{\mathrm{saw}}}z)\). Such a modulation with amplitude equal 2π shifts the spin wave in the Kz direction by ksaw, making the spin wave unreadable, as ksawσz ≫ 1. Next, two pulses with kx components separated by 2k arriving at the same time are written to the ensemble. Then, square-shaped (sq) modulation \(\varphi _{{\mathrm{acS}}}(x,z) = \varphi _{{\mathrm{acS}}}^{{\mathrm{sq}}}(k_{{\mathrm{sq}}}x)\) with ksq = 2k is applied. The amplitude and phase of this modulation are chosen so that the first three Fourier coefficients are in following relations: \(c_{ - 1}^{{\mathrm{sq}}} = c_0^{{\mathrm{sq}}} = - c_1^{{\mathrm{sq}}}\). This way the two pulses with non-zero kx component are combined in a way reminiscent of a two mode beamsplitter transformation29 resulting in constructive interference in the mode with kx = −k. Note that the spin wave component corresponding to the first pulse is transformed (split) as well, but because of shifted Kx and most importantly Kz component it does not take part in the interference. At this stage the first readout is performed during which all readable (zero Kz) spin wave components are converted to light pulses. To read out the first pulse, all the previous transformations are undone by applying versions of previous modulations shifted by half a period in reversed order. At the very end of the protocol, the first pulse is retrieved.
Reconfigurable ac-Stark Echo Memory
For the experimental demonstration we begin by moving the spin waves outside the zero Kz to allow storage of subsequent incoming optical pulses. This configuration, most reminiscent of the GEM12 and already proposed as a way to reverse pulses order in the two-level GEM,26 here operates best with a triangle-shaped grating (pattern A), which can be conventionally written in a closed form:
with ktri = 9.6 rad/mm \(\hat e_{z}\) for which most essentially the zeroth order \(c_{0}^{{\mathrm{tri}}} \propto \left| {{\mathrm{sinc}}({\cal A}{\mathrm{/}}2)} \right|\) disappears periodically with modulation strength \({\cal A}^{{\mathrm{tri}}}\) (with period equal 2π) except for \({\cal A}^{{\mathrm{tri}}} = 0\). With this scheme, we may thus apply a grating with \({\cal {A}}^{\mathrm{tri}} = 2{\pi}\) and move the pulse out of the Kz = 0 plane. Due to the periodicity of \(c_{0}^{\mathrm{tri}}\) in the modulation strength \({\cal A}^{{\mathrm{tri}}}\), if a subsequent pulse is stored, the first and any previous pulse remains phase-mismatched at consecutive grating operations with amplitude \({\cal A}^{{\mathrm{tri}}} = 2\pi\). To retrieve the pulses we apply a pattern with the same amplitude shifted by a half of period in the spatial domain (pattern B), that restores the spin waves to the Kz = 0 plane.
The scheme lends itself to both first-in, first-out (FIFO) and last-in, first-out (LIFO) operation, as shown in Fig. 2. For the FIFO operation on two pulses, after storage of a second pulse, we apply a shifted pattern B to simultaneously transfer the first pulse back to the Kz = 0 plane and phase-mismatch the second pulse. After the first retrieval operation, the phase matching is restored for the second pulse with pattern A.
Operation of the ac-Stark Echo Memory and spin-wave Mach–Zehnder interferometer. a–d Simulated time- and wavevector resolved spin-wave density S(Kz,t) (Spin wave) during operation of the memory with corresponding (measured) Control and ac-Stark field sequences along with measured input-output signal traces (solid fill) as well as proper simulation results (line). a, b correspond to storage and retrieval of two coherent optical pulses in the last-in, first-out (LIFO) a and first-in, first-out (FIFO) configurations b. c is the LIFO configuration for storage of three pulses. d Mach–Zehnder interferometer configuration for pulses stored at different times, presented for a specific choice of phase leading to constructive interference in the second port (port b). e ac-Stark triangle-wave (tri) modulation patterns for storage (pattern A) retrieval (pattern B) of subsequent pulses. Pattern B is a shifted by a half of a period version of pattern A with the same amplitude. The same patterns are used in the Mach–Zehnder interferometer case. f Ramsey fringes, i.e., light intensities registered in two ports (port a, port b) of the beamsplitter as a function of two-photon detuning δ. The error bars correspond to standard error of the mean (s.e.m) derived from many collected signal traces for each data point
The efficiency of our memory is currently limited by the optical depth of the ensemble as well as available coupling power. By comparing the intensity of light at the input and output of the memory we obtain write-in efficiency for the first pulse of about 59 and 44% for the second pulse. For immediate retrieval (as for the second pulse in LIFO scheme) we achieve 35% efficiency, while net storage and retrieval efficiency is equal 44% × 35% = 15%. For the pulses that are manipulated the efficiency is diminished by dephasing due to the ac-Stark light intensity inhomogeneities.30
Programmable beamsplitting of stored optical pulses
To demonstrate the beamsplitting capability for pulses arriving at different times we use again the triangle-wave modulation (tri) in the z-direction, with ktri = 22 rad/mm. After storage of two subsequent pulses (which is done the same way as in FIFO and LIFO demonstration using pattern A) we apply the shifted pattern B for a half of period T, modulating the spin wave with amplitude π instead of 2π (see Fig. 2d). This way the two pulses are combined and Kz = 0 component of resulting spin wave becomes the first output port of the temporal-mode beamsplitter. Then, after the first readout, we modulate the remaining part again with pattern B with amplitude \({\cal {A}} \approx {2.25}{\pi}\) to transfer a part of the second port to readable Kz = 0 plane, then the second readout is performed. Note that it is crucial to always perform the first readout as otherwise the unread spin wave will interfere and spoil the operation of the second output port. It is thus necessary to simulate the operation of this scheme to a full extent, including possibly imperfect first readout which can affect the second output port.
To characterize the interference of two pulses we change the relative phase between the pulses by varying the two-photon detuning δ. Fringes in the intensity registered in the two output ports appear accordingly. Essentially, the phase difference between the two interfering spin waves is the product of the two-photon detuning δ and the time between two storage operations τ. Furthermore, as we move outside the two-photon resonance the interaction becomes inefficient. This behavior is reminiscent of the well-known Ramsey interference. In Fig. 2f we plot the total number of photons collected after the first (port a) and second (port b) readout as a function of the two-photon detuning δ. The observed behavior is properly predicted by the simulation described in detail in Methods. The maximal efficiency achievable in this case (triangle-shaped grating) calculated using the provided Fourier formalism assuming perfect readout is 81% and 60% for port a and b respectively.
The relative phase between the pulses can be also modified within the spin-wave domain. To demonstrate this, we implement another interference protocol; instead of splitting the first pulse into many orders we simply shift its Kz component by ksaw using sawtooth wave modulation:
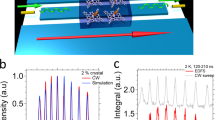
in the z-direction. Then, the second pulse is written to the memory and the resulting spin wave is modulated using a triangle-shaped grating of depth \({\cal {A}}^{{\mathrm{tri}}} \approx 1.16{\pi}\) satisfying the equation \(\left| {c_0^{{\mathrm{tri}}}} \right| = \left| {c_1^{{\mathrm{tri}}}} \right| = \left| {c_{ - 1}^{{\mathrm{tri}}}} \right| \approx 0.53\). The spatial period of the tri modulation is chosen to satisfy \({\bf{k}}_{{\mathrm{tri}}} = {\bf{k}}_{{\mathrm{saw}}} = 22\,{\mathrm{rad/mm}}\,\hat e_z\), thus the pulses are combined in such a manner that the zeroth order of the first pulse overlaps with first diffraction order of the second pulse and vice versa. The first interferometer port is again a resulting Kz = 0 spin wave component, so it can be completely read-out without any additional manipulations. The second port this time is well defined and lies at a plane with Kz = ktri. Thus, in principle the second port could be restored completely by applying reversed sawtooth pattern shifting back the spin wave by −ksaw to the readable region in wavevector space. Due to our setup limitations (see Methods) we probe the second port by applying the tri modulation with an amplitude equal π and subsequently the phase-matched component (Kz = 0) is released. The relative phase between interfering components can be manipulated by changing the phase of one of the gratings (saw or tri), as for any shifted periodic modulation \(\varphi _{{\mathrm{acS}}}^{{\mathrm{periodic}}}(\xi - \zeta )\) the complex amplitudes of subsequent orders change as cn ~ einζ. We directly witness this behavior by shifting the sawtooth grating portrayed in Fig. 3a in the z-direction and measuring interference fringes in the total energy of the released pulses. In Fig. 3c we plot the resulting interference pattern, accompanied by a proper simulation, showing the interference in wavevector space (Fig. 3b). Theoretical maximal efficiency taken as the ratio of cumulative energy of two output ports to total input energy under perfect readout conditions is however limited in this case by \(2\left| {c_0^{{\mathrm{tri}}}} \right|^2 \approx 56{\mathrm{\% }}\). Yet, the rest (unread part) of the spin wave remains in the memory and could be in principle retrieved using proper manipulation.
Asymmetric interferometer with geometric phase control. a The sawtooth-shaped grating (saw) used to shift the spin waves in one Kz direction. b Simulated time and wavevector resolved spin-wave density S(Kz,t) for a one phase point showing the longitudinal (Kz) spin wave mode-mixing during interferometer operation. The most of the spin wave remaining in the memory after two readouts is concentrated around Kz = −22 rad/mm and Kz = 44 rad/mm. Due to the symmetry the contribution outside the Kz range (around Kz = 44 rad/mm) will be the same as around Kz = −22 rad/mm. c Intensity interference fringes for two consecutively retrieved ports (first–port a, second–port b) as a function of sawtooth grating phase ζ. Error bars correspond to s.e.m derived from many collected signal traces for each data point
Transverse space interference and manipulation
To go beyond a single transverse mode we now add the Kx dimension to the scheme. In a simple yet highly robust scenario, we map two equally bright pulses arriving at the same time yet into two different spin waves with Kx = ±k, where k = 75.4 rad/mm. We then apply a sinusoidal grating modulation (pattern presented in Fig. 4a):
with \({\bf k}_{\mathrm{sin}} = 2k\hat e_x\) and \({\cal {A}}^{{\mathrm{sin}}} \approx 0.92\pi\) that again satisfies \(\left| {c_0^{{\mathrm{sin}}}} \right| = \left| {c_1^{{\mathrm{sin}}}} \right| = \left| {c_{ - 1}^{{\mathrm{sin}}}} \right| = {\cal C} \approx 0.55\). In this way the output ports at Kx = ±k are mixtures of both input ports in the 50:50 ratio. We then again use the fact that shifting the grating position ζ changes the phase at orders ±1 by ±ζ. We may thus write the (lossy) beamsplitter transformation as:
Spin-wave interference induced by ac-Stark shift manipulation in the transverse-wavevector space. a The sinusoidally shaped grating pattern used to apply transverse mode (Kx) beamsplitter transformation by ac-Stark modulating the spin waves. b Intensity interference fringes for two transverse-mode ports separated by 2k detected on the sCMOS camera situated in the far field of the ensemble. The grating phase ζ is changed using a piezo-actuated mirror. The error bars correspond to the standard error of the mean (s.e.m) taken as square root of the registered photon numbers
We scan the phase using a piezo-actuated mirror mount in the far field of the ensemble (see Methods for details of the imaging setup) and observe high-visibility interference fringes. Notably, we obtain average visibility of 95% by comparing maximum and minimum intensities observed at each port, as portrayed in Fig. 4b. As in the previous section, the theoretical maximal efficiency in this case (assuming perfect readout) is limited by \(2{\cal C}^2 \approx 60{\mathrm{\% }}\).
Simultaneous spin-wave processing in two dimensions
Finally, we combine the longitudinal and transverse manipulations to exhibit the time-space interference of two sequentially stored pulses. To access the time-space beamsplitting we design the square-wave grating
in the x − z direction \(\varphi _{{\mathrm{acS}}}^{{\mathrm{sq}}}({\bf{k}}_{{\mathrm{sq}}} \cdot (x,z))\), where \({\bf{k}}_{{\mathrm{sq}}} = 12\,{\mathrm{rad/mm}}\,\hat e_x + 5\,{\mathrm{rad/mm}}\,\hat e_z\). The periodic collapse-revival behavior of a \(c_0^{{\mathrm{sq}}} = \left| {{\mathrm{cos}}({\cal {A}}^{{\mathrm{sq}}}{\mathrm{/}}2)} \right|\) allows us to use this very grating for both subsequent storage and interference of two coherent pulses. By applying the square-wave modulation (sq, pattern A in Fig. 5a) of amplitude \({\cal {A}}^{{\mathrm{sq}}} = \pi\) after arrival of the first pulse and \({\cal {A}}^{{\mathrm{sq}}} = \pi {\mathrm{/}}2\) after the second pulse is stored we combine the pulses in t − x space. As in previous cases, the Kz = 0 component of the processed spin wave becomes the first port of the Mach–Zehnder interferometer. To sample the second port (which is distributed into successive diffraction orders \(c_{n \ne 0}^{{\mathrm{sq}}}\)) we use sawtooth grating in the z-direction \(\varphi _{{\mathrm{acS}}}^{{\mathrm{saw}}}\left( {k_{{\mathrm{saw}}}z} \right)\) with \(k_{{\mathrm{saw}}} = {\bf{k}}_{{\mathrm{sq}}} \cdot \hat e_z = 5\,{\mathrm{rad/mm}}\) (pattern B in Fig. 5b) to transfer the 1-st order to readable Kz = 0 space, and perform the readout. The simulation reveals that in this protocol the two output ports turn out to not be in perfectly opposite phases. The same behavior is observed in the experiment, as demonstrated in Fig. 5d. We attribute this effect to imperfect retrieval of the first port which in turn partially leaks to the second read-out operation. We envisage that further simulations will facilitate a more elaborate scheme that could yield two output ports that are perfectly in opposite phases, as in experiments described in Sec. “Programmable beamsplitting of stored optical pulses” and “Transverse space interference and manipulation”. In this case, the theoretical maximal efficiency for perfect readout is 100% for the first and 40% for the second port. However, as already mentioned we only sample the second port using sawtooth grating. We envisage that using more complex grating the second port could also be retrieved with 100% efficiency in the ideal case.
Processing and interference in the two-dimensional space. a Phase modulation patterns used to split spin waves in the tilted wavevector-space direction (pattern A) and shift them in the Kz direction (pattern B). b Example of simulated and measured time traces of the scheme demonstrating spin-wave processing in two wavevector-space dimensions. Shaded regions correspond to total light intensity measured for both transverse wavevectors on the same photodiode. Phase is chosen to maximize output in port b. c Simulated wavevector-space spin wave densities at different time instants of the protocol, with subsequent numbers corresponding to marked positions in (a). In the protocol the spin wave with amplitude α is first created by storing a single coherent pulse (1). Next, the spin wave is split using pattern A (2) and another pulse is stored to create spin wave with amplitude β (3). Pattern A is then applied again to cause interference of the two stored pulses (4). Readout is then performed to first observe the output port corresponding roughly to α + β, and after shifting the spin wave in the Kz direction with pattern B the output port corresponding to the α − β component. d portrays intensities registered in the two output ports as a function of relative phase between pulses. Solid lines correspond to the simulated result. The horizontal error bars are related to the signal phase fluctuations (s.e.m) in our experimental setup
Rapidly-reprogrammable double pattern imaging system. HWP—half-wave plate, QWP—quarter-wave plate, PZT—piezoelectric transducer, AOM—acousto-optic modulator. The AOM diffracts the input beam onto disparate regions of the SLM, which are then simultaneously imaged onto the MOT after being combined on the polarizing beamsplitter (PBS). The final PBS projects both light fields onto the z polarization. Desired patterns are prepared using an iterative optimization algorithm with camera feedback
Discussion
We have demonstrated a reprogrammable device that processes atomic spin waves through interference. Starting with the application of the ac-Stark shift control facilitating a temporally multimode cold-atomic memory for light, we have extended the concept of ac-Stark control to enable interference of coherent spin-wave states stored in the memory. In particular, the processing is performed simultaneously in two dimensions of the wavevector space. With this, we simultaneously exploit temporal and spatial multiplexing. We show how to perform spin-wave interference between light pulses stored both at different times, as well as sent to the memory at different angles. By switching only a pair of patterns we achieve a substantial degree of reprogrammability and control (see Fig. 6), which paves the way towards creating complex unitary quantum networks through spin-wave interference.
The demonstrated SMIP lends itself to many critical schemes in quantum and classical telecommunication, including the quantum memory-enabled superadditive communication31,32,33,34 or implementation of a receiver operating with an error rate below the standard quantum limit35, as well as quantum metrology through collective measurements on many optical pulses.36,37 The ability of programming interference of stored states provides a robust tool for probing fundamental properties of quantum systems. Recently, a tunable beamsplitter transformation has been used to demonstrate Hong–Ou–Mandel interference between two microwave quantum memories.38 The techniques presented here pave the way towards programmable complex interference experiments which can be used to reveal fundamental properties of a given quantum system.
The ac-Stark control owes its versatility to the possibly a very high speed of switching and operation, as compared with the magnetic field gradients. This feature makes it applicable to recently developed short-lived quantum memories that operate in the ladder atomic scheme in warm atomic vapors and achieve very low noise levels.39,40 The high speed of the ac-Stark control also facilitates real-time feedback processing that could lead to the realization of an even broader class of operations, including enhanced single-photon generation through multiplexing.6,41,42,43 Here, such a scheme could also include engineering of photonic spatial and temporal mode. This could be taken even further with techniques used in stationary-light experiments, where the amplitude of the stored spin-wave is non-destructively reshaped using a multi-laser field.44,45
The universality of the current approach is limited by access only to pure phase modulation of spin waves, that inherently produces many diffraction orders, rather than a specific desired pattern. An interesting approach to achieve universality of performed operations, rather than just control of phase in the wavevector-domain, would be to implement a three-step protocol. It has been demonstrated that for optical frequency-bin modes a pair of electro-optics modulator and a pulse shaper46 are sufficient to perform an arbitrary unitary operation. In our case to obtain arbitrary input-output relation for many stored pulses we would first store the pulses in the memory and apply the phase modulation as presented in the current work. Next, the pulses would be simultaneously read-out and stored again in the memory with an electro-optic modulator changing the phase of each time-bin. Final modulation in the spin-wave domain would yield an arbitrary operation, achieving universality in terms of time-bin input-output operation. In turn, the linear-optical scheme of quantum computation becomes feasible.47 The number of modes that can be efficiently processed would be limited by the optical depth. In general, a set of concatenated memories, as proposed in,22 could facilitate universal operations within our ac-Stark modulation protocol.
Furthermore, note that here we did not use the ac-Stark shift during write and read operations of the optical memory, and thus the two-photon absorption line is not broadened. Thus, the Gradient Echo Memory advantage of avoiding reabsorption of stored light is not yet exploited. Combined with larger optical densities this could significantly improve the efficiency of the presented memory.14
Finally, by bringing the presented techniques to spin waves that involve a Rydberg state,48,49,50,51,52 the attainable range of operations between storage modes could be enriched with nonlinear interactions in order to realize efficient and deterministic quantum gates for photonic states. This could be particularly advantageous in engineering complex correlations within the spatial domain of a Rydberg atomic ensemble.53
Methods
Light-atom coupling simulations
To correctly predict efficiencies during storage and retrieval as well as non-trivial shapes of spin waves created in the atomic ensemble. We choose to describe the system within the three-level model described by an interaction picture Hamiltonian within the rotating wave approximation. It is subsequently reduced using the typical adiabatic elimination approach by setting the time derivatives of all excited-state coherences and populations to zero. The coupled equations are then most conveniently expressed in terms of Rabi frequency of the signal field \({\mathrm{\Omega }} = {\cal {E}}d_{{\rm{eg}}}{\mathrm{/}}\bf{\hbar}\), where deg is the dipole moment of the relevant transition, and the coupling field \({\mathrm{\Omega }}_C = {\cal {E}}_Cd_{{\rm{eh}}}{\mathrm{/}}\bf{\hbar}\). With the coupling coefficient equal \(g = \omega \left| {d_{eg}} \right|^2N{\mathrm{/}}2\mathbf{\hbar} c\epsilon _0\) and in the frame co-moving with the pulses (t → t − z/c) the equations take the following form (see refs. 54,55,56):
where we have also introduced Γ = 2π × 6 MHz as the excited-state |e〉 decay rate and γ ≈ 2π × 10 kHz as the intrinsic spin-wave decoherence rate, dominated by motional dephasing. The one-photon Δ = 2π × 20 MHz and two-photon δ detunings are defined as in Fig. 1b. In the first equation, the two terms in the nominator correspond to the two-photon and one-photon processes, respectively. In the second equation, the first term corresponds to the Raman interaction, while the second term is the free evolution under the ac-Stark shift Hamiltonian due to the coupling light, which includes both the additional phase acquired as well as the power broadening. Even though the ac-Stark modulation is applied only during dark periods of the memory, for completeness we include its influence as an additional term in Eq. (11B) given by iΔacSS. Note that in all cases the atom number density N is implicitly z-dependent, and so is the coupling constant g. In the simulation we model this dependence as a Gaussian function in the z dimension with a width of 5 mm. Finally, we also add a small imaginary component to the ac-Stark shift ΔacS → (1 + isgn(ΔacS)γacS)ΔacS with γacS ~ 0.1, which effectively simulates dephasing due to inhomogeneous ac-Stark light intensity.
We determine the coupling constant g by observing single-photon off-resonant absorption. This allows us to experimentally determine its peak value as g0 ≈ 200 cm−1 μs−1, which corresponds to the optical depth OD ≈ 11. For the coupling field, we take short pulses with smooth slopes (modeling ~100 ns experimental rise times) and peak ΩC ≈ 2π × 9 MHz = 1.5Γ. Typical signal field intensities correspond to peak Ω ≈ 2π × 50 kHz. The evolution is simulated using the XMDS package57 on a two-dimensional z–t grid, or three-dimensional x–z–t grid for the results in Section F. For this case, we also include a diffraction term in Eq. (11A), although the diffraction effects prove to be negligible for the plane-wave modes we work with.
Pattern preparation and imaging
The ac-Stark laser is frequency-stabilized using an offset beat-note lock.58 It is then spatially filtered using a single-mode fiber and amplified using a tapered amplifier (Toptica, BoosTA) to 1.5 W. The output beam is then reshaped using a cylindrical lens to better fit the shape of the elongated atomic ensemble. Simultaneously, an acousto-optical modulator (AOM) situated in the far field of the spatial-light modulator (SLM) is used to control the position of the beam at the SLM and carve out ~2 μs long pulses. With this setup, depicted in Fig. 6, we may select which region of the SLM is illuminated by changing the frequency of the AOM, which is done in real time using a direct digital synthesizer (DDS). On the SLM matrix, we display two patterns in two disparate regions. The SLM surface is then imaged onto a D-shape mirror which sends each pattern on a different path. The two paths are joined on a polarizing beamsplitter (PBS) before the vacuum chamber and now the two patterns overlap. Note that in the current configuration we loose half of the power at the final PBS. An additional mirror placed in the far field of the SLM is used for fine adjustment of grating position in the vertical direction with the help of a piezoelectric transducer (PZT), which is used to scan the grating phase ζ as in Sec. “Transverse space interference and manipulation”.
By flipping the flip mirror patterns can also be observed on a camera situated at the same image plane as the atomic ensemble. The camera provides feedback to the computer program that controls the SLM, which is used to actually generate the desired pattern, with a particular focus on intensity homogeneity. The program operates by first mapping the SLM coordinates onto the camera pixels using a National Instruments Vision module, and then iteratively adjusting the SLM display to achieve an intensity distribution closest to the target one. The optimization procedure begins with a white rectangle displayed on the SLM. Next, at each iteration, the error distribution i.e., the difference between pattern observed on camera an the target is calculated. According to that error, the SLM pattern is changed proportionally.
As demonstrated, at this point our setup already allows rapid switching between two patterns that could be used in short-lived quantum memories.39,40 We envisage that the setup may be extended to feature more patterns that could be rapidly reprogrammed, by for example using a two-dimensional AOM to scan the beam through the atomic ensemble, or by using a set of AOMs to transfer many multiplexed images displayed with an SLM. This would unavoidably increase the complexity of the setup. In consequence, fast rapid spatial-light modulators and deformable mirrors that can already be reprogrammed during ~100 μs could serve as a highly viable solutions.59 On the other hand, simpler patterns could also be rapidly generated by sweeping the frequencies in a setup based on acousto-optic deflectors.60,61
Code availability
Computer code used to process data in this study is available from the corresponding authors upon reasonable request.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Reim, K. F. et al. Multipulse addressing of a raman quantum memory: configurable beam splitting and efficient readout. Phys. Rev. Lett. 108, 263602 (2012).
Vernaz-Gris, P., Huang, K., Cao, M., Sheremet, A. S. & Laurat, J. Highly-efficient quantum memory for polarization qubits in a spatially-multiplexed cold atomic ensemble. Nat. Commun. 9, 363 (2018).
Wang, H. et al. Quantum interference of stored dual-channel spin-wave excitations in a single tripod system. Phys. Rev. A. 83, 043815 (2011).
Lee, M.-J. et al. Experimental demonstration of spinor slow light. Nat. Commun. 5, 5542 (2014).
Pu, Y.-F. et al. Experimental realization of a multiplexed quantum memory with 225 individually accessible memory cells. Nat. Commun. 8, 15359 (2017).
Parniak, M. et al. Wavevector multiplexed atomic quantum memory via spatially-resolved single-photon detection. Nat. Commun. 8, 2140 (2017).
Ding, D.-S., Zhou, Z.-Y., Shi, B.-S., Guo, G.-C. & Harris, S. E. Single-photon-level quantum image memory based on cold atomic ensembles. Nat. Commun. 4, 183601 (2013).
Gündoğan, M., Mazzera, M., Ledingham, P. M., Cristiani, M. & de Riedmatten, H. Coherent storage of temporally multimode light using a spin-wave atomic frequency comb memory. New J. Phys. 15, 045012 (2013).
Kutluer, K., Mazzera, M. & de Riedmatten, H. Solid-state source of nonclassical photon pairs with embedded multimode quantum memory. Phys. Rev. Lett. 118, 210502 (2017).
Tiranov, A. et al. Temporal multimode storage of entangled photon pairs. Phys. Rev. Lett. 117, 240506 (2016).
Nunn, J. et al. Multimode memories in atomic ensembles. Phys. Rev. Lett. 101, 260502 (2008).
Hosseini, M. et al. Coherent optical pulse sequencer for quantum applications. Nature 461, 241 (2009).
Hosseini, M., Sparkes, B. M., Campbell, G., Lam, P. K. & Buchler, B. C. High efficiency coherent optical memory with warm rubidium vapour. Nat. Commun. 2, 174 (2011).
Sparkes, B. M. et al. Gradient echo memory in an ultra-high optical depth cold atomic ensemble. New J. Phys. 15, 085027 (2013).
Albrecht, B., Farrera, P., Heinze, G., Cristiani, M. & de Riedmatten, H. Controlled rephasing of single collective spin excitations in a cold atomic quantum memory. Phys. Rev. Lett. 115, 160501 (2015).
Sinclair, N. et al. Spectral multiplexing for scalable quantum photonics using an atomic frequency comb quantum memory and feed-forward control. Phys. Rev. Lett. 113, 053603 (2014).
Dai, H.-N. et al. Holographic storage of biphoton entanglement. Phys. Rev. Lett. 108, 210501 (2012).
Sinclair, N., Oblak, D., Thiel, C. W., Cone, R. L. & Tittel, W. Properties of a rare-earth-ion-doped waveguide at sub-kelvin temperatures for quantum signal processing. Phys. Rev. Lett. 118, 100504 (2017).
Saglamyurek, E. et al. An integrated processor for photonic quantum states using a broadband light-matter interface. New J. Phys. 16, 065019 (2014).
Yang, T.-S. et al. Multiplexed storage and real-time manipulation based on a multiple degree-of-freedom quantum memory. Nat. Commun. 9, 3407 (2018).
Campbell, G., Hosseini, M., Sparkes, B. M., Lam, P. K. & Buchler, B. C. Time- and frequency-domain polariton interference. New J. Phys. 14, 033022 (2012).
Campbell, G. T. et al. Configurable unitary transformations and linear logic gates using quantum memories. Phys. Rev. Lett. 113, 063601 (2014).
Dudin, Y. O. et al. Entanglement of Light-Shift Compensated Atomic Spin Waves with Telecom Light. Phys. Rev. Lett. 105, 260502 (2010).
Sparkes, B. M., Hosseini, M., Hétet, G., Lam, P. K. & Buchler, B. C. ac Stark gradient echo memory in cold atoms. Phys. Rev. A. 82, 043847 (2010).
Chanelière, T. & Hétet, G. Light-shift-modulated photon-echo. Opt. Lett. 40, 1294 (2015).
Hétet, G. & Guéry-Odelin, D. Spin wave diffraction control and read-out with a quantum memory for light. New J. Phys. 17, 073003 (2015).
Su, S.-W. et al. Setting a disordered password on a photonic memory. Phys. Rev. A. 95, 061805 (2017).
Bajcsy, M., Zibrov, A. S. & Lukin, M. D. Stationary pulses of light in an atomic medium. Nature 426, 638–641 (2003).
Parniak, M. et al. Quantum optics of spin waves through ac Stark modulation. Phys. Rev. Lett. 122, 063604 (2019).
Leszczyński, A. et al. Spatially resolved control of fictitious magnetic fields in a cold atomic ensemble. Opt. Lett. 43, 1147 (2018).
Guha, S. Structured optical receivers to attain superadditive capacity and the Holevo limit. Phys. Rev. Lett. 106, 240502 (2011).
Klimek, A., Jachura, M., Wasilewski, W. & Banaszek, K. Quantum memory receiver for superadditive communication using binary coherent states. J. Mod. Opt. 63, 2074 (2016).
Jarzyna, M., Lipińska, V., Klimek, A., Banaszek, K. & Paris, M. G. A. Phase noise in collective binary phase shift keying with Hadamard words. Opt. Express 24, 1693 (2016).
Czajkowski, J., Jarzyna, M. & Demkowicz-Dobrzański, R. Super-additivity in communication of classical information through quantum channels from a quantum parameter estimation perspective. New J. Phys. 19, 073034 (2017).
Becerra, F. E. et al. Experimental demonstration of a receiver beating the standard quantum limit for multiple nonorthogonal state discrimination. Nat. Photonics 7, 147 (2013).
Demkowicz-Dobrzański, R., Jarzyna, M. & Kołodyński, J. Quantum limits in optical interferometry. Prog. Opt. 60, 345 (2015).
Hou, Z. et al. Deterministic realization of collective measurements via photonic quantum walks. Nat. Commun. 9, 1414 (2018).
Gao, Y. Y. et al. Programmable interference between two microwave quantum memories. Phys. Rev. X 8, 021073 (2018).
Kaczmarek, K. T. et al. High-speed noise-free optical quantum memory. Phys. Rev. A. 97, 042316 (2018).
Finkelstein, R., Poem, E., Michel, O., Lahad, O. & Firstenberg, O. Fast, noise-free memory for photon synchronization at room temperature. Sci. Adv. 4, eaap8598 (2018).
Mazelanik, M., Dąbrowski, M. & Wasilewski, W. Correlation steering in the angularly multimode Raman atomic memory. Opt. Express 24, 21995 (2016).
Nunn, J. et al. Enhancing multiphoton rates with quantum memories. Phys. Rev. Lett. 110, 133601 (2013).
Kaneda, F., Xu, F., Chapman, J. & Kwiat, P. G. Quantum-memory-assisted multi-photon generation for efficient quantum information processing. Optica 4, 1034 (2017).
Everett, J. L. et al. Dynamical observations of self-stabilizing stationary light. Nat. Phys. 13, 68 (2016).
Park, K.-K., Cho, Y.-W., Chough, Y.-T. & Kim, Y.-H. Experimental demonstration of quantum stationary light pulses in an atomic ensemble. Phys. Rev. X 8, 021016 (2018).
Lu, H. H. et al. Electro-optic frequency beam splitters and tritters for high-fidelity photonic quantum information processing. Phys. Rev. Lett. 120, 030502 (2018).
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).
Wei, R., Zhao, B., Deng, Y., Chen, Y.-A. & Pan, J.-W. Deterministic spin-wave interferometer based on the Rydberg blockade. Phys. Rev. A. 83, 63623 (2011).
Ding, D. S. et al. Entanglement between low- and high-lying atomic spin waves. Phys. Rev. A. 94, 052326 (2016).
Distante, E., Padrón-Brito, A., Cristiani, M., Paredes-Barato, D. & de Riedmatten, H. Storage enhanced nonlinearities in a cold atomic rydberg ensemble. Phys. Rev. Lett. 117, 113001 (2016).
Mirgorodskiy, I. et al. Electromagnetically induced transparency of ultra-long-range Rydberg molecules. Phys. Rev. A. 96, 011402 (2017).
Distante, E. et al. Storing single photons emitted by a quantum memory on a highly excited Rydberg state. Nat. Commun. 8, 14072 (2017).
Busche, H. et al. Contactless nonlinear optics mediated by long-range Rydberg interactions. Nat. Phys. 13, 655 (2017).
Parniak, M., Pęcak, D. & Wasilewski, W. Multimode Raman light-atom interface in warm atomic ensemble as multiple three-mode quantum operations. J. Mod. Opt. 63, 2039 (2016).
Kołodyński, J., Chwedeńczuk, J. & Wasilewski, W. Eigenmode description of Raman scattering in atomic vapors in the presence of decoherence. Phys. Rev. A. 86, 013818 (2012).
Cho, Y.-W. et al. Highly efficient optical quantum memory with long coherence time in cold atoms. Optica 3, 100 (2016).
Dennis, G. R., Hope, J. J. & Johnsson, M. T. XMDS2: fast, scalable simulation of coupled stochastic partial differential equations. Comput. Phys. Commun. 184, 201 (2013).
Lipka, M., Parniak, M. & Wasilewski, W. Optical frequency locked loop for long-term stabilization of broad-line DFB laser frequency difference. Appl. Phys. B 123, 238 (2017).
Andersen, G., Gelsinger-Austin, P., Gaddipati, R., Gaddipati, P. & Ghebremichael, F. Fast, compact, autonomous holographic adaptive optics. Opt. Express 22, 9432 (2014).
Römer, G. & Bechtold, P. Electro-optic and acousto-optic laser beam scanners. Phys. Procedia 56, 29–39 (2014).
Kong, C. et al. Ultra-broadband spatiotemporal sweeping device for high-speed optical imaging. Opt. Lett. 43, 3546 (2018).
Acknowledgements
We thank K. Banaszek for generous support. This work has been funded by the National Science Centre, Poland (NCN) (Grants No. 2015/19/N/ST2/01671, 2016/21/B/ST2/02559, 2017/25/N/ST2/01163 and 2017/25/N/ST2/00713) and by the Polish MNiSW “Diamentowy Grant” (Projects No. DI2013 011943 and DI2016 014846). The research is supported by the "Quantum Optical Technologies'' project carried out within the International Research Agendas programme of the Foundation for Polish Science co-financed by the European Union under the European Regional Development Fund.
Author information
Authors and Affiliations
Contributions
M.M., M.P., and W.W. planned the experiment. M.M. and M.P. performed the experiment, analyzed the data, and wrote the manuscript with input from other authors. M.P. performed the simulation. M.M., M.P., A.L., and M.L. built the experimental setup. W.W. supervised the project. M.M. and M.P. contributed equally to this work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mazelanik, M., Parniak, M., Leszczyński, A. et al. Coherent spin-wave processor of stored optical pulses. npj Quantum Inf 5, 22 (2019). https://doi.org/10.1038/s41534-019-0136-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-019-0136-0
This article is cited by
-
Coherent optical two-photon resonance tomographic imaging in three dimensions
Communications Physics (2023)
-
Optical-domain spectral super-resolution via a quantum-memory-based time-frequency processor
Nature Communications (2022)
-
Massively-multiplexed generation of Bell-type entanglement using a quantum memory
Communications Physics (2021)