Abstract
Spin qubits hosted in silicon (Si) quantum dots (QD) are attractive due to their exceptionally long coherence times and compatibility with the silicon transistor platform. To achieve electrical control of spins for qubit scalability, recent experiments have utilized gradient magnetic fields from integrated micro-magnets to produce an extrinsic coupling between spin and charge, thereby electrically driving electron spin resonance (ESR). However, spins in silicon QDs experience a complex interplay between spin, charge, and valley degrees of freedom, influenced by the atomic scale details of the confining interface. Here, we report experimental observation of a valley dependent anisotropic spin splitting in a Si QD with an integrated micro-magnet and an external magnetic field. We show by atomistic calculations that the spin-orbit interaction (SOI), which is often ignored in bulk silicon, plays a major role in the measured anisotropy. Moreover, inhomogeneities such as interface steps strongly affect the spin splittings and their valley dependence. This atomic-scale understanding of the intrinsic and extrinsic factors controlling the valley dependent spin properties is a key requirement for successful manipulation of quantum information in Si QDs.
Similar content being viewed by others
Introduction
How microscopic electronic spins in solids are affected by the crystal and interfacial symmetries has been a topic of great interest over the past few decades and has found potential applications in spin-based electronics and computation.1,2,3,4,5,6,7 While the coupling between spin and orbital degrees of freedom has been extensively studied, the interplay between spin and the momentum space valley degree of freedom is a topic of recent interest. This spin-valley interaction is observed in the exotic class of newly found two-dimensional materials,8,9,10 in carbon nanotubes11 and in silicon12,13,14—the old friend of the electronics industry.
Progress in silicon qubits in the last few years has come with the demonstrations of various types of qubits with exceptionally long coherence times, such as single spin up/down qubits,15,16 two-electron singlet-triplet qubits,17,18 three-electron exchange-only19 and hybrid spin-charge qubits20 and also hole spin qubits21 realized in silicon (Si) quantum dots (QDs). The presence of the valley degree of freedom has enabled valley based qubit proposals22 as well, which have potential for noise immunity. To harness the advantages of different qubit schemes, quantum gates for information encoded in different bases are required.9,23,24 A controlled coherent interaction between multiple degrees of freedom, like valley and spin, might offer a building block for promising hybrid systems.
An interesting interplay between spin and valley degrees of freedom, which gives rise to a valley dependent spin splitting, has been observed in Si QDs in recent experiments.15,25,26,27 Although bulk silicon has six-fold degenerate conduction band minima, in quantum wells or dots, electric fields and often in-plane strain in addition to vertical confinement results in only two low lying valley states (labeled as v− and v+ in Fig. 1b) split by an energy gap known as the valley splitting. SOI enables the control of spin resonance frequencies of the valley states by gate voltage, an effect measured in refs.16,25. However, the ESR frequencies and their Stark shifts were found to be different for the two valley states.25 In another work, an inhomogeneous magnetic field, created by integrated micro-magnets in a Si/SiGe quantum dot device, was used to electrically drive ESR.15 Magnetic field gradients generated in this way act as an extrinsic spin-orbit coupling and thus can affect the ESR frequency.28 Remarkably, although SOI is a fundamental effect arising from the crystalline structure, the ESR frequency differences between the valley states observed in refs.15,25 have different signs when the external fields are oriented in the same direction with respect to the crystal axes. In this work we will show that the atomic scale details of the Si interface determine these signs.
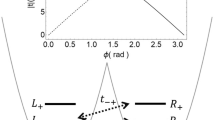
Valley dependent anisotropic ESR in a Si QD with integrated micro-magnets. a False-color image of the experimental device showing the estimated location of the quantum dot (magenta colored circle) and two Co micro-magnets (green semi-transparent rectangles). The external magnetic field (Bext) was rotated clockwise in-plane, from the [110] (θ = 0°) crystal orientation towards \([1\bar 10]\left( {\theta = 90^ \circ } \right)\). b Lowest energy levels of a Si QD in an external magnetic field. The valley-split levels v− and v+ are found to have unequal Zeeman splittings (EZS(v±) = hfv±), with ESR frequencies \(f_{v_ - } \ne f_{v_ + }\). In the experiment, all the measured spin splittings are much larger than the valley splitting and are therefore above the anticrossing point of the spin and valley states. c Both measured (red circles) and calculated \(f_{v_ - } - f_{v_ + }\) as a function of θ, for Bext = 0.8 T. The anisotropy in \(f_{v_ - } - f_{v_ + }\) is governed by both internal (intrinsic SOI) and external (micro-magnetic fields) factors. The anisotropy due to the intrinsic SOI, calculated from atomistic tight binding method, for a specifically chosen (discussed later) vertical electric field and interface step configuration, is labeled as “Bext (TB)”. The micro-magnetic field is separated into a homogeneous (\({\bf{B}}_{{\mathrm{micro}}}^\theta\)) and an inhomogeneous (ΔBθ) part. The inclusion of \({\bf{B}}_{{\mathrm{micro}}}^\theta\) in this case (labeled “\({\bf{B}}_{{\mathrm{ext}}} + {\bf{B}}_{{\mathrm{micro}}}^\theta\) (TB)”), shifts the curve away from the experiment. The addition of ΔBθ introduces additional anisotropy (labeled “\({\bf{B}}_{{\mathrm{ext}}} + {\bf{B}}_{{\mathrm{micro}}}^\theta + {\mathrm{\Delta }}{\bf{B}}^\theta\) (TB)”) and shifts the curve towards the experiment. An effective-mass calculation, with fitted SOI and dipole coupling parameters, is also presented with a cyan solid line. To further clarify the labeling, we want to point out that we label the curves based on the B-field components that are used in simulations, with the SOI included in all cases. d Both measured (red circles) and calculated \(f_{v_ - }\), as a function of θ, for Bext = 0.8 T. Calculation with the intrinsic SOI shows negligible change in GHz scale, while the addition of \({\bf{B}}_{{\mathrm{micro}}}^\theta\) results in anisotropy close to the experimental data. ΔBθ has negligible effect on \(f_{v_ - }\). Hence, the anisotropy of \(f_{v_ - }\) is mainly dictated by the homogeneous part of the micro-magnetic field
To understand and achieve control over the coupled behavior between spin and valley degrees of freedom, several key questions need to be addressed, such as (1) What causes the device-to-device variability?, (2) Can an artificial source of interaction, like inhomogeneous B-field, completely overpower the SOI effects of the intrinsic material?, (3) What knobs and device designs can be utilized to engineer the valley dependent spin splittings?
Results
Experiment and theory
Here we report experimentally measured anisotropy in the ESR frequencies of the valley states \(f_{v_ - }\) and \(f_{v_ + }\) and their differences \(f_{v_ - } - f_{v_ + }\), as a function of the direction (θ) of the external magnetic field (Bext) in a quantum dot formed at a Si/SiGe heterostructure with integrated micro-magnets. At specific angles of the external B-field, we also measure the spin splittings of the two valley states as a function of the B-field magnitude (Bext). By performing spin-resolved atomistic tight binding (TB) calculations of the quantum dots confined at ideal versus non-ideal interfaces, we evaluate the contribution of the intrinsic SOI with and without the spatially varying B-fields from the micro-magnets to the spin splittings, thereby relating these quantities to the microscopic nature of the interface and elucidating how spin, orbital and valley degrees of freedom are intertwined in these devices. Finally, by combining all the effects together, we explain the experimental measurements and address the key questions raised in the introduction.
We show that the SOI and micro-magnetic fields all make essential contributions to the dependence of the spin splitting on the magnetic field orientation. We also show that physically realistic choices for the interface condition and of the vertical electric field yield quantitative agreement with the experimental measurements. We show that a Dresselhaus-like SOI makes \(f_{v_ \pm }\) anisotropic in a Si QD, even without any micro-magnetic field. The valley dependence of the Dresselhaus coefficient makes \(f_{v_ - } \ne f_{v_ + }\) and \(f_{v_ - } - f_{v_ + }\) anisotropic. This Dresselhaus SOI, missing in bulk Si, results due to the interface inversion asymmetry. Consequently, the details of the interface, like the presence of monoatomic steps, control both the sign and magnitude of the Dresselhaus SOI and \(f_{v_ - } - f_{v_ + }\). The micro-magnetic fields can be separated into two parts, a homogeneous (spatial average, \({\bf{B}}_{{\mathrm{micro}}}^\theta\)) and an inhomogeneous (spatially varying, ΔBθ) magnetic field. Both of these fields depend on the direction of Bext, but not on its magnitude (see Methods and Supplementary Section S4), hence the superscript θ. The homogeneous component vectorially adds to Bext, modifies \(f_{v_ \pm }\) and makes them anisotropic. Interface steps can cause the spatial distribution of the valley states to be non-identical. Therefore a spatially varying magnetic field can contribute to \(f_{v_ - }\) and \(f_{v_ + }\) differently. The inhomogeneous micro-magnetic field, in a similar fashion as its homogeneous counterpart, adds to the anisotropy of \(f_{v_ - } - f_{v_ + }\). The contributions of the different components can be distinguished because the contributions arising from the homogeneous and inhomogeneous magnetic fields are independent of Bext, while the contribution arising from SOI is proportional to Bext.
First we show that the experimental measurements (anisotropy of \(f_{v_ - }\) and \(f_{v_ - } - f_{v_ + }\) in Fig. 1 and Bext dependence in Fig. 2) agree well with the theoretical calculations including all the components: SOI and the homogeneous and inhomogeneous micro-magnetic fields. Then we discuss the effects of the different components separately (SOI in Fig. 3 and the inhomogeneous micro-magnetic field in Fig. 4) in detail.
Measured ESR frequencies, (\(f_{v_ \pm }\)) and their differences for the two valley states as a function of the external B-field magnitude Bext along two crystal directions, and comparison with theoretical calculations. a \(f_{v_ - } - f_{v_ + }\) and b \(f_{v_ - }\) with Bext along [110] (θ = 0°) (bottom panel) and \([1\bar 10]\left( {\theta = 90^ \circ } \right)\) (top panel). As in Fig. 1c,d, the calculations progressively include SOI (labeled “Bext (TB)”), homogeneous (labeled “Bext + Bmicro (TB)”), and gradient (labeled “Bext + Bmicro + ΔB (TB)”) B-field of the micro-magnet. The cyan solid lines are the effective mass calculations and the red circles are the experimental data. The dependence (slope) of \(f_{v_ - } - f_{v_ + }\) on Bext in (a) comes from the SOI, while the micro-magnetic fields provide a shift independent of Bext
Effect of the intrinsic SOI on \(f_{v_ \pm }\) in a Si QD. a Calculated \(f_{v \pm }\) as a function of θ, in a QD with ideal (flat) interface, for Bext = 0.8 T, without any micro-magnet. The anisotropies in these curves are in the MHz range and will appear flat on a GHz scale, like the SOI line (labeled "Bext (TB)") of Fig. 1d. b Schematic of a QD wave function near a monoatomic step at the interface. The distance between the dot center and the step edge is denoted by x0. c Computed Dresselhaus parameters β± as a function of x0. β± changes sign between the two sides of the step. d QD wave functions subjected to multiple interface steps. Four different cases are shown (c1(5), c2(3), c3(4), c4(4)) that are used in Figs. 3e, f and also in Figs. 4c, d. The number in parentheses is the total number of steps within the QD. Though c3 and c4 has the same number of steps, the location of the steps are different. c3 is the step configuration used in Figs. 1 and 2. e Calculated \(f_{v_ - } - f_{v_ + }\) as a function of θ, for different interface conditions, for Bext = 0.8 T. Interface steps affect both the magnitude and sign of \(f_{v_ - } - f_{v_ + }\). f \(f_{v_ - } - f_{v_ + }\) with respect to Bext along [110] (θ = 0°)/ \([\bar 1\bar 10]\) (θ = 180°) (bottom panel) and \([1\bar 10]\) (θ = 90°)/\([\bar 110]\) (θ = 270°) (top panel). \(f_{v_ - } - f_{v_ + }\) for c3 (red lines with circular marker), in both Figs. 3e, f, corresponds to the SOI lines (blue dashed lines with diamond marker) of Figs. 1c and 2a. The parabolic confinement and E z used here are the same as that of Figs. 1 and 2, except for Fig. 3c, where a smaller dot (with a parabolic confinement in both x and y corresponding to orbital energy splitting of 9.4 meV) is used to accommodate for large variation in dot location
Effect of inhomogeneous magnetic field on \(f_{v_ - } - f_{v_ + }\). a 1D cut of the wave functions of the two valley states close to a step edge, highlighting their spatial differences. A large vertical E-field, E z = 30 MVm−1 is used here to show a magnified effect. b The change in \(f_{v_ - } - f_{v_ + }\) due to the inhomogeneous B-field (ΔB) alone as a function of the distance x0 between the dot center and a step edge, as defined in Fig. 3b. c Angular dependence of \({\mathrm{\Delta }}\left( {f_{v_ - } - f_{v_ + }} \right)^{{\mathrm{\Delta }}{\bf{B}}}\) for the various step configurations of Fig. 3d (same color code) computed from atomistic TB. d \({\mathrm{\Delta }}\left( {f_{v_ - } - f_{v_ + }} \right)^{{\mathrm{\Delta }}{\bf{B}}}\) as a function of Bext. \({\mathrm{\Delta }}\left( {f_{v_ - } - f_{v_ + }} \right)^{{\mathrm{\Delta }}{\bf{B}}}\) shows negligible dependence on Bext. \({\mathrm{\Delta }}\left( {f_{v_ - } - f_{v_ + }} \right)^{{\mathrm{\Delta }}{\bf{B}}}\) for c3 (red lines with circular marker), in Figs. 4c, d, corresponds to the contribution of ΔB (the difference between the black solid curve/lines with circular markers and green dashed curve/lines with square markers) of Figs. 1c and 2a. The fields used in the simulations of c and d are the same as that of Figs. 1 and 2, whereas the fields used for b are the same as that of Fig. 3c
Anisotropy
The external magnetic field in the experimental device is swept from the [110] to \([1\bar 10]\) crystal orientation. Details of the device (shown in Fig. 1a) and the measurement technique of the spin resonance frequency can be found in ref.15. A schematic of the energy levels of interest is shown in Fig. 1b depicting the v− and v+ valley states with different spin splittings, where v− is defined as the ground state. In the experiment, the lowest valley-orbit excitation is well below the next excitation, justifying this four-level schematic in the energy range of interest.
Figures 1c, d show how the SOI and both the micro-magnetic fields come into play to explain the experimentally measured anisotropic spin splittings. The atomistic calculation with SOI alone (labeled “Bext (TB)”) for a QD at a specifically chosen, as discussed below, non-ideal interface and vertical electric field (E z ) qualitatively captures the experimental trend of \(f_{v_ - } - f_{v_ + }\) in Fig. 1c, but fails to reproduce the anisotropy of the measured \(f_{v_ - }\) in Fig. 1d in the larger GHz scale. The differences between the experimental data and the SOI-only calculations in both figures arise from the micro-magnets present in the experiment. The inclusion of the homogeneous part of the micro-magnetic field creates an anisotropy in the total magnetic field (Supplementary Fig. S7), which captures the anisotropy of \(f_{v_ - }\) in Fig. 1d very well (\(f_{v_ - } \approx g\mu \left| {{\bf{B}}_{{\mathrm{ext}}} + {\bf{B}}_{{\mathrm{micro}}}^\theta } \right|{\mathrm{/}}h\), where g is the Landé g-factor, μ is the Bohr magneton and h is the Planck constant), but quantitative match with the experimental data in Fig. 1c is not obtained. Next, we also incorporate the inhomogeneous part of the micro-magnetic field, and witness a close quantitative agreement in the anisotropy of \(f_{v_ - } - f_{v_ + }\), while the anisotropy of \(f_{v_ - }\) is unaffected. This experiment-theory agreement of Fig. 1c is achieved for a specific choice of interface condition and E z , whose influence will be discussed later. Here, we conclude that mainly the intrinsic SOI and the extrinsic inhomogeneous B-field govern the anisotropy of \(f_{v_ - } - f_{v_ + }\) on the MHz scale, while the anisotropy in the total homogeneous magnetic field introduced by the micro-magnet dictates the anisotropy of \(f_{v_ - }\) (and \(f_{v_ + }\)) on the larger GHz scale.
Magnetic field dependence
In Fig. 2, we show that the measurements of the spin splittings as a function of Bext can not be quantitatively explained as well, without the inclusion of all three components: SOI and both the homogeneous and inhomogeneous applied magnetic fields. The bottom panels show \(f_{v_ - } - f_{v_ + }\) (Fig. 2a) and \(f_{v_ - }\) (Fig. 2b) for Bext along [110] (θ = 0°), whereas the top panels correspond to the B-field along \([1\bar 10]\) (θ = 90°). In Fig. 2b, \(f_{v_ - }\) depends on Bext through g−μBtot/h, with Btot = |Bext + Bmicro|. The addition of Bmicro causes a change in Btot and shifts \(f_{v_ - }\) to coincide with the experimental data. The contributions of ΔB and SOI are negligible here in the GHz scale.
On the other hand, comparing the calculated \(f_{v_ - } - f_{v_ + }\) from SOI alone (labeled “Bext (TB)”) with the experimental data (in both the top and bottom panels of Fig. 2a), it is clear that the experimental B-field dependence of \(f_{v_ - } - f_{v_ + }\) (the slope, \(\frac{{d\left( {f_{v_ - } - f_{v_ + }} \right)}}{{dB_{{\mathrm{ext}}}}}\)) is captured from the effect of intrinsic SOI. However there is a shift between the SOI curve and the experimental data (different shift for θ = 0° and θ = 90°). The addition of Bmicro alone does not result in the necessary shift to match the experiment. Only after adding ΔB can a quantitative match with the experiment be achieved. Again the experiment-theory agreement is conditional on the interface condition and E z . Moreover, we see that the addition of ΔB does not change the dependency on Bext. Therefore, to properly explain the observed experimental behavior, we can ignore neither the SOI, which is responsible for the change in \(f_{v_ - } - f_{v_ + }\) with Bext, nor the inhomogeneous B-field which shifts \(f_{v_ - } - f_{v_ + }\) regardless of Bext.
Discussion
The only knobs we have to adjust to obtain a quantitative agreement between the experiment and the atomistic TB calculations, are (1) E z and (2) interfacial geometry, i.e., how many atomic steps at the interface lie inside the dot and where they are located relative to the dot center. These adjustments have to be done iteratively since the steps and E z not only affect the intrinsic SOI but also the influence of the inhomogeneous B-field. It is easy to separate out the contribution of the SOI from the micro-magnet in the Bext dependence of \(f_{v_ - } - f_{v_ + }\). It will be shown in Figs. 3 and 4 that, the slope, \(\frac{{d\left( {f_{v_ - } - f_{v_ + }} \right)}}{{dB_{{\mathrm{ext}}}}}\) originates from the SOI, while the micro-magnetic field shifts \(f_{v_ - } - f_{v_ + }\) independent of Bext. First we individually match the experimental “slope” from the SOI and the “shift” from the contribution of the micro-magnet for some combinations of the two knobs. Finally both effects together quantitatively match the experiment for E z = 6.77 MVm−1, and an interface with four evenly spaced monoatomic steps at −24.7, −2.9, 18.7, 40.4 nm from the dot center along the x ([100]) direction. This combination also predicts a valley splitting of 34.4 μeV in close agreement with the experimental value, given by 29 μeV.27 To describe the QD, a 2D simple harmonic (parabolic confinement) potential was used with orbital energy splittings of 0.55 and 9.4 meV characterizing the x and y ([010]) confinement respectively. As the interface steps are parallel to y direction, the orbital energy splitting along y has negligible effects, but the strong y confinement significantly reduces simulation time.
To further our understanding, we have complemented the atomistic calculations with an effective mass (EM) based analytic model with Rashba and Dresselhaus-like SOI terms (Supplementary Section S1), as used in earlier works.25,29,30,31 We have also developed an analytic model to capture the effects of the inhomogeneous magnetic field (Supplementary Section S2). Although our large-scale atomistic tight-binding simulation enables us to quantitatively capture the effects of the SOI and the atomic-scale details of the interface automatically, they are computationally expensive. The EM model, benchmarked with our atomistic results, allows us to get quick insight with the help of a set of fitting parameters. The contributions of the SOI and ΔB on \(f_{v_ - } - f_{v_ + }\) obtained from these models are shown in Eqs. (1) and (2), respectively.
Here, α± and β± are the Rashba and Dresselhaus-like coefficients respectively, l z is the spread of the electron wave function along z, \(\left\langle {x_ \pm } \right\rangle\) and \(\left\langle {y_ \pm } \right\rangle\) are the intra-valley dipole matrix elements, ϕ is the angle of the external magnetic field with respect to the [100] crystal orientation and \(\frac{{dB_i^\phi }}{{dj}}\) are the magnetic field gradients along different directions (i, j = x, y, z) for a specific angle ϕ. It is clear from these expressions that to match \(f_{v_ - } - f_{v_ + }\) the difference in SOI and dipole moment parameters between the valley states are relevant (but not their absolute values). The parameters used to match the experiment are β− − β+ = −2.5370 × 10−15 eV · m, α− − α+ = 9.4564 × 10−19 eV · m, \(\left\langle {x_ - } \right\rangle - \left\langle {x_ + } \right\rangle\) = −0.169 nm, \(\left\langle {y_ - } \right\rangle - \left\langle {y_ + } \right\rangle = 0\) nm and l z = 2.792 nm. These fitting parameters in the EM calculations enable us to obtain an even better match with the experimental data compared to TB in Figs. 1c and 2a (cyan solid lines). Here we want to point out that the accuracy of the numerically calculated micro-magnetic field values depends on our estimation of the dot location. But as we calculate (β− − β+) and (α− − α−) independently by comparing the measured \(\frac{{d\left( {f_{v_ - } - f_{v_ + }} \right)}}{{dB_{{\mathrm{ext}}}}}\) for [110] and \([1\bar 10]\) with Eq. (1) (Supplementary Section S5), any uncertainty in the estimated dot location or the micro-magnetic field values does not effect the extracted SOI parameters.
As shown in Figs. 1 and 2, three physical attributes play a key role in explaining the experimental data, 1) SOI, 2) Bmicro, and 3) ΔB. Each of these contribute to \(f_{v_ \pm }\), and only their sum can accurately reproduce the experimental data for a specific interface condition and vertical electric field, the two knobs mentioned in earlier paragraph. In Figs. 3 and 4, we show separately the effects of (1) and (3) respectively. We show how the contributions of SOI and ΔB are modulated by the nature of the confining interface (knob 2). The influence of E z (knob 1) on the effects of SOI and ΔB are shown in the Supplementary Figs. S3 and S4 respectively. We also show how Bmicro modifies the total homogeneous B-field in the Supplementary Fig. S7.
Spin-orbit interaction in a Si QD and valley dependent spin-splitting
The intrinsic SOI in a Si QD makes \(f_{v_ \pm }\) anisotropic. Figure 3a shows the angular dependence of \(f_{v_ \pm }\) for a Si QD with a smooth interface, without any micro-magnetic field, calculated from TB. Both \(f_{v_ - }\) and \(f_{v_ + }\) show a 180° periodicity but they are 90° out of phase. From analytic effective mass study (Supplementary Section S1), we understand that the anisotropic contribution from the Dresselhaus-like interaction, caused by interface inversion asymmetry,31 results in this angular dependence in \(f_{v_ \pm }\). Moreover, the different signs of the Dresselhaus coefficients β± for the valley states, give rise to a 90° phase shift between \(f_{v_ - }\) and \(f_{v_ + }\). It is important to notice that the change in \(f_{v_ \pm }\) is in MHz range. So, in GHz scale, like the blue curve (diamond markers) in Fig. 1d, this change is not visible. However, if we compare \(f_{v_ - }\) and \(f_{v_ + }\) for this ideal interface case, we see \(f_{v_ - } > f_{v_ + }\) at θ = 0° and \(f_{v_ - } < f_{v_ + }\) at θ = 90°, which does not explain the experimentally measured anisotropy. We now discuss the remaining physical parameters needed to obtain a complete understanding of the experiment.
The atomic-scale details of a Si QD interface actually define the Dresselhaus SOI. It is well-known that the interface between Si/SiGe or Si/SiO2 has atomic-scale disorder, with monolayer atomic steps being a common form of disorder.32 To understand how such non-ideal interfaces can affect SOI, we first introduce a monolayer atomic step as shown in Fig. 3b and vary the dot position laterally relative to the step, as defined by the variable x0. By fitting the EM solutions to the TB results (Supplementary Section S5), we have extracted β± and plotted them in Fig. 3c as a function of x0. It is seen that β± changes sign as the dot moves from the left to the right of the step edge. Both the sign and magnitude of β± depends on the distribution of the wave function between the neighboring regions with one atomic layer shift between them, as shown in Fig. 3b. To understand this behavior, we have to understand the atomic arrangements in a Si crystal, where the nearest neighbors of a Si atom lie either in the [110] or [1\(\bar 1\)0] planes. A monoatomic shift of the vertical position of the interface results in a 90° rotation of the atomic arrangements about the [001] axis, which results in a sign inversion of the Dresselhaus coefficient of that region31 (Supplementary Section S6). So whenever there is a monoatomic step at the interface, β changes sign between the two sides of the step. A dot wave function spread over a monoatomic step therefore samples out a weighted average of two βs with opposite signs.29,30 Thus the interface condition of a Si QD determines both the sign and strength of the effective Dresselhaus coefficients.
Next, we investigate the influence of interface steps on \(f_{v_ - } - f_{v_ + }\). Figure 3e shows the anisotropy of \(f_{v_ - } - f_{v_ + }\) with various step configurations shown in Fig. 3d. \(f_{v_ - } - f_{v_ + }\) exhibits a 180° periodicity, with extrema at the [110], \([1\bar 10]\), \([\bar 1\bar 10]\), \([\bar 110]\) crystal orientations. Both the sign and magnitude of \(f_{v_ - } - f_{v_ + }\) depends on the interface condition. Since β± decreases when a QD wave function is spread over a step edge, the smooth interface case (green curve) has the highest amplitude. Figure 3f shows that the slope of \(f_{v_ - } - f_{v_ + }\) with Bext changes sign for a 90° rotation of Bext and is strongly dependent on the step configuration. The step configuration labeled c3 in Fig. 3d is used to match the experiment in Figs. 1 and 2. So the curves for c3 in both Figs. 3e, f correspond to the SOI results of Figs. 1c and 2a. It is key to note here that, as E z also influences \(\left| {f_{v_ - } - f_{v_ + }} \right|\) and \(\left| {\frac{{d\left( {f_{v_ - } - f_{v_ + }} \right)}}{{dB_{{\mathrm{ext}}}}}} \right|\), shown in Supplementary Fig. S3, a different combination of interface steps and E z can also produce these same SOI results of Figs. 1c and 2a, but might not result in the necessary contribution from micro-magnet to match the experiment. Now the dependence of \(f_{v_ - } - f_{v_ + }\) on the interface condition will cause device-to-device variability, while the dependence on the direction and magnitude of Bext can provide control over the difference in spin splittings. These results thus give us answers to key questions 1 and 3 asked in introduction.
Inhomogeneous micro-magnetic field in a Si QD and valley dependent spin-splitting
Figure 4 illustrates how the inhomogeneous magnetic field alone changes \(f_{v_ - } - f_{v_ + }\) (denoted as \({\mathrm{\Delta }}\left( {f_{v_ - } - f_{v_ + }} \right)^{{\mathrm{\Delta }}{\bf{B}}}\)). In the presence of interface steps the wave functions for the v− and v+ valley states shift away from each other. This shift in an inhomogeneous magnetic field results in different \(f_{v_ - }\) and \(f_{v_ + }\). This can be understood from Figs. 4a, b, and/or Eq. (2). Interface steps generate strong valley-orbit hybridization33,34 causing the valley states to have non-identical wave functions (Fig. 4a), and hence different dipole moments, \(\left( {\left\langle {x_ - } \right\rangle - \left\langle {x_ + } \right\rangle } \right) \ne 0\) and/or \(\left( {\left\langle {y_ - } \right\rangle - \left\langle {y_ + } \right\rangle } \right) \ne 0\), as opposed to a flat interface case, which has \(\left\langle {x_ \pm } \right\rangle = \left\langle {y_ \pm } \right\rangle = 0\). Thus the spatially varying magnetic field has a different effect on the two wave functions, thereby contributing to the difference in ESR frequencies between the valley states. Figure 4b shows \({\mathrm{\Delta }}\left( {f_{v_ - } - f_{v_ + }} \right)^{\Delta {\bf{B}}}\) as a function of the dot location relative to a step edge, x0 (as in Fig. 3b) and illustrates that ΔB has the largest contribution to \(f_{v_ - } - f_{v_ + }\) when the step is in the vicinity of the dot. Since ΔBθ vectorially adds to Bext, an anisotropic \({\mathrm{\Delta }}\left( {f_{v_ - } - f_{v_ + }} \right)^{{\mathrm{\Delta }}{\bf{B}}}\) is seen in Fig. 4c with and without the various step configurations portrayed in Fig. 3d. We also see that \({\mathrm{\Delta }}\left( {f_{v_ - } - f_{v_ + }} \right)^{{\mathrm{\Delta }}{\bf{B}}}\) in Fig. 4c is negligible for a flat interface, but is significant when interface steps are present. Also, \({\mathrm{\Delta }}\left( {f_{v_ - } - f_{v_ + }} \right)^{{\mathrm{\Delta }}{\bf{B}}}\) is almost independent of Bext, as shown in Fig. 4d. The curves labeled c3 in both Figs. 4c, d correspond to the contribution of ΔB in Figs. 1c and 2a. Now E z also influences \(\left| {{\mathrm{\Delta }}\left( {f_{v_ - } - f_{v_ + }} \right)^{{\mathrm{\Delta }}{\bf{B}}}} \right|\), as shown in Supplementary Fig. S4. Thus a different combination of interface steps and E z can also produce these same ΔB results of Figs. 1c and 2a, but might not result in the necessary SOI contribution to match the experiment. Therefore, only a specific combination of these two knobs results in the final all-inclusive experiment-theory agreement.
Distinguishable effects of SOI and inhomogeneous magnetic field
It is important to figure out how to differentiate between the contributions of the SOI and the micro-mangetic fields in an experimental measurement. A comparison between Figs. 3f and 4d (also between Eqs. (1) and (2)) reveals that any dependence of \(f_{v_ - } - f_{v_ + }\) on Bext can only come from the SOI and not from the inhomogeneous magnetic field. This indicates that the experimental B-field dependency in Fig. 2a can not be explained without the SOI. So the effect of the SOI cannot be ignored even in the presence of a micro-magnet and this answers key question 2 raised in the introduction. However, engineering the micro-magnetic field will allow us to engineer the anisotropy of \(f_{v_ - } - f_{v_ + }\) (key question 3). Also, the influence of interface steps will cause additional device-to-device variability (key question 1).
SOI vs micro-magnet driven ESR in Si QDs
Now the understanding of an enhanced SOI effect compared to bulk, brings forward an important question, whether it is possible to perform electric-dipole spin resonance (EDSR) without the requirement of micro-magnets. Here, we predict that (Fig. 5) for similar driving amplitudes as used here the SOI-only EDSR can offer Rabi frequencies close to 1 MHz, which is around five times smaller than the micro-magnet based EDSR. Moreover, the Rabi frequency of the SOI-EDSR will strongly depend on the interface condition35 (Supplementary Section S7) and can be difficult to control or improve. On the other hand, with improved design (stronger transverse gradient field) we can gain more advantage of the micro-magnets and drive even faster Rabi oscillations. However, we also predict that, both the SOI and inhomogeneous B-field contribute to the E z dependence of \(f_{v_ \pm }\) (Supplementary Section S3) and make the qubits susceptible to charge noise.25 As these two have comparable contribution, both of their effects will add to the charge noise induced dephasing of the spin qubits in the presence of micro-magnets.
Calculated Rabi frequencies (fRabi) with SOI only, inhomogeneous B-field only and both SOI and inhomogeneous B-field for different direction of the external magnetic field for both v−(panel a) and v+ (panel b) valley states. Interface condition, vertical e-field and parabolic confinement for the dot used in these simulations are the same as that used to match the experimental data in Figs. 1 and 2. The valley and orbital splittings that we get from the simulations are around 34.4 μeV and 0.48 meV, respectively. The dot radius is around 35 nm. The fastest Rabi frequencies for SOI only are around 1 MHz, which are least five times smaller compared to that of the gradient B-field for θ = 0°. It is important to note here that the micro-magnet geometry was designed to maximize the Rabi frequency at θ = 0°. The details of the fRabi calculation are discussed in Supplementary Section S7
Possible application of the spin-valley interaction in a Si QD
The coupled spin and valley behavior observed in this work may in principle enable us to simultaneously use the quantum information stored in both spin and valley degrees of freedom of a single electron. For example, a valley controlled not gate9 can be designed in which the spin basis can be the target qubit, while the valley information can work as a control qubit. If we choose such a direction of the external magnetic field, where the valley states have different spin splittings, an applied microwave pulse in resonance with the spin splitting of v−, will rotate the spin only if the electron is in v−. So we get a NOT operation of the spin quantum information controlled by the valley quantum information. Spin transitions conditional to valley degrees of freedom are also shown in ref.15 and an inter-valley spin transition, which can entangle spin and valley degrees of freedom, is observed in ref.27.
Conclusion
To conclude, we experimentally observe anisotropic behavior in the electron spin resonance frequencies for different valley states in a Si QD with integrated micro-magnets. We analyze this behavior theoretically and find that intrinsic SOI introduces 180° periodicity in the difference in the ESR frequencies between the valley states, but the inhomogeneous B-field of the micro-magnet also modifies this anisotropy. Interfacial non-idealities like steps control both the sign and magnitude of this difference through both SOI and inhomogeneous B-field. We also measure the external magnetic field dependence of the resonance frequencies. We show that the measured magnetic field dependence of the difference in resonance frequencies originates only from the SOI. We conclude that even though the SOI in bulk silicon has been typically ignored as being small, it still plays a major role in determining the valley dependent spin properties in interfacially confined Si QDs (A few works on metal-oxide-semiconductor based Si QDs without any micro-magnets have appeared (arXiv:1703.03840, Nat. Commun. 9, 1768 (2018)) subsequent to our submission, that validate our findings and predictions about the spin-orbit interaction, its anisotropy and device-to-device variability). These understandings help us answer the key questions from the introduction, which are crucial for proper operation of various qubit schemes based on silicon quantum dots.
Methods
Theory
For the theoretical calculations, we use a large scale atomistic tight binding approach with spin resolved sp3d5s* atomic orbitals with nearest neighbor interactions.36 Typical simulation domains comprise of 1.5–2 million atoms to capture realistic sized dots. Spin-orbit interactions are directly included in the Hamiltonian as a matrix element between p-orbitals following the prescription of Chadi.37 The advantage of this approach is that no additional fitting parameters are needed to capture various types of SOI such as Rashba and Dresselhaus SOI in contrast to k.p theory. We introduce monoatomic steps as a source of non-ideality consistent with other works.32,34,38 We do not include strain in the calculations, in order to keep the model considered as minimal as possible; homogeneous strain adds effects similar to electric fields (Supplementary Section S8) and any inhomogeneity in strain, in the presence of atomic steps, adds effects similar to a slight change in the location of steps. The Si interface is modeled with Hydrogen passivation, without using SiGe. This interface model is sufficient to capture the SOI effects of a Si/SiGe interface discussed in refs.29,30,31. We use the methodology of ref.39 to model the micro-magnetic fields (Supplementary Section S4). Full magnetization of the micro-magnet is assumed. This causes the value of the magnetization of the micro-magnet to be saturated and makes it independent of Bext. However, a change in the direction of Bext changes the magnetization. We include the effect of inhomogeneous magnetic field perturbatively, with the perturbation matrix elements, \(\left\langle {\psi _m} \right|\frac{1}{2}g\mu {\mathrm{\Delta }}{\bf{B}}^\phi \left| {\psi _n} \right\rangle\) = \(\frac{1}{2}g\mu \mathop {\sum}\limits_{i,j} \left\langle {\psi _m} \right|\frac{{dB_i^\phi }}{{dj}}j\left| {\psi _n} \right\rangle\). Here, ψ n and ψ m are atomistic wave functions calculated with homogeneous magnetic field. For further details about the numerical techniques, see NEMO3D ref.36.
Experiment
Method details about the experiment can be found in ref.15. The dot location in this experiment is different from ref.15. The device was electrostatically reset by shining light using an LED and all the measurements were done with a new electrostatic environment (a new gate voltage configuration). The quantum dot location is estimated by the offsets of the magnetic field created by the micro-magnets extrapolated from the measurements shown in Fig. 2 and comparing to the simulation results shown in Supplementary Section S4. We also observed that the Rabi frequencies were different from ref.15 when applying the same microwave power to the same gate, which qualitatively indicates that the dot location is different.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Datta, S. & Das, B. Electronic analog of the electro-optic modulator. Appl. Phys. Lett. 56, 665(R) (1990).
Wolf, S. et al. Spintronics: a spin based electronics vision for the future. Science 294, 1488–1495 (2001).
Žutić, I., Fabian, J. & Das Sarma, S. Spintronics: fundamentals and applications. Rev. Mod. Phys. 76, 323 (2004).
Loss, D. & Vincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A. 57, 120 (1998).
Petta, J. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Koppens, F. et al. Driven coherent oscillations of a single electron spin in a quantum dot. Nature 442, 766–771 (2006).
Hanson, R. et al. Spins in few electron quantum dots. Rev. Mod. Phys. 79, 1217 (2007).
Xiao, D., Liu, G.-B., Feng, W., Xu, X. & Yao, W. Coupled spin and valley physics in monolayers of MoS2 and other group VI dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012).
Gong, Z. et al. Magnetoelectric effects and valley-controlled spin quantum gates in transition metal dichalcogenide bilayers. Nat. Commun. 4, 2053 (2013).
Xu, X., Yao, W., Xiao, D. & Heinz, T. Spins and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343–350 (2014).
Laird, E. A., Pei, F. & Kouwenhoven, L. P. A valley–spin qubit in a carbon nanotube. Nat. Nanotech. 8, 565–568 (2013).
Renard, V. T. et al. Valley polarization assisted spin polarization in two dimensions. Nat. Commun. 6, 7230 (2015).
Yang, C. et al. Spin-valley lifetimes in a silicon quantum dot with tunable valley splitting. Nat. Commun. 4, 2069 (2013).
Hao, X., Ruskov, R., Xiao, M., Tahan, C. & Jiang, H. Electron spin resonance and spin-valley physics in a silicon double quantum dot. Nat. Commun. 5, 3860 (2014).
Kawakami, E. et al. Electrical control of a long-lived spin qubit in a Si/SiGe quantum dot. Nat. Nanotechnol. 9, 666–670 (2014).
Veldhorst, M. et al. An addressable quantum dot qubit with fault tolerant control fidelity. Nat. Nanotechnol. 9, 981–985 (2014).
Maune, B. M. et al. Coherent singlet-triplet oscillations in a silicon-based double quantum dot. Nature 481, 344–347 (2011).
Wu, X. et al. Two-axis control of a singlet-triplet qubit with integrated micromagnet. Proc. Natl. Acad. Sci. USA 111, 11938 (2014).
Eng, K. et al. Isotopically enhanced triple quantum dot qubit. Sci. Adv. 1 no. 4, e1500214 (2015).
Kim, D. et al. Quantum control and process tomography of a semiconductor quantum dot hybrid qubit. Nature 511, 70–74 (2014).
Maurand, R. et al. A CMOS silicon spin qubit. Nat. Commun. 7, 13575 (2016).
Culcer, D., Sariava, A. L., Koiller, B., Hu, X. & Das Sarma, S. Valley-based noise resistant quantum computation using Si quantum dots. Phys. Rev. Lett. 108, 126804 (2012).
Rohling, N. & Burkard, G. Universal quantum computing with spin and valley states. New J. Phys. 14, 083008 (2012).
Rohling, N., Russ, M. & Burkard, G. Hybrid spin and valley quantum computing with singlet-triplet qubits. Phys. Rev. Lett. 113, 176801 (2014).
Veldhorst, M. et al. Spin-orbit coupling and operation of multivalley spin qubits. Phys. Rev. B 92, 201401(R) (2015).
Scarlino, P. et al. Second-harmonic coherent driving of a spin qubit in SiGe/Si quantum dot. Phys. Rev. Lett. 115, 106802 (2015).
Scarlino, P. et al. Dressed photon-orbital states in a quantum dot: Inter-valley spin resonance. Phys. Rev. B 95, 165429 (2017).
Tokura, Y., van der Wiel, W. G., Obata, T. & Tarucha, S. Coherent single electron spin control in a slanting Zeeman field. Phys. Rev. Lett. 96, 047202 (2006).
Golub, L. E. & Ivchenko, E. L. Spin splitting in symmetrical SiGe quantum wells. Phys. Rev. B 69, 115333 (2004).
Nestoklon, M. O., Golub, L. E. & Ivchenko, E. L. Spin and valley-orbit splittings in SiGe/Si heterostructures. Phys. Rev. B 73, 235334 (2006).
Nestoklon, M. O., Ivchenko, E. L., Jancu, J.-M. & Voisin, P. Electric field effect on electron spin splitting in SiGe/Si quantum wells. Phys. Rev. B 77, 155328 (2008).
Zandvliet, H. J. W. & Elswijk, H. B. Morphology of monatomic step edges on vicinal Si(001). Phys. Rev. B 48, 14269 (1993).
Gamble, J. K., Eriksson, M. A., Coppersmith, S. N. & Friesen, M. Disorder-induced valley-orbit hybrid states in Si quantum dots. Phys. Rev. B 88, 035310 (2013).
Friesen, M., Eriksson, M. A. & Coppersmith, S. N. Magnetic field dependence of valley splitting in realistic Si/SiGe quantum wells. Appl. Phys. Lett. 89, 202106 (2006).
Huang, W., Veldhorst, M., Zimmerman, N. M., Dzurak, A. S. & Culcer, D. Electrically driven spin qubit based on valley mixing. Phys. Rev. B 95, 075403 (2017).
Klimeck, G. et al. Atomistic simulation of realistically sized nanodevices using NEMO 3D: part I—models and benchmarks. IEEE Trans. Electron Dev. 54, 2079–2089 (2007).
Chadi, D. J. Spin-orbit splitting in crystalline and compositionally disordered semiconductors. Phys. Rev. B 16, 790 (1977).
Kharche, N., Prada, M., Boykin, T. B. & Klimeck, G. Valley splitting in strained silicon quantum wells modeled with 2° miscuts, step disorder, and alloy disorder. Appl. Phys. Lett. 90, 092109 (2007).
Goldman, J. R., Ladd, T. D., Yamaguchi, F. & Yamamoto, Y. Magnet designs for a crystal lattice quantum computer. Appl. Phys. A 71, 11 (2000).
Acknowledgements
This work was supported in part by ARO (W911NF-12-0607); development and maintenance of the growth facilities used for fabricating samples is supported by DOE (DE-FG02-03ER46028). This research utilized NSF-supported shared facilities (MRSEC DMR-1121288) at the University of Wisconsin-Madison. Computational resources on nanoHUB.org, funded by the NSF grant EEC-0228390, were used. M.P.N. acknowledges support from ERC Synergy Grant. R.F. and R.R. acknowledge discussions with R. Ruskov, C. Tahan, and A. Dzurak.
Author information
Authors and Affiliations
Contributions
R.F. performed the g-factor calculations, explained the underlying physics and developed the theory with guidance from R.R. R.F., R.R., E.K., P.S. and M.P.N. analyzed the simulation results and compared with experimental data in consultation with L.M.K.V., M.F., S.N.C. and M.A.E. E.K. and P.S. performed the experiment and analyzed the measured data. D.R.W. fabricated the sample. D.E.S. and M.G.L. grew the heterostructure. R.F. and R.R. wrote the manuscript with feedback from all the authors. R.R. and L.M.K.V. initiated the project, and supervised the work with S.N.C, M.F. and M.A.E.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ferdous, R., Kawakami, E., Scarlino, P. et al. Valley dependent anisotropic spin splitting in silicon quantum dots. npj Quantum Inf 4, 26 (2018). https://doi.org/10.1038/s41534-018-0075-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-018-0075-1
This article is cited by
-
Low disorder and high valley splitting in silicon
npj Quantum Information (2024)
-
Mapping of valley splitting by conveyor-mode spin-coherent electron shuttling
npj Quantum Information (2024)
-
Compilation and scaling strategies for a silicon quantum processor with sparse two-dimensional connectivity
npj Quantum Information (2023)
-
Anisotropy with respect to the applied magnetic field of spin qubit decoherence times
npj Quantum Information (2022)
-
A silicon singlet–triplet qubit driven by spin-valley coupling
Nature Communications (2022)