Abstract
Einstein–Podolsky–Rosen (EPR) steering describes a quantum nonlocal phenomenon in which one party can nonlocally affect the other’s state through local measurements. It reveals an additional concept of quantum non-locality, which stands between quantum entanglement and Bell nonlocality. Recently, a quantum information task named as subchannel discrimination (SD) provides a necessary and sufficient characterization of EPR steering. The success probability of SD using steerable states is higher than using any unsteerable states, even when they are entangled. However, the detailed construction of such subchannels and the experimental realization of the corresponding task are still technologically challenging. In this work, we designed a feasible collection of subchannels for a quantum channel and experimentally demonstrated the corresponding SD task where the probabilities of correct discrimination are clearly enhanced by exploiting steerable states. Our results provide a concrete example to operationally demonstrate EPR steering and shine a new light on the potential application of EPR steering.
Similar content being viewed by others
Introduction
In the original discussion of Einstein–Podolsky–Rosen (EPR) paradox,1 Schrödinger2,3 described a quantum non-local phenomenon that Alice can steer Bob’s state through her local measurements. Since then, great efforts have been made to understand quantum nonlocality. It was not until 2007, Wiseman, Jones, and Doherty revisited Schrödinger’s discussion and formulated the concepts of quantum non-locality as quantum entanglement, EPR steering, and Bell non-locality in terms of quantum information tasks.4,5 It is now clear that all steerable states are entangled, but not all steerable states exhibit the Bell non-locality,4,5 which implies that EPR steering sits between quantum entanglement and Bell non-locality. This hierarchy also holds for all possible positive operator valued measures.6 EPR steering has recently drawn plenty of attention.7 For example, several theoretical studies including the verification of EPR steering based on steering inequalities8 and all-versus-nothing proof,9 no-cloning of quantum steering,10 temporal steering,11,12,13,14,15 quantification of steerability,16,17,18 and one-way EPR steering19 have been reported as well as the corresponding experiments.20,21,22,23,24,25,26 There are also other interesting steering experiments, such as the high-order steering27 and loophole-free steering.28,29,30 Moreover, the parallel works based on the continuous variable systems31,32,33,34,35,36,37,38,39 have been reported.
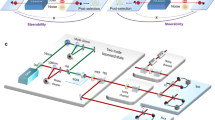
Similar to the necessary and sufficient verification of quantum entanglement with a quantum information task named quantum channel discrimination,40 which refers to the task of distinguishing among different quantum operations,41,42,43 EPR steering can be characterized necessarily and sufficiently based on a quantum task named subchannel discrimination (SD).17 As an extension of the quantum channel generally representing the physical transformation of information from an initial state to a final state in which the quantum operation is trace-preserving for all input states,44 a subchannel is a completely positive operator that does not increase the trace in the density matrix space.17 A series of subchannels {Λ h } h , that constitute a channel Λ satisfying \({\mathrm{\Lambda }} = \mathop {\sum}\nolimits_h {\kern 1pt} {\mathrm{\Lambda }}_h\), can be treated as a decomposition of the channel into its different evolutionary branches with the corresponding probability Tr(Λ h [ρ]) for any state ρ, as shown in Fig. 1a. Here, \({\mathrm{\Lambda }}_h[\rho ] = K_h\rho K_h^\dagger\), where the Kraus operators K h are the explicit matrix descriptions of Λ h and satisfy \(\mathop {\sum}\nolimits_h K_h^\dagger K_h = {\mathbb{I}}\). The SD task allows one to distinguish in which subchannel the quantum evolution occurs, whereas this information is lost if the process is described simply in the framework of the quantum channel. Moreover, SD tasks might lead to the emergence of new quantum phenomena and applications in quantum information processing, such as the SD-based quantum key distribution.45
The process of subchannel discrimination (SD). a The collection of subchannels {Λ h } h composing a quantum channel Λ. b The protocol for realizing the Kraus operators K ij using the entanglement-breaking channel (EBC) scenario. The state ρ is measured along the z direction with output result i after passing through the intermediate subchannel A j . A new state is prepared based on the value of i. c The single-qubit protocol for SD in the case of two measurement settings. The unitary operation U related to the intermediate subchannels A0 and A1 is demonstrated with the qubit state ρ and an auxiliary qubit \(\left| 0 \right\rangle\) which is finally measured along z with output result j. After the EBC, the measurement along a direction \(\vec n\) is performed on the signal qubit, and the result b is obtained. d The two-qubit protocol for SD with multiple measurement settings. One of the two qubits, in a state ρ AB , is sent to Bob, and the other is sent to Alice. On Bob’s side, the qubit passes through one of the unitary gates g m with probability 1/m before the evolution K ij . Alice chooses one of the measurement directions \(\vec n_i\) based on the result b|g m from Bob and obtains the result a
Recently, it has been proven that for any bipartite state, we can verify it is steerable if there exists an SD task in which the successful discrimination probability is enhanced by this state compared with the case employing single-qubit states; otherwise, if no such SD tasks exist, it is unsteerable.17 Also, such an SD task presents an operational method to characterize EPR steering. However, the detailed construction of such subchannels has not been investigated up to now. In this article, we design a feasible collection of concrete subchannels and experimentally demonstrate EPR steering with the corresponding SD task.
Results
SD task for the two-setting case
First, we would like to introduce the detailed SD task in the simplest case with two measurement settings. In this work, we consider a channel consisting of four subchannels Λ ij (i, j = 0 or 1), where the corresponding Kraus operators are denoted by K ij . We exploit an entanglement-breaking channel (EBC)46 to limit the bound established in the single-qubit protocol. The Kraus operators K ij are implemented with the EBC, as illustrated in Fig. 1b, where A j (j = 0 or 1) is regarded as the intermediate subchannel and satisfies \(K_{ij} = \left| i \right\rangle \left\langle i \right| \cdot A_j\) (i, j = 0 or 1) (see Methods). Since the information of i is included in the output ρ out , the SD task is transformed into the task of distinguishing A j based on i. To realize {A j } j , a unitary operation U is performed on a quantum system consisting of a target qubit in the state ρ and an auxiliary qubit initially in the state \(\left| 0 \right\rangle\),47 as shown in Fig. 1c. In this work, the operation is represented as follows,
A j is determined according to the output j measured along the z direction on the auxiliary qubit. The SD task in single-qubit protocol is completed by guessing j according to the output b that is measured along a direction \(\vec n\) on the target qubit. Since the target qubit only carries the classical information after the EBC, \(\vec n\) is optimized to be z to maximize the success probability \(P_\rho ^{\mathrm{s}}\). With the input state ρ, the results of different strategies for guessing j are denoted by \(p_\rho ^{c0},p_\rho ^{c1}\) (guessing j is the constant 0 or 1 regardless of b, respectively), \(p_\rho ^{00},p_\rho ^{01}\) (guessing j = b or j = b ⊕ 1 where ⊕ represents addition modulo 2, respectively). The success probability is denoted as \(P_\rho ^{\mathrm{s}} = {\mathrm{max}}\left\{ {p_\rho ^{c0},p_\rho ^{c1},p_\rho ^{00},p_\rho ^{01}} \right\}\), and the upper-bound probability Ps in the single-qubit case is obtained by optimizing the input state, which implies \(P^{\mathrm{s}} = {\mathrm{max}}_\rho \left\{ {P_\rho ^{\mathrm{s}}} \right\}\).
We now consider the two-qubit Werner states ρ AB 48 with the form of,
where η ∈ [0,1], \(\left| {\mathrm{\Phi }} \right\rangle\) is the maximally entangled state, and \({\mathbb{I}}{\mathrm{/}}4\) is the maximally mixed state. As illustrated in Fig. 1d in the two-setting case (m = 1, and g1 is identical), the task is that Alice guesses j and announces to Bob based on a which is obtained by measuring along \(\vec n_i\) (chosen according to b). Since b ∈ {0, 1}, there are two directions \(\vec n_i\) along which Alice can choose to measure. In this work, we follow two rules to design the SD tasks, i.e., (i) the success probability of maximally entangled state is 100%; (ii) the success probability of maximally mixed state is 50%. Thus, the success probability of SD task \(P_{\rho _{AB}}\) equals to 1/2 + η/2. In the linear EPR steering inequalities, \(C_n^{{\mathrm{LHS}}}\) denotes the bound established by the local hidden state model where n is the number of measurement settings.20 In the case of n = 2, \(C_2^{{\mathrm{LHS}}} = \eta _2^ \ast\) where \(\eta _2^ \ast = 1{\mathrm{/}}\sqrt 2\) is the visibility bound of the Werner states. When \(\eta > \eta _2^ \ast\), \(\rho _{\rho _{AB}}\) is steerable. For the single-qubit protocol, by directly calculating, we find \(P^{\mathrm{s}} = 1{\mathrm{/}}2 + C_2^{{\mathrm{LHS}}}{\mathrm{/}}2\) (see Section I of the Supplemental Material for details (See the Supplemental Material.)). Thus, if Bob finds \(P_{\rho _{AB}} > P^{\mathrm{s}}\), the steerability from Alice to Bob is observed.
SD task for the multi-setting cases
EPR steering from Alice to Bob relates to the number of settings measured by Alice.4,49 For some predictably steerable states, steering fails because of the very limited number of measurement settings.25 To capture as much information about the states as possible to demonstrate EPR steering, it is necessary for Alice to apply multiple measurement settings to approach the predictions of infinite measurement settings. In this work, we consider the regularly spaced directions which are given by the Platonic solids with the number of measurement settings n corresponding to 2, 3, 4, 6, and 10.20 Compared with the optimal measurement settings introduced in,49 here, the two-setting and three-setting measurements are optimal and EPR steering can be affirmed necessarily and sufficiently. For other multi-setting cases, the optimal measurements don’t correspond to the regularly spaced directions and are difficult to realize in experiment. Moreover, the diffence between the results in this work and the predictions of the optimal measurements is very small (see Section I of the Supplemental Material (See the Supplemental Material.)). To experimentally realize such a task, on Bob’s side, the qubit equiprobably evolves through several unitary gates g m before the Kraus operators K ij , as illustrated in Fig. 1d, and the details can be found in Section I of the Supplemental Material (See the Supplemental Material.). The corresponding measurement setting based on Bob’s result b|g m , which denotes that b is obtained under the gate operation g m , is then implemented on Alice’s side. In fact, for each g m , the SD process can still be regarded within the framework of two measurement settings. In the single-qubit protocol with n measurement settings, denoting \(P_{m,\rho }^{\mathrm{s}}\) for each g m , the total success probability is obtained as \(P_n^s = {\mathrm{max}}_\rho \left\{ {\mathop {\sum}\nolimits_m {\kern 1pt} 1{\mathrm{/}}mP_{\rho ,m}^{\mathrm{s}}} \right\}\). Similarly, for the two-qubit state ρ AB , \(P_{\rho _{{{AB}}},{\kern 1pt} n} = \mathop {\sum}\nolimits_m {\kern 1pt} 1{\mathrm{/}}m{\kern 1pt} P_{\rho _{{{AB}}},m}\). Furthermore, similar with the two-setting case, we have \(C_n^{{\mathrm{LHS}}} = \eta _n^ \ast\) and \(P_n^{\mathrm{s}} = 1{\mathrm{/}}2 + C_n^{{\mathrm{LHS}}}{\mathrm{/}}2\) (see Section I of the Supplemental Material for details (See the Supplemental Material.)) when the multiple measurement settings are selected based on the Platonic solids.20 As a result, the constructed SD task provides an operational method to characterize the steerability of Werner states. If the success probability of SD is enhanced by using the two-qubit state ρ AB , i.e., \(P_{\rho _{AB}} > P^{\mathrm{s}}\), then ρ AB is steerable from Alice to Bob regardless of the number of measurement settings; otherwise, under n measurement settings performed by Alice, i.e., \(P_{\rho _{{{AB}}},{\kern 1pt} n} \le P_n^{\mathrm{s}}\), Alice fails to steer Bob’s states.
Compared with the two-setting case in which there are four subchannels, the multi-setting cases can be regarded as multi-subchannel discrimination tasks where more subchannels consisting of gates g m and the corresponding Kraus operators K ij are required, and the reconstructed subchannels could be expressed as \(K_{ijm}^\prime = K_{ij} \cdot g_m\). Following the similar method designing subchannels for Werner states, we can also create the corresponding subchannels for other types of two-qubit states, like the Bell diagonal states (see Section I of the Supplemental Material (See the Supplemental Material.)).
Experimental setup
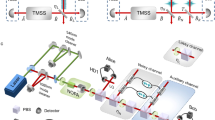
The unitary operation U shown in Fig. 1c can be decomposed into several parts, including two control-not (CNOT) gates (CNOT1 and CNOT2) and the other unitary evolutions E, V1, V2, and V3, and implemented in an optical Sagnac-like interferometer (SLI), as illustrated in Fig. 2 (see Methods). And U could be expressed as
where \({\mathbb {I}}_C\) is the identical operation on the control qubit. To obtain the bound Ps and verify the setup, the single-qubit protocol is performed with the input state denoted as \(\rho (\theta ) = {\mathrm{cos}}{\kern 1pt} \theta \left| {\mathrm{H}} \right\rangle + {\mathrm{sin}}{\kern 1pt} \theta \left| {\mathrm{V}} \right\rangle\) where \(\left| {\mathrm{H}} \right\rangle\) and \(\left| {\mathrm{V}} \right\rangle\) represent the horizonal and vertical polarizations of the photons, respectively. For the two-qubit protocol, Werner states are prepared via the spontaneous parametric down conversion process by pumping the nonlinear crystal of periodically poled KTiOPO4 (PPKTP) which is placed in a polarization Sagnac interferometer.50 Here, \(\left| {\mathrm{\Phi }} \right\rangle\) is prepared to be \(\left( {\left| {\mathrm{HH}} \right\rangle + \left| {\mathrm{VV}} \right\rangle } \right){\mathrm{/}}\sqrt 2\). The experimental Werner states ρ AB are prepared with an average fidelity of 98.3 ± 0.2%. The detailed experimental preparation can be found in Methods.
Logic circuit and experimental setup. a The logic circuit for implementing U. b The integrated experimental setup. One photon is sent to Bob, and the other is sent to Alice. On Bob’s side, each one of the gates g m before the Sagnac-like interferometer (SLI) is realized using a combination of a quarter-wave plate (QWP), a half-wave plate (HWP) and a QWP; the photons are measured along the z direction using an HWP and a polarized beam splitter (PBS). On Alice’s side, in the single-qubit protocol, the photons are detected directly to provide a coincidence signal. While, in the two-qubit protocol, Alice measures her photons along a direction \(\vec n_i\) that is chosen based on the result b|g m received from Bob. The photons on both sides are detected by single-photon detectors (SPD). Finally, Alice’s measurement result is sent to coincidence units, unit0 and unit1, to coincide with the corresponding results from port0 and port1, respectively. c The unit used to prepare the investigated entangled states. The polarization Sagnac interferometer is used to prepare the maximally entangled state \(\left| {\mathrm{\Phi }} \right\rangle\) to be fed into the dual-wavelength PBS and HWP, i.e., HWP2. An additional unit M, in which the dashed gray part inserted with a long enough birefringent crystal (BC) assists in preparing the maximally mixed component \({\mathbb {I}}{\mathrm{/}}4\), is placed at the port to Alice to produce the mixed state ρ AB . Two moveable shutters are used to adjust the parameter η. BS beam splitter, DM dichroic mirror. d Experimental realization of U with the SLI constructed from a homemade beam splitter, with half of it coated as a PBS and the other half coated as a non-polarized beam splitter (NBS)
Experimental results
In the case of two measurement settings, the results \(p_\rho ^{c0},p_\rho ^{c1},p_\rho ^{00}\) and \(p_\rho ^{01}\) are presented in Fig. 3a which show that the input states ρ(θ) should be optimized to obtain the upper-bound value Ps. More results in the single-qubit protocol with multiple measurement settings are presented in Section III of the Supplemental Material (See the Supplemental Material.). The Werner state ρ AB is identified to be steerable when the SD performance is enhanced with \(P_{\rho _{AB}} > P^s\), see Fig. 3b, c. By contrast, when \(P_{\rho _{AB},{\kern 1pt} n} \le P_n^s\) (n = 2, 3, 4, 6, 10), Alice fails to steer Bob’s state via the corresponding SD task. As the number of measurement settings increases, the bound established for the single-qubit approach decreases, whereas the success probability achieved by employing steerable resources remains constant, as illustrated in Fig. 3d. All error bars in this work are estimated as the standard deviation from the statistical variation of the photon counts, which is assumed to follow a Poisson distribution. As the error bars on the experimental probabilities are very small, roughly 0.002, they are not shown in the figures.
Experimental results for the SD task. a The probabilities of successful discrimination with single-qubit states in the case of two measurement settings. The curves and symbols represent the theoretical predictions and experimental results, respectively. b,c The experimental results in the two-qubit protocol with two and six measurement settings, respectively. The blue lines represent the theoretical predictions. The pink and green dots in b and c represent the corresponding experimental results, with the pink and green solid lines representing the single-qubit upper bounds for two and six measurement settings, respectively. The black dashed lines represent the single-qubit upper bound for the infinite number of measurement settings. d The comparison of the single-qubit upper bounds Ps with the results \(P_{\rho _{{AB}}}\) obtained using the prepared maximally entangled state (blue dots) for different number of measurement settings. The success probabilities \(P_{\rho _{{AB}}}\) are lower than the theoretical predictions, which can be primarily attributed to imperfect experimental manipulation. The brown squares represent the theoretical predictions of the upper bound for single-qubit states, whereas the experimental results are represented by the purple triangles. The bound Ps established for the single-qubit approach decreases, and it is very close to the value with infinite measurement settings when the number of measurement setting is equal to ten. The experimental error bars which are very small and not shown are estimated as the standard deviation
Moreover, by means of the SD task, the difference between EPR steering and entanglement can be characterized in an operational way. It is found that the success probability achieved using unsteerable Werner states ρ AB cannot surpass the single-qubit bound when \(\eta \le \eta _{10}^ \ast \approx 0.524\) in the case of ten measurement settings.20 However, ρ AB is still entangled when η > 1/3. This implies that the success probability of SD cannot be enhanced by using unsteerable entangled states, which is experimentally verified by the two pink dots in Fig. 4a. The concurrences of these two pink dots are measured to be 0.154 ± 0.008 and 0.223 ± 0.009, which verify that the states are entangled.51 We further investigate EPR steering with Bell-local states. Theoretically, the Bell inequality will be violated when \(\eta > 1{\mathrm{/}}\sqrt 2\),48 and according to ref. 52, ρ AB is a Bell-local state when η ≤ 0.683. We measure the Bell-CHSH parameter S53 which is shown as the function of \(P_{\rho _{{AB}}}\) in Fig. 4b. The success probabilities of SD using three Bell-local states which are represented by the dark red dots in Fig. 4 are enhanced, and therefore, these states are steerable.
Experimental results of investigating different kinds of correlations via the SD task. a The probabilities of successful discrimination for the case of ten measurement settings. The colored dots represent the experimental results, and the blue line represents the theoretical prediction. The dark red solid line and black dashed lines represent the upper bounds in the case of the single-qubit protocol for ten and infinite measurement settings, respectively. b The experimental results for the Bell-CHSH parameter S as a function of the success probability of SD, \(P_{\rho _{{AB}}}\), in the case of ten measurement settings. The colored dots represent the experimental results. The green solid line represents the upper bound of local-hidden-variable model. The dark red dashed line represents the single-qubit upper bound. The experimental error bars which are very small and not shown are estimated as the standard deviation
Discussion
Based on the proof of the necessary and sufficient characterization of EPR steering, we designed and experimentally implemented an SD task to demonstrate EPR steering using two-qubit Werner states. The methods for decomposing a quantum evolution into sub-channels can be helpful for gaining a thorough understanding of complex open-system dynamics. The enhanced probabilities of successful discrimination achieved using EPR steering provides a concrete example of the application. Moreover, this practical task offers an intuitive means of operationally distinguishing the different concepts of quantum nonlocality.
Compared with the previous experiments using steering inequalities to investigate EPR steering, in which Bob measures along several directions when steered by Alice,20,25 our work exhibits a particular feature that the measurement performed on Bob’s qubit is restricted to a single direction, which is z in this work. This feature implies that the SD task offers a convenient approach for identifying EPR steering. Another character of the SD task is the measurement sequence of Alice and Bob. In the previous works,4,21 considering that Alice steers Bob, Bob performs the measurements after receiving the measurement results from Alice. However, in the SD task, the sequence is reversed, which means Alice begins to measure her qubit after Bob’s measurements.
As EPR steering can be regarded as the one-side device-independent quantum information task,45 the steering-enhanced SD task, where Bob trusts his experimental device while Alice’s side is device-independent, shows the potential application in one-side device-independent quantum key distribution. Furthermore, in our work, the SD task on Bob’s side is implemented based on the one-way classical communication (from Bob to Alice). Considering the situation that Bell non-locality relates to the two-side device-independent quantum information task,5,45 one might extend the SD task demonstrating EPR steering to investigate the Bell non-locality. For instance, a similar quantum information task referring to a bipartite SD problem (SD tasks on both sides) with two-way classical communications, which relates to the communication complexity problem,54,55 might be used to characterize Bell non-locality in an operational way.
Methods
The detailed expressions of A j and K ij in the two-setting case
Following the theoretical method to determine A j which is introduced in Section I of the Supplemental Material in detail (See the Supplemental Material.), we can obtain the expressions of A0, A1 in the two-setting case as below
Considering the Kraus operators K ij which satisfy \(K_{ij} = \left| i \right\rangle \left| i \right\rangle \cdot A_j\) (i, j = 0 or 1), we can get
For multi-setting cases, the corresponding expressions of A j and K ij can be obtained using the similar method which is shown in Section I of the Supplemental Material (See the Supplemental Material.).
Experimental implementation of the unitary operation U
We construct an inherently stable optical interferometer, namely, a Sagnac-like interferometer (SLI), to realize this operation U (see Fig. 2b). The path and polarization degree of freedom of the photons are used as the auxiliary qubit, which is initially in the state \(\left| 0 \right\rangle\), and the probe qubit, respectively. A homemade beam splitter, of which one half is coated as a PBS and the other half is coated as a non-polarized beam splitter (NBS), acts as the input-output coupling element of the interferometer. Each single-qubit gate evolution of the probe qubit (the polarization of photons), i.e., V1,V2, and V3, is realized through a combination of two HWPs. The operation E on the auxiliary qubit is realized by adjusting the ratio of the numbers of photons on the \(\left| 0 \right\rangle\) and \(\left| 1 \right\rangle\) paths, which is achieved by means of a continuously variable neutral density filter (CVF) crossing both paths. For the first CNOT gate, the path qubit is the control qubit, while the polarization is used as the target qubit. Thus, the polarization of photons on the \(\left| 0 \right\rangle\) path remains the same, whereas the polarization on the \(\left| 1 \right\rangle\) path reverses, meaning that the polarization \(\left| {\mathrm{H}} \right\rangle\) is flipped to \(\left| {\mathrm{V}} \right\rangle\) and \(\left| {\mathrm{V}} \right\rangle\) is flipped to \(\left| {\mathrm{H}} \right\rangle\). This process is realized by placing one HWP on each of the two paths; HWP0, located on the \(\left| 0 \right\rangle\) path, is set at 0° for phase compensation, while HWP1 is set at 45° to reverse the polarizations of \(\left| H \right\rangle\) and \(\left| V \right\rangle\). The second CNOT gate is the inverse of the first CNOT gate; the polarization is treated as the control qubit affecting the target qubit, which is the qubit related to the path information. This gate is implemented in the PBS part of the homemade beam splitter. In detail, the \(\left| {\mathrm{H}} \right\rangle\) polarization remains unchanged (retaining the same path information), while the \(\left| {\mathrm{V}} \right\rangle\) polarization flips to the other path. The imperfect optical elements, especially the homemade beam splitter, would reduce the visibility of the interferometer and introduce system errors.
To realize {g m } in the multi-setting cases, several wave plates including HWPs and quarter-wave plates (QWPs) are employed. This part is explained in detail in Section II of the Supplemental Material (See the Supplemental Material.).
Preparation of the experimental states
To obtain the single-qubit upper bound and verify the setup, we perform the SD task using the following single-qubit state ρ(θ),
In this case, the photons on Bob’s side are prepared as the state expressed in Eq. (6), and the photons on Alice’s side are detected directly to provide coincidence signals. ρ(θ) are simply prepared with a half-wave plate (HWP) set at the angel θ/2 following a polarized beam splitter (PBS). The upper bound is then \(P^{\mathrm{s}} = {\mathrm{max}}_{\rho (\theta )}\left\{ {P_{\rho (\theta )}^{\mathrm{s}}} \right\}\).
The investigated ρ AB states are manufactured by combining the maximally entangled state \(\left| \Phi \right\rangle\) and the maximally mixed state \({\mathbb{I}}{\mathrm{/}}4\). \(\left| \Phi \right\rangle\) is prepared via the spontaneous parametric down conversion process where a χ(2) nonlinear crystal of periodically poled KTiOPO4 (PPKTP) is pumped by an ultraviolet laser with a peak wavelength of 404.1 nm and a spectrum width of 0.05 nm. The crystal is placed in a polarization Sagnac interferometer,50 as illustrated in Fig. 2c. The dichroic mirror (DM) is designed to exhibit high transmission at 404 nm and high reflection at 808 nm. A dual-wavelength polarization beam splitter (PBS) is employed as the input-output coupling element of the Sagnac interferometer, and a dual-wavelength HWP set at 45° is used to change the vertically polarized component of the ultraviolate photon to the horizonal polarization to pump the PPKTP crystal. The crystal is placed in a thermoelectric oven with the temperature set at 28.5 ± 0.1 °C. The maximally entangled state \(\left| {\mathrm{\Phi }} \right\rangle\) is prepared with a brightness of ~18,000 pairs s−1 mW−1, which is filtered using 3 nm bandwidth filters, and the state fidelity is 95.5 ± 0.4%. As shown in Fig. 2c, a part of the input of unit M still remains as the maximally entangled state \(\left| {\mathrm{\Phi }} \right\rangle \left\langle {\mathrm{\Phi }} \right|\), and the other part is used to prepare the maximally mixed state \({\mathbb{I}}{\mathrm{/}}4\) with the dashed gray part in unit M. Two HWPs are set at 22.5° and a birefringent calcite crystal (BC) of 10 mm in length is employed to induce decoherence between the horizonal and vertical polarizations of the photons. The shutters are used to adjust the ratio between \(\left| {\mathrm{\Phi }} \right\rangle \left\langle {\mathrm{\Phi }} \right|\) and \({\mathbb{I}}{\mathrm{/}}4\) to control the parameter η.
Data availability
All relevant data and program codes are available from the corresponding author upon the reasonable request.
References
Einstein, A., Podolsky, B. & Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 0777–0780 (1935).
Schrodinger, E. Discussion of probability relations between separated systems. Proc. Camb. Philos. Soc. 31, 555–563 (1935).
Schrodinger, E. Probability relations between separated systems. Proc. Camb. Philos. Soc. 32, 446–452 (1936).
Wiseman, H. M., Jones, S. J. & Doherty, A. C. Steering, entanglement, nonlocality, and the Einstein-Podolsky-Rosen paradox. Phys. Rev. Lett. 98, 140402 (2007).
Jones, S. J., Wiseman, H. M. & Doherty, A. C. Entanglement, einstein-podolsky-rosen correlations, bell nonlocality, and steering. Phys. Rev. A 76, 052116 (2007).
Quintino, M. T. et al. Inequivalence of entanglement, steering, and Bell nonlocality for general measurements. Phys. Rev. A 92, 032107 (2015).
Cavalcanti, D. & Skrzypczyk, P. Quantum steering: a review with focus on semidefinite programming. Rep. Prog. Phys. 80, 024001 (2017).
Cavalcanti, E. G., Jones, S. J., Wiseman, H. M. & Reid, M. D. Experimental criteria for steering and the Einstein-Podolsky-Rosen paradox. Phys. Rev. A 80, 032112 (2009).
Chen, J. L. et al. All-versus-nothing proof of Einstein-Podolsky-Rosen steering. Sci. Rep. 3, 2143 (2013).
Chiu, C. Y., Lambert, N., Liao, T. L., Nori, F. & Li, C. M. No-cloning of quantum steering. Npj Quantum Inf. 2, 16020 (2016).
Chen, Y. N. et al. Entanglement swapping and testing quantum steering into the past via collective decay. Phys. Rev. A 88, 052320 (2013).
Chen, Y. N. et al. Temporal steering inequality. Phys. Rev. A 89, 032112 (2014).
Bartkiewicz, K., Cernoch, A., Lemr, K., Miranowicz, A. & Nori, F. Temporal steering and security of quantum key distribution with mutually unbiased bases against individual attacks. Phys. Rev. A 93, 062345 (2016).
Chen, S. L. et al. Quantifying non-markovianity with temporal steering. Phys. Rev. Lett. 116, 020503 (2016).
Chen, S. L. et al. Spatio-temporal steering for testing nonclassical correlations in quantum networks. Sci. Rep. 7, 3728 (2017).
Skrzypczyk, P., Navascues, M. & Cavalcanti, D. Quantifying Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 112, 180404 (2014).
Piani, M. & Watrous, J. Necessary and sufficient quantum information characterization of Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 114, 060404 (2015).
Costa, A. C. S. & Angelo, R. M. Quantification of Einstein-Podolski-Rosen steering for two-qubit states. Phys. Rev. A 93, 020103 (2016).
Bowles, J., Vértesi, T., Quintino, M. T. & Brunner, N. One-way Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 112, 200402 (2014).
Saunders, D. J., Jones, S. J., Wiseman, H. M. & Pryde, G. J. Experimental EPR-steering using Bell-local states. Nat. Phys. 6, 845–849 (2010).
Sun, K. et al. Experimental demonstration of the Einstein-Podolsky-Rosen steering game based on the all-versus-nothing proof. Phys. Rev. Lett. 113, 140402 (2014).
Bartkiewicz, K., Cernoch, A., Lemr, K., Miranowicz, A. & Nori, F. Experimental temporal quantum steering. Sci. Rep. 6, 38076 (2016).
Liu, Z. D. et al. Experimental test of single-system steering and application to quantum communication. Phys. Rev. A 95, 022341 (2017).
Wollmann, S., Walk, N., Bennet, A. J., Wiseman, H. M. & Pryde, G. J. Observation of genuine one-way Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 116, 160403 (2016).
Sun, K. et al. Experimental quantification of asymmetric Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 116, 160404 (2016).
Xiao, Y. et al. Demonstration of multisetting one-way Einstein-Podolsky-Rosen steering in two-qubit systems. Phys. Rev. Lett. 118, 140404 (2017).
Li, C. M. et al. Genuine high-order Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 115, 010402 (2015).
Smith, D. H. et al. Conclusive quantum steering with superconducting transition-edge sensors. Nat. Commun. 3, 1628 (2012).
Bennet, A. J. et al.Arbitrarily loss-tolerant Einstein-Podolsky-Rosen steering allowing a demonstration over 1 km of optical fiber with no detection loophole. Phys. Rev. X 2, 031003 (2012).
Wittmann, B. et al. Loophole-free Einstein–Podolsky–Rosen experiment via quantum steering. New J. Phys. 14, 053030 (2012).
Reid, M. D. Demonstration of the Einstein-Podolsky-Rosen paradox using nondegenerate parametric amplification. Phys. Rev. A 40, 913–923 (1989).
Olsen, M. K. & Bradley, A. S. Bright bichromatic entanglement and quantum dynamics of sum frequency generation. Phys. Rev. A 77, 023813 (2008).
Midgley, S. L. W., Ferris, A. J. & Olsen, M. K. Asymmetric Gaussian steering: when Alice and Bob disagree. Phys. Rev. A 81, 022101 (2010).
He, Q. Y. & Reid, M. D. Genuine multipartite Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 111, 250403 (2013).
He, Q. Y., Gong, Q. H. & Reid, M. D. Classifying directional Gaussian entanglement, Einstein-Podolsky-Rosen steering, and discord. Phys. Rev. Lett. 114, 060402 (2015).
He, Q. Y., Rosales-Zarate, L., Adesso, G. & Reid, M. D. Secure continuous variable teleportation and Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 115, 180502 (2015).
Händchen, V. et al. Observation of one-way Einstein-Podolsky-Rosen steering. Nat. Photon. 6, 598–601 (2012).
Kogias, I., Lee, A. R., Ragy, S. & Adesso, G. Quantification of Gaussian quantum steering. Phys. Rev. Lett. 114, 060403 (2015).
Armstrong, S. et al. Multipartite Einstein-Podolsky-Rosen steering and genuine tripartite entanglement with optical networks. Nat. Phys. 11, 167–172 (2015).
Piani, M. & Watrous, J. All entangled states are useful for channel discrimination. Phys. Rev. Lett. 102, 250501 (2009).
Acín, A. Statistical distinguishability between unitary operations. Phys. Rev. Lett. 87, 177901 (2001).
D’Ariano, G. M., Lo Presti, P. & Paris, M. G. A. Using entanglement improves the precision of quantum measurements. Phys. Rev. Lett. 87, 270404 (2001).
Lloyd, S. Enhanced sensitivity of photodetection via quantum illumination. Science 321, 1463–1465 (2008).
Nielsen, M. A. & Chuang, I. L. Quantum computation and quantum information, New edn (Cambridge University Press, New York, 2010).
Branciard, C., Cavalcanti, E. G., Walborn, S. P., Scarani, V. & Wiseman, H. M. One-sided device-independent quantum key distribution: security, feasibility, and the connection with steering. Phys. Rev. A 85, 010301 (2012).
Horodecki, M., Shor, P. W. & Ruskai, M. B. Entanglement breaking channels. Rev. Math. Phys. 15, 629–641 (2003).
Stinespring, W. F. Positive functions on C*-algebras. Proc. Am. Math. Soc. 6, 211–216 (1955).
Werner, R. F. Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys. Rev. A 40, 4277–4281 (1989).
Evans, D. A. & Wiseman, H. M. Optimal measurements for tests of Einstein-Podolsky-Rosen steering with no detection loophole using two-qubit Werner states. Phys. Rev. A 90, 012114 (2014).
Kim, T., Fiorentino, M. & Wong, F. N. C. Phase-stable source of polarization-entangled photons using a polarization Sagnac interferometer. Phys. Rev. A 73, 012316 (2006).
Wootters, W. K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245–2248 (1998).
Hirsch, F., Quintino, M. T., Vértesi, T., Navascués, M. & Brunner, N. Better local hidden variable models for two-qubit Werner states and an upper bound on the Grothendieck constant K G (3). Quantum 1, 3 (2017).
Clauser, J. F., Horne, M. A., Shimony, A. & Holt, R. A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880–884 (1969).
Brukner, C., Zukowski, M., Pan, J. W. & Zeilinger, A. Bell’s inequalities and quantum communication complexity. Phys. Rev. Lett. 92, 127901 (2004).
Buhrman, H. et al. Quantum communication complexity advantage implies violation of a Bell inequality. Proc. Natl Acad. Sci. USA 113, 3191–3196 (2016).
Acknowledgements
This work was supported by National Key Research and Development Program of China (Grants Nos. 2016YFA0302700 and 2017YFA0304100), the National Natural Science Foundation of China (Grant Nos. 61327901, 61725504, 11274297, 61322506, 11325419, and 11774335), Anhui Initiative in Quantum Information Technologies (AHY060300 and AHY020100), the Key Research Program of Frontier Sciences, CAS (Grants No. QYZDY-SSW-SLH003), the Fundamental Research Funds for the Central Universities (Grant Nos. WK2030380015, WK2470000020 and WK2470000026) and the Youth Innovation Promotion Association and Excellent Young Scientist Program CAS. J.L.C. acknowledges the support by National Basic Research Program of China under Grant No. 2012CB921900 and NSF of China (Grant Nos. 11175089, 11475089).
Author information
Authors and Affiliations
Contributions
K.S. and X.J.Y. contributed equally to this work. J.S.X. and K.S. designed the experiment. K.S. performed the experiment with the help from Y.X. and X.Y.X. X.J.Y. took charge of the theoretical proof in assistance of J.L.C. and Y.C.W. K.S., X.J.Y. and J.S.X. wrote the paper. All authors read the manuscript and discussed the results. J.S.X., C.F.L. and G.C.G. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sun, K., Ye, XJ., Xiao, Y. et al. Demonstration of Einstein–Podolsky–Rosen steering with enhanced subchannel discrimination. npj Quantum Inf 4, 12 (2018). https://doi.org/10.1038/s41534-018-0067-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-018-0067-1
This article is cited by
-
Activation of Einstein–Podolsky–Rosen steering sharing with unsharp nonlocal measurements
Scientific Reports (2024)
-
Stronger EPR-steering criterion based on inferred Schrödinger–Robertson uncertainty relation
Scientific Reports (2024)
-
Dynamics of multipartite quantum steering for different types of decoherence channels
Scientific Reports (2023)
-
Optimization of tripartite quantum steering inequalities via machine learning
Quantum Information Processing (2023)
-
Steady-state quantum steering in a largely detuned optomechanical cavity
Quantum Information Processing (2023)