Abstract
The ability to manipulate electron spins with voltage-dependent electric fields is key to the operation of quantum spintronics devices, such as spin-based semiconductor qubits. A natural approach to electrical spin control exploits the spin–orbit coupling (SOC) inherently present in all materials. So far, this approach could not be applied to electrons in silicon, due to their extremely weak SOC. Here we report an experimental realization of electrically driven electron–spin resonance in a silicon-on-insulator (SOI) nanowire quantum dot device. The underlying driving mechanism results from an interplay between SOC and the multi-valley structure of the silicon conduction band, which is enhanced in the investigated nanowire geometry. We present a simple model capturing the essential physics and use tight-binding simulations for a more quantitative analysis. We discuss the relevance of our findings to the development of compact and scalable electron–spin qubits in silicon.
Similar content being viewed by others
Introduction
Silicon is a strategic semiconductor for quantum spintronics, combining long spin coherence and mature technology.1 Research on silicon-based spin qubits has seen a tremendous progress over the past 5 years. In particular, very long coherence times have been achieved with the introduction of devices based on the nuclear-spin-free 28Si isotope, enabling the suppression of hyperfine coupling, the main source of spin decoherence.2 Single qubits with fidelities exceeding 99% as well as a first demonstration of a two-qubit gate have been reported.3,4,5
Finding a viable pathway towards large-scale integration is the next step. To this aim, access to electric-field-mediated spin control would facilitate device scalability, circumventing the need for more demanding control schemes based on magnetic-field-driven spin resonance. Electric-field control requires a mechanism coupling spin and motional degrees of freedom. This so-called spin–orbit coupling (SOC) is generally present in atoms and solids—due to a relativistic effect, electrons moving in an electric-field gradient experience in their reference frame an effective magnetic field. In the case of electrons in silicon, however, SOC is intrinsically very weak.
Possible approaches to circumvent this limitation have so far relied either on the introduction of micromagnets, generating local magnetic field gradients and hence an artificial SOC,6,7,8,9 or on the use of hole spins,10 for which SOC is strong. In both cases, relatively fast coherent spin rotations could be achieved through resonant radio-frequency (RF) modulation of a control gate voltage. While the actual scalability of these two solutions remains to be investigated, other valuable opportunities may emerge from the rich physics of electrons in silicon nanostructures.1,11,12,13,14,15,16
Silicon is indeed an indirect band-gap semiconductor with six degenerate conduction-band valleys. This degeneracy is lifted in quantum dots (QD) where quantum confinement leaves only two low-lying valleys that can be coupled by potential steps at Si/SiO2 interfaces. The resulting valley eigenstates, which we label v1 and v2, are separated by an energy splitting Δ ranging from a few tens of μeV to a few meV.17,18,19,20 Δ depends on the confinement potential, and can hence be tuned by externally applied electric fields.4,21,22 Even if weak,23 SOC can couple valley and spin degrees of freedom when, following the application of a magnetic field, E Z ~ Δ, where EZ is the Zeeman energy splitting. It has been shown that this operating regime can result in enhanced spin relaxation.3,22,24
Here we demonstrate that it can be exploited to perform electric-dipole spin resonance (EDSR).25,26,27,28 This functionality is enabled by the use of a QD with a low-symmetry confinement potential. We discuss the implications of these results for the development of silicon spin qubits.
Results
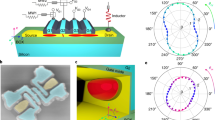
The experiment is carried out on a silicon nanowire device fabricated on a 300-mm diameter silicon-on-insulator (SOI) wafer using an industrial-scale fabrication line.10 The device, shown in the schematic of Fig. 1a and in the scanning electron micrograph of Fig. 1b, consists of an undoped, 30-nm-wide and 12-nm-thick silicon channel oriented along [110], with n-doped contacts. Two 35 nm-wide top-gates (gate 1 and gate 2), spaced by 30 nm, partially cover the channel. An additional gate (gate 3) is located on the opposite side at a distance of 50 nm from the nanowire. Electron transport measurements were performed in a dilution refrigerator with a base temperature T = 15 mK. At this temperature, two QDs in series, labeled as QD1 and QD2, can be defined by the accumulation voltages Vg1 and Vg2 applied to gate 1 and gate 2, respectively. The two QDs are confined against the nanowire edge covered by the gates, forming so-called “corner” dots,29,30 as confirmed by tight-binding (TB) simulations of the lowest energy states, whose wave-functions are shown in Fig. 1c. We tune the electron filling of QD1 and QD2 down to relatively small occupation numbers n1 and n2, respectively (n1, n2 < 10, as inferred from the threshold voltage at room temperature and the charging energy10). The side gate is set to a negative Vg3 = −0.28 V in order to further push the QD wave-functions against the opposite nanowire edges.
Device schematics. a Sketch of the sample and measurement setup. The silicon nanowire with the source/drain extensions is colored in yellow, the two top gates in green, and the side gate in violet. The gate oxides are colored in orange and the buried oxide (BOX) of the SOI in blue. b Colorized device top view obtained by scanning electron microscopy before the deposition of the spacers of a device similar to the one used in the experiment. False-colors as in a. c Sketch of the transverse cross-section of the device along the dashed line in b with the spacer in gray. The cross-section of the silicon nanowire (yellow background) shows a color map of the square of the tight-binding wave function of the lowest conduction band state
In the limit of vanishing inter-dot coupling and odd occupation numbers, both QD1 and QD2 have a spin-1/2 ground state. At finite magnetic field, B, the respective spin degeneracies are lifted by the Zeeman energy EZ = gμBB, where μB is the Bohr magneton and g is the Landé g-factor, which is close to the bare electron value (g ≃ 2) for electrons in silicon.31 In essence, our experiment consists in measuring electron transport through the double dot while driving EDSR in QD2. The polarized spin in QD1 acts as an effective “spin filter” regulating the current flow as a function of the spin admixture induced by EDSR in QD2. This Pauli blockade regime can be achieved only when the double dot is biased in a charge/spin configuration where inter-dot tunneling is forbidden by spin conservation.32 The simplest case involves the inter-dot charge transition (n1 = 1, n2 = 1) → (n1 = 0, n2 = 2), where one electron tunnels from QD1 into QD2. The two electrons may indeed form singlet (S) or triplet (T) states. While the singlet S(1, 1) and triplet T(1, 1) states are only weakly split by exchange interations and magnetic field and may both be loaded, the triplet T(0, 2) states remain typically out of reach because they must involve some orbital excitation of QD2. The system may hence be trapped for long times in the T(1, 1) states since tunneling from T(1, 1) to the S(0, 2) ground-state is forbidden by Pauli exclusion principle.32 This scenario can be generalized to the (n1, n2) → (n1 − 1, n2 + 1) transitions where n1 and n2 are odd integers. The current is strongly suppressed unless EDSR mixes T(1, 1) and S(1, 1) by rotating the spin in QD2.
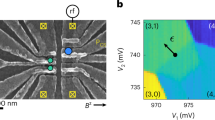
Because the opposite (0, 2) → (1, 1) transition (or, more generically, (n1 − 1, n2 + 1) → (n1, n2)) is never blocked (there is always a (1, 1) spin singlet to tunnel to), the Pauli blockade regime can be revealed by source-drain current rectification.33 Figure 2 presents measurements of the source-drain current, Ids, as a function of (Vg1, Vg2) in a charge configuration exhibiting Pauli rectification. Figure 2a corresponds to a source–drain bias voltage Vds = −2.5 mV and a magnetic field B = 0.7 T. Current flows within characteristic triangular regions32 where the electrochemical potential of dot 1, μ1(n1, n2), is lower than the electrochemical potential of dot 2, μ2(n1 − 1, n2 + 1). The energy detuning ε between the two electrochemical potentials increases when moving along the red arrow. Current contains contributions from both elastic (i.e., resonant) and inelastic inter-dot tunneling. Figure 2b shows that reversing the bias voltage (i.e., Vds = 2.5 mV) yields the desired Pauli rectification characterized by truncated current triangles (In Supplementary Note 1 we discuss the presence of a concomitant valley-blockade effect similar to the one shown by Hao et al.12).
Pauli Spin Blockade. a Map of the current Ids as a function of Vg1 and Vg2 at finite Vds = −2.5 mV around a pair of triangles showing current rectification. The magnetic field B = 0.7 T is parallel to x − y (see axes on Fig. 1) The number of electrons in each dot is given between parentheses, with n, m integers. b Same as a at opposite Vds = +2.5 mV. c Current as a function of detuning and magnetic field. The detuning axis is highlighted by a red arrow in a. d Same as c at opposite Vds = +2.5 mV with detuning axis defined in b
The extent of the spin-blockade region measured along the detuning axis corresponds to the energy splitting, ΔST, between singlet and triplet states in the (n1 − 1, n2 + 1) charge configuration (which is equivalent to (0, 2)), basically the singlet-triplet splitting in QD2 (In the case of non-degenerate triplet states at finite B, ΔST is the splitting with respect to the triplet state, T0, with zero spin projection along B). We find ΔST = 1.9 meV. Figure 2c, d shows Ids as a function of B and ε for negative and positive Vds, respectively. As expected,33 in the non-spin blocked polarity (Fig. 2c) Ids shows essentially no dependence on B. In the opposite polarity, spin blockade is lifted at low field (B ≲ 0.1 T), due to spin–flip cotunneling,34,35 as well as at B = 0.31 T. This unexpected feature will be discussed later.
We now focus on the spin resonance experiment. To manipulate the spin electrically, we set Vg1 and Vg2 in the spin blocked region and apply a microwave excitation of frequency ν on gate 2. Figure 3a displays Ids as a function of B and ν at constant power at the microwave source (the power at the sample depends on ν and is estimated to be −53 dBm ≃ 0.7 mV peak at ν ≈ 9.6 GHz). Several lines of increased current are visible in this plot, highlighting resonances along which Pauli spin blockade is lifted. They are labeled A, B, C and V. In the simplest case, spin resonance occurs when the microwave photon energy matches the Zeeman splitting between the two spin states of a doublet, i.e., when hν = EZ = gμBB. We assign such a resonance to line A, because line A extrapolates to the origin (B = 0, ν = 0). Its slope gives gA = 1.980 ± 0.005, which is compatible with the g-factor expected for electrons in silicon.31 Also line C extrapolates to the origin but with approximately half the slope (i.e., gC = 0.96 ± 0.01). We attribute this line to a second-harmonic driving process.36
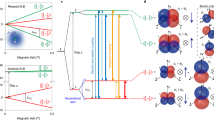
Spin Resonance. a Color plot of the measured drain current Ids as function of the magnetic field B and microwave frequency ν. The gates are biased in the spin-blockade regime. Three different measurements are gathered for clarity. EDSR transitions are revealed by oblique straight lines, labeled with letters A, B, and C. A vertical line (V) is also present. Line C is the weak feature that starts around ≈0.63 T close to line B in the smallest inset. The faint vertical line at ≈0.61 T is an artifact. b Diagram of the energy levels of a system with spin S = 1/2 and two valleys (v1, v2) as function of magnetic field. At low magnetic field, the two lowest (highest) levels belongs to valley v1 (v2). Near the anti-crossing field BV, the states \(\left| {v_1, \uparrow } \right\rangle\) and \(\left| {v_2, \downarrow } \right\rangle\) hybridize due to SOC. The spin and valley composition of the hybridized states is quantified by the color scale on the right. The possible EDSR transitions are marked with green arrows (within v1 or v2) and orange/violet arrows (between v1 and v2). c Sketch of the possible EDSR transitions in panel b as function of magnetic field and microwave frequency
We now focus on resonances B and V. The slope of line B is also compatible with the electron g-factor (gB = 2.00 ± 0.01). However, line B crosses zero-frequency at BV = 0.314 ± 0.001 T, corresponding exactly to the magnetic field at which the non-dispersive resonance V appears. Consequently, line B can be assigned to transitions between spin states associated with two distinct orbitals. When these spin states cross at BV, Pauli spin blockade is lifted independently of the microwave excitation leading to the non-dispersive resonance V (see Supplementary Note 1 for details on the lifting of spin blockade at BV).
In order to understand the experimental EDSR spectrum of Fig. 3a, we neglect in a first approximation the hybridization between the two QDs and consider only QD2 filled with one electron. We have developed a model that accounts for the mixing between spin and valley states due to SOC. In our silicon nanowire geometry, the confinement is strongest along the z direction (normal to the SOI substrate), so that the low-energy levels belong to the Δ±z valleys. Valley coupling at the Si/SiO2 interface lifts the two-fold valley degeneracy,1,17,18,19,20 resulting in two spin-degenerate valley eigenstates v1 and v2 with energies E1 and E2, respectively, and a valley splitting Δ = E2 − E1. The expected energy diagram of the one-electron spin-valley states is plotted as a function of B in Fig. 3b (see Supplementary Note 2). The lowest spin-valley states can be identified as \(\left| {v_1, \downarrow } \right\rangle\), \(\left| {v_1, \uparrow } \right\rangle\)/\(\left| {v_2, \downarrow } \right\rangle\) anti-crossing at B = BV, and \(\left| {v_2, \uparrow } \right\rangle\) (the spin being quantized along B). From this energy diagram we assign the resonant transitions observed in Fig. 3a as follows: line A corresponds to EDSR between states \(\left| {v_1, \downarrow } \right\rangle\) and \(\left| {v_1, \uparrow } \right\rangle\) (and between states \(\left| {v_2, \downarrow } \right\rangle\) and \(\left| {v_2, \uparrow } \right\rangle\)); line B arises from EDSR between states \(\left| {v_1, \uparrow } \right\rangle\) and \(\left| {v_2, \downarrow } \right\rangle\);37 line V is associated with the anti-crossing between states \(\left| {v_1, \uparrow } \right\rangle\) and \(\left| {v_2, \downarrow } \right\rangle\) when E Z = Δ. We can thus measure Δ = gμBBV = 36 μeV. Note that the experimental EDSR spectrum does not capture all possible transitions since some of them fall out of the scanned (B, ν) range. Figure 3c shows the expected EDSR spectrum starting from ν = 0 and B = 0. The measured region is indicated in light blue (lower values of ν and B could not be explored due to the onset of photon-assisted charge pumping and to the lifting of spin blockade, respectively).
The RF magnetic field associated with the microwave excitation on gate 2 is too weak to drive conventional ESR.25 Since a pure electric field cannot couple opposite spin states, SOC must be involved in the observed EDSR. The atomistic spin–orbit Hamiltonian primarily couples the different p orbitals of silicon;38 the Δ±z states are, however, linear combinations of s and p z orbitals with little admixture of p x and p y , which explains why the SOC matrix elements are weak in the conduction band of silicon. Yet the mixing between \(\left| {v_1, \uparrow } \right\rangle\) and \(\left| {v_2, \downarrow } \right\rangle\) by “inter-valley” SOC can be strongly enhanced when the splitting between these two states is small enough. We can capture the main physics and identify the relevant parameters using the simplest perturbation theory in the limit \(B \ll B_V\). The states \(\left| \Downarrow \right\rangle\) ≡ \(\left| {v_1, \downarrow } \right\rangle\) and \(\left| \Uparrow \right\rangle\) ≡ \(\left| {v_1, \uparrow } \right\rangle\) indeed read to first order in the spin–orbit Hamiltonian HSOC:
where:
Therefore, \(\left| {v_1, \uparrow } \right\rangle\) admixes a significant fraction of \(\left| {v_2, \downarrow } \right\rangle\) when the splitting Δ − gμBB between these two states decreases. As \(\left| {v_2, \downarrow } \right\rangle\) can be coupled to \(\left| {v_1, \downarrow } \right\rangle\) by the RF electric field, this allows for Rabi oscillations between \(\left| \Uparrow \right\rangle\) and \(\left| \Downarrow \right\rangle\). Along line A, the Rabi frequency at resonance (hν = gAμBB) reads:
where δVg2 is the amplitude of the microwave modulation on gate 2, D(r) = ∂Vt(r)/∂Vg2 is the derivative of the total potential Vt(r) in the device with respect to the gate potential Vg2, and:
is the matrix element of D(r) between valleys v1 and v2. The gate-induced electric field essentially drives motion in the (yz) plane. \(D_{v_1v_2}\) is small yet non negligible in SOI nanowire devices because the v1 and v2 wavefunctions show out of phase oscillations along z, and can hence be coupled by the vertical electric field. The field along y does not result in a sizable \(D_{v_1v_2}\) unless surface roughness disorder couples the motions along z and in the (xy) plane.39,40 Although \(C_{v_1v_2}\) is weak in silicon, SOC opens a path for an electrically driven spin resonance \(\left| \Downarrow \right\rangle\) → \(\left| \Uparrow \right\rangle\) through a virtual transition from \(\left| {v_1, \downarrow } \right\rangle\) to \(\left| {v_2, \downarrow } \right\rangle\), mediated by the microwave field, and then from \(\left| {v_2, \downarrow } \right\rangle\) to \(\left| {v_1, \uparrow } \right\rangle\), mediated by SOC. Note, however, that the above equations are only valid at small magnetic fields where perturbation theory can be applied. A non-perturbative model valid at all fields is introduced in the Supplementary Note 2. It explicitly accounts for the anti-crossing (and strong hybridization by SOC) of states \(\left| {v_1, \uparrow } \right\rangle\) and \(\left| {v_2, \downarrow } \right\rangle\) near B = BV,12,22,24 but features the same matrix elements as above. This model shows that the Rabi frequency is maximal near B = BV, and confirms that there is a concurrent spin resonance \(\left| {v_1, \uparrow } \right\rangle\) ↔ \(\left| {v_2, \downarrow } \right\rangle\), shifted by the valley splitting Δ = 36 μeV (lines B/B' on Fig. 3c), as well as, in principle, a possible resonance \(\left| {v_1, \downarrow } \right\rangle\) ↔ \(\left| {v_2, \uparrow } \right\rangle\) (line D).
We have validated the above interpretation against sp3d5s* TB calculations. TB is well suited to that purpose as it accounts for valley and SOC at the atomistic level. We consider a simplified single-gate device model capturing the essential geometry (Fig. 4a). A realistic surface roughness disorder with rms amplitude ΔSR = 0.4 nm41 is included in order to reduce the valley splitting down to the experimental value.20 A detailed description of the TB calculations is given in the Supplementary Note 3. The top panel of Fig. 4b shows the B dependence of the energy of the first four TB states \(\left| 1 \right\rangle\)…\(\left| 4 \right\rangle\). An anti-crossing is visible between states \(\left| 2 \right\rangle\) and \(\left| 3 \right\rangle\) at BV = 0.3 T. We calculate \(\left| {C_{v_1v_2}} \right|\) = 1.8 μeV and \(\left| {D_{v_1v_2}} \right|\) = 70 μV/V. The B dependence of the TB Rabi frequency f on line A is shown in the bottom panel of Fig. 4b. There is a prominent peak near B = BV where \(\left| 2 \right\rangle\) and \(\left| 3 \right\rangle\) have a mixed \(\left| {v_1, \uparrow } \right\rangle\)/\(\left| {v_2, \downarrow } \right\rangle\) character. The maximum Rabi frequency \(f_{{\mathrm{max}}} \simeq e\delta V_{{\rm g}2}\left| {D_{v_1v_2}} \right|{\mathrm{/}}\left( {\sqrt 2 h} \right)\) is limited by \(D_{v_1v_2}\) while the full width at half maximum of the peak, \({\mathrm{\Delta }}B_{{\mathrm{FWHM}}} \simeq 12\left| {C_{v_1v_2}} \right|{\mathrm{/}}\left( {\sqrt 7 g\mu _{\rm B}} \right)\) = 0.07 T is controlled by the SOC matrix element \(C_{v_1v_2}\) (see Supplementary Note 3). The Rabi frequency remains however sizable over a few ΔBFWHM. We point out that \(C_{v_1v_2}\) and \(D_{v_1v_2}\) may depend on the actual roughness at the Si/SiO2 interface.
TB calculations results. a Electrostatic model of the device. The silicon wire appears in yellow, SiO2 in blue, HfO2 in orange and the gate in green. We did not include the lateral gate in the simulations. b TB energy levels as a function of the magnetic field B || y, and TB Rabi frequency along line A (identified by the green arrows) as a function of the magnetic field for a reference microwave amplitude δVg2 = 1 mV. The points are the TB data and the solid lines are the analytical model developed in Supplementary Note 3. The TB valley splitting energy Δ ~ 36 μeV is in good agreement with the experimental value. The Rabi frequency shows a prominent peak near the anti-crossing field BV. c, Experimental measurement of EDSR current as a function of the angle θ between an in-plane magnetic field B ⊥ z and the nanowire axis x (θ = 0°), and TB Rabi frequency f2 as a function of θ
The calculated Rabi frequencies compare well against those reported for alternative silicon based systems. For example, the expected Rabi frequency is around 4.2 MHz for B = 0.35 T, close to anticrossing field BV, and for a microwave excitation amplitude δVg2 = 0.7 mV, close to the experimental value (see Fig. 4b). This frequency is comparable with those achieved with coplanar antennas3,42 and in some experiments with micromagnets.7,9
One of the most salient fingerprint of the above EDSR mechanism is the dependence of f on the magnetic field orientation. Indeed, it must be realized that \(C_{v_1v_2}\) may vary with the orientation of the magnetic field (as the spin is quantized along B in Eq. (2)). Actually, symmetry considerations supported by TB calculations show that \(C_{v_1v_2}\) and hence f are almost zero when B is aligned with the nanowire axis, due to the existence of a (yz) mirror plane perpendicular to that axis (see Supplementary Note 4). As a simple hint of this result, we may consider a generic Rashba SOC Hamiltonian of the form \(H_{{\mathrm{SOC}}} \propto ({\bf{E}} \times {\bf{p}}) \cdot {\boldsymbol{\sigma }}\), where E is the electric field, p the momentum, and σ the Pauli matrices. Symmetric atoms on each side of the (yz) plane contribute to \(C_{v_1v_2}\) with opposite E x and p x components. Therefore, only the ∝ (E y p z − E z p y )σ x component of HSOC makes a non-zero contribution to \(C_{v_1v_2}\), but does not couple opposite spins when B || x. The current on line A is, to a first approximation, proportional to f2.43,44 The TB f2 is plotted in Fig. 4c as a function of the angle θ between an in-plane magnetic field B ⊥ z and the nanowire axis x. It shows the ∝ sin2 θ dependence expected from the above considerations. The experimental Ids, also plotted in Fig. 4c, shows the same behavior, supporting our interpretation. The fact that Ids remains finite for B || x may be explained by the fact that the (yz) symmetry plane is mildly broken by disorder and voltage biasing.
In a recent work, Huang et al.45 proposed a mechanism for EDSR based on electrically induced oscillations of an electron across an atomic step at a Si/SiO2 or a Si/SiGe hetero-interface. The step enhances the SOC between the ground and the excited state of the same valley. The Rabi frequency is, however, limited by the maximal height of the step that the electron can overcome (typically 1 nm). The EDSR reported here has a different origin. It results from the finite SOC and dipole matrix elements between the ground-states of valleys v1 and v2. These couplings are sizable only in a low-symmetry dot structure such as a corner QD,29 where there is only one mirror plane (see Supplementary Note 4). Indeed, we have verified that more symmetric device structures with at least two symmetry planes show a dramatic suppression of the SOC matrix element (since, as hinted above, each mirror rules out two out of three components in HSOC, leaving no possible coupling). This is the case of a typical nanowire field-effect transistor with the gate covering three sides of the nanowire channel, for which TB calculations give no EDSR since \(C_{v_1v_2} = 0\) whatever the spin or magnetic field orientation. Conversely, the design of QDs without any symmetry left should maximize the opportunities for EDSR.
Discussion
In conclusion, we have reported an experimental demonstration of electric-dipole, spin-valley resonance mediated by intrinsic SOC in a silicon electron double QD. Although SOC is weak in silicon, its effect can be enhanced in the corner QDs of an etched SOI device, owing to their reduced symmetry. SOC enables EDSR on the spin–split doublet of the first, lowest energy valley by mixing the up-spin state of that valley with the down-spin state of the second valley. The EDSR Rabi frequency is strongly enhanced near the corresponding anti-crossing, namely when the valley and Zeeman splittings are close enough. This enhancement comes with a price though, since we expect the spin relaxation time T1 (and presumably also the spin coherence time T2) to be simultaneously reduced.22,24 Therefore, we anticipate that the efficiency of the reported EDSR mechanism for spin qubit manipulation will be conditioned by the possibility to tune the valley splitting Δ, in order to bring the qubit near the anti-crossing point for manipulation, then away from the anti-crossing point to mitigate decoherence. Given the strong dependence of the valley splitting on gate voltages in silicon-based devices,21,46 this possibility appears within reach and will be addressed in future experiments.
Methods
The silicon nanowire transistors are manufactured on a 300 mm SOI processing line.10 First, silicon nanowires are etched from a SOI wafer with a 12-nm thick undoped silicon layer and a 145-nm thick buried oxide. The nanowire channels are oriented along the [110] direction. The width W of the nanowires, initially defined by deep ultra-violet lithography, is trimmed down to about 30 nm by a well-controlled etching process. Two parallel top-gates, ≃35 nm wide and spaced by ≃30 nm are patterned with e-beam lithography in order to control the double QD. An additional side gate is also placed parallel to the nanowire at a distance of 50 nm in order to strengthen confinement in the corner dots of the Si nanowire. The gate stack consists in a 2.5-nm thick layer of SiO2, a 1.9-nm thick layer of HfO2, a thin (≃5 nm) layer of TiN metal and a much thicker (≃50 nm) layer of polysilicon. Then, insulating SiN spacers are deposited all around the gates and are etched. Their width is deliberately large (≃25 nm) in order to cover completely the nanowire channel between the two gates and protect it from subsequent ion implantation. Arsenic and phosphorous are indeed implanted in order to achieve low resistance source/drain contacts. The wide spacers also limit dopant diffusion from the heavily implanted contact regions into the channel. The dopants are activated by spike annealing followed by silicidation. The devices are finalized with a standard microelectronics back-end of line process.
The devices are first screened at room temperature. Those showing the best performances (symmetrical characteristics for both top gates with no gate leakage current, low subthreshold swing) are cleaved from the original 300-mm wafer in order to be mounted on a printed-circuit-board chip carrier with high-frequency lines. The sample is measured in a wet dilution fridge with a base temperature T = 15 mK. The magnetic field is applied by means of a 2D superconducting vector magnet in the (xy) plane parallel to the SOI wafer.
All terminals are connected with bonding wires to DC lines; gate 2 is also connected with a bias-tee to a microwave line. The DC block is a low rise-time Tektronik PSPL5501A, while the RF filter is made with a 10 kΩ SMD resistance mounted on the chip carrier plus a wire acting as inductor. The DC voltages are generated at room temperature by custom battery-powered opto-isolated voltage sources. The microwave signal is generated by a commercial analog microwave generator (Anritsu MG3693C). The RF line is equipped with a series of attenuators at room temperature and in the cryostat for signal thermalization (1 K), with a total attenuation of ≃38 dB at 10 GHz. The current in the nanowire is measured by a custom transimpedance amplifier with a gain of 109 V/A and then digitized by a commercial multimeter (Agilent 34410A).
The TB calculations are performed with the sp3d5s* model of ref. 47. The potential in the device is calculated with a finite-volume Poisson solver, then the eigenstates of the dot are computed with an iterative Jacobi–Davidson solver. The Rabi frequencies are obtained from Eq. (3).
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Zwanenburg, F. A. et al. Silicon quantum electronics. Rev. Mod. Phys. 85, 961 (2013).
Tyryshkin, A. M. et al. Electron spin coherence exceeding seconds in high-purity silicon. Nat. Mater. 11, 143 (2012).
Veldhorst, M. et al. An addressable quantum dot qubit with fault-tolerant control-fidelity. Nat. Nanotechnol. 9, 981 (2014).
Laucht, A. et al. Electrically controlling single-spin qubits in a continuous microwave field. Sci. Adv. 1, e1500022 (2015).
Veldhorst, M. et al. A two-qubit logic gate in silicon. Nature 526, 410 (2015).
Pioro-Ladrière, M. et al. Electrically driven single-electron spin resonance in a slanting zeeman field. Nat. Phys. 4, 776 (2008).
Kawakami, E. et al. Electrical control of a long-lived spin qubit in a Si/SiGe quantum dot. Nat. Nanotechnol. 9, 666 (2014).
Rančić, M. J. & Burkard, G. Electric dipole spin resonance in systems with a valley-dependent g factor. Phys. Rev. B 93, 205433 (2016).
Takeda, K. et al. A fault-tolerant addressable spin qubit in a natural silicon quantum dot. Sci. Adv. 2, e1600694 (2016).
Maurand, R. et al. A CMOS silicon spin qubit. Nat. Commun. 7, 13575 (2016).
Nestoklon, M. O., Golub, L. E. & Ivchenko, E. L. Spin and valley-orbit splittings in SiGe/Si heterostructures. Phys. Rev. B 73, 235334 (2006).
Hao, X., Ruskov, R., Xiao, M., Tahan, C. & Jiang, H. Electron spin resonance and spin-valley physics in a silicon double quantum dot. Nat. Commun. 5, 3860 (2014).
Schoenfield, J. S., Freeman, B. M. & Jiang, H. Coherent manipulation of valley states at multiple charge configurations of a silicon quantum dot device. Nat. Commun. 8, 64 (2017).
Jock, R. M. et al. Probing low noise at the MOS interface with a spin-orbit qubit. Preprint at https://arxiv.org/abs/1707.04357 (2017).
Veldhorst, M. et al. Spin-orbit coupling and operation of multivalley spin qubits. Phys. Rev. B 92, 201401(R) (2015).
Ruskov, R., Veldhorst, M., Dzurak, A. S. & Tahan, C. Electron g-factor of valley states in realistic silicon quantum dots. Preprint at https://arxiv.org/abs/1708.04555 (2017).
Sham, L. J. & Nakayama, M. Effective-mass approximation in the presence of an interface. Phys. Rev. B 20, 734 (1979).
Saraiva, A. L., Calderon, M. J., Hu, X., Das Sarma, S. & Koiller, B. Physical mechanisms of interface-mediated intervalley coupling in si. Phys. Rev. B 80, 081305(R) (2009).
Friesen, M. & Coppersmith, S. N. Theory of valley-orbit coupling in a Si/SiGe quantum dot. Phys. Rev. B 81, 115324 (2010).
Culcer, D., Hu, X. & Das Sarma, S. Interface roughness, valley-orbit coupling, and valley manipulation in quantum dots. Phys. Rev. B 82, 205315 (2010).
Goswami, S. et al. Controllable valley splitting in silicon quantum devices. Nat. Phys. 3, 41 (2007).
Yang, C. H. et al. Spin-valley lifetimes in a silicon quantum dot with tunable valley splitting. Nat. Commun. 4, 2069 (2013).
Rashba, E. I. Theory of electric dipole spin resonance in quantum dots: mean field theory with gaussian fluctuations and beyond. Phys. Rev. B 78, 195302 (2008).
Huang, P. & Hu, X. Spin relaxation in a Si quantum dot due to spin-valley mixing. Phys. Rev. B 90, 235315 (2014).
Golovach, V. N., Borhani, M. & Loss, D. Electric-dipole-induced spin resonance in quantum dots. Phys. Rev. B 74, 165319 (2006).
Nowack, K. C., Koppens, F. H. L., Nazarov, Y. V. & Vandersypen, L. M. K. Coherent control of a single electron spin with electric fields. Science 318, 1430 (2007).
Nadj-Perge, S., Frolov, S. M., Bakkers, E. P. A. M. & Kouwenhoven, L. P. Spin-orbit qubit in a semiconductor nanowire. Nature 468, 1084 (2010).
Pribiag, V. S. et al. Electrical control of single hole spins in nanowire quantum dots. Nat. Nanotechnol. 8, 170 (2013).
Voisin, B. et al. Few-electron edge-state quantum dots in a silicon nanowire field- effect transistor. Nano. Lett. 14, 2094 (2014).
Gonzalez-Zalba, M. F., Barraud, S., Ferguson, A. J. & Betz, A. C. Probing the limits of gate-based charge sensing. Nat. Commun. 6, 6084 (2015).
Feher, G. Electron spin resonance experiments on donors in silicon. i. electronic structure of donors by the electron nuclear double resonance technique. Phys. Rev. 114, 1219 (1959).
Hanson, R., Petta, J. R., Tarucha, S. & Vandersypen, L. M. K. Spins in few-electron quantum dots. Rev. Mod. Phys. 79, 1217 (2007).
Ono, K., Austing, D. G., Tokura, Y. & Tarucha, S. Current rectification by pauli exclusion in a weakly coupled double quantum dot system. Science 297, 1313 (2002).
Lai, N. S. et al. Pauli spin blockade in a highly tunable silicon double quantum dot. Sci. Rep. 1, 110 (2011).
Yamahata, G. et al. Magnetic field dependence of pauli spin blockade: a window into the sources of spin relaxation in silicon quantum dots. Phys. Rev. B 86, 115322 (2012).
Scarlino, P. et al. Second-harmonic coherent driving of a spin qubit in a Si/SiGe quantum dot. Phys. Rev. Lett. 115, 106802 (2015).
Scarlino, P. et al. Dressed photon-orbital states in a quantum dot: Intervalley spin resonance. Phys. Rev. B 95, 165429 (2017).
Chadi, D. J. Spin-orbit splitting in crystalline and compositionally disordered semiconductors. Phys. Rev. B 16, 790 (1977).
Gamble, J. K., Eriksson, M. A., Coppersmith, S. N. & Friesen, M. Disorder-induced valley-orbit hybrid states in Si quantum dots. Phys. Rev. B 88, 035310 (2013).
Boross, P., Széchenyi, G., Culcer, D. & Pályi, A. Control of valley dynamics in silicon quantum dots in the presence of an interface step. Phys. Rev. B 94, 035438 (2016).
Bourdet, L. et al. Contact resistances in trigate and finfet devices in a non-equilibrium green’s functions approach. J. Appl. Phys. 119, 084503 (2016).
Pla, J. J. et al. A single-atom electron spin qubit in silicon. Nature 489, 541 (2012).
Koppens, F. H. L. et al. Detection of single electron spin resonance in a double quantum dot. J. Appl. Phys. 101, 081706 (2007).
Schroer, M. D., Petersson, K. D., Jung, M. & Petta, J. R. Field tuning the g factor in InAs nanowire double quantum dots. Phys. Rev. Lett. 107, 176811 (2011).
Huang, W., Veldhorst, M., Zimmerman, N. M., Dzurak, A. S. & Culcer, D. Electrically driven spin qubit based on valley mixing. Phys. Rev. B 95, 075403 (2017).
Takashina, K., Ono, Y., Fujiwara, A., Takahashi, Y. & Hirayama, Y. Valley polarization in Si(100) at zero magnetic field. Phys. Rev. Lett. 96, 236801 (2006).
Niquet, Y. M., Rideau, D., Tavernier, C., Jaouen, H. & Blase, X. Onsite matrix elements of the tight-binding hamiltonian of a strained crystal: application to silicon, germanium, and their alloys. Phys. Rev. B 79, 245201 (2009).
Acknowledgements
This work was supported by the European Union’s Horizon 2020 research and innovation program under grant agreement No 688539 MOSQUITO. Part of the calculations were run on the TGCC/Curie and CINECA/Marconi machines using allocations from GENCI and PRACE. We thank Cosimo Orban for the 3D rendering of the sample.
Author information
Authors and Affiliations
Contributions
H.B., R.L., L.H., S.B., and M.V. led device fabrication. A. Corna performed the experiment with help from R.M., A. Crippa and D.K.-P. under the supervision of X.J., S.D.F. and M.S. L. B. and Y.-M.N. did the modeling and simulations. M.V., X.J., S.D.F. and M.S led the all project. All authors co-wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Corna, A., Bourdet, L., Maurand, R. et al. Electrically driven electron spin resonance mediated by spin–valley–orbit coupling in a silicon quantum dot. npj Quantum Inf 4, 6 (2018). https://doi.org/10.1038/s41534-018-0059-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-018-0059-1
This article is cited by
-
Non-symmetric Pauli spin blockade in a silicon double quantum dot
npj Quantum Information (2024)
-
Electrical manipulation of the spins in phosphorene double quantum dots
Scientific Reports (2024)
-
Pipeline quantum processor architecture for silicon spin qubits
npj Quantum Information (2024)
-
Bounds to electron spin qubit variability for scalable CMOS architectures
Nature Communications (2024)
-
Field programmable spin arrays for scalable quantum repeaters
Nature Communications (2023)