Abstract
Measurements approaching the ultimate quantum limits of sensitivity are central in quantum information processing, quantum metrology, and communication. Quantum measurements to discriminate multiple states at the single-photon level are essential for optimizing information transfer in low-power optical communications and quantum communications, and can enhance the capabilities of many quantum information protocols. Here, we theoretically investigate and experimentally demonstrate the discrimination of multiple coherent states of light with sensitivities surpassing the quantum noise limit (QNL) at the single-photon level under realistic conditions of loss and noise based on strategies implementing globally-optimized adaptive measurements with single photon counting and displacement operations. These discrimination strategies can provide realistic advantages to enhance information transfer at low powers, and are compatible with photon number resolving detection, which provides robustness at high powers, thus allowing for surpassing the QNL at arbitrary input power levels under realistic conditions.
Similar content being viewed by others
Introduction
Assessing the information about the state of a quantum system is fundamentally limited by quantum noise. This task requires performing measurements discriminating among different states, and when these states are nonorthogonal, discrimination cannot be performed perfectly due to their intrinsic overlap.1 Measurements for the discrimination of nonorthogonal states, such as coherent states, can enable secure communications2,3,4,5,6,7,8,9,10,11 and assist quantum information protocols for quantum repeaters,12,13 quantum computing,14,15,16 entanglement generation with high fidelity,17,18 quantum signatures,19,20 and quantum finger printing.21,22 Moreover, efficient discrimination measurements of multiple coherent states can enhance information transfer in communication,23,24,25,26 and, by performing collective measurements over long sequences of states, allow for achieving the ultimate limits for classical information transfer (classical capacity27) in communication channels with loss and noise.28,29,30
Quantum mechanics allows for measurements that in principle achieve the ultimate sensitivity limits for the discrimination of nonorthogonal states.1,31 These measurements can optimize many quantum information and communication protocols. The lowest error probability allowed by quantum mechanics for discriminating nonorthogonal states, such as coherent states with different phases, is referred to as the Helstrom bound.1 This bound is much lower than the limit of ideal conventional measurements, referred to as the quantum noise limit (QNL), which can be reached by the homodyne (heterodyne) measurement for two (multiple) phase states.6 Strategies for the discrimination of two coherent states below the QNL have been investigated theoretically32,33,34 and demonstrated experimentally,35,36,37 including the optimal strategy saturating the Helstrom bound34 based on photon counting and real-time feedback.35 The discrimination of multiple coherent states below the QNL was first investigated by Bondurant38 generalizing the optimal two-state strategy in34 to four states. Further theoretical39,40,41,42,43 and experimental work demonstrated that the discrimination of multiple states below the QNL44 can be achieved with current technologies,45 and that some realizable measurements show the same exponential scaling as the Helstrom bound in the limit of high powers.38,39,40 Recent work showed that photon-number resolution (PNR) provides robustness against realistic noise for discrimination of multiple states.41,42 And an experimental realization with detectors with finite PNR demonstrated multiple-state discrimination below the QNL at high input-power levels, which provides advantages for coded communication over heterodyne measurements.23
Discrimination of multiple states surpassing the QNL in the single-photon regime has a large potential for applications in quantum information12,13,14,15,16 and enhancing information transfer in low-power communication.23,24,25,26 Moreover, optimized measurements for nonorthogonal states at the single-photon level can potentially be used to enhance the rate of secure communications in quantum key distribution (QKD) with coherent states,7,8,9,46 which require states at low powers to ensure security. However, even though theoretical advancements have shown that this discrimination task is possible,43 the discrimination of multiple states surpassing the QNL at the single-photon level under realistic conditions with noise and loss has not been experimentally demonstrated.
Here, we theoretically investigate and experimentally demonstrate the discrimination of multiple nonorthogonal states at the single-photon level below the QNL based on adaptive measurements, globally optimized displacement operations, and photon counting. These strategies are compatible with PNR detection to extend discrimination to high powers,23,45 and thus enable discrimination strategies of multiple states below the QNL at arbitrary input-power levels under realistic conditions. These optimized discrimination measurements more closely approach the quantum limits of detection for multiple states at the single-photon level, and can be used to optimize quantum information protocols assisted by coherent states, and enhance information transfer in optical communication. We show that these optimized measurements can provide advantages for increasing information transfer with coherent states at low powers25 beyond what can be achieved with the heterodyne measurement at the QNL. We expect that these measurements can be used in joint-detection schemes over sequences of coherent states for approaching the quantum limits for information transfer at the single-photon level.24
Results
Optimized discrimination measurements
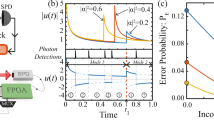
Figure 1a shows the measurement scheme for the discrimination of multiple nonorthogonal states \(\left\{ {\left| {\alpha _k} \right\rangle } \right\}\) below the QNL at the single-photon level implementing N adaptive measurements based on displacement operations \(\hat D(\beta )\) optimized to minimize the probability of error (P e). This optimization gives rise to discrimination strategies surpassing the QNL at arbitrary input power levels under realistic noise and loss requiring just a few adaptive measurements, while being compatible with PNR, which increases robustness at high powers.23 Compared to previous strategies described in ref. 43 that require measurements with infinite feedback bandwidth, the optimized strategies discussed here are based on a finite number of adaptive measurements, which is practical and allows for the demonstration of multi-state discrimination beyond the QNL at the single-photon level with current technologies.
Optimized discrimination of multiple states. a Discrimination of an input coherent state \(\left| {\alpha _k} \right\rangle \in \left\{ {\left| {e^{i\phi _k}\left| {\alpha _k} \right|} \right\rangle } \right\}\) where \(\phi _k = \frac{{2\pi k}}{M}\) (k = 1, 2, .., M) implementing N adaptive measurements based on optimized displacement operations \(\hat D(\beta )\) and single-photon counting with fast feedback. This strategy discriminates multiple states below the quantum noise limit (QNL) at arbitrary input power levels with a small number of adaptive measurements. b Probability of error for the discrimination of four nonorthogonal states \(\left\{ {\left| \alpha \right\rangle ,\left| {i\alpha } \right\rangle ,\left| { - \alpha } \right\rangle ,\left| { - i\alpha } \right\rangle } \right\}\) with three different optimized strategies: flat optimization, sequential optimization, and historical optimization, as a function of the mean photon number \(\left\langle n \right\rangle = \left| \alpha \right|^2\) based on N = 10 optimized adaptive measurements with perfect detection efficiency DE = 1 and visibility \({\cal V} = 100\%\) of the displacement operation. The QNL and the Helstrom bound are shown for reference, as well as the non-optimized strategy. c, d Examples of ratios \(\left| \beta \right|{\mathrm{/}}\left| \alpha \right|\) of the displacement field \(\left| \beta \right|\) to input amplitude \(\left| \alpha \right|\) for optimized strategies corresponding to c sequential optimization for \(\left\langle n \right\rangle\) from 0.2 to 5 and d historical optimization for 100 possible detection histories D H. These ratios are the result of global optimizations that minimize the probability of error (see main text for details). SPD single-photon detector, M mirror
The optimized strategies implement globally optimized displacements \(\hat D(\beta )\) of the input state \(\left| {\alpha _k} \right\rangle\) from a set of states with (see Note) \(\left| {\alpha _k} \right\rangle \in \left\{ {\left| {e^{i\phi _k}\left| {\alpha _k} \right|} \right\rangle } \right\}\) (\(\phi _k = \frac{{2\pi k}}{M}\) (k = 1, 2, .., M)) to the vacuum state \(\left| 0 \right\rangle\), single-photon counting, and recursive Bayesian inference. In a given adaptive measurement j (j = 1, 2, .., N), the displacement of the input state \(\left| {\alpha _k} \right\rangle\) results in state \(\left| \psi \right\rangle = \hat D( - \beta )\left| {\alpha _k} \right\rangle\), which is followed by photon counting with probability of n photon detection given by \({{P}}\left( {n\left| {\alpha _k,\beta } \right.} \right) = \kern-5pt \left| {\left\langle n \right|\hat D( - \beta )\left| {\alpha _k} \right\rangle } \right|^2 = \frac{{\bar n^n}}{{n!}}e^{ - \bar n}\). Here \(\bar n = \left| \alpha \right|^2 + \left| \beta \right|^2\) − \(2{\cal V}\left| \alpha \right|\left| \beta \right|{\rm{cos}}\left[ {{\rm{arg}}\left( {\alpha _k} \right) - {\rm{arg}}(\beta )} \right]\) is the mean photon number of the state \(\left| \psi \right\rangle\) and \({\cal V}\) is the visibility of the displacement operation.23,45 After an adaptive-measurement period j, the strategy estimates the posterior probabilities of the possible input states \(\left\{ {\left| {\alpha _k} \right\rangle } \right\}\) in j based on the photon detection result d j ∈ {0, 1, ...} and the displacement field β as:
where P post \(\left( {\left\{ {\left| {\alpha _k} \right\rangle } \right\}\left| {\beta ,d_j} \right.} \right)\) and \({{P}}_{{\rm{prior}}}^j\left( {\left\{ {\left| {\alpha _k} \right\rangle } \right\}} \right)\) are the posterior and prior probabilities in j, respectively, for all possible input states \(\left\{ {\left| {\alpha _k} \right\rangle } \right\}\), and \(\mathop {\sum}\nolimits_{\left\{ {\left| {\alpha _k} \right\rangle } \right\}}\) indicates the sum over all states \(\left\{ {\left| {\alpha _k} \right\rangle } \right\}\). The discrimination strategy uses recursive Bayesian inference to update prior probabilities P prior \(\left( {\left\{ {\left| {\alpha _k} \right\rangle } \right\}} \right)\) in subsequent adaptive measurements, so that the posterior probability estimated in adaptive measurement j, P post \(\left( {\left\{ {\left| {\alpha _k} \right\rangle } \right\}\left| {\beta ,d_j} \right.} \right)\), is defined as the prior probability \({{P}}_{{\rm{prior}}}^{j + 1}\left( {\left\{ {\left| {\alpha _k} \right\rangle } \right\}} \right)\) for the next adaptive measurement, j + 1. The phase of the displacement field β in j + 1 is chosen to test the most likely state based on the maximum-posterior probability criterion: the phase of β is set equal to the phase of the state for which P post is maximum. This criterion for choosing the phases of β is applied to all the optimized strategies described below.
The overall probability of error P e after the last adaptive measurement N can be expressed as:
where [β] is the set of all the displacement fields used in all the adaptive measurements j = 1, .., N, which can be optimized to minimize the final probability of error. \(\mathop {{max}}\nolimits_{\{ \alpha \} }\) takes the maximum over input states \(\left\{ {\left| {\alpha _k} \right\rangle } \right\}\) of \(P_{{\rm{prior}}}^N\left( {\left\{ {\alpha _k} \right\}} \right)P\left( {d_N\left| {\left\{ \alpha \right\},\left[ {\beta ^{\rm{opt}}} \right]} \right.} \right)\), which is proportional to the posterior probability in N, and the sum \(\mathop {\sum}\nolimits_{D_{\rm H}}\) is realized over all detection histories D H = {d 1, d 2, ..., d N } with occurrence probabilities \(P_{D_{\rm H}}\). Note that \(P_{{\rm{prior}}}^N\left( {\left\{ {\alpha _k} \right\}} \right)\) in Eq. (2) depends on the detection histories D H and the displacement fields [β] in all the previous adaptive measurements. The freedom to choose [β] allows for finding global optimizations of the set of displacement field amplitudes [β] that minimize the overall probability of error, and gives rise to different discrimination strategies with different complexities and degrees of sensitivity. These optimized strategies for which \(\left| \beta \right|\) ≠ \(\left| \alpha \right|\) enable measurements surpassing the QNL in the low-power regime, a task that measurements without optimized amplitudes (non-optimized strategies) for which \(\left| \beta \right|\) = \(\left| \alpha \right|\) cannot achieve.
The simplest optimized discrimination strategy finds a constant value of the amplitude of the displacement field \(\left| \beta \right|\) over all the N adaptive measurements to minimize the probability of error, so that
Figure 1b shows the probability of error for the discrimination of four nonorthogonal coherent states \(\left\{ {\left| \alpha \right\rangle ,\left| {i\alpha } \right\rangle ,\left| { - \alpha } \right\rangle ,\left| { - i\alpha } \right\rangle } \right\}\) achieved by this strategy for N = 10. We observe that this strategy is sufficient to surpass the QNL for multiple states at the single-photon level. This strategy, which we call “flat optimization,” is the discrete version of that described in ref. 43 and only requires a finite N, which translates to measurements with finite bandwidth and provides advantages for realistic implementations.
Performing more sensitive measurements requires implementing global optimization over the magnitudes of the displacement fields [β] in individual adaptive measurements. A simple strategy that we refer to as “sequential optimization” implements N-optimized displacement amplitudes [β] = {β 1, β 2, ..., β N } one in each adaptive measurement, but optimized simultaneously so that
Figure 1b shows the improved performance of this strategy over the “flat optimization” strategy. This “sequential optimization” strategy is similar to the optimal discrimination strategy for two states described by Dolinar,34 but for multiple states. We observe that the displacement amplitude ratio \(\left| \beta \right|{\rm{/}}\left| \alpha \right|\) starts with a large value and decreases as a function of time, as seen in Fig. 1c. However, in contrast to the optimal measurement for two states,34 the displacement magnitude ratio is not a monotonically decreasing function of time, and may not be optimal as N → ∞.
Higher sensitivities for discrimination of multiple states can be achieved by strategies based on globally optimized displacement operations that are conditional on the detection histories. These strategies have as many optimal displacement amplitudes as the number of possible detection histories D H minus one. For detectors without PNR capabilities, i.e., with only two possible detection outcomes, the number of detection histories is 2N, and the displacement amplitudes \([\beta ] = \left\{ {\beta _1,\beta _2,...,\beta _{2^N - 1}} \right\}\) are optimized to minimize the final probability of error
These strategies, which we refer to as “historical optimization,” generalize strategies for discrimination of multiple states based on coherent displacements, photon counting and finite number of adaptive measurements with maximum posterior probability criteria.
Figure 1b shows the improved performance of the historical optimization strategy over the “flat optimization” and the “sequential optimization.” The historical optimization is closer to the Helstrom limit for a small number of adaptive measurements. Figure 1d shows the highly complex evolution of the optimized displacement amplitudes for this strategy for 100 possible detection histories D H for N = 10. It is unknown if the historical optimization strategy would reach the Helstrom limit for N → ∞. Since the number of parameters to globally optimize grows as 2N, finding the optimal [β] for large N numerically becomes computationally intensive. However, this strategy as well as the flat and sequential optimization strategies can be realized experimentally with current technologies. Once optimal displacements for different strategies are determined, they can be coded in a high-bandwidth electronic controller. The controller updates the values of phase and amplitudes of the optimal displacements conditioned on detection results in each adaptive measurement using fast feedback. In this way, the overhead in computation time for estimating the optimal [β] is done offline, and the complexity in the implementation of different strategies becomes comparable in the experiment. This method allows us to experimentally demonstrate discrimination of multiple nonorthogonal states below the QNL at the single-photon level.
Experimental demonstration
Figure 2a shows a schematic of the experimental demonstration of optimized strategies for the discrimination of four coherent states \(\left| {\alpha _k} \right\rangle \in \left\{ {\left| \alpha \right\rangle ,\left| {i\alpha } \right\rangle ,\left| { - \alpha } \right\rangle ,\left| { - i\alpha } \right\rangle } \right\}\) below the QNL. A 633 nm laser with an acousto–optic modulator prepares flat top 27 μs long pulses defining the temporal extent of the input state \(\left| {\alpha _k} \right\rangle\). Phase modulator (PM1) prepares the phase of \(\left| {\alpha _k} \right\rangle\) with a given mean photon number \(\left\langle n \right\rangle\) calibrated with a transfer-standard calibrated detector.47 Phase (PM2) and amplitude (AM) modulators prepare the phase and the amplitude of the optimal displacement fields [β] for different optimized discrimination strategies. The displacement operations are performed by interference in a 99/1 beam splitter (BS2), achieving an average visibility of the displacement operation of \({\cal V}_{{\rm Exp}} = 99.6(1)\%\). An avalanche photodiode single-photon detector (SPD) with detection efficiency of DE = 84.0(5)% detects the photons in the displaced state \(\left| \psi \right\rangle = \hat D( - \beta )\left| {\alpha _k} \right\rangle\). A field-programmable gate array (FPGA) processes the detection results d j and prepares the optimal displacements \(\hat D\left( {\left[ \beta \right]} \right)\) for subsequent adaptive measurements in real time with AM and PM2 for a specific discrimination strategy (see Methods). The experimental rate is 11 kHz with a 50% duty cycle: 50% of the time is used either for performing the experiment or for calibration of the phase and AM modulators; the other 50% of the time is used for active stabilization of the interferometer using a 780 nm laser, a differential detector and a piezo (PZT), as in refs. 23,45. Figure 2b, c shows an example of the target (b) and observed intensity for (c) optimized displacement amplitudes [β] for the sequential optimized strategy for \(\left\langle n \right\rangle\) = 0.5 with N = 10. This experimental setup achieves an overall detection efficiency of DEExp = 70.5(7)% and is compatible with PNR detection, which increases robustness at high powers.23 We use our experiment to demonstrate globally optimized strategies for the discrimination of multiple coherent states below the QNL at the single-photon level without correction for detection inefficiencies or dark counts.
Experimental implementation of multi-state discrimination with optimized displacements. a Experimental configuration of strategies with optimized discrimination of four nonorthogonal coherent states \(\left\{ {\left| \alpha \right\rangle ,\left| {i\alpha } \right\rangle ,\left| { - \alpha } \right\rangle ,\left| { - i\alpha } \right\rangle } \right\}\) implementing N = 10 adaptive measurements. A phase modulator PM1 prepares the input state, and phase PM2 and amplitude AM modulators prepare the optimized displacements [β]. The displacement operation is implemented by interference in a 99/1 beam splitter (BS2), and a field-programmable gate array (FPGA) processes the detection result from the single-photon detector (SPD) to prepare the optimized displacements [β] for subsequent adaptive measurements. The phase of [β] is controlled with a 2-bit fast multiplexer switch and PM2, and its amplitude with a 1-byte depth digital-to-analog converter (DAC) and the AM. SMF single-mode fiber, DM dichroic mirror, PZT piezo, AOM acousto–optic modulator. b, c Example of the intensity \(\left| \beta \right|^2\) of the optimized displacement field [β] for the sequential global optimization strategy for N = 10, DE = 70%, \({\cal V}\) = 99.6% and \(\left\langle n \right\rangle\) = 0.5 for b target and c observed
Figure 3 shows the experimental results of the discrimination of four nonorthogonal coherent states below the QNL at the single-photon level based on three optimized strategies: flat optimization, sequential optimization, and historical optimization. Included in the figure are the non-optimized strategy, the Helstrom bound, the ideal QNL, and the QNL scaled to the same system detection efficiency (70%) as in our experiment. The theoretical predictions are shown in dashed lines and are based on numerical simulations using Eq. (2) with the optimal displacements [β] for the flat, sequential, and historical optimization strategies satisfying Eq. (3), Eq. (4), and Eq. (5), respectively, with the experimental parameters DEExp = 70%, visibility \({\cal V}_{{\rm Exp}} = 99.6\%\) and dark counts of 0.1% per pulse. We observe that the strategy based on displacements without optimized amplitudes does not surpass the QNL at the single-photon level, in agreement with previous work.38,43,44,45,48 On the other hand, discrimination measurements with globally optimized displacements can surpass the QNL at the single-photon level even with moderate detection efficiency and visibility with just ten adaptive measurements. We observe that sequential and historical optimizations provide similar advantages within the experimental noise with error probabilities about 10% below the QNL at \(\left\langle n \right\rangle\) = 1, and provide slightly greater advantages than the flat optimization. Moreover, compared to a system with the same DE (70%), optimized measurement strategies surpass the QNL at very small powers, which is essential for enhancing information transfer in optical communication at low powers beyond classical limits24,25,26 and may provide advantages for increasing security in QKD with coherent states. In addition, these strategies can extend discrimination to high powers and increase robustness by implementing PNR detection, which broadens their capabilities for general tasks in quantum information and communications.
Experimental results. Error probability for the discrimination of four nonorthogonal states \(\left\{ {\left| \alpha \right\rangle ,\left| {i\alpha } \right\rangle ,\left| { - \alpha } \right\rangle ,\left| { - i\alpha } \right\rangle } \right\}\) with three optimized strategies, flat (light-brown dots) sequential (green dots) and historical (blue dots) optimization, and the non-optimized strategy (magenta dots). The Helstrom bound (black line) and the QNL (red line) are shown for reference together with the QNL with the same experimental conditions of detection efficiency DEExp = 70% (gray line). While discrimination strategies without optimized displacements do not surpass the QNL at the single-photon level, globally optimized strategies can reach error rates below the QNL without any correction for detection efficiency as shown for \(\left\langle n \right\rangle\) = 1. Furthermore, for a system with the same DE = 70%, optimized strategies surpass the QNL at arbitrary small powers in the presence of noise and imperfections. Error bars represent 1 statistical standard deviation from 4 runs of 1 × 105 independent experiments per data point. The theoretical predictions (dashed lines) are based on numerical simulations with the experimentally determined detection efficiency DEExp = 70%, visibility of the displacement \({\cal V}_{{\rm Exp}} = 99.6\%\), and dark counts of 0.1% per pulse
Discussion
We investigated the potential advantages of optimized strategies for multiple states for increasing information transfer in communication. Recent theoretical work showed that nonconventional receivers for coherent states based on photon counting can provide higher communication rates than what is possible with conventional ones.25,26,49 The optimized discrimination strategies for multiple states presented here can achieve higher levels of information transfer than both non-optimized strategies and what could be achieved with coherent states and heterodyne detection25 at the single photon level. Figure 4 shows the mutual information achieved by the “flat optimization” discrimination measurement for four states \(\left\{ {\left| \alpha \right\rangle ,\left| {i\alpha } \right\rangle ,\left| { - \alpha } \right\rangle ,\left| { - i\alpha } \right\rangle } \right\}\) with DE = 1 and N = 10. This optimized measurement surpasses the capacity of the heterodyne measurement using an arbitrary number of coherent states in the single-photon regime at \(\left\langle n \right\rangle\) = 1,25 which is not possible with non-optimized strategies. Other optimized measurements are expected to provide greater advantages over the heterodyne measurement in the single-photon regime. However, we note that flat optimization may be easier to implement than sequential and historical optimizations, and may be more practical in communication, albeit with a slightly lower attainable sensitivity. This example shows the potential of optimized measurements for low-power communication with multiple states to increase capacity based on single-state decoding,50 which can be further optimized with larger alphabets and optimal distribution of the input states.25 Moreover, optimized discrimination strategies can assist joint quantum measurements over sequences of coherent states51,52 with multiple phases24 in approaching the ultimate limits in capacity53,54 at the single-photon level. While in the present work we used long pulses and feedback with a SPD with deadtime of about 35 ns, the optimized strategies investigated here can be implemented using feed forward, instead of feedback, by splitting the input state in space and using optical delay lines, as described in refs. 48,55, allowing for higher repetition rates with much shorter pulses. Together with fast electronic controllers and gated SPD56,57 reaching >GHz speeds, these optimized strategies could allow for high sensitivity measurements at higher communication rates.
Mutual information of optimized discrimination measurements. The flat optimization strategy achieves higher mutual information than non-optimized measurements, and surpasses the achievable capacity of heterodyne measurement over coherent states in a range of input powers in the single-photon regime from 0.5 to 2 photon number with just N = 10 adaptive measurements and four states. Other optimized measurements are expected to provide greater advantages in capacity. The Gaussian limit corresponds to the achievable capacity with arbitrary Gaussian states and operations; the Holevo bound corresponds to the ultimate limit in capacity
It has been shown46 that optimized measurements of two nonorthogonal coherent states based on post-selection can lead to higher secret key rates in QKD than what can be achieved with homodyne measurements and post selection.55,58 The optimization methods described here for measurements with definite outcomes may be useful for increasing the rate in QKD protocols with measurements without post selection.55,58 These measurements may lead to higher rates than the heterodyne detection, and could be experimentally investigated with our current setup.
Conclusion
Optimized measurements for the discrimination of multiple nonorthogonal states at the single-photon level can increase the information transfer in communications and enhance security in quantum communication. We demonstrate discrimination of multiple nonorthogonal states below the QNL at the single-photon level under realistic loss, noise, and system imperfections based on globally optimized strategies requiring only a few adaptive measurements. These optimized discrimination measurements can enable low-power communication with multi-level encoding surpassing the QNL; yield higher information transfer at low powers; and could have applications in QKD with multiple coherent states. Our work makes measurements achieving sensitivities beyond conventional Gaussian measurements a more realistic alternative to enhance information transfer beyond what can be achieved with conventional technologies. We expect that this work will motivate further theoretical and experimental research in finding optimal measurements for multiple coherent states and their applications in quantum information processing and communication.
Methods
Preparation of the displacement field
The field FPGA provides two digital signals to control the phase of the displacement field β, and eight digital signals plus one clock to control its amplitude \(\left| \beta \right|\), which corresponds to the optimized displacements [β] for a given discrimination strategy. To control the phase of β, we use a voltage source together with a 4-to-1 fast multiplexer switch with 210 MHz bandwidth. The output of the multiplexer switches among the four voltages based on the two digital inputs from the FPGA, and controls the voltage to PM2 to provide four possible phase shifts: {0, π/2, π, 3π/2} (The phase of the input state is prepared with PM1 using the same technique.) To control the displacement field amplitude \(\left| \beta \right|\), we use the AM and a digital-to-analog converter (DAC) with maximum update rate of 210 MSPS. The DAC receives eight digital signals from the FPGA and outputs a 1-byte depth analog voltage, which is sent to the input of the AM. The DAC is updated by a 48 MHz clock provided by the FPGA, which allows for updating the amplitude of the displacement field as soon as a new value of \(\left| \beta \right|\) is available from the FPGA. The total latency of the circuitry to update the AM input voltage is <35 ns.
Note
This information encoding scheme is referred to as M-ary phaseshift keying (M-PSK) in coherent communication
Data availability
The authors declare that the main data supporting the finding of this study are available within the article.
References
Helstrom, C. W. Quantum detection and estimation theory, Mathematics in Science and Engineering Vol. 123 (Academic Press, 1976).
Huttner, B., Imoto, N., Gisin, N. & Mor, T. Quantum cryptography with coherent states. Phys. Rev. A 51, 1863–1869 (1995).
Bennett, C. H. Quantum cryptography using any two nonorthogonal states. Phys. Rev. Lett. 68, 3121–3124 (1992).
Grosshans, F. & Grangier, P. Continuous variable quantum cryptography using coherent states. Phys. Rev. Lett. 88, 057902 (2002).
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002).
Weedbrook, C. et al. Gaussian quantum information. Rev. Mod. Phys. 84, 621–669 (2012).
Sych, D. & Leuchs, G. Coherent state quantum key distribution with multi letter phase-shift keying. New J. Phys. 12, 053019 (2010).
Leverrier, A. & Grangier, P. Unconditional security proof of long-distance continuous-variable quantum key distribution with discrete modulation. Phys. Rev. Lett. 102, 180504 (2009).
Leverrier, A. & Grangier, P. Continuous-variable quantum-key-distribution protocols with a non-gaussian modulation. Phys. Rev. A 83, 042312 (2011).
Qi, B., Lougovski, P., Pooser, R., Grice, W. & Bobrek, M. Generating the local oscillator “locally” in continuous-variable quantum key distribution based on coherent detection. Phys. Rev. X 5, 041009 (2015).
Soh, D. B. S. et al. Self-referenced continuous-variable quantum key distribution protocol. Phys. Rev. X 5, 041010 (2015).
van Loock, P. et al. Hybrid quantum repeater using bright coherent light. Phys. Rev. Lett. 96, 240501 (2006).
van Loock, P., Lütkenhaus, N., Munro, W. J. & Nemoto, K. Quantum repeaters using coherent-state communication. Phys. Rev. A 78, 062319 (2008).
Munro, W. J., Nemoto, K. & Spiller, T. P. Weak nonlinearities: a new route to optical quantum computation. New J. Phys. 7, 137 (2005).
Nemoto, K. & Munro, W. J. Nearly deterministic linear optical controlled-not gate. Phys. Rev. Lett. 93, 250502 (2004).
Ralph, T. C., Gilchrist, A., Milburn, G. J., Munro, W. J. & Glancy, S. Quantum computation with optical coherent states. Phys. Rev. A 68, 042319 (2003).
Kilin, S. Y. & Mikhalychev, A. B. Optical qudit-type entanglement creation at long distances by means of small cross-kerr nonlinearities. Phys. Rev. A 83, 052303 (2011).
van Loock, P. Optical hybrid approaches to quantum information. Laser Photon. Rev. 5, 167–200 (2011).
Collins, R. J. et al. Realization of quantum digital signatures without the requirement of quantum memory. Phys. Rev. Lett. 113, 040502 (2014).
Croal, C. et al. Free-space quantum signatures using heterodyne measurements. Phys. Rev. Lett. 117, 100503 (2016).
Arrazola, J. M. & Lütkenhaus, N. Quantum communication with coherent states and linear optics. Phys. Rev. A 90, 042335 (2014).
Guan, J.-Y. et al. Observation of quantum fingerprinting beating the classical limit. Phys. Rev. Lett. 116, 240502 (2016).
Becerra, F. E., Fan, J. & Migdall, A. Photon number resolution enables quantum receiver for realistic coherent optical communications. Nat. Photonics 9, 4853 (2015).
Rosati, M., Mari, A. & Giovannetti, V. Multiphase hadamard receivers for classical communication on lossy bosonic channels. Phys. Rev. A 94, 062325 (2016).
Lee, J., Ji, S.-W., Park, J. & Nha, H. Gaussian benchmark for optical communication aiming towards ultimate capacity. Phys. Rev. A 93, 050302 (2016).
Tan, S.-H., Dutton, Z., Nair, R. & Guha, S. Finite codelength analysis of the sequential waveform nulling receiver for M-ary PSK. in Proceedings of the IEEE International Symposium on Information Theory (ISIT), Hong Kong, 2015, 729–733 (IEEE Press, New York, 2015).
Caves, C. M. & Drummond, P. D. Quantum limits on bosonic communication rates. Rev. Mod. Phys. 66, 481–537 (1994).
Giovannetti, V. et al. Classical capacity of the lossy bosonic channel: the exact solution. Phys. Rev. Lett. 92, 027902 (2004).
Giovannetti, V., Garcia-Patron, R., Cerf, N. J. & Holevo, A. S. Ultimate classical communication rates of quantum optical channels. Nat. Photonics 8, 796800 (2014).
Mari, A., Giovannetti, V. & Holevo, A. S. Quantum state majorization at the output of bosonic gaussian channels. Nat. Commun. 5, 3826 (2014).
Yuen, H., Kennedy, R. & Lax, M. Optimum testing of multiple hypotheses in quantum detection theory. IEEE Trans. Inf. Theory 21, 125–134 (1975).
Kennedy, R. S. A near-optimum receiver for the binary coherent state quantum channel. MIT Technical Report No. 110 (Research Laboratory of Electronics, 1972) unpublished.
Takeoka, M. & Sasaki, M. Discrimination of the binary coherent signal: Gaussian-operation limit and simple non-gaussian near-optimal receivers. Phys. Rev. A 78, 022320 (2008).
Dolinar, S. J. An optimum receiver for the binary coherent state quantum channel. MIT Res. Lab. Electron. Quart. Progr. Rep. 111, 115–120 (1973).
Cook, R. L., Martin, P. J. & Geremia, J. M. Optical coherent state discrimination using a closed-loop quantum measurement. Nature 446, 774–777 (2007).
Wittmann, C. et al. Demonstration of near-optimal discrimination of optical coherent states. Phys. Rev. Lett. 101, 210501 (2008).
Tsujino, K. et al. Quantum receiver beyond the standard quantum limit of coherent optical communication. Phys. Rev. Lett. 106, 250503 (2011).
Bondurant, R. S. Near-quantum optimum receivers for the phase-quadrature coherent-state channel. Opt. Lett. 18, 1896–1898 (1993).
Nair, R., Yen, B. J., Guha, S., Shapiro, J. H. & Pirandola, S. Symmetric m-ary phase discrimination using quantum-optical probe states. Phys. Rev. A 86, 022306 (2012).
Izumi, S. et al. Displacement receiver for phase-shift-keyed coherent states. Phys. Rev. A 86, 042328 (2012).
Izumi, S., Takeoka, M., Ema, K. & Sasaki, M. Quantum receivers with squeezing and photon-number-resolving detectors for m-ary coherent state discrimination. Phys. Rev. A. 87, 042328 (2013).
Li, K., Zuo, Y. & Zhu, B. Suppressing the errors due to mode mismatch for M-ary PSK quantum receivers using photon-number-resolving detector. IEEE Photon. Technol. Lett. 25, 2182–2184 (2013).
Müller, C. R. & Marquardt, C. A robust quantum receiver for phase shift keyed signals. New. J. Phys. 17, 032003 (2015).
Müller, C. et al. Quadrature phase shift keying coherent state discrimination via a hybrid receiver. New J. Phys. 14, 083009 (2012).
Becerra, F. E. et al. Experimental demonstration of a receiver beating the standard quantum limit for multiple nonorthogonal state discrimination. Nat. Photonics 7, 147–152 (2013).
Wittmann, C., Andersen, U. L., Takeoka, M., Sych, D. & Leuchs, G. Demonstration of coherent-state discrimination using a displacement-controlled photon-number-resolving detector. Phys. Rev. Lett. 104, 100505 (2010).
Gentile, T. R., Houston, J. M. & Cromer, C. L. Realization of a scale of absolute spectral response using the national institute of standards and technology high-accuracy cryogenic radiometer. Appl. Opt. 35, 4392–4403 (1996).
Becerra, F. E. et al. M-ary-state phase-shift-keying discrimination below the homodyne limit. Phys. Rev. A 84, 062324 (2011).
Takeoka, M. & Guha, S. Capacity of optical communication in loss and noise with general quantum gaussian receivers. Phys. Rev. A 89, 042309 (2014).
Shannon, C. E. A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423 (1948).
Guha, S. Structured optical receivers to attain superadditive capacity and the holevo limit. Phys. Rev. Lett. 106, 240502 (2011).
Jarzyna, M., Lipińska, V., Klimek, A., Banaszek, K. & Paris, M. G. A. Phase noise in collective binary phase shift keying with hadamard words. Opt. Express 24, 1693–1698 (2016).
Holevo, A. S. The capacity of the quantum channel with general signal states. IEEE Trans. Inf. Theory 44, 269–273 (1998).
Schumacher, B. & Westmoreland, M. D. Sending classical information via noisy quantum channels. Phys. Rev. A 56, 131–138 (1997).
Sych, D. & Leuchs, G. Practical receiver for optimal discrimination of binary coherent signals. Phys. Rev. Lett. 117, 200501 (2016).
Bienfang, J. C. & Restelli, A. Characterization of an advanced harmonic subtraction single-photon detection system based on an InGaAs/Inp avalanche diode. Proc. SPIE 9858, Advanced Photon Counting Techniques X, 98580Q. 5 May. https://www.spiedigitallibrary.org/conference-proceedings-of-spie/9858/98580Q/Characterization-of-an-advanced-harmonic-subtraction-single-photon-detection-system/10.1117/12.2228331.short?SSO=1 (2016).
Zhang, J., Itzler, M. A., Zbinden, H. & Pan, J.-W. Advances in ingaas/inp single-photon detector systems for quantum communication. Light Sci. Appl. 4, e286 (2015).
Heid, M. & Lütkenhaus, N. Efficiency of coherent-state quantum cryptography in the presence of loss: Influence of realistic error correction. Phys. Rev. A 73, 052316 (2006).
Acknowledgements
This work was supported by NSF Grant PHY-1653670 and PHY-1521016.
Author information
Authors and Affiliations
Contributions
F.E.B. analyzed the theoretical measurement strategies, and designed the experimental implementation of the optimized receiver. F.E.B., A.R.F. and M.T.D. performed the measurements and analyzed the experimental results. All authors contributed to writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ferdinand, A.R., DiMario, M.T. & Becerra, F.E. Multi-state discrimination below the quantum noise limit at the single-photon level. npj Quantum Inf 3, 43 (2017). https://doi.org/10.1038/s41534-017-0042-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-017-0042-2
This article is cited by
-
Quantum receiver enhanced by adaptive learning
Light: Science & Applications (2022)
-
Energy and bandwidth efficiency optimization of quantum-enabled optical communication channels
npj Quantum Information (2022)
-
Determination of the asymptotic limits of adaptive photon counting measurements for coherent-state optical phase estimation
npj Quantum Information (2022)
-
Experimental demonstration of single-shot quantum and classical signal transmission on single wavelength optical pulse
Scientific Reports (2019)
-
Optimized communication strategies with binary coherent states over phase noise channels
npj Quantum Information (2019)