Abstract
Identifying and ameliorating dominant sources of decoherence are important steps in understanding and improving quantum systems. Here, we show that the free induction decay time (\(T_2^*\)) and the Rabi decay rate (ΓRabi) of the quantum dot hybrid qubit can be increased by more than an order of magnitude by appropriate tuning of the qubit parameters and operating points. By operating in the spin-like regime of this qubit, and choosing parameters that increase the qubit’s resilience to charge noise (which we show is presently the limiting noise source for this qubit), we achieve a Ramsey decay time \(T_2^*\) of 177 ns and a Rabi decay time 1/ΓRabi exceeding 1 μs. We find that the slowest ΓRabi is limited by fluctuations in the Rabi frequency induced by charge noise and not by fluctuations in the qubit energy itself.
Similar content being viewed by others
Introduction
There has been much progress in the development of qubits in semiconductor quantum dots,1 making use of one,2,3,4,5,6,7,8,9,10,11 two,12,13,14,15,16,17,18,19,20 and three quantum dots21,22,23,24,25,26 to host qubits. Charge noise is often the leading source of decoherence in semiconductor qubits,27 and an advantage of using two or more quantum dots to host a single qubit is the ability to work at sweet spots, a technique pioneered in superconducting qubits,28 that make the qubit more resistant to charge noise.29,30,31,32,33,34,35,36
In this work we focus on one such qubit, the quantum dot hybrid qubit (QDHQ),37,38,39,40,41,42,43,44,45 which is formed from three electrons in a double quantum dot, and can be viewed as a hybrid of a spin qubit and a charge qubit. Fast, full electrical control of the QDHQ was recently implemented experimentally using ac gating,46 demonstrating a free induction decay (FID) time of 11 ns through operation in the spin-like operating region (see Fig. 1). While QDHQ gating times are fast, substantial further improvements in QDHQ coherence times are required to achieve the high-fidelity gating necessary for fault-tolerant operation.47 True sweet spots, which are used to increase resistance to noise and thus increase coherence, are defined by a zero derivative of the qubit energy with respect to a parameter subject to noise. Sweet spots are usually found at specific points of zero extent in parameter space, so that non-infinitesimal noise amplitude temporarily moves a qubit off the sweet spot. The spin-like regime of the QDHQ has no true sweet spot; however, it has a large and extended region of small dEQ/dε, where EQ is the qubit energy and ε is the detuning between the two quantum dots.
Energy spectrum and pulse sequences for the QDHQ. Main panel: Energy vs. detuning of the qubit states |0〉 and |1〉 as well as a leakage state |L〉. The QDHQ Hamiltonian, described in Supplementary Section 1, is parameterized using two tunnel couplings Δ1(2) between the ground state of the left dot and the ground (excited) state of the right dot, and the asymptotic energy splitting ER between the ground and excited states of the right dot. In the spin-like region (green, right), the logical states are differentiated by their spin configurations. The four pulse sequences used in this work are shown as functions of the detuning: the non-adiabatic Larmor (I) and Ramsey (II) sequences, and the microwave-pulsed Rabi (III) and Ramsey (IV) sequences. See Supplementary Section 4 for details. Inset, SEM image of a device lithographically identical to the one used in the experiments; white dashed circles indicate the locations of the double dot. Voltage pulses are applied to gates L and R, and a quantum point contact is used to measure the electron occupancy of the dots
Here, we show that the spin-like operating regime for the QDHQ can be made resilient to charge noise by appropriate tuning of the internal parameters of the qubit. By measuring dEQ/dε, we are able to identify dot tuning parameters that increase resiliency to charge noise. These measurements show that the three-electron QDHQ can be tuned in-situ in ways that have a predictable and understandable impact on the qubit coherence: the qubit dispersion can be tuned smoothly by varying device gate voltages, and we find that the dephasing rate is proportional to dEQ/dε, consistent with a charge noise dephasing mechanism. Reducing dEQ/dε significantly enhances the coherence of the qubit. We have achieved an increase the coherence times by more than an order of magnitude over previous work, decreasing the Rabi decay rate ΓRabi from 67.1 to 0.98 MHz, and increasing the FID time \(T_2^*\) to as long as 177 ns. These parameters correspond to an infidelity contribution from pure dephasing of about 1%.
Results
Figure 1 shows the energy levels of the QDHQ as a function of the detuning ε. At negative detuning the energy difference between the |0〉 and |1〉 states is dominated by the Coulomb energy, while at large positive detunings, where both logical states have the same electron configuration (one electron on the left and two on the right), the energy difference is dominated by the single-particle splitting ER between the lowest two valley-orbit states in the right dot. Here, the logical states are described by their spin configuration: |0〉 = |↓〉|S〉 and |1〉 = \(\sqrt {1{\rm{/}}3} \)|↓〉|T0〉−\(\sqrt {2{\rm{/}}3} \)|↑〉|T−〉, where |↓〉 and |↑〉 represent the spin configuration of the single electron in the left quantum dot and |S〉, |T0〉, and |T−〉 represent the singlet (S) and triplet (T0, T−) spin configurations of the two electrons in the right quantum dot. The tunnel coupling Δ1(2) describes the anticrossings between the right dot ground (first excited) state and left dot ground state.
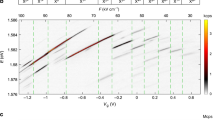
Figure 2a–g shows results of FID measurements for four different values of the measured dEQ/dε, performed using the pulse sequence of diagram IV of Fig. 1, in order to determine \(\Gamma _2^*{\rm{ = }}1{\rm{/}}T_2^*\). For short times (panels a, c, e), Ramsey fringes are visible for all dEQ/dε; in contrast, for tFree = 22 ns, Ramsey fringes are attenuated in Fig. 2b (large dEQ/dε), yet are still clearly visible in Fig. 2f (small dEQ/dε). As shown in Fig. 2g, by tuning the qubit to achieve dEQ/dε = 0.0025, Ramsey fringes are still visible at tFree = 120 ns, and at this tuning a Gaussian fit to the Ramsey fringe amplitude (shown in Fig. 2h) yields \(T_2^*{\rm{ = }}177 \pm 9\,{\rm{ns}}\). Fits to the Ramsey fringe amplitude of the other three detunings are shown in Fig. 2i, demonstrating a strong correlation between small dEQ/dε and long \(T_2^*\). Although we have shown Gaussian fits in Fig. 2, consistent with quasistatic charge noise, we note that the FID decay also can be fit by an exponential decay, which would be consistent with noise that is dominated by only a few two-level fluctuators,48 and therefore we cannot distinguish between these two limiting cases (see Supplemental Material for fit parameters extracted from exponential decays).
Changing the dot tuning and ε to achieve small dEQ/dε decreases the FID rate by more than an order of magnitude. a–g Plots showing the probability P1 of being in state |1〉 after applying the Ramsey pulse sequence of diagram IV in Fig. 1, for qubit tunings characterized by different dEQ/dε values. Two tFree time windows are shown for three tunings, corresponding to dEQ/dε = 0.028 (a, b), dEQ/dε = 0.012 (c, d), dEQ/dε = 0.0042 (e, f), and a single time window is shown for dEQ/dε = 0.0025 (g). Comparing b, d, f, and g, we see that the FID rate decreases as dEQ/dε decreases. h, i Oscillation amplitudes as a function of tFree, normalized by their value at tFree = 0 are obtained at the ε values indicated by black arrows in g (h) and a–f (i); fits to both \({\rm{exp}}( - {({t_{{\rm{Free}}}}{\rm{/}}T_2^*)^2})\) (values shown) and \({\rm{exp}}( - {t_{{\rm{Free}}}}{\rm{/}}T_2^*)\) are plotted. j \(\Gamma _2^*\) vs. dEQ/dε, obtained from a fit to \({\rm{exp}}( - {({t_{{\rm{Free}}}}{\rm{/}}T_2^*)^2})\), as in i (values extracted from a fit to \({\rm{exp}}( - {t_{{\rm{Free}}}}{\rm{/}}T_2^*)\) can be found in Supplementary Section 6), for several different tunings and a range of ε. The data are well fit to Eq. (1) (blue line, σε = 4.39 ± 0.32 μeV), providing evidence that \(\Gamma _2^*\) is limited by charge noise. All error bars are standard deviations
Figure 2j shows \(\Gamma _2^*{\rm{ = }}1{\rm{/}}T_2^*\) for a wide range of dEQ/dε, demonstrating a significant improvement in coherence for reduced values of dEQ/dε. For a Gaussian distribution of quasistatic fluctuations of the detuning parameter, with a standard deviation of σε, one expects that15, 27
In Fig. 2j, we observe such a linear relation between \(\Gamma _2^*\) and dEQ/dε, with a fitting constant σε = 4.39 ± 0.32 μeV.
We now turn to a discussion of the Rabi decay time, 1/ΓRabi, and its dependence on the qubit dispersion dEQ/dε. Figure 3a shows both EQ and dEQ/dε as a function of detuning, calculated using the measured tuning parameters for Fig. 3b–e (see Supplementary Section 1 and 4), showing the decrease in the slope dEQ/dε with increasing ε. Figure 3b–e shows Rabi oscillation measurements, performed with a microwave burst of duration tRF and acquired at the detunings labeled b–e in Fig. 3a, showing that with increasing ε (and therefore decreasing dEQ/dε) the Rabi decay rate ΓRabi decreases by more than an order of magnitude for the data reported here.
Rabi decay rate is limited by charge noise and applied microwave power, Aε. a Plots of EQ = hfQ (black) and dEQ/dε (red) vs. ε for the tuning used in b–e. Here, fQ is the qubit frequency, and the spectroscopy methods used are described in Supplementary Section 4. b–e Rabi oscillations of the probability P1 of being in state |1〉, all obtained at the same tuning but at different ε, ranging from ~210 to 340 μeV. ΓRabi clearly decreases as dEQ/dε decreases. The decrease in fRabi between b–e is caused by the decreased coupling to the left dot as ε is increased (see Eq. (2)). Aε is nominally the same but changes slightly between b–e due to changes in fQ as discussed in Supplementary Section 5. f Rabi oscillations, taken at a different device tuning, demonstrating over 100 coherent Xπ/2 rotations within a Rabi decay time. g Rabi oscillations demonstrating a Rabi decay time longer than 1 μs, taken at a device tuning differing from those in b–f. h ΓRabi, obtained by fitting to an exponential decay, plotted as a function of dEQ/dε for measurements at multiple tunings and operating points, with Aε within 10% of 25 μeV. Here, the black line has slope 2, indicating that ΓRabi depends quadratically on dEQ/dε, consistent with ΓRabi being limited by fluctuations of fQ.48, 50 Here, the different tunings are labeled with different colors (red, green, and blue), as specified in Supplementary Section 1. i Rabi oscillations taken at ε = 323 μeV (dEQ/dε = 0.005), as a function of the microwave amplitude Aε, showing that the Rabi decay rate ΓRabi ∝ Aε, consistent with ΓRabi being limited by fluctuations of fRabi for small values of dEQ/dε
For quantum gates, the contribution to infidelity arising from qubit decoherence is minimized when the ratio of the gate duration to the Rabi decay time is minimized. The data in Fig. 3f, acquired at a different dot tuning, show that this ratio can be made small enough that an Xπ/2 gate can be performed over 100 times within one Rabi decay time. In the absence of any other nonideality in the experiment, this would limit the fidelity of an Xπ/2 rotation on the Bloch sphere to 99.0% and would represent a sevenfold improvement over previous results.46
It is also interesting to consider how long the Rabi decay time, 1/ΓRabi, itself can be. Figure 3g shows Rabi oscillations acquired at a different dot tuning and a very small dEQ/dε = 0.005. Here, ΓRabi = 0.98 MHz, representing a decrease by more than a factor of 30 from previously reported Rabi decay rates.46
The decay of Rabi oscillations is caused by at least two different mechanisms,49 both of which are observed in these experiments. First, for relatively large values of dEQ/dε, fluctuations in EQ from charge noise dominate the decoherence. This is similar to FID measurements, with the important difference that the microwave drive effectively reduces the range of frequencies decohering the qubit. This results in Rabi decoherence rates ΓRabi that are slower than the FID rates \(\Gamma _2^*\) at the same dEQ/dε. For this mechanism, the Rabi decay is expected to be exponential and depend quadratically on dEQ/dε.48, 50 Figure 3h shows ΓRabi vs. dEQ/dε and a quadratic fit to the data; the data are well described by this functional form, and decreasing dEQ/dε yields nearly two orders of magnitude decrease in ΓRabi.
Second, charge noise can also cause fluctuations in the rotation rate fRabi itself,49 and as dEQ/dε becomes small, these fluctuations become the dominant source of decoherence. This second decay process is expected to yield a decay rate proportional to the drive amplitude Aε, and as shown in Fig. 3i we observe this proportionality in the experiment for small dEQ/dε. Thus, for small dEQ/dε, fluctuations in fRabi dominate the Rabi decay rate. In contrast to the Rabi decay process discussed above, in which the applied microwave pulse narrows the frequency range of charge fluctuations contributing to the decay, charge fluctuations over a wide bandwidth are expected to contribute to this decay process. This contribution can be seen by applying the rotating wave approximation to Eq. (S1) in Supplementary Section 1, which yields an approximate form for fRabi that is valid at large detunings:
σε can then be related to σRabi, the standard deviation of fluctuations in fRabi, by
We therefore expect the decay rate from this mechanism to be proportional to dEQ/dε rather than to the square of dEQ/dε, explaining its dominance at small dEQ/dε.
Discussion
In this work we have shown that the internal parameters of the QDHQ can alter the qubit dispersion dEQ/dε over a wide range, resulting in large tunability in both the decoherence rates and the Rabi frequencies achievable. The dominant dephasing mechanism for Rabi oscillations switches from fluctuations in the qubit energy EQ to fluctuations in the Rabi frequency fRabi at the smallest values of dEQ/dε. By decreasing dEQ/dε we have reduced both the Rabi and the Ramsey decoherence rates, important metrics for achieving high-fidelity quantum gate operations, by more than an order of magnitude compared with previous work, demonstrating ΓRabi as small as 0.98 MHz and \(T_2^*{\rm{ = }}1{\rm{/}}\Gamma _2^*\) as long as 177 ns. These coherence times exhibit the utility of the extended near-sweet spot in the QDHQ for improving qubit performance in the presence of charge noise.
Methods
The Si/SiGe device is operated in a region where magnetospectroscopy measurements3, 51 have indicated that the valence electron occupation of the double dot is (1,2) for the qubit states studied here. Manipulation pulse sequences were generated using Tektronix 70001 A arbitrary waveform generators and added to DC gate voltages on gates L and R using bias tees (PSPL5546). Because of the frequency-dependent attenuation of the bias tees, corrections were made to the applied pulses during the adiabatic detuning pulses, as described in Supplementary Section 5. The qubit states were mapped to the (1,1) and (1,2) charge occupation states as described in ref. 46. A description of the methods used to measure the qubit dispersion and lever arm can be found in Supplementary Section 4.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120–126 (1998).
Koppens, F. H. L. et al. Driven coherent oscillations of a single electron spin in a quantum dot. Nature 442, 766–771 (2006).
Simmons, C. B. et al. Tunable spin loading and T1 of a silicon spin qubit measured by single-shot readout. Phys. Rev. Lett. 106, 156804 (2011).
Pla, J. J. et al. A single-atom electron spin qubit in silicon. Nature 489, 541–545 (2012).
Veldhorst, M. et al. An addressable quantum dot qubit with fault-tolerant control-fidelity. Nat. Nanotech. 9, 981–985 (2014).
Kawakami, E. et al. Electrical control of a long-lived spin qubit in a Si/SiGe quantum dot. Nat. Nanotech. 9, 666–670 (2014).
Yoneda, J. et al. Fast electrical control of single electron spins in quantum dots with vanishing influence from nuclear spins. Phys. Rev. Lett. 113, 267601–267605 (2014).
Veldhorst, M. et al. A two-qubit logic gate in silicon. Nature 526, 410–414 (2015).
Scarlino, P. et al. Second-harmonic coherent driving of a spin qubit in a Si/SiGe quantum dot. Phys. Rev. Lett. 115, 106802 (2015).
House, M. G. et al. High-sensitivity charge detection with a single-lead quantum dot for scalable quantum computation. Phys. Rev. Appl. 6, 044016–044016 (2016).
Takeda, K. et al. A fault-tolerant addressable spin qubit in a natural silicon quantum dot. Sci. Adv. 2, 1600694 (2016).
Levy, J. Universal quantum computation with spin-1/2 pairs and Heisenberg exchange. Phys. Rev. Lett. 89, 147902 (2002).
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Foletti, S., Bluhm, H., Mahalu, D., Umansky, V. & Yacoby, A. Universal quantum control of two-electron spin quantum bits using dynamic nuclear polarization. Nat. Phys. 5, 903–908 (2009).
Petersson, K. D., Petta, J. R., Lu, H. & Gossard, A. C. Quantum coherence in a one-electron semiconductor charge qubit. Phys. Rev. Lett. 105, 246804 (2010).
Maune, B. M. et al. Coherent singlet-triplet oscillations in a silicon-based double quantum dot. Nature 481, 344–347 (2012).
Wang, K., Payette, C., Dovzhenko, Y., Deelman, P. W. & Petta, J. R. Charge relaxation in a single-electron Si/SiGe double quantum dot. Phys. Rev. Lett. 111, 046801 (2013).
Shi, Z. et al. Coherent quantum oscillations and echo measurements of a Si charge qubit. Phys. Rev. B 88, 075416 (2013).
Wu, X. et al. Two-axis control of singlet-triplet qubit with an integrated micromagnet. Proc. Nat. Acad. Sci. USA 111, 11938 (2014).
Harvey-Collard, P. et al. Nuclear-driven electron spin rotations in a single donor coupled to a silicon quantum dot. Preprint at https: //arxiv.org/pdf/1512.01606v1.pdf (2015).
DiVincenzo, D. P., Bacon, D., Kempe, J., Burkard, G. & Whaley, K. B. Universal quantum computation with the exchange interaction. Nature 408, 339 (2000).
Laird, E. A. et al. Coherent spin manipulation in an exchange-only qubit. Phys. Rev. B 82, 075403 (2010).
Gaudreau, L. et al. Coherent control of three-spin states in a triple quantum dot. Nat. Phys. 8, 54–58 (2011).
Medford, J. et al. Self-consistent measurement and state tomography of an exchange-only spin qubit. Nat. Nanotech. 8, 654–659 (2013).
Eng, K. et al. Isotopically enhanced triple-quantum-dot qubit. Sci. Adv. 1, 1500214 (2015).
Russ, M. & Burkard, G. Asymmetric resonant exchange qubit under the influence of electrical noise. Phys. Rev. B 91, 235411 (2015).
Dial, O. E. et al. Charge noise spectroscopy using coherent exchange oscillations in a singlet-triplet qubit. Phys. Rev. Lett. 110, 146804 (2013).
Vion, D. et al. Manipulating the quantum state of an electrical circuit. Science 296, 886–889 (2002).
Taylor, J. M., Srinivasa, V. & Medford, J. Electrically protected resonant exchange qubits in triple quantum dots. Phys. Rev. Lett. 111, 050502 (2013).
Medford, J. et al. Quantum-dot-based resonant exchange qubit. Phys. Rev. Lett. 111, 050501 (2013).
Kim, D. et al. Microwave-driven coherent operations of a semiconductor quantum dot charge qubit. Nat. Nano 10, 243–247 (2015).
Fei, J. et al. Characterizing gate operations near the sweet spot of an exchange-only qubit. Phys. Rev. B 91, 205434 (2015).
Reed, M. et al. Reduced sensitivity to charge noise in semiconductor spin qubits via symmetric operation. Phys. Rev. Lett. 116, 110402 (2016).
Martins, F. et al. Noise suppression using symmetric exchange gates in spin qubits. Phys. Rev. Lett. 116, 116801 (2016).
Shim, Y.-P. & Tahan, C. Charge-noise-insensitive gate operations for always-on, exchange-only qubits. Phys. Rev. B 93, 121410 (2016).
Nichol, J. M. et al. High-fidelity entangling gate for double-quantum-dot spin qubits. npj Quant. Inform. 3, 1–4 (2017).
Shi, Z. et al. Fast hybrid silicon double-quantum-dot qubit. Phys. Rev. Lett. 108, 140503 (2012).
Koh, T. S., Coppersmith, S. N. & Friesen, M. High-fidelity gates in quantum dot spin qubits. Proc. Nat. Acad. Sci. USA 110, 19695–19700 (2013).
Kim, D. et al. Quantum control and process tomography of a semiconductor quantum dot hybrid qubit. Nature 511, 70–74 (2014).
Ferraro, E., De Michielis, M., Mazzeo, G., Fanciulli, M. & Prati, E. Effective hamiltonian for the hybrid double quantum dot qubit. Quant. Inform. Process 13, 1155–1173 (2014).
Mehl, S. Quantum computation with three-electron double quantum dots at an optimal operation point. Preprint at https://arxiv.org/pdf/1507.03425v1.pdf. (2015).
De Michielis, M., Ferraro, E., Fanciulli, M. & Prati, E. Universal set of quantum gates for double-dot exchange-only spin qubits with intradot coupling. J. Phys. A Math Theor. 48, 065304 (2015).
Cao, G. et al. Tunable hybrid qubit in a GaAs double quantum dot. Phys. Rev. Lett. 116, 086801 (2016).
Wong, C. H. High-fidelity ac gate operations of a three-electron double quantum dot qubit. Phys. Rev. B 93, 035409 (2016).
Chen, B.-B. et al. Spin blockade and coherent dynamics of high-spin states in a three-electron double quantum dot. Phys. Rev. B 95, 035408 (2017).
Kim, D. et al. High-fidelity resonant gating of a silicon-based quantum dot hybrid qubit. npj Quant. Inform. 1, 15004 (2015).
Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012).
Ithier, G. et al. Decoherence in a superconducting quantum bit circuit. Phys. Rev. B 72, 134519 (2005).
Yan, F. et al. Rotating-frame relaxation as a noise spectrum analyser of a superconducting qubit undergoing driven evolution. Nat. Commun. 4, 2337 (2013).
Jing, J., Huang, P. & Hu, X. Decoherence of an electrically driven spin qubit. Phys. Rev. A 90, 022118 (2014).
Shi, Z. et al. Tunable singlet-triplet splitting in a few-electron Si/SiGe quantum dot. Appl. Phys. Lett. 99, 233108 (2011).
Acknowledgements
This work was supported in part by ARO (W911NF-17-1-0274, W911NF-12-0607, W911NF-08-1-0482), NSF (DMR-1206915, PHY-1104660, DGE-1256259), and the Vannevar Bush Faculty Fellowship program sponsored by the Basic Research Office of the Assistant Secretary of Defense for Research and Engineering and funded by the Office of Naval Research through grant N00014-15-1-0029. Development and maintenance of the growth facilities used for fabricating samples is supported by DOE (DE-FG02-03ER46028). We acknowledge the use of facilities supported by NSF through the UW-Madison MRSEC (DMR-1121288). The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office (ARO), or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein.
Author information
Authors and Affiliations
Contributions
B.T. performed electrical measurements with L.W.S. and J.C., developed measurement techniques with D.K. and R.H.F., and analyzed the data with Y.Y., M.A.E., M.F., and S.N.C. D.W.R. developed hardware and software for the measurements. C.B.S. fabricated the quantum dot device. D.E.S. and M.G.L. prepared the Si/SiGe heterostructure. All authors contributed to the preparation of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Thorgrimsson, B., Kim, D., Yang, YC. et al. Extending the coherence of a quantum dot hybrid qubit. npj Quantum Inf 3, 32 (2017). https://doi.org/10.1038/s41534-017-0034-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-017-0034-2
This article is cited by
-
Reducing charge noise in quantum dots by using thin silicon quantum wells
Nature Communications (2023)
-
Impact of charge noise on electron exchange interactions in semiconductors
npj Quantum Information (2022)
-
Review of performance metrics of spin qubits in gated semiconducting nanostructures
Nature Reviews Physics (2022)
-
Devitalizing noise-driven instability of entangling logic in silicon devices with bias controls
Scientific Reports (2022)
-
A silicon singlet–triplet qubit driven by spin-valley coupling
Nature Communications (2022)