Abstract
We propose a quantum generalisation of a classical neural network. The classical neurons are firstly rendered reversible by adding ancillary bits. Then they are generalised to being quantum reversible, i.e., unitary (the classical networks we generalise are called feedforward, and have step-function activation functions). The quantum network can be trained efficiently using gradient descent on a cost function to perform quantum generalisations of classical tasks. We demonstrate numerically that it can: (i) compress quantum states onto a minimal number of qubits, creating a quantum autoencoder, and (ii) discover quantum communication protocols such as teleportation. Our general recipe is theoretical and implementation-independent. The quantum neuron module can naturally be implemented photonically.
Similar content being viewed by others
Introduction
Artificial neural networks mimic biological neural networks to perform information processing tasks. They are highly versatile, applying to vehicle control, trajectory prediction, game-playing, decision making, pattern recognition (such as facial recognition, spam filters), financial time series prediction, automated trading systems, mimicking unpredictable processes, and data mining.1, 2 The networks can be trained to perform tasks without the programmer necessarily detailing how to do it. Novel techniques for training networks of many layers (deep networks) are credited with giving impetus to the neural networks approach.3
The field of quantum machine learning is rapidly developing though the focus has arguably not been in the connection to neural networks. Quantum machine learning, see e.g. refs. 4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19 employs quantum information processing (QIP).20 QIP uses quantum superpositions of states with the aim of faster processing of classical data as well as tractable simulation of quantum systems. In a superposition each bit string is associated with two numbers: the probability of the string and the phase,21 respectively. The phase impacts the future probabilities via a time evolution law. There are certain promising results that concern quantum versions of recurrent neural networks, wherein neurons talk to each other in all directions rather than feeding signals forward to the next layer, e.g. with the purpose of implementing quantum simulated annealing.10, 16, 22, 23 In ref. 24 several papers proposing quantum neural network designs are discussed and critically reviewed. A key challenge to overcome is the clash between the nonlinear, dissipative dynamics of neural network computing and the linear, reversible dynamics of quantum computing.24 A key reason for wanting well-functioning quantum neural networks is that these could do for quantum inputs what classical networks can do for classical inputs, e.g., compressing data encoded in quantum superpositions to a minimal number of qubits.
We here accordingly focus on creating quantum generalisations of classical neural networks, which can take quantum inputs and process them coherently. Our networks contribute to a research direction known as quantum learning,25,26,27,28,29 which concerns learning and optimising with truly quantum objects. The networks provide a route to harnessing the powerful neural network paradigm for this purpose. Moreover they are strict generalisations of the classical networks, providing a clear framework for comparing the power of quantum and classical neural networks.
The networks generalise classical neural networks to the quantum case in a similar sense to how quantum computing generalises classical computing. We start with a common classical neural network family: feedforward perceptron networks. We make the individual neurons reversible and then naturally generalise them to being quantum reversible (unitary). This resolves the classical-quantum clash mentioned above from ref. 24. An efficient training method is identified: global gradient descent for a quantum generalisation of the cost function, a function evaluating how close the outputs are to the desired outputs. To illustrate the ability of the quantum network we apply it to (i) compressing information encoded in superpositions onto fewer qubits (an autoencoder) and (ii) re-discovering the quantum teleportation protocol—this illustrates that the network can work out QIP protocols given only the task. To make the connection to physics clear we describe how to simulate and train the network with quantum photonics.
We proceed as follows. Firstly, we describe the recipe for generalising the classical neural network. Then it is demonstrated how the network can be applied to the tasks mentioned above, followed by a discussion of the results. Finally, we present a design of a quantum photonic realisation of a neural module.
Results
Classical neural networks are composed of elementary units called neurons. We begin with describing these, before detailing how to generalise them to quantum neurons.
Quantum neural networks
The neuron
A classical neuron is depicted at the top of Fig. 1. In this case, it has two inputs (though there could be more). There is one output, which depends on the inputs (bits in our case) and a set of weights (real numbers): if the weighted sum of inputs is above a set threshold, the output is 1, else it is 0.
Diagram summarising our method of generalising the classical irreversible neuron with Heaviside activation function, first to a reversible neuron represented by a permutation matrix (P), and finally to a quantum reversible computation, represented by a unitary operator (U). The top neuron is a classical neuron taking two inputs in1 and in2 and giving a corresponding output out.1 \(a_j^{(l)}\) labels the output of the j-th neuron in the l-th layer of the network
We will use the following standard general notation. The j-th neuron in the l-th layer of a network takes a number of inputs, \(w_{jk}^{(l)}\), and an output, \(a_k^{(l - 1)}\) where k labels the input. The inputs are each multiplied by a corresponding weight, \(w_{jk}^{(l)}\), and an output, \(a_j^{(l)}\), is fired as a function of the weighted input \(z_j^{(l)} = \mathop {\sum}\nolimits_{k = 1}^n {w_{jk}^{(l)}a_k^{(l - 1)}}\), where n is the number of inputs to the neuron (top of Fig. 1). The function relating the output to the weighted input is called the activation function. This is normally taken to be a non-linear function \(f\left( {\mathop {\sum}\nolimits_i {\left( {{r_i}{a_i}} \right)} } \right) \ne \mathop {\sum}\nolimits_i {{r_i}f\left( {{a_i}} \right)}\) for inputs a i and real numbers r i ).1 Commonly it is the Heaviside step function or a sigmoid.1 For example, the neuron in the top of Fig. 1 with a Heaviside activation function gives an output of the form:
This paper aims to generalise the classical neuron to a quantum mechanical one. In the absence of measurement, quantum mechanical processes are required to be reversible, and more specifically, unitary, in a closed quantum system.20, 30 This suggests the following procedure for generalising the neuron first to a reversible gate and finally to a unitary gate:
Irreversible → reversible: For an n-input classical neuron having (in1, in2, ..., in n ) → out, create a classical reversible gate taking (in1, in2, ..., in n , 0) → (in1, in2, ..., in n , out). Such an operation can always be represented by a permutation matrix.31 This is a clean way of rendering the classical neuron reversible. The extra ‘dummy’ input bit is used to make it reversible30; in particular, some of the ‘2 bits in −1 bit out’ functions the neuron can implement require 3 bits to be made reversible in this manner.
Reversible → unitary: Generalise the classical reversible gate to a quantum unitary taking input \(\left( {{{\left| {{\psi _{{\rm{in}}}}} \right\rangle }_{1,2,...,n}}\left| 0 \right\rangle } \right) \to {\left| {{\psi _{{\rm{out}}}}} \right\rangle _{1,2,...,n,{\rm{out}}}}\), such that the final output qubit is the output of interest. This is the natural way of making a permutation matrix unitary.
If the input is a mixture of states in the computational basis and the unitary a permutation matrix,32 the output qubit will be a mixture of \(\left| 0 \right\rangle\) or \(\left| 1 \right\rangle\): this we call the classical special case. This way the quantum neuron can simulate any classical neuron as defined above. The generalisation recipe summarised in Fig. 1 also illustrates how any irreversible classical computation can be recovered as a special case from reversible classical computation (by ignoring the dummy and copied bits), which in turn can be recovered as a special case from quantum computation.
The network
In order to form a neural network, classical neurons are connected together in various configurations. Here, we consider feedforward classical networks, where neurons are arranged in layers and each neuron in the l-th layer is connected to every neuron in the (l − 1)-th and (l + 1)-th layers, but with no connections within the same layer. For an example of such a classical network, see Fig. 2a. Note that in this case the same output of a single neuron is sent to all the neurons in the next layer.1, 2
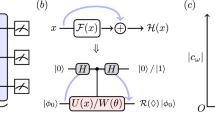
Neural network implementations of a a classical autoencoder and b a quantum autoencoder, respectively. The blue boxes represent the data compression devices after the training procedures. a A classical autoencoder taking two inputs \({\rm{i}}{{\rm{n}}_1} = a_1^{(0)}\) and \({\rm{i}}{{\rm{n}}_2} = a_2^{(0)}\) and compressing them to one hidden layer output \(a_1^{(l)}\). The final output layer is used in training and is trained to reconstruct the inputs. The notation here follows ref. 1. b A quantum autoencoder that can accommodate two input qubits that are entangled. c A plot of the quantum autoencoder cost function w.r.t. the number of steps used in the training procedure. In this example the input state is picked uniformly at random from \(\left( {1{\rm{/}}\sqrt 2 } \right)\left\{ {\left| {00} \right\rangle + \left| {11} \right\rangle ,\left| {00} \right\rangle - \left| {11} \right\rangle } \right\}\). The cost function can be seen to converge to zero, showing that the network has learned to compress the input state onto one qubit and then later recreate the input state. The non-monotonic decrease is to be expected as we are varying the input states. Qualitatively identical graphs of the cost function converging to 0 were also obtained for other examples of 2 orthogonal input states, including for the case of 3 input qubits and 1 bottleneck qubit
To make the copying reversible, in line with our approach of firstly making the classical neural network reversible, we propose the recipe:
Irreversible → reversible: For a classical irreversible copying operation of a bit b → (b, b), create a classical reversible gate, which can be represented by a permutation matrix,30 taking (b, 0) → (b, b).
In the quantum case the no-cloning theorem shows one cannot do this in the most naive way.20 For a 2-qubit case, one can use a CNOT for example to copy in the classical computational basis30: \(\left| b \right\rangle \left| 0 \right\rangle \to \left| b \right\rangle \left| b \right\rangle\), if \(\left| b \right\rangle \in \left\{ {\left| 0 \right\rangle ,\left| 1 \right\rangle } \right\}\). Thus one may consider replacing the copying with a CNOT. However when investigating applications of the network we realised that there are scenarios (the autoencoder in particular) where entanglement between different neurons is needed to perform the task. We have therefore chosen the following definition:
Reversible → unitary: The classical CNOT is generalised to a general 2-qubit ‘fan-out’ unitary U F , with one dummy input set to \(\left| 0 \right\rangle\), such that \(\left| b \right\rangle \left| 0 \right\rangle \to {U_F}\left| b \right\rangle \left| 0 \right\rangle\). As this unitary does not in general copy quantum states that are non-orthogonal we call it a ‘fan-out’ operation rather than a copying operation, as it distributes information about the input state into several output qubits. Note that a quantum network would be trained to choose the unitary in question.
Efficient training with gradient descent
A classical neural network is trained to perform particular tasks. This is done by randomly initialising the weights and then propagating inputs through the network many times, altering the weights after each propagation in such a way as to make the network output closer to the desired output. A cost function, C, relating the network output to the desired output is defined by
where \({\vec y^{(L)}}\) is a vector of the desired outputs from each of the final layer l = L neurons and \({\vec a^{(L)}}\) is the vector of actual outputs, which depends on the network weights, and \(\left| {\left( . \right)} \right|\) is the l 2-norm. The cost function is minimised to zero when the weights propagate the input in such a way that the network output vector equals the desired output vector.
Since the weights are continuous variables, the numerical partial derivatives of the cost function w.r.t. each weight can be found by approximating \(\frac{{\partial C}}{{\partial w}} \approx \frac{{C(w + \epsilon ) - C(w)}}{\epsilon }\). After each propagation, these partial derivatives are computed and the weights are altered in the direction of greatest decrease of the cost function. Specifically, each weight \(w_{jk}^{(l)}\) is increased by \({\rm{\delta }}w_{jk}^{(l)}\), with
where η is an adjustable non-negative parameter. This training procedure is known as gradient descent.1
Note that gradient descent normally also requires a continuous and differentiable activation function, to allow small changes in the weights to relate to small changes in the cost. For this reason, the Heaviside activation function has traditionally been replaced by a sigmoid function.1, 2 Nevertheless, gradient descent has also been achieved using Heaviside activation functions, by taking the weights as Gaussian variables and taking partial derivatives w.r.t. the means and standard deviations of the appropriate Gaussian distributions.33, 34
In the reversible generalisation, where each neuron is replaced by a permutation matrix, we find that the output is no longer a function of the inputs and continuous weights, but rather of the inputs and a discrete set of permutation matrices. However, in the generalisation to unitaries, for a gate with n inputs and outputs, there exist an infinite number of unitaries, in contrast with the discrete set of permutation matrices. This means that the unitaries can be parametrised by continuous variables, which once again allows the application of gradient descent.
Given that any unitary matrix U can be expressed as U = e iH, where H is a Hermitian matrix,20 and that such matrices can be written as linear combinations of tensor products of the Pauli matrices and the identity, it follows that a general N-qubit unitary can be expressed as
where σ i are the Pauli matrices for i ∈ {1, 2, 3} and σ 0 is the 2 × 2 identity matrix. This parametrisation allows the use of the training rule of Eq. (3), but replacing the weight \(w_{jk}^{(l)}\) with a general parameter \({\alpha _{{j_1},...,{j_N}}}\) of the unitary U N :
A simpler and less general form of U N has been sufficient for the tasks discussed in this paper:
where \(\left\{ {\left| {{\tau _j}} \right\rangle } \right\}_{j = 1}^4 = \left\{ {V\left| {00} \right\rangle ,V\left| {01} \right\rangle ,V\left| {10} \right\rangle ,V\left| {11} \right\rangle } \right\}\). V is a general 2-qubit unitary of the form of Eq. (4). Each T j is similarly a general 1-qubit unitary and one can see, using the methods of35 on Eq. (4), that this can be expressed as a linear combination of the Pauli matrices, σ j :
where \(\Omega = \sqrt {\alpha _1^2 + \alpha _2^2 + \alpha _3^2}\).35 To extend this to higher dimensional unitaries, see e.g. ref. 36
The cost function we use for the quantum neural networks is, with experimental feasibility in mind, determined by the expectation values of local Pauli matrices (σ 1, σ 2, σ 3) on individual output qubits, j. It has the form
where f ij is a real non-negative number (in the examples to follow f ij ∈ {0, 1}). We note in the classical mode of operation, where the total density matrix state is diagonal in the computational basis, only σ 3 will have non-zero expectation, and the cost function becomes the same as in the classical case (Eq. (2)) up to a simple transformation.
It is important to note that the number of weights grow polynomially in the number of neurons. Each weight shift is determined by evaluating the cost function twice to get the RHS of Eq. (5). Thus the number of evaluations of the cost function for a given iteration of the gradient descent grows polynomially in the number of neurons. The training procedure is efficient in this sense. Here we do not attempt to provide a proof that the convergence to zero cost-function, where possible, will always take a number of iterations that grows polynomially in the number of neurons. Note also that the statements about the efficiency of the training procedure refer to the physical implementation with quantum technology: the simulation of quantum systems with a classical computer is, with the best known methods, in general inefficient.
Example: autoencoder for data compression
We now demonstrate applications of our quantum generalisation of neural networks described in the previous section. We begin with autoencoders. These compress an input signal from a given set of possible inputs onto a smaller number of bits, and are ‘work-horses’ of classical machine learning.2
Classical autoencoder
Autoencoders are commonly achieved by a feedforward neural network with a bottleneck in the form of a layer with fewer neurons than the input layer. The network is trained to recreate the signal at a later layer, which necessitates reversibly compressing it (as well as possible) to a bit size equal to the number of neurons in the bottleneck layer.2 The bottleneck layer size can be varied as part of the training to find the smallest compression size possible, which depends on the data set in question. After the training is complete, the post-bottleneck part of the network can be discarded and the compressed output taken directly from after the bottleneck.
In Fig. 2a a basic autoencoder designed to compress two bits into a single bit is shown. (Here the number of input bits, j max = 2.) The basic training procedure consists of creating a cost function:
with which the network is trained using the learning rule of Eq. (3). If the outputs are identical to the inputs (to within numerical precision), the network is fully trained. The final layer is then removed, revealing the second last layer, which should enclose the compressed data. The number of neurons in a given hidden layer for a classical neuron will not exceed j max. Once the network is trained, the removal of the post-bottleneck layer(s) will yield a last layer of fewer neurons, achieving dimensional reduction.2
Quantum autoencoder
We now generalise the classical autoencoder as shown in Fig. 2a to the quantum case. We generalise the neurons labelled 1, 2 and 3 in Fig. 2a into unitary matrices U 1, U 2 and U 3, respectively, with the addition of a ‘fan-out’ gate, U F , as motivated in the previous sections. The result is shown in Fig. 2b as a quantum circuit model. (We follow the classical convention that this neural network is drawn with the input neurons as well, but they are identity operators which let the inputs through regardless, and can be ignored in the simulation of the network.) The input state of interest in12 is on 2 qubits, each fed into a different neuron, generalising the classical autoencoder in Fig. 2a. From each of these neurons, one output qubit each is led into the bottleneck neuron U 1, followed by a fan-out of its output. We add as an extra desideratum that the compressed bit, the output of U 1, is diagonal in the computational basis. The final neurons have the task of recreating \(\left| {{\rm{i}}{{\rm{n}}_{{\rm{12}}}}} \right\rangle\) on the outputs labelled 6 and 8 respectively.
This means that a natural and simple cost function is
Training is then conducted via global gradient descent of the cost w.r.t. the \({\alpha _{{j_1},...,{j_N}}}\) parameters, as defined in Eq. (5). During the training the network was fed states from the given input set, picked independently and identically for each step (i.i.d). Standard speed-up techniques for learning were used, e.g., a momentum term.1, 2 In training with a variety of two possible orthogonal input states including superposition states, the cost function of the quantum autoencoder converged towards zero through global gradient descent in every case, starting with uniformly randomised weights, \({\alpha _{{j_1},...,{j_N}}} \in \left[ { - 1,1} \right]\). For two non-orthogonal inputs and a 1-qubit bottleneck the cost-function will not converge to zero as is to be expected, but the training rather results in an approximately compressing unitary. Figure 2c shows the network learning to compress in the case of two possible inputs: \(\left( {\left| {00} \right\rangle + \left| {11} \right\rangle } \right){\rm{/}}\sqrt 2\) and \(\left( {\left| {00} \right\rangle - \left| {11} \right\rangle } \right){\rm{/}}\sqrt 2\). One can force the compressed output to be diagonal in a particular basis by adding an extra term to the cost-function (e.g., desiring the expectation values of Pauli X and Y to be zero in the case of a single qubit will push the network to give an output diagonal in the Z-basis).
Example: neural network discovers teleportation protocol
With quantum neural networks already shown to be able to perform generalisations of classical tasks, we now consider the possibility of quantum networks discovering solutions to existing and potentially undiscovered quantum protocols. We propose a quantum neural network structure that can, on its own, work out the standard protocol for quantum teleportation.20
The design and training of this network is analogous to the autoencoder and the quantum circuit diagram is shown in Fig. 3a. The cost function used was:
A fully trained network can teleport the state \(\left| \psi \right\rangle\) (from Alice) to the output port of qubit 6 (to Bob). Once trained properly, \({\rho _{{\rm{ou}}{{\rm{t}}_{\rm{1}}}}}\) will no longer be \(\left| \psi \right\rangle \left\langle \psi \right|\), as the teleportation has ‘messed up’ Alice’s state.37
Diagram of the neural network (a) and plot of the convergence of the cost function (b) for the neural network discovery of the teleportation protocol. a A circuit diagram of a quantum neural network that can learn and carry out teleportation of the state \(\left| \psi \right\rangle\) from Alice to Bob using quantum entanglement. The standard teleportation protocol allows only classical communication of 2 bits20; this is enforced by only allowing two connections, which are dephased in the Z-basis (D). U 1,U 2 and U 3 are unitaries. The blue line is the boundary between Alice and Bob. b A plot of the teleportation cost function w.r.t. the number of steps used in the training procedure. The cost function can be seen to converge to zero. The non-monotonic decrease is to be expected as we are varying the input states. The network now teleports any qubit state: picking 1000 states at random from the Haar measure (uniform distribution over the Bloch sphere) gives a cost function distribution with mean 5.0371 × 10−4 and standard deviation 1.7802 × 10−4, which is effectively zero
In order to train the teleportation for any arbitrary state \(\left| \psi \right\rangle\) (and to avoid the network simply learning to copy \(\left| \psi \right\rangle\) from Alice to Bob), the training inputs are randomly picked from the axis intersection states on the surface of the Bloch sphere.20 Figure 3b shows the convergence of the cost function during training, simulated on a classical computer. As can be seen, the training was found to be successful, i.e., the cost function converged towards zero. This held for all tests with randomly initialised weights.
Discussion
Quantum vs. classical
Can these neural networks show some form of quantum supremacy? The comparison of classical and quantum neural networks is well-defined within our set-up, as the classical networks correspond to a particular parameter regime for the quantum networks. A key type of quantum supremacy is that the quantum network can take and process quantum inputs: it can for example process \(\left| + \right\rangle\) and \(\left| - \right\rangle\) differently. Thus, there are numerous quantum tasks it can do that the classical network cannot, including the two examples above. We anticipate that they will moreover, in some cases be able to process classical inputs faster, by turning them into superpositions—investigating this is a natural follow-on from this work.
We also mention that we term our above design a quantum neural network with classical learning parameters, as the parameters in the unitaries are classical. It seems plausible that allowing these parameters to be in superpositions, while experimentally more challenging, could give further advantages.
While adding the ancillary qubits ensures that the network is a strict generalisation of the classical network, it can of course be experimentally and numerically simpler to omit these. Then one would sacrifice performance in the classical mode of operation, and the network may not be as good as a classical network with the same number of neurons for all tasks.
Visualising the cost function landscape
To gain intuitive understanding, one can visualise the gradient descent in 3D by reducing the number of free parameters. We sampled the cost surface and gradient descent path of a one-input neuron (4 × 4 unitary matrix). With the second qubit expressed as the dummy-then-output qubit, the task for the neuron was \(\left| + \right\rangle \otimes \left| 0 \right\rangle \to \left| + \right\rangle \otimes \left| 0 \right\rangle\) and \(\left| - \right\rangle \otimes \left| 0 \right\rangle \to \left| - \right\rangle \otimes \left| 1 \right\rangle\). We optimised, similarly to Eq. (6), over unitaries of the form
where \(\left| \tau \right\rangle = {\rm{cos}}(\theta {\rm{/}}2)\left| 0 \right\rangle + {e^{i\phi }}{\rm{sin}}(\theta {\rm{/}}2)\left| 1 \right\rangle\) and \(\left| {{\tau ^ \bot }} \right\rangle = {\rm{sin}}(\theta {\rm{/}}2)\left| 0 \right\rangle <$> <$>- {e^{i\phi }}{\rm{cos}}(\theta {\rm{/}}2)\left| 1 \right\rangle\). We performed gradient descent along the variables θ and ϕ as shown by the red path in Fig. 4.
Scaling to bigger networks
The same scheme can be used to make quantum generalisations of networks whose generalised neurons have more inputs/outputs and connections. Figure 5 illustrates an M-qubit input quantum neuron with a subsequent N-qubit fan-out gate.
Diagram of the quantum generalisation of a classical neuron with M inputs and N outputs. The superscripts inside the square brackets of the unitaries represent the number of qubits that the respective unitaries act on. U [M+1] is the unitary that represents the quantum neuron with an M-qubit input and U [N] is the fan-out gate that fans out the output in the final port of U [M+1] in a particular basis
If one wishes the number of free parameters of a neuron to grow no more than polynomially in the number of inputs, one needs to restrict the unitary. It is natural to demand it to be a polynomial length circuit of some elementary universal gates, in particular if the input states are known to be generated by a polynomial length circuit of a given set of gates, it is natural to let the unitary be restricted to that set of gates.
The evaluation of the cost function can be kept to a sensible scaling if we restrict it to be a function of local observables on each qubit, in particular a function of the local Pauli expectation values, as was used in this paper, for which case a vector of 3n expectation values suffices for n qubits.
Methods
Quantum photonics neuron module
To investigate the physical viability of these quantum neural networks we consider quantum photonics. This is an attractive platform for QIP: it has room temperature operation, the possibility of robust miniaturisation through photonic integrated circuits; in general it harnesses the highly developed optical fibre-related technology for QIP purposes.38 Moreover optical implementations have been viewed as optimal for neural networks, in the classical case, due to the low design cost of adding multiple connections (as light passes through light without interacting).39 A final motivation for choosing this platform is that the tuning can be naturally implemented, as detailed below.
We design a neuron as a module that can then be connected to other neurons. This makes it concrete how experimentally complex the network would be to build and operate, including how it could be trained.
The design employs the Cerf–Adami–Kwiat (C–A–K) protocol,40 where a single photon with polarisation and multiple possible spatial modes encodes the quantum state; the scheme falls into the category of hyper-entangling schemes, which entangle different degrees of freedom. One qubit is the polarisation; digital encodings of the spatial mode labels give rise to the others. With four spatial modes this implements 3 qubits, with basis \(\left| {0{\rm{/}}1} \right\rangle \left| {H{\rm{/}}V} \right\rangle \left| {0{\rm{/}}1} \right\rangle\), where H/V are two different polarisation states, and the other bits label the four spatial modes. The first bit says whether it is in the top two or bottom two pairs of modes and the last bit whether it is the upper or lower one in one of those pairs. This scheme and related ones such as in refs. 41, 42 are experimentally viable, theoretically clean and can implement any unitary on a single photon spread out over spatial modes. In such a single photon scenario they do not scale well however. The number of spatial modes grows exponentially in the number of qubits. Thus for larger networks our design below would need to be modified to something less simple, e.g., accepting probabilistic gates in the spirit of the KLM scheme,43 or using measurement-based cluster state quantum computation approaches.38
Before describing the module we make the simplifying restriction that there is one input qubit to the neuron and one dummy input. We will ensure that the designated output qubit can be fed into another neuron, as in Fig. 6a.
Diagrams showing the structure of the proposed quantum optical neuron module: a the basic structure of inputs and outputs, b a more detailed circuit diagram, and c the structure of the experimental implementation. a Simplifying restriction: the first neuron takes one input and one dummy input and its designated output is fed into the next neuron. b A circuit diagram of the neural module. Following C–A–K there are 3 qubits, with basis \(\left| {0{\rm{/}}1} \right\rangle \left| {H{\rm{/}}V} \right\rangle \left| {0{\rm{/}}1} \right\rangle\), where H/V label different polarisation states, and the other bits label the four spatial modes. We define the input to the module to be carried by the middle (polarisation) qubit. The neuron U 1 has the form of Eq. (6), modifying the output conditional on the input state. The swaps ensure that the next neuron module U 2 also gets the input via the polarisation. c The optics circuit of the neuron module. There are four spatial modes labelled \(\left| {00} \right\rangle ,\left| {01} \right\rangle ,\left| {10} \right\rangle\) and \(\left| {11} \right\rangle\). Initially only \(\left| {00} \right\rangle\) and \(\left| {10} \right\rangle\) have non-zero amplitudes and the second spatial qubit is not manipulated. The polarisation of the single photon is also manipulated. The two beamsplitters in bold at points A and D are variable (and can be replaced by Mach–Zehnder interferometers with variable phase). B and E are variable phase shifters and C shows a variable polarisation shifter. G and F are the two spatial modes available before a splitting occurs at H via a polarising beamsplitter, where the (fixed) polarisation rotator implements SWAP1. The beamsplitters with extra inputs at I allow for an additional spatial qubit to be manipulated, with J, K and L representing the components required for a SWAP gate. Before entering the second unitary, the second level splitting modes are brought close
We propose to update the neural network by adjusting both variable polarisation rotators, and spatial phase shifters in a set of Mach–Zehnder interferometers as shown in Fig. 6c. In this we are able to change the outputs from each layer of the network. The spatial shift could be induced by varying the strain or temperature on the waveguides at given locations, to change their refractive indices and hence the relative phase; this may have additional difficulties in that silicon waveguides are birefringent.44 Alternatively we can tune both polarisation and spatial qubits via the electro–optic effect.
This circuit can be made more robust and miniaturised using silicon or silica optical waveguides.38 They have been extensively used to control spatial modes and recently also polarisation.45 Several labs can implement the phase shifting via heaters or the electro–optic effect. Conventionally phase shifters built upon the electro–optic effect are known to work in the megahertz region and have extremely low loss.38 For many applications this would be considered slow, but our tuning only requires (in the region of) a few thousand steps. Taking into account that each step requires approximately 1000 repetitions, around 300 for each of the three Pauli measurements, a learning task could be completed in the order of seconds. While it appears that this effect will be the limiting factor in terms of speed, photodetectors are able to reach reset times in the tens of nanoseconds, while the production of single photons through parametric down conversion has megahertz repetition rates.46
Data availability
This is a theoretical paper and there is no experimental data available beyond the numerical simulation data described in the paper.
References
Nielsen, M. A. Neural Networks and Deep Learning (Determination Press, 2015).
Azoff, E. M. Neural Network Time Series Forecasting of Financial Markets (Wiley, 1994).
LeCunn, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
Schuld, M., Sinayskiy, I. & Petruccione, F. An introduction to quantum machine learning. Contemp. Phys. 56, 172–185 (2014).
Biamonte, J. et al. Quantum Machine Learning. Preprint at https://arxiv.org/abs/1611.09347 (2016).
Lloyd, S., Mohseni, M. & Rebentrost, P. Quantum algorithms for supervised and unsupervised machine learning. Preprint at https://arxiv.org/abs/1307.0411 (2013).
Lloyd, S., Mohseni, M. & Rebentrost, P. Quantum principal component analysis. Nat Phys 10, 631–633 (2014).
Montanaro, A. Quantum pattern matching fast on average. Algorithmica 10, 16–39 (2017).
Aaronson, S. Read the fine print. Nat. Phys. 11, 291–293 (2015).
Garnerone, S., Zanardi, P. & Lidar, D. A. Adiabatic quantum algorithm for search engine ranking. Phys. Rev. Lett. 108, 230506 (2012).
Harrow, A. W., Hassidim, A. & Lloyd, S. Quantum algorithm for linear systems of equations. Phys. Rev. Lett. 103, 150502 (2009).
Lloyd, S., Garnerone, S. & Zanardi, P. Quantum algorithms for topological and geometric analysis of big data. Nat. Commun. 7, 10138 (2016).
Rebentrost, P., Mohseni, M. & Lloyd, S. Quantum support vector machine for big data classification. Phys. Rev. Lett. 113, 130503 (2014).
Wiebe, N., Braun, D. & Lloyd, S. Quantum algorithm for data fitting. Phys. Rev. Lett. 109, 050505 (2012).
Adcock, J. et al. Advances in quantum machine learning https://arxiv.org/abs/1512.02900 (2015).
Heim, B., Rønnow, T. F., Isakov, S. V. & Troyer, M. Quantum versus classical annealing of Ising spin glasses. Science 348, 215–217 (2015).
Gross, D., Liu, Y. K., Flammia, S. T., Becker, S. & Eisert, J. Quantum state tomography via compressed sensing. Phys. Rev. Lett. 105, 150401 (2010).
Dunjko, V., Taylor, J. M. & Briegel, H. J. Quantum-enhanced machine learning. Phys. Rev. Lett. 117, 130501 (2016).
Wittek, P. (ed.) Quantum Machine Learning (Academic, 2014).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge University Press, 2000).
Garner, A. J. P., Dahlsten, O. C. O., Nakata, Y., Murao, M. & Vedral, V. A framework for phase and interference in generalized probabilistic theories. New. J. Phys. 15, 093044 (2013).
Lechner, W., Hauke, P. & Zoller, P. A quantum annealing architecture with all-to-all connectivity from local interactions. Sci. Adv. 1, e1500838 (2015).
Wiebe, N., Kapoor, A. & Svore, K. M. Quantum deep learning. Preprint at https://arxiv.org/abs/1303.5904 (2015).
Schuld, M., Sinayskiy, I. & Petruccione, F. The quest for a quantum neural network. Quant. Inf. Process. 13, 25672586 (2014).
Bisio, A., Chiribella, G., D’Ariano, G. M., Facchini, S. & Perinotti, P. Optimal quantum learning of a unitary transformation. Phys. Rev. A 81, 032324 (2010).
Sasaki, M. & Carlini, A. Quantum learning and universal quantum matching machine. Phys. Rev. A 66, 022303 (2002).
Sentís, G., Guţă, M. & Adesso, G. Quantum learning of coherent states. EPJ Quant. Technol. 2, 17 (2015).
Banchi, L., Pancotti, N. & Bose, S. Quantum gate learning in qubit networks: Toffoli gate without time-dependent control. NPJ Quant. Inf. 2, 16019 (2016).
Palittapongarnpim, P., Wittek, P., Zahedinejad, E., Vedaie, S. & Sanders, B. C. Learning in quantum control: high-dimensional global optimization for noisy quantum dynamics. Neurocomputing (in press, available online) doi: 10.1016/j.neucom.2016.12.087 (2016).
Feynman, R. P. Quantum mechanical computers. Found. Phys. 16, 507531 (1986).
Muthukrishnan, A. Classical and Quantum Logic Gates: An Introduction to Quantum Computing. Rochester Center for Quantum Information (online seminar notes). Retrieved from http://www.optics.rochester.edu/~stroud/presentations/muthukrishnan991/LogicGates.pdf (1999).
Curtis, C. W. & Reiner, I. Representation Theory of Finite Groups and Associative Algebras (AMS Chelsea Publishing, 1962).
Bartlett, P. L. & Downs, T. Using random weights to train multilayer networks of hard-limiting units. IEEE Trans. Neural Netw. 3, 202–210 (1992).
Downs, T. & Gaynier, R. J. The use of random weights for the training of multilayer networks of neurons with heaviside characteristics. Math. Comput. Model. 22, 53–61 (1995).
Rowell, D. Computing the Matrix Exponential the Cayley-Hamilton Method. Department of Mechanical Engineering, MIT (online lecture notes). Retrieved from http://web.mit.edu/2.151/www/Handouts/CayleyHamilton.pdf (2004).
Hedemann, S. R. Hyperspherical parameterization of unitary matrices. Preprint at https://arxiv.org/abs/1303.5904 (2013).
Wilde, M. M. Quantum Information Theory (Cambridge University Press, 2013).
Rudolph, T. Why I am optimistic about the silicon-photonic route to quantum computing. Preprint at https://arxiv.org/abs/1607.08535 (2016).
Rojas, R. Neural Networks (Springer, 1996).
Cerf, N. J., Adami, C. & Kwiat, P. G. Optical simulation of quantum logic. Phys. Rev. A. 57, R1477–R1480 (1998).
Reck, M., Zeilinger, A., Bernstein, H. J. & Bertani, P. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 73, 58–61 (1994).
Clements, W. R., Humphreys, P. C., Metcalf, B. J., Kolthammer, W. S. & Walmsley, I. A. An optimal design for universal multiport interferometers. Preprint at https://arxiv.org/abs/1603.08788 (2016).
Knill, E., Laamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).
Humphreys, P. C. et al. Strain-optic active control for quantum integrated photonics. Opt. Express 22, 21719–21726 (2014).
Sansoni, L. et al. Polarization entangled state measurement on a chip. Phys. Rev. Lett. 105, 200503 (2010).
Bonneau, D. et al. Fast path and polarization manipulation of telecom wavelength single photons in lithium niobate waveguide devices. Phys. Rev. Lett. 108, 053601 (2012).
Acknowledgements
We acknowledge discussions with Stefanie Baerz, Abbas Edalat, William Clements, Alex Jones, Mio Murao, Maria Schuld, Vlatko Vedral, and Alejandro Valido, as well as discussions and detailed comments from Doug Plato, Mihai Vidrighin and Peter Wittek. We are grateful for funding from the the EU Collaborative Project TherMiQ (Grant Agreement 618074), the London Institute for Mathematical Sciences, the Royal Society, a Leverhulme Trust Research Grant (No. RPG-2014-055), and a programme grant from the UK EPSRC (EP/K034480/1). A related and independently derived study appeared on the pre-print arXiv server shortly following that of the present study: J. Romero, J. Olson, and A. Aspuru-Guzik, ″Quantum autoencoders for efficient compression of quantum data,″ arXiv:1612.02806 [quant-ph] (2016).
Author information
Authors and Affiliations
Contributions
All authors made substantial contributions and were involved in drafting and writing up the work, as well as in the final approval of the completed version.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wan, K.H., Dahlsten, O., Kristjánsson, H. et al. Quantum generalisation of feedforward neural networks. npj Quantum Inf 3, 36 (2017). https://doi.org/10.1038/s41534-017-0032-4
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-017-0032-4
This article is cited by
-
Information compression via hidden subgroup quantum autoencoders
npj Quantum Information (2024)
-
Quantum autoencoders using mixed reference states
npj Quantum Information (2024)
-
Discrete-time quantum walk-based optimization algorithm
Quantum Information Processing (2024)
-
Estimating quantum mutual information through a quantum neural network
Quantum Information Processing (2024)
-
Classification of data with a qudit, a geometric approach
Quantum Machine Intelligence (2024)