Abstract
Quantum key distribution provides an efficient means to exchange information in an unconditionally secure way. Historically, quantum key distribution protocols have been based on binary signal formats, such as two polarization states, and the transmitted information efficiency of the quantum key is intrinsically limited to 1 bit/photon. Here we propose and experimentally demonstrate, for the first time, a high-dimensional quantum key distribution protocol based on space division multiplexing in multicore fiber using silicon photonic integrated lightwave circuits. We successfully realized three mutually unbiased bases in a four-dimensional Hilbert space, and achieved low and stable quantum bit error rate well below both the coherent attack and individual attack limits. Compared to previous demonstrations, the use of a multicore fiber in our protocol provides a much more efficient way to create high-dimensional quantum states, and enables breaking the information efficiency limit of traditional quantum key distribution protocols. In addition, the silicon photonic circuits used in our work integrate variable optical attenuators, highly efficient multicore fiber couplers, and Mach-Zehnder interferometers, enabling manipulating high-dimensional quantum states in a compact and stable manner. Our demonstration paves the way to utilize state-of-the-art multicore fibers for noise tolerance high-dimensional quantum key distribution, and boost silicon photonics for high information efficiency quantum communications.
Similar content being viewed by others
Introduction
Quantum key distribution (QKD) is an attractive quantum technology that provides a means to securely share secret keys between two clients (Alice and Bob).1,2,3,4 Traditional QKD is based on binary signal formats, such as the BB84 protocol where the quantum information is encoded in the polarization domain.5 Four polarization states create a set of two mutually unbiased basis (MUBs) in a two-dimensional Hilbert space which are used for establishing quantum keys between two parties. In these binary QKD systems the information efficiency is limited to 1 bit/photon. Recently, tremendous efforts have been put into developing novel protocols to increase the information efficiency.6,7,8,9,10 High-dimensional QKD (HD-QKD) based on qudit encoding (unit of information in a N dimension space) is an efficient technique to achieve high information efficiency for QKD systems.11,12,13,14,15,16,17,18 Furthermore, HD-QKD protocols exhibit higher resilience to noise, allowing for lower signal-to-noise ratio (SNR) of the received signal,10 which in turn may be translated into longer transmission distances.19 One interesting way to achieve HD-QKD is to use space division multiplexing technology, where the spatial dimension is used to carry the quantum states. In this context, optical angular momentum (OAM) modes has been proposed for HD-QKD protocol, and demonstrated over a free-space link using discrete components. QKD systems will eventually be merged with optical fiber transmission, so as to combine the classical internet with a quantum internet.20,21,22,23 However, the transmission of OAM modes over long distance fiber links is very challenging due to inter-modal crosstalk. An alternative approach is to use separate cores in multicore fibers (MCFs), which have been widely studied for in ultra-high capacity fiber communication, owing to the large potential multiplicity of cores and the low crosstalk between cores.24, 25
On the other hand, photonic integration has played a critical role in recent quantum information revolution by integrating functionalites of traditional discrete bulky components into ultra-compact chips.26, 27 Photonic integrated circuits (PICs) provide excellent optical phase stability, making them particularly suitable for manipulating quantum states in compact chips with low energy consumption. Binary QKD systems have been demonstrated using integrated circuits.28, 29 Silicon photonics technology has been a powerful means to combine the assets of integrated photonics with complementary metal-oxide semiconductor technologies. In this paper, we demonstrate the first HD-QKD protocol based on MCFs using silicon PICs. We prove that manipulation of the high dimensional quantum states in MCFs is feasible. We successfully prepare three mutually unbiased bases with four dimensional quantum states (ququart) and send these through a seven-core fiber. High fidelity is obtained in tomography measurements. Stable and low quantum bit error rate (QBER), below threshold limits, is achieved for more than 10 min.
Results
Protocol definition
Most of the QKD protocols are based on the concept of MUBs. For instance the bases {B 0 = |Φ0,i i = 0, 1, …, N−1〉} and {B 1 = |Φ1, j j =0, 1, …, N−1〉} are orthogonal bases of a N-dimensional Hilbert space H N . These bases are defined as mutually unbiased if and only if
In other words in a set of MUBs {B 0, B 1, B 2,…, B k, B n} if we measure a state in B n basis, and this state was prepared in B k basis (with k ≠ j), all the outputs are equally probable. It has been proven that the maximum number of the MUBs in a Hilbert space of dimension N is N + 1, where N is a integer power of a prime number.30 In our analysis we consider the case of three MUBs reported in Eq. (2) for an Hilbert space of four dimension (N = 4). The main difference is related to the tolerable threshold of the QBER and the maximum achievable value of secret key rate. A more detailed discussion follows in next paragraph. The set of the three MUBs, used in the proposed HD-QKD system, can be defined as a linear combination of:
We can easily prove that the set M 0, M 1, M 2 satisfies the mutually unbiased assumption, |〈M 0|M 1〉|2 = |〈M 0|M 2〉|2 = |〈M 1|M 2〉|2 = 1/4. Physically, |A〉, |B〉, |C〉, and |D〉 represent the quantum states related to the four individual cores of a multi-core fiber, as shown in the inset of Fig. 1a. By tuning the Mach–Zehnder interferometers (MZIs), situated in the transmitter chip, Alice creates a quantum superposition between cores. In this way she prepares one of the states in the three MUBs. A random number generator is used for basis and states choice. Before the quantum measurement, Bob randomly choose one of the three MUBs tuning the corresponding MZI. In such a way, Bob creates interference between different cores and he correctly measures the quantum states sent by Alice. As in the BB84 protocol, after the measurements, a distillation process is required. In this procedure Alice and Bob discard all the data related to a different basis choice. At this point Alice and Bob share an identical quantum key, useful for encryption and decryption of the plain text.
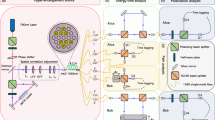
a Schematic of the HD-QKD based on MCF using silicon PIC for Alice and Bob. The inset shows the cross-section of the multi-core fiber, where four cores are used. b, d Shows the fabricated silicon PIC for Alice and Bob, respectively. c Presents the picture of the fabricated chips with a 1 euro coin, indicating the compact size of the silicon PICs
Secret key rate
One of the most important parameters in a communication system is the achievable rate. In particular, in a QKD system, the major criterion is represented by the secret key rate: number of bit/s or bit/pulse that Alice and Bob can establish as useful key. A general formula for the standard protocols can be written as:
where I AB represents the classical mutual information between Alice and Bob (I XY = H(X)−H(X|Y)), and the marginal entropy is defined as \(H\left( X \right) = \mathop {\sum}\nolimits_{x \in X} {p\left( x \right)\log p\left( x \right)} \). The right term of Eq. (3), min(I AE and I BE), is related to the quantum mutual information between Alice and Eve or Bob and Eve. In the following analysis we consider only the mutual information between Alice and Eve, but a more complete analysis can be done: in this way the secret key rate value is estimated with a lower bound. Furthermore, we work under the assumption of trusted-device scenario, in which Eve cannot modify the efficiency of Bobs detectors. In case of ququart QKD system the final secret key rate formula must be adapted. The mutual information between Alice and Bob is:
where N is the dimension of the Hilbert space and F = 1−D represents the fidelity of Bob. D is defined as the disturbance in the communication link. In order to extract a bound on the final secret key rate, we should define the best strategy for Eve. In the following analysis we consider two different kinds of Eve’s strategy. Individual attacks (IAs), where Eve monitors the ququarts independently from each other, and coherent attacks (CAs). CAs instead are less conservative on Eve’s strategy, in fact she can monitor more quantum states jointly. Intuitively CAs are less stringent than IAs.
Let’s start our analysis under the assumption of IAs where Eve uses a universal quantum cloning machine for qudits. By focusing on the two MUBs we retrieve the mutual information between Alice and Eve depending on the number of states N. In the case of ququarts encoding we define four different quantum states as |0〉, |1〉, |2〉, |3〉. The most general symmetric eavesdropping strategy for ququarts can be written as:
Under the assumption of symmetric attacks (Eve treats all the input states with the same strategy) and following the approach defined in10 the fidelity is: \(F = Tr\left( {\left| {{\psi _i}} \right\rangle \left\langle {{\psi _i}} \right|\rho _B^{out}} \right)\), where \(\rho _B^{out}\) is the reduced density operator of the state send to Bob. The maximum value of Eve’s mutual information is:
where the corresponding optimal fidelity for Eve is:
In other words, Eq. (5) represents the ability of Eve to distinguish between N non-orthogonal states. In the case of IAs, the term I AE can be easily formulated using F E instead of F in Eq. (4). By using Eq. (3) we can define an upper bound on the disturbance D introduce by Eve. We highlight that this limit increases with the Hilbert space dimension (see Supplementary Information Table S1). As evidence we report in Fig. 2 the theoretical mutual information in case of different Hilbert space dimension (from N = 2 to N = 8) and under the assumption of IAs and CAs. The intersections between the x-axis and the color filled/dashed lines represent the QBER thresholds. The higher N used in the system, the higher QBER threshold is allowed in the key generation. This means that higher dimension used in the QKD protocol leads to higher resilience to noise, allowing lower SNR for the received signal, which can be be translated into longer transmission distances. Following the same approach it is possible to defined a bound on Eve’s information related to the case of N + 1 MUBs.10
Let’s now consider a different strategy for Eve. As introduced above in case of CAs, Eve collects a finite number of ququart pulses, n < ∞. In this case under the assumption made in10 and 31, it is possible to define an upper bound on Eve’s information. The condition I AB ≥ log2(N)/2 is a sufficient case for guaranteeing the security under CAs, if the key dimension l is much greater than n.31 To be stressed that all the previous bounds are true under the assumption of infinity key length, but a different approach can be used for defining security under the case of finite-key scenario.
High-dimensional decoy state analysis
Most of the QKD systems encode the bit information using different degrees of freedom like polarization, phase and time, carried by a train of weak coherent pulses (WCPs). This idea, although unconditionally secure from a theoretical point of view, is subjected to some limitation on a practical realization. In fact, WCPs are obtained by attenuated laser with a mean photon number per pulse, μ, lower than one. However, the Poissonian distribution of the laser does not guarantee a non zero probability of multi-photon states. In that case, Eve can easily stop all the single photon pulses and split the multi-photon pulses (PNS—photon number splitting attack). In such a way Eve can measure the same information as Bob and after information reconciliation Alice, Eve, and Bob share the same key. In order to overcome this problem a simple strategy can be adopted-decoy state method. During the transmission process, Alice randomly changes the mean photon number per pulse.32 A intensity tunable laser or a real time variable optical attenuator (VOA1) can be used to create different levels of mean photon numbers. From a theoretical point of view this technique, used with infinite different number of decoy states, permits to avoid the PNS attack and to increment the key rate for further distances. However, as reported and proved in,32 two different decoy values (plus a vacuum measurement), are sufficient to establish a good compromise between rate and security. Our analysis follows the same procedure as introduced in,32 by using a practical implementation of decoy-state method with two weak decoy-states (with average photon flux ν < μ < 1) and a vacuum state. The final secret key rate can be written as:
where M is the number of bases used in the protocol (in our QKD experiment we used M = 2), D is the overall QBER as already defined is the disturbance in the communication link, e 1 is the error-rate of the single-photon state and f(D) is the efficiency of the error correction code (f(D) = 1.05). The Shannon entropy in case of high-dimensionality can be adapted as h HD(x) = −xlog2(x/(D−1))−(1−x)log2(1−x). The gain of the signal decoy state (i.e., the probability of obtaining a detection when the signal state μ is sent) is defined like \({Q_u} = {Y_0} + 1 - \exp \left( { - \eta \mu } \right)\), where Y 0 is the yield of the vacuum state (probability of the dark counts) and η is the overall efficiency (η = η Bob η AB η d ). The link transmittance parameter \({\eta _{{\rm{AB}}}} = {10^{ - {\alpha _f}L/10}}\), where α f [dB/km] is the fiber losses (average losses of a MCF about 0.2 dB/km) and L is the link distance in kilometer. e 0 is the QBER associated to the vacuum state (e 0 = (N−1)/N) corresponding to the probability of a random dark count in one of the N detectors. The values of Q u and D can be directly measured when Alice send the signal state to Bob. Q 0 can be directly estimated as Q 0 = e −μ Y 0. Note that Q 0 log2(N) indicates the gain relative to the dark counts, where Eve has no information. However, the gain and the error of the single photon state (Q 1 and e 1) must be approximated by the following formulas:
By using the decoy-state method is possible to avoid the main problem of the multi-photon state generated by the WCPs, used in the current experiment. This technique allows to establish an higher secret key rate for longer distances comparing the performance of the same protocol without decoy-state.
Experimental results
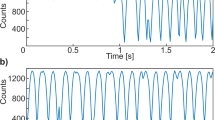
The experimental scheme of the proposed HD-QKD based on MCF using silicon PICs is shown in Fig. 1a (the detailed experimental setup is presented in Supplementary Information, Fig. S2). WCPs (10 ns wide, see also Supplementary Information) are injected into the transmitter chip (Alice, Fig. 1b). The silicon PIC for Alice is used to prepare the high-dimensional quantum states. The detailed schematic of the chip design is found in Fig. S1 in Supplementary Information. A VOA1 is used to thermally tune the pulse power to prepare the decoy states. Cascaded MZIs associated with the four thermally tunable phase shifters are used to prepare the quantum states in the three MUB sets with mean number of photons per pulse, μ, lower than 1. As an example, MZI 1 can be set so that light goes to the upper arm. At the same time, MZI 2 can be set as a 3 dB coupler. In this case, M 0 basis is prepared, and states |A〉+|B〉 and |A〉−|B〉 can be prepared by controlling the phase difference between the two output arms of MZI 2 to 0 or π, which is obtained through thermally controlling φ1 and φ2. Similarly, the other quantum states can be prepared by configuring the corresponding MZIs and phase shifters. The total insertion loss of Alice chip is 15 dB, which includes the coupling losses of the grating coupler with the input single mode fiber and the grating coupler based MCF fan-in/fan-out (FI/FO), and all the losses by other components on the chip. The quantum states are coupled to four cores of a multi-core fiber through an apodized grating coupler based MCF FI/FO.33, 34 After the MCF, the quantum states are coupled into Bobs chip (Fig. 1d) through the MCF FI/FO coupler, and randomly measured in one of the MUBs by configuring the corresponding phase shifters and MZIs. For instance, by configuring MZI 4 as a 3 dB coupler and setting MZI 6 and MZI 7 to directly go through, Bob is configured to receive the quantum states in base M 0. In order to measure correctly the quantum states, it is critical to obtain balanced losses for the four spatial channels, which is enabled by four VOAs introduced in BOB’s chip. The total insertion loss of Bob chip is 8 dB. We firstly measured the state tomography of the 3 MUBs. Figure. 3a, b show the theoretically and the experimental data acquired for the three MUBs. In this measurements, a weak coherent pulse with μ < 0.1 at 10 kHz was injected to Alice, and Bob acquires data for 30 s. The resulting fidelity of the corresponding matrices are 0.973 ± 0.006; 0.981 ± 0.0064;0.975 ± 0.006 with an average value of 0.976 ± 0.0109. Secondly, as a proof of concept, 3 m of MCF is used to prove a real-time QKD experiment with two MUBs with a 5 kHz repetition rate (currently limited by the on-chip thermal heaters, see supplementary information). Alice, by using a PRBS sequence (8 bit) generated by an FPGA, randomly chooses one of the four states in one of the two bases and set the corresponding heaters in order to create the required quantum state. Moreover, by randomly tuning the VOA1 we implement the decoy-state technique. In particular the decoy values are reported in Table 1, and represents the signal and decoy state parameters. By using the same procedure, Bob’s heaters are configured in one of the two MUBs. The choice of the basis is randomly decided by a PRBS sequence (7 bit), generated by the same FPGA. In the succeeding distillation process, counts measured in the wrong basis are discarded. In Fig. 4a we presents the QBER as a function of time and with an average value of μ = 0.276 ± 0.006 and ν = 0.153 ± 0.004 photon per pulse. Good and stable QBER performance with an average value of 13% is achieved for more than 10 min, which is well below both coherent attach limit and individual attach limit. In Fig. 4b we report the measured value of the decoy-state gain Q u . The average value of 43.8 × 10−2 ± 0.9 × 10−2 indicates the low losses present on Alice side and the stability of the MCFs grating coupler.
State tomography of the three MUBs: a, b, c represent the theoretical matrices of the different MUBs; d, e, f show the experimental measurements of the same basis. The state tomography were obtained with 30 s of integration time using a CW 1550 nm laser modulated with a 10 ns pulse at 10 kHz of repetition rate and a mean photon per pulse of 0.2 ± 0.006. By using the (classical) definition of fidelity (F(x, y) = ∑ i (p i q i )1/2, where x and y are random variables and q i and p i are the vector of probability distribution), we obtain an average fidelity of 0.977 ± 0.01
Experimental results. a QBER for 10 min of acquired data. The blue line represents the average QBER about 13%, which is well below the limits of both coherent attach and individual attacks. b Measured value of the signal-state gain Q u . The average value of 43.8 × 10−2 ± 0.9 × 10−2 indicates the low losses present on Alice side and the stability of the MCFs grating coupler
Discussion
The results reported in Fig. 4a, b show a stable and good demonstration of the HD-protocol. The average value of 13% of the QBER, obtained over 10 min of measurement, represents a good point for the key extraction. Moreover, thanks to the on-chip VOA1, we implemented a real-time decoy state technique. The experiment was performed using two of three MUBs prepared and showed in Fig. 3. We would like to highlight that the maximum number of MUBs in an Hilbert space of four-dimension is five. However, by using five MUBs we will compromise the final secret key rate. In fact, although the security increases using more bases, the secret key rate (Eq. (7)) scales dependently with the number of the bases. As reported in Table S1 of the Supplementary information, for a space of four-dimension and in the case of IAs, less than 6.5% of disturbance can be gained in the QBER threshold respect to a leak of a factor 6/10 on the key rate. The user must choose a trade off between security and rate, depending on the actual conditions of the channel. As a comparison, the case of multiple independent quantum keys (one per each core) in a MCF must be considered. The final composed rate would possibly be higher as compared to the HD one. However more strict requirements must be satisfied. As an example, the QBER of the classical BB84 protocol must be lower than 11% (Fig. 2), and after a long transmission distance the fluctuation of phase and polarization due to the perturbation in the fiber becomes relevant. Furthermore, if we introduce the concept of photon information efficiency 14 our HD-QKD allows a gain of 0.65 bit/detected photon (from 0.806 to 1.461). In Fig. 5 we show the simulation of the secret key rate as a function of the link distance in the case of HD-QKD with decoy state, BB84 QKD with decoy state and HD-QKD without decoy state. It follows that the best performance in terms of rate and achievable distance is reached with the case of HD-QKD and decoy-state. We also traced, as a comparison, the experimental data acquired by using the four VOAs integrated in Bob’s chip in order to simulate the link losses. It is well known in optical communication, that phase and polarization of coherent light is changed in a long optical fiber transmission. This effect is mainly due to the environment changes during transmission. In a MCF, each core acts independently from the other with very low crosstalk. However the phase and polarization of photons drift independently in each core. In our experiment this effect was mitigated by the short link distance, but in a real QKD system it must be considered. A close loop phase stabilization system can be implemented for a longer transmission distance, as reported in.35 In order to avoid influence by polarization drift, two different strategies can be used. Firstly, a two dimensional grating coupler associated with an MZI36 can be used to couple with the cores of the MCF, so that the polarization for each core can be tuned independently. Moreover, the polarization dependence can be solved by an on-chip polarization diversity circuit37, 38 for Bob’s chip. In addition, Bob is performing interference between cores for receiving quantum states in different basis, thus the time delay between each cores should be matched after long transmission. This problem can be solved by introducing a cascaded delay28 on Alice chip.
Comparison between experimental data and theoretical simulation. We overlapped the experimental data with the expected theoretical rate as a function of the link distance. The parameters used are: p dark = 2 × 10−8, η d = 0.1, α loss = 0.2 dB/km, u = 0.3, v = 0.15 for the decoy rates. Blue solid line is the rate without decoy state in case of WCP HD-QKD. Red and black solid lines are the simulated decoy state key rate for qubit or ququart encoding
The pulse rate used in this experiment of 10 kHz (for characterization) and 5 kHz (for the real-time QKD experiment) represents the main limitation for a long link deployment of this technology. The main limitation is the slow thermal dynamics of the heaters used in our experiment. In fact, despite a very high extinction ratio and good stability, the thermal tunable MZIs on Alice’s and Bob’s chips have low switching time of 66 and 27 μs for rise and fall time, as detailed in Supplementary Information. In order to overcome this problem, two main ideas can be implemented. Different kinds of material, such as graphene, that has ultra-high thermal conductivity enabling sub-microsecond tuning speed can be investigated.39, 40 Ultra-high speed p-i-n or p-n junction,41, 42 or silicon-lithium niobate hybrid integration43 can also be utilized for the phase shifters to further increase the repetition rate. The insertion loss of receiver chip is critical for final key rate. Our current device has an insertion loss of 8 dB, which attributes from the ~4 dB coupling loss of the grating couplers. More efficient grating couplers44 can be applied to improve the coupling loss. In addition, significant improvements will be achieved by introducing an aluminum (Al) mirror below the grating couplers to improve the coupling efficiency.45, 46
Once these technical problems is solved, the idea of space multiplexing HD-QKD can be considered feasible for an end-to-end high-rate transmission over long distance. Moreover, thanks to the advantages of state of the art silicon photonics, laser sources can be integrated on Alice chip in order to create a miniaturized quantum transmitter. Transistors, switches, digita-analog converters (DACs) and other electronic devices can also be integrated on a silicon substrate creating a stable and powerful chip. On the receiver side, fully demonstration of single photon detector on chip was already proved during the last years.47 The best solution for HD-QKD is based on single photon arrays. In this way the scalability of the process can be improved and higher capacity protocols can be implemented.
Materials and methods
Device fabrication
The silicon PICs was fabricated on the commercial SOI wafer with top silicon thickness of 250 nm and buried oxide layer (BOX) of 1 μm. A single step of standard SOI processing, including e-beam lithography and inductively coupled plasma etching was first used to fabricate the whole silicon PIC simultaneously. A 1500 nm thick layer of SiO2 was then deposited on top of the chip by plasma-enhanced chemical vapor deposition. The chip surface was then polished, and the top SiO2 was thinned down to 1 μm accordingly. The 1 μm SiO2 was used as an isolation layer between the silicon waveguide and the Ti heaters fabricated later to avoid potential optical losses. Afterwards, the 100 nm thick titanium heaters are formed by e-beam lithography followed by metal deposition and liftoff process. After that, the thick Au/Ti contact layer was fabricated by UV lithography followed by metal deposition and liftoff process. The chip was then cleaved and wire-bonded to a PCB board, and controlled by field programmable gate array (FPGA) for system experiment.
Electronic design
The chip-to-chip HD-QKD based on space-division multiplexing is feasible thank to a real time control of the different MZIs presented on the silicon chip. These MZIs, as reported above, are controlled by heaters: conductor material which change his property when a voltage is applied. In order to tune in real-time these MZIs, different electrical signals are required in the transmitter and receiver side. An Altera FPGA board emits eight digital parallel outputs every 0.2 ms, which are converted into analog voltages by eight DACs. Then, these analog signals are send to the transmitter and the receiver PCB board by flat cables.
References
Lo, H. K. & Chau, H. F. Unconditional security of quantum key distribution over arbitrarily long distances. Science 283, 2050–2056 (1999).
Hwang, W.-Y. Quantum key distribution with high loss: toward global secure communication. Phys. Rev. Lett. 91, 057901 (2003).
Lo, H. K., Curty, M. & Tamaki, K. Secure quantum key distribution. Nat. Photon. 8, 595 (2014).
Bacco, D. et al. Experimental quantum key distribution with finite-key analysis for noisy channels. Nat. Commun. 4, 2363 (2013).
Bennett, C. H. & Brassard, G. Quantum cryptography: public key distribution and coin tossing, in Proceeding of IEEE international conference on computer, systems & signal processing 175179, (1984).
Mirhosseini, M. et al. High-dimensional quantum cryptography with twisted light. N. J. Phys. 17, 033033 (2015).
Cotler, J. S. & Shor, P. W. A new relativistic orthogonal states quantum key distribution protocol. Quantum Inf. Comput. 14, 13–14 (2014).
Bacco, D. et al. Two-dimensional distributed-phase-reference protocol for quantum key distribution. Sci. Rep. 6, 36756 (2016).
Mafu, M. et al. Higher-dimensional orbital-angular-momentum-based quantum key distribution with mutually unbiased bases. Phys. Rev. A 88, 032305 (2013).
Cerf, N. J., Bourennane, M., Karlsson, A. & Gisin, N. Security of quantum key distribution using d-level system. Phys. Rev. Lett. 88, 127902 (2002).
Etcheverry, S. et al. Quantum key distribution session with 16-dimensional photonic states. Sci. Rep. 3, 2316 (2013).
Mower, J. et al. High-dimensional quantum key distribution using dispersive optics. Phys. Rev. A 87, 062322 (2013).
Bunandar, D. et al. Practical high-dimensional quantum key distribution with decoy states. Phys. Rev. A 91, 022336 (2015).
Zhong, T. et al. Photon-efficient quantum key distribution using timeenergy entanglement with high-dimensional encoding. N. J. Phys. 17, 022002 (2015).
Walborn, S. P., Lemelle, D. S., Almeida, M. P. & Ribeiro, P. H. S. Quantum key distribution with higher-order alphabets using spatially encoded qudits. Phys. Rev. Lett. 96, 090501 (2006).
Nunn, J. et al. Large-alphabet time-frequency entangled quantum key distribution by means of time-to-frequency conversion. Opt. Express 21, 15959–15973 (2013).
Zhang, Z. et al. Unconditional security of time-energy entanglement quantum key distribution using dual-basis interferometry. Phys. Rev. Lett. 112, 120506 (2014).
Lee, C. et al. Entanglement-based quantum communication secured by nonlocal dispersion cancellation. Phys. Rev. A 90, 062331 (2014).
Niu, M. Y., Xu, F., Shapiro, J. H. & Furrer, F. Finite-key analysis for time-energy high-dimensional quantum key distribution. Phys. Rev. A 94, 052323 (2016).
Gröblacher, S. et al. Experimental quantum cryptography with qutrits. N. J. Phys. 8, 75 (2006).
D’Ambrosio, V. et al. Complete experimental toolbox for alignment-free quantum communication. Nat. Commun. 3, 961 (2012).
Vallone, G. et al. Free-space quantum key distribution by rotation-invariant twisted photons. Phys. Rev. Lett. 113, 060503 (2014).
Paterson, C. et al. Atmospheric turbulence and orbital angular momentum of single photons for optical communication. Phys. Rev. Lett. 94, 153901 (2005).
Mizuno, T. et al. 32-core Dense SDM unidirectional transmission of PDM-16QAM signals over 1600 km using crosstalk-managed single-mode heterogeneous multicore transmission line. In Optical Fiber Communication Conference (OFC), postdeadline Papers Th5C.3, (2016).
Dynes, J. F. et al. Quantum key distribution over multicore fiber. Opt. Express 24, 8081–8087 (2016).
Matthews, J. C. F., Politi, A., Stefanov, A. & O’Brien, J. L. Manipulation of multiphoton entanglement in waveguide quantum circuits. Nat. Photon. 3, 346–350 (2009).
Politi, A., Cryan, M. J., Rarity, J. G., Yu, S. & OBrien, J. L. Silica-on-silicon waveguide quantum circuits. Science 320, 646–649 (2008).
Sibson, P. et al. Chip-based quantum key distribution. Nat. Commun. 8, 13984 (2017).
Ma, C. et al. Integrated silicon photonic transmitter for polarization-encoded QKD. Optica 3, 1274–1278 (2016).
Boykin, P. O., Sitharam, M., Tarifi, M. & Wocjan, P. Real mutually unbiased bases. arXiv:quant-ph/0502024.
Hall, M. J. W. Quantum information and correlation bounds. Phys. Rev. A 55, 100–112 (1997).
Lo, H.-K., Ma, X. & Chen, K. Decoy state quantum key distribution. Phys. Rev. Lett. 94, 230503 (2005).
Ding, Y., Ou, H. & Peucheret, C. Ultra-high-efficiency apodized grating coupler using fully etched photonic crystals. Opt. Lett. 38, 2732–2734 (2013).
Ding, Y. et al. On-chip grating coupler array on the SOI platform for fan-in/fan-out of MCFs with low insertion loss and crosstalk. Opt. Express 23, 3292–3298 (2015).
Caas, G. et al. High-dimensional decoy-state quantum key distribution over 0.3 km of multicore telecommunication optical fibers. arXiv:1610.01812 (2016).
Caspers, J. N., Wang, Y., Chrostowski, L., & Mojahedi, M. Active polarization independent coupling to silicon photonics circuit. In SPIE Photonics Europe, 91330G-91330G-11 (2014).
Bogaerts, W. et al. A polarization-diversity wavelength duplexer circuit in silicon-on-insulator photonic wires. Opt. Express 15, 1567–1578 (2007).
Van Laere, F. et al. Focusing polarization diversity grating couplers in silicon-on-insulator. J. Lightwave Technol. 27, 612–618 (2009).
Gan, S. et al. A highly efficient thermo-optic microring modulator assisted by graphene. Nanoscale 7, 20249–20255 (2015).
Yan, S. et al. Slow-light-enhanced energy efficiency for the graphene microheater on silicon photonic crystal waveguides. arXiv:1607.07571 (2016).
Png, C. E., Chan, S. P., Lim, S. T. & Reed, G. T. Optical phase modulators for MHz and GHz modulation in silicon-on-insulator (SOI). J. Lightwave Technol. 22, 1573–1582 (2004).
Liu, A. et al. High-speed optical modulation based on carrier depletion in a silicon waveguide. Opt. Express 15, 660–668 (2007).
Chen, L., Xu, Q., Wood, M. G. & Reano, R. M. Hybrid silicon and lithium niobate electro-optical ring modulator. Optica 1, 112–118 (2014).
Vermeulen, D. et al. High-efficiency fiber-to-chip grating couplers realized using an advanced CMOS-compatible silicon-on-insulator platform. Opt. Express 18, 18278–18283 (2010).
Ding, Y., Peucheret, C., Ou, H. & Yvind, K. Fully etched apodized grating coupler on the SOI platform with −0.58 dB coupling efficiency. Opt. Lett. 39, 5348–5350 (2014).
Ding, Y. et al. Reconfigurable SDM switching using novel silicon photonic integrated circuit. Sci. Rep. 6, 39058 (2016).
Tosi, A., Calandri, N., Sanzaro, M. & Acerbi, F. Low-noise, low jitter, high detection efficiency InGaAs/InP single-photon Avalanche diode. IEEE J. Sel. Top. Quantum Electron. 20, 3803406 (2014).
Acknowledgements
This work is supported by the Danish Council for Independent Research (DFF-1337-00152 and DFF-1335-00771), by the Center of Excellence, SPOC (Silicon Photonics for Optical Communications (ref DNRF123) and from the People Program (Marie Curie Actions) of the European Union’s Seventh Framework Program (FP7/2007-2013) under REA grant agreement n° 609405 (COFUNDPostdocDTU).
Author information
Authors and Affiliations
Contributions
Y. D., D. B., X. C., and X. Z. proposed the idea. Y. D. designed and fabricated the silicon PICs. K. D. designed the electrical controlling circuits. Y. D., D. B., and K. D. performed the system experiment. D. B. carried out the theoretical analysis on the proposed protocol. Y. D., D. B., K. R., and L. K. Oxenlwe discussed the results. All authors contributed to the writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ding, Y., Bacco, D., Dalgaard, K. et al. High-dimensional quantum key distribution based on multicore fiber using silicon photonic integrated circuits. npj Quantum Inf 3, 25 (2017). https://doi.org/10.1038/s41534-017-0026-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-017-0026-2
This article is cited by
-
Self-supervised dynamic learning for long-term high-fidelity image transmission through unstabilized diffusive media
Nature Communications (2024)
-
Ultrahigh-fidelity spatial mode quantum gates in high-dimensional space by diffractive deep neural networks
Light: Science & Applications (2024)
-
Practical high-dimensional quantum key distribution protocol over deployed multicore fiber
Nature Communications (2024)
-
High-dimensional single photon based quantum secure direct communication using time and phase mode degrees
Scientific Reports (2024)
-
Information processing at the speed of light
Frontiers of Optoelectronics (2024)