Abstract
We demonstrate a coherent spin shuttle through a GaAs/AlGaAs quadruple-quantum-dot array. Starting with two electrons in a spin-singlet state in the first dot, we shuttle one electron over to either the second, third, or fourth dot. We observe that the separated spin-singlet evolves periodically into the m = 0 spin-triplet and back before it dephases due to nuclear spin noise. We attribute the time evolution to differences in the local Zeeman splitting between the respective dots. With the help of numerical simulations, we analyze and discuss the visibility of the singlet-triplet oscillations and connect it to the requirements for coherent spin shuttling in terms of the inter-dot tunnel coupling strength and rise time of the pulses. The distribution of entangled spin pairs through tunnel coupled structures may be of great utility for connecting distant qubit registers on a chip.
Similar content being viewed by others
Introduction
Single electron spins in semiconductor quantum dots have been proposed as a candidate qubit platform that may allow scalable quantum information processing.1, 2 Recent progress in semiconductor quantum-dot structures have shown long single-spin coherence times and high-fidelity coherent operations.3,4,5,6,7 Furthermore, linear arrays have been successfully scaled to triple and quadruple dots,8,9,10,11,12 and 2 × 2 arrays have been demonstrated as well.13 However, there are practical limitations to the size of tunnel-coupled quantum dot arrays in one or two dimensions. Integrating larger numbers of qubits can be achieved by coherently connecting distant qubit registers on a chip.14,15,16,17 Such coherent links could also serve to connect different functions such as memory and processor units.2 As an alternative to coherent spin–spin coupling at a distance, the physical transfer of electrons across the chip while preserving the spin information can serve as an interface between separated quantum dot arrays.2, 18 This is similar in spirit to experiments with trapped ions that were shuttled around through segmented ion traps.19, 20 To our knowledge, there are no demonstrations of the transfer of single electron spins coherently through arrays of three or more coupled quantum dots. (A closely related work appeared subsequent to our submission. H. Flentje et al., Coherent long-distance displacement of individual electron spins. arXiv:1701.01279)
Various physical mechanisms have been proposed to controllably transfer single charges through confined structures, including Thouless pumps,21, 22 charge pumps 23, and surface acoustic waves,24 and several of these approaches have been experimentally demonstrated with quantum dot devices.12, 25, 26 Furthermore, charge transfer with preservation of spin projection was shown using surface acoustic waves27 and charge pumps.28 However, none of these approaches has proceeded to measure the preservation of spin coherence during the shuttling processes. The main obstacle towards spin coherent transfer is the short dephasing time due to nuclear spins in GaAs, the commonly used host material for shuttling experiments so far (\(T_2^*\) of 10–30 ns).29
In this Article we explore the coherent shuttling of single electron spins through a quadruple-quantum-dot array by applying gate-voltage pulses to push the electron through the array. Starting with two electrons in a spin-singlet state in a single dot at one extremity, we shuttle one of these two electrons to the second, third, and fourth dot. We probe the preservation of spin coherence by subsequently attempting to bring the two electrons back onto the first dot. Through the Pauli exclusion principle, this is allowed only if the spin singlet state is still preserved. Starting from an analysis of the spin-shuttle performance, we discuss two adiabaticity conditions of the transfer, one for coherent single-spin shuttling and one for distributing entangled states.
Results
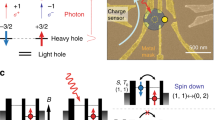
To study the preservation of spin coherence while shuttling electrons around, we initialize the two electrons in a spin-singlet state in the leftmost dot, then move one electron over to either the second, third, or fourth dot and back, and probe whether the spin-singlet phase is still preserved after shuttling. Spin-singlet initialization is done by waiting for thermal equilibration in the (2000) charge state (point I in Fig. 1b). Next, one of the electrons is shuttled to one of the other three dots by ramping the voltages on gates P1 and P4 from position I to position A, B, or C in Fig. 1b in 2.5 ns. The ramp is chosen slow enough such that the electron motion is adiabatic with respect to the inter-dot tunnel coupling to ensure that the electron moves to the neighboring dots in a well-controlled and reproducible manner, see Fig. 2a. At the same time, the transfer should not be too slow so that the transfer is non-adiabatic in the spin sector and furthermore can be completed well within the \(T_2^*\). Furthermore, by tuning the dot-reservoir couplings to be much smaller (~kHz) than the inter-dot tunnel couplings, the shuttling of an electron to any of the dots can be implemented in one step—as opposed to dot by dot—without a significant probability of losing the electron to the reservoirs when passing through the (1000) region, see Fig. 2b. After the forward shuttle, this electron is pulled back towards dot 1 for a spin measurement (point M in Fig. 1b). If the spin state remains a singlet, the two electrons can both reside in dot 1 and the charge sensor will indicate charge state (2000). If the spin-state has changed to a triplet, the second electron is stuck on dot 2 due to Pauli-spin-blockade30 and the charge sensor will record (1100). We calibrated the read-out fidelities to be over 95% for both the spin-triplet and spin-singlet (see Supplementary Information Section IV). Through this method of spin-to-charge conversion we can tell whether the phase between the two electron spins has changed during shuttling.
Device image and spin shuttling protocol. a Scanning electron microscope image of a sample nominally identical to the one used for the measurements. Dotted circles indicate the intended quantum dot positions and squares indicate Fermi reservoirs in the 2DEG, which are connected to ohmic contacts. The RF reflectance of SD1 and/or SD2 are monitored in order to determine the occupancies of the four dots in the linear array.(Reproduced from ref. 10, with the permission of AIP Publishing) b Charge stability diagram that includes the regions with two electrons involved in the shuttling sequence. Horizontal traces are averaged over 200 sweeps with a scan rate of 4.4 ms per sweep. The (1010) (or (1100)) region fading into the (1000) region occurs due to the slow unloading of the electron in dot 3 (or dot 2) relative to the scan rate. Labels indicate the number of electrons on each of the four dots. The dot array is initialized with two electrons on the leftmost dot, allowing them to relax to the spin-singlet ground state (point I). Then, a gate voltage pulse takes the system to point A, B, or C, resulting in the transfer of one of the two electrons to the second, third, or fourth dot, respectively. After the gate voltage pulse, the system returns to point (M), and the spin state is measured using Pauli spin blockade. We infer a spin-singlet (triplet) state when the signal of SD1 reads (2000) ((1100)) for an integration time of 5 μs. The data shown here was chosen since it clearly shows all the relevant charge transitions. The corresponding data with the settings used in Fig. 3 is shown in Supplementary Information Section II
Adiabaticity requirements for shuttling. a Schematic energy diagram for shuttling from (2000) (I) to (1100) a. The rise time of the applied gate voltage pulse is chosen such that the charge motion is adiabatic with respect to the inter-dot tunnel coupling, causing one of the electrons to move to dot 2, but non-adiabatic with respect to the spin Hamiltonian causing the spin singlet state to be preserved. As a consequence, the system is taken from S(2000) to \(\frac{{ \uparrow \downarrow - \downarrow \uparrow }}{{\sqrt 2 }}\)(1100) (orange dashed arrow). b A similar energy diagram when linearly moving between points I and C in Fig. 1b (Supplementary Information Section II). Lines are depicted for spin-less states. When inter-dot tunnel rates are tuned to be larger than the rate of change of the detuning (controlled by the ramp rate of V P1−V P4) and the dot-reservoir tunnel rates, the charge state adiabatically follows its original energy branch without crossing over to other branches and without the electron escaping to the reservoir (the horizontal dashed line indicates the Fermi-level). Furthermore, as in panel a, the detuning ramp rate must be fast enough such that the spin singlet is preserved during the charge transfer
The main experimental observations are as follows. When shuttling one of the electrons to dot 2 and varying the waiting time in that dot (point A in Fig. 1b), we observe that the singlet-return probability oscillates sinusoidally with a frequency of 103 ± 5 MHz (see Fig. 3a). When shuttling to dot 3, a similar oscillation is observed (see Fig. 3b), albeit at a frequency of 118 ± 7 MHz. For dot 4 we record an oscillation with a frequency of 185 ± 14 MHz (see Fig. 3c). The oscillations have a contrast of 0.63 ± 0.12, 0.62 ± 0.14, and 0.57 ± 0.15 and decay on a timescale of 14 ± 3, 13 ± 3, and 7 ± 2 ns, respectively.
Coherent shuttling and S-T 0 oscillations. a–c Measured spin-singlet probability as a function of the waiting time in the (1100), (1010), or (1001) charge state (error bars indicate 95% confidence intervals). This waiting time occurs in between separating the electrons and trying to bring them back together. The spin-singlet probability is fitted with a Gaussian damped cosine function with a constant phase shift. The fitted S-T 0 oscillation frequencies are: 103 ± 5, 118 ± 7, and 185 ± 14 MHz respectively. The fitted contrasts are 0.63 ± 0.12, 0.62 ± 0.14, and 0.57 ± 0.15. The damping is attributed to the random nuclear fields in the two dots and the phase shift accounts for the additional shuttle towards the measurement point. d Bloch sphere representation of a singlet-triplet qubit. For a spin singlet distributed over two separated dots, the exchange interaction J is small and the Zeeman energy difference between the dots, \(\Delta E_z^{i,j}\), dominates
Discussion
The observed oscillations can be interpreted in terms of qubit evolutions between the singlet state, S, and the m = 0 triplet state, T 0, around two orthogonal axes governed by the exchange term, \(J{\vec \sigma _i} \cdot {\vec \sigma _j}/4\), and a local difference in Zeeman energy, \(\Delta E_z^{i,j}\left( {\sigma _i^z - \sigma _j^z} \right)/2\), where \({\vec \sigma _i}\) is the Pauli matrix for the spin in dot i. These two axes are depicted in the Bloch sphere of Fig. 3d. The magnitude of J depends on the overlap of the two electron wavefunctions. Inside the (2000) region, J is of order 1 meV with S the ground state, allowing us to initialize in S. As we move from (2000) toward (1100), J gradually decreases up to the point where \(\Delta E_z^{i,j}\) dominates. For (1010) and (1001), J is negligibly small. A difference in Zeeman splittings could result from a difference in local magnetic fields.31, 32 In the present experiment, the local fields are identical but the g-factors are different between the dots.28 In this case, and as observed, \(\Delta E_z^{i,j}\) increases linearly with B ext. Then, starting with a (2000) singlet, separating the electrons across two dots kick-starts a coherent S-T 0 evolution around \(\Delta E_z^{i,j}\).32 Since \(\Delta E_z^{i,j}\) is different for different pairs of dots, the frequency of the S-T 0 oscillations is dependent on the location of the two electrons (see also ref. 33, where a three-electron state in a triple dot was adiabatically transferred from ↑1 S 23 to ↑2 S 13, where the subscripts refer to the dot number). The damping of the oscillation on a timescale of about 10 ns is due to the hyperfine interaction with the randomly oriented nuclear spins in the host material of the two dots.3
To test this interpretation of the measurements in Fig. 3 in terms of S-T 0 oscillations, we have measured the Zeeman energy in each dot using electric-dipole-spin-resonance (EDSR) measurements.34 For this aim we modified the gate voltage settings in order to implement single-spin read-out, using the single-spin CCD protocol of ref. 28. Chirped microwave signals were applied to gate P3 to adiabatically invert a spin from its initial state ↑ to ↓. The \(\Delta E_z^{i,j}\) extracted from the individual spin resonance frequencies for magnetic fields 2.7 to 4.7 T are depicted in Fig. 4a. Extrapolating to 2.3 Tesla using a fit through the data points, we observe that the sequence of the frequency differences corresponds to that obtained from the S-T 0 oscillations, but the absolute values differ. This could be due to the fact that the gate voltages used for the EDSR measurements were different from those used for the S-T 0 oscillations by 5–15 mV. In EDSR measurements on dots 1 and 4, we have found comparable changes in the spin splittings with similar gate voltage changes (Supplementary Information Section V). Within this offset, the three distinct oscillation frequencies in the data of Figs. 3a–c support the interpretation that one of the electrons was shuttled controllably from dot 1 to dots 2, 3, and 4, whilst preserving phase coherence.
Zeeman energy differences and simulated S-T 0 oscillation contrasts. a The Zeeman energy in each dot is determined using EDSR measurements for a range of magnetic field strengths28, 34 and is fitted to E z = |g 1 μ B B + g 3 μ B B 3|, resulting in \(g_1^{{\rm{dot1}}} = - 0.4332 \pm 0.0005\), \(g_3^{{\rm{dot1}}} = \left( {0.47 \pm 0.03} \right){10^{ - 3}}\)/T2, \(g_1^{{\rm{dot2}}} = - 0.4353 \pm 0.0004\), \(g_3^{{\rm{dot2}}} = \left( {0.46 \pm 0.04} \right){10^{ - 3}}\)/T2, \(g_1^{{\rm{dot3}}} = - 0.4361 \pm 0.0006\), \(g_3^{{\rm{dot3}}} = \left( {0.47 \pm 0.04} \right){10^{ - 3}}\)/T2, \(g_1^{{\rm{dot4}}} = - 0.4372 \pm 0.0004\), \(g_3^{{\rm{dot4}}} = \left( {0.47 \pm 0.03} \right){10^{ - 3}}\)/T2. The solid data points represent the differences in Zeeman energy between dot n (n = 2,3,4) and dot 1 as a function of magnetic field, extracted from the EDSR measurements (error bars account for the expected fluctuations of ± 15 MHz from the quasi-static nuclear field and ± 5 MHz from the frequency resolution of the measurement, for each of the two resonance measurements used in the frequency difference calculation). Solid curves represent the difference between the fit of dot n and dot 1. Open circles show the Zeeman energy differences extracted from Figs. 3a–c (error bars indicate the fitting uncertainty). b The contrast of the simulated coherent oscillation when pulsing from point I to point A in Fig. 1b. The simulation assumes a linear ramp from start to end over 2.50 ns. c Similar to b but pulsing to point B and varying the tunnel coupling between dots 2 and 3. d Similar to b but pulsing to point C and varying the tunnel coupling between dots 3 and 4. The tunnel couplings were set to t 12 = 1.2, t 23 = 2.6, and t 34 = 4.3 GHz if not varied. These values correspond to the peak positions in the tunnel coupling dependencies. Note that the maximum in d is lower and occurs for a higher tunnel coupling than that in c because the ramp rate is higher for d (same ramp duration but higher pulse amplitude)
The oscillation contrast provides quantitative information on the spin-singlet component in the two-electron state after shuttling. In the experiment, the measured contrasts are well below unity. To investigate whether the reduced contrasts are due to dephasing upon shuttling or have a different origin, we numerically simulate the shuttling process. The simulations compute the spin evolution taking into account the finite rise time of the gate voltage pulse, the inter-dot tunnel couplings, the Zeeman energy differences, and inelastic relaxation. Starting from a S(2000) state, we calculated the population of the various states after pulsing the dot levels in a way that resembles the shuttle experiments (see Supplementary Information Section VI for the details of the simulation). For simplicity, we initially leave out inelastic relaxation as well as the return pulse used for spin read-out. Figs. 4b–d show the numerically computed contrast for the S-T 0 oscillations after shuttling to the (1100), (1010), and (1001) charge regions, as a function of the inter-dot tunnel coupling. For the inter-dot transition from (2000) to (1100) the contrast is peaked around 1.2 GHz (see Fig. 4b). Starting with small tunnel coupling, increasing the tunnel coupling results in an increasing probability that the charge is (adiabatically) transferred. Obviously, if both charges stay in the first dot, there will be no S-T 0 oscillations. If the charge initially stays behind in the first dot and then tunnels inelastically to a next dot at a (random) later time, the spin phase will be out of sync with the case of a adiabatic charge transfer. This also reduces the S-T 0 oscillation contrast. As tunnel couplings increase further, the transition from a Hamiltonian dominated by spin exchange to one dominated by the Zeeman energy difference becomes wider, which eventually results in a spin-adiabatic transition. In this case, the system adiabatically moves from S(2000) to ↓↑(1100) and the amplitude of the S-T 0 oscillations gradually vanishes. When moving from (1100) to (1010) and (1001), the spin eigenbasis does not change and we can afford higher tunnel couplings without a rapid degradation of the contrast (see Figs. 4c and d). The gradual decreases in contrast seen at higher tunnel couplings occurs because the electron is increasingly delocalized over the strongly coupled dots, and the plots show the amplitude of the T 0 oscillations for a single charge state only.
Adding to the simulation the return path introduces additional phase shifts and offsets in the simulated S-T 0 oscillations vs. waiting time, without a significant further effect on the contrast of the oscillations (see Supplementary Information Section VI). Overall, the contrast in the simulated oscillations does not exceed 0.65–0.8. This is only about 10% larger than the experimentally observed contrasts, which also incur measurement infidelities of 4–5%. This suggests that the tunnel coupling between dots 1 and 2 in the experiment was close to the optimal value of around 1.2 GHz. Importantly, the contrast of the S-T 0 oscillations being only 60–65% does not imply a loss of phase coherence by 30–35%, but is mostly due to the difficulty in satisfying competing adiabaticity conditions. If the (forward) pulse rise time is too fast, the charge transition is non-adiabatic: the charge does not follow the pulse but stays in (2000). At this point, there are two possibilities. The first is that the electron stays in S(2000) throughout the subsequent waiting time and return pulse. In this case, phase coherence of the spin singlet state is clearly preserved, but there is no contribution to the contrast of the S-T 0 oscillations. Taking t 12 = 1.2 GHz, t 23 = 2.6 GHz, and t 34 = 4.3 GHz, a 2.5 ns rise time, and the Zeeman energy differences extracted from Fig. 3, we estimate such events to occur with up to 32% probability, accounting for most of the reduction in contrast. The second possibility is that the electron spin inelastically relaxes from S(2000) to a (1100), (1010), or (1001) state. If this relaxation time is comparable to or longer than the inverse Zeeman energy difference, the relaxed spin will start the S-T 0 oscillation at a random time, leading to phase randomization. In this case coherence is truly lost. Given that the relaxation time in the experiment is not known, it is difficult to estimate the contribution to decoherence accurately, but we expect it is in the 1–2% range. Finally, if the forward pulse rise time is too slow, the spin transition is adiabatic: the singlet is rotated to ↓↑ as the charge state moves from (2000) to (1100), (1010), or (1001). Since ↓↑ is an eigenstate of the Hamiltonian when exchange interaction is small, there will again be no contribution to the contrast of S-T 0 oscillations. However, for an equally slow return pulse, the spin state is rotated back from ↓↑ to singlet, hence there is no loss of phase coherence. We estimate the probability for this to happen in the present experiment to be up to 1.8%. Additionally, if the initial state is a superposition state of the (initial) Hamiltonian, there will be dephasing during the pulse if the pulse is too slow.
In summary, from comparing the measured and simulated contrasts as a function of shuttling distance, we conclude that reduced contrasts arise mainly from the fact that the charge transfer is not fully adiabatic and to a less extent to the fact that the spin transfer is not fully diabatic. An additional small reduction in contrast is due to a loss of phase coherence associated with inelastic tunneling at a random time after the forward pulse. Other mechanisms that could compromise phase coherence during shuttling are the spin–orbit interaction and hyperfine interaction. Spin–orbit interaction would induce a deterministic spin rotation as an electron moves across the array.35 In the present experiment, the effect of spin–orbit interaction is minimized for motion along the inter-dot axis by the choice of alignment of the gate design with respect to the crystallographic axes and the external magnetic field (see Fig. 1a).10 The slowly varying hyperfine interaction gives rise to random nuclear fields in each of the quantum dots for every shuttle run. In our experiment the nuclear spin distribution specific to the final charge state contributed to the damping of the S-T 0 oscillations. However, when shuttling rapidly through large dot arrays, the effect of random nuclear fields increasingly averages away, and the spin is preserved better than if the electron stayed in a single charge state.36 The decrease of the coherence time observed in Fig. 3c for example is presumably due to a smaller electron wave function in dot 4, resulting in a larger random nuclear field.37 Both hyperfine and spin–orbit interaction are significantly weaker in silicon than in GaAs, so spin shuttles in silicon should be even more robust.
To quantify the fidelity of the spin transfer, we can take two approaches. First, we can define the spin transfer fidelity as the probability that the initial state is preserved as is after moving one electron to one of the other dots. In the present experiment, the spin transfer fidelity then corresponds to the contrast of the S-T 0 oscillations (apart from the reduction in contrast from the measurement infidelity). This would be 65–70% in the present experiment. A second meaningful definition for the spin transfer fidelity is given by the probability of reversible mapping of the initial spin state to a well-defined final spin state upon shuttling, preserving the purity of the state. That would be 1−p, with p the probability that phase coherence is lost, which we here estimate to be 98–99%.
Finally, we explore the limits of the achievable spin transfer fidelity in the absence of spin–orbit and hyperfine interaction. The loss of phase coherence from inelastic tunneling can be reduced by increasing the tunnel coupling or by elongating the pulse rise time, so that the charge transfer meets more closely the ideal adiabaticity condition. In order to simultaneously stay in the spin singlet state (diabatic spin transfer), the difference in Zeeman splittings could be reduced. For a Zeeman energy difference ten times smaller than ΔE z,12, it is possible to achieve simultaneously (near-perfect) adiabatic charge transfer and (near-perfect) diabatic spin transfer, resulting in a 99.7% probability to preserve the spin singlet upon shuttling. Finally, we note that for the transfer of a single-spin state (that is, not a spin that is part of an entangled pair), we only need to achieve adiabatic charge transfer, with no adiabaticity requirements for the spin transfer, relaxing the constraints that need to be met to achieve spin transfer with near-unity fidelity.
Conclusion
We demonstrate a coherent spin-shuttle though a quadruple-quantum-dot device. The main observation is a coherent singlet-triplet oscillation that occurs when one electron of a spin-singlet pair is shuttled to a distant dot. Such an oscillation can only be observed if the coherence is preserved during shuttling. The key requirement for a coherent spin shuttle in the presence of differences in Zeeman splitting between the dots in the array, is that the motion through the array be adiabatic with respect to the inter-dot tunnel couplings for the spin phase to be preserved. For distributing entangled states such as the spin singlet, an additional condition is that the transitions must be non-adiabatic with respect to the spin exchange strength. This demonstration and analysis open up new avenues for large scale solid-state quantum computation, whereby single electrons are shuttled and entanglement is distributed across the chip.38, 39
Methods
The quadruple-quantum-dot array is formed electrostatically in a two-dimensional electron gas (2DEG) 90 nm below the surface of a GaAs/AlGaAs heterostructure, see Fig. 1a. (Reproduced from ref. 10, with the permission of AIP Publishing) Gate electrodes fabricated on the surface are biased with appropriate voltages to selectively deplete regions of the 2DEG and define the linear array of four quantum dots, designated as dots 1, 2, 3, and 4 counting from the left. A sensing dot (SD1) next to the quantum dot array is used for non-invasive charge sensing using radiofrequency (RF) reflectometry to monitor the number of electrons in each dot.40 We denote the charge state occupation of the array as (nmpq) referring to the number of electrons in dots 1, 2, 3, and 4 respectively. We tune the quadruple dot such that it is occupied with two electrons in total. Together the two electrons can form a spin-singlet state S, or one of the three triplet states T 0, T −, and T +. An in-plane magnetic field B ext = 2.3 T is applied to split the T − and T + states from the T 0 state. In order to shuttle electrons back and forth through the array within the dephasing time \(T_2^*\) of a few tens of ns, all inter-dot tunnel couplings are tuned to about 1 GHz and higher (see Supplementary Information Section III for the procedure). The device is cooled inside a dilution refrigerator to a base temperature of ~22 mK (see Supplementary Information Section I for more details on the measurement setup).
Data availability
The authors declare that the main data supporting the finding of this study are available within the article and its Supplementary Information files.
References
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120 (1998).
Taylor, J. M. et al. Fault-tolerant architecture for quantum computation using electrically controlled semiconductor spins. Nat. Phys. 1, 177–183 (2005).
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Nowack, K. C., Koppens, F. H., Nazarov, Y. V. & Vandersypen, L. M. K. Coherent control of a single electron spin with electric fields. Science 318, 1430–1433 (2007).
Hanson, R., Kouwenhoven, L. P., Petta, J. R., Tarucha, S. & Vandersypen, L. M. K. Spins in few-electron quantum dots. Rev. Mod. Phys. 79, 1217–1265 (2007).
Kawakami, E. et al. Electrical control of a long-lived spin qubit in a Si/SiGe quantum dot. Nat. Nanotechnol. 9, 666–670 (2014).
Veldhorst, M. et al. A two-qubit logic gate in silicon. Nature 526, 410–414 (2015).
Medford, J. et al. Self-consistent measurement and state tomography of an exchange-only spin qubit. Nat. Nanotechnol. 8, 654–659 (2013).
Eng, K. et al. Isotopically enhanced triple-quantum-dot qubit. Sci. Adv. 1, e1500214 (2015).
Baart, T., Fujita, T., Reichl, C., Wegscheider, W. & Vandersypen, L. Coherent spin-exchange via a quantum mediator. Nat. Nanotechnol. 12, 26–30 (2017).
Takakura, T. et al. Single to quadruple quantum dots with tunable tunnel couplings. Appl. Phys. Lett. 104, 113109 (2014).
Baart, T. A., Jovanovic, N., Reichl, C., Wegscheider, W. & Vandersypen, L. M. K. Nanosecond-timescale spin transfer using individual electrons in a quadruple-quantum-dot device. Appl. Phys. Lett. 109, 043101 (2016).
Thalineau, R. et al. A few-electron quadruple quantum dot in a closed loop. Appl. Phys. Lett. 101, 103102 (2012).
Childress, L., Sørensen, A. S. & Lukin, M. D. Mesoscopic cavity quantum electrodynamics with quantum dots. Phys. Rev. A 69, 042302 (2004).
Trifunovic, L. et al. Long-distance spin-spin coupling via floating gates. Phys. Rev. X 2, 011006 (2012).
Hassler, F., Catelani, G. & Bluhm, H. Exchange-interaction of two spin qubits mediated by a superconductor. Phys. Rev. B 92, 235401 (2015).
Schuetz, M. J. A. et al. Universal quantum transducers based on surface acoustic waves. Phys. Rev. X 5, 031031 (2015).
Oskin, M., Chong, F. T., Chuang, I. L. & Kubiatowicz, J. Building quantum wires: the long and the short of it. In Proc. 30th Annual International Symposium on Computer Architecture. IEEE. 374–385 (2003).
Kielpinski, D., Monroe, C. & Wineland, D. J. Architecture for a large-scale ion-trap quantum computer. Nature 417, 709–711 (2002).
Nakajima, S. et al. Topological Thouless pumping of ultracold fermions. Nat. Phys. 12, 296–300 (2016).
Gefen, Y. & Thouless, D. J. Zener transitions and energy dissipation in small driven systems. Phys. Rev. Lett. 59, 1752–1755 (1987).
Aleiner, I. L. & Andreev, A. V. Adiabatic charge pumping in almost open dots. Phys. Rev. Lett. 81, 1286–1289 (1998).
Pothier, H., Lafarge, P., Urbina, C., Esteve, D. & Devoret, M. H. Single-electron pump based on charging effects. EPL (Europhys. Lett.) 17, 249 (1992).
Shilton, J. M. et al. High-frequency single-electron transport in a quasi-one-dimensional GaAs channel induced by surface acoustic waves. J. Phys. Condensed Matter 8, L531 (1996).
Hermelin, S. et al. Electrons surfing on a sound wave as a platform for quantum optics with flying electrons. Nature 477, 435–438 (2011).
McNeil, R. P. G. et al. On-demand single-electron transfer between distant quantum dots. Nature 477, 439–442 (2011).
Bertrand, B. et al. Fast spin information transfer between distant quantum dots using individual electrons. Nat. Nanotechnol. 11, 672–676 (2016).
Baart, T. A. et al. Single-spin CCD. Nat. Nanotechnol. 11, 330–334 (2016).
Chekhovich, E. et al. Nuclear spin effects in semiconductor quantum dots. Nat. Mater. 12, 494–504 (2013).
Ono, K., Austing, D. G., Tokura, Y. & Tarucha, S. Current rectification by Pauli exclusion in a weakly coupled double quantum dot system. Science 297, 1313–1317 (2002).
Tokura, Y., van der Wiel, W. G., Obata, T. & Tarucha, S. Coherent single electron spin control in a slanting zeeman field. Phys. Rev. Lett. 96, 047202 (2006).
Foletti, S., Bluhm, H., Mahalu, D., Umansky, V. & Yacoby, A. Universal quantum control of two-electron spin quantum bits using dynamic nuclear polarization. Nat. Phys. 5, 903–908 (2009).
Nakajima, T. et al. Phase control of local and non-local entanglement in a triple spin qubit. 1–26. arXiv:1604.0223 (2016).
Shafiei, M., Nowack, K., Reichl, C., Wegscheider, W. & Vandersypen, L. Resolving spin-orbit- and hyperfine-mediated electric dipole spin resonance in a quantum dot. Phys. Rev. Lett. 110, 107601 (2013).
Schreiber, L. et al. Coupling artificial molecular spin states by photon-assisted tunnelling. Nat. Commun. 2, 556 (2011).
Echeverria-Arrondo, C. & Sherman, E. Y. Relaxation of flying spin qubits in quantum wires by hyperfine interaction. Phys. Rev. B—Condensed Matter Mater. Phys. 87, 1–5 (2013).
Erlingsson, S. I. & Nazarov, Y. V. Hyperfine-mediated transitions between a Zeeman split doublet in GaAs quantum dots: the role of the internal field. Phys. Rev. B 66, 155327 (2002).
Saraga, D. S. & Loss, D. Spin-entangled currents created by a triple quantum dot. Phys. Rev. Lett. 90, 166803 (2003).
Taylor, J. M. et al. Solid-state circuit for spin entanglement generation and purification. Phys. Rev. Lett. 94, 1–4 (2005).
Barthel, C. et al. Fast sensing of double-dot charge arrangement and spin state with a radio-frequency sensor quantum dot. Phys. Rev. B 81, 161308 (2010).
Acknowledgements
We acknowledge useful discussions with the members of the Delft spin qubit team and J.M. Taylor and experimental assistance from M. Ammerlaan, J. Haanstra, R. Roeleveld, R. Schouten, M. Tiggelman and R. Vermeulen. This work is supported by the Netherlands Organization of Scientific Research (NWO) Graduate Program, the Intelligence Advanced Research Projects Activity (IARPA) Multi-Qubit Coherent Operations (MQCO) Program, the Japan Society for the Promotion of Science (JSPS) Postdoctoral Fellowship for Research Abroad, and the Swiss National Science Foundation.
Author information
Authors and Affiliations
Contributions
T.F. and T.A.B. performed the experiment and analyzed the data, C.R. and W.W. grew the heterostructure, T.F., T.A.B., and L.M.K.V. contributed to the interpretation of the data, and T.F., T.A.B., and L.M.K.V. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fujita, T., Baart, T.A., Reichl, C. et al. Coherent shuttle of electron-spin states. npj Quantum Inf 3, 22 (2017). https://doi.org/10.1038/s41534-017-0024-4
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-017-0024-4
This article is cited by
-
Qubit-controlled directional edge states in waveguide QED
npj Quantum Information (2023)
-
Review of performance metrics of spin qubits in gated semiconducting nanostructures
Nature Reviews Physics (2022)
-
A shuttling-based two-qubit logic gate for linking distant silicon quantum processors
Nature Communications (2022)
-
Parametric longitudinal coupling between a high-impedance superconducting resonator and a semiconductor quantum dot singlet-triplet spin qubit
Nature Communications (2022)
-
Two-qubit sweet spots for capacitively coupled exchange-only spin qubits
npj Quantum Information (2021)