Abstract
Selecting effective corrosion inhibitors from the vast chemical space is not a trivial task, as it is essentially infinite. Fortunately, machine learning techniques have shown great potential in generating shortlists of inhibitor candidates prior to large-scale experimental testing. In this work, we used the corrosion responses of 58 small organic molecules on the magnesium alloy AZ91 and utilized molecular descriptors derived from their geometry and density functional theory calculations to encode their molecular information. Statistical methods were applied to select the most relevant features to the target property for support vector regression and kernel ridge regression models, respectively, to predict the behavior of untested compounds. The performance of the two supervised learning approaches were compared and the robustness of the data-driven models were assessed by experimental blind testing.
Similar content being viewed by others
Introduction
Magnesium (Mg), the lightest structural metal, is a promising material in automotive and aeronautic engineering due to its outstanding mechanical properties as well as in medical industries due to its biocompatibility1,2,3. However, Mg-based materials have to be protected from corrosion to facilitate their application in advanced engineering applications, as Mg is a highly reactive metal. Surface coatings depict a reliable and effective strategy to realize the corrosion protection of Mg by adding a barrier layer between the substrate and the service environment3,4,5. However, scratches or cracks in the protective coating may lead to severe local corrosion reactions6. This can be mitigated by incorporating corrosion inhibitors into the coatings that will be released on demand and inhibit corrosion in the damaged areas6,7,8. It is noteworthy that direct embedding of corrosion inhibitors into a coating matrix9 may impair their functionality by no or limited release10,11 or may release all corrosion inhibitors at once without control once a defect occurs12. Application of layered double hydroxides (LDHs) intercalated with corrosion inhibitors is one of the promising routes to achieve a controllable active corrosion protection12,13,14. An LDH is an inorganic sheet-like clay with a brucite structure in its pure Mg(OH)2 form. Thanks to the anion exchange property of the LDH structure, the corrosion inhibitors can be intercalated into this layered structure and their release can be subsequently triggered by exchanging with an aggressive corrosive species (e.g. chloride) to suppress corrosion reactions12. Aside from the inorganic corrosion inhibitors commonly intercalated in the LDHs such as vanadate12, tungstate15, and molybdate16, organic corrosion inhibitors have gained more and more attention recently because a large number of organic compounds have shown promising corrosion inhibition for Mg and its alloys7. Furthermore, it has been demonstrated that small organic molecules can be intercalated into LDHs17,18,19.
However, pure experimental studies on the intercalation of new organic molecules into LDHs can be time-consuming, especially when considering the large number of candidate molecules to choose from20. Aside from that, identification of an effective organic corrosion inhibitor to be intercalated into LDHs (see Fig. 1) to protect a specific type of Mg alloy can be very challenging due to the large number of organic compounds with potentially useful properties21. Luckily, machine learning-based approaches promise to facilitate the screening of useful compounds.
Machine learning (ML) has developed rapidly in recent years due to the augmentation of algorithms and technological advances in computing hardware22. While influencing our daily life23,24, machine learning algorithms have also gained an important role in material science25,26. Different algorithms have been applied in material discovery such as compound prediction27,28,29, structure prediction30,31 and predicting material properties such as band gap32, superconductivity33, bulk and shear moduli34 and to identify effective corrosion inhibitors based on quantitative structure-property relationships (QSPRs)35,36. For the latter, a number of different machine learning algorithms (e.g. neural networks, kernel ridge regression, and random forests)21,37,38 were successfully developed to predict the corrosion inhibiting effect of small organic compounds for different types of Mg and its alloys7,21,37, Aluminum alloys35,36,39, and Copper-based materials40. Naturally, a sufficiently large, diverse, and reliable training dataset and a suitable modeling framework (usually based on one or more machine learning algorithms), are two of the crucial prerequisites for the development of predictive QSPR models. A third key step is the selection of relevant input features which can either be selected by chemical intuition38 or based on statistical methods37. Random forests (RFs) have proven to be a useful algorithm for dealing with feature selection problems due to their ability to calculate the importance of each feature41. The presence of correlated features, on the other hand, has been shown to affect their ability to identify important features, potentially lowering their accuracy42,43,44. To address this issue, a combination of random forests and recursive feature elimination (RFE) is commonly used43,44 and its potential to select relevant features to model corrosion inhibition efficiencies (IEs) of small organic molecules has been demonstrated in a recent study37.
In this work, corrosion inhibition responses of 58 small organic molecules on Mg alloy AZ91 from a previous work7 were used to train a QSPR model. AZ91 was the selected substrate in this study because our previous experimental work45 proved that LDHs can be directly synthesized at the surface of this alloy as a conversion layer. The corrosion inhibition efficiencies of the samples in the used dataset exhibit a higher variance than those used in other Mg alloy prediction models21,37,38 so far which renders the use of a machine learning algorithm with good generalization capabilities a necessity. A potential algorithm that can be employed to establish the QSPR workflow are support vector machines (SVMs) which represent one of the most powerful, precise and robust supervised learning methods due to their good theoretical foundations and generalization capacity46,47. They have been widely applied to solve various complex real-world problems such as: image classification48, hand-written character recognition49 and face detection50 in the past twenty years46. Applying the same principle as SVMs, support vector regression (SVR) was developed to solve regression problems with high accuracy51,52,53. SVR52 has been used to develop a predictive model to investigate the influence of the outdoor environment on the corrosion rates of metallic materials54,55. Furthermore, Liu et al.56 developed a QSPR model based on SVR for Q235 steel using a limited number of organic compounds, demonstrating that SVR is well suited for small datasets. However, the use of small training datasets may lead to overfitting and the validation of the prediction is an essential part of the model development. Therefore, SVR was chosen for the QSPR model construction in this work to investigate its applicability for Mg-based datasets, and the quality of the predictions was evaluated using experimental blind testing. Moreover, approaches based on kernel ridge regression (KRR)57,58 have already been applied to predict the effect of small organic molecules on the corrosion behavior of commercially pure Mg21. As a result, the KRR approach was chosen as a benchmark for comparing the performance of the SVR model. Unlike existing models36,37,38, where the number of selected features used to build the model was chosen manually, a two-step feature selection method was proposed in this work, where the optimal number of features is determined by the model. In the end, the QSPR model developed in this work can assist the selection of an effective organic corrosion inhibitor from a large number of organic compounds, whose intercalation into the LDHs will be further investigated to achieve the goal of corrosion protection for AZ91.
Results and discussion
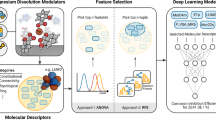
The model construction in this work is based on the workflow shown in Fig. 2. Further investigations of the feature selection were carried out which is a key element in the development of an ML model that predicts the corrosion IEs of small organic molecules. Based on the selected features, two different QSPR models (based on SVR and KRR algorithms) were trained to predict the IEs of small organic molecules on AZ91 and their accuracy was subsequently validated and compared based on experimental blind testing using ten compounds which were not part of the initial dataset.
A database of 58 small organic molecules and their corrosion responses on AZ91 are employed as training database. First a pool of molecular descriptors to encode their molecular structure is generated and exposed to a two-step sparse feature selection approach. The most relevant descriptors are subsequently used to train supervised machine learning models to predict the behavior of untested chemicals. The small organic molecules for this step are selected following our previously published ExChem21 approach.
Feature selection
A pool of 2876 distinct molecular descriptors was generated as input features for the development of a QSPR model. After omitting all molecular descriptors with constant values, the remaining 876 were exposed to feature selection. An RFE based on random forests approach was adopted to select a 25-tuple of features out of the initial 876 features in the first step. More details on the selection process of the selected 25 features are available in the ’Methods’ section. An additional step was added to the feature selection by gradually decreasing the number of used input features, starting from the 25-tuple features that were selected using RFE in the first step (see the feature selection section of Fig. 2). In the second step of the feature importance investigation, the initially selected 25 features were removed one-by-one in 24 steps. Instead of applying RFE, the SVR and KRR models were used directly to select features at each step together with hyperparameter optimization and cross validations. At each step, there is more than one possibility to remove a feature from the previous step, e.g. there are twenty-five possibilities to remove one feature from the selected 25 features. Attempts across all possibilities were conducted and the possibility with the lowest averaged root mean squared error (RMSE) of the IEs for the test sets in the cross validation was selected at each step and plotted in Fig. 3. The averaged RMSEs for the train sets in the cross validation corresponding to the plot in Fig. 3 are listed in the Supplementary Table 1. For the selected possibility, the removed feature was defined as the least important feature in the previous step. In the end, the selected 25 features were ordered according to the previously defined importance, obtaining an order of importance for the features.
The trend of the black line in Fig. 3 shows that the optimal number of features selected for the SVR model equals eight, since the resulting model exhibits the lowest RMSE. The selected molecular descriptors are P_VSA_LogP_2, Mor28e, HOMO, MATS4v, Mor06s, GATS4p, MATS8m, and Mor15v, ordered by their suggested feature importance. Except for the highest occupied molecular orbital (HOMO) which is obtained from DFT calculations, the other seven features are from three descriptor categories (P_VSA-like descriptors59, 3D-MoRSE descriptors60 and 2D autocorrelations61) obtained from the chemoinformatic software package alvaDesc62. P_VSA-like descriptors are based on the van der Waals surface area of the compounds by summing up all the atomic contributions. 3D-MoRSE descriptors incorporate the whole molecule structure information by summarizing the atomic pairwise information related to the scattering parameter based on electron diffraction and then weighted by either of the properties, e.g. mass, Sanderson electronegativity, van der Waals volume, and atomic polarizability. The 2D autocorrelations descriptors are calculated to provide the interdependence between atomic properties (analogous to the 3D-MoRSE descriptors), which are connected by a log function63. All these three descriptor categories focus on calculating the spatial distribution of a generic molecular property rather than only considering the atomic configurations.
In the KRR model, the optimal number of features resulted in eleven as shown in Fig. 3. The eleven selected features were identified as Mor15v, HOMO, MATS8m, Mor30e, nRNH2, C-018, GATS4p, MATS2i, Mor11e, Mor06s, Mor28e, ordered by their feature importance. It is noteworthy that six out of the eleven features are identical with those selected for the SVR model. The overlapping features are Mor15v, HOMO, MATS8m, GATS4p, Mor06s, Mor28e. This finding implies that the HOMO energies derived from DFT calculations, 3D-MoRSE descriptors, and 2D autocorrelations descriptors seem to encode crucial structural information concerning the prediction of the corrosion inhibition efficiency of small organic molecules for AZ91. This observation agrees well with the conclusion from Schiessler et al.37 where DFT calculated features as well as 3D-MoRSE descriptors were identified as important input features for an artificial neural network using IEs of small organic molecules for the Mg-based alloy ZE41 as a target property.
Apart from these three feature groups, a number of features encoding functional group counts and atom-centered fragments were identified for the top eleven features in the KRR model, e.g. nRNH2 which directly encodes the number of aliphatic primary amines. All five compounds that contain nRNH2 moieties in our dataset are amino acids (Cysteine, Glutamic acid, Glycine, DL-norleucine, and DL-phenylalanine) which exhibit negative inhibition efficiencies. This finding agrees well with the conclusion in Ref. 7 that amino acids accelerated corrosion of Mg alloys. The corrosion acceleration behavior of amino acids can be attributed to the solubility of their corresponding magnesium complex in water64,65. The feature C-018 from the class of atom-centered fragments represents =CHX, where “=” depicts a double bond and X any of the following heteroatoms: O, N, S, P, Se, or any halogen. In the =CHX fragment, a sp2-hybridized carbon atom is directly connected to a hydrogen and one of heteroatoms that are denoted as X. In our training dataset, this specific functional group is present in the compounds Kojic acid, Maltol, and Uracil (X represents either O or N) whereas all three organic molecules display negative IE values, as shown in Supplementary Fig. 1. It has been proven that the complexes formed by these three compounds with magnesium are water-soluble65,66,67. Compared to the capability to form complexes with metal ions, the solubility of these complexes in water appears to be a more decisive factor in determining the efficiency of the organic inhibitors. This observation agrees well with the work from Lamaka et al.7 and Anjum et al.19 that organic compounds whose complexes have a low solubility in water exhibited a high inhibiting effect since they delay corrosion by forming a protective barrier layer.
Some of the molecular descriptors obtained from the chemoinformatics tool are arcane and cannot be easily linked to physical properties since they are derived from extensive mathematical manipulations of the chemical structure. Pearson tests provided a better understanding of the correlation between the used input features and IEs as well as a measure for their statistical significance. The Pearson correlation coefficient measures the linear relationship between two sets of data, which varies between −1 and 1 with 0 implying no correlation while −1 and 1 implying exact negative and positive correlations, respectively68. For both models, the correlation between the individual features and the IEs is moderate to weak since the values of the determined correlation coefficients in Fig. 4a, b are not higher/lower than ±0.5, where the most pronounced negative and positive correlations are −0.5 and 0.2, respectively. This observation agrees well with the findings of Guyon et al.69 that the selected features are on their own not necessarily the most relevant with respect to the target property. For the correlation between the selected features, neither of the correlations is considered as a strong relationship (>0.9) and most of the correlations (over 90%) are interpreted as weak relationships (0.1−0.39) or are negligible (<0.1) according to the definitions in the work of Schober et al.68. Moreover, the p-value between the used input features and IEs was calculated and illustrated in Supplementary Fig. 2, where the p-value is an indicative measure whether the correlation is statistically significant. The weak correlations between most of the selected features largely ensure that there is no redundant feature selected as input for the models. Although most of the selected features are only weakly correlated with the target property itself, the results indicate that they can still be used to build a predictive model when used as a group due to underlying synergistic effects which is in good agreement with previous works37,38.
In summary, the feature selection method proposed in this work is able to increase the accuracy of the predictions in the cross-validation stage by applying the step-wise reduction to the group of features which was selected based on RFE in the first step. Moreover, the proposed method can be employed to perform RFE for SVR with a radial basis function (RBF) kernel, since only the linear kernel is currently supported in scikit-learn70. Another advantage of this proposed method is that there is no prerequisite on the number of features to be selected, therefore all possible combinations of feature groups are explored in the feature selection and a comprehensive exploration can be guaranteed.
Model validation
Hyperparameters for the SVR and KRR models were optimized in a grid search with 5-fold cross validations together with the feature importance investigation. As a result, the set of hyperparameters for the SVR (random_state=10, C = 17, γ = 0.1) and the KRR (random_state = 10, α = 0.1, γ = 0.1) were selected respectively. For both models, the value selected for the random state parameter (random_state) is identical which indicates the same split of the dataset into train and test sets in the cross validations. After the selection of the hyperparameters, the full initial dataset was used to fit the two models and then these models were applied to predict the behavior of the blind test compounds to evaluate their robustness. The experimental and predicted values for the 10 compounds in the blind tests are listed in Table 1. The predicted values for the piperazine derivatives 1 and 2 are marked in brown for both models as their predicted acceleration efficiencies are significantly less negative than the corresponding experimental values, which are beyond the inhibition efficiency range of the chemicals used as initial dataset in this work. However, it is noteworthy that both compounds were correctly predicted to accelerate the dissolution of AZ91. These two compounds were excluded in the following analysis since they are outside of the domain of applicability of the used initial dataset.
The SVR and KRR models performed similarly well for the full initial dataset, the blue points in Fig. 5a, b, where the predicted and experimental values correlated well with an RMSE of around 10%. The performance of some of the blind test compounds that were under- or overestimated, circled by red and blue dashed circles or ellipses in Fig. 5, results in a relatively high RMSE value for both employed models (84% for SVR and 69% for KRR). Moreover, there is no strong positive correlation between the predicted and experimental values for the eight compounds (3-10) for both the SVR (coefficient = −0.571, p-value = 0.140) and KRR (coefficient = 0.005, p-value = 0.991) models as these statistical metrics are heavily affected by the outliers. Due to the relatively large deviation between predicted and experimental values for the eight compounds, an area of overlap between mild inhibitors and mild accelerators was introduced for compounds with experimentally determined values in the range of -30%<IE<30%. For compounds in this area, the predicted values were considered as reliable estimates if they fell within this range. From Fig. 5, it can be seen that both SVR and KRR models underestimated 5-Nitrouracil (6, IEpred,KRR = −82%, IEpred,SVR = −68%) and Trimethylolpropane (10, IEpred,KRR = −49%, IEpred,SVR = −48%) in a similar way. There are other two outliers (2-Hydroxycinnamic acid (3) and Trimesic acid (8)) in the SVR model as shown in Fig. 5a. Even though there are two more outliers in the SVR model, it is important to note that the predicted values for the other four compounds in the blind test set correlated well with the corresponding experimental values for the acetic acid 4 (IEpred,SVR = −21%, IE\({}_{\exp.}=\) −14%), the pyrazole 5 (IEpred,SVR = 9%, IE\({}_{\exp.}=\) 16%) as well as the aliphatic (7 (IEpred,SVR = 37%, IE\({}_{\exp.}=\) 30%)) and aromatic (9 (IEpred,SVR = 34%, IE\({}_{\exp .}=\) 52%)) carboxylic acids with an RMSE of 11% and an R2 of 0.782 in the SVR model. The RMSE and R2 calculated for the same non-outlier compounds (4, 5, 7, 9) in the KRR model are 33% and 0.385, respectively. These observations indicate that both the SVR and KRR models are able to provide good estimates for the four blind test compounds (4, 5, 7, 9). For the compounds where the predictions yielded reliable estimates based on the SVR (4, 5, 7, 9) and the KRR (3, 4, 5, 7, 8, 9) models, the Pearson correlation coefficient and p-value were calculated between their predicted and experimental values. The predicted values of the SVR model (coefficient=0.93, p-value = 0.071) show a higher correlation with the experimental results than the KRR model (coefficient = 0.60, p-value = 0.214) while the p-value of the SVR model indicates statistical relevance of the prediction. The difference between these two models for the given dataset is that the SVR model can provide a higher accuracy of predictions for the non-outlier compounds while there are fewer outliers in the KRR model.
The correlation between the predicted values and the measured values from experiments (IEs in %) is displayed for (a) SVR model and (b) KRR model. The blue points represent the full initial dataset (58 compounds, the names and IEs were listed in the Supplementary Table 2). The orange points depict the blind test compounds. Please note that 1-Acetylpiperazine (1) and 1-Amino-4-methylpiperazine (2) were excluded from the plot. Although their estimates were qualitatively correct (1: IEpred,SVR = -172%, IEpred,KRR = −108%, IE\({}_{\exp }\) = −563%; 2: IEpred,SVR = −195%, IEpred,KRR = −109%, IE\({}_{\exp }=\) −517%), their measured values were far outside the models domain. The corresponding structures of the plotted blind test compounds are shown at the bottom of the figure. Red and blue dashed circles or ellipses mark the over- and underestimated compounds, respectively.
Moreover, modulators exhibiting an aliphatic primary amine (nRNH2), e.g. in an amino acid, or fragments with the general formula R=CHX cause elevated corrosion rates in experimental studies7. The results indicate that small organic molecules that exhibit either of the above-mentioned functional moiety can most likely be excluded from the screening for effective corrosion inhibitors. However, they might have beneficial properties for other applications such as battery electrolyte additives where a controlled dissolution of the Mg-based anode material is required71. One out of the 10 compounds (5-Nitrouracil (6)) in the blind test set contained a =CHX fragment, suggesting that it has a negative IE value. However, in contrast to the predicted negative inhibition efficiency, the experimental result showed that 5-Nitrouracil gave adequate inhibition performance. This could be attributed to the nitro compounds of 5-Nitrouracil which have been proven to be able to assist the corrosion protection of a variety of alloys72,73,74. Furthermore, while Uracil has a negative IE value (-151%), its substitution with a nitro moiety, 5-Nitrouracil, results in a highly potent corrosion inhibitor (78%), indicating that the nitro moiety plays a significant role in corrosion protection. This observation is, however, not captured by neither of the employed models because of the limited information on the effect of a nitro functionality in our dataset as there are only two compounds (5-Nitrobarbituric acid and 3-Methyl-2-nitrobenzoic acid) that exhibit this functional moiety. This strongly indicates that future experimental dataset need to include more compounds with a nitro moiety to enable the model to recuperate the impact of this group on the corrosion inhibiting effect.
To gain more insights of the compounds which are outliers, the pairwise distances based on the input features were calculated between the compounds in the blind test and the initial dataset used in building the models to evaluate the highly similar structures for each blind test compound. A value of 1 in the similarity matrix suggests high similarity while a value of 0 indicates no similarity. Figure 6a, b show the similarity matrix for the eight blind test compounds and the initial data set for the SVR and KRR models, respectively. The top 5 similar structures (containing the names and the inhibition efficiencies) for 5-Nitrouracil (6) are shown in Fig. 6 for both models. A similarity order from high to low can be extracted for these 5 structures in SVR (Uracil, Glycine, 5-Nitrobarbituric acid, DL-Phenylalanine, Glutamic acid) and KRR (Uracil, Maltol, Kojic acid, Fumaric acid, Urea). It is noteworthy that there are obvious similarity differences for some of the top 5 similar structures such as the difference between Uracil and Urea in the KRR model as shown in Fig. 6b. This indicates the limitation of the dataset used in this work where there are only 58 data points in total. As a consequence, there are not enough structures in the dataset with higher or comparable similarities to the similarity between Uracil and the blind test compound 5-Nitrouracil (6). The IEs of these 5 similar structures are ordered by similarity in Table 2. The same process was applied to extract the top 5 similar structures and list their IEs in Table 2 for all the other outliers. Naturally, the predicted value for each outlier is heavily influenced by the IEs of the top 5 similar structures. For example, because the IEs of the top five similar structures for compound 3 in the SVR model are all positive, the IE value predicted by the model will be positive as well. This indicates that our models are able to capture the similarity connections existing in the dataset and make according predictions. The similarity connections are however limited by the small size of our dataset, resulting in the appearance of these outliers. The learning curves for the SVR and KRR models (as illustrated in the Supplementary Fig. 3) show that the averaged RMSEs for the test sets in the cross validation decrease as the size of the training set increases, although the averaged RMSEs of the test sets for both models are higher relative to that of the train sets. One possible remedy is to expand the dataset, so the averaged RMSEs of the test sets can consistently decrease by adding additional training data.
Similarity matrix of the 8 blind test compounds and the 58 compounds in the dataset for the (a) SVR model and (b) KRR model. The top 5 similar structures containing the names and the inhibition efficiencies for 5-Nitrouracil (6) are plotted in the figure as an example. The values below the names are the similarity values. The color scale corresponds to the values in the matrix where dark blue indicates low / no, green moderate and yellow high similarity values.
In this work, the performance of two supervised machine learning approaches (SVR and KRR) were assessed concerning their robustness to predict the corrosion inhibition of small organic compounds for AZ91. The blind tests for the models were carried out to assess the reliability of each model. With the dataset expanding in size and diversity in the future, similarity connections can be improved to increase the domain of applicability of the model. Either of the described model approaches can then be applied to predict the corrosion inhibition behaviors of a large amount of organic compounds with higher confidence and select promising inhibitors for AZ91, thus significantly decreasing material costs and environmental impact of experiments while accelerating the discovery of effective corrosion inhibitors.
In summary, small organic molecules exhibit great potential to control the corrosion behavior of magnesium-based materials. Selecting effective organic corrosion inhibitors from the vast space of available compounds is not a trivial task and it cannot be solved by time- and resource-consuming experimental investigations alone. QSPR models based on supervised learning techniques such as SVR and KRR create great efficiencies in screening for effective agents for corrosion control.
In this work, the RBF kernel was used to develop two predictive data-driven models based on the available experimental IEs of organic compounds for AZ91 from a previous work7. A pool of 876 input features derived from the cheminformatics software package and DFT were generated and exposed to an initial feature selection based on RFE to identify the feature group consisting of 25 features with the highest relevance for the target property. These 25 features were subsequently gradually reduced to find the optimal number of features for the respective method and the results indicate that lowest RMSE is obtained for 8 features in the SVR and for 11 features in the KRR approach. There is a considerable overlap between the two groups of selected features as the energy levels of the HOMO derived from DFT, 3D-MoRSE descriptors, and 2D autocorrelations descriptors ended up in the final model for both cases, which agrees well with the findings in our previous work37.
Blind tests were carried out to assess the performance of the two model frameworks that were investigated in this work. Of the ten compounds in the blind tests, 1-Acetylpiperazine (1) and 1-Amino-4-methylpiperazine (2) were predicted correctly to be strong accelerators with IE values more negative than −100% by both models. However, the experimentally derived values were far outside the training IE range and hence, their predicted values strongly underestimated. For the other eight compounds, 2-Hydroxyphenylacetic acid, 3-Methylpyrazole, Tartronic acid, and Pyromellitic acid were correctly predicted by both models, where the values predicted by the SVR model are closer to the real values compared to the KRR model. In addition, both models identified 5-Nitrouracil and Trimethylolpropane as outliers, although there are two more outliers for the SVR model. For each of the outliers, there is a distinct variation for the IEs of its top 5 highly similar structures extracted from the dataset, which might ultimately cause the false prediction of the IE value. This indicates that the similarity connection of the structures is limited by available data.
In conclusion, the two-step feature selection method proposed in this paper can select the most relevant features while improving the prediction accuracy of the SVR and KRR-based QSPR models. After first reducing the pool of available features to a 25-tuple using RFE, this feature set is subsequently systemically screened for the best n-tuple to train the predictive model, rather than relying on human intuition to choose the number and composition of input features. Despite the limited training dataset, the SVR-based model predicted robust estimates for the anti-corrosion performance of four and the KRR-based model of six members of the blind test set whereas the SVR predictions were closer to the experimental results while the KRR model generalized better, resulting in fewer detected outliers. Outliers, on the other hand, are not always a bad thing because they provide guidance on which structural leitmotifs should be tested next to increase the domain of applicability and robustness of the models. According to our results, substitution of the uracil parent system with a nitro moiety (5-Nitrouracil (6)) results in a highly potent corrosion inhibitor (IE = 78%) compared to uracil (IE = −151%). However, our model fails to correctly predict the behavior of this compound, and this structural leitmotif should therefore be the target of upcoming experiments to broaden the domain of applicability of our model. The new data points will subsequently be used to augment the training database and as a consequence to improve the accuracy of the predictions for broader area of chemical space. Feeding more training samples to the model will facilitate an active design of experiments thereby accelerating the selection of potent inhibitors for AZ91 and other materials. This work demonstrates that data-driven models based on SVR and KRR approaches not only provide a reliable basis to generate predictive models and that they can be applied to predict the corrosion inhibition efficiencies of small organic molecules for Mg-based materials. Next, the selected inhibitors will be investigated for intercalation in LDH to achieve an active corrosion protection of AZ91. Finally, the machine-learning based strategies developed in this work can also be adapted to explore quantitative structure-property relationships in different application fields given sufficient training data is available to train the respective models.
Methods
58 organic compounds were extracted from the work of Lamaka et al.7 for AZ91 and used as database in this work. These 58 organic compounds were selected based on the following three requirements: the concentration of the tested inhibitor was 0.05 M in 0.5 wt.% sodium chloride electrolyte (NaCl) pH neutral aqueous solution, molecular weight (<350 Da) and inhibition efficiencies ranging from −250% to 100%. The concentration was selected to be 0.05 M due to the fact that the majority of organic compounds were measured in this concentration for AZ91 and other concentrations influenced the inhibition efficiency of a chemical compound7. The chemical space was explored in a limited range of molecular weight since we are interested in seeking for small molecular organic inhibitors. The selection of the inhibition efficiency range is a balance between the large number of compounds, which is beneficial to build a model, and the small range from the side of the accelerators since the exploration of strong accelerators is out of interest in this work.
Feature generation and selection
After the data extraction, the molecular structures of these 58 compounds were built and optimized in the DFT calculations at the TPSSh/def2SVP level of theory using the quantum chemical software package Gaussian 1675. DFT-calculated features, especially the highest occupied (HOMO) and the lowest unoccupied molecular orbital (LUMO), have been shown to be correlated to the corrosion inhibition efficiencies of small organic molecules for some Mg-based materials38,76,77. The optimized structures from DFT were subsequently used as input in the cheminformatics software package alvaDesc 1.0.2262 to generate more features, which were then combined with the HOMO and LUMO features to the initial feature set. There are over 800 features for each compound in the initial feature set, which significantly exceeds the number of compounds in the initial dataset. At first, RFE based on random forests was applied to select the 25-tuple features, thus initially reducing the feature space. These selected 25 features can be different if the selection procedure is repeated due to the random initialization in the random forests. The selection procedure was repeated 50 times, obtaining 50 different groups of selected top 25 features. These 50 distinct groups of features obtained in step 1 are fed into the 5-fold cross validation (as shown in Supplementary Fig. 4) of the SVR model. The feature group with the lowest averaged test RMSE of the cross validation in the SVR model was picked out of the 50 feature groups and is the basis for searching the most relevant features for the SVR and KRR models, respectively. The 25 features were reduced in a stepwise manner (one feature per step) to remove insignificant features in the model training. In each step, there is more than one possibility to remove one of the total features and all possibilities were investigated. The option which yielded the lowest averaged test RMSE was selected at each step and the preserved features were used for the next step. The number of considered features ranged from 25 to 1. Applying this method, the most relevant features which obtained the lowest averaged test RMSE for the SVR and KRR models were selected, respectively. After the selection of the optimal features for each model, the continued stepwise procedure resulted in an order of importance for the selected features, depending on their removed order.
Support vector regression and kernel ridge regression
SVR52,78 and KRR58 approaches were selected to build the QSPR models for the prediction of inhibition efficiency of small organic compounds for AZ91 alloy with the assist of an RBF kernel. A kernel function can map the nonlinear distribution data in the input space to a higher-dimensional space where the regression can be in a linear form. RBF kernel was selected in this work since it is the most widely used kernel in SVM79 and Smola et al.80 pointed out that the RBF kernel is generally a reasonable choice for datasets with little information on their shape. After applying the same feature selection process to each model, the most relevant features were obtained. In this work, the high-dimensional input vector is composed of the previously identified most relevant features and the target values are the experimental inhibition efficiency extracted from the work of Lamaka et al.7. The regression is achieved by ε-SVR and KRR, and the results obtained from these two methods are compared and discussed in this work. The difference between these two methods is their error loss functions. While KRR applies a squared error loss, SVR employs an ε-insensitive loss as illustrated in the Supplementary Fig. 5. Hyperparameters such as γ of the RBF kernel (as seen in the Supplementary Fig. 6), the regularization parameter C, which manages the trade-off between the smoothness and overfitting of the ε-SVR, and the regularization parameter α for a similar trade-off function in the KRR model, are tuned in a 5-fold grid search to find optimal values with respect to the target property. Except for these three mentioned parameters, the random state parameter (random_state) which controls the split of the train and test sets was also tuned in the 5-fold grid search to avoid the biased split because of the relatively small dataset (58 compounds) and large inhibition efficiency range (from −250% to 100%). The distribution of the inhibition efficiencies is provided in the Supplementary Fig. 7.
Similarity calculation
The similarity calculation used in this work is based on a distance metric where the selected input features are the coordinates of each compound in the corresponding high-dimensional feature space. The RBF kernel used in the SVR and KRR model was applied in the similarity calculation, which is defined as
where x and y are the vectors of the selected input features for two compounds, respectively.
Corrosion experiments
The dataset used in building the SVR and KRR models was extracted from the work of Lamaka et al.7 and therefore the validation for these two models (blind tests) has been carried out with the same experimental setup and under the same conditions. For the selection of the compounds in the blind tests, Trimesic acid and Pyromellitic acid were suggested by experimentalists based on chemical intuition, whereas the remaining candidates were selected by following the ExChem approach described in a previous work21, using a database of 7094 commercially available compounds provided by Thermo Fisher Scientific. The IE of compounds was calculated based on a hydrogen evolution test, in which the amount of evolved hydrogen due to the corrosion of magnesium is measured during immersion in a NaCl solution. 0.5 g of AZ91 Mg chips with the surface area of 430 ± 29 cm2/g from the same batch used in work of Lamaka et al. was immersed in 0.5 wt.% NaCl solution without (reference solution) and with the untested compounds. The chemical composition of the AZ91 chips is identical to the work of Lamaka et al. and is provided in the Supplementary Table 3. The concentration of compounds was 0.05 M and the pH of solutions was adjusted to 7 ± 0.1 by NaOH/HCl. The hydrogen evolution measurements were repeated three times for each solution and the average of calculated IEs was used for the corresponding blind test data point. The IE was defined by the following equation
where \({V\,}_{{{{{\rm{H}}}}}_{2}}^{0}\) and \({V\,}_{{{{{\rm{H}}}}}_{2}}^{{{{\rm{Inh}}}}}\) are the volumes of H2 evolved after 20 h of immersion in the reference NaCl solution and the NaCl solution containing the investigated chemical compound, respectively. More details on the hydrogen evolution tests are available in the original publication7.
Data availability
The authors declare that the primary data supporting the results of this study can be found in the paper and its supplementary information. The data used in this study is available at https://doi.org/10.5281/zenodo.8135985.
Code availability
The code used for this study is available at https://doi.org/10.5281/zenodo.8135985.
References
Tan, J. & Ramakrishna, S. Applications of magnesium and its alloys: a review. Appl. Sci. 11, 6861 (2021).
Landkof, B. Magnesium Alloys and their Applications, p. 168–172 (John Wiley & Sons, Inc, 2000).
Luan, B., Yang, D., Liu, X. & Song, G.-L. Corrosion of Magnesium Alloys, p. 541–564 (Elsevier, 2011).
Chen, X.-B., Easton, M., Birbilis, N., Yang, H.-Y. & Abbott, T. Corrosion Prevention Of Magnesium Alloys 282–312 (Woodhead Publishing Limited, 2013).
Pommiers, S., Frayret, J., Castetbon, A. & Potin-Gautier, M. Alternative conversion coatings to chromate for the protection of magnesium alloys. Corros. Sci. 84, 135–146 (2014).
Zhang, G. et al. Corrosion protection properties of different inhibitors containing peo/ldhs composite coating on magnesium alloy az31. Sci. Rep. 11, 1–14 (2021).
Lamaka, S. et al. Comprehensive screening of mg corrosion inhibitors. Corros. Sci. 128, 224–240 (2017).
Hu, H., Nie, X. & Ma, Y. Magnesium Alloys-Properties in Solid and Liquid States 67–108 (IntechOpen, 2014).
Latnikova, A. Polymeric Capsules For Self-healing Anticorrosion Coatings. Ph.D. thesis (Universität Potsdam, 2012).
Denissen, P. J., Shkirskiy, V., Volovitch, P. & Garcia, S. J. Corrosion inhibition at scribed locations in coated aa2024-t3 by cerium-and dmtd-loaded natural silica microparticles under continuous immersion and wet/dry cyclic exposure. ACS Appl. Mater. Interfaces 12, 23417–23431 (2020).
Yin, Y., Prabhakar, M., Ebbinghaus, P., da Silva, C. C. & Rohwerder, M. Neutral inhibitor molecules entrapped into polypyrrole network for corrosion protection. Chem. Eng. J. 440, 135739 (2022).
Zheludkevich, M. et al. Active protection coatings with layered double hydroxide nanocontainers of corrosion inhibitor. Corros. Sci. 52, 602–611 (2010).
Zhang, X. et al. Active corrosion protection of mg–al layered double hydroxide for magnesium alloys: a short review. Coatings 11, 1316 (2021).
Jing, C., Dong, B., Raza, A., Zhang, T. & Zhang, Y. Corrosion inhibition of layered double hydroxides for metal-based systems. Nano Mater. Sci. 3, 47–67 (2021).
Li, D. et al. Anticorrosion organic coating with layered double hydroxide loaded with corrosion inhibitor of tungstate. Prog. Org. Coat. 71, 302–309 (2011).
Yu, X. et al. One-step synthesis of lamellar molybdate pillared hydrotalcite and its application for az31 mg alloy protection. Solid State Sci. 11, 376–381 (2009).
Poznyak, S. et al. Novel inorganic host layered double hydroxides intercalated with guest organic inhibitors for anticorrosion applications. ACS Appl. Mater. Interfaces 1, 2353–2362 (2009).
Zhang, F. et al. Corrosion resistance of superhydrophobic layered double hydroxide films on aluminum. Angew. Chem. 120, 2500–2503 (2008).
Anjum, M. J. et al. Green corrosion inhibitors intercalated mg: Al layered double hydroxide coatings to protect mg alloy. Rare Metals 40, 2254–2265 (2021).
Tabish, M. et al. Reviewing the current status of layered double hydroxide-based smart nanocontainers for corrosion inhibiting applications. J. Mater. Res. Technol. 10, 390–421 (2021).
Würger, T. et al. Exploring structure-property relationships in magnesium dissolution modulators. npj Mater. Degrad. 5, 1–10 (2021).
Schmidt, J., Marques, M. R., Botti, S. & Marques, M. A. Recent advances and applications of machine learning in solid-state materials science. npj Comput. Mater. 5, 1–36 (2019).
Popel, M. et al. Transforming machine translation: a deep learning system reaches news translation quality comparable to human professionals. Nat. Commun. 11, 1–15 (2020).
Sharma, S., Bhatt, M. & Sharma, P. Face recognition system using machine learning algorithm. In 2020 5th International Conference on Communication and Electronics Systems (ICCES), 1162–1168 (IEEE, 2020).
Gormley, A. J. & Webb, M. A. Machine learning in combinatorial polymer chemistry. Nat. Rev. Mater. 6, 642–644 (2021).
Hart, G. L., Mueller, T., Toher, C. & Curtarolo, S. Machine learning for alloys. Nat. Rev. Mater. 6, 730–755 (2021).
Faber, F. A., Lindmaa, A., Von Lilienfeld, O. A. & Armiento, R. Machine learning energies of 2 million elpasolite (a b c 2 d 6) crystals. Phys. Rev. Lett. 117, 135502 (2016).
Schmidt, J., Chen, L., Botti, S. & Marques, M. A. Predicting the stability of ternary intermetallics with density functional theory and machine learning. J. Chem. Phys. 148, 241728 (2018).
Kim, K. et al. Machine-learning-accelerated high-throughput materials screening: Discovery of novel quaternary heusler compounds. Phys. Rev. Mater. 2, 123801 (2018).
Graser, J., Kauwe, S. K. & Sparks, T. D. Machine learning and energy minimization approaches for crystal structure predictions: a review and new horizons. Chem. Mater. 30, 3601–3612 (2018).
Oliynyk, A. O., Adutwum, L. A., Harynuk, J. J. & Mar, A. Classifying crystal structures of binary compounds ab through cluster resolution feature selection and support vector machine analysis. Chem. Mater. 28, 6672–6681 (2016).
Zhuo, Y., Mansouri Tehrani, A. & Brgoch, J. Predicting the band gaps of inorganic solids by machine learning. J. Phys. Chem. Lett. 9, 1668–1673 (2018).
Isayev, O. et al. Materials cartography: representing and mining materials space using structural and electronic fingerprints. Chem. Mater. 27, 735–743 (2015).
De Jong, M. et al. A statistical learning framework for materials science: application to elastic moduli of k-nary inorganic polycrystalline compounds. Sci. Rep. 6, 1–11 (2016).
Winkler, D. A. et al. Using high throughput experimental data and in silico models to discover alternatives to toxic chromate corrosion inhibitors. Corros. Sci. 106, 229–235 (2016).
Galvão, T. L., Novell-Leruth, G., Kuznetsova, A., Tedim, J. & Gomes, J. R. Elucidating structure–property relationships in aluminum alloy corrosion inhibitors by machine learning. J. Phys. Chem. C 124, 5624–5635 (2020).
Schiessler, E. J. et al. Predicting the inhibition efficiencies of magnesium dissolution modulators using sparse machine learning models. npj Comput. Mater. 7, 1–9 (2021).
Feiler, C. et al. In silico screening of modulators of magnesium dissolution. Corros. Sci. 163, 108245 (2020).
White, P. A. et al. Towards materials discovery: assays for screening and study of chemical interactions of novel corrosion inhibitors in solution and coatings. New J. Chem. 44, 7647–7658 (2020).
Kokalj, A. Molecular modeling of organic corrosion inhibitors: calculations, pitfalls, and conceptualization of molecule–surface bonding. Corros. Sci. 193, 109650 (2021).
Chen, R., Dewi, C., Huang, S. & Caraka, R. Selecting critical features for data classification based on machine learning methods. J. Big Data 7, 1–26 (2020).
Kubus, M. et al. The problem of redundant variables in random forests. Acta Univ. Danub. Oecon. 6, 7–16 (2018).
Darst, B. F., Malecki, K. C. & Engelman, C. D. Using recursive feature elimination in random forest to account for correlated variables in high dimensional data. BMC Genet. 19, 1–6 (2018).
Biau, G. & Scornet, E. A random forest guided tour. Test 25, 197–227 (2016).
Shulha, T. et al. In situ formation of ldh-based nanocontainers on the surface of az91 magnesium alloy and detailed investigation of their crystal structure. J. Magnes. Alloy. (2021).
Thurnhofer-Hemsi, K., López-Rubio, E., Molina-Cabello, M. A. & Najarian, K. Radial basis function kernel optimization for support vector machine classifiers. Preprint at https://arxiv.org/pdf/2007.08233.pdf (2020).
Cervantes, J., Garcia-Lamont, F., Rodríguez-Mazahua, L. & Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 408, 189–215 (2020).
Kaur, P., Pannu, H. S. & Malhi, A. K. Plant disease recognition using fractional-order zernike moments and svm classifier. Neural. Comput. Appl. 31, 8749–8768 (2019).
Bhowmik, T. K., Ghanty, P., Roy, A. & Parui, S. K. Svm-based hierarchical architectures for handwritten bangla character recognition. Int. J. Doc. Anal. Recognit. 12, 97–108 (2009).
Je, H.-M., Kim, D. & Bang, S. Y. Human face detection in digital video using svmensemble. Neural Process. Lett. 17, 239–252 (2003).
Awad, M. & Khanna, R. Efficient learning machines, p. 67–80 (Springer, 2015).
Okujeni, A. et al. A comparison of advanced regression algorithms for quantifying urban land cover. Remote Sens. 6, 6324–6346 (2014).
Wehbe, B., Hildebrandt, M. & Kirchner, F. Experimental evaluation of various machine learning regression methods for model identification of autonomous underwater vehicles. In 2017 IEEE International Conference on Robotics and Automation (ICRA), 4885–4890 (IEEE, 2017).
Fang, S., Wang, M., Qi, W. & Zheng, F. Hybrid genetic algorithms and support vector regression in forecasting atmospheric corrosion of metallic materials. Comput. Mater. Sci. 44, 647–655 (2008).
Zhi, Y., Fu, D., Zhang, D., Yang, T. & Li, X. Prediction and knowledge mining of outdoor atmospheric corrosion rates of low alloy steels based on the random forests approach. Metals 9, 383 (2019).
Liu, Y. et al. A machine learning-based qsar model for benzimidazole derivatives as corrosion inhibitors by incorporating comprehensive feature selection. Interdiscip. Sci. Comput. Life Sci. 11, 738–747 (2019).
Schölkopf, B., Luo, Z. & Vovk, V.Empirical Inference: Festschrift In Honor Of Vladimir N. Vapnik (Springer Science & Business Media, 2013).
Murphy, K. P. Machine Learning: A Probabilistic Perspective (MIT press, 2012).
Labute, P. A widely applicable set of descriptors. J. Mol. Graph. 18, 464–477 (2000).
Devinyak, O., Havrylyuk, D. & Lesyk, R. 3d-morse descriptors explained. J. Mol. Graph. 54, 194–203 (2014).
Hollas, B. An analysis of the autocorrelation descriptor for molecules. J. Math. Chem. 33, 91–101 (2003).
Mauri, A. alvadesc: a tool to calculate and analyze molecular descriptors and fingerprints. In Ecotoxicological QSARs, 801–820 (Springer, 2020).
Caballero, J. Computational modeling to explain why 5, 5-diarylpentadienamides are trpv1 antagonists. Molecules 26, 1765 (2021).
Reid, B., Agri-Minerals, P. E. & Headquarters, C. Nop petition for inclusion of magnesium oxide to the national list of substances allowed. Cell 850, 261–0807 (2013).
Case, D. R., Zubieta, J., Gonzalez, R. & Doyle, R. P. Synthesis and chemical and biological evaluation of a glycine tripeptide chelate of magnesium. Molecules 26, 2419 (2021).
Murakami, Y. Complexing behavior of kojic acid with metal ions. i. mg (ii) and mn (ii) chelates. Bull. Chem. Soc. Jpn 35, 52–56 (1962).
Kufelnicki, A. Complexes of uracil (2, 4-dihydroxypyrimidine) derivatives. part i. cu (ii), ca (ii) and mg (ii) coordination with uracil and related compounds in aqueous solution. Pol. J. Chem. 76, 1559–1570 (2002).
Schober, P., Boer, C. & Schwarte, L. A. Correlation coefficients: appropriate use and interpretation. Anesth. Analg. 126, 1763–1768 (2018).
Guyon, I., Weston, J., Barnhill, S. & Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 46, 389–422 (2002).
Pedregosa, F. et al. Scikit-learn: machine learning in python. J. Mach. Learn. Res. 12, 2825–2830 (2011).
Würger, T. et al. Data-driven selection of electrolyte additives for aqueous magnesium batteries. J. Mater. Chem. A 10, 21672–21682 (2022).
Deyab, M. Corrosion inhibition of heat exchanger tubing material (titanium) in msf desalination plants in acid cleaning solution using aromatic nitro compounds. Desalination 439, 73–79 (2018).
Aslam, J. et al. Inhibitory effect of 2-nitroacridone on corrosion of low carbon steel in 1 m hcl solution: An experimental and theoretical approach. J. Mater. Res. Technol. 9, 4061–4075 (2020).
Eddy, N. O., Ameh, P. O. & Essien, N. B. Experimental and computational chemistry studies on the inhibition of aluminium and mild steel in 0.1 m hcl by 3-nitrobenzoic acid. J. Taibah Univ. Sci. 12, 545–556 (2018).
Frisch, M. et al. Gaussian 16 revision c. 01, 2016. Gaussian Inc. Wallingford CT1 (2016).
Ju, H., Kai, Z.-P. & Li, Y. Aminic nitrogen-bearing polydentate schiff base compounds as corrosion inhibitors for iron in acidic media: a quantum chemical calculation. Corros. Sci. 50, 865–871 (2008).
Barouni, K. et al. Amino acids as corrosion inhibitors for copper in nitric acid medium: Experimental and theoretical study. J. Mater. Environ. Sci 5, 456–463 (2014).
Chang, C.-C. & Lin, C.-J. Libsvm: a library for support vector machines. ACM Trans. Intell. Syst. 2, 1–27 (2011).
Shi, H., Xiao, H., Zhou, J., Li, N. & Zhou, H. Radial basis function kernel parameter optimization algorithm in support vector machine based on segmented dichotomy. In 2018 5th International Conference on Systems and Informatics (ICSAI), 383–388 (IEEE, 2018).
Smola, A. J. & Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 14, 199–222 (2004).
Acknowledgements
Funding by the Helmholtz-Zentrum Hereon I2B project MUFfin is greatfully acknowledged. The authors thank Thermo Fisher Scientific for providing a chemical database used for the blind test selection.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
X.L., B.V., T.W., S.V.L., M.L.Z., and C.F.: contributed to the conception and design of the study. B.V. and S.V.L.: provided experimental data. X.L., T.W., and C.F.: built the two machine learning models. X.L. and C.F.: wrote the first draft of the manuscript. All authors contributed to the manuscript revision, read, and approved the submitted version.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, X., Vaghefinazari, B., Würger, T. et al. Predicting corrosion inhibition efficiencies of small organic molecules using data-driven techniques. npj Mater Degrad 7, 64 (2023). https://doi.org/10.1038/s41529-023-00384-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41529-023-00384-z
This article is cited by
-
DATACORTECH: artificial intelligence platform for the virtual screen of aluminum corrosion inhibitors
npj Materials Degradation (2024)
-
Gravimetric inhibition efficiency prediction model of AA7075-T7351 alloy using Treculia africana extract in 1.0 M HCl through input feature optimization
Surface Science and Technology (2024)