Abstract
The leading theory of primary radiation damage in materials, by Norgett, Robinson, and Torrens (NRT), assumes that materials are homogeneous. This is inadequate for most engineering materials, which have rich microstructures. The lack of alternative theories has led to the widespread assumption that the microstructure only affects defect recombination and not defect production. We extend the NRT formalism to account for microstructural variations and explicitly include the damage caused in a phase by primary knock-on atoms that are produced in another nearby phase. Our approach reveals new insight on the interplay between radiation damage and microstructure, and converges to conventional NRT at suitably large length-scales. Applying it to real two-phase nuclear alloys we discover a reversal of primary radiation damage localisation when grain size is < 1 μm: in some fine-grained superalloys more damage is produced in the matrix than the precipitates, and the opposite is true for coarse-grained superalloys of same composition.
Similar content being viewed by others
Introduction
Materials that are subject to high energy radiation undergo changes in their atomic structure, which then evolve into larger microstructural defects, often with detrimental changes to the material properties. Thus, understanding radiation-matter interaction is of paramount importance in advancing materials for a range of applications, from nuclear energy and nuclear technologies to outer space and radio-pharmaceutical production.
When a high-energy neutron interacts with a material, it displaces an atom from its original site in the crystal lattice. These displaced atoms are known as the primary knock-on atoms, or PKAs, which then go on to create subsequent cascades of atomic collisions. In this sense, the damage is not directly caused by neutron collisions, but by the interaction and stopping of PKAs displacing further atoms within the material. The total number of displacements per atom (dpa) is a common metric of the primary radiation damage in the material1. While many of the defects created by these displacements annihilate within pico-seconds of the collision event, residual defects are left behind, and their accumulation and evolution leads to range of material-specific radiation effects, such as swelling, embrittlement, growth, chemical segregation and enhanced corrosion2,3. As this microstructural evolution is primary dictated by the dose rate, exposure time, and temperature effects, accurately determining the dose rate, dpa, and how the microstructure affects them, is of utmost importance.
Methods to calculate the damage that neutrons cause to a material have been developed since the 1940’s4, and fall into one of two categories: analytical coarse-grained methods, such as the Kinchin-Pease5,6 and NRT7,8 models; and explicit atomic-scale simulations such as molecular dynamics and Monte Carlo simulations. While the former are fast and yield useful values for engineering application, they do so by approximating the material as an amorphous solid of homogeneous composition. For most engineering materials, this assumption is often inadequate. This is especially true when the mean free path of PKAs is in the range of nano- to micro-meters9, which is commensurate with that of engineering materials’ microstructures. On the other hand, atomic-scale simulations provide an accurate description of the collision cascade event, with pico-meter and femto-second resolution, but they are too costly to extend beyond nano-meter length scale and nano-second timescale. Thus, neither approach can provide information of radiation damage at the microstructural length scale. This has led to the development of multi-scale approaches10,11, which feed the results of atomic-scale simulations into larger scale models e.g., discrete dislocation dynamics, phase field modeling, kinetic Monte Carlo, or rate theory. However, these are still computationally intensive approaches that require significant user input and development.
One way to fulfill this gap, is to considers each constituent phase of a material as separate bulk phases, and perform NRT calculations on each phase separately. While this technique has provided insight in selected cases12, it assumes that all damage within a phase is caused by PKAs generated in that same phase, and that PKAs of one material do not contribute to damage in another phase, which is unphysical. This approach is only appropriate when the phases are much larger than the mean free path of the PKAs. As we show in this paper, this approach can lead to significant errors, even qualitatively wrong answers, for some engineering alloys.
When damage is caused by ions rather than neutrons, it can be accurately modelled using binary collision approximation (BCA) simulations, such as the commonly used SRIM/TRIM packages13,14. BCA uses a Monte Carlo algorithm to calculate the ion passage, deposition, and collision cascade displacements within the material7,13,14,15,16. In all BCA models, materials are assumed to be as amorphous. Consequently, they cannot account for channelling effects, which can play an important role in the angular-dependent shape and range of collision cascades17. BCA calculations have the appropriate length and time scales to account for micro-structural features and are a promising technique to bridge the gap in methodology to study spatial distribution of damage in heterogeneous microstructure. However, there is no established method to integrate the interaction between radiation and microstructural features within the BCA formalism.
The nuclear industry routinely adopts the NRT formulation because its simplicity allows for a like-for-like comparison when investigating new materials or new radiation conditions18. However, the limitations of the NRT method are important, particularly for modern superalloys, composites, and hybrid materials. Here we expand the NRT formulation, to account for spatial heterogeneities. We do so by combining both BCA and NRT theories to quantify the degree of localisation and spatial distribution of primary radiation damage production in materials with arbitrarily heterogeneous microstructures. In Section 2.1 we present an overview of the theoretical framework to expand the NRT model, with further details provided in the methods section and supplementary information. Sections 2.2–2.4 then demonstrates the method through case studies, and investigates over what length scales the method is superior to the approximation of a homogeneous material. A discussion is presented in Section 3.
Results
Theoretical framework
Our approach, which we call RAΔAЯ, aims to extend the NRT formulation to include the interplay between microstructural heterogenieties and primary radiation damage generation. In the limit of a homogeneous distribution of species, our method must collapse into the analytical NRT solution. We will show that in the limit of macroscopic, distribution of constituent phases (i.e., grains larger than PKA’s mean free path) the method also collapses into the NRT solutions applied to each phase individually.
The NRT model separates primary damage into two processes: first the incident neutron flux (ϕN) interacts with the material to produce a PKA flux (ϕPKA), according to known interaction cross-sections19,20,21. Second, the PKAs travel through the material causing further displacements. Traditional NRT theory uses the Lindhard-Scharff-Schiott (LSS) theory22,23,24 to determine the portion of the PKA energy that displaces atoms in a bulk material 8. Alternatively, this energy can be calculated from BCA simulations which describe the energy imparted to the material by the PKA as a function of depth14. In principle the total damage produced by a neutron flux can be calculated with a set of BCA simulations: one set for every PKA species and for every PKA energy that is created by the neutron flux, with the results summed and weighted accordingly25,26. For a homogeneous single-phase material, this is a large but feasible set of calculations.
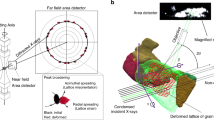
To apply this approach to heterogeneous microstructures, one must consider that the PKAs will cross the interface between two different phases. The damage produced in a uniform small volume of material (a target voxel) is caused by all PKAs generated in all other (source) voxels within a sphere of radius ∣r−r0∣ as shown schematically in Fig. 1. Some of these voxels may reside in a different phase, and across one or more interfaces.
Mathematically, we describe the damage K as
where S is the number of PKAs generated isotropically at the source voxel given a neutron flux ϕN, F is the fraction of those PKAs whose path intersect the target voxel, and f is the damage per ion that the target voxel experiences due to those PKAs. S is obtained by interrogating databases of known nuclear interaction cross-sections (see Methods); F is derived deterministically using a geometric argument presented in the Methods section, however, it could also be calculated through statistical sampling. f is not known a-priori. In principle f could be calculated explicitly from a large set of BCA simulations, if these were repeated with statistical significance for each PKA species, PKA energy, source location, source direction and interface distance. This is computationally intractable for any geometry more complex than an infinite planar 2D interface. We propose a computationally efficient and accurate way to reduce the parameter space, which results in an analytical description of f. An overview is provided below, and a detailed derivation is given in the Methods section. In the result section, this is validated against a set of explicit BCA calculations for simple planar interfaces (section 2.2) before applying it to solve Eq. (1) for arbitrary (section 2.3) and realistic (section 2.4) microstructures.
The parameter space of f was reduced by removing the interface distances as a simulation parameter and predicting damage profiles from the BCA damage profiles of the constituent (bulk) phases. Damage in a single phase is defined as a function of the PKA energy, and fitted to a continuous function that is consistent with LSS theory22,23,24,27. The function is linear in the limit of the electronic stopping regime and is a power-law in the limit of the nuclear stopping regime. The damage profile across an interface is then taken by splicing the (fitted) damage profiles of the constituent bulk phases, such that the PKA energy is continuous. This means the damage profile is not a continuous function of the distance, but is a continuous function of PKA energy. This is illustrated schematically in Fig. 2, where a PKA creates two different damage profiles (represented by the ovals) in the two materials (left and right). Each damage profile has a characteristic range (length of oval) and magnitude of damage (width of oval), and the PKA reaches given energies E1 and E2 at two different distances. In a composite material (central cartoon), the damage is approximated by the damage that the same PKA creates in the constituent bulk phases when it has the same energy, which may not be at the same distance.
Blue indicates material A and orange indicates material B. Ovals indicate the displacement cascade within the material, where the width of oval represents the magnitude of displacements and the length represents the depth at which displacements occur. The horizontal lines represent the distance in the different materials at which the PKA reaches a specific energy. a, c Show the damage profile in pure materials. b Shows the damage profile in the composite material.
Method validation
For validation, we compare the predictions from the current method to explicit BCA calculations of damage profile across a planar interface for a range of PKA initial energies, material compositions, and interface distance. Difference curves between the explicit BCA simulation and the proposed approximation for all combinations are provided in the supplementary information. Figure 3 shows two representative examples of such radiation damage profiles, with the absolute damage curves shown in the top panel, where the black line is the explicit BCA simulation, and the coloured lines are from the proposed approximation. The difference curve is shown in the bottom panel. In this example, a 100 keV Fe ion crosses an interface at 20 nm between Fe and Al layers.
Shown are a 100 keV Fe ion across an a Fe-Al interface and b Al-Fe interface at 20 nm from the surface. Shading represents the composition of the materials (red=Al, blue=Fe). Top panels: Damage profiles. Black line shows the exact profile, calculated with explicit BCA simulations of the layered materials. Coloured lines show the predicted damage of the novel method, using the piecewise damage function in Eq. (13). Bottom Panel: Difference curve between the exact profile and proposed method.
Our method (coloured lines) of using the damage profiles in constituent phases is in good agreement with the explicit BCA simulation of the composite structure (black line). There is a sharp discontinuity at the interface of the explicit calculation due to the sudden change in threshold displacement energy, Ed, and cascade chemical composition. This effect is discussed in greater detail in later sections. While the method does not capture the exact profile at the discontinuity, the agreement is excellent beyond a few nano-meters from the interface, where the cascade particles of the neighbouring phase have come to rest and all new damage is caused by particles of same chemistry as the phase in which they travel.
Extensive statistical analysis was performed to evaluate the accuracy of the method. From all simulations conducted, across the whole length of the profiles 90% of points had an error of less than 5.7%. The error is strongly correlated with the relative difference in atomic number ΔZ between the two material layers, with materials that have similar Z having minimal discrepancies. This is shown in Fig. 4a, where the mean and standard deviation of the error for each material pair are plotted as a function of ΔZ. Large discrepancies between the profiles were also found to only occur in the very near vicinity of the interface. The average and standard deviation of the distance from the interface where the error exceeds 10% is shown in Fig. 4b. This is again correlated with ΔZ, and with all large errors occurring within 40 nm of the interface. ∣ΔZ∣ is usually much less than 20 for most engineering alloys, and average errors are therefore less than 2%, and are concentrated within 2 nm–5 nm of the interface. For the microstructures and chemical compositions considered in this paper, the size of the distribution features observed are larger than this narrow region and are hence cannot be artifacts of the method. This provides confidence in using our analytical formulation to perform high-throughput calculations across arbitrary interfaces.
In essence, the method predicts the radiation damage profile by a PKA (or any ion) in a multi-phase material/composite using only the damage and energy profiles of the PKA in the constituent phases. One direct application of the method is in parametric studies of ion irradiation of layered materials. Greater benefit becomes apparent when investigating more complex 2D and 3D microstructures, which would not be feasible using explicit BCA calculations.
Application to a model microstructure
Figure 5 shows an example application of the RAΔAЯ method using Eq. (1), applied to an idealised 2D microstructure containing a circular particle of W/Mg (white phase) with radius 50 nm embedded in a matrix of Al/Fe (black phase). The top half of the figure shows the microstructure, while the bottom half of the figure shows the resulting spatial distribution of primary radiation damage when the microstructure is exposed to a typical pressurised water reactor (PWR) neutron flux. The particle and the matrix experience substantially different rates of damage when exposed to the same neutron flux. There is a distribution in damage in both phases approaching the interface, due to the transmission of PKAs between the phases.
In the case of W embedded in Al, the damage in W decreases near the edges of the particle, while the damage in Al increases near the interface. This can be explained by the fact that heavier W PKAs produce more damage than Al PKAs in the Al phase, and the inverse occurs in the W phase, where Al PKAs from the Al phase produce less damage than W PKAs. An inverted distribution is observed in the Fe/Mg system, where less damage is produced in the Mg particle compared to the Fe matrix, and a discontinuity is observed at the interface, with a minimum at the edge of the matrix and a maximum at the edge of the particle. This is due to self-screening effects discussed below.
Application to a real alloy’s microstructure
Figure 6a, modified from Teng et al.28, shows a ferritic superalloy that has an Fe matrix and NiAl secondary phase precipitates29,30. This material was selected because the two phases it comprises have similar physical and nuclear properties, thus it is an ideal candidate for the NRT assumptions of homogeneity. Specifically, the supperalloy contain both light (Al) and heavy (Fe/Ni) elements, with similar thermal neutron scattering cross sections (σFe ≈ 12b, σNiAl ≈ 10b), slightly different atomic densities (NFe = 8.5 × 1022 cm−3, NNiAl = 4.9 × 1022 cm−3) and the same threshold displacement energies (Ed,Fe = Ed,NiAl = 40 eV). Yet, our results show that the damage production, even in this system, is far from homogeneous: figure 6b–d shows the spatial distribution of primary radiation damage in the material calculated (b) using the NRT formula, which assumes the material to be homogeneous, (c) treating each phase as a bulk isolated material and applying NRT to each separately, and (d) with our method, which explicitly accounts for microstructural complexity. A common colour scale is used for figures (b–d).
a TEM image modified from ref. 28 showing sample microstructure (light phase is NiAl, dark phase is ferrite). Bottom row shows the calculated dpa using: the NRT formula for a homogeneous mixture (b); the NRT formula of each phase separately (c); our proposed method, RAΔAЯ, which explicitly takes into account the microstructure (d).
The assumption of homogeneity is not applicable here, as it fails to capture the significant difference in radiation damage rate in the two phases — up to 30% extra damage in the Fe matrix compared to the NiAl precipitates. Interestingly, when the phases are treated in isolation (i.e., they are assumed to be large enough that all damage is caused by PKAs generated within the same phase), the results are qualitatively opposite to those of our method. This discrepancy is entirely explained by PKAs travelling from one phase into the other, where they may be able to do more or less damage per unit distance travelled, depending on their mass, kinetic energy and material’s Ed.
To confirm that this is not an artifact of our method, but a physical insight into the interplay of microstructure and primary radiation damage, we repeat the calculations on microstructures with increasingly larger grains (see Fig. 7), which shows that our method converges to the results of the macroscopic approximation for sufficiently large particles (of order 100 μm in the case of Fe/NiAl). At some large length scale, most of the damage in a phase is produced by PKAs originating within the same phase, and so each phase can be treated separately as a bulk material as done previously12, except for a thin boundary region near the interface. We find this assumption holds when the particle diameter or grain size exceeds twice the dominant PKA’s range. However, if at least one of the phases is smaller, the approximation of the independent bulk phases results in local under- or over-estimation of the damage production rate, and may even affect the macroscopic average damage production rate. We have observed a similar behaviour in several other engineering alloys used int he nuclear industry, including nickel superalloys and Zr alloys. This finding cautions against treating constituent phases of a material separately, as that can be a worse approximation than assuming a homogeneous solid solution.
Our method also reveals that there is substantial variation within each phase, as shown in figure 6d. In the Fe matrix phase, regions surrounded by a high density of secondary phase receive substantially more damage than regions further away from precipitates. This difference is due to the effects of the microstructure on the PKA paths. The lighter Al PKAs generated within the NiAl phase, leave their phase of origin and approximately a third of the total ballistic energy is deposited in the matrix, as shown in Fig. 8. Conversely, the heavier Fe and Ni PKAs remain localised to their origin phase and do not cause significant damage in the neighbouring phase.
Discussion
The combined results of the previous section show that phase composition and morphology of a microstructure have remarkable effects on the spatial distribution of primary radiation damage production. Importantly, this interplay between radiation damage production and microstructure is independent of any additional effects that interfaces may have on the recombination of defects after they are produced. The latter is a well-studied phenomenon31,32,33, which has driven the development or radiation-tolerant materials for the last decade34,35,36. In fact, the assumption that primary damage production cannot be controlled is so widespread that defect recombination is often ascribed as the only contributing factor to radiation tolerance of a material31,33. However, in light of the current findings, it is possible that in some cases part of the benefit of refined grain sizes lies in a reduced defect production rate, in addition to the well-documented enhanced defect recombination rate.
This paper introduces a general framework to calculate the interplay between microstructure and primary radiation damage distribution. This framework is formally exact, but requires a prohibitive number of calculations (e.g., BCA simulations) to be applied to realistic microstructures. Thus, we introduce a method, called RAΔAЯ, to predicting the damage profile of a PKA as it crosses an interfaces based solely on the PKA energy-damage profile of the parent materials. The RAΔAЯ method was validated against explicit BCA calculations of damage across planar interfaces, and was shown to produce accurate results, with < 5% root mean square error and a computational saving of 6+ orders of magnitude. Specifically, calculations such as Fig. 6 are performed in the order of 100 cpu hr, while it would take 5.4 × 109 cpu hr to obtain the same results through a large set of conventional BCA simulations (see SI for calculation details), which is clearly impracticable.
The computational speed-up, which is central to our method, becomes even greater in 3D volumes, and for 2D images that are larger and/or have higher resolution than the ones presented here. The computational gains are chiefly due to the high-throughput approach to calculating radiation damage across planar interfaces, which reduces the parameter space of the BCA simulations that need to be run: simulations need only be run for each PKA species and energy in the constituent materials. They do not need to be run for all possible interface permutations that the PKA will encounter — other than for validation purpose as shown in section 2.2. Additionally, the data generated is used to create a library that can be reused for later simulations. This makes our approach highly scalable, and it becomes progressively faster as more materials are added to the database.
The best accuracy in our benchmark is obtained when the interfaces are very close or very far from the location where the PKA is produced. For shallow interfaces, the collision cascade has not developed enough to alter the profile in the post-interface material, resulting in minimal discrepancy. For deep interfaces, most of the profile remains that of the initial material, with minimal region afterwards in which a discrepancy can occur. For intermediate interface depths, where the discrepancy is largest, it remains below 5% for all test cases. This provides an estimate for the uncertainty in the results, when the method is applied to 2D or 3D micro-structures. The results shown in the previous section show local deviations in radiation damage rate in the order of 30%, which is well above the uncertainty of the method.
A surprising insight from the RAΔAЯ method is that sometimes the primary radiation damage exhibits a maxima and or minima on either or both sides of an interface, while other times it results in a monotonic transition from one phase to another. The behaviour depends on the combination of the chemical species (specifically their cross-sections and atomic mass/charge), the atomic density N and the threshold displacement energy Ed of the phases. The relative contribution of each of those three variables is analysed in Fig. 9, which shows the damage distribution between a natural Fe matrix (Ed = 40 eV, N = 8.49 × 1022 cm−3), and a particles of diameter 1 μm made of a fictitious Fe-like material that shares the same material properties as true Fe except for one parameter: in one case (dashed orange line) the atomic density N is doubled, in the second case (dot-dashed green line) Ed is doubled, and in the third case (solid blue line) the atomic mass and charge have been changed to that of Al (which has approximately half the mass and charge of Fe).
Changing only Ed causes a proportional reduction in damage, with the material with double the Ed experiencing half the dpa, in agreement with the NRT formulation, and no other significant effect at the interface. When the density is changed, a screening effect is observed. In the denser phase, the PKAs cannot travel as far as they would in the less dense phase. Therefore fewer particles originating from the denser phase can reach the less dense side of the interface to cause damage. This results in a localised minimum damage region in the less dense phase, and a localised maximum in the denser phase. Far from the interface the profile has the same value, as the dpa in homogeneous materials is independent of density, in agreement with NRT theory. When the chemical species is changed, a similar screening effect is seen. The range of a PKA is dependent on the mass and charge of the PKA, with heavier and higher charged ions travelling shorter distances. As a result, the phase with heavier constituent atoms plays the same role as the denser material, and vice versa. The local maxima and minima are much more pronounced in this case as both the mass and charge of Al are approximately half that of Fe, both contributing to the PKA range, and hence screening effect.
In a real material, combinations of the above effects will be observed. This is further complicated by the fact that the damage experienced by each phase will strongly depend on the nuclear cross-sections of the isotopes in both phases for the given flux. The cross sections determine how many PKAs of each energy are produced and are available to cross the interface and interact with the second phase, while also altering the amount of damage experienced by the phase in which they originate. Importantly, considering individual interface effects will not reveal a-priori how the effects will combine at a given length scale, as evidenced in Fig. 6, and what will happen when multiple secondary phases are in close proximity to each other with overlapping interface effects.
Applying the RAΔAЯ approach to real-life alloys, we gain physical insight into the interplay between microstructure and radiation damage. Taking the example of a ferritic superalloy designed for nuclear applications (ferrite with NiAl precipitates of ~100 nm size), and exposing it to a typical PWR neutron flux, we show that widely used assumption of homogeneity is inadequate, even when the constituent phases have similar physical and neutronic properties (such as Fe and NiAl). One finding obtained from our method is that performing NRT calculations on the constituent phases (i.e., treating them as separate macroscopic phases) can lead to less accurate results than the assumption of homogeneity. In the example of the ferritic superalloy, our approach shows that the NiAl particles receive 30% less damage than the surrounding ferrite matrix, which is the opposite of what is predicted by NRT calculations carried out on phase separately as independent bulk phases. More precisely, this is a relative error of 106%. The discrepancy is entirely explained in terms of the transport of PKAs across phases: when a two-phase microstructure is sufficiently refined, a substantial fraction of the total damage is caused by PKAs that originate in another phase. This can lead to a reduction in damage in one phase and an increase in another, or local changes within a phase due to proximity to another phase. The key determining factor for this effect is the length scale of the microstructure, compared to the average range of the PKAs. In sufficiently large grains (approximately double the average range of the PKAs) our results converge to those obtained from NRT calculations of macroscopic bulk phases. However, for most modern engineering alloys and composites, we caution against making assumptions of homogeneity, or assuming (macroscopic) bulk phases; instead we recommend using the method proposed above.
Methods
Computational details for neutron and BCA calculations
All calculations were performed using a sample isotropic neutron flux for the core of a pressurised water reactor (PWR) 37. For each material considered, the resulting PKA fluxes were calculated using the SPECTRA-PKA code38, with a resolution of 2 logarithmically spaced bins per magnitude (see supplementary information for neutron flux and convergence details).
BCA simulations were carried out using the iradina software39, with incident ion energy equal to the logarithmic mid point of the PKA bins. For each BCA simulation, 105 ions were run. 100 equally spaced cells were used, and the simulation length was set to 1.1 times the PKA range 9. The PKA energy-depth profile in a material is obtained by running a simulation in the “Quick Calculation” mode and subtracting the energy deposited in each cell (the sum of the electronic and ballistic energies) from the initial PKA energy E0. The damage-depth profile is calculated using the method developed by Stoller14 and modified by Crocombette and Wambeke40, whereby the ballistic energy available for displacements obtained from “Full Cascade” simulations is used in the NRT formula.
Deterministic calculation of the spatial distribution of primary radiation damage
The term S, F and f of Eq. (1) are detailed here. The source term S is
where the PKA flux, ϕPKA, is calculated from neutron cross-sections databases using SPECTRA-PKA19,20,21, and Ns and V are the number density, and volume of the source voxel, respectively. Voxels are cubic with side length p.
For an isotropic neutron flux, PKAs are generated isotropically, and a simple conservation argument can be used to determine the solid angle fraction, F3D, of PKAs that a target voxel at a distance ∣r−r0∣ from the PKA source receives. In three dimensions, this is
where the area of the voxel that the sphere intersects is approximated as the square face of the voxel p2. In two dimensions voxels are equivalent to image pixels, and F becomes
For non-isotropic fluxes, e.g., ion irradiation experiments, equations (3) and (4) can be multiplied by an angular weighting function to account for the angular distribution of PKA production. In this formulation, there is no net loss/gain of PKAs by leaving/entering the plane of the image. Consideration about finite size effects are discussed below.
Finally, the PKA flux that interacts with the target voxel is converted into a damage rate through the function f, which combines the NRT theory with BCA results. Specifically,
where the ballistic energy per ion T is deposited into each BCA cell of pre-specified length l at location r. In the next section, we outline how this energy is calculated when the PKA crosses an interface. T is then normalised to the size of the voxel, \(\frac{p}{l}\), and used to calculate the number of atomic displacements in each voxel following the NRT model. The last term converts this quantity to dpa/s by dividing by the atomic density Nt and volume V of the target voxel.
Analytical solution for the damage distribution across interfaces
The decay of an ion’s kinetic energy through a material occurs in two regimes; a linear region due to electronic stopping, followed by a power law region due to nuclear stopping. This change in regimes occurs when the particle has a reduced LSS energy22,23,24 of approximately ϵLSS = 0.327. We produce analytical energy-depth profiles by fitting the average energy as a function of depth, E(r), of a PKA with initial energy E0, to the function 27
where A, m and c are parameters. As the energy loss of the PKA must be smooth and continuous between the two regimes, m and A can be solved to give
where d, c and ϵ are fitting parameters. If the PKA is created with an energy that immediately places it within the nuclear stopping regime, ϵ = E0, and A further reduces to
The energy available for displacements is the sum of the PKA energy and the energy contained within the cascade particles. As a first-order approximation, we assume that the spatial distribution of cascade particles, and the displacements they cause at a given location, is only dependent on the initial energy of the PKA, E0, and the current energy of the PKA at that location, E. The damage profile that a PKA generates in a second phase across an interface is therefore the same profile that an equivalent PKA would produce if it had originated from within the second phase with the same initial energy E0, and was offset such that the current PKA energy E was the same. We express the PKA ballistic energy available to cause damage, T, at a given distance r from the source as
where Tdam,r is the BCA average damage-energy profile of the specified PKA in the constituent material at location r, and is not explicitly dependent on the location of interfaces in a composite. However, T is implicitly dependent on the interface locations, as the energy at given distance from the source in a composite material is not known a-priori and must be found by using the average energy-depth profiles given in Eq. (6). The PKA energy is obtained by the function \({{{\mathcal{E}}}}\)
where x is the array of interface locations. \({{{\mathcal{E}}}}\) is a piecewise function such that before an interface the energy-depth profile is that of the first material, and after the interface, the energy-depth profile is that of the second material with the depth offset such the profile is continuous at the interface. For a series of layers (A, B, C,...) the ballistic energy can hence be expressed as
Finite size effects
The damage produced in a target voxel is due to the sum of all PKAs originating in all neighbouring voxels within one PKA range, as described by Eq. (1) and Fig. 1. As the simulation volume is necessarily finite, one must take into account the contribution of PKAs originating outside the simulation volume, to avoid an artificial reduction in damage near the simulation’s edge. Several approaches exist to solve the problem either exactly or approximately, including the use periodic boundaries, reflective boundaries, tessellation and buffer layers.
For model microstructures, we partition the simulation volume into an inner region (the window) and a surrounding region (the buffer). Only the results of the window are shown here. Given that the the range of PKAs is known a priori, it is possible to counter the finite size effects entirely by using a buffer layer of width equal to maximum PKA range. In practice, suitable convergence is obtained with substantially narrower buffer layers, since the average PKA range is much lower than the maximum PKA range, which is dominated by few PKAs with high energy (details in supplementary information).
For real microstructures, we padded the region of interest with replicas of the same image, flipped and tiled to ensure a continuous boundary at the edge of the simulation. This effectively creates a fictitious but representative volume of material to use as buffer, and in the limit of a large cell, it is equivalent to applying reflective boundary conditions. Further details are provided in the supplementary information.
Data availability
The data that support the findings of this study, beyond what is provided in the supporting information, may be available from the corresponding author upon reasonable request.
Code availability
The code used to produce the findings of this study may be made available by contacting the authors, subject to export controls checks and non-disclosure agreements.
References
Nordlund, K. et al. Primary radiation damage: A review of current understanding and models. J. Nucl. Mater. 512, 450–479 (2018).
Raj, B. & Vijayalakshmi, M. Ferritic steels and advanced ferritic-martensitic steels. In Comprehensive Nuclear Materials, 97–121 (Elsevier, 2012).
Zinkle, S. Radiation-induced effects on microstructure. In Comprehensive Nuclear Materials, 65–98 (Elsevier, 2012).
Wigner, E. P. Theoretical physics in the metallurgical laboratory of Chicago. J. Appl. Phys. 17, 857–863 (1946).
Kinchin, G. H. & Pease, R. S. The displacement of atoms in solids by radiation. Rep. Prog. Phys. 18, 1–51 (1955).
Kinchin, G. H. & Pease, R. S. The mechanism of the irradiation disordering of alloys. J. Nucl. Energy 1, 200–202 (1955).
Torrens, I. M. & Robinson, M. T. Computer simulation of atomic-displacement cascades in solids in the binary-collision approximation. Phys. Rev. B 9, 5008 (1974).
Norgett, M. J., Robinson, M. T. & Torrens, I. M. A proposed method of calculating displacement dose rates. Nucl. Eng. Des. 33, 50–54 (1975).
Ziegler, J. F. & Biersack, J. P. The stopping and range of ions in matter. In Treatise on Heavy-Ion Science, Vol. 6, 93–129 (Springer US, 1985).
Gilbert, M. et al. Perspectives on multiscale modelling and experiments to accelerate materials development for fusion. J. Nucl. Mater. 554, 153113 (2021).
Nordlund, K. Historical review of computer simulation of radiation effects in materials. J. Nucl. Mater. 520, 273–295 (2019).
Adrych-Brunning, A., Gilbert, M. R., Sublet, J.-C., Harte, A. & Race, C. P. Modelling the interaction of primary irradiation damage and precipitates: Implications for experimental irradiation of zirconium alloys. J. Nucl. Mater. 498, 282–289 (2018).
Ziegler, J. F. SRIM-2003. Nucl. Instrum. Methods Phys. Res. Sect. B 219-220, 1027–1036 (2004).
Stoller, R. et al. On the use of SRIM for computing radiation damage exposure. Nucl. Instrum. Methods Phys. Res. Sect. B 310, 75–80 (2013).
Robinson, M. T. Computer simulation studies of high-energy collision cascades. Nucl. Instrum. Methods Phys. Res. Sect. B 67, 396–400 (1992).
Smith, R. Atomic and Ion Collisions in Solids and at Surfaces (Cambridge University Press, 2005).
Robinson, M. T. The binary collision approximation. Radiat. Eff. Defects Solids 1, 3–20 (1994).
ASTM Standard E521-16. Standard Practice for Investigating the Effects of Neutron Radiation Damage Using Charged-Particle Irradiation.” ASTM International, West Conshohocken, PA, Pages 1-21, https://doi.org/10.1520/E0521-16, (2016).
Gilbert, M. R., Marian, J. & Sublet, J.-C. Energy spectra of primary knock-on atoms under neutron irradiation. J. Nucl. Mater. 467, 121–134 (2015).
Gilbert, M. R. & Sublet, J.-C. Pka distributions: Contributions from transmutation products and from radioactive decay. Nucl. Mater. Energy 9, 576–580 (2016).
Gilbert, M. R. & Sublet, J.-C. Differential dpa calculations with spectra-pka. J. Nucl. Mater. 504, 101–108 (2018).
Lindhard, J., Nielsen, V. & Scharff, M. Integral equations governing radiation effects. Mat.-Fys. Medd. - K. Dan. Vidensk. Selsk. 33, 10 (1963).
Lindhard, J., Scharff, M. & Schiott, H. E. Range concepts and heavy ion ranges. Mat.-Fys. Medd. - K. Dan. Vidensk. Selsk. 33, 14 (1963).
Lindhard, J., Nielsen, V. & Scharff, M. Approximation method in classical scattering by screened coulomb fields. Mat.-Fys. Medd. - K. Dan. Vidensk. Selsk. 36, 1–31 (1968).
Mohammadi, A., Hamidi, S. & Asadabad, M. A. The use of the SRIM code for calculation of radiation damage induced by neutrons. Nucl. Instrum. Methods Phys. Res., Sect. B 412, 19–27 (2017).
Saha, U., Devan, K. & Ganesan, S. A study to compute integrated dpa for neutron and ion irradiation environments using SRIM-2013. J. Nucl. Mater. 503, 30–41 (2018).
Winterbon, K. B., Sigmund, P. & Sanders, J. B. Spatial distribution of energy deposited by atomic particles in elastic collisions. Mat.-Fys. Medd. - K. Dan. Vidensk. Selsk. 37, 5–70 (1970).
Teng, Z. K. et al. Characterization of nanoscale NiAl-type precipitates in a ferritic steel by electron microscopy and atom probe tomography. Scr. Mater. 63, 61–64 (2010).
Huang, S. et al. Effect of al on the NiAl-type b2 precipitates in ferritic superalloys. Metall. Mater. Trans. A 43, 3423–3427 (2012).
Song, G. et al. Ferritic alloys with extreme creep resistance via coherent hierarchical precipitates. Sci. Rep. 5, 16327 (2015).
Odette, G., Alinger, M. & Wirth, B. Recent developments in irradiation-resistant steels. Annu. Rev. Mater. Res. 38, 471–503 (2008).
Ackland, G. Controlling radiation damage. Science 327, 1587–1588 (2010).
Bai, X.-M., Voter, A. F., Hoagland, R. G., Nastasi, M. & Uberuaga, B. P. Efficient annealing of radiation damage near grain boundaries via interstitial emission. Science 327, 1631–1634 (2010).
Beyerlein, I. et al. Radiation damage tolerant nanomaterials. Mater. Today 16, 443–449 (2013).
Demkowicz, M. J., Bellon, P. & Wirth, B. D. Atomic-scale design of radiation-tolerant nanocomposites. MRS Bull. 35, 992–998 (2010).
Han, W. et al. Design of radiation tolerant materials via interface engineering. Adv. Mater. 25, 6975–6979 (2013).
FISPACT-II. Reference input spectra (2018). https://fispact.ukaea.uk/wiki/Reference_input_spectra.
Gilbert, M. R. Spectra-pka is available as a utility within fispact-ii and now also available to download from GitHub at. (2018). https://github.com/fispact/SPECTRA-PKA.
Borschel, C. & Ronning, C. Ion beam irradiation of nanostructures – a 3d monte carlo simulation code. Nucl. Instrum. Methods Phys. Res., Sect. B 269, 2133–2138 (2011).
Crocombette, J.-P. & Wambeke, C. V. Quick calculation of damage for ion irradiation: implementation in iradina and comparisons to SRIM. EPJ Nuclear Sci. Technol 5, 7 (2019).
Acknowledgements
This research was supported by an Australian Government Research Training Program (RTP) Scholarships. MIB acknowledges the Tyree foundation for financial support through a philanthropic Tyree UNSW nuclear engineering scholarship.
Author information
Authors and Affiliations
Contributions
M.I.B. (first author) performed all the calculations, data analysis, and theory implementation, and drafted the manuscript. E.G. Obbard contributed through insightful discussion, interpretation of the data, and providing computational hardware. P.A.B. (corresponding author) contributed to conception, supervision, computational design, and financial support. All authors contributed to editing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Brand, M.I., Obbard, E.G. & Burr, P.A. Spatial distribution of primary radiation damage in microstructures. npj Mater Degrad 7, 23 (2023). https://doi.org/10.1038/s41529-023-00337-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41529-023-00337-6