Abstract
In this work, we developed a QSAR model using the K-Nearest Neighbor (KNN) algorithm to predict the corrosion inhibition performance of the inhibitor compound. To overcome the small dataset problems, virtual samples are generated and added to the training set using a Virtual Sample Generation (VSG) method. The generalizability of the proposed KNN + VSG model is verified by using six small datasets from references and comparing their prediction performances. The research shows that for the six datasets, the proposed model is able to make predictions with the best accuracy. Adding virtual samples to the training data helps the algorithm recognize feature-target relationship patterns, and therefore increases the number of chemical quantum parameters correlated with corrosion inhibition efficiency. This proposed method strengthens the prospect of ML for developing material designs, especially in the case of small datasets.
Similar content being viewed by others
Introduction
Corrosion is an electrochemical process between metal surfaces and a corrosive environment that can cause huge losses in various industrial fields, especially in the oil and gas industries1,2. One of the most economical and effective strategies to prevent metal damage due to corrosion is the use of corrosion inhibitors2,3,4. Various organic compounds have been used as corrosion inhibitors to protect metals, for example, nitrogen-containing heterocyclic compounds such as imidazole derivatives, benzimidazoles, and pyridines5, plant extracts6,7,8, and commercial drugs9,10. Experimental and theoretical investigations based on density functional theory (DFT) in evaluating various candidates for potential inhibitor compounds require intensive resources, costs, and time. Nowadays, the machine learning (ML) based quantitative structure-activity relationships (QSAR) approach has become a reliable method in revealing the relationship between structural properties of chemical compounds and biological activities. The approach is widely used to explore various inhibitor candidate compounds11,12,13,14 because the electronic properties and chemical reactivity can be quantified against the structure compound chemistry.
Quantum chemical descriptors derived from DFT calculations15 and molecular dynamics simulations16 have been implemented in the development of QSAR models using various ML algorithms to evaluate inhibitor performance. An artificial neural network (ANN) model was applied to predict the corrosion inhibition potential of 11 thiophene-derived compounds with 7 quantum chemical descriptors, resulted in a determinant coefficient (R2) of 0.95817. The ANN was also used to predict the efficiency of corrosion inhibition in a chloride solution of 28 amino acids with 12 quantum chemical descriptors, resulted in R2 of 0.999 and a predictive sum of squares 19.18118. Quadri et al.19 reported that the ANN model implemented on a dataset of 20 pyridazine derivatives gave a root mean square error (RMSE) value of 10.5637. Another QSAR study was also developed to predict 41 pyridine-quinoline-derived compounds with 20 quantum chemical descriptors using a combination of Genetic Algorithm and ANN (GA-ANN) with an average value of RMSE = 8.8%20. Liu et al.21 used an SVM model with 11 descriptors to evaluate 20 benzimidazole derivatives, reported correlation coefficient (r) and RMSE values of 0.9589 and 4.45, respectively. Meanwhile, several other literatures discussing corrosion reported that ANN and support vector machine (SVM) were unreliable when applied to small datasets22,23. Beltran-Perez et al.24 developed an Autoregressive with Exogeneous Inputs ARX model for examining commercial drugs as corrosion inhibitors in steel.
The number of features and samples of the datasets in the studies reported above range from 7 to 20 and 11–69, respectively, this might be classified as small datasets. Research25 mentioned that small dataset problems refer to the case of small amount of samples, where the number of samples is less than 50 in respect to engineering applications or less than 30 in regard to academic research. Since the availability of high-quality datasets is a key factor in ML for corrosion26,27, then its related model must have a sufficient number of samples28. Small datasets cannot fully reveal all population features due to lack of information29, and these lead to overfitting28,29, bias30,31, decreased accuracy32,33, poor generalization skills34, and often make learning algorithms difficult to produce accurate predictions35. Solving small dataset problems is important in developing a QSAR model for predicting corrosion resistance with a limited number of data samples.
Most ML research for corrosion aims to improve the accuracy of a predictive model. For that reason, Roy et al26. used descriptors selection for predicting corrosion resistance in multi-principal element alloys. Their feature selection preprocessing showed both promise and perils of using ML for such a complex chemical phenomenon. We develop an ML-based QSAR model using the K-Nearest Neighbor (KNN) equipped with VSG method to evaluate the corrosion inhibition performance of inhibitor compounds derived from a series of datasets found in previous studies. The KNN method is chosen because, among learning algorithms, it is the simplest and has good performance when working with small datasets36. Meanwhile, virtual sample generation (VSG) is chosen because it is the most prominent and popular technique for solving small dataset problems, namely by adding virtual samples to the training data25. In this study, all quantum chemical descriptors are considered important features and the addition of virtual samples to the training is intended to increase their relevance and correlation with the target of inhibition efficiencies.
Following the introduction, materials and methods are described in more detail covering datasets, quantum chemical descriptors, KNN algorithm, virtual sample generation method, model development and validation, and assessment metrics. Furthermore, the results of the research are presented along with discussions aimed at knowing the determination of the model and its performance advantages when compared to the previous models. This paper concludes that the KNN + VSG model is proven to outperform the previous model, and that the VSG method is very appropriate to be applied in the field of material sciences of small datasets.
Results and discussion
Correlation analysis
Small datasets have at least two characteristics, namely, uneven distribution of observations and the high-value gap between data. These are problems for machine learning algorithms to learn patterns accurately35. Virtual samples are generated and added to the training in hopes of addressing the problems. To illustrate how virtual samples help the ML algorithm to learn, in the following, we give an example of adding virtual samples affects the distributions of a descriptor ELUMO against IE and their histograms for the thiophene and its derivatives dataset. Figures 1a, 2a, b show the characteristics of a small dataset with an uneven distribution and a high-value gap between data. The addition of virtual samples makes the distribution more even and the gap between data values becomes smaller as shown in Figs. 1b, 2c, d. With this improved distribution and histogram, the algorithm more easily recognizes patterns even though the number of actual data is small35.
The effect of adding virtual samples is further analyzed using correlation calculation to see the strength of the relationship between the descriptors and the corrosion inhibition efficiency (IE). Some literatures37,38,39 used these calculations of correlation for their feature selection method to get an increase in the model accuracy. The features that correlate with the target are selected to get the best model38,40. This study uses the Spearman correlation coefficient as in Eq. (5) with a 95% confidence interval or a 5% significance level to describe how sensitive the IE responses to the increase or decrease of monotonous descriptors. The sign 1 means both the descriptor and IE samples are correlated (p value <0.05). The sign 0 means the two samples are not correlated (p value ≥0.05). Tables 1–7 present a complete picture of the effect of adding virtual samples to the learning of the KNN algorithm on the correlation between each descriptor and the IE target for all datasets.
It can be seen in Table 1, based on the p value of 0.05, there are only four descriptors that are correlated with the IE target, namely Hammet constant, ELUMO, energy gap, and molecular volume, while three other descriptors (dipole moment, EHOMO, molecular surface area) are not correlated (sign = 0). This situation reduces the ability of ML algorithms to recognize patterns. With the addition of virtual samples, there is an improvement in the status of the three descriptors so that all descriptors are correlated with IE (sign = 1). The addition of virtual samples improves the correlation between descriptors and the target for the Thiophene and Its Derivatives dataset. This is the status that every ML algorithm expects in recognizing patterns. In Table 2, for the Benzimidazole Derivatives dataset, there is only 1 descriptor (EHOMO) not correlated with IE. The use of virtual samples improves the status of this descriptor so that the whole descriptors of the dataset are correlated with IE, making it easier for the ML algorithm to capture the pattern.
Table 3 shows that for the Amino Acids, as many as 8 features are not correlated with IE, namely: EHOMO, adsorption energy, total energy, dipole x, dipole y, dipole z, molecular surface area, and molecular volume. In such circumstances, the performance of the ML algorithm is not optimal because the number of uncorrelated features is more than that of their correlated counterparts. The addition of virtual samples reduces the level of feature uncorrelatedness to only 1 feature, namely molecular volume. On the Pyridines and Quinolones dataset that consists of 20 descriptors (Table 4), the addition of virtual samples improves the status of descriptor’s correlation. Learning without virtual samples results in 15 correlated and the remaining five are not correlated. With the addition of virtual samples, only two descriptors are not correlated, namely dipole moment and electronegativity.
The most striking observation on the benefits of virtual samples in ML performance is found in the Commercial Drugs and Pyridazine Derivatives datasets, as presented in Tables 5, 6. In Commercial Drugs, from 10 descriptors, there is no single descriptor has correlation with IE, but the addition of virtual samples increases the number of correlated descriptors into 8 with 2 stay uncorrelated, namely pKa and ELUMO. In the Pyridazine Derivatives dataset (Table 6), the correlation between attributes shows that there is only 1 descriptor, namely the total energy with the status of correlated before adding the virtual samples. The presence of virtual samples changes the status of correlation from one into nine descriptors, only two, namely dipole moment and electronegativity, are still uncorrelated.
Overall, the experiment shows that virtual samples affect the status of descriptors from uncorrelated to mostly correlated. This correlation (between the descriptor and IE) is needed to get the best model so that it improves the performance of the model37,41. The experiment shows that the use of virtual samples in the KNN algorithm (Table 7), significantly decreases the RMSE values from 12.122 to 1.639, 12.89 to 3.88, 45.711 to 3.888; 20.424 to 2.707%; 7.113 to 3.858; and 12.848 to 1.135 each for the thiophene and its derivatives, benzimidazole derivatives, amino acids and their related compounds, pyridines and quinolones, commercial drugs, and pyridazine derivatives datasets. This clearly indicates that the addition of virtual samples improves the performance of the KNN model in making predictions of corrosion inhibition efficiencies.
Comparisons to different models
This section compares the exploratory power of different models, and at the moment, the effect of material representation is not discussed yet. Comparisons are made purely regarding ML performance parameters. The generalizability of our proposed KNN + VSG model is verified with the six datasets in Table 8, and its performance was compared with the performance of the ANN, GA-ANN, SVM, and ARX models from related previous references. The RMSE metric is used to assess the prediction error for each model, while R2 is used to assess the suitability of the model predictions with observations. The experimental results of corrosion inhibitor prediction for the six datasets are presented in Table 7, where the RMSE_CV is the prediction error tested during cross-validation training, and the RMSE is that tested using a testing set, while NA stands for not available information. The RMSE values marked with an asterisk (*) are prediction errors that are tested using the entire datasets. As the RMSE_CV and RMSE represent cross-validation training and testing errors, respectively, their values become a measure of whether overfitting occurs.
For the KNN model, bad suitability of the model predictions is observed for its very low determination coefficient values below 0.50. For the KNN + VSG model, it can be seen that RMSE < RMSE_CV values are true for all datasets. It means that the KNN + VSG prediction of all datasets are in good-fitting42. The use of virtual samples in small datasets facilitates ML algorithms and effectively improves the quality of prediction fitting. In general, for all datasets, adding virtual samples significantly decreases RMSE and increases R2 values, and therefore improves the performance of KNN model43. The range of RMSE values of 7.113−45.711 decreases to 1.135−3.888 after adding virtual samples, and the coefficient of determination increases from a maximum of 0.50 to a minimum of 0.96 after the implementation of the VSG.
Based on the RMSE and R2 values, the KNN + VSG model performs better than all other models do for the same datasets. The model performance improvement is so obvious on the RMSE values from 5.836 to 1.639, 6.79 to 3.88, 4.45 to 3.88, 5.157 to 3.888, 8.831 to 2.707, 4.870 to 3.858, 10.5637 to 1.1350, each for the thiophene and its derivatives, benzimidazole derivatives, amino acids and their compounds, pyridines and quinolones, commercial drugs, and pyridazines derivatives datasets. The improvement is also supported by the relatively high determination coefficient of the proposed model ranging from 0.96 to 0.99, as compared to that of the previous models, ranging from −0.65 to 0.99.
The superiority of the proposed model performance can be observed through the visual representation of prediction data. Figure 3a–f presents the KNN + VSG model prediction data for thiophene and its derivatives, benzimidazole derivatives, amino acids and their compounds, pyridines and quinolones, commercial drugs, and pyridazines derivatives datasets, respectively. The same data from other models are also presented for comparison, except for the last dataset where the associated data is not available. It can be seen that compared to the previous model for the same dataset, the prediction data of the KNN + VSG model is relatively closer to the prediction line, indicating that this model is superior to the previous models44.
In particular, we discuss the case of implementing the ARX model on the Commercial Drugs dataset because the suitability is visually very poor (Fig. 3e). This can happen because the data pattern from the Commercial Drugs dataset which is predicted using the linear ARX model24 is nonlinear. This linear ARX model approach causes the prediction of IE to be unrealistic, especially for the following five data, sulfadiazine (106.31%), metacyclic (111.72%), glycine (124.03%), ethosuximide (158.88%), and hexetidine (259.25%). The KNN + VSG model can overcome the problems faced by the ARX model, such as poor suitability and unrealistic IE predictions being realistic, namely 82.51, 82.96, 93.19, 96.71, and 93.93% for ethosuximide, hexetidine, metacyclic, glycine, and sulfadiazine.
In summary, the KNN + VSG model is used to predict the efficiency of corrosion inhibition on the surface of the material based on computational and/or experimental data, which are classified as small datasets. In general, the addition of virtual samples helps increase the number of quantum chemical descriptors that correlate with IE as a target. Consequently, it improves the performance of the model with much lower errors and high determination coefficient values. Predictive performance assessment using RMSE and R2 shows that the proposed model performs better than the ANN17, SVM16, SVM21, ANN18, GA-ANN, ARX24, and ANN19 models do when working on the same dataset as used in this research. Model development is open for improvement either in an algorithm or preprocessing, and this research shows that VSG preprocessing is appropriate for solving small dataset problems in corrosion research.
Methods
Datasets, samples, and descriptors
This study uses six small datasets from previous studies about corrosion inhibition efficiencies. Their name, number of samples, number of descriptors, associated models, and users are listed in Table 8. Almost all datasets have samples less than 50, except Commercial Drugs, with 69 samples. It’s not too much of a stretch to classify them as small datasets. For all the datasets, the number of dimensions (descriptors) are lower than that of samples, ranging from 7 to 20. Different ML algorithms had been implemented into the datasets to make predictions of inhibition efficiencies, namely ANN-based, SVM, and ARX.
Thiophene and its derivatives dataset has 11 samples with seven quantum chemical descriptors, namely: Hammett constant, dipole moment, HOMO, LUMO, gap energy, molecular surface area, and molecular volume17. The benzimidazole derivative dataset was adopted from the work45 and described by ref. 16. This dataset consists of 20 samples and 11 descriptors: HOMO, LUMO, polarizability, molecular volume, ionization potential, electron affinity, electrophilicity, total negative natural charges of all non-hydrogen atoms, the fraction of electrons transferred, ΛNICS(1)B, and ΛNICS(1)I. The amino acids dataset consists of 28 samples and 12 descriptors, taken directly from ref. 18. The descriptors associated with this dataset are HOMO, LUMO, gap energy, binding energy, adsorption energy, total energy, dipole moment, dipole x, dipole y, dipole z, molecular surface area, and molecular volume. The dataset of 41 Pyridines and Quinolines is taken from ref. 20. This dataset consists of 20 quantum chemical descriptors are HOMO, LUMO, gap energy, ionization potential, electron affinity, electronegativity, global hardness, global softness, dipole moment, polarizability, electrophilicity, electron donor capacity, electron acceptor capacity, the fraction of electrons transferred, NBO atomic charge, adsorption energy, hydrophobicity, molecular volume, molecular surface area, and solvent accessible surface area. The Commercial drugs dataset was obtained from ref. 24. This dataset consists of ten descriptors: molecular weight, acid dissociation constant, octanol-water partition coefficient, water solubility, polar surface area, polarizability, HOMO, LUMO, electrophilicity, and the fraction of electrons transferred. The pyridazine derivatives dataset is taken from19 with 11 quantum chemical descriptors, namely total energy, gap energy, HOMO, LUMO, dipole moment, ionization potential, electron affinity, electronegativity, global hardness, global softness, and the fraction of transferred electrons.
Corrosion inhibition is highly dependent on the chemical reactivity of the inhibitor molecule represented in various quantum chemical descriptors20. Hammett constant indicates the negativity of an atom. A negative value indicates that the atom acts as an electron donor, whereas a positive value indicates that the atom acts as an electron acceptor. The dipole moment describes the ability of molecules to interact with the metal surface dipole. Gap energy shows the level of inhibitor molecular binding ability to be adsorbed by the metal surface. Molecular surface area and molecular volume are parameters to measure the ability of molecules to prevent access to corrosive agents on metal surfaces. Since physisorption and chemisorption are related to the electronic interaction with the metal surface, the polarization of the charge around the molecule is very influential. Molecular polarizability has something to do with the distribution of electron density around the molecule, and the ability of the molecule to distort the electron density. Ionization potential is defined as the amount of energy needed to release one outer electron of the atom used to measure the reactivity of atoms or molecules. Electron affinity is the energy needed to capture 1 mole of electrons. Electrophilicity illustrates the ability of a molecule to absorb electrons. Total negative natural charges of all non-hydrogen atoms represent the amount of charge carried by all non-hydrogen atoms of the molecule. A fraction of electrons transferred is the number of electrons flowing from the inhibitor molecules to the metal surface atoms. Electron transfer occurs due to differences in electronegativity between inhibitor molecules and metal surface atoms. NICS(1)B and NICS(1)I are aromaticity parameters calculated from the center of the benzene ring and the center of the imidazole ring, respectively. The total energy refers to the ability of inhibitor molecules to be adsorbed on metal surfaces. In general, the mechanism of corrosion inhibition is related to the interaction between inhibitor molecules and metal surfaces. Inhibitor molecules can be adsorbed on the metal surface through chemisorption and physisorption. Therefore, adsorption energy and binding energy are important molecular descriptors46,47. Electronegativity is related to the ability of inhibitor molecules to attract electrons so that electron equilibrium is achieved. Global hardness indicates the resistance of a molecule to transfer charges, while global softness shows the capacity of a molecule to receive charges. Electron donor capacity explains the tendency of molecules to donate charges, while electron acceptor capacity explains the tendency of molecules to receive charges. Natural bonding orbital is an analysis of interacting charges, which can be used to show the type and value of the atomic charge. Hydrophobicity is related to the ability of molecules to form an adsorbed layer through a hydrophobic mechanism. Solvent accessible surface area is the surface area of the molecule that is accessible by a solvent. This parameter is also related to the ability of the molecule to prevent the access of corrosive agents to the metal surface. Molecular weight is considered a parameter related to the size of the molecule. The acid dissociation constant is related to the acidity of a solution. The octanol-water partition coefficient is the concentration of a particular substance in the liquid phase of an octanol-water mixture (between the hydrophobic phase and the hydrophilic phase). Water solubility is related to the solubility of a substance in water. The polar surface area is the surface of the molecule associated with the accumulation of charge.
KNN algorithm
The KNN prediction of the testing set is based on the result of the K-nearest neighbor’s distance to the training set, which is calculated using the Euclidean distance function as in Eq. (1)48
with x and p are descriptors of training and testing sets, respectively, while m is the number of descriptors. The K target values from the training set are averaged to obtain predictive results as in Eq. (2)48
where yi is the ith target and y is the result of testing prediction.
Virtual sample generation method
The VSG method is used to generate virtual samples using bush topology adopted from ref. 49, with a slight modification to get the best virtual samples by selecting the best paths of the smallest errors. Virtual samples are generated on those paths by interpolation techniques using Eqs. (3) and (4)
where, xi and x(i+1) are the ith and (i + 1)th feature vectors, while xvs is the virtual sample feature vector, and yi and yi+1 are the ith and the (i + 1)th targets, while yvs is the virtual sample target. The value of t = [0,1] is used to determine the number of virtual samples inserted between two data points.
The number of inserts are exercised to get an optimum value that increases the number of correlated features, stability of the models, and prediction accuracy. For this purpose, the number of virtual samples generated between two data points is determined to be 10. If the number of training samples is n, then the number of virtual samples will be (n − 1) × 10. From the overall validation, k models that have the smallest errors have been selected. If there are (n − 1) × 10 virtual samples for each models then the total number of virtual samples will be (n − 1) × 10 × k. These virtual samples are added into the training set to train the machine learning algorithm to get the final model. In this study, k = 10 is chosen to represent 10 different experiments.
Model development
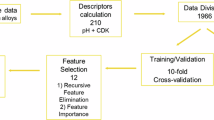
In principle, the VSG technique can be implemented on any algorithm. For the preliminary study, three algorithms, namely, K-Nearest Neighbor (KNN), Decision Tree (DT), and Random Forest (RF), are chosen to exercise ML models. For all six datasets used in this research, the KNN produces the most consistent results of error lower than reference values. It also shows the most stable error for varying number of virtual samples (see Supplementary Table 1 and Supplementary Fig. 1). Therefore, the KNN is chosen to build an ML model to predict inhibition efficiencies for the six datasets. This study uses the KNN algorithm of the Python programming language. All other parameters and arrangements are defaults as stipulated in sci-kit learn release 0.23.250. Figure 4 illustrates the model development, where the dataset is split into training and testing sets with a ratio of 70:30, except for the benzimidazole derivatives and commercial drugs, where the training and testing sets were determined following the previous related literature. For Benzimidazole derivatives, sample number 1–16 are used for training and number 17–20 are used for testing. For Commercial Drugs, all samples are used for training except eight samples for testing. At the preprocessing stage, both training and testing sets are normalized to avoid the sensitivity problem of certain features of prediction results. Virtual samples produced by the VSG method are added into the training set to train the KNN algorithm, and this combination model is then evaluated using the testing set to see its accuracy level in making a prediction. The performances of the model are also evaluated to see the effectiveness of adding virtual samples, before they are finally compared to that of other previous models.
Model validation
Both actual and virtual samples are used to train the KNN algorithm by implementing Monte Carlo cross-validation (MCCV), which randomly selects any pair of 70:30 actual sample partition51, 70 for training and 30 for testing. For each random pair of training-testing partitions, virtual samples are generated along the lines connecting all-two training data for all possible paths depending on the number of training samples. Each pair is associated with \(\frac{{\left( {n - 1} \right)!}}{2}\) different path for distributing virtual samples, where n is the number of actual training samples. Using actual and virtual samples on each path, the training produces a temporary model, and its performance of RMSE is measured using the corresponding testing set52,53,54. A threshold θ is determined to select a temporary model that meets the criteria, its RMSE ≤θ. In the beginning, an RMSE value from a related reference model is chosen as θ. For a certain pair, a smaller θ is set up when there are more than k temporary models that meet the criteria. This process is repeated until it generates k models with the smallest RMSE values, and the associated virtual samples are stored. The virtual samples are then added to the training set to train the KNN algorithm to produce a final model.
Assessment metrics
Three performance metrics, including Spearman’s rank correlation coefficient (r), determination coefficient R-squared (R2), and root mean square error (RMSE), are used to analyze and assess the performance of the model. The Spearman correlation coefficient, measuring the strength and direction of the monotonous relationship between two variables, is calculated using Eq. (5)
where,
The coefficient of determination of R-squared (R2) measures the fitting degree of a model44, where a value approaching one indicates a good fit, as formulated in Eq. (6).
The RMSE measures the deviation between the predicted value and the real value44 and is calculated using Eq. (7)
where Yi, \(\bar Y\), and \(\widehat {Y_i}\)are observed, average observed, and predicted values, respectively, and n is the number of samples.
Data availability
The datasets that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The codes that support the findings of this study are available from the corresponding author upon reasonable request.
References
Finšgar, M. & Jackson, J. Application of corrosion inhibitors for steels in acidic media for the oil and gas industry: a review. Corros. Sci. 86, 17–41 (2014).
Tiu, B. D. B. & Advincula, R. C. Polymeric corrosion inhibitors for the oil and gas industry: design principles and mechanism. React. Funct. Polym. 95, 25–45 (2015).
Kadhim, A. et al. Corrosion inhibitors. A review. Int. J. Corros. Scale Inhib. 10, 54–67 (2021).
Miralrio, A. & Vázquez, A. E. Plant extracts as green corrosion inhibitors for different metal surfaces and corrosive media: a review. Processes 8, 8 (2020).
Keshavarz, M. H. et al. Simple approach to predict corrosion inhibition efficiency of imidazole and benzimidazole derivatives as well as linear organic compounds containing several polar functional groups. Zeitschrift fur Anorg. und Allg. Chemie 642, 906–913 (2016).
Majd, M. T. et al. Probing molecular adsorption/interactions and anti-corrosion performance of poppy extract in acidic environments. J. Mol. Liq. 304, 112750 (2020).
Alrefaee, S. H. et al. Challenges and advantages of using plant extract as inhibitors in modern corrosion inhibition systems: Recent advancements. J. Mol. Liq. 321, 114666 (2021).
Salleh, S. Z. et al. Plant extracts as green corrosion inhibitor for ferrous metal alloys: a review. J. Clean. Prod. 304, 127030 (2021).
El-Haddad, M. N. & Fouda, A. E. A. S. Evaluation of Curam drug as an ecofriendly corrosion inhibitor for protection of stainless steel-304 in hydrochloric acid solution: chemical, electrochemical, and surface morphology studies. J. Chinese Chem. Soc. 68, 826–836 (2021).
Farahati, R. et al. Experimental and computational study of penicillamine drug and cysteine as water-soluble green corrosion inhibitors of mild steel. Prog. Org. Coatings. 142, 105567 (2020).
Neves, B. J. et al. QSAR-based virtual screening: advances and applications in drug discovery. Front. Pharmacol. 9, 1–7 (2018).
Toropov, A. A. & Toropova, A. P. QSPR/QSAR: state-of-art, weirdness, the future. Molecules 25, 1292 (2020).
Belghiti, M. E. et al. Computational simulation and statistical analysis on the relationship between corrosion inhibition efficiency and molecular structure of some hydrazine derivatives in phosphoric acid on mild steel surface. Appl. Surf. Sci. 491, 707–722 (2019).
Winkler, D. A. Predicting the performance of organic corrosion inhibitors. Metals 7, 1–8 (2017).
Mendoza, R. L. C. et al. Density functional theory and electrochemical studies: structure-efficiency relationship on corrosion inhibition. J. Chem. Inf. Model. 55, 2391–2402 (2015).
Li, L. et al. The discussion of descriptors for the QSAR model and molecular dynamics simulation of benzimidazole derivatives as corrosion inhibitors. Corros. Sci. 99, 76–88 (2015).
Khaled, K. F. & Al-Mobarak, N. A. A predictive model for corrosion inhibition of mild steel by thiophene and its derivatives using artificial neural network. Int. J. Electrochem. Sci. 7, 1045–1059 (2012).
Khaled, K. F. & Sherik, A. Using neural networks for corrosion inhibition efficiency prediction during corrosion of steel in chloride solutions. Int. J. Electrochem. Sci. 8, 9918–9935 (2013).
Quadri, T. W. et al. Development of QSAR-based (MLR/ANN) predictive models for effective design of pyridazine corrosion inhibitors. Mater. Today Commun. 30, 103163 (2022).
Ser, C. T. et al. Prediction of corrosion inhibition efficiency of pyridines and quinolines on an iron surface using machine learning-powered quantitative structure-property relationships. Appl. Surf. Sci. 512, 145612 (2020).
Liu, Y. et al. A machine learning‑based QSAR model for benzimidazole derivatives as corrosion inhibitors by incorporating comprehensive feature selection. Interdiscip. Sci. Comput. Life Sci. 11, 738–747 (2019).
Zhi, Y. et al. Long-term prediction on atmospheric corrosion data series of carbon steel in China based on NGBM(1,1) model and genetic algorithm. Anti-Corrosion Methods Mater 66, 403–411 (2019).
De Masi, G. et al. Machine learning approach to corrosion assessment in subsea pipelines. MTS/IEEE Ocean. 2015 - Genova Discovering Sustainable Ocean Energy for a New World 8–13 (2015).
Beltran-Perez, C. et al. A general use QSAR-ARX model to predict the corrosion inhibition efficiency of drugs in terms of quantum mechanical descriptors and experimental comparison for lidocaine. Int. J. Mol. Sci. 23, 5086 (2022).
Chen, Z. S. et al. A PSO based virtual sample generation method for small sample sets: applications to regression datasets. Eng. Appl. Artif. Intell. 59, 236–243 (2017).
Roy, M. A. et al. Machine-learning-guided descriptor selection for predicting corrosion resistance in multi-principal element alloys. npj Mater. Degrad. 6, 9 (2022).
Coelho, L. B. et al. Reviewing machine learning of corrosion prediction in a data-oriented perspective. npj Mater. Degrad. 6, 8 (2022).
Chen, Z. S. et al. Integrating virtual sample generation with input-training neural network for solving small sample size problems: application to purified terephthalic acid solvent system. Soft Comput. 25, 6489–6504 (2021).
Li, D. C. et al. A new approach for manufacturing forecast problems with insufficient data: the case of TFT-LCDs. J. Intell. Manuf. 24, 225–233 (2013).
Luo, H. & Paal, S. G. Reducing the effect of sample bias for small data sets with double-weighted support vector transfer regression. Comput. Civ. Infrastruct. Eng. 36, 248–263 (2021).
Asanya, K. C. et al. Robust Bayesian approach to logistic regression modeling in small sample size utilizing a weakly informative student’s t prior distribution. Commun. Stat. Theory Methods. 52, 1–11 (2021).
Wang, X. & Yao, J. Linear regression estimation methods for inferring standard values of snow load in small sample situations. Math. Probl. Eng. 2020, 1–10 (2020).
Liu, Q. et al. A new support vector regression model for equipment health diagnosis with small sample data missing and its application. Shock Vib. 2021 (2021). https://doi.org/10.1155/2021/6675078.
Liu, B. et al. Small dataset modeling and application of plant medicine extraction. Commun. Comput. Inform. Sci. 1006, 381–392 (2019).
Li, D. C. et al. Using virtual samples to improve learning performance for small datasets with multimodal distributions. Soft Comput. 23, 11883–11900 (2019).
Raikwal, J. S. & Saxena, K. Performance evaluation of SVM and K-nearest neighbor algorithm over medical data set. Int. J. Comput. Appl. 50, 35–39 (2012).
Kumar, S. & Chong, I. Correlation analysis to identify the effective data in machine learning: Prediction of depressive disorder and emotion states. Int. J. Environ. Res. Public Health. 15, 2907 (2018).
Vettoretti, M. & Di Camillo, B. A variable ranking method for machine learning models with correlated features: In-silico validation and application for diabetes prediction. Appl. Sci. 11, 7740 (2021).
Moedjahedy, J. et al. CCrFS: combine correlation features selection for detecting phishing websites using machine learning. Futur. Internet. 14, 229 (2022).
Ying, X. An overview of overfitting and its solutions. J. Phys. Conf. Ser. 1168, 022022 (2019).
Yan, L. et al. Corrosion rate prediction and influencing factors evaluation of low-alloy steels in marine atmosphere using machine learning approach. Sci. Technol. Adv. Mater. 21, 359–370 (2020).
Giola, C. et al. Learning curves: a novel approach for robustness improvement of load forecasting. Eng. Proc. 5, 38 (2021).
Brumen, B. et al. Overview of machine learning process modelling. Entropy 23, 1123 (2021).
Hassan, A. H. M. et al. Visualization & prediction of COVID-19 future outbreak by using machine learning. Int. J. Inf. Technol. Comput. Sci. 13, 16–32 (2021).
Song-Qing, H. et al. 3D-QSAR study and molecular design of benzimidazole derivatives as corrosion inhibitors. Chem. J. Chinese Univ. 32, 2402 (2011).
Kozlica, D. K. et al. Synergistic effect of 2-mercaptobenzimidazole and octylphosphonic acid as corrosion inhibitors for copper and aluminium – An electrochemical, XPS, FTIR and DFT study. Corros. Sci. 182, 109082 (2021).
Kokalj, A. Corrosion inhibitors: physisorbed or chemisorbed? Corros. Sci. 196, 109939 (2022).
Imandoust, S. B. & Bolandraftar, M. Application of K-nearest neighbor (KNN) approach for predicting economic events: theoretical background. Int. J. Eng. Res. Appl. 3, 605–610 (2013).
Sutojo, T. et al. Investigating the impact of synthetic data distribution on the performance of regression models to overcome small dataset problems. Proc. 2020 International Seminar on Application for Technology of Information and Communication (iSemantic). 125–130 (IEEE, 2020).
Xu, Q. S. & Liang, Y. Z. Monte Carlo cross validation. Chemom. Intell. Lab. Syst. 56, 1–11 (2001).
Jun Lv, Y. et al. Steel corrosion prediction based on support vector machines. Chaos Solitons Fractals. 136, 109807 (2020).
Zhou, C. et al. A novel stacking heterogeneous ensemble model with hybrid wrapper-based feature selection for reservoir productivity predictions. Complexity 2021, 1–12 (2021).
Zhang, Y. et al. Data augmentation strategy for small sample short‐term load forecasting of distribution transformer. Int. Trans. Electr. Energy Syst. 30, e12209 (2019).
Scikit-learn. Scikit-learn user guide - Release 0.23.2. (2020).
Acknowledgements
The author sincerely thanks LPPM Dian Nuswantoro University Semarang Indonesia, for the support. T.S. acknowledges scholarship support from Dian Nuswantoro University Semarang Indonesia. M.A. acknowledges scholarship support from LPDP (Lembaga Pengelola Dana Pendidikan) Indonesia.
Author information
Authors and Affiliations
Contributions
T.S. designed the algorithms, provided technical expertize on machine learning, and wrote the manuscript. M.A. extracted data from the literature, performed DFT analysis, and drafted the manuscript. S.R. and H.K.D. contributed to the main idea and methodology, interpreted the results and discussion, and reviewed the manuscript. A.S. and G.F.S. performed the data analysis.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sutojo, T., Rustad, S., Akrom, M. et al. A machine learning approach for corrosion small datasets. npj Mater Degrad 7, 18 (2023). https://doi.org/10.1038/s41529-023-00336-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41529-023-00336-7
This article is cited by
-
Laying the experimental foundation for corrosion inhibitor discovery through machine learning
npj Materials Degradation (2024)
-
DATACORTECH: artificial intelligence platform for the virtual screen of aluminum corrosion inhibitors
npj Materials Degradation (2024)
-
Diffusive migration behavior of single atoms in aluminum alloy substrates: Explaining machine-learning-accelerated first principles calculations
Science China Materials (2024)
-
Searching the chemical space for effective magnesium dissolution modulators: a deep learning approach using sparse features
npj Materials Degradation (2023)