Abstract
The question of silicate glass chemical durability is at the heart of many industrial and environmental issues, with certain glasses, such as bioglasses, needing to transform rapidly, while others, like nuclear glasses, extremely slowly. Due to the wide diversity of the chemical composition for these types of materials and their metastability—no thermodynamic equilibrium can be reached between glass and solution—the evaluation of chemical durability remains a scientific challenge. In this article, we review the current state of knowledge on glass alteration mechanisms and kinetics, and point to some perspectives for glasses for which no direct experimental validation is currently possible. Thanks to the development of novel techniques and international collaborations, a better understanding of the mechanisms involved has been achieved. Mechanistic models have been developed at some specific scales, although holistic models still need further development to link the various scales and perform reliable predictions.
Similar content being viewed by others
Introduction
Silicate glasses are manmade materials with various applications in our daily life, ranging from tableware, labware, windows in construction, insulation, and reinforcement, to high technology fields such as optical lenses, displays, fibers, biomedicine, and nuclear waste disposal, all due to their ability to be customized1,2,3. Among glass materials’ properties, chemical durability is important in many of the above-mentioned applications. In particular, the reaction of a glass in aqueous environments and its alteration behavior is critical in applications such as biomedicine (e.g., bone repair)4, where fast and controllable dissolution is preferred, or in agriculture to supply plants with nutrients5. For nuclear waste disposal, on the contrary, it is essential6 to maintain waste glass long-term stability to prevent the release of radioactive elements into the biosphere for periods of thousands to hundreds of thousands of years. Silicate glasses can also be produced naturally on Earth. Basaltic glasses are volcanic glasses found in different settings such as hyaloclastites and pillow-lavas, and in various locations, including submarine, subglacial, or lacustrine environments. Understanding their alteration mechanisms and rates is a preliminary step toward the understanding of different natural phenomena such as volcano slope stability7, the chemical mass balance of the oceans8, and the geological history of the planet Mars9.
The term ‘silicate glass’ refers to any kind of vitreous materials in which SiO2 is the most abundant oxide. Among others, these include the well-known categories of soda-lime glasses, borosilicate glasses, aluminosilicate glasses, etc. The terms ‘alteration’ or ‘corrosion’ refer to the transformation of the glass into solid alteration products and aqueous species. The term ‘dissolution’ is employed when glass transforms into aqueous species only.
The alteration of silicate glasses is a complex phenomenon that depends both on the nature of the glass material, i.e., its chemical composition, structure (short and medium-range order), and bonding, and also on the environmental conditions, such as temperature, pH, Eh, and solution chemistry. The plethora of influencing parameters makes alteration difficult to predict from simple descriptors or parameters arising from structural analysis or tests performed in accelerated conditions. Calculation of a glass alteration rate can be further complicated by the fact that different mechanisms or different coupled mechanisms can control glass alteration during the reaction. This has led scientists to distinguish three main kinetic regimes depending on which mechanism or set of mechanisms control the alteration process: the initial dissolution rate regime (stage I), the residual alteration rate regime (stage II), and (for some glasses) a sudden potential acceleration of the alteration (stage III) (Fig. 1). Stage I takes place in diluted and renewed solutions. A high concentration of dissolved silica which reduces the affinity for matrix dissolution and the formation of a passivating alteration layer on the glass surface allows the establishment of stage II with low residual rates, while massive precipitation of secondary phases can trigger an acceleration of alteration (stage III). In this article, we review the progress made in understanding silicate glass alteration mechanisms (second section), and then focus on the three aforementioned kinetic regimes (third section). Note that most of the knowledge and examples given in this article are based on glass behavior in liquid water. However, a separate section gives information on glass interaction with water vapor, as atmospheric alteration is also a key aspect of glass degradation.
(Reprinted from Vienna et al.62 with permission, copyright John Wiley and Sons).
An introduction to the mechanisms of glass alteration
In contact with water, the glass surface first reaches an electrochemical equilibrium10 before undergoing chemical attack through ion-exchange and hydrolysis reactions of metal–oxygen bonds, driven by the difference between the chemical potential of the solid and that of the fluid11. Because of this, the concentration of glass species in the solution increases, meaning a decrease in the Gibbs free energy of the glass-solution system. The behavior of silicate glass also depends on the fact that the reaction between silica and water (Eq. 1) is reversible12
Therefore, in a solution containing orthosilicic acid, matrix dissolution slows down and above the saturation level, precipitation reactions take place, generally on the glass surface. Furthermore, Si atoms facing water and bound to O atoms of the glass network (Si tetrahedra not fully hydrolyzed) can form silanol groups, which can, in turn, condensate to reform siloxane bonds (Eq. 2).
These reactions of precipitation and condensation can involve other elements from the glass or supplied by the solution. They result in the formation of an alteration layer, generally composed of a Si-rich hydrated and porous layer, called a gel, and secondary phases13. In some circumstances, the gel layer can be transport-limiting for aqueous species. It then becomes a passivating layer. Figure 2 summarizes the main features of silicate glass alteration.
a Representation of a cross section of an altered piece of glass. The alteration layer is generally made up of a hydrated layer (also called ‘interdiffusion’ or ‘leached’ layer), the gel layer (amorphous hydrated polymerized Si-rich material) which can be made of several sub-layers depending on how it forms, and secondary phases (precipitates). b Scanning electron microscopy image of a piece of SON68 glass, a 30 oxide borosilicate glass (Table 1), altered for 2 months at 150 °C in deionized water. The sample was broken and observed from the edge. Secondary phases precipitated on the top of the gel layer consist of poorly crystallized phyllosilicates. c Transmission Electron Microscopy bright field image of a SON68 glass sample (composition given in Table 1) altered for 26 years at 90 °C in granitic water. Pores within the gel can be seen in bright.
The rate of glass alteration can be described as the rate at which the glass hydrates and transforms into new, thermodynamically more stable phases (alteration products) and dissolved ions. It can be determined from a mass balance based on the glass components present in the leachate and those retained in the alteration layer. In practice, one focuses on elements not retained in the alteration layer. Such elements are called alteration tracers.
Difficulties arise when trying to link processes described at atomic scale to the observations made at macroscopic level. Glass displays a disordered structure at medium range (>5 Å) characterized by a broad distribution of bond distances and bond angles. See for instance the case of ISG, a 6-oxide borosilicate glass used as a reference material within the glass corrosion community (Table 1)14, in which Si‒O‒Si bond angle ranges between 120 and 180°, and Si‒O bond distance between 1.5 and 1.75 Å, with significant differences between the bulk and the glass surface15. Therefore, a simple reaction, such as the hydrolysis of Si‒O‒Si, can be more or less easy depending on its local configuration because of a large distribution of the activation energy16. A mesoscale approach is thus necessary to bridge the gap between the atomic level, where first principles or molecular dynamics (MD) calculations can be performed, and the macroscopic level. Moreover, the reacting surface of the glass is usually covered with an alteration layer, which means that local conditions at the reaction front (pH, concentration of dissolved species) are potentially different from those of the bulk solution17. Another difficulty arises from the chemical complexity of multicomponent glasses, as glass/water interaction cannot be described by a simple solid/liquid thermodynamic equilibrium, such as that applicable for pure amorphous silica11. Although one could theoretically define a state corresponding to an equilibrium between the glass phase and the liquid phase, based on enthalpy and entropy contributions18, this equilibrium is not achievable in practice because secondary phases with low solubility and fast precipitation rates will control the solution chemistry, maintaining the glass-solution system well away from saturation. Because of the high complexity of the system and the difficulties listed above, empirically-inspired approaches are still widely used to assess glass durability. Nonetheless, progress has been achieved in the understanding of glass alteration over recent years, thanks to the development of new simulation methods, analytical techniques, and international efforts14,19.
Molecular mechanisms of glass alteration
The macroscopic behavior of a glass in contact with water is the consequence of the accumulation of countless mechanisms at the atomistic level, involving species from the solution and from the glass. These mechanisms are related to adsorption/desorption, exchange, hydrolysis and bond reformation, Ostwald ripening (gel maturation), precipitation, and the transport of reactants and products through the alteration layer. In recent years, many studies based on atomistic simulation techniques have been dedicated to better understanding these mechanisms both qualitatively and quantitatively. A review of the methods available is proposed in the recent literature20. Figure 3 provides some examples of the advanced simulation methods used to understand glass alteration mechanisms. In the following sections, we discuss the outcomes of the most relevant studies on the basic processes of glass alteration: Adsorption, exchange, and hydrolysis. Note that because of the timescale accessible to current atomistic simulations (ps to ns timescale), not all the processes listed above have been studied yet.
1. Formation of a porous and hydrated gel layer and Ostwald ripening studied by classical molecular dynamics with dissociative potentials (MD). 2. Inward water diffusion, ion-exchange, outward solvated glass cation diffusion. 3. Water adsorption at the solution–gel interface (or at the glass surface at the beginning of the reaction) studied by ab initio methods. 4. Hydrolysis/condensation reactions studied by ab initio molecular dynamics or potential mean force methods. 5. Precipitation of secondary phases studied by classical geochemical simulator (The saturation index (SI) is calculated by comparing the chemical activities of the dissolved ions of the mineral (ion activity product, IAP) with their solubility product (Ksp)).
Water adsorption on glass
Recent studies have focused on the chemical reactions occurring at the glass (pure silica, bioactive glass, borosilicate glass)–water interface. Results show that water molecules have a higher affinity for alkali or alkaline earth cations or non-bridging oxygen atoms (NBO) than Si‒O‒Si linkages21. Water dissociates and forms Na‒OH, Ca‒OH, and NBO‒H groups. When a film of water molecules is simulated at the glass surface, collective motions occur, and protons resulting from the dissociation of water molecules jump onto water molecules before being captured by a cation or an NBO at the glass surface. These results have been confirmed by classical molecular dynamics (MD) with shell-model potentials22. However, no particular affinity between small Si‒O‒Si rings (size 2 or 3) and water molecules has been observed, although the large local stresses concentrated on the small rings should favor their hydrolysis23.
Mahadevan et al. studied the chemisorption of water on a silica surface by classical MD using a dissociative potential for water specially fitted to represent silica–water interfaces24. As inferred from experiments, a water molecule can form two Si‒OH after dissociation and reaction with the glass surface. Interestingly, silanol groups were observed several Angstroms inside the bulk either by migration of the water molecule through channels or by migration of protons jumping from NBO to NBO with the help of the water molecules. Some non-dissociated water molecules are also present a few Angstroms inside the bulk. When defects like IIISi are present, they readily react with the water molecules25. These results obtained at atomic scale indicate that, unlike most silicate crystals which have a more compact structure, the reactive zone of a silicate glass is not a surface but a volume, whose size depends on both the connectivity of the silicate network and the pH.
To go deeper in our understanding of the chemical processes at work, first principle calculations using the DFT method have been performed simulating an interface between a SiO2–B2O3–Na2O glass and water26. Both a single water molecule and a film of water molecules were simulated. Adsorption energy calculations showed that three coordinated B atoms (IIIB) have a lower affinity for water molecules than four-coordinated B atoms (IVB). However, IIIB atoms are more accessible to water molecules than IVB atoms, which explains why it has been observed experimentally that IIIB atoms are preferentially dissolved rather than IVB27,28. This relationship between the quantity of accessible sites and the alteration rate has also been pointed out in a SiO2–CaO system29. In this work, the β- and γ-CaO–SiO2 polymorphs were simulated at the atomistic level and despite the smaller hydration energy of the γ-polymorph, its hydration rate was much slower because it contained a considerably lower quantity of reactive sites. Jabraoui’s study also confirmed (i) the high affinity between Na atoms and water molecules, and (ii) that the Na/H2O exchange allows the penetration of water inside the bulk glass. This process is complex and involves several hydrogen bonds, in addition to the direct bonding between the O of the water molecule and Na of the glass. Following this work, it seems important to consider a “real” aqueous solution (i.e., a liquid represented by a sufficiently large number of water molecules) rather than isolated water molecules, to grasp the complexity of the interactions at the glass–water interfaces.
Water diffusion/ion exchange at the glass–water interface
Beyond adsorption, hydration, and exchanges between water and mobile glass cations (alkaline, alkaline earth elements) have been studied experimentally and by using different molecular simulation techniques. The importance of the glass topology, in particular the ring size distribution, was underlined decades ago by Bunker13. Water molecules are able to penetrate the glass by diffusion only if voids with diameters larger than ~0.7 nm are available (the water molecule diameter is equal to 0.28 nm). Otherwise, water penetration occurs mainly through hydrolysis reactions. This threshold at around 0.7 nm is important, as it separates two diffusion regimes: liquid-state diffusion above the threshold with Dapp of the order of 10−9 m2.s−1 and solid-state diffusion below with Dapp < 10−15 m2.s−1. Note that recent MD simulations have tended to lower the threshold below 0.5 nm in pure silica30. Interestingly, it was shown recently that, owing to complexity of the topology and the existence of multiple pathways for water molecules, actual gels cannot be characterized by a unique Dapp30. It is thus better to consider both open channels and closed pores. In simplified systems, MD techniques provided a more detailed description of water diffusion mechanisms involving alkali–H2O exchanges, proton diffusion, and a possible braking role of the glass surface on the water diffusion31,32,33. In porous silica, a proxy for the gel of multicomponent glasses, the diffusion of water molecules is impacted by the topology of the porous network. In particular, water diffusion slows down in low connected pores33. Ohkubo et al. also observed a large decrease in the water diffusion compared to diffusion in bulk water in simulated gels prepared from an alumino-borosilicate glass after removing the soluble species (B and Na)32. A water diffusion coefficient of 8 × 10−16 m2/s was calculated. The interactions between the water molecules and the atoms located at the interface between the reticulated network and the pores are responsible for this low diffusivity compared to water self-diffusion (~2 × 10−9 m2/s at room temperature). Similar observations were obtained with a cylindrical pore dug out in a silica glass containing pure water or alkalis in water31. The water diffusion coefficient decreases as the ionic radius of the alkali increases.
In a system simulated by ReaxFF34 and consisting of three layers (pure silica, an intermediate gel layer (i.e., hydrated silica), and water), water molecules diffused significantly more slowly in the gel than in bulk water35. At ambient temperature, the decrease factor is roughly equal to 30 compared to the diffusion coefficient of bulk water. Moreover, as the gel–water interactions proceed, the gel network becomes more reticulated because of the hydrolysis of the weakest Qn species (Qn stands for the reticulation of the silicate network; n is the number of bridging O linking a Si atom to the network, n can vary from 0 to 4), and because of the cross-linking siloxane bonds. Interestingly, the gel repolymerization could be linked to the drop in the alteration rate, as pores formed by the release of mobile species tend to close30,36,37. When a system with a SiO2‒Na2O glass in interaction with water was simulated with the same ReaxFF potentials used in Rimsza and Du’s work38, different reactions occurred depending on the depth. Near the surface, H2O dissociated to form a Si‒OH group accompanied by a Na+/H+ exchange. Deeper below the surface, H2O dissociation mechanisms always occurred in conjunction with H+ jumps from NBO to NBO. Finally, below the subsurface region, only H+ jumps were observed. These mechanisms have been confirmed in a recent simulation by Mahadevan on aluminosilicate glasses with varying Na contents39. When the Na2O content increases, water penetrates faster and silanol groups form more deeply. In addition, some dissolved Na atoms remain close to the glass surface, surrounded by water molecules.
The possibility for a proton to jump from site to site has also been evidenced in a work using DFT calculations dedicated to the hydration of aluminosilicate glasses40. After the bond dissociation, Si‒OH and Al‒OH groups formed. During the remaining simulations, different reactions of proton exchanges around the Si or Al sites were observed.
Using Car Parrinello Molecular Dynamics, Tilocca et al. showed that in dry bioactive glasses with quite a low SiO2 content, Na ions can migrate by a jump process with the initial and final polyhedra around the Na sharing common O atoms41. It is also possible for a Na ion to pass temporarily through a Ca site during its migration, due to the considerable flexibility of the glass network. When the glass surface is in contact with water, Na ions can exchange with H2O molecules inducing water dissociation42.
Coupling experiments and classical MD simulations, the blocking role of Ca in relation to the water diffusion has been evidenced43. In particular, in the composition domain investigated in the study, an increasing content of CaO in the glass resulted in a decrease in the amount of bottlenecks larger than that of the water molecule, which in turn led to a drop in water diffusivity. In borosilicate glasses, the mixing of IIIB and IVB complexifies the mechanisms16. When a Na+ near a BO4− is exchanged with a hydronium ion, one B‒O‒Si bond breaks, and the IVB is converted into a IIIB. In parallel, a silanol group forms and the hydronium dissociates.
The examples given here emphasize the complexity of the ion-exchange processes taking place in silicate glasses. They account for the experimental observations related to water labeled with isotopes such as 2H = D or 18O, where, even in simple soda-lime glasses, the exchange ratio D/Na can vary from 1 to 344,45. Furthermore, they explain how ion-exchange and water ingress in the solid work together, as experimentally evidenced by Rutherford backscattering (RBS) and Resonant nuclear reaction analysis (RNRA) techniques applied to various samples of natural and nuclear glasses altered between 60 and 200 °C46. Regarding the time scales accessible to the simulation techniques, it is still not possible to numerically investigate low apparent diffusivity determined experimentally in a passivating gel, where values lower than 10−20 m2/s have been reported30,47,48. This would however be of great interest in order to explain the cause and the dynamics of passivation.
Hydrolysis
The investigation of hydrolysis mechanisms by first principles calculations began several decades ago by focusing on F1‒O‒F2 bridges (F1,2 = Si or Al) in reduced clusters, Qn entities, or small –O‒Si‒O‒ rings49,50,51,52. It appeared that the results depended on several factors, namely the cluster size, the cluster termination types, and the number of water molecules around the cluster50,53. For instance, Pelmenschikov demonstrated that the activation energy for hydrolysis, Ehydrolysis, i.e., energy barrier necessary to form the activated complex, increases significantly when a Si‒O‒Si linkage is embedded in a crystalline structure; the larger the connections with the structure, the higher the Ehydrolysis. From Pelmenschikov’s results, it can be inferred that the breaking of the last bond around a SiO4 tetrahedron in pure silica will be the easiest, energetically. This would confirm a hypothesis made in the 1980s, leading to the widely used macroscopic first order law (Eq. (3), Table 3) to calculate a glass dissolution rate as a function of the concentration of dissolved silica54.
Despite the above-mentioned limitations, calculations with small clusters are of interest and enable the topological characterization of the different steps leading to the bond breaking. In particular, it has been shown that during the Si‒O‒Si breakage, an intermediate five-coordinated Si atom is formed conjointly with the H2O dissociation, before the equilibration of the final configuration formed with two separated SiO4 entities containing Si‒OH groups52.
Work by Kagan et al. has proposed a statistical analysis of different sites at the surface of a silica–water system, using the potential mean force (PMF) method to determine the activation energies for hydrolysis of various linkages55. The force fields used in this study were those developed specially to simulate hydrated silica systems by classical molecular dynamics24,56. The Q3 to Q2 and Q2 to Q1 conversions have Ehydrolysis equal to 58.6 kJ/mol. The Q4 to Q3 conversion has a lower activation energy because of local strains around the Q4 entities on the silica surface. Ehydrolysis associated with the Q1 to Q0 conversion is equal to 52.7 kJ/mol. The fact that the hydrolysis of the last bond around a Qn entity corresponds to the lowest energy barrier is in agreement with Pelmenschikov’s work57. It was also shown that Ehydrolysis of a ‒Si(OH)3 group is only slightly dependent on the nature of the connected Si58. This conclusion was derived from calculations on a surface of quartz, where –Si(OH)3 groups were connected to either an edge site, a kink site, or a terrace site.
To our knowledge, Zapol et al.’s work is the only study dedicated to hydrolysis mechanisms in borosilicate glasses using ab initio methods59. The authors showed that Ehydrolysis necessary for the dissociation of B‒O‒B and B‒O‒Si linkages are lower in acid conditions compared to neutral or basic conditions, which is in fair agreement with experimental observations pointing out that the preferential dissolution of B compared to Si increases with decreasing pH60,61. Moreover, the Ehydrolysis for B‒O‒B and B‒O‒Si linkages dissociation are much lower in acid and neutral conditions compared to the Ehydrolysis for Si‒O‒Si dissociation, but the gap decreases in basic conditions.
As a whole, despite progress in this area, there is still a lack of statistics in the determination of the activation energies for the dissociation of the various linkages in silicate glasses to account for structural disorder in these materials. This limits the use of these data to investigate macroscopic systems.
Mechanisms responsible for the initial dissolution rate
At the macroscopic level, the initial dissolution rate, r0, depends on both the glass composition and environmental factors such as pH, temperature, and the solution composition62,63. From a mechanistic standpoint, r0 results from the following processes described above: adsorption, exchange, and hydrolysis reactions. We remind the reader that in this regime, the solution remains undersaturated, with no secondary phases able to form in the conditions tested. From the state of knowledge previously discussed, we can make several observations: (1) The mechanisms at molecular level are extremely complicated, as they involve collective effects of water molecules and concern not only a linkage but the whole local environment around a given atom (at least the second shell of cations undergoing hydrolysis). (2) The release of a glass cation by exchange or hydrolysis involves local structural reconfigurations after its release, such as the possible change in coordination of the surrounding cations, the formation of silanol groups, or the diffusion of protons or water molecules. To date, scientists have not yet investigated all the linkages and configurations even within simple silicate glasses by classical MD or ab initio techniques. Therefore, some fundamental parameters of glass dissolution are missing. (3) Ion-exchange and hydration processes are intimately coupled with hydrolysis of covalent bonds forming the silicate network. The way the first mechanism impacts dissolution of Si from the glass is not yet understood. The main theory for glass dissolution relies on that developed for silicate minerals in the 1980s64. This approach, inherited from the transition state theory (TST), supposes that dissolution of the entire mineral or glass is controlled by an elementary reaction. The theory was later improved by Oelkers, who considered a series of elementary reactions as the reaction progresses65. However, glasses differ from minerals in their structural disorder and in the possibility of water diffusion within the structure after exchanges with lattice modifier cations. It has been shown experimentally that the degree of disorder within the glassy structure, generated by fine-tuning the cooling rate of the molten glass, significantly impacts r028.
Mechanisms responsible for the residual rate
It has taken many years for the glass corrosion community to understand the fundamental reasons for the drop in the alteration rate, but it seems well established now that a thermodynamic effect and a transport-limiting effect work together66. The thermodynamic effect can be seen as a decrease in the chemical affinity for the hydrolysis of the silicate network (Si‒O‒M linkages, M = glass formers). The transport-limiting effect is related to the formation of a Si-rich gel layer, whose structure reorganizes and becomes a diffusion barrier for aqueous species. In a transient period between Stages I and II, the concentrations of glass network formers in solution increase and eventually reach steady states. These are interpreted in a first approximation as the saturation of the fluid with respect to the alteration layer. Since the alteration layer is generally made up of several phases, several competing equilibria must be considered. This makes the system impossible to describe by a single equation, unless it can be demonstrated that a single reaction controls the whole system. Such a demonstration applied to multicomponent glasses has not yet clearly established67. Moreover, even if only a gel forms on the glass surface, it is difficult to consider that a single thermodynamic equilibrium can describe the system because the gel does not necessarily form by precipitation of aqueous species, and does not necessarily have a constant composition and structure in volume and time68. A time and depth-dependent composition and structure would suppose that the equilibrium continuously changes69. In that case, a solid solution model would then be preferable to accommodate these dynamics70.
A combination of simulation and analytical techniques, including MD simulation39,71, atom-probe tomography (APT)48, time of flight secondary ion mass spectrometry depth profiling (ToF-SIMS)72, transmission electron microscopy (TEM)73, spectroscopic ellipsometry (SE)74, infrared spectroscopy (IR)75,76, nuclear magnetic resonance spectroscopy (NMR)71, and H218O and dye diffusivity measurement30, have been deployed on ISG glass14. The goal was to better understand the mechanisms of gel formation and maturation. Using different Si isotopic ratios in the leaching solution and in the glass, and post mortem characterizations, it was demonstrated that the gels formed in circum-neutral and slightly alkaline pHs resulted from an in situ reorganization of the silicate network after partial detachment of Si enabled the release of the soluble elements30,77. This reorganization implies that condensation reactions of siloxane bonds occur before all the bonds linking one Si tetrahedron to another are hydrolyzed. In these cases, only the outermost gel layer is in equilibrium with the bulk solution. Another qualitative proof of in situ replacement was supplied a long time before the collaborative work on ISG by post mortem characterization of highly irradiated glasses which were embodied in the gel part of the fission tracks inherited from the parent glass78. A gel formed by the precipitation of dissolved species would not have kept such features. Although the interfacial congruent dissolution/precipitation (ICDP) model is valid for most silicate minerals79, it is now clear that the formation of gel layers on glass can proceed in different ways. The weight of the local mechanism compared to the complete dissolution/precipitation process depends on the glass composition and the pH69,80,81. This point of view remains widely debated in the literature69,78,80,82,83, as certain authors claim that the ICDP model can be generalized to any kind of silicate material82,83. Several promising ways to settle this controversy and develop a general theory for silicates would be to:
-
(1)
Investigate the behavior of various polymorphs to understand how the structure of the dissolving material impacts the characteristics of the alteration layer (see for instance the work comparing albite glasses and crystals84,85).
-
(2)
Explore a broad compositional domain from highly depolymerized to highly polymerized glasses under both acid and basic pH conditions.
-
(3)
Probe the dissolving materials at atomic and nanoscopic scales into both the structure of the materials and the reactivity of the surfaces by spiking solutions or solids with isotopes and monitoring their behavior with advanced analytical techniques30,82,86, or by using in operando techniques such as in situ TEM or Raman17.
The existence of a residual alteration rate was postulated for the first time in 1984 by Grambow, who argued that no thermodynamic equilibrium between the glass surface and the solution could take place, and that hydration of the glass would never stop54. It was then experimentally verified in 199087. Beyond Grambow’s hypothesis, several other possible individual or coupled rate-controlling mechanisms have been evaluated, such as ion-exchange88,89,90, precipitation of secondary phases89, gel dissolution91, and diffusion of water30, silicon90, or tracing elements47 through the gel, but no definitive demonstration has been made. Consequently, no model is currently comprehensive enough to accurately predict the residual rate of a given glass altered in a given set of experimental conditions (kinetic models are discussed in section “Holistic models for glass alteration”). Several factors account for this profusion of hypotheses: (1) many intrinsic and extrinsic factors affect glass behavior (composition and structure of the glass, temperature, pH, solution composition, and radioactivity), making the development of a unified approach challenging. (2) residual rates are generally extremely low (3 to 5 orders of magnitude lower than r0), resulting in small amounts of alteration products, which in turn make detailed characterizations difficult. Last but not least, (3) the discovery of a correlation does not mean that the root causes have been identified. There is still some work to be done to develop a truly comprehensive understanding of the residual rate. It could start from the observation that the interfacial dissolution/precipitation mechanism and the leaching mechanism constitute two extreme cases, and that all the intermediate situations are possible and can be explored by a glass/solution system, even during an experiment.
Effects of solution composition
Both the pH and the ions in solution can affect the mechanisms of silicate glass alteration13,63,92,93. The pH affects the molecular mechanisms of bond breaking and bond reforming, as most of the chemical reactions involve H+ or OH−26,59. The pH also affects the speciation of elements in water, and thus the equilibria between solid phases and the aqueous species91. Siaq diminishes the rate at which Siglass detaches from the surface. This effect, related to the reversibility of the dissolution of SiO2 in water (Eq. 1), impacts the whole alteration process as, except for highly depolymerized glasses which undergo ion-exchange, the other glass constituents cannot be released if Si‒O‒Si bonds are not broken. The first order rate laws were derived on the basis of this observation (see section “Continuous scale models”)54
where r is the glass corrosion rate, r0 is the initial (or forward) dissolution rate, [H4SiO4] is the activity of orthosilicic acid at the glass surface, and K is the equilibrium constant (which equals the activity of orthosilicic acid at saturation).
It is worth noting that certain silicate glasses are more soluble than amorphous silica (SiO2am). This is the case, for instance, for Al-free high B, Na content glasses69. In other words, despite the saturation of the solution with respect to SiO2am, the glass still dissolves and releases orthosilicic acid. Consequently, the solution becomes supersaturated until it reaches the threshold where SiO2 particles precipitate. The addition of a small amount of Al to these glasses decreases their apparent solubility, which dramatically affects the mechanisms of gel formation once silica saturation conditions are reached69.
Certain elements other than Siaq in solution can also affect the mechanisms of bond breaking63 or the diffusivity of the passivating layer94, but the greatest influence of exogenous elements is on the nature of secondary phases formed during the alteration process86,92,95,96,97,98,99,100,101. There has been a general observation that the elements such as Fe, Mg, or Ni precipitating with Si to form silicate minerals will increase glass alteration rate. To form these precipitates, Si can be supplied either by the solution or by the gel layer. In the first case, the drop in the concentration of Si triggers the dissolution of the gel, and thus sustains glass alteration. The other reason is that secondary silicate phases do not passivate the glass surface, at least in short-term experiments. If the gel is passivating, the consumption of Si makes the gel more porous, less dense, and this accelerates the transport of reactants and products. Some examples are given in the following sections. There is a wide variety of silicate minerals which can form during glass alteration: amorphous silicates, phyllosilicates, calcium silicate hydrates, zeolites… In a first approximation, the consequence on glass durability depends on the type and rate of secondary phases formed91.
Effects of microorganisms
Although most of the studies on glass alteration published in the literature to date have focused on abiotic processes, it has also been established that microorganisms can interact with glass, leading to potential synergistic effects102. Microorganisms (bacteria, fungi) have been shown to impact glass alteration by a variety of mechanisms, especially through a direct impact of bacteria attached to the glass surface103 and also by the possible effect of microbial metabolites excreted by the cells104. The formation of a biofilm on the glass surface is not systematic. It depends on physical and chemical factors, which may be influenced by the glass composition and particularly by the presence of nutrients in the glass (Fe, Mn, P…), surface (substrate and organism) hydrophobicity, charge distribution, solution chemistry (i.e., pH and ionic strength), contact angle, and roughness104. Biofilm formation on the glass surface can act as a diffusion barrier for aqueous species, induce mechanical stress, or favor the formation of secondary phases (biomineralization)102. Depending on which mechanism dominates in the conditions of interest, the effects of microorganisms can either enhance or reduce glass alteration105,106. For nuclear waste glasses under geological storage conditions, the direct effect of microorganisms on glass alteration should be neglected, but redox reactions involving multivalent elements such as Fe or S could impact the local chemical conditions that could indirectly impact the glass. These potential indirect effects require further investigations.
Effects of irradiation
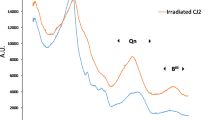
Nuclear waste glasses contain fission products (mostly β and γ emitters) and minor actinides (mostly α emitters). Radioactivity can affect glass durability either through structural damage within the glass structure or through the radiolysis of the interfacial water, modifying the chemical environment in the zone under reaction. Most of the structural damage within a glass is due to recoil nuclei associated with α decay107. Defects in the solid are usually in the form of dangling bonds (non-bridging oxygen atoms and peroxy bridges), oxygen-deficient centers, molecular oxygen, and coordination changes of certain network formers such as boron108,109. In borosilicate glasses, ballistic damage causes an increase in tri-coordinated B species at the expense of four-coordinated B species, with a detrimental consequence on the fraction of Na modifier110. The impact of irradiation on the medium-range order results in an increase in the disorder111,112. MD simulations reveal an increase in the mean ring size in the glass, which can increase water diffusion in the material113,114. Healing processes have been observed, which can mitigate the detrimental effects mentioned above111,115.
Alpha-emitters are generally low soluble elements which are highly retained in the gel and secondary phases107. The gel also can undergo radiation damages that could impact its thermodynamic and transport properties. The consequences on the glass of such changes require further investigation73.
Together, the different types of structural change can impact Stages I and II of glass alteration owing to a significantly higher reactivity of the reacting interface as compared to a non-irradiated glass sample109. The differences in behavior between alpha-irradiated and non-irradiated specimen depend on both the glass composition and the dose of irradiation, until a plateau is reached corresponding to a complete irradiation of the whole sample116,117. In general, simple glasses and high doses mean a greater impact. Regarding the mechanisms involved, the potential effects of irradiation on gel properties, the speciation of certain redox-sensitive species, and the nature of secondary phases remain subjects of investigation, especially when considering the complex scenarios expected for nuclear waste glass in a geological repository.
Effect of surrounding reactive solids
The presence of other solids near glass can change the driving forces for glass dissolution and thus the overall dynamics of the system. The effects on glass durability resulting from interactions with other solids chiefly depend on the transport of chemical species in the fluid between the dissimilar solids. If transport is slow or the distance is large, the effect will be small, and vice versa. We detail two emblematic examples: nuclear waste glass in interaction with a metallic canister, and bioactive glass interacting with bone.
Nuclear waste glass
Materials in contact with or near a borosilicate nuclear glass may include carbon steel118,119,120,121,122,123,124,125, stainless steel126,127,128,129,130, and their corrosion products, including magnetite (Fe3O4)131,132,133,134,135,136, goethite (FeOOH)134, iron hydroxide (Fe(OH)3)120, siderite (FeCO3)123, or various types of cementitious materials137,138. Several mechanisms have been identified: (1) precipitation of iron-silicates, which suppresses the saturation of Si in solution, and continuously drives glass alteration at a higher rate than that of glass altered without the presence of metals and their corrosion products118,121,122,123,124,125,139. (2) sorption120,128,131,133,134 and precipitation132 of silica onto the surface of metallic iron and Fe-containing corrosion products. (3) adverse effects of Fe2+ and Fe3+ cations140,141, which can strongly acidify the solution. (4) incorporation of Fe into the glass alteration layer, potentially deteriorating the passivating properties of the gel121,122,123,124,125. It is generally believed that like precipitation in the bulk solution, the precipitation of iron-silicates in porous gels may act as a sink for silicates, because these precipitates remove Si from the gel and hinder condensation reactions and gel maturation125,136,142. As a result, the gel is destabilized and the alteration rate of glass increases. In addition, the formation of Fe- and Si-containing phyllosilicates consumes hydroxyl ions and induces a pH decrease, resulting in the enhancement of glass alteration via the ion-exchange mechanism142. Finally, (5) enhanced alteration driven by the localized corrosion of metals129,143 (Fig. 4). More details regarding the corrosion interactions between different materials can be found in a recent review article143. The presence of cement near the glass can have opposite effects (increase or decrease glass alteration) depending on the pH137,144. In this case, the role of Ca is key.
The anodic dissolution of stainless steel (SS) creates a high concentration of metal cations (Mn+) on the interior surface of the SS canister. These metal cations hydrolyze, acidify the local solution, and attack the glass through ion-exchange reactions. In addition, a cathodic reaction occurs on the exterior surface of the SS canister, raising the alkalinity in the surrounding environment and subsequently assisting the precipitation of secondary phase minerals that could adversely impact glass alteration. (Reprinted from Guo et al.129, with permission, copyright Springer Nature).
Bioactive glass
Bioactive silicate glasses are used in medicine to stimulate bone regeneration4. The four-component glass 45S5 (Table 1) was discovered 50 years ago by Larry Hench, and since then more than a million patients have undergone surgery where this glass is used to repair bone defects in the jaw and in orthopedics4. For such applications, glass particles are pressed into the bone defect. The bioactivity of the glass is intimately linked to its alteration properties. Bone bonding is attributed to the precipitation of a hydroxycarbonate apatite (HCA) layer on the altered glass surface, which interacts with collagen fibrils of damaged bone to form a bond. Furthermore, the release of Si and Ca from the glass stimulates osteogenesis, and HCA provides a surface suitable for osteogenic cell attachment and proliferation. The mechanism of HCA precipitation is well understood. First, the glass undergoes ion-exchange, leading to a rapid release of Na and an increase in the pH near the glass surface. High local pH promotes hydrolysis and a condensation reaction of the remaining silica layer. The migration of Ca and P through the silica layer eventually leads to the formation of an amorphous film of Ca–P, which reacts with carbonate ions and hydroxyl groups to crystallize HCA4. The high pH near the glass surface is also known for its bactericidal properties145. The biological interactions of the HCA layer are complicated and less understood. They involve protein actions, incorporation of collagen fibrils, attachment of bone progenitor cells, cell differentiation, the excretion of bone extracellular matrix, and eventually its mineralization146. There are many other applications of bioglasses and many other compositions than that of glass 45S5, including glasses from other families (borate, phosphate glasses)147.
Atmospheric alteration
The literature on glass alteration by water vapor is quite limited compared to that in liquid water. A recent review by Majérus et al.148 concluded that the alteration of silicate glass in relative humidity (RH) <100% differs from that in liquid water at high S/V because the hydration process does not involve element release into the fluid, but rather a redistribution within the alteration layer, except for the elements which could be volatilized149. Therefore, the flux of water molecules, the local chemistry near the glass surface, and the porosity of the hydrated layer differ from the liquid medium. This results from the difference in the mechanisms between the two media, so that glasses that are classified as the most durable in aqueous phase can be the least durable in vapor phase150,151. In other words, to date, good knowledge of how a glass behaves in liquid water cannot be used to infer its behavior in vapor phase.
The RH plays a key role, as it determines the number of layers of water molecules that build on the glass surface152. In general, the hydration rate (in this situation, the authors refer to hydration rate instead of alteration, corrosion, or leaching rate) increases with RH and temperature153. Depending on the glass composition, temperature, and RH, the hydration rate can be constant or decreasing following a square root of time dependency, potentially related to a diffusion-controlled behavior154,155. Even in a square root of time behavior, the apparent activation energy is high (>60 kJ.mol−1), suggesting that coupled processes of transport of reactive species and bond breaking operate simultaneously. A recent study showed that some elements such as B or I can be volatilized during atmospheric alteration at 90 °C156. This makes the hydrated layer more porous and reactive than expected.
Secondary phases form more rapidly in atmospheric conditions because of the confined conditions. This could be explained by the local conditions at the glass surface that differ from that in liquid water. Bates et al. estimated that the S/V—where V is the volume occupied by the water molecules adsorbed on the glass surface S—is 109 times greater in vapor phase than in liquid phase157. Abrajano et al. estimated a pH of about 10–12 in the film of water formed in vapor phase for an initial pH of 6–7151. Various salts can precipitate with alkalis and volatile species such as chlorine, sulfate, carbon dioxide… Moreover, silicate minerals such as calcium silicate hydrates, zeolites, or clay-type minerals can also form. The precipitation of secondary phases gives direct effects, such as a modification of the visual appearance of the material along with changes to the chemical conditions at the glass surface, promoting or reducing further alteration148.
The main lesson from the recent work in this field is that the current understanding of glass alteration in atmospheric conditions cannot be deduced from knowledge obtained in liquid water. Although the processes at a molecular level are the same, the interplays between the mechanisms differ and this has an impact on the macroscopic behavior of the material. Therefore, there is a need to connect the various scales in order to decipher the rate-limiting steps depending on all the intrinsic and extrinsic variables.
Kinetics of glass alteration
In this paper, we have followed the widely used description of glass alteration in three kinetic regimes (Fig. 1)62: Stage I for ion-exchange and matrix dissolution, with no backward reaction of condensation and precipitation capable of impacting the solution chemistry or the properties and reactivity of the glass surface; Stage II for the residual rate regime associated with a Si-saturated solution, a passivating gel, and potential secondary phases; and Stage III for a potential acceleration of glass alteration due to the partial or total loss of the protectiveness of the gel.
Stage I
Among the three kinetic regimes listed above, Stage I may be seen as the most simple, as the glass undergoes only dissolution and the solution remains far from saturation, meaning that no backward reaction can occur. However, owing to the complexity of the glass structure, predicting r0 remains challenging. To date, no model has been developed which is capable of predicting, a priori and without resorting to empirical parameters, the initial dissolution rate of a silicate glass in a given environment. In this regime, the most common practice is to calculate the glass dissolution rate from the release of Si into the solution from static (batch) or dynamic (flow through) leaching experiments. This release is generally linear with time and congruent with the other glass elements. This is also true for glass modifiers sensitive to ion-exchange, but only if the glass is highly polymerized and the pH not too acidic. Otherwise, glass modifiers are released incongruently and faster than Si due to a fast H+/Na+ exchange. As an example, the dealkalized layer is about 100-nm thick in champagne bottles which have held wine for many years158. In lead-crystal bottles, unlike Pb, Na and K also undergo preferential leaching in acetic acid solutions simulating beverages159. Pb, which is a major health hazard, is strongly retained in the alteration layer because the silicate network repolymerizes after the release of alkali. An estimate of the time necessary to reach a steady state as a function of the interdiffusion coefficient and matrix dissolution is given by Frugier et al.91.
Figure 5 shows the typical evolution of the normalized mass losses calculated from Si and Na concentrations in the solution. In a static experiment, the normalized mass loss for an element i is given by:
where C(i) is the concentration of an element i in the solution, V the volume of solution, S the glass surface area, xi the mass fraction of i in the glass, and \({\sum} {NL(i)_{{\mathrm{samplings}}}}\) represents the contribution of the various samples taken in the leachate. The glass composition is known (nominal or analyzed composition), concentrations of i and solution volume are monitored over time, and S is treated with simple considerations. Depending on the authors, either the specific surface area determined from gas adsorption methods or the geometric surface using spheres as proxies for glass particles have been considered. Furthermore, a glass surface area can be considered as constant or decreasing with time160. For more details, see Fournier et al.161. In most kinetic studies, S is treated with simple considerations which do not take into account what actually happens at small scale. From a general standpoint, this issue must be considered cautiously, as several studies have reported significant changes to the reacting surface area during the reaction due to roughening48, pitting162,163,164, or cracking165.
r0 is derived from the NL(Si), after verifying that the release of Si is linear, the intercept is near zero, and the concentration of Si in solution is low, so that the solution is far from saturation:
where ρ is the glass density.
Another accurate way to calculate r0 is to monitor the retreat of the glass surface as a function of time. This can be performed by vertical scanning interferometry (VSI), after coating a small portion of the surface to serve as a reference85,166. But, if a gel forms, this technique will underestimate r0.
Among the various parameters impacting the magnitude of r0, we find the temperature and the pH yield effects, which are well understood, while the effects of glass composition167 and solution composition are less understood. The effect of temperature and pH can be modeled with an Arrhenius law and a power law, respectively:
where k is a kinetic constant, Ea an apparent activation energy, and η a coefficient for the pH dependency. Similarly to crystals, r0 against pH displays a V-shape curve with a minimum at a pH corresponding to the zero net proton charge (pHznpc), and an increase in both acid and basic regions for highly polymerized glasses60,168,169,170, or a continuously decreasing trend for low polymerized glasses171, as reported for silicate minerals. There has been no systematic study on the effect of solution chemistry on r0. Several potential mechanisms have been identified, such as the formation of outer-sphere or inner-sphere complexes between cations in solution and surface sites, the modification of the electric potential of the interfacial double layer, the nucleation of secondary phases, or the modification of the interfacial pH17,92,144,172,173. These effects can account for a supplementary term in Eq. (7), as suggested by previous work on silicate minerals174.
A challenging task for the glass community is to understand the effect of glass composition on r0. Table 1 summarizes the values of r0 determined or recalculated at 90 °C and pH90°C 9 for some nuclear, bioactive, natural, and industrial common glasses. It can be seen that r0 varies widely depending on the glass composition. At the first order, the Si content plays a major role—glass durability increases with increasing Si content—but the other glass constituents can dramatically and non-linearly affect r0. The case of Al is particularly interesting. Depending on the authors, the addition of Al to silicate glasses increases175 or decreases176 their chemical durability. This apparent contradiction can be explained if one considers the various effects of Al on a glass structure. On the one hand, except in peraluminous glasses, Al decreases the amount of sodium ions bonded to NBOs by increasing sodium ions for charge compensation of [AlO4]− tetrahedral units177. It also increases the glass network connectivity and results in a decrease in water diffusivity, and when present in a glass, stabilizes four-fold coordinated Mg and Zn, which then act as glass formers175. All these effects increase glass durability. But on the other hand, first principle calculations have demonstrated that Q4Al‒Q4Si linkages are easier to hydrolyze than Q4Si‒Q4Si. This result can explain why it is that in highly polymerized glasses with the same fraction of NBO, a higher Al content yields higher r0176. The example of aluminum highlights the complexity of the mechanisms involved, and the difficulty of attributing a single effect of a given element on the durability of silicate glasses.
The first approaches attempting to develop predictive models for r0 relied on thermodynamic models178,179. Reasonable trends were obtained between r0 and the free energy of hydration of glasses, although the hypothesis that glass can be seen as the sum of pure oxides is questionable given that the mixing enthalpy and the entropy tied to the structural disorder were not considered. Later, statistical approaches180 or Monte Carlo simulations with probabilities of dissolution of glass network formers fitted from experimental data36,181,182 were developed. However, the incomplete set of mechanisms incorporated in these models have prevented accurate predictions from being made. Recently, advanced techniques have been developed, such as science informed machine learning (ML) which overcome the intrinsic limitations of classical ML approaches (violation of the laws of physics, or unreliable extrapolations)183 or quantitative structure properties relationship (QSPR) approaches. These link structural descriptors to various glass properties, including r0184,185,186,187. The efficiency of these approaches is partly due to the recent improvements made in modeling glass structures by MD. The development of new interatomic potentials enables simulated structures to be in fair agreement with actual ones, even for borosilicate glasses which were previously poorly modeled because of the various coordinations of B atoms188. With these structural models, it has become possible to determine the number of constraints per atom, nc, and apply the topological constraints theory (TCT)189,190 or determine a mean bond strength, Fnet, that can be correlated to r0. Suitable linear correlations between nc (or Fnet) and log(r0) were obtained with these models, if one considers restricted compositional domains191,192,193. However, several limitations have been pointed out. These models require calibration, and the dissolution rate of an unknown glass can be calculated only if one knows the dissolution rate of a reference glass or a set of references glasses (training set). With a broad compositional domain, the uncertainties for the predictions remain much larger than for the measured rates. An uncertainty with a factor of ∼7 was calculated for a compositional domain with r0 spanning 5.5 orders of magnitude61, compared to a relative uncertainty of just 30% for a measured value of r0161. These limitations mean more effort is necessary in order to better refine the structural descriptors. For example, in the TCT approach no difference is made between Si and Al, as both have 4 bond stretching constraints and 5 bond bending constraints per atom, whereas as discussed above, Al impacts glass durability when substituted for Si176. In the Fnet approach, instead of taking the M‒O bond strength, first principles calculations could be performed to estimate the energy barrier for hydrolysis of the various M‒O‒M′ bonds59.
Stage II
As indicated above, Stage II of glass corrosion begins when the concentrations of low soluble glass network formers (Si, Al, Zr…) in solution have reached steady states. The corresponding alteration rate is called the residual rate, as the affinity for matrix dissolution is minimum. This residual rate, rr, is highly dependent on the glass composition—several studies have reported wide variations of rr for only slight glass compositional variations98,194,195—but not in the same way as for the initial dissolution rate180,196. In other words, knowledge of r0 cannot be used to predict rr196. This is because the rate-controlling mechanisms are not the same.
Various experimental protocols have been used to measure rr. In general, crushed glass is placed in contact with a given volume of deionized water in a Teflon or stainless steel vessel, and placed in an oven at the target temperature180,194,196,197. From that point on, two strategies are possible. Either a series of small vessels is prepared and each vessel is used for a particular duration, or a single vessel is used and the solution is sampled at various time durations. Samples are analyzed by classical solution analysis methods, such as ICP-OES or ICP-MS. The residual rate is derived from NL(i) calculated for the tracer elements (Eq. 4). In that case, alkalis or boron are used as glass dissolution tracers, instead of silicon. The criteria taken into account for selecting a tracer include high solubility in the test conditions and a low retention in the alteration layer. In most studies on nuclear glass, B has been considered as an ideal tracer198. Recently, it has been shown that when ISG is corroded in Stage II, some B is retained within an inner layer close to the pristine glass surface, called the reactive zone as it is also richer in hydrogenated species48,61. In general, the question of the tracer must always remain central when studying the glass dissolution.
During experiments, the volume of sampled solution can be replaced by fresh water (pseudo-dynamic test) or not (static test). To better monitor the glass response for a given solution composition, experiments can be conducted in dynamic conditions199,200,201. The use of glass powder ensures a high S/V ratio and thus increases the accuracy of the rate determination from solution analysis. An alternative approach consists in altering polished glass coupons at low S/V in a solution pre-saturated in glass network formers. This protocol offers a better control of the geometry of the reacting glass and opens up the possibility of running depth profiling analysis77,86.
For glasses that can form a passivating gel, rr usually starts diminishing proportionally to t−1/2 (the concentration of tracer elements released into the solution increases proportionally to t1/2). The rest of the curve depends on both the glass composition and the alteration conditions (pH, solution composition): it can be continuously decreasing, constant, or fluctuating180,196,202,203,204. There is no general practice for calculating rr. In some studies, the authors considered the long-term near constant rate when calculating rr, while in others the authors used the value corresponding to the most advanced stage of reaction in the tested conditions but without checking that the rate was at its minimum. This can make inter-study comparisons difficult. Table 2 summarizes values of rr for SON68 glass, the reference non-radioactive glass which simulates the R7T7 glass produced at La Hague. Data came from various experiments conducted at 90 °C in deionized water, in Si-rich solution, in synthetic clayey groundwater, or at various pHs imposed by a strong acid or base. All the protocols described above have little impact on the rr. This reveals that in this regime, glass behavior is not sensitive to S/V. Only the experiment in groundwater had a significant impact on rr. This can be explained by both a pH effect and the precipitation of Mg-silicate at the expense of the passivating gel92. The impact of pH on rr is not clear. On the one hand, the pH seemed to have a minor impact on SON68 between pH 7 and 10.5 (Table 2), but on the other hand, it significantly affected the residual rate of ISG61,205,206. Note that in Gin et al. the pH of the pH 8 and pH 7 experiments fluctuated, despite numerous manual corrections206. The mechanisms governing the residual rate also depend on T. It has been found that the apparent activation energy measured in the Stage II regime was close to that determined when glass undergoes only dissolution (stage I)47.
Stage III
Stage III of glass corrosion is characterized by a sudden increase of the alteration rate. The period of slow corrosion in Stage II before the alteration takes off is very sensitive to both glass composition and environmental conditions. The resumption can happen after a minute, a few decades, or perhaps never. This issue is particularly serious for nuclear glasses, because it must be demonstrated that Stage III is unlikely if one wants to develop a performance model based on Stage II. As recalled in a recent review paper, Stage III has been widely investigated in the past207. It has been established that when alteration resumes, the corresponding rate, rres, can be close to but is always less than the initial dissolution rate measured in the same (T, pH) conditions208,209,210,211. Interestingly, it has been found that the lower the pH, the lower the ratio rres/r0208. This means that for a given glass, hyperalkaline media favor Stage III with rates close to r0, whereas circum-neutral pH media, such as those of most ground waters, favor alteration rates close to rr. In his review, Fournier concluded that the stage III is mostly associated with the precipitation of zeolites and, to a lesser extent, calcium-silicate-hydrates (CSH)207, although other causes such as the formation of cracks within the passivating layer212 or an increase in the reacting surface area165 have been reported. The zeolites and CSH precipitate at the expense of the passivating gel, and do not form a diffusion barrier for aqueous species, at least in the experimental test conditions86,213. At low temperatures in natural environments, it is not known if zeolitization of basaltic glass is associated with fast alteration rates214. Jantzen et al. developed a powerful approach based on observations and thermodynamic considerations to predict if a glass is likely to reach Stage III, depending on its composition215,216,217. The authors found that the Si/Al ratio of the gel is the key point. If Si/Al <1, glasses tend to remain in Stage II even if clay minerals precipitate, whereas if Si/Al >1, the presence of alkali or OH− in the leachate (strong bases) generate zeolites accompanied by a marked increase of the glass dissolution rate. However, this approach does not tell us when alteration will resume, and at what rate. To date, mostly thermodynamic models have been tested, showing that zeolite precipitation can occur and control glass dissolution depending on the glass and the solution composition204,218,219.
Holistic models for glass alteration
Here we discuss the models able to calculate the glass dissolution rate and the formation of alteration products, compared to time and environmental conditions.
Two kinds of models have been developed: continuous scale models including a single equation or a set of equations, and probabilistic models based on Monte Carlo (MC) algorithms.
Continuous scale models
The most popular continuous scale models are summarized in Table 3. The questions discussed here focus on whether these models can simulate the transition between Stages I and II and the residual rate regime, and if they are able to assess the risk of Stage III. We will not discuss the theoretical bases of these rate laws, but only their application to account for experimental observations. Some models simulate the decrease in the rate with an affinity term only54,65,220,221, while others couple an affinity term and the transport of aqueous species through the passivating gel and/or the transport of water in the pristine glass91,222,223,224,225,226. The affinity term (1-IAP/IAPsat) describes the degree of saturation of the solution with respect to the dissolving phase in terms of an adequate ion activity product IAP, with the index “sat” denoting saturation. The affinity-based rate laws suppose that either a thermodynamic equilibrium between the outer surface of the reacting material and the solution can stop further glass dissolution65,220,221, or that the thermodynamic equilibrium applies between the buried glass surface and the interfacial solution224. The predictions of these affinity-type models are at odds with observations on borosilicate glass, where alkalis and boron continue to dissolve even when concentrations of low soluble glass network formers (elements forming the outer surface) have reached saturation87. For this type of glass, it is thought that alteration proceeds beyond saturation of the fluid through the dissolution of B, because (1) B‒O‒Si linkages break faster than Si‒O‒Si linkages, and (2) dissolution of B is irreversible (B‒O‒Si bonds cannot reform), therefore B cannot contribute to the polymerization of the passivating layer. But this is not so clear-cut, since a recent study on ISG has shown that the activation energies for the hydrolysis of the two kinds of bonds are very close and that a high concentration of B and Ca in solution seems to limit further B release61. Therefore, at least for this type of glass, the dissolution of B and the transport of B(OH)3 and B(OH)4− through the gel could be rate-limiting in Stage II. For basaltic glass, the rate law proposed by Daux et al. predicts that the rate is zero when a solution is saturated with the leached outer layer made up of Si, Al, and Fe221. Techer et al. proposed an affinity term only based on Si, applied at the pristine glass surface, and added a diffusion term of Si through the gel layer222. The model predicts that the rate is zero when the concentration of Si at the glass surface reaches saturation. However, when there was a rapid reaction progress (long duration, high S/V, static conditions), an extremely slow but not zero residual rate was measured197. Therefore, the two models developed for basaltic glass (Table 3) cannot account for this low rr.
For B-free glasses with no or a low amount of non-bridging oxygens (NBO), such as obsidian, albite, or nepheline glass, the existence of a residual rate has not been demonstrated. At the first order, it depends on whether the glass structure allows water molecules to diffuse in the pristine material. If water can diffuse in the solid, alteration could proceed through ion exchange, hydrolysis reactions, and local rearrangements16,76,227. This can be considered as a residual alteration even if no glass components are released into the solution. Another possible cause of a residual alteration could be the difference in chemical potential between the altered glass surface in equilibrium with the bulk solution and the pristine glass surface. A significant difference would account for the maintenance of a residual transformation of the pristine glass into alteration products, with a potential supplemental effect if alteration products are transport-limiting for water molecules. A recent MD study to compare the behavior of vitreous albite (NaAlSi3O8) with its crystalline polymorph demonstrated that water can diffuse in the glassy structure but not in the crystal85. This structural difference was assumed to impact the formation mechanism of the passivating layer. It remains to be shown whether the glassy form exhibits a non-zero residual rate.
Direct evidence using isotopic (29Si, 18O) markers has been obtained showing that a dense gel layer can be transport-limiting for water molecules and some dissolved glass species30,61. The kinetic models coupling affinity and diffusive transport are therefore a priori better able to predict the residual rate of these glasses. However, it remains unclear which chemical species are involved in the diffusion-limiting mechanism. It is likely that several of them can play a role, depending on the gel characteristics (porosity, surface charge) and the environmental conditions (T, pH…). Progress here could come from the identification of the chemical species diffusing in the gel and the direct measurement of the diffusion coefficients of these species. Another important aspect concerns the formation dynamics of the passivating layer. Recent experimental studies have shown that the passivating gel undergoes local reorganization, leading to pore ripening, and a decrease in the reactivity with water30,228. Except for the model developed by Ma et al.225, none of the models listed above take into account the effect of maturation.
Overall, when considering the glass/gel/solution system, there is still some progress to be made in identifying the rate-limiting mechanisms and their inclusion in a reactive transport model in order to be able to make accurate predictions. This will benefit from the progress made in the development of advanced analytical techniques17,209,229, along with simulation techniques at molecular and mesoscopic levels230.
The precipitation of secondary phases is a key phenomenon for Stage II. In most of the experimental studies, secondary phases form at the expense of the passivating gel (Fig. 7). When secondary phases precipitate, they change the solution chemistry, which in turn can change the rate of formation or dissolution of the passivating gel. From a modeling standpoint, the data required to take secondary phases into account include, in order of priority, the solubility product, and the kinetics of precipitation. The rate laws listed above are implemented in reactive transport codes, which use thermodynamic databases with most of the secondary phases which can form.
A kinetic model was used by Fournier et al. to account for Stage III glass corrosion. The model was applied to ISG altered in NaOH solutions231. The authors used the GRAAL model associated with additional equations for nucleation and the growth of zeolites. Despite the use of fitting parameters, the modeling exercise was helpful and showed that, subject to knowing the composition and the solubility of the gel as a function of pH, it is possible to predict when and at what rate the alteration will resume. It is worth noting that, at laboratory scale, the nature and both the solubility and passivating properties of gels able to form in various environments need to be understood and calculated before a mechanistic model can predict the behavior of glass in both Stages II and III. At a longer timescale, the modeling of nuclear glasses in disposal environments requires an integrated approach and the use of a model relying on the relevant mechanisms. More complicated, slow processes that could impact the durability of glass packages, such as the sealing of cracks by secondary phases formed in Stages II or III, should be considered, especially in a best estimate approach. An illuminating example was given by the alteration of a fractured archeological glass block from the Roman period, altered for 1800 years in seawater. It was demonstrated that the precipitation of clay minerals and calcite within the cracks dramatically diminished the contribution of the internal surfaces to the global alteration of the block. After a few centuries, their contribution became negligible even though their surface was initially 100 times greater than the outer surface232. A simple model based on a constant contribution of all the surfaces would therefore be extremely over-conservative.
Probabilistic models
Probabilistic models based on the MC algorithm constitute another kind of kinetic models. They link the elementary mechanisms at the atomistic scale to the dissolution rates at the macroscopic level. This approach has been widely applied to both minerals233,234,235 and glasses113,182,236,237. The parameters are generally fitted from ab initio calculations233 or empirically, to reproduce certain experimental behaviors238. Despite some limitations discussed below, it is worth emphasizing the use of these models, as interesting results have already been obtained and the technique is still in development. Let us discuss a few examples.
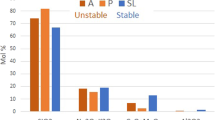
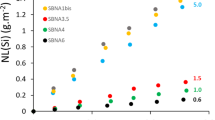
To simulate glasses within the compositional ranges (61 − x)SiO2–17B2O3–18Na2O–4CaO–xZrO2236 or (70 − 2x)SiO2–xAl2O3–15B2O3–(15 + x)Na2O237, glass cations were placed at the nodes of an ordered cubic network (each atom is surrounded by six neighbors). Then some bonds were broken, depending on the coordination number of the cations in the glass: zero for VIZr, two for IVSi or IVAl, IVB, and three for IIIB. O atoms were not explicitly displayed, and Na and Ca atoms were not bound to the network. A 2D or 3D glass–water interface with thousands to millions of atoms and water molecules was prepared, and probabilities were implemented for bond breaking (Si‒Si, Si‒Al, Al‒Al) and dissolved cation (Si, Al) redeposition on the glass surface. Note that a single set of probabilities was assigned for a given series of glasses. A simulation consists in accumulating thousands to millions of events (dissolution–redeposition) to monitor the glass behaviors. Step by step, the soluble elements in contact with water were dissolved in solution, leading to the formation of a gel-like altered layer composed of low or non-soluble elements (Si, Al, and Zr in this example). The alteration rate decreased with time because redeposition prevented the accessibility of water to the soluble elements, but once the Si and Al saturation was reached, the rate dropped sharply to zero, as no diffusion mechanisms were implemented, except for one attempt to introduce ion diffusion in the liquid phase239. Owing to the limitations preventing the calculation of rr, simulations have mostly focused on the effects of soluble or hardener elements on r0, the transition between Stages I and II, and the characteristics of the alteration layer (thickness, interfacial roughness, pore volume, pore size). For instance, it has been seen that r0 decreases with increasing Zr content in the glass, because Zr cannot dissolve. However, at high reaction progress rates, high Zr content glasses are much less durable than low Zr content glasses, as Zr prevents gel maturation and pore closing236,238,240. This nonlinear effect of Zr has been confirmed experimentally by porosity investigation using small-angle X-ray and neutron scattering (SAXS, SANS) and the diffusion of dyes monitored by time-of-flight secondary ion mass spectrometry (ToF-SIMS) techniques36,240 (Fig. 6).
Glasses ((61−x)SiO2–xZrO2–17B2O3–18Na2O–4CaO) were studied both by a MC model and experimentally. a On the left, cross section of altered glass specimen in Stage I and corresponding values of r0 measured at 90 °C, neutral pH. On the right, cross section of the same glasses at a faster reaction progress. This example highlights the nonlinear effect of Zr, which can be explained when considering its role in Si dissolution and gel maturation. b TEM image of the gel formed on the Zr-free glass of the series (x = 0) and the corresponding simulated gel obtained by MC. Both display the same features with the closing of the porosity near the outer surface. c Comparison of the gel morphologies based on the exponent of the SAXS power law as a function of the ZrO2 content in glass composition after 106 computation steps for the simulated glasses and after 39 days of corrosion for the real glasses. Data adapted from Cailleteau et al.36 with permission, copyright Springer Nature, and Cailleteau et al.240 with permission, copyright American Chemical Society.
The impact of NBO, the Si/B ratio, boroxol rings, or Al2O3 content has been investigated in alumino-borosilicate glasses181,237. The quantity of NBO is a key factor that increases the glass dissolution rate. The impact of NBO concentration on glass dissolution rate is nonlinear: at low concentration, the glass dissolution rate is proportional to Q3, whereas at high concentration, glass clusters surrounded by Q1 and Q2 species are released to solution without being dissolved. Furthermore, when the B atoms are clustered within boroxol rings, the glass dissolution rate increases. A clear synergy between the Al and B has been shown. The B release changes in a nonlinear manner when the Al2O3 content increases, with a maximum B release observed for an intermediate Al2O3 content237. This behavior relies on the dynamics of gel reorganization.
MC modeling has also been used to investigate radiation-induced structural damage in glass and its consequences on chemical durability113. Modifications of the local structural characteristics induced by ballistic effects (depolymerization, change in the local angles) were not sufficient to account for the experimental observations on r0. For that, it is necessary to consider other mechanisms not implemented in the current Monte Carlo approach, such as the acceleration of water diffusion in the irradiated structure.
Despite the interesting results summarized above, the simulation of the glass structure by an ordered lattice constitutes only a rough approximation. The consequences of this oversimplification have been evaluated by comparing the r0 of an ordered structure to that of a disordered structure prepared by classical MD241. It appears important to represent the surface roughness accurately, because of the strong correlation between this parameter and r0 (the number of sites accessible to water increases with increasing the interfacial roughness). Hence, using a structure prepared by classical MD represents a clear improvement. Unfortunately, this approach remains limited due to the difficulty of simulating structural relaxation after a hydrolysis or condensation reaction that has occurred within a disordered structure. To overcome this difficulty, a model based on patchy particles is currently being developed, allowing for a very fast structural relaxation in parallel with the MC procedure230. This promising approach opens the door to the simulation of the complete alteration process using a MC approach based on a more realistic glass network.
Concluding remarks
Significant progress has been made over recent years in deciphering glass behaviors in natural, industrial, or living environments. Progress has come from both understanding the fundamental processes at molecular level and integrating that knowledge in models. Zooming in at the molecular level reveals extremely complex and dynamic processes. The challenge now is to identify the relevant mechanisms to be implemented in macroscopic models. The overall picture and the applications must always be kept in mind. Experiments in laboratories as well as observations of natural systems have demonstrated that silicate glasses can self-passivate by forming amorphous gels on their surfaces, but the fate of the protected glass strongly depends on the environment. The mechanisms of gel formation are still under debate, although recent results strongly suggest that a continuum exists between the ICDP model and the leaching/in situ reorganization model.
For applications requiring very resistant glasses, secondary phases can be seen as a threat for the pseudo-equilibrium achieved when the glass is protected by a gel, as they are thermodynamically more stable than the amorphous passivation layer and have poor diffusion properties. Therefore, they can form at the expense of the passivating layer. Stages II and III of glass corrosion result from these competitions. It is worth noting that the frontier between a passivating gel and secondary phases is not always clear, as illustrated in Fig. 7 with various cases. In Fig. 7a and c, gels form by in situ reorganization of the silicate network after preferential dissolution of alkalis and boron, whereas in Fig. 7b, a series of amorphous layers forms by congruent dissolution of the glass and reprecipitation. Note that, those solid phases can act as a sink for hazardous elements contained in the glass107,204,242,243,244. This can dramatically reduce the source term of vitrified wastes. Furthermore, in some cases, precipitation of secondary phases can reduce the renewal of fresh water on the glass surface, resulting in increased durability of the glass232,245,246.
a TEM cross section of SON68 glass altered in Mg-rich clayey groundwater at 70 °C for 224 days (Adapted from De Echave et al.97 with permission, copyright Elsevier). The growth of the Mg-bearing phyllosilicates on the gel surface consumes Si and Al in the gel, resulting in bigger pores near the precipitates. b SEM image of the inner part of the alteration layer formed on a 9-oxide borosilicate glass altered at 150 °C, pH 1 for 96 h (adapted from Geisler et al.259 with permission, copyright Elsevier). The oscillating banding pattern (ptz) forms an inner amorphous zone resulting from glass dissolution followed by interfacial reprecipitation. This example illustrates the fact that the alteration layer can be formed by different mechanisms. c TEM cross section of ISG altered at 70 °C for 385 days in cement water (adapted from Ferrand et al.260 with permission, copyright MDPI). High pH (pH70°C ~ 10) favors the precipitation of calcium-silicate-hydrates at the expense of the passivating gel.
For some applications, the formation of an alteration layer on glass, whatever its composition, is detrimental. For instance, this is the case for (1) tableware, which can lose its transparency after a few cleaning cycles in a dishwasher247, (2) commercial window glass during the storage period, which can undergo atmospheric alteration248, (3) stained-glass windows, which can lose shine and luminosity after decades or centuries of exposure to acid rain and pollutant deposits249,250, and (4) ampoules, vials, or cartridges for pharmaceutical use, as alteration products can delaminate and contaminate the active products251. For all these situations, a deeper understanding of the mechanisms involved can help to find solutions to delay or limit the detrimental effects of aging. As seen above the case of bioactive glass is the opposite. The formation of secondary phases is wanted, and must occur quickly, as that is the way bioactive glasses alter to form HCA to repair damaged bones in the human body4. Unmet challenges always require more research147. In particular, the role of cations released by glass on cell stimulation has to be better understood.
Future challenges and perspectives
The previous sections have shown that there are still some unresolved issues regarding the mechanisms controlling the three stages of glass corrosion. These fundamental limitations prevent the development of predictive models without the use of empirical convoluted parameters. Having predictive models available, with calculated or measured fundamental parameters from first principles or specific experiments, is mandatory for systems that cannot be investigated with a comprehensive experimental approach. This is typically the case for nuclear waste glasses, which require the best estimation of their performance over hundreds of thousands of years, or natural glasses which evolve slowly in natural (i.e., complex) environments at a geological timescale. To overcome this difficulty, current performance assessment models take into account over-conservatisms252,253. For other applications which can be directly tested, it seems less important to have predictive models, but they could offer the opportunity to efficiently design glasses with targeted properties, or to find efficient solutions for current problems of aging.
The case of nuclear glasses is certainly the most complicated system of glass science considered to date. These materials include dozens of oxides, the geometry of the glass block is complicated due to the cracks formed during the cooling stage, the thermal, chemical, and hydraulic boundary conditions are time-dependent and involve many coupled phenomena. Furthermore, the radioactivity yields specific effects, and the timescale that needs to be considered for the safety assessment of the disposal site is beyond any direct validation254. That is why a rigorous, multi-scale approach has been developed, with fundamental understanding being integrated in models, then compared to the results from dedicated experiments, or natural or archeological analogs232,255.
From a general standpoint, it is clear that silicate glasses do not behave like crystallized silicates, even though they are made up of the same basic units. Disorder in a glass structure yields isotropic properties and specific behaviors, mainly in the way of forming alteration products. In that sense, there is still some work to be done to develop a universal theory for silicates. Both experimental and digital tools have made progress, and it is now possible to envisage strategies for reactive transport codes or probabilistic codes to implement various coupled mechanisms with parameters calculated with atomistic simulations based on first principles. The next major result may well be the calculation of the initial dissolution rate of a silicate glass with only parameters calculated at the atomic level. Such a result would open the gate to fully predictive models able to design materials with tailored properties, or to calculate their durability in conditions where experiments are currently impossible or costly.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Mauro, J. C., Philip, C. S., Vaughn, D. J. & Pambianchi, M. S. Glass science in the United States: current status and future directions. Int. J. Appl. Glass Sci. 5, 2–15 (2014).
Mauro, J. C. Decoding the glass genome. Curr. Opin. Solid State Mat. Sci. 22, 58–64 (2018).
Morse, D. L. & Evenson, J. W. Welcome to the glass age. Int. J. Appl. Glass Sci. 7, 409–412 (2016).
Jones, J. R. Review of bioactive glass: from Hench to hybrids. Acta Biomater. 9, 4457–4486 (2013).
Waclawska, I. & Szumera, A. Reactivity of silicate-phosphate glasses in soil environment. J. Alloy. Compd. 468, 246–253 (2009).
Lee, W. E., Ojovan, M. I., Stennett, M. C. & Hyatt, N. C. Immobilisation of radioactive waste in glasses, glass composite materials and ceramics. Adv. Appl. Ceram. 105, 3–12 (2006).
Schiffman, P., Watters, R. J., Thompson, N. & Walton, A. W. Hyaloclastites and the slope stability of Hawaiian Volcanoes: Insights from the Hawaiian Scientific Drilling Project’s 3-km drill core. J. Volcanol. Geotherm. Res. 151, 217–228 (2006).
Walton, A. W., Schiffman, P. & Macpherson, G. L. Alteration of hyaloclastites in the HSDP 2 Phase 1 Drill Core: 2. Mass balance of the conversion of sideromelane to palagonite and chabazite. Geochem. Geophys. Geosyst. 6, 27 (2005).
Minitti, M. E., Weitz, C. M., Lane, M. D. & Bishop, J. L. Morphology, chemistry, and spectral properties of Hawaiian rock coatings and implications for Mars. J. Geophys. Res. -Planets 112, 24 (2007).
Baucke, F. G. K. Glass electrodes: why and how they function. Ber. Bunsen-Ges. Phys. Chem. Chem. Phys. 100, 1466–1474 (1996).
Conradt, R. Chemical durability of oxide glasses in aqueous solutions: a review. J. Am. Ceram. Soc. 91, 728–735 (2008).
Iler, R. K. The Chemistry of Silica: Solubility, Polymerization, Colloid and Surface Properties and Biochemistry of Silica (Wiley, 1979).
Bunker, B. C. Molecular mechanisms for corrosion of silica and silicate-glasses. J. Non Cryst. Sol. 179, 300–308 (1994).
Gin, S. et al. An international initiative on long-term behavior of high-level nuclear waste glass. Mater. Today 16, 243–248 (2013).
Lu, X. N., Ren, M. G., Deng, L., Benmore, C. J. & Du, J. C. Structural features of ISG borosilicate nuclear waste glasses revealed from high-energy X-ray diffraction and molecular dynamics simulations. J. Nucl. Mater. 515, 284–293 (2019).
Geneste, G., Bouyer, F. & Gin, S. Hydrogen-sodium interdiffusion in borosilicate glasses investigated from first principles. J. Non Cryst. Sol. 352, 3147–3152 (2006).
Geisler, T., Dohmen, L., Lenting, C. & Fritzsche, M. B. K. Real-time in situ observations of reaction and transport phenomena during silicate glass corrosion by fluid-cell Raman spectroscopy. Nat. Mater. 18, 342 (2019).
Linard, Y., Advocat, T., Jegou, C. & Richet, P. Thermochemistry of nuclear waste glasses: application to weathering studies. J. Non Cryst. Sol. 289, 135–143 (2001).
Frankel, G. S. et al. A comparative review of the aqueous corrosion of glasses, crystalline ceramics, and metals. NPJ Mater. Degrad. 2, 17 (2018).
Du, J. C. & Rimsza, J. M. Atomistic computer simulations of water interactions and dissolution of inorganic glasses. NPJ Mater. Degrad. 1, 12 (2017).
Tilocca, A. & Cormack, A. N. Modeling the water-bioglass interface by ab initio molecular dynamics simulations. ACS Appl. Mater. Interfaces 1, 1324–1333 (2009).
Tilocca, A. & Cormack, A. N. Surface signatures of bioactivity: MD simulations of 45S and 65S silicate glasses. Langmuir 26, 545–551 (2010).
D’Souza, A. S. & Pantano, C. G. Hydroxylation and dehydroxylation behavior of silica glass fracture surfaces. J. Am. Ceram. Soc. 85, 1499–1504 (2002).
Mahadevan, T. S. & Garofalini, S. H. Dissociative chemisorption of water onto silica surfaces and formation of hydronium ions. J. Phys. Chem. C. 112, 1507–1515 (2008).
Mahadevan, T. S. & Du, J. C. Evaluating water reactivity at silica surfaces using reactive potentials. J. Phys. Chem. C. 122, 9875–9885 (2018).
Jabraoui, H., Charpentier, T., Gin, S., Delaye, J. M. & Pollet, R. Atomic insights into the events governing the borosilicate glass–water interface. J. Phys. Chem. C. 125, 7919–7931 (2021).
Arena, H. et al. Characterization of the boron profile and coordination in altered glass layers by EEL spectroscopy. Micron 141, 9 (2021).
Angeli, F. et al. Effect of thermally induced structural disorder on the chemical durability of International Simple Glass. NPJ Mater. Degrad. 2, 11 (2018).
Wang, Q. Q., Manzano, H., Guo, Y. H., Lopez-Arbeloa, I. & Shen, X. D. Hydration mechanism of reactive and passive dicalcium silicate polymorphs from molecular simulations. J. Phys. Chem. C. 119, 19869–19875 (2015).
Gin, S. et al. Dynamics of self-reorganization explains passivation of silicate glasses. Nat. Commun. 9, 9 (2018).
Collin, M. et al. Molecular dynamics simulations of water structure and diffusion in a 1 nm diameter silica nanopore as a function of surface charge and alkali metal counterion identity. J. Phys. Chem. C. 122, 17764–17776 (2018).
Ohkubo, T., Gin, S., Collin, M. & Iwadate, Y. Molecular dynamics simulation of water confinement in disordered aluminosilicate subnanopores. Sci. Rep. 8, 11 (2018).
Rimsza, J. M. & Du, J. C. Nanoporous silica gel structures and evolution from reactive force field-based molecular dynamics simulations. NPJ Mater. Degrad. 2, 10 (2018).
van Duin, A. C. T. et al. ReaxFF(SiO) reactive force field for silicon and silicon oxide systems. J. Phys. Chem. A 107, 3803–3811 (2003).
Rimsza, J. M. & Du, J. C. Interfacial structure and evolution of the water-silica gel system by reactive force-field-based molecular dynamics simulations. J. Phys. Chem. C. 121, 11534–11543 (2017).
Cailleteau, C. et al. Insight into silicate-glass corrosion mechanisms. Nat. Mater. 7, 978–983 (2008).
Jollivet, P. et al. Investigation of gel porosity clogging during glass leaching. J. Non Cryst. Sol. 354, 4952–4958 (2008).
Deng, L. et al. Reaction mechanisms and interfacial behaviors of sodium silicate glass in an aqueous environment from reactive force field-based molecular dynamics simulations. J. Phys. Chem. C. 123, 21538–21547 (2019).
Mahadevan, T. S. & Du, J. C. Atomic and micro-structure features of nanoporous aluminosilicate glasses from reactive molecular dynamics simulations. J. Am. Ceram. Soc. 104, 229–242 (2021).
Bouyer, F., Geneste, G., Ispas, S., Kob, W. & Ganster, P. Water solubility in calcium aluminosilicate glasses investigated by first principles techniques. J. Solid State Chem. 183, 2786–2796 (2010).
Tilocca, A. Sodium migration pathways in multicomponent silicate glasses: Car-Parrinello molecular dynamics simulations. J. Chem. Phys. 133, 10 (2010).
Tilocca, A. & Cormack, A. N. The initial stages of bioglass dissolution: a Car-Parrinello molecular-dynamics study of the glass-water interface. Proc. R. Soc. A-Math. Phys. Eng. Sci. 467, 2102–2111 (2011).
Mansas, C. et al. Drivers of water transport in glass: chemical or topological effect of the glass network? J. Phys. Chem. C. 121, 16201–16215 (2017).
March, P. & Rauch, F. Leaching studies of soda lime silica glass using deuterium-enriched and O-18-enriched solutions. Glastech. Ber. -Glass Sci. Technol. 63, 154–162 (1990).
Richter, T., Frischat, G. H., Borchardt, G. & Scherrer, S. Short-time leaching of a soda lime glass in H2O and D2O. Phys. Chem. Glasses 26, 208–212 (1985).
Petit, J. C. et al. Hydrated-layer formation during dissolution of complex silicate-glasses and minerals. Geochim. Cosmochim. Acta 54, 1941–1955 (1990).
Chave, T., Frugier, P., Ayral, A. & Gin, S. Solid state diffusion during nuclear glass residual alteration in solution. J. Nucl. Mater. 362, 466–473 (2007).
Gin, S. et al. Atom-Probe Tomography, TEM and ToF-SIMS study of borosilicate glass alteration rim: a multiscale approach to investigating rate-limiting mechanisms. Geochim. Cosmochim. Acta 202, 57–76 (2017).
Criscenti, L. J., Kubicki, J. D. & Brantley, S. L. Silicate glass and mineral dissolution: calculated reaction paths and activation energies for hydrolysis of a Q(3) si by H3O+ using ab initio methods. J. Phys. Chem. A 110, 198–206 (2006).
Laurence, P. R. & Hillier, I. H. Towards modelling bioactive glasses: quantum chemistry studies of the hydrolysis of some silicate structures. Comput. Mater. Sci. 28, 63–75 (2003).
Kubicki, J. D. & Sykes, D. Molecular-orbital calculations on the vibrational-spectra of Q(3)T-(OH) species and the hydrolysis of a 3-membered aluminosilicate ring. Geochim. Cosmochim. Acta 59, 4791–4797 (1995).
Xiao, Y. T. & Lasaga, A. C. Ab initio quantum mechanical studies of the kinetics and mechanisms of quartz dissolution: OH- catalysis. Geochim. Cosmochim. Acta 60, 2283–2295 (1996).
Pelmenschikov, A., Strandh, H., Pettersson, L. G. M. & Leszczynski, J. Lattice resistance to hydrolysis of Si-O-Si bonds of silicate minerals: Ab initio calculations of a single water attack onto the (001) and (111) beta-cristobalite surfaces. J. Phys. Chem. B 104, 5779–5783 (2000).
Grambow, B. In MRS Proceedings (eds. Stone, J. A., Jantzen, C. M. & Ewing, R. C.) 15 (Cambridge University Press). Volume 44, (1985).
Kagan, M., Lockwood, G. K. & Garofalini, S. H. Reactive simulations of the activation barrier to dissolution of amorphous silica in water. Phys. Chem. Chem. Phys. 16, 9294–9301 (2014).
Lockwood, G. K. & Garofalini, S. H. Bridging oxygen as a site for proton adsorption on the vitreous silica surface. J. Chem. Phys. 131, 8 (2009).
Pelmenschikov, A., Leszczynski, J. & Pettersson, L. G. M. Mechanism of dissolution of neutral silica surfaces: Including effect of self-healing. J. Phys. Chem. A 105, 9528–9532 (2001).
Nangia, S. & Garrison, B. J. Ab initio study of dissolution and precipitation reactions from the edge, kink, and terrace sites of quartz as a function of pH. Mol. Phys. 107, 831–843 (2009).
Zapol, P., He, H. Y., Kwon, K. D. & Criscenti, L. J. First-principles study of hydrolysis reaction barriers in a sodium borosilicate glass. Int. J. Appl. Glass Sci. 4, 395–407 (2013).
Inagaki, Y., Kikunaga, T., Idemitsu, K. & Arima, T. Initial dissolution rate of the international simple glass as a function of pH and temperature measured using microchannel flow-through test method. Int. J. Appl. Glass Sci. 4, 317–327 (2013).
Gin, S. et al. Insights into the mechanisms controlling the residual corrosion rate of borosilicate glasses. NPJ Mater. Degrad. 4, 9 (2020).
Vienna, J. D., Ryan, J. V., Gin, S. & Inagaki, Y. Current understanding and remaining challenges in modeling long-term degradation of borosilicate nuclear waste glasses. Int. J. Appl. Glass Sci. 4, 283–294 (2013).
Jollivet, P., Gin, S. & Schumacher, S. Forward dissolution rate of silicate glasses of nuclear interest in clay-equilibrated groundwater. Chem. Geol. 330, 207–217 (2012).
Aagaard, P. & Helgeson, H. C. Thermodynamic and kinetic constraints on reaction-rates among minerals and aqueous-solutions. 1. Theoretical considerations. Am. J. Sci. 282, 237–285 (1982).
Oelkers, E. H. General kinetic description of multioxide silicate mineral and glass dissolution. Geochim. Cosmochim. Acta 65, 3703–3719 (2001).
Van Iseghem, P. et al. Environmental issues and waste management technologies in the materials and nuclear industries Xii. In Ceramic Transactions Vol. 207 (eds. Cozzi, A. & Ohji, T.) 115 (Amer Ceramic Soc, 2009).
Gin, S., Jegou, C., Frugier, P. & Minet, Y. Theoretical consideration on the application of the Aagaard-Helgeson rate law to the dissolution of silicate minerals and glasses. Chem. Geol. 255, 14–24 (2008).
Vernaz, E. & Gin, S. Scientific basis for nuclear waste management Xxiv. In Materials Research Society Symposium Proceedings Vol. 663 (eds. Hart, K. P. & Lumpkin, G. R.) 217–225 (Materials Research Society, 2000).
Gin, S. et al. A general mechanism for gel layer formation on borosilicate glass under aqueous corrosion. J. Phys. Chem. C. 124, 5132–5144 (2020).
Munier, I., Crovisier, J. L., Grambow, B., Fritz, B. & Clement, A. Modelling the alteration gel composition of simplified borosilicate glasses by precipitation of an ideal solid solution in equilibrium with the leachant. J. Nucl. Mater. 324, 97–115 (2004).
Collin, M. et al. Structure of International Simple Glass and properties of passivating layer formed in circumneutral pH conditions. NPJ Mater. Degrad. 2, 12 (2018).
Collin, M. et al. ToF-SIMS depth profiling of altered glass. NPJ Mater. Degrad. 3, 10 (2019).
Mir, A. H. et al. Effect of decades of corrosion on the microstructure of altered glasses and their radiation stability. NPJ Mater. Degrad. 4, 9 (2020).
Ngo, D. et al. Spectroscopic ellipsometry study of thickness and porosity of the alteration layer formed on international simple glass surface in aqueous corrosion conditions. NPJ Mater. Degrad. 2, 9 (2018).
Ngo, D. et al. Hydrogen bonding interactions of H2O and SiOH on a boroaluminosilicate glass corroded in aqueous solution. NPJ Mater. Degrad. 4, 14 (2020).
Kaya, H., Ngo, D., Gin, S. & Kim, S. H. Spectral changes in Si-O-Si stretching band of porous glass network upon ingress of water. J. Non Cryst. Sol. 527, 6 (2020).
Gin, S. et al. Origin and consequences of silicate glass passivation by surface layers. Nat. Commun. 6, 8 (2015).
Dran, J. C., Petit, J. C. & Brousse, C. Mechanism of aqueous dissolution of silicate-glasses yielded by fission tracks. Nature 319, 485–487 (1986).
Ruiz-Agudo, E., Putnis, C. V. & Putnis, A. Coupled dissolution and precipitation at mineral-fluid interfaces. Chem. Geol. 383, 132–146 (2014).
Gin, S. et al. The controversial role of inter-diffusion in glass alteration. Chem. Geol. 440, 115–123 (2016).
Schalm, O., Nuyts, G. & Janssens, K. Some critical observations about the degradation of glass: The formation of lamellae explained. J. Non Cryst. Sol. 569, 120984 (2021).
Geisler, T. et al. The mechanism of borosilicate glass corrosion revisited. Geochim. Cosmochim. Acta 158, 112–129 (2015).
Hellmann, R. et al. Nanometre-scale evidence for interfacial dissolution-reprecipitation control of silicate glass corrosion. Nat. Mater. 14, 307–311 (2015).
Hamilton, J. P., Pantano, C. G. & Brantley, S. L. Dissolution of albite glass and crystal. Geochim. Cosmochim. Acta 64, 2603–2615 (2000).
Perez, A. et al. Comparing the reactivity of glasses with their crystalline equivalents: the case study of plagioclase feldspar. Geochim. Cosmochim. Acta 254, 122–141 (2019).
Gin, S. et al. The fate of silicon during glass corrosion under alkaline conditions: a mechanistic and kinetic study with the International Simple Glass. Geochim. Cosmochim. Acta 151, 68–85 (2015).
Petit, J. C., Magonthier, M. C., Dran, J. C. & Mea, G. D. Long-term dissolution rate of nuclear glasses in confined environments: does a residual chemical affinity exist? J. Mater. Sci. 25, 3048–3052 (1990).
Ojovan, M. I., Pankov, A. & Lee, W. E. The ion exchange phase in corrosion of nuclear waste glasses. J. Nucl. Mater. 358, 57–68 (2006).
Frugier, P., Gin, S., Lartigue, J. E. & Deloule, E. Scientific basis for nuclear waste management Xxix. In Materials Research Society Symposium Proceedings Vol. 932 (ed. VanIseghem, P.) 305 (Materials Research Soc, 2006).
Ferrand, K., Abdelouas, A. & Grambow, B. Water diffusion in the simulated French nuclear waste glass SON 68 contacting silica rich solutions: experimental and modeling. J. Nucl. Mater. 355, 54–67 (2006).
Frugier, P. et al. SON68 nuclear glass dissolution kinetics: current state of knowledge and basis of the new GRAAL model. J. Nucl. Mater. 380, 8–21 (2008).
Jollivet, P. et al. Effect of clayey groundwater on the dissolution rate of the simulated nuclear waste glass SON68. J. Nucl. Mater. 420, 508–518 (2012).
Elia, A., Ferrand, K. & Lemmens, K. Determination of the forward dissolution rate for international simple glass in alkaline solutions. MRS Adv. 2, 661–667 (2017).
Collin, M., Fournier, M., Charpentier, T., Moskura, M. & Gin, S. Impact of alkali on the passivation of silicate glass. NPJ Mater. Degrad. 2, 10 (2018).
Arena, H. et al. Impact of Fe, Mg and Ca elements on glass alteration: Interconnected processes. Geochim. Cosmochim. Acta 239, 420–445 (2018).
Arena, H. et al. Impact of Zn, Mg, Ni and Co elements on glass alteration: additive effects. J. Nucl. Mater. 470, 55–67 (2016).
De Echave, T. et al. Effect of clayey groundwater on the dissolution rate of SON68 simulated nuclear waste glass at 70 degrees C. J. Nucl. Mater. 503, 279–289 (2018).
Curti, E., Crovisier, J. L., Morvan, G. & Karpoff, A. M. Long-term corrosion of two nuclear waste reference glasses (MW and SON68): a kinetic and mineral alteration study. Appl. Geochem. 21, 1152–1168 (2006).
Abdelouas, A. et al. Surface layers on a borosilicate nuclear waste glass corroded in MgCl2 solution. J. Nucl. Mater. 240, 100–111 (1997).
Bouakkaz, R., Abdelouas, A., El Mendili, Y., Grambow, B. & Gin, S. SON68 glass alteration under Si-rich solutions at low temperature (35-90 degrees C): kinetics, secondary phases and isotopic exchange studies. RSC Adv. 6, 72616–72633 (2016).
Van Iseghem, P. et al. Scientific basis for nuclear waste management Xxix. In Materials Research Society Symposium Proceedings Vol. 932 (ed. VanIseghem, P.) 293 (Materials Research Soc, 2006).
Weaver, J. L. et al. Microbial interactions with silicate glasses. NPJ Mater. Degrad. 5, 11 (2021).
Hutchens, E. Microbial selectivity on mineral surfaces: possible implications for weathering processes. Fungal Biol. Rev. 23, 115–121 (2009).
Bos, R., van der Mei, H. C. & Busscher, H. J. Physico-chemistry of initial microbial adhesive interactions—its mechanisms and methods for study. Fems Microbiol. Rev. 23, 179–230 (1999).
Perez, A. et al. Bioalteration of synthetic Fe(III)-, Fe(II)-bearing basaltic glasses and Fe-free glass in the presence of the heterotrophic bacteria strain Pseudomonas aeruginosa: Impact of siderophores. Geochim. Cosmochim. Acta 188, 147–162 (2016).
Perez, A. et al. Direct and indirect impact of the bacterial strain Pseudomonas aeruginosa on the dissolution of synthetic Fe(III)- and Fe(II)-bearing basaltic glasses. Chem. Geol. 523, 9–18 (2019).
Gin, S., Jollivet, P., Tribet, M., Peuget, S. & Schuller, S. Radionuclides containment in nuclear glasses: an overview. Radiochim. Acta 105, 927–959 (2017).
Peuget, S., Delaye, J. M. & Jegou, C. Specific outcomes of the research on the radiation stability of the French nuclear glass towards alpha decay accumulation. J. Nucl. Mater. 444, 76–91 (2014).
Tribet, M. et al. New Insights about the Importance of the Alteration Layer/Glass Interface. J. Phys. Chem. C. 124, 10032–10044 (2020).
Maugeri, E. A. et al. Calorimetric study of glass structure modification induced by a decay. J. Am. Ceram. Soc. 95, 2869–2875 (2012).
Charpentier, T. et al. Self-healing capacity of nuclear glass observed by NMR spectroscopy. Sci. Rep. 6, 6 (2016).
Lonartz, M. I. et al. The effect of heavy ion irradiation on the forward dissolution rate of borosilicate glasses studied in situ and real time by fluid-cell raman spectroscopy. Materials 12, 13 (2019).
Jan, A., Delaye, J. M., Gin, S. & Kerisit, S. Monte Carlo simulation of the corrosion of irradiated simplified nuclear waste glasses. J. Non Cryst. Sol. 519, 6–13 (2019).
Jan, A., Delaye, J. M., Gin, S. & Kerisit, S. Molecular dynamics simulation of ballistic effects in simplified nuclear waste glasses. J. Non Cryst. Sol. 505, 188–201 (2019).
Mir, A. H. et al. Defect recovery and damage reduction in borosilicate glasses under double ion beam irradiation. Epl 112, 6 (2015).
Tribet, M. et al. 2nd International summer school on nuclear glass wasteform: structure, properties and long-term behavior. In Procedia Materials Science Vol. 7 (eds. Angeli, F. et al.) 209–215 (Elsevier Science Bv, 2014).
Mougnaud, S. et al. Heavy ion radiation ageing impact on long-term glass alteration behavior. J. Nucl. Mater. 510, 168–177 (2018).
McVay, G. L. & Buckwalter, C. Q. Effect of iron on waste‐glass leaching. J. Am. Ceram. Soc. 66, 170–174 (1983).
Burns, D., Upton, B. & Wicks, G. G. Interactions of SRP waste glass with potential canister and overpack metals. J. Non Cryst. Sol. 84, 258–267 (1986).
Kim, S., Lee, J.-G., Choi, J., Lee, G. & Chun, K. Effects of metals, metal oxides and metal hydroxide on the leaching of simulated nuclear waste glass. Radiochimica Acta 79, 199–206 (1997).
De Combarieu, G. et al. Glass–iron–clay interactions in a radioactive waste geological disposal: an integrated laboratory-scale experiment. Appl. Geochem. 26, 65–79 (2011).
Burger, E. et al. Impact of iron on nuclear glass alteration in geological repository conditions: a multiscale approach. Appl. Geochem. 31, 159–170 (2013).
Michelin, A. et al. Silicate glass alteration enhanced by iron: origin and long-term implications. Environ. Sci. Technol. 47, 750–756 (2013).
Michelin, A. et al. Effect of iron metal and siderite on the durability of simulated archeological glassy material. Corros. Sci. 76, 403–414 (2013).
Dillmann, P., Gin, S., Neff, D., Gentaz, L. & Rebiscoul, D. Effect of natural and synthetic iron corrosion products on silicate glass alteration processes. Geochimica et. Cosmochimica Acta 172, 287–305 (2016).
Bates, J. K., Gerding, T. J. & Woodland, A. B. Parametric effects of glass reaction under unsaturated conditions. MRS Online Proc. Libr. Arch. 176, 347 (1989).
Woodland, A. B., Bates, J. K. & Gerding, T. J. Parametric Effects on Glass Reaction in the Unsaturated Test Method. (Argonne National Lab. ANL-91/36, 1991).
Barkatt, A., Sousanpour, W., Barkatt, A. & Boroomand, M. A. Effects of metals and metal oxides on the leaching of nuclear waste glasses. MRS Online Proc. Libr. Arch. 26, 689 (1983).
Guo, X. L. et al. Self-accelerated corrosion of nuclear waste forms at material interfaces. Nat. Mater. 19, 310–316 (2020).
Guo, X. L. et al. Near-field corrosion interactions between glass and corrosion resistant alloys. npj Mater. Degrad. 4, 8 (2020).
Bart, G. et al. Borosilicate glass corrosion in the presence of steel corrosion products. MRS Online Proc. Libr. Arch. 84, 459 (1986).
Inagaki, Y. et al. In Materials Research Society Symposium-Proceedings 257 (1996).
Grambow, B., Zwicky, H., Bart, G., Bjorner, I. & Werme, L. Modeling of the effect of iron corrosion products on nuclear waste glass performance. MRS Online Proc. Libr. Arch. 84, 471 (1986).
Werme, L. et al. Chemical corrosion of highly radioactive borosilicate nuclear waste glass under simulated repository conditions. J. Mater. Res. 5, 1130–1146 (1990).
Björner, I.-K., Christensen, H., Hermansson, H., Tsukamoto, M. & Werme, L. Corrosion of radioactive, crushed waste glass. MRS Online Proc. Libr. Arch. 127, 113 (1988).
Rebiscoul, D. et al. Reactive transport processes occurring during nuclear glass alteration in presence of magnetite. Appl. Geochem. 58, 26–37 (2015).
Suzuki-Muresan, T. et al. Alteration of vitrified intermediate level nuclear waste in alkaline media: effects of cementitious materials, pH and temperature. RSC Adv. 8, 37665–37680 (2018).
Ferrand, K., Liu, S. & Lemmens, K. In 2nd International summer school on nuclear glass wasteform: structure, properties and long-term behavior. In Procedia Materials Science Vol. 7 (eds. Angeli, F. et al.) 223–229 (Elsevier Science Bv, 2014).
Francisco, P. C. M. et al. Interaction of Fe-II and Si under anoxic and reducing conditions: Structural characteristics of ferrous silicate co-precipitates. Geochim. Cosmochim. Acta 270, 1–20 (2020).
Jain, V. & Pan, Y. Performance of sUrrogate High-level Waste Glass in the Presence of Iron Corrosion Products. No. INIS-FR-2903 (Center for Nuclear Waste Regulatory Analyses, 2004).
Pan, Y.-M., Jain, V. & Pensado, O. Degradation of high-level waste glass under simulated repository conditions. J. Non Cryst. Sol. 319, 74–88 (2003).
Aréna, H. et al. Impact of iron and magnesium on glass alteration: characterization of the secondary phases and determination of their solubility constants. Appl. Geochem. 82, 119–133 (2017).
Guo, X. L. et al. Near-field corrosion interactions between glass and corrosion resistant alloys. NPJ Mater. Degrad. 4, 15 (2020).
Mercado-Depierre, S., Angeli, F., Frizon, F. & Gin, S. Antagonist effects of calcium on borosilicate glass alteration. J. Nucl. Mater. 441, 402–410 (2013).
Waltimo, T. et al. Fine-tuning of bioactive glass for root canal disinfection. J. Dent. Res. 88, 235–238 (2009).
Hench, L. L. & Polak, J. M. Third-generation biomedical materials. Science 295, 1014 (2002).
Hench, L. L. & Jones, J. R. Bioactive glasses: frontiers and challenges. Front. Bioeng. Biotechnol. 3, 12 (2015).
Majerus, O. et al. Glass alteration in atmospheric conditions: crossing perspectives from cultural heritage, glass industry, and nuclear waste management. NPJ Mater. Degrad. 4, 16 (2020).
Zhang, H., Suzuki-Muresan, T., Morizet, Y., Gin, S. & Abdelouas, A. Investigation on boron and iodine behavior during nuclear glass vapor hydration. NPJ Mater. Degrad. 5, 10 (2021).
Narayanasamy, S. et al. Influence of composition of nuclear waste glasses on vapor phase hydration. J. Nucl. Mater. 525, 53–71 (2019).
Abrajano, T. A., Bates, J. K. & Mazer, J. J. Aqueous corrosion of natural and nuclear waste glasses. 2. Mechanisms of vapor hydration of nuclear waste glasses. J. Non Cryst. Sol. 108, 269–288 (1989).
Asay, D. B. & Kim, S. H. Evolution of the adsorbed water layer structure on silicon oxide at room temperature. J. Phys. Chem. B 109, 16760–16763 (2005).
Abrajano, T. A., Bates, J. K. & Byers, C. D. Aqueous corrosion of natural and nuclear waste glasses. 1. Comparative rates of hydration in liquid and vapor environments at elevated-temperatures. J. Non Cryst. Sol. 84, 251–257 (1986).
Bouakkaz, R., Abdelouas, A. & Grambow, B. Kinetic study and structural evolution of SON68 nuclear waste glass altered from 35 to 125 degrees C under unsaturated H2O and D2O18 vapour conditions. Corros. Sci. 134, 1–16 (2018).
Cummings, K., Lanford, W. A. & Feldmann, M. Weathering of glass in moist and polluted air. Nucl. Instrum. Methods Phys. Res. Sect. B-Beam Interact. Mater. At. 136, 858–862 (1998).
Zhang, H. H., Suzuki-Muresan, T., Morizet, Y., Gin, S. & Abdelouas, A. Investigation on boron and iodine behavior during nuclear glass vapor hydration. NPJ Mater. Degrad. 5, 9 (2021).
Bates, J. K., Seitz, M. G. & Steindler, M. J. The relevance of vapor-phase hydration aging to nuclear waste isolation. Nucl. Chem. Waste Manag. 5, 63–73 (1984).
Jupille, J. Glass surfaces: structure and physical chemistry. C. R. Acad. Sci. Ser. IV-Phys. Astrophys 2, 303–320 (2001).
Angeli, F., Jollivet, P., Charpentier, T., Fournier, M. & Gin, S. Structure and chemical durability of lead crystal glass. Environ. Sci. Technol. 50, 11549–11558 (2016).
Jegou, C., Gin, S. & Larche, F. Alteration kinetics of a simplified nuclear glass in an aqueous medium: effects of solution chemistry and of protective gel properties on diminishing the alteration rate. J. Nucl. Mater. 280, 216–229 (2000).
Fournier, M. et al. Glass dissolution rate measurement and calculation revisited. J. Nucl. Mater. 476, 140–154 (2016).
Guittonneau, C. et al. A 25-year laboratory experiment on French SON68 nuclear glass leached in a granitic environment—first investigations. J. Nucl. Mater. 408, 73–89 (2011).
Chinnam, R. K., Hutchison, C., Pletser, D. & Lee, W. E. Degradation of international simple glass cracks and surface. MRS Adv. 1, 4215–4220 (2016).
Palomar, T. & Llorente, I. Decay processes of silicate glasses in river and marine aquatic environments. J. Non Cryst. Sol. 449, 20–28 (2016).
Neill, L. et al. Various effects of magnetite on international simple glass (ISG) dissolution: implications for the long-term durability of nuclear glasses. NPJ Mater. Degrad. 1, 11 (2017).
Icenhower, J. P. & Steefel, C. I. Dissolution rate of borosilicate glass SON68: a method of quantification based upon interferometry and implications for experimental and natural weathering rates of glass. Geochim. Cosmochim. Acta 157, 147–163 (2015).
Neeway, J. J., Rieke, P. C., Parruzot, B. P., Ryan, J. V. & Asmussen, R. M. The dissolution behavior of borosilicate glasses in far-from equilibrium conditions. Geochim. Cosmochim. Acta 226, 132–148 (2018).
Strachan, D. Glass dissolution as a function of pH and its implications for understanding mechanisms and future experiments. Geochim. Cosmochim. Acta 219, 111–123 (2017).
Advocat, T., Crovisier, J. L., Vernaz, E., Ehret, G. & Charpentier, H. Hydrolysis of R7T7 Nuclear Waste Glass in Dilute Media—Mechanisms and Rate as a Function of pH. Vol. 212 (Materials Research Soc, 1991).
Inagaki, Y. et al. Initial dissolution rate of a Japanese simulated high-level waste glass P0798 as a function of pH and temperature measured by using micro-channel flow-through test method. J. Nucl. Sci. Technol. 49, 438–449 (2012).
Sessegolo, L. et al. Alteration rate of medieval potash-lime silicate glass as a function of pH and temperature: a low pH-dependent dissolution. Chem. Geol. 550, 15 (2020).
Gin, S., Godon, N., Mestre, J. P., Vernaz, E. Y. & Beaufort, D. Experimental investigation of aqueous corrosion of R7T7 nuclear glass at 90-degrees-C in the presence of organic-species. Appl. Geochem. 9, 255–269 (1994).
Gin, S., Jegou, C. & Vernaz, E. Use of orthophosphate complexing agents to investigate mechanisms limiting the alteration kinetics of French SON 68 nuclear glass. Appl. Geochem. 15, 1505–1525 (2000).
Lasaga, A. C. Chemical weathering rates of silicate minerals. In Reviews in Mineralogy Vol. 31 (eds. White, A. F. & Brantley, S. L.) 23–86 (Mineralogical Soc Amer, 1995).
Smets, B. M. J. & Tholen, M. G. W. Leaching of glasses with molar composition 20Na2O.10RO.xAl2O3.(70-x)SiO2. J. Am. Ceram. Soc. 67, 281–284 (1984).
Hamilton, J. P., Brantley, S. L., Pantano, C. G., Criscenti, L. J. & Kubicki, J. D. Dissolution of nepheline, jadeite and albite glasses: Toward better models for aluminosilicate dissolution. Geochim. Cosmochim. Acta 65, 3683–3702 (2001).
Piovesan, V., Bardez-Giboire, I., Perret, D., Montouillout, V. & Pellerin, N. Effect of composition on peraluminous glass properties: An application to HLW containment. J. Nucl. Mater. 483, 90–101 (2017).
Jantzen, C. M. & Plodinec, M. J. Thermodynamic model of natural, medieval and nuclear waste glass durability. J. Non Cryst. Sol. 67, 207–223 (1984).
Paul, A. Chemical durability of glasses—thermodynamic approach. J. Mater. Sci. 12, 2246–2268 (1977).
Frugier, P., Martin, C., Ribet, I., Advocat, T. & Gin, S. The effect of composition on the leaching of three nuclear waste glasses: R7T7, AVM and VRZ. J. Nucl. Mater. 346, 194–207 (2005).
Kerisit, S. & Pierce, E. M. Monte Carlo simulations of the dissolution of borosilicate and aluminoborosilicate glasses in dilute aqueous solutions. Geochim. Cosmochim. Acta 75, 5296–5309 (2011).
Devreux, F., Ledieu, A., Barboux, P. & Minet, Y. Leaching of borosilicate glasses. II. Model and Monte-Carlo simulations. J. Non Cryst. Sol. 343, 13–25 (2004).
Liu, H. et al. Predicting the dissolution kinetics of silicate glasses by topology-informed machine learning. NPJ Mater. Degrad. 3, 12 (2019).
Pedone, A. & Menziani, M. C. Computational modeling of silicate glasses: a quantitative structure-property relationship perspective. Springe. Ser. Mater. Sci. 215, 113–135 (2015).
Oey, T. et al. The role of the network-modifier’s field-strength in the chemical durability of aluminoborate glasses. J. Non Cryst. Sol. 505, 279–285 (2019).
Krishnan, N. M. A. et al. Predicting the dissolution kinetics of silicate glasses using machine learning. J. Non Cryst. Sol. 487, 37–45 (2018).
Mascaraque, N., Bauchy, M. & Smedskjaer, M. M. Correlating the network topology of oxide glasses with their chemical durability. J. Phys. Chem. B 121, 1139–1147 (2017).
Tuheen, M. I., Deng, L. & Du, J. C. A comparative study of the effectiveness of empirical potentials for molecular dynamics simulations of borosilicate glasses. J. Non Cryst. Sol. 553, 15 (2021).
Bauchy, M. Deciphering the atomic genome of glasses by topological constraint theory and molecular dynamics: a review. Comput. Mater. Sci. 159, 95–102 (2019).
Smedskjaer, M. M. et al. Topological principles of borosilicate glass chemistry. J. Phys. Chem. B 115, 12930–12946 (2011).
Gin, S. et al. Can a simple topological-constraints-based model predict the initial dissolution rate of borosilicate and aluminosilicate glasses? NPJ Mater. Degrad. 4, 10 (2020).
Lu, X. N., Deng, L., Gin, S. & Du, J. C. Quantitative structure-property relationship (QSPR) analysis of ZrO2-containing soda-lime borosilicate glasses. J. Phys. Chem. B 123, 1412–1422 (2019).
Pignatelli, I., Kumar, A., Bauchy, M. & Sant, G. Topological control on silicates’ dissolution kinetics. Langmuir 32, 4434–4439 (2016).
Gin, S., Frugier, P., Jollivet, P., Bruguier, F. & Curti, E. New insight into the residual rate of borosilicate glasses: effect of S/V and glass composition. Int. J. Appl. Glass Sci. 4, 371–382 (2013).
Mir, A. H. et al. Effect of decades of corrosion on the microstructure of altered glasses and their radiation stability. NPJ Mater. Degrad. 4, 11 (2020).
Gin, S., Beaudoux, X., Angeli, F., Jegou, C. & Godon, N. Effect of composition on the short-term and long-term dissolution rates of ten borosilicate glasses of increasing complexity from 3 to 30 oxides. J. Non Cryst. Sol. 358, 2559–2570 (2012).
Parruzot, B., Jollivet, P., Rebiscoul, D. & Gin, S. Long-term alteration of basaltic glass: Mechanisms and rates. Geochim. Cosmochim. Acta 154, 28–48 (2015).
Scheetz, B. E., Freeborn, W., Anderson, C., Zolensky, M. & White, W. B. In Materials Research Society Vol. 44, 129 (1985).
Neeway, J., Abdelouas, A., Grambow, B. & Schumacher, S. Dissolution mechanism of the SON68 reference nuclear waste glass: New data in dynamic system in silica saturation conditions. J. Nucl. Mater. 415, 31–37 (2011).
Icenhower, J. P. & Steefel, C. I. Experimentally determined dissolution kinetics of SON68 glass at 90 degrees C over a silica saturation interval: Evidence against a linear rate law. J. Nucl. Mater. 439, 137–147 (2013).
Pierce, E. M., Richards, E. L., Davis, A. M., Reed, L. R. & Rodriguez, E. A. Aluminoborosilicate waste glass dissolution under alkaline conditions at 40 degrees C: implications for a chemical affinity-based rate equation. Environ. Chem. 5, 73–85 (2008).
Ebert, W. L. & Bates, J. K. A comparison of glass reaction at high and low glass-surface solution volume. Nucl. Technol. 104, 372–384 (1993).
Ribet, S., Muller, I. S., Pegg, I. L., Gin, S. & Frugier, P. Scientific Basis for Nuclear Waste Management Xxviii. In Materials Research Society Symposium Proceedings Vol. 824 (eds. Hanchar, J. M., StroesGascoyne, S. & Browning, L.) 309–314 (Materials Research Soc, 2004).
Inagaki, Y. et al. Aqueous alteration of Japanese simulated waste glass P0798: effects of alteration-phase formation on alteration rate and cesium retention. J. Nucl. Mater. 354, 171–184 (2006).
Fournier, M. et al. Effect of pH on the stability of passivating gel layers formed on International Simple Glass. J. Nucl. Mater. 524, 21–38 (2019).
Gin, S. & Mestre, J. P. SON 68 nuclear glass alteration kinetics between pH 7 and pH 11.5. J. Nucl. Mater. 295, 83–96 (2001).
Fournier, M., Gin, S. & Frugier, P. Resumption of nuclear glass alteration: state of the art. J. Nucl. Mater. 448, 348–363 (2014).
Fournier, M., Gin, S., Frugier, P. & Mercado-Depierre, S. Contribution of zeolite-seeded experiments to the understanding of resumption of glass alteration. NPJ Mater. Degrad. 1, 13 (2017).
Ryan, J. V. et al. In-situ monitoring of seeded and unseeded stage III corrosion using Raman spectroscopy. NPJ Mater. Degrad. 3, 7 (2019).
Neeway, J. J. et al. Acceleration of glass alteration rates induced by zeolite seeds at controlled pH. Appl. Geochem. 113, 9 (2020).
Piovesan, V. et al. Chemical durability of peraluminous glasses for nuclear waste conditioning. NPJ Mater. Degrad. 2, 10 (2018).
Ojovan, M. I. On alteration rate renewal stage of nuclear waste glass corrosion. MRS Adv. 5, 111–120 (2020).
Ribet, S. & Gin, S. Role of neoformed phases on the mechanisms controlling the resumption of SON68 glass alteration in alkaline media. J. Nucl. Mater. 324, 152–164 (2004).
Crovisier, J. L., Advocat, T. & Dussossoy, J. L. Nature and role of natural alteration gels formed on the surface of ancient volcanic glasses (Natural analogs of waste containment glasses). J. Nucl. Mater. 321, 91–109 (2003).
Jantzen, C. M., Trivelpiece, C. L., Crawford, C. L., Pareizs, J. M. & Pickett, J. B. Accelerated leach testing of GLASS (ALTGLASS): I. Informatics approach to high level waste glass gel formation and aging. Int. J. Appl. Glass Sci. 8, 69–83 (2017).
Jantzen, C. M., Brown, K. G. & Pickett, J. B. Durable glass for thousands of years. Int. J. Appl. Glass Sci. 1, 38–62 (2010).
Jantzen, C. M., Trivelpiece, C. L., Crawford, C. L., Pareizs, J. M. & Pickett, J. B. Accelerated leach testing of glass (ALTGLASS): II. Mineralization of hydrogels by leachate strong bases. Int. J. Appl. Glass Sci. 8, 84–96 (2017).
Zhen-Wu, B. Y. et al. zeo19: a thermodynamic database for assessing zeolite stability during the corrosion of nuclear waste immobilization glasses. NPJ Mater. Degrad. 4, 2 (2020).
Strachan, D. M. & Neeway, J. J. Effects of alteration product precipitation on glass dissolution. Appl. Geochem. 45, 144–157 (2014).
Bourcier, W. L., Peiffer, D. W., Knauss, K. G., McKeegan, K. D. & Smith, D. K. A Kinetic-model for Borosilicate Glass Dissolution Based on the Dissolution Affinity of a Surface Alteration Layer Vol. 176 (Materials Research Soc, 1990).
Daux, V., Guy, C., Advocat, T., Crovisier, J. L. & Stille, P. Kinetic aspects of basaltic glass dissolution at 90 degrees C: role of aqueous silicon and aluminium. Chem. Geol. 142, 109–126 (1997).
Techer, I., Advocat, T., Lancelot, J. & Liotard, J. M. Basaltic glass: alteration mechanisms and analogy with nuclear waste glasses. J. Nucl. Mater. 282, 40–46 (2000).
Frugier, P., Minet, Y., Rajmohan, N., Godon, N. & Gin, S. Modeling glass corrosion with GRAAL. NPJ Mater. Degrad. 2, 35 (2018).
Grambow, B. & Muller, R. First-order dissolution rate law and the role of surface layers in glass performance assessment. J. Nucl. Mater. 298, 112–124 (2001).
Ma, T. Q. et al. A mechanistic model for long-term nuclear waste glass dissolution integrating chemical affinity and interfacial diffusion barrier. J. Nucl. Mater. 486, 70–85 (2017).
Grambow, B. Nuclear Waste Glass Dissolution, Mechanism, Model and Application (1987).
Gouze, B., Cambedouzou, J., Parres-Maynadie, S. & Rebiscoul, D. How hexagonal mesoporous silica evolves in water on short and long term: Role of pore size and silica wall porosity. Microporous Mesoporous Mat. 183, 168–176 (2014).
Ngo, D. et al. Spectroscopic ellipsometry study of thickness and porosity of the alteration layer formed on international simple glass surface in aqueous corrosion conditions. NPJ Mater. Degrad. 2, 20 (2018).
Schreiber, D. K., Perea, D. E., Ryan, J. V., Evans, J. E. & Vienna, J. D. A method for site-specific and cryogenic specimen fabrication of liquid/solid interfaces for atom probe tomography. Ultramicroscopy 194, 89–99 (2018).
Kerisit, S., Mahadevan, T. & Du, J. C. Patchy particle model of hydrated amorphous silica. J. Non Cryst. Sol. 556, 8 (2021).
Fournier, M., Frugier, P. & Gin, S. Application of GRAAL model to the resumption of International Simple Glass alteration. NPJ Mater. Degrad. 2, 21 (2018).
Verney-Carron, A., Gin, S. & Libourel, G. Archaeological analogs and the future of nuclear waste glass. J. Nucl. Mater. 406, 365–370 (2010).
Kurganskaya, I. & Luttge, A. Kinetic Monte Carlo simulations of silicate dissolution: model complexity and parametrization. J. Phys. Chem. C. 117, 24894–24906 (2013).
Luttge, A. & Arvidson, R. S. Reactions at surfaces: a new approach integrating interferometry and kinetic simulations. J. Am. Ceram. Soc. 93, 3519–3530 (2010).
Bouissonnie, A., Daval, D. & Ackerer, P. Dissolution anisotropy of pyroxenes: a surrogate model for steady-state enstatite dissolution resulting from stochastic simulations of the hydrolysis process. J. Phys. Chem. C. 124, 13113–13126 (2020).
Arab, M. et al. Aqueous alteration of five-oxide silicate glasses: experimental approach and Monte Carlo modeling. J. Non Cryst. Sol. 354, 155–161 (2008).
Kerisit, S., Ryan, J. V. & Pierce, E. M. Monte Carlo simulations of the corrosion of aluminoborosilicate glasses. J. Non Cryst. Sol. 378, 273–281 (2013).
Ledieu, A., Devreux, F., Barboux, P. & Minet, Y. Contribution of Monte Carlo modeling to understanding the alteration of nuclear glasses by water. Nucl. Sci. Eng. 153, 285–300 (2006).
Kerisit, S., Pierce, E. M. & Ryan, J. V. Monte Carlo simulations of coupled diffusion and surface reactions during the aqueous corrosion of borosilicate glasses. J. Non Cryst. Sol. 408, 142–149 (2015).
Cailleteau, C., Devreux, F., Spalla, O., Angeli, F. & Gin, S. Why do certain glasses with a high dissolution rate undergo a low degree of corrosion? J. Phys. Chem. C. 115, 5846–5855 (2011).
Kerisit, S. & Du, J. C. Monte Carlo simulation of borosilicate glass dissolution using molecular dynamics-generated glass structures. J. Non Cryst. Sol. 522, 7 (2019).
Valcke, E. et al. Scientific basis for nuclear waste management Xxix. In Materials Research Society Symposium Proceedings Vol. 932 (ed. VanIseghem, P.) 999 (Materials Research Soc, 2006).
Utton, C. A. et al. Chemical durability of vitrified wasteforms: effects of pH and solution composition. Mineral. Mag. 76, 2919–2930 (2012).
Sterpenich, J. Crystal-chemistry of alteration products of vitrified wastes: implications on the retention of polluting elements. Waste Manag. 28, 120–132 (2008).
Verney-Carron, A., Gin, S., Frugier, P. & Libourel, G. Long-term modeling of alteration-transport coupling: application to a fractured Roman glass. Geochim. Cosmochim. Acta 74, 2291–2315 (2010).
Strachan, D. M., Crum, J. V., Ryan, J. V. & Silvestri, A. Characterization and modeling of the cemented sediment surrounding the Iulia Felix glass. Appl. Geochem. 41, 107–114 (2014).
Martinek, K. P., Wang, C., Krausch, G. & Radlein, E. Local clouding of glass after machine dishwashing. Glass Sci. Technol. 78, 12–17 (2005).
Alloteau, F. et al. Efficacy of zinc salts to protect glass against atmospheric alteration. Part I: Effects of a spraying treatment. J. Am. Ceram. Soc. 104, 2039–2051 (2021).
Sterpenich, J. & Libourel, G. Using stained glass windows to understand the durability of toxic waste matrices. Chem. Geol. 174, 181–193 (2001).
Ferrand, J. et al. Browning phenomenon of medieval stained glass windows. Anal. Chem. 87, 3662–3669 (2015).
Guglielmi, M. et al. Laboratory intercomparison for the evaluation of the delamination propensity of glass containers for pharmaceutical use. Int. J. Appl. Glass Sci. 12, 135–144 (2021).
Gin, S. et al. Scientific basis for nuclear waste management Xxviii. In Materials Research Society Symposium Proceedings Vol. 824 (eds. Hanchar, J. M., StroesGascoyne, S. & Browning, L.) 327–332 (Materials Research Society, 2004).
Jeong, J. et al. Progress of the long-term safety assessment of a reference disposal system for high level wastes in Korea. Prog. Nucl. Energy 90, 37–45 (2016).
Poinssot, C. & Gin, S. Long-term behavior science: the cornerstone approach for reliably assessing the long-term performance of nuclear waste. J. Nucl. Mater. 420, 182–192 (2012).
Libourel, G. et al. The use of natural and archeological analogues for understanding the long-term behavior of nuclear glasses. C. R. Geosci. 343, 237–245 (2011).
Gin, S. et al. Can a simple topological-constraints-based model predict the initial dissolution rate of borosilicate and aluminosilicate glasses? NPJ Mater. Degrad. 4, 6 (2020).
Perera, G., Doremus, R. H. & Lanford, W. Dissolution rates of silicate-glasses in water at pH 7. J. Am. Ceram. Soc. 74, 1269–1274 (1991).
Sepulveda, P., Jones, J. R. & Hench, L. L. In vitro dissolution of melt-derived 45S5 and sol-gel derived 58S bioactive glasses. J. Biomed. Mater. Res. 61, 301–311 (2002).
Geisler, T. et al. Aqueous corrosion of borosilicate glass under acidic conditions: a new corrosion mechanism. J. Non Cryst. Sol. 356, 1458–1465 (2010).
Ferrand, K. et al. Dissolution kinetics of international simple glass and formation of secondary phases at very high surface area to solution ratio in young cement water. Materials 14, 21 (2021).
Acknowledgements
Authors are grateful to Pierre Frugier and Nicolas Bisbrouck from CEA, and Tomo Suzuki-Mauresan from University of Nantes for fruitful scientific discussions, and Beverley Marshall from Ibl84 for improving the English. This work was funded by CEA (VESTALE project).
Author information
Authors and Affiliations
Contributions
S.G. supervised the work and wrote most of the paper. J.M.D. wrote the section on molecular mechanisms of glass alteration. F.A. and S.C. contributed to the discussion and deeply reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gin, S., Delaye, JM., Angeli, F. et al. Aqueous alteration of silicate glass: state of knowledge and perspectives. npj Mater Degrad 5, 42 (2021). https://doi.org/10.1038/s41529-021-00190-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41529-021-00190-5
This article is cited by
-
Mechanisms and energetics of calcium aluminosilicate glass dissolution through ab initio molecular dynamics-metadynamics simulations
npj Materials Degradation (2024)
-
Effect of structural disorder induced by external irradiation with heavy ions on the alteration of a four oxide borosilicate glass
npj Materials Degradation (2024)
-
Formation and evolution of secondary phases and surface altered layers during borosilicate glass corrosion in pore water
npj Materials Degradation (2024)
-
Vapor-phase crystallization from a hydrous silicate melt: an experimental simulation of diktytaxitic texture
Contributions to Mineralogy and Petrology (2024)
-
Alteration of medieval stained glass windows in atmospheric medium: review and simplified alteration model
npj Materials Degradation (2023)