Two-phase transport in a cemented waste package considering spatio-temporal evolution of chemical conditions

Abstract

The long-term evolution of cemented waste packages is governed by (bio)chemical reactions between waste, cement, and barrier materials, and by transport processes inside the waste package and through openings in the waste package hull. Inside a waste package, gases can be generated by pH-dependent anoxic corrosion of metals and the degradation of organic matter. The (bio)chemical reactions consume water and will not proceed under dry conditions. The degradation of cementitious materials lowers the alkaline pH of the pore water. The modeling of such a complex feedback system shows that the internal structure of a waste package and the exchange of mass with the environment (boundary conditions) are major factors that determine the importance of process couplings. The (bio)chemical reactions are controlled by internal re-distribution of water predominantly via vapor transport. Calculated gas generation rates were found to be affected by dry-out processes inside the drum.

Introduction

The disposal of low- and intermediate-level radioactive wastes (L/ILW) in a deep geological repository is the preferred option in many countries worldwide. The Swiss repository design includes a multi-barrier concept, where waste matrix, waste packages, emplacement containers, and the clay host rock act as barriers to ensure the long-term isolation of radioactive waste and to minimize the long-term release of radionuclides from the repository with a view to the applicable regulatory limits¹. For all the stakeholders, understanding the behavior and long-term evolution of single barriers and the barrier system as a whole is of fundamental interest, as it serves as the basis for a reliable performance assessment of the repository^2,3.

The prediction of repository evolution is difficult, as, on different spatial scales, a complex system of interacting physical and (bio)chemical processes exists^4,5. Most studies on the evolution of the repository near field recognize the link between chemical and physical processes, but they treat processes separately because couplings between processes are assumed to be weak^6,7,8 or due to lack of appropriate modeling tools⁵. Complete re-saturation of the repository is expected to be delayed for very long times, possibly up to 10⁵ years, by the low permeability of the host rock and due to gas production by corrosion of metals and degradation of organic wastes^9,10,11. Waste-cement interactions are of specific importance, as the L/ILW repository contains large amounts of cementitious materials. The latter materials are used for waste conditioning, production of emplacement containers, backfilling the void space, and for providing tunnel support. The alkaline conditions in terms of high pH induced by the presence of cement paste slow down gas generation by metal corrosion and degradation of organic materials. Simultaneously the CO₂ generated by the degradation of organic matter degrades cementitious materials and lowers the pH.

One of the controlling factors in the feedback system between physical and chemical processes is the transport of water under partially saturated conditions, as most (bio)chemical reactions require the presence of a minimal water amount as solvent^12,13. Availability of water in terms of liquid (water) saturation is locally reduced due to gas production from the corrosion of metals and the degradation of organic matter, which both consume water. Other reactions, specifically carbonation of cementitious materials, will release water and increase liquid saturation¹⁴. Although most chemical processes in a repository are well understood, little attention has been paid to the comparative interaction between transport processes and the rate of different chemical reactions, especially with a view to water availability and considering the chemical heterogeneity of the materials⁵. In this context and for applications related to deep geologic disposal of radioactive waste in Canada, the T2GGM model was developed by Suckling et al.¹⁵. These authors used the two-phase flow code TOUGH2 in combination with a gas generation model (GDM), which accounts for gas generation and water consumption due to corrosion processes and degradation of organic matter. It seems that studies using this code are the only ones that have investigated systematically the feedback system between gas and water transport, water consumption by (bio)chemical processes, and chemical reactivity changes at low relative humidity in a cement-based repository¹⁶. These investigations predicted that a repository in low-permeable sedimentary rock will be dry for very long times and that gas production is limited by (slow) water inflow.

The feedback of water availability on gas generation is specifically important on the waste package level, as an intact waste package hull prevents free exchange of gases and water with the environment. Existing models of waste packages often focus on the performance under repository conditions^17,18, gas generation due to the degradation of organics^19,20,21 and corrosion^21,22,23. On the one hand, with an intact hull, initially present water might be completely consumed and chemical reactions may stop with time. On the other hand, gas production in the waste package might cause a considerable pressure build-up leading to the mechanical failure of the hull and enable transport pathways. Note that also the initial state of waste packages disposed of in a deep geological repository might not be well known. During long-term interim storage, the coupled physical and chemical processes are already active and might change the condition in waste packages, specifically if non-airtight cover lids are applied to prevent overpressure in those packages²⁴.

The feedback system requires consideration of the coupling effects of hydrodynamic and chemical reactions in both unsaturated and partially saturated conditions. Two-phase reactive transport modeling is an efficient tool to improve the understanding of the complex interaction and feedback between different physical and chemical processes. Senger et al.²⁵ used a 3D site-scale two-phase flow model to investigate metal corrosion and H₂ development in backfilled emplacement caverns. Croisé et al.²⁶ investigated the influence of metal corrosion by considering water consumption and saturation-dependent corrosion rates. Askarieh et al.²⁷ used the GAMMON model to simulate the chemical and microbial degradation of cellulose in a nuclear waste repository. The BRAGFLO code²⁸ developed at Sandia National Laboratories was used to simulate brine and gas flow in the Waste Isolation Pilot Plant (WIPP) repository for performance assessment. The code incorporates a baseline gas generation model accounting for the corrosion of iron and microbial degradation of cellulose and possibly plastics and rubber²⁹. Small et al.^19,30 published several papers on the interplay between the degradation of organic wastes and the corrosion of metallic wastes in low- and intermediate-level radioactive waste (LLW/ILW). Vikman et al.³¹ presented an 18-year study of an in-situ nuclear waste repository, which indicates that the heterogeneous chemical conditions provide optimal niches for microbial action, thus affecting the gas generation rate. Duro et al.³² reported an assessment of the evolution of the redox conditions in the low- and intermediate-level nuclear waste repository SFR1 in Sweden, in which both metal corrosion and organic degradation were simulated by the numerical tool PHREEQC. However, the model neither considered gas diffusion and transport nor chemical heterogeneity effects. Trotignon et al.³³ used TOUGHREACT to simulate the atmospheric carbonation of concrete in intermediate-low level waste (ILLW), while Seigneur et al.³⁴ developed a numerical model to study the durability of the cementitious materials in nuclear waste repository subjected to the atmospheric CO₂ carbonation. Previously, the gas generation and more general the geochemical evolution of several typical waste sorts were investigated under repository conditions with the help of thermodynamic modeling^35,36. There, a mixing-tank approach was adopted, i.e., the content of specific waste packages was homogenized. The long-term evolution of the waste package was simulated by considering kinetically controlled metal corrosion, dissolution of aggregates, degradation of organic matter, gas generation, and mortar/concrete carbonation subject to a complete water balance. For most waste sorts, the evolution of waste packages stopped after the initial amount of water was consumed. In waste sorts with a high amount of organic matter the production of CO₂ caused degradation of cementitious materials and drop of pH, which in turn accelerated corrosion and potentially also the degradation of organic matter³⁵.

In view of the results from these calculations, the question arose whether or not the mixing-tank approach is an appropriate approach or if internal material heterogeneities of waste packages have a stronger influence on the geochemical evolution and gas generation, as in reality waste packages are highly heterogeneous and rarely exhibit well-mixed conditions.

This subject is addressed in this modeling study by adopting the reactive multi-species multi-phase code OGS-MP-LT³⁷ which is part of the OpenGeoSys framework³⁸. The OGS-MP-LT code contains an effective parameterization for the degradation of cementitious materials and was complemented with kinetic rate laws for organic degradation and corrosion in terms of gas generation and water consumption coupled to the two-phase transport solver.

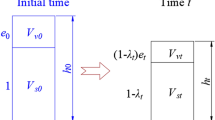
The customized code was used to model water and gas transport influenced by chemical reactions in a simplified cemented waste package that contains mixed organic and metallic wastes (Fig. 1). The generic waste package concept reported in this study accounts for a cemented mixed solid waste sort used for the previous modeling study³⁵. The original waste sort mainly consists of readily degradable cellulose, slowly degradable organic materials (plastic, polyvinyl chloride (PVC), and rubber), carbon steel, cement paste, and quartz sand as aggregate for the backfill mortar. Most water is bound in the residual form in the pore space. This waste form was chosen due to the expected high reactivity (presence of cellulose) as well as its complex geometry. The waste material was originally collected in 20 or 100 dm³ drums that are compacted in a steel tube of 485 mm diameter (Fig. 1). The tube was then placed in a 200 dm³ steel drum on a base layer of reinforced concrete and the void space was backfilled with reinforced backfill mortar. The bottom and the top of the tube is open and in direct contact with the backfill mortar, while the tube wall is impermeable. For simplicity and the absence of information about the base layer of reinforced concrete, it was assumed in the model that the concrete base layer is identical in composition and properties with the backfill mortar. The top of the steel drum is closed with a cover lid, keeping a small air-filled gap between cover lid and backfill mortar. The cover lid contains a cap that can be opened to allow escape of gases and to dry out the drum and prevent corrosion during interim storage. To simplify model implementation, the cover lid was assumed to be easily permeable to gas (cap open) also in a deep geologic repository. Not being in direct contact with the backfill mortar, the cover lid is not explicitly considered in the model. Instead, the gas-filled gap between cover lid and backfill mortar was implemented as an open boundary which connects directly to an outer gas atmosphere.

Fig. 1: Conceptualization of the generic waste package.

The model implementation preserves the geometry of the real waste package in a radial-symmetric setup. Waste and backfill mortar are implemented as porous media, while steel tube and outer steel walls are represented by impermeable model boundaries. The top cover is open and allows free gas exchange with an outer atmosphere.

Due to the high computational demand of such numerical simulations, only one scenario with well-defined boundary conditions was considered that can be investigated without accounting for the evolution of a waste package over the whole lifetime of a typical L/ILW repository of 10⁵ years³⁹.

Note that during the lifetime of a repository, the conditions around a waste package in terms of pressure, liquid saturation, and composition of the gas phase might change considerably with time⁵. In this study, as an outer state, an oxygen-depleted atmosphere was chosen, with constant pressure and a relative humidity of 60%. The presence of CO₂ in atmospheric amounts was considered, because it allows backfill carbonation induced from outside to be compared with internal backfill carbonation by CO₂ produced by degradation of organic waste. Moreover, the integrity of the waste package hull controls the possibility and magnitude of mass exchange between the interior of the waste package with its surrounding atmosphere. For the selected scenario a partly intact waste package was assumed which allows free gas exchange through the cover lid in form of an open top cap. This configuration enabled us to explore whether or not the chemical processes inside the waste package can be slowed down due to the availability of water, to which degree the slowing down is controlled by the outer atmosphere, in what parts of the waste package the slowing down occurs, and eventually how fast this slowing-down is achieved in comparison to the repository lifetime or to the expected evolution of waste package components (hull integrity, degradation of organic, or metallic waste).

Results

Evaluation of model results

The methodology for the present work is described in the subsequent “Methods” section. Due to the complexity of the involved processes and their coupling, the complete analysis of a single model realization requires the combined investigation of several processes and corresponding parameterizations. In this study, model calculations up to 157 years are presented. The time period is mainly limited by computational resources and efficiency of the code, which is not optimized for production runs. The period covered by the modeling is short compared to geological disposal, while it is sufficiently long to show the system evolution until equilibration with the given boundary condition is nearly achieved.

To make such analysis more traceable, the model results are presented in terms of major subject areas of interest such as gas generation and transport, mass fluxes over the open boundary, evolution of water content, and changes of material properties and chemical conditions. In this study, the terms ‘flow’, ‘advection’, and ‘advective flux’ are used, if the liquid phase or the gas phase, or dissolved gases in liquid phase or gas components are transported due to pressure gradients. The terms ‘diffuse’ and ‘diffusive flux’ denote the diffusive transport driven by concentration gradients in case of dissolved gases or gas components. The terms ‘transported’ or ‘fluxes’ without further specification are used, if no differentiation between advection and diffusion is necessary, or both processes are lumped together. Additional visualization of results can be found in Supplementary Figs. 6–10.

Gas and water transport

The choice of initial and boundary conditions determines the gas and water transport in the early stage of the simulation. The initial uniform liquid saturation is high in the backfill and relatively low in the waste (Fig. 2) and is not in equilibrium with the non-uniform water pressure in the drum (see also Supplementary Fig. 6). The liquid water is driven by gravitational force toward the bottom which results toward the top of the backfill in a small decrease in liquid saturation. Gas flow is toward the under-pressured backfill mortar. These internal equilibration processes are soon suppressed by other processes.

Fig. 2: Temporal and spatial evolution of liquid saturation.

Distribution of liquid saturation in drum after a 0.01, b 10, c 50, and d 150 years. The residual liquid saturation is 0.2.

The generation/consumption of gases and water due to chemical reactions causes an increase in gas pressure and (usually) a decrease in liquid saturation (Fig. 2). The strongest changes are found in the waste domain, where gas pressure increases by about 0.3 × 10⁵ Pa after 10 years. The overpressures in the waste domain degrade with time as water consumption lowers liquid saturation (Fig. 2). Chemical processes are partly controlled by the reactivity function that stops the reactions once the relative humidity approaches a threshold value. The spatio-temporal evolution of relative humidity and gas generation reflects the evolution of the liquid saturation.

Gas fluxes across the top boundary with time are shown in Fig. 3. Positive flux values indicate transport from the interior of the drum toward the outside, while negative fluxes indicate mass transport into the drum. At the early phase of the simulation (from 0 to 0.1 years), the system is dominated by equilibration processes caused by the initial conditions. Gas fluxes are relatively low as the composition of the gas phase and the pressures are comparable on both sides of the boundary. Only the relative humidity inside the drum is much higher than outside. This induces quickly a strong diffusive humidity flux out of the drum, resulting in a growing de-saturating zone at the top of the drum (Fig. 2).

Fig. 3: Gas fluxes across the upper boundary with time.

Dashed lines marked with additional black crosses are fluxes calculated with a refined mesh (up to 50 years only). Positive fluxes denote fluxes out of the drum, while negative fluxes denote flux direction into the drum.

From 0.1 years up to 10–30 years, fluxes across the boundary are dominated by outflow of gas generated in the waste compartment (Fig. 3). Hydrogen flux is higher than the methane flux because gas production is dominated by steel corrosion. Nitrogen is diffusing into the drum due to diffusive equilibration of the gas composition between the drum and outer reservoir. After 10 years, vapor transport decreases strongly because most of the water in the drum has already been consumed by chemical reactions or has left the drum via gas phase. The fluxes of hydrogen and methane decrease only after 30–40 years when gas production in the waste compartment is limited by the availability of water.

Water balance

The water balance in the drum is of specific interest along with the induced spatial distribution of saturation and its impact on gas generation. Figure 4 shows the integrated amount of water in the drum. The amount of water that corresponds to residual saturation is marked specifically as chemical reactivity ceases at residual saturation. In addition, the two-phase transport parameterization does not allow to decrease liquid saturation below the residual saturation of 0.2 (Fig. 2).

Fig. 4: Water balance in the drum.

The absolute amount of water in the model is shown in blue. The residual amount of water (dashed black line) is slightly decreasing due to porosity changes. The integrated contributions to water decrease are marked as negative to indicate that they are subtracted from the amount of water. The decrease is caused by the consumption of water due to (bio-)chemical reactions and the flux of water vapor and liquid water from the drum to the atmosphere through the open top. Dashed lines marked with black crosses are values calculated with a refined mesh (up to 50 years only).

The removal of water from the drum is caused by two processes, (i) the consumption of water by chemical reactions and (ii) the transport of water vapor across the top boundary. For both processes, the amount of water removed from the drum with time is also shown in Fig. 4. The consumption of water by chemical processes dominates the water balance in the drum. Note that our simplified implementation of the atmospheric boundary condition allows an artificial advective liquid flux across the top boundary. However, the amount of water flowing as liquid water out of the drum across the boundary is much less than the amount of water escaping from the drum via gas phase. Still, most water in the drum is consumed by gas generation reactions. In addition, liquid fluxes across the top boundary decrease once the adjacent concrete approaches a saturation that is in equilibrium with a relative humidity of 0.6 imposed by the outer atmosphere. Hence, this artifact does not significantly change the evolution of the waste drum.

After 150 years of simulation time, the amount of water available for reactions is very small and will be present mainly in the backfill mortar (compare the trend in Fig. 2). In there, water consumption by corrosion is limited due to the small amount of iron present and corrosion is slow due to the high pH value of the pore solution. In addition, the aggregate-cement reaction is among the slowest reactions and related to this, water consumption is also very low. Gas and liquid permeability are relatively low too, which slows down transport of water out of the backfill material. At any point inside the drum, the gas flux is typically several orders of magnitude higher than the flux of liquid. This is also true for the transport of components. Therefore, the water flux is strongly dominated by humidity transport in the gas phase.

The simulations show that the humidity fluxes across the boundary and inside the drum are not high enough to equilibrate the differences in the water content between backfill, waste, and outer reservoir (across the boundary). The results suggest that it takes only slightly more than 157 years to nearly dry out the drum. Specifically, the low permeability of the backfill mortar limits the advective transport of water and delays the equilibration process.

In the very long term, the amount of water in the drum available for chemical reactions will decrease further. It eventually reaches a value which is on average still higher than the residual saturation (0.2) but below 0.214, the liquid saturation equivalent to a relative humidity imposed by the outer atmosphere. It can be expected that, in the long-term, water vapor influx across the top boundary controls water-consuming reactions in the drum, in particular gas production.

Gas generation rates

Figure 5 shows the gas generation rates within the drum as a function of time (solid lines). The dashed lines show expected rates without reduction in chemical reactivity or dependence of pH (dashed lines). The absolute pH-dependent gas generation rate for H₂ is not identical to those reported by Wieland et al.^35,36. In the latter study, a mixing-tank approach was employed where pH is high everywhere in the waste package, while in this study high hydrogen gas generation was observed in the waste compartment due to the low pH. After about 40 years of simulation time, the gas generation rates decrease rapidly due to the decrease in liquid saturation and the associated drop in chemical reactivity. The gas production rates continue to decrease and approach very low values within a period of 157 years. Gas production is limited by water availability, which is controlled in the long term by the difference in relative humidity inside and outside the drum.

Fig. 5: Gas generation in the waste package with time.

Solid lines are model results for gas generation, dashed lines are calculated rates for a mixing-tank model with unlimited availability of water³⁵.

In Fig. 6, the spatial evolution of gas generation is shown for hydrogen. Initially and after 10 years, gas generation is close to a homogeneous distribution in the waste compartment. Hydrogen gas production in the backfill compartment is hardly visible, as it is more than 100 times smaller than that in the waste compartment. After 50 and 150 years, the spatial distribution of gas production mirrors the distribution of chemical reactivity which coincides with the liquid saturation pattern in Fig. 2.

Fig. 6: Temporal and spatial evolution of H₂ gas generation rates.

H₂ gas generation [mol m⁻³ a⁻¹] in the modeled drum after a 0.01, b 10, c 50, and d 150 years.

Backfill mortar degradation and its consequences

With the help of the look-up table, porosity change, fluid volume change, and pH change due to mortar degradation can be effectively parameterized in terms of aggregate-cement reaction and carbonation (compare “Methods” section). The carbonation process is largely driven by the transport of gaseous CO₂ from the waste compartment toward the backfill material. In addition, some CO₂ enters the drum across the top boundary. The aggregate-cement reaction depends only on the pH of the pore water and the degree of degradation of the mortar. Both processes, aggregate-cement reaction and carbonation might be suppressed by a decrease in chemical reactivity caused by a lack of water. In addition, these are competing processes which might proceed simultaneously. The accumulated amount of CO₂ consumed during carbonation and the accumulated amount of dissolved quartz aggregate with time are shown in Fig. 7.

Fig. 7: Simulation results for concrete degradation and induced changes for pore water pH and porosity.

a Initial cumulated CO₂ gas consumed by carbonation [mol m⁻³], b cumulated CO₂ gas consumed by carbonation after 150 years, c initial cumulated dissolved quartz [mol m⁻³], d cumulated dissolved quartz after 150 years, e initial pore water pH in the drum, f pore water pH after 150 years, g initial porosity, h porosity change after 150 years. The negative values in blue colors in (h) denote a reduction of porosity, while positive values in brown colors denote an increase in porosity.

In accordance with the CO₂ flux (Fig. 3) across the top boundary, carbonation caused by in-diffusion of CO₂ is small due to the low concentration of CO₂ outside the drum. In addition, the backfill region near the top boundary is nearly dried out at the start of the waste package evolution (Fig. 2) which decreases the chemical reactivity and broadens the carbonation front. Backfill materials in contact with the waste compartment are prone to carbonation due to the transport of gaseous CO₂ produced in large amounts in the waste compartment (compare also Supplementary Fig. 7). The upper contact area between waste and backfill is nearly fully carbonated after 150 years as this is the dominating transport pathway for CO₂ toward the open top boundary. The latter transport is reflected by the accumulated CO₂ consumed by carbonation in Fig. 7b. The backfill material at the bottom waste/backfill interface shows much less carbonation. The CO₂ flux across the top boundary is very small (Fig. 3). Therefore, it can be concluded that in the model scenario nearly all CO₂ produced in the drum is consumed by carbonation of the backfill. Once the mortar between the waste and the top boundary is fully carbonated, or completely de-saturated, CO₂ can be easily transported out of the drum.

The degree of mortar degradation due to aggregate-cement reaction is reflected by the accumulated amount of silica aggregate dissolved after 150 years (Fig. 7d). The reaction is not far advanced after 150 years. Total degradation of mortar would require the dissolution of about 5100 mol m⁻³ aggregate, while not more than 1150 mol m⁻³ have been dissolved after 150 years. The progress of the aggregate-cement reaction is slowed down at the bottom and top of the drum by the concurrent carbonation reaction. Both reactions decrease the pH value of the mortar pore water. As a consequence, aggregate dissolution decelerates. The competition between both reactions is clearly visible in regions where high carbonation occurred, because the amount of silica consumed by the aggregate-cement reaction is reduced (Fig. 7b, d). In addition, after 150 years, the aggregate-cement reaction is diminished in the top backfill region due to reduced chemical reactivity (dry conditions in Fig. 2, see also Supplementary Fig. 10 for chemical reactivity).

Both mortar degradation processes, i.e., carbonation and aggregate-cement reaction, decrease the pH (Fig. 7e, f) and affect the porosity (Fig. 7g, h). The change of pH after 150 years by aggregate-cement reaction is relatively small, i.e., pH is still above 11, as the reaction is not yet very far progressed. Full carbonation of the backfill is achieved in the backfill on top of the waste compartment. This reduces the pH in the middle of the upper carbonated region to 7.7–8. As the extension of this region is small, the overall effect on steel corrosion is limited. It should be noted that the progress of carbonation fronts in the investigated partially water-saturated system is mainly controlled by the diffusive flux of CO₂ in the gas phase. A slowing down in carbonation with time is visible at the upper boundary, which is caused by the decrease of the CO₂ flux with increasing carbonation depth. This is typically observed in case of a diffusion-dominated transport regime. Porosity clogging was not observed as the thermodynamic calculations for the look-up table did not show a strong porosity decrease upon carbonation. On the contrary, hydrated cement phases with relatively high molar volumes are replaced by denser carbonate with a lower molar volume, which gives rise to a net increase of porosity for the fully carbonated medium (Fig. 8a). According to Huet et al.⁴⁰, porosity clogging during carbonation in CO₂-rich environment is related to the transport of dissolved calcium in the liquid phase with mass fluxes similar to CO₂ fluxes toward the carbonation front causing accumulation of carbonate. For the system with low liquid saturation investigated in this study, the mass flux of CO₂ in the gas phase is much higher than the expected flux of dissolved calcium in the liquid phase. This will prevent accumulation of additional carbonate at the carbonation front and porosity clogging can be excluded in the drum.

Fig. 8: Material parameters and pore water changes due to cement degradation as stored in the look-up table.

a Porosity, b liquid volume, c pH, and d decadic logarithm of quartz dissolution rate are plotted, depending on CO₂ addition (for mortar carbonation) and quartz dissolution (for aggregate-cement reaction). Blue colors indicate a decrease and red colors indicate an increase of the parameter with regard to the un-degraded system.

While the aggregate-cement reaction does not lower pH significantly within 150 years, it decreases the backfill porosity from 0.095 to only 0.08. The porosity decrease is slightly stronger near the top and bottom layers of the waste compartment, because both the aggregate-cement reaction and carbonation affect the backfill. In the fully carbonated top backfill region, a slight porosity increase was observed in accordance with the effective parameterization of the mortar degradation (Fig. 7h). The total void space (porosity) in the drum was reduced from initially 0.0372 to 0.0349 m³ after 157 years.

Discussion

The modeling study demonstrates the importance of, and the difficulties associated with process couplings between transport and (bio)chemical processes. The realistic internal structure of the investigated waste package, i.e., the heterogeneous distribution of materials with different chemical and transport properties, and the exchange of mass with the surrounding atmosphere (via the top boundary condition) are key factors that determine the waste package evolution.

The calculated temporal evolution of gas generation rates and water consumption are very different to those calculated with the mixing-tank approach reported by Wieland et al.^35,36. The latter authors investigated two cases, (i) the complete isolation of the waste package from the surrounding (steel hull intact) and (ii) a case where water (of neutral pH) can freely enter the waste package (permeable steel hull). In the former case, all chemical reactions (including gas generation) stopped, once all water in the waste package was consumed. In the latter case, chemical reactions proceeded until chemical equilibrium was reached, i.e., all metals were corroded and all organic wastes were degraded. In both cases, metal corrosion and hydrogen production increased, once the pH dropped below 10.5. In this study, the reactive transport model is based on a more realistic, spatial separation between waste, backfill, and package components. Therefore, already the initial geochemical conditions in the compartments may deviate strongly from the averaged (mixing-tank) system. This difference has direct consequences for gas generation and water consumption, which are much higher as compared to the mixing-tank model for the investigated waste package.

The major factor limiting chemical processes is the drying out of those parts of the drum with the highest water consumption. Due to the separation of waste and backfill material, the pH value in the waste is low, and therefore metal corrosion and associated consumption of water are high. The chemical reactivity in the waste compartment is controlled by the availability of water, which is controlled by the transport of water, specifically as vapor. The transport of liquid and of humidity in the gas phase is limited by the low permeability of the surrounding backfill material. Nearly dry conditions are achieved in large parts of the drum at the end of the simulation period of 157 years. This is a very short period compared to the lifetime of a repository. The top boundary allows quite high fluxes compared to a nearly completely intact outer hull, which only allows gas to escape through small holes. From the mass balance of water, it clearly appears that water consumption inside the waste package is the main process responsible for drying out the waste package. It can also be expected that a waste package hull is still largely intact after 157 years. Therefore, if mass transfer (vapor diffusion) into the waste package is limited by a largely unperforated waste package hull, it will be possible to achieve dry conditions within a few hundred years inside waste packages similar to the one investigated in this study.

The simulations show that mixing-tank models are not necessarily conservative with regards to the temporal evolution of waste packages in the sense that they may systematically over- or under-predict specific processes within a given time period. To be able to assess whether or not a model leads to conservative predictions, a good knowledge of the processes and in particular the process couplings is needed.

A major source of uncertainty in the model is the representation of the inner waste compartment. At the time being, it is uncertain as to whether the compressed waste packages in the steel tube can be represented in terms of a porous medium with averaged properties and whether or not the chosen material parameters are appropriate. Other sources of uncertainty might originate from the parameters that have been selected for the two-phase flow model, for instance, the diffusion coefficients used for each gas component in both gas and liquid phases or the van Genuchten model parameters. A detailed sensitivity analysis allows the quantification of the influence of parameter uncertainties on the evolution of waste packages.

The model presented in this study highlights the importance of process coupling for predictions of the evolution of waste packages during long-term storage, as significant amounts of reactive wastes might be consumed. Quantification of metal corrosion as well as organic degradation and mortar degradation during long-term storage are required in order to account for changes in the inventory of reactive wastes and backfill materials that are placed in a deep geological repository.

The model application shows that carbonation of backfill material due to exposure to atmospheric CO₂ is limited, for example during interim storage. This is in agreement with the study of Trotignon et al.³³ on the carbonation of concrete structures in an underground repository during the operation period. As for other cementitious materials with low permeability, carbonation fronts slow down with time and carbonation is limited at low relative humidity. Nevertheless, pre-carbonated zones might become important specifically in the presence of preferred pathways or heterogeneous structures, as they do not bind/retard CO₂ further leading to preferred pathways for CO₂ migration into other parts of the waste package. The model also demonstrates that within 157 years, the aggregate-cement reaction has limited influence on the chemical evolution of the system, as the change of pH inside the backfill mortar is small.

Further extension of the current model to interim storage conditions is an obvious perspective. Most waste packages have often been stored for decades in interim storage facilities before being disposed of in the final repository. Ventilation caps of waste packages might be opened to allow gases to escape and avoid problems with mechanical integrity caused by excessive gas production during interim storage. External humidity in interim storage facilities is kept low which allows the drying out of waste packages and suppresses the corrosion of metals. Nevertheless, conditions are oxic during interim storage and therefore, the corresponding modeling scenario requires the availability of gas generation rates by the degradation of organic matter and the corrosion of metal in these conditions. To the best of our knowledge, a consistent parameter set of the chemical kinetics of degradation processes in oxic conditions is presently lacking.

For the current simulations, a special version of the OpenGeoSys V6 framework was used. Although the code is one to two orders of magnitude faster than a fully coupled reactive transport code³⁷, calculation times are still up to 2 weeks for the waste package application with a coarse discretization. The long computing time is a consequence of the time step size that can only be limited within 1 × 10⁻⁴ years due to constraints imposed by the carbonation of cementitious materials. Clearly, this limits the applicability of the approach, as it does not allow for extensive parameter sensitivity studies or screening of the parameter space with probabilistic methods. The use of a relatively coarse mesh might change system evolution and calculated changes, as concentration and pressure gradients are not properly resolved at all simulation times. We tested this by conducting calculations with a finer mesh and found good agreement for calculated values (Figs. 3 and 4). Further details can be found in Supplementary Note 3.

Nevertheless, there is some potential for further optimization in terms of computational efficiency and parallelization of the current implementation. Further work on computational schemes is required to improve their applicability to long-term predictions of the evolution of waste forms in a repository for radioactive waste, e.g., by high-performance-computing methods or alternative methods for representing chemical processes (e.g., by machine learning). Increased computational efficiency might be expected with these methods, which allows a more rigorous benchmarking of the current model, including parameter uncertainty, to be achieved in the future.

Methods

Modeling of coupled processes on waste package scale

The evolution of a cementitious waste package for L/ILW is governed by several tightly coupled transport and chemical processes. In this study, the temporal and spatial evolution of gas and liquid transport is influenced by chemical reactions and mass exchange with an outer atmosphere. The description of the bio(chemical) processes is based on a model applied by Wieland et al.^35,36.

Several simplifying assumptions are necessary for the modeling procedure. For simplicity, mechanical effects such as concrete/mortar cracking were not considered, although they might strongly influence mass transport in cementitious backfill⁴¹. Thermal effects on transport and chemical processes were also excluded. Since, in the Swiss concept, gas production by radiolysis is believed to be related to specific waste sorts and only produces minor amounts of gas compared to other processes, it was ignored in this work⁴². In the calculated scenario, the atmosphere was assumed to be oxygen-free. This assumption enforces anoxic conditions for metal corrosion and degradation of organic matter which are anticipated to occur in the long term in a deep geological repository.

The unknown complex structure of compacted 20 dm³ waste containing steel drums cannot be modeled with numerical tools. It is safe to assume that the integrity of the steel drums is destroyed during compaction, and that numerous cracks and holes allow the transport of liquid and gas in the inner waste compartment (Fig. 1). Hence, the inside part of the steel tube was implemented as a porous medium with averaged material properties. The detailed geometric information on this type of waste package is given in Supplementary Note 3.

Chemical processes

The model mimics only the key chemical processes, which are relevant in terms of gas production, water consumption and may interact strongly with gas and water transport in the waste package. The following chemical processes have been included:

• 1. (Microbial) Degradation of organic materials resulting in the production of CO₂ and CH₄

• 2. Anoxic corrosion of metals, for example, steel walls of waste packages and corrosion of iron/steel waste

• 3. Degradation of the backfill mortar by siliceous aggregate-cement interaction

• 4. Carbonation of the backfill mortar caused by influx of atmospheric CO₂ or CO₂ generated during the degradation of organic materials.

The first three reactions are considered to be kinetically controlled and will occur over relatively long periods of time, typically more than hundreds or thousands of years until reactions end. The fourth reaction, carbonation of the backfill mortar, is expected to be nearly instantaneous and controlled by the transport of CO₂ and the availability of water.

The approach reported by Wieland et al.³⁵ was implemented for the degradation of organic materials. Details on the underlying simplifications, the processes considered and further links to more detailed degradation reactions, rates, and pathways are further given in Chapter 2 of Diomidis et al.¹⁰. In summary, the organic waste materials are classified into two groups. Group 1 comprises fast degrading organic matter, which mainly consists of cellulose. Group 2 accounts for the slowly degrading organics matter which includes, e.g., polystyrene, plastic materials, and rubber.

Group 1 organics were modeled in terms of cellulose degradation, which can be described in the presence of water according to the following overall chemical reaction:

$${\mathrm{C}}_6{\mathrm{H}}_{10}{\mathrm{O}}_5 + {\mathrm{H}}_2{\mathrm{O}} \to 3\,{\mathrm{CO}}_2 + 3\,{\mathrm{CH}}_4.$$

(1)

The degradation of the slowly degrading organics (polystyrene, plastic) in group 2 was tentatively represented in terms of the following chemical reaction:

$${\mathrm{C}}_8{\mathrm{H}}_8 + 6{\mathrm{H}}_2{\mathrm{O}} \to 3{\mathrm{CO}}_2 + 5{\mathrm{CH}}_4$$

(2)

For both groups, the gas generation rate as well as the water consumption rate correspond to the degradation rate of the organics. The temporal behavior of the degradation of both types of organics was expressed in terms of a first-order kinetics:

$$m\left( t \right) = m\left( 0 \right) \cdot {\mathrm{exp}}\left( { - \lambda t} \right)$$

(3)

where m(0) refers to the initial mass of organic material [kg] and λ denotes the degradation rate [a⁻¹]. Hence, it was assumed that the degradation of organics follows a first-order kinetics.

The total gas generation rate R [mol a⁻¹] for each waste group can be expressed as follows:

$$R = m\left( {\mathrm{t}} \right) \cdot k_{\mathrm{D}}$$

(4)

k_D [mol kg⁻¹ a⁻¹] represents the amount of gas generated from one kg of waste over one year. The degradation rate λ and the specific gas generation rate k_D are related and their values cannot be varied independently³⁵.

The implemented parameters for the gas generation of the two waste groups are listed in Table 1. The water consumption rates for each waste group were calculated by combining reactions (1) and (2) with Eq. (3). The rates for the production of CH₄ and CO₂ were calculated with the help of the gas generation rate (Eq. 4).

Table 1 Organic degradation parameters, gas generation rates and rates for water consumption for two waste groups in accordance with earlier studies^4,35,36,67.

It was assumed that all steel components of the waste package are made of carbon steel. The anoxic corrosion of the steel can be expressed in terms of the following overall reaction^43,44:

$$3\,{\mathrm{Fe}} + 4{\mathrm{H}}_2{\mathrm{O}} \to {\mathrm{Fe}}_3{\mathrm{O}}_4 + {\mathrm{4}}\,{\mathrm{H}}_2$$

(5)

Anoxic corrosion of iron and steel is kinetically controlled, and its rate is mainly pH-dependent. The corrosion rate is significantly accelerated under near-neutral conditions (pH <10.5) compared to alkaline conditions (pH ≥10.5). The corrosion rates R_Fe can be expressed in terms of mol Fe consumed with a value of 0.28 mol m⁻² a⁻¹ when the pH value is below 10.5, while under alkaline conditions, the iron consumption rate drops to 0.0028 mol m⁻² a⁻¹. These values are identical to those previously used^35,36 and are in accordance with those used by Diomidis et al.¹⁰. According to the overall reaction (5), the related hydrogen production and water consumption rates are 4/3 R_Fe.

In the model, corrosion rates for steel were calculated based on the available surface areas (Table 2). The inner surface of the outer drum and the surfaces of the steel tube were explicitly considered according to the waste package geometry. Steel waste is homogeneously distributed inside the waste compartment (inner tube) in a form of a time-invariant surface area per volume. For simplicity and due to its small contribution to gas generation, the corrosion of mortar reinforcement steel was excluded in the model. The top lid of the drum was not considered in the model, as outlined before. Moreover, the model did not trace if any surface of the iron has been completely consumed, which would stop the corrosion reaction. Note that simulations for this study covered only a relatively short time period, in which a maximum corrosion depth of 300 µm in 150 years was reached (see corrosion rate in Supplementary Table 7).

Table 2 Areas for steel surfaces as calculated from the waste description given in Wieland et al.³⁵.

The composition of the backfill mortar is given in Table 3. The setup represents a typical mortar used for waste conditioning. Two different types of cement are used, a typical OPC (CEM I) and a sulfate-resisting OPC (CEM I, HTS = haute teneur en silice) similar to the one described by Lothenbach and Wieland⁴⁵. Silica fume (Micropoz) and clinoptilolite were assumed to have a very high reactivity, i.e., they possess a high surface area and react very fast during cement hydration. The aggregates, sand and quartz sand, were considered as quartz which is an inert component during cement hydration. The aggregates have the same grain size (1.5 mm diameter) and dissolve over time according to a pH-dependent rate⁴⁶ provided by a look-up table (Fig. 8c).

Table 3 Composition of the (simplified) backfill mortar, for a waste package.

The calculated equilibrium composition for the fully hydrated mortar is given in Table 4. The recipe and the thermodynamic setup was taken from previous work³⁵. Therefore, the composition is very similar to the one given in Table 3.2 of Wieland et al.³⁵ for the combined equilibration of waste and backfill. Portlandite is not present in the fully hydrated mortar, as it is consumed due to the reaction with silica fume and clinoptilolite. The release of the alkalis from the clinker minerals and clinoptilolite gives rise to a calculated pH of about 13.

Table 4 Initial properties and phase composition of the fully hydrated backfill mortar calculated using the input data listed in Table 3 and normalized to a volume of 1 m³.

The numerical model uses a look-up table which contains changes of material properties upon degradation of the backfill mortar. It considers porosity changes, water consumption in terms of volume changes of the liquid phase, pH changes, and pH-dependent quartz dissolution rates. The general procedure used to generate this look-up table has been explained by Huang et al.³⁷, more details on the specific setup for this work are summarized in Supplementary Note 1. The equilibrated mortar is the starting composition for the degradation calculations that span the look-up table. Only two degradation reactions were considered: (a) reaction between siliceous aggregates with cement phases and (b) carbonation upon reaction with intruding CO₂. Both degradation mechanisms successively dissolve calcium-bearing cement phases to form carbonates in case of carbonation or calcium silicate hydrates (C-S-H) with low Ca/Si (C/S) ratio in case of the aggregate-cement reaction. The 2D isoline plots displayed in Fig. 8 represent the parametrization of mortar degradation, which depicts the evolution subjected to the coupling effects of carbonation in terms of added moles of CO₂ per unit volume, and aggregate-cement reaction in terms of moles of quartz dissolved per unit volume. The look-up table parameters were normalized with respect to a reference volume, i.e., the volume of the initial fully hydrated mortar.

The net porosity change originating from the aggregate-cement reaction is small, while for carbonation the replacement of hydrated cement phases with denser carbonates decreases significantly the volume of solid phases during carbonation and increases porosity of the fully carbonated material (Fig. 8a). The dissolution of hydrated cement phases during carbonation also releases considerable amounts of water, while the amount of water consumed during aggregate-cement reaction is small (Fig. 8b). It should be noted that porosity and liquid volume are not identical. The porosity was calculated from the volume occupied by solids with regard to a reference volume, which is the total volume of the un-degraded starting system (Supplementary Note 1). The liquid volume, however, was calculated during equilibration of the system and not scaled to any reference volume. For both degradation mechanisms, a strong drop in pH value was observed (Fig. 8c). The existence of C-S-H with a minimal C/S ratio of 0.8 buffers the pH at a value close to 10 for large parts of the look-up table. Only if C-S-H is completely converted into carbonates after adding large amounts of CO₂, the pH decreases further in the presence of free CO₂.

The evolution of pH upon mortar degradation is directly reflected by the decrease of quartz dissolution rates with progressing degradation (Fig. 8d). Details on the calculation of the quartz dissolution rate and how the cement-aggregate reaction influences pH evolution are given in Supplementary Note 1.

Capturing all aspects of the movement of carbonation fronts in cementitious media with macroscopic continuum scale models is non-trivial and has led to increasingly more complex experiments and models⁴⁷. The review of Qiu⁴⁸ reports numerous internal material factors and external environmental factors that can influence carbonation processes, e.g., relative humidity, temperature, CO₂ concentration. In our simplified model, however, the cement composition was considered as the only internal material factor in the look-up table.

Experimental investigations show that carbonation fronts are not sharp^49,50 which is in part attributed to the influence of chemical reaction kinetics^14,50. The effect of the characteristic time of carbonation reaction to a characteristic diffusion time was discussed for example by Muntean et al.⁴⁷. In general, if the characteristic time for reaction is much longer than the time for diffusion of CO₂ then the zone of reaction is small as compared to the progress of the reaction front. This is frequently observed for OPC-based materials^47,51. The influence of chemical reaction kinetics was not considered for the look-up table, for simplicity and due to lack of experimental data.

In our model approach, the progress of carbonation fronts is still influenced by competition with the aggregate-cement reaction as well as porosity and liquid saturation changes as these properties enhance or reduce CO₂ transport in the gas phase. Furthermore, a sharp carbonation front is smeared out in a region with reduced chemical reactivity as only part of the CO₂ in a node/volume is consumed.

It is known that iron corrosion rates⁵² and more generally (bio)chemical reactions are strongly inhibited in a dry environment with limited water availability. As soon as the relative humidity is lower than a threshold value, these reactions almost stop⁵³. In fact, threshold values might be different for different reactions⁵³. For example, corrosion of an iron surface exposed to the atmosphere was found to slow down strongly below a first threshold relative humidity of 0.55 and was even further reduced below a second threshold value of 0.2⁵⁴. For reactions in porous media, the threshold value depends specifically on the pore size distribution, connecting (partial) liquid saturation of the medium with the relative humidity of the gas phase⁵⁵. In contrast, carbonation fronts move fastest at about 50–70% relative humidity in most concrete materials^56,57,58. At higher humidity, the CO₂ fluxes slow down as increasingly more pores are water-filled and fast diffusion in gas-filled pores is replaced by slow diffusion in water-filled pores. At lower humidity, however, there is insufficient water in larger pores to drive carbonation reactions.

In this study, an approach implemented by Trotignon et al.³³ was employed to account for the slowing down of chemical reactions at dry conditions. The various reaction rates were multiplied with a function R(t) to scale chemical reactivity with relative humidity RH of the gas phase. This chemical reactivity R was calculated for each time step and finite element (FE)-node. R varied between zero, if no reaction takes place due to lack of water, and one, if the reaction is not limited by the availability of water. R was multiplied with hydrogen, methane, and CO₂ gas generation rates, water consumption rates, quartz dissolution rate (for aggregate-cement reaction), and with the amount of CO₂ used for the carbonation reaction.

A phenomenological approach proposed by Bazant and Najjar⁵⁹ was implemented for Fe-nodes that represent the backfill mortar:

$$R = \left( {1 + \left( {7.5 - 7.5{\mathrm{RH}}} \right)^4} \right)^{ - 1}$$

(6)

in which the reactivity decreases progressively from 1 to zero as liquid saturation approaches residual saturation.

Following Suckling et al.¹⁵, a linear ramp was implemented for FE-nodes in the inner waste compartment.

$$R = \left\{ {\begin{array}{*{20}{c}} {1\,\,\,\,\,\,\,\,\,\,1\, < \,X} \\ {X\,\,\,0\, < \,X \,<\, 1} \\ {0\, \,\,\,\,\,\,\,\,\,\,X\, < \,0} \end{array},\,{\mathrm{where}}\,X = \frac{{{\mathrm{RH}} - {\mathrm{RH}}_{{\mathrm{min}}}}}{{{\mathrm{RH}}_{{\mathrm{max}}} - {\mathrm{RH}}_{{\mathrm{min}}}}}.} \right.$$

(7)

The reactivity varies linearly between RH_min = 0.6 and RH_max = 1. The definitions of the reactivity functions are given in terms of RH (Fig. 9b), but are connected to the saturation of the medium via Kelvins equation (Supplementary Eq. (9)) which relates the relative humidity with the radius of the largest water-filled pore in a porous medium⁶⁰. This allows the saturation dependence of chemical reactivity to be plotted for both materials as shown in Fig. 9a.

Fig. 9: Chemical reactivity dependence on liquid saturation.

Evolution of the chemical reactivity function R with respect to a liquid saturation S_L and b relative humidity RH in waste and backfill mortar. Liquid saturation and relative humidity are related via Kelvin’s law.

Modeling methodology and implementation

To assess the influence of process couplings on system evolution, the following feedback mechanisms were implemented in the OpenGeoSys-MP-LT code (Fig. 10). Details on the implementation of the look-up table approach and on the feedback between degradation of cementitious materials and transport processes are reported by Huang et al.³⁷. In addition, the extended model links gas generating and water-consuming reactions for degradation of organic matter and anoxic corrosion of metals via source/sink terms to the two-phase flow transport part (Supplementary Note 2).

Fig. 10: Implemented transport and chemical process and their couplings.

Specific couplings between multi-phase multi-component transport and chemical processes for drum simulations (modified from Huang et al.³⁷).

Corrosion of steel was implemented as described in Wieland et al.³⁶. The outer drum surface and the surfaces of the steel tube (Fig. 1) were considered explicitly via the FE-discretization (compare, e.g., Supplementary Fig. 4). A hydrogen flux boundary condition was applied to the FE-nodes that form these boundaries. Corrosion in the waste compartment was implemented as a source term for hydrogen. The contribution to water consumption was calculated at each node/element depending on the local hydrogen generation rate. Kinetic rates, look-up table, and multi-phase transport were explicitly coupled via the pH dependence of iron/steel corrosion¹⁰. In the current model implementation, steel corrosion and organic degradation reaction do not influence porosity nor do they change pH or alter mortar degradation.

For cementitious materials, degradation was parameterized in terms of a look-up table that provides pH, porosity, liquid volume, and kinetic rates for the dissolution of (quartz) aggregate depending on the progress of carbonation and aggregate-cement reaction. From the change in liquid volume due to aggregate dissolution (−H₂O in Fig. 10) and carbonation (+H₂O in Fig. 10) liquid consumption/release rates were calculated for each node (if cement was present). In the look-up table, changes in pore water composition or pH as a result of changes of liquid saturation were excluded. We assumed that the waste compartment is only composed of steel and organic waste. Therefore, the look-up table approach was not used for the waste compartment and pH was assumed to be below 10.5 from the beginning.

The degree of carbonation was calculated for each node based on the amount of CO₂ that reaches a node/volume by transport. The CO₂ is removed from the gas and liquid phase at the node after reaction. The aggregate-cement reaction was calculated based on the dissolution rate of quartz aggregate provided by the look-up table.

Reaction rates for corrosion, degradation of organic matter, and mortar degradation were reduced via a common chemical reactivity factor calculated from liquid saturation/relative humidity.

In the numerical model, the waste package was simplified to a 2D radial geometry and the simulation domain is thus half of the cross-section of the drum (Fig. 1). Discretization was relatively coarse with 249 cells to limit the duration of computing runs to manageable times. Model results calculated with a refined mesh are further discussed in Supplementary Note 3.

The two-phase transport relevant gas, water, and material properties are provided in Supplementary Tables 3–5. The model only considers capillary condensation and not additionally adsorbed water as reported by Davie et al.⁶¹ or Zhang and Angst⁶². The model captures the main features of moisture transport in cementitious materials, although only advective transport of liquid water and advection and diffusion of moisture in the gas phase was implemented. For example, anomalous transport behavior caused by the interplay between adsorbed water, water films, and capillary water is not captured⁶².

The model accounts for two materials with different properties, the tube filled with waste in the center of the drum, and the backfill mortar that fills the space between the tube and the wall of the drum (Fig. 1). For real waste packages, the waste and backfill materials were not well characterized and citable references do not exist. Specifically, porosity, permeability, and other two-phase flow transport parameters were unknown and values had to be estimated. In case of the backfill mortar, it was known that the calculated porosity (Table 4) is comparable to experimental data. In case of the inner waste compartment, however, no information was available. For the two-phase transport in the backfill, properties were chosen similar to a typical high-performance concrete with relatively low porosity described by Croisé et al.²⁶. For the waste, it was assumed that the permeability is much higher as compared to the backfill, while gas entry pressures in the capillary pressure–saturation relation are much lower. In case of dry concretes with porosities similar to the backfill mortar, effective gas diffusion coefficients are known to be 1 × 10⁻⁷ – 1 × 10⁻⁸ m² s⁻¹ (see, e.g., Linares et al.⁶³ and Boumaaza et al.⁶⁴). For simplicity, the same pore gas diffusion coefficient of 3.3 × 10⁻⁷ m² s⁻¹ was used for all gases in the two materials. This results in effective gas diffusion coefficients of 5.3 × 10⁻⁸ m² s⁻¹ in dry waste and 2.5 × 10⁻⁸ m² s⁻¹ in dry backfill mortar. In this model, completely dry materials are at residual liquid saturation. For comparison, the diffusion coefficient of water vapor in air at 20 °C is 0.242 × 10⁻⁴ m² s^−1 65. The diffusion of dissolved gases in the liquid phase was also considered using the diffusion coefficient listed in Supplementary Table 4.

In order to come up to the correct numerical solution, it was necessary to ensure that the numerical time step was smaller than the time needed for a reactant to move between adjacent spatial grid points⁶⁶. In the modeled scenario, the fastest transport process that controls the time step size was the transport of CO₂ in the gas phase. CO₂ is removed at each time step at numerical nodes where carbonation occurs due to instantaneous carbonation. In reality, specifically at short times and at high CO₂ concentrations, reaction fronts are smoothed by reaction kinetics^50,51. It was observed that instantaneous consumption of CO₂ forms sharp reaction fronts which move slowly through the material, driven by the transport of CO₂ in the gas phase. Changes in chemical reactivity are partly controlled by the transport of water vapor in the gas phase. However, as water vapor is not completely removed from the water-consuming, kinetically controlled processes, the transport of water vapor is not the process limiting the time step.

Kinetically controlled processes, for example, gas production and aggregate-cement reaction, were all comparably slow and they were well resolved by the time step size.

The top of the drum was assumed to be in contact with an anoxic outer atmosphere with a relative humidity of 0.6. The atmosphere is composed of 10⁻⁵ molar fraction hydrogen, 2 × 10⁻⁵ molar fraction methane, 4 × 10⁻⁴ molar fraction CO₂, and ~0.97 molar fraction nitrogen. The gas pressure was fixed to 1 atm (1.01325 × 10⁵ Pa). The boundary nodes at the top of the model were kept at a capillary pressure of 6.75 × 10⁷ Pa which sets saturation close to the residual value and also corresponds to 0.6 relative humidity.

At the start of the simulation, a starting condition close to liquid saturation (S_w = 0.9) was assumed for the backfill compartment, while liquid saturation of the waste compartment was significantly lower (S_w = 0.33). The composition of the gas phase was similar to the outer (boundary) gas composition, while the relative humidity was very close to 1 for both materials (see Supplementary Table 6). A uniform pressure equal to 1 atm was applied within the domain.