Abstract
When exposed to irradiation—e.g., in nuclear power plant environments—minerals may experience alterations in their atomic structure which, in turn, result in changes in their physical and chemical properties. Herein, we mimic via Ar+ implantation the effects of neutron irradiation on calcite (CaCO3) and dolomite (CaMg(CO3)2) – two carbonate minerals that often find use as aggregates in concrete: a material that is extensively used in the construction of critical structural and safety components in nuclear power plants. By a pioneering combination of nanoscale quantifications of mineral dissolution rates (i.e., a proxy for chemical durability) in alkaline solutions, vibrational (infrared and Raman) spectroscopy, and molecular simulations, we find that irradiation minimally affects the atomic structure and properties of these carbonate minerals. This insensitivity to radiation arises from the predominantly ionic nature of the interatomic bonds in these minerals which can relax and recover their initial configuration, thus ensuring minimal damage and permanent alterations to these minerals following radiation exposure. The outcomes have significant implications on the selection, use, and specification of mineral aggregates for use in nuclear concrete construction.
Similar content being viewed by others
Introduction
Carbonates are common minerals that make up nearly 20% of sedimentary rocks at the Earth’s surface.1 Limestone, a sedimentary rock composed mainly of calcite (CaCO3) and dolomite (CaMg(CO3)2), often finds use as a mineral aggregate in concrete.2,3,4,5 Recent studies have shown that aggregates may be altered upon exposure to irradiation, resulting in decreases in the compressive strength and elastic modulus of concrete at fluence levels above 1.0 × 1019 n/cm2.6 Under prolonged neutron irradiation, aggregates and their mineral constituents may feature volume expansions or enhancements in their reactivity, e.g., enhanced dissolution rate.7 The cement paste, because of its poor crystallinity, has been shown to be relatively less affected by neutron irradiation.8 Such alterations can detrimentally affect the structural integrity of concrete – an issue of particular importance in nuclear power plants (NPPs).6,7,9,10,11
Volume changes produced in nuclear power plant concretes may result from expansion, drying shrinkage, and radiation (e.g., neutron, and γ–rays) effects on the aggregate and cement paste. Aggregates and the minerals therein, which occupy >70% of the volume of concrete and are disproportionately affected by radiation exposure, dominantly affect volume changes and the durability of concrete. Thus, damage and cracking of concrete can occur due to mechanical expansive stresses resulting from the irradiation-induced volume changes of the aggregates and the onset of dissolution-facilitated alkali-silica reaction (ASR) or alkali-carbonate reaction (ACR) for siliceous or carbonaceous aggregates.12,13
Studies of irradiation-induced alterations of the atomic structure and reactivity of minerals have mainly focused on silicates such as quartz: SiO2, albite: NaAlSi3O8, and almandine: Fe3Al2Si3O12—which were observed to form disordered structures following their irradiation.7,9,10 However, the effects of irradiation on carbonates remain less clear. For example, for calcite, whereas some studies reported negligible changes both in its atomic structure and dissolution kinetics,7,14 others indicate an evolution toward an amorphous atomic structure with increasing fluence.15,16 Analogous studies on dolomite have not been undertaken. Dolomite and calcite exhibit similar structures, wherein layers of carbonate \(({\mathrm{CO}}_3^{2 - })\) groups separate layers of different cations (Ca2+ in calcite, or Ca2+ and Mg2+ in dolomite) (see Fig. 1). Both minerals can be described by a rhombohedral unit cell, but the alternating Ca-Mg arrangement in dolomite reduces its symmetry, i.e., vis-à-vis calcite, from R-3c to R-3. Despite the structural similarity of these two light-metal carbonates, significant differences have been observed with respect to their dissolution kinetics,17,18 solubility,19 and thermal expansion behavior.20 These differences have been explained in terms of the differences in the properties of the C‒O, Ca‒O, and Mg‒O bonds (e.g., bonding energy, interatomic distance, etc.).20 As such, it may be envisioned that irradiation influences the structure and properties of these two carbonate minerals distinctly.21 Therefore, this study examines and compares the effects of irradiation on calcite’s and dolomite’s atomic structures and reactivities in aqueous solutions. Vertical scanning interferometry (VSI) provides high vertical resolution (~2 nm) topographical data of reacting surfaces, enabling measurements of dissolution rates of irradiated layers with thickness < 500 nm. The combination of nanoscale (VSI) analytics and molecular dynamics (MD) simulations implemented herein provides a general overview of the effects of radiation damage, and offers an analysis of how changes in the atomic structures of minerals result in changes in their chemical durability. The outcomes offer new insights into the mechanism of irradiation damage of light-metal carbonates at the atomic scale and inform the selection of durable mineral aggregates for the production of concrete that may find use in both nuclear-energy/-waste disposal applications.
The crystal structure of a pristine calcite and b pristine dolomite projected along the [100] direction as visualized using VESTA.82 Ca, Mg, C, and O atoms are shown in blue, orange, black, and red, respectively. The unit cell is outlined in black. c The unit cell of calcite projected along the [001] direction
Results and discussion
Dissolution behavior of pristine and irradiated carbonates in alkaline solutions
Figure 2 shows the dissolution rates of calcite and dolomite before and following irradiation. Dissolution rates of pristine calcite and dolomite as reported by Plummer et al.,24 Busenberg et al.,25 Chou et al.,17 Shiraki et al.22 and Dolgaleva et al.23 are also shown for comparison.17,22,23,24,25 In general, it was observed that the dissolution rate remained unchanged for 6 ≤ pH ≤ 10, and decreased thereafter as the pH increased, in relation to the increase in the carbonate-ion activity in solution.26 The dissolution rate of carbonates in alkaline solutions is controlled by the pH-dependent concentrations of dissolved \({\mathrm{H}}_2{\mathrm{CO}}_3^ \ast\), \({\mathrm{HCO}}_3^ -\), and \({\mathrm{CO}}_3^{2 - }\) at the solid–water interface.27 In highly alkaline solutions, the sorption of hydroxyl ions by the mineral surface leads to a higher surface pH due to the formation of negatively-charged surface groups, which may reduce the rate of carbonate detachment.27 It should be noted that although the literature data considered herein were obtained under the same pH,17,22,23,24,25 the dissolution rates, especially of calcite, show considerable variability on account of differences including particle size distribution, solution chemistry, and sample source.22,28 Nevertheless, our measured dissolution rates lie within typical ranges observed previously, and in fact agree closely with the data of Chou et al. obtained at 25 °C.17,22,23,24,25
The dissolution rates of calcite (blue squares) and dolomite (red triangles) as a function of the solvent pH before (open symbols) and following (solid symbols) irradiation. The shaded region denotes the range of dissolution rates reported by Plummer et al.,24 Busenberg et al.,25 Chou et al.,17 Shiraki et al.,22 and Dolgaleva et al.23 for calcite dissolution under similar conditions of pH, flow rate, and temperature
Overall, it was observed that the dissolution rate of dolomite is lower than that of calcite over the entire range of pH considered.17 The slower dissolution kinetics of dolomite has been attributed to the rapid release of Ca2+, which leaves the solid enriched in a MgCO3 component whose protonation and hydrolysis control the overall dissolution rate.29,30 Although the dissolution rates for both pristine and irradiated calcite are within the range of published values (see Fig. 2), upon irradiation, a uniform decrease in the dissolution rates of calcite over the entire pH range probed was observed. This is postulated to be on account of ion implantation, at the energies and fluence implemented herein inducing the reorganization of existing dislocations in the crystal structure in an effect similar to annealing,31 which would result in a consequent reduction in the dissolution rate (and elsewhere, has been observed to result in an increase in calcite’s hardness).32,33 This effect is more prominent in the case of calcite, i.e., rather than dolomite on account of the calcite being a pure and oriented single crystal as compared to the natural dolomite sections. In the case of dolomite, irradiation appears to impose no effect on its dissolution rate. Thus, it can be concluded that irradiation affects carbonate mineral dissolution rates in a much more limited manner than observed for silicates.32,34 For example, quartz, albite, and almandine have shown increases in their dissolution rate upon irradiation by a factor of 1000 times, 20 times, and 2 times, respectively.7,9,10
Effect of irradiation on the atomic structure of carbonate minerals
Irradiation can significantly affect the crystal structure of minerals by altering: (i) coordination numbers, (ii) bond lengths, (iii) bond angles, and/or (iv) their medium-range order.7,9,10 Such alterations and defect formation can produce substantial structural changes, such as loss of crystallinity, i.e., amorphization. Here, vibrational (Fourier-transform Infrared (FTIR) and Raman) spectroscopy techniques were used to evaluate disordering. The main difference between these two techniques is the nature of molecular bonding that they assess. Specifically, whereas Raman spectroscopy measures the change in the polarizability of the molecular bond during vibration, FTIR measures the change in the dipole moment during vibrations.35 The degree of structural disordering can be revealed using FTIR from (i) the number and the intensity of peaks, and (ii) the displacement of a given peak from its reference position.36 For example, disordering is associated with a decrease in the number of FTIR peaks, and a shift of their positions toward lower wavenumbers.
Figure 3 shows the FTIR spectra of calcite and dolomite, before and following irradiation. The FTIR spectra of these carbonate minerals revealed known major peaks at 1435–1450, 876–881, and 712–730 cm−1 and minor peaks at 2530–2550 and 1812–1818 cm−1,37 which are related to the stretching and bending modes of the \({\mathrm{CO}}_3^{2 - }\) groups.15,37,38 The similarity in the atomic structures of dolomite and calcite is reflected in their FTIR spectra. Notably, the two major absorption peaks of dolomite (i.e., around 876–881 and 712–730 cm−1) lie between those of calcite and magnesite (MgCO3).38 Broadly speaking, the FTIR spectra of the irradiated carbonates are indistinguishable from those of the non-irradiated samples, especially for dolomite. The minor peak broadening at 876 and 712 cm−1 observed in the case of irradiated calcite (see Fig. 3a) is postulated to be on account of the ion implantation-induced reorganization of existing defects in the crystal structure,31 which could have resulted in the observed reduction in dissolution rate as noted above. Previously, Nagabhushana et al.15 showed both reduction in the peak intensity and peak broadening upon ion implantation in calcite for peaks corresponding to the \({\mathrm{CO}}_3^{2 - }\) group’s bending and stretching modes. This was attributed to the breakage of carbonate bond (‒C‒O‒) or changes in the crystallite size due to irradiation-induced volume expansion.15 However, it should be noted that the implantation energy used by Nagabhushana et al. was 100 MeV, which is almost 3 orders of magnitude greater than what was used in the current study.
The Raman spectra of calcite and dolomite before and following irradiation, are shown in Fig. 4. It is noted that similar to the FTIR observations, the positions and intensities of the 6 major peaks that characterize the chemical bonding of the carbonates remained fairly unchanged.39,40 These peaks which are described in Table 1 include: a major peak located at 1085 cm−1 (calcite) or 1100 cm−1 (dolomite), which reflects the symmetric \({\mathrm{CO}}_3^{2 - }\) stretching (ν1),39 two medium peaks at 280 (calcite)/304 (dolomite) and 154 (calcite)/179 (dolomite) cm−1, which are assigned to external \({\mathrm{CO}}_3^{2 - }\) rotational and translational modes, respectively,39 and two weak peaks at 710 (calcite)/725 (dolomite) and 1434 (calcite)/1445 (dolomite) cm−1, which are related to symmetric \({\mathrm{CO}}_3^{2 - }\) deformation (ν4) and antisymmetric \({\mathrm{CO}}_3^{2 - }\) stretching (ν3).41 In addition, a peak located at 1747 (calcite)/1765 (dolomite) cm−1 corresponds to a \({\mathrm{CO}}_3^{2 - }\) internal mode that originates from the out-of-plane \({\mathrm{CO}}_3^{2 - }\) ion bending (ν2).39,41 Our data suggest that both the pristine and irradiated materials share similar chemical bonding modes on their surface, i.e., \({\mathrm{CO}}_3^{2 - }\) stretching, rotation, translation, or bending. Therefore, the results from both Raman and FTIR spectroscopy show that irradiation did not significantly alter the structure of carbonates, consistent with the results of Pignatelli et al., which employed cross-sectional transmission electron microscopy/selected area electron diffraction (SAED).7
Representative Raman spectra of pristine and irradiated a calcite in the 125‒2000 cm−1 wavenumber region, and b dolomite in the 125‒2000 cm−1 wavenumber region. The peaks are essentially similar before and following irradiation. Fluorescence is more obvious when using a 532 nm laser as typical for a lower wavelength laser source. Although use of a lower wavelength source induced greater fluorescence, this source probes the depth of the material corresponding to the zone affected by irradiation
New insights from molecular dynamics simulations into structure and reactivity
Molecular dynamics simulations provide direct insight into the effects of irradiation (ballistic impacts) on the structures of calcite and dolomite. For example, first, Fig. 5a shows the evolution of the density of these two phases upon irradiation. In contrast to the behavior observed in silicates,7,9,10,42,43 irradiation did not result in significant changes in the bulk densities of the carbonates. In fact, after deposition of 900 × 1018 keV of total kinetic energy, the simulated densities of calcite and dolomite remained effectively unchanged as compared to their initial (pristine state) values of 2.71 g/cm3 and 2.89 g/cm3, respectively, in agreement with previous observations.21,34,44 In contrast, quartz has been shown to exhibit a 15% decrease in density, and complete amorphization, at the same radiation exposure conditions.7 The significant volume expansion and implied density reduction that was indicated via our MD simulations for an incident energy of 1 keV7 was later found to be an artifact stemming from an insufficient system size and relaxation time, which resulted in damage saturation of the system after a small number of high-energy collision cascades. This issue was avoided in the current study by using a larger system size, as demonstrated by Krishnan et al.,45 or a smaller incident energy (600 eV). The electron paramagnetic/spin resonance (EPR/ESR) studies from Kabacinśka et al.46 indicate that changes in the hardness or elastic modulus of materials may arise from electron spinning. Our MD simulations do not take electronic behavior into account. Nonetheless, the lack of change in density as ascertained herein does not contradict the results of Kabacinśka et al.,46 e.g., since density does not always scale with hardness, as shown previously.47,48 In agreement with the vibrational spectroscopy observations, careful inspection of the simulated atomic structures – following irradiation – also did not reveal major structural damage in the calcite or dolomite structures. For example, only subcritical structural modifications (e.g., defect reorganization or distortion) were observed as indicated in Fig. 3. As such, the substantial resistance of carbonate minerals to irradiation can be attributed to the non-directional nature of the ionic bonds (e.g., Ca‒O and Mg‒O bonds) in these minerals which can readily recover their initial geometry after radiation exposure, i.e., cessation of the ballistic cascade.7 In general, the resistance to radiation-induced atomic alterations is dominated by the competition between the short-range covalent bonds (i.e., that induce localized electronic charge between neighboring atoms) and the long-range ionic bonds (i.e., that produce a collection of electrostatically charged spherical ions).49 As such, following exposure to ballistic collisions, the amount of structural alterations that result depends on the ability of the system to rapidly recrystallize; a process which is facilitated in primarily ionic systems which are able to rapidly regain their pristine – most thermodynamically favorable – structure.49 This nature of rapid reorganization to the pristine state is hindered in dominantly covalently bonded systems, since the directional nature of atomic bonds prevents local structural reorganizations, thereby hindering the tendency for recrystallization, resulting in the accumulation of atomic defects.49,50
Coming back to chemical durability (dissolution rates), recently Pignatelli et al. and Hsiao et al. have shown that mineral and glass dissolution rates are, to the first order, controlled by the topology of their atomic networks.9,51 Specifically, it has been highlighted that dissolution rates, for a given solution composition, are determined by the number of topological constraints per atom (nc, unitless) as represented by an Arrhenius-like function:51,52,53,54 \(D_r = D_{r0}{\mathrm{exp}}\left( {\frac{{ - n_cE_0}}{{RT}}} \right)\), where Dr is the dissolution rate, Dr0 is a rate constant that depends on the solution chemistry, R is the gas constant, E0 is the energy required to break a unit topological constraint and T is the thermodynamic temperature. As such, the variation in the dissolution rates before and following irradiation can be expressed as: \(\frac{{D_r^{{\mathrm{irr}}}}}{{D_r^{{\mathrm{prist}}}}} = {\mathrm{exp}}\left( {\frac{{ - \Delta n_cE_0}}{{RT}}} \right)\), where \(D_r^{{\mathrm{irr}}}\) and \(D_r^{{\mathrm{prist}}}\) are the dissolution rates of the irradiated and pristine solute, respectively, and \(\Delta n_c\) is the change in the number of topological constraints per atom upon irradiation.9 By application of this framework, and from knowledge of the pre- and post-irradiation dissolution rates, it is indicated that the limited change in the dissolution rates of calcite and dolomite, before and following irradiation is likely on account of insignificant changes in the number of constraints. This conclusion is unsurprising since the MD simulations above also indicate that the connectivity (e.g., coordination numbers) of the atomic networks of calcite and dolomite remained unaffected by irradiation. This analysis confirms that, despite the small and potentially transient structural changes induced upon irradiation (e.g., distortion of the carbonate groups), irradiation does not induce significant permanent changes in the structure, and consequently the chemical durability of carbonates.
Taken together, by using Ar+ implantation as a proxy for neutron irradiation, this study evaluates the extent of damage that calcite and dolomite—two archetypical carbonate minerals—experience after irradiation by probing changes in both atomic structure and dissolution kinetics, i.e., reactivity. As such, our results highlight that irradiation induces substantially smaller – and if anything, conservative (i.e., the reactivity reduces) changes – in the chemical durability (i.e., mineral dissolution rates) of carbonates as compared to common silicate minerals (i.e., especially those that are fully polymerized, and in which the silicate-groups are percolating). This can be explained by the observation that the atomic structures and connectivity of the carbonate phases remain broadly unaffected by irradiation. This behavior arises from their non-directional ionic bonds, which can recover their initial geometry after each ballistic cascade. This is why radiation damage in carbonates, even if induced, presents a reversible character.32 The resistance to irradiation-induced structural alteration is controlled by the competition between covalent and ionic bonds in the system, and the ability for a structure to recrystallize to its thermodynamically most favored state depends mostly on its ionic nature. Conversely, recrystallization is hindered in structures that are covalently bonded, whose directional character inhibit structural reorganizations, thereby retaining structural defects. These conclusions are supported by our MD simulations which reveal no changes in the atomic densities of both calcite and dolomite after exposure to irradiation, in an ideal system (i.e., no impurities or defects),21,34,55 although the sample may experience some form of defect reorganization that could decrease their aqueous dissolution rates. This is unlike the case of framework silicate aggregates whose volumetric expansion, change (reduction) in mechanical properties, and reduced chemical durability render them poorly suited for use in nuclear concrete construction. This suggests that it would be appropriate to especially prescribe and specify the use of (solely) carbonate-based aggregates in the design and construction specifications of nuclear power plants and other relevant facilities.
Methods
Sample preparation and ion-irradiation
Synthetic single-crystals of (100)-oriented calcite with dimensions of 1 cm × 1 cm × 1 mm (l × w × h) were sourced from MTI Corporation. Naturally occurring dolomite from Sussex County, NJ was obtained from Ward’s Science and sectioned to dimensions of 1 cm × 1 cm × 1 mm using a low-speed diamond saw (IsoMetTM 1000, Buehler Inc.). One side of the dolomite coupons was successively polished using 400, 600, 800, and 1200 grit SiC abrasives and then with diamond paste from 6, 3, 1, and ¼ µm prior to ion implantation.
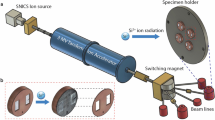
To simulate neutron irradiation, calcite and dolomite were exposed to Ar+ ions, which induce similar damage as neutrons while offering precise beam control and ease of handling.56 The as-received calcite and polished dolomite samples were irradiated at the Michigan Ion Beam Laboratory (MIBL) at ambient temperature using a 400 keV Ar+ ion beam to a total fluence of 1.0 × 1014 ions/cm2. The ion or neutron fluence and the system’s temperature determine the extent of irradiation-induced damage and disordering that is produced (e.g., displacements per atom: dpa).57 For example, a typical neutron fluence after 40 years of operation in nuclear power plants is around 1019 n/cm2.6 To induce the same extent of disordering via ion bombardment, the fluence must be around 105 times lower.57 Thus, an Ar+ fluence of 1014 ions/cm2 was chosen herein. Further, increasing the incident energy beyond 100 eV has been shown to not affect lattice distortion and atomic density.45,58 It is noted that the medium recoil energy for 400 keV Ar+ ions is a factor of 4 lower than for neutrons, although the damage recovery rates of the two are similar.59 The concentration of implanted Ar+ ions as a function of depth was calculated using SRIM (Stopping and Range of Ions in Matter) using the “detailed calculation with full damage cascade method” based on the incident energy of the ion beam (400 keV), the displacement energies for each atom, i.e., Ca, Mg, C, and O which are 25, 25, 28, and 28 eV, respectively, and the ideal compositions and densities of the solids (calcite: 2.71 g/cm3 and dolomite: 2.87 g/cm3). These calculations indicate ion-influenced depths of around 500 nm and 430 nm for calcite and dolomite, respectively (see Fig. 6). The presence of impurities and defects that may affect the actual ion-implanted depths was not considered in the SRIM calculations.
The representative Ar+ ion concentrations as a function of the distance from the implantation surface (located at x = 0 nm). The ion concentration when multiplied by the implantation fluence (1014 ions/cm2) reveals the number density of implanted Ar+ ions per unit volume. This calculation assumes defect-free, stoichiometric single crystals
Scanning Electron Microscopy-Energy Dispersive X-ray Spectroscopy (SEM-EDS)
To ascertain the composition of dolomite, SEM-EDS analysis was carried out on powdered samples with an average particle diameter of around 20 μm. The particulates were gold-coated to a thickness of around 6-to-7 nm and examined using backscattered electrons using a Phenom G-2 SEM (15 kV, 80 pA). The field-of-view (FoV) selected was larger than 10000 μm2 and more than three repeat measurements were carried out for each sampling area (see Table 2). The slightly higher concentration of Ca relative to the reference value (1-to-2 mol%) likely arises from the presence of 1–2 mol% CaCO3 as vaterite (a hexagonal polymorph of CaCO3),60 as confirmed by X-ray diffraction.
X-ray Diffraction (XRD)
The presence of mineral impurities in the natural dolomite samples was examined using a Bruker D8-Advance powder x-ray diffractometer in θ–θ Bragg-Brentano geometry, using Cu-Kα radiation (λ = 1.5406 Å) at an accelerating voltage of 40 kV and a beam intensity of 40 mA. A 2θ range of 20° to 75°, a step size of 0.02°, and an exposure time of 0.5 s/step were used. The XRD pattern of the sample is qualitatively similar to the International Centre for Diffraction Data (ICDD) reference for dolomite (Code: 00–001–0942), as shown in Fig. 7. The presence of vaterite impurity was identified from the diffraction peak at 2θ = 26.64°.61
Fourier-transform infrared spectroscopy (FTIR) and Raman spectroscopy
FTIR was carried out on pristine and irradiated calcite and dolomite samples using Attenuated Total Reflectance Fourier-Transform Infrared Spectroscopy (ATR-FTIR, PerkinElmer Spectrum Two) at room temperature. Here, polished calcite and dolomite surfaces were pressed using around 90 N of force onto a diamond/ZnSe composite crystal to ensure good contact and generate total internal reflection. The spectra reported herein were obtained by averaging 4 scans over the wavenumber range of 2000–400 cm−1 at a resolution of 1 cm−1.
The peaks observed in a Raman spectrum arise from specific molecular vibration or rotation modes. Both the pristine and implanted dolomite samples were probed using a Renishaw inVia confocal Raman microscope with an incident laser beam of near-infrared wavelength of 532 nm. The laser penetration depth in Raman spectroscopy depends on the wavelength of the incident beam, the confocal hole size, the numerical aperture of the objective (NA = 0.85), and the magnification offered by the objective (×100). The penetration depth for the spectra shown herein is calculated to be around 464 nm for a wavelength of 532 nm, implying that the acquired signal is dominated by the material in the irradiation-affected (damaged) region. The spectra were obtained at 1 cm−1 resolution over 10 s of exposure of the CCD detector in the wavenumber region 125–2000 cm−1. Three spectra were collected at 2 different areas on the mineral surfaces (each having a spot diameter of 100 µm).
Vertical scanning interferometry (VSI) for quantifying mineral dissolution rates
The dissolution rates of pristine and irradiated calcite and dolomite surfaces were measured using a flow-through cell (PermeGear) at room temperature (22 ± 1 °C). Alkaline solutions with pH 10, 12, and 13 – i.e., to mimic the chemical environment in concrete – were prepared by adding reagent-grade NaOH to deionized water (>18 MΩ cm). The pH of the solutions was measured using a ThermoFisher Scientific Orion Versa Star Pro pH Benchtop Multiparameter Meter calibrated over the range of 2 ≤ pH ≤ 13. The solutions were injected into the cell (volume = 0.708 mL) at a flow-rate of 1.0 mL/min using a peristaltic pump. These flow conditions have been shown to be sufficient to prevent supersaturation with respect to phases such as Ca(OH)2, Mg(OH)2, CaCO3, and MgCO3.22,62,63,64,65 The dissolution rates of calcite and dolomite were measured using vertical scanning interferometry (VSI) by observing the surface retreat after 2 h of reaction for pristine calcite, 4 h for irradiated calcite, and 6 h for pristine and irradiated dolomite. These periods of solution contact resulted in dissolution depths < 300 nm across all samples. This implies that the zone of the mineral that dissolves is well-within the ion-influenced regions as simulated using SRIM. A 50 × Mirau objective (N.A. = 0.55, lateral resolution 0.163 μm) was used to measure surface height (change) over a total field of view (FoV) of 1374 μm × 974 μm. To offer a height reference for the VSI measurements, a portion of the sample surface was covered with an inert silicone mask (Silicone Solutions SS-38). Thus, the masked area that is revealed after peeling off the silicone mask serves as an unreacted “reference.” The topographical images acquired were analyzed using Gwyddion (ver. 2.48). The absolute height difference between the reacted (dissolved) and masked areas when divided by the molar volume and the period of dissolution reveals the molar dissolution rate. The error bars shown signify one standard deviation of the average dissolution rate for three unique samples. The dissolution rate for each sample is the average of at least three measurements made across different areas on the sample. Additional details on the VSI methodology can be found elsewhere.9,10
Molecular dynamics (MD) simulations
To examine the nature of irradiation-induced damage at the atomic level, MD simulations of calcite and dolomite were carried out using LAMMPS following an established method.9,45,66,67,68 Herein, a randomly selected atom from within the structure of calcite and dolomite (i.e., Ca, Mg, C or O), known as primary knock-on atom (PKA), is accelerated to a kinetic energy of 600 eV, resulting in the formation of ballistic cascades. Note that, based on the predicted energy loss of colliding neutrons, this deposited kinetic energy (600 eV) corresponds to a neutron energy roughly ranging from 4-to-13 keV. The weighted collision probabilities of the different atoms with an incident neutron were based on the neutron cross-sections of the respective elements shown in Table 3a. The neutron cross sections are energy-dependent at low energy (< 10 keV), and typically decay logarithmically with increasing energy and then oscillate for energies ranging from 10 keV to 10 MeV. In Table 3a, the cross-sections were selected so as to account for a deposited energy of 600 eV. For a given incident particle, the accumulation of irradiation damage (e.g., the number of induced ballistic cascades) is determined by the incident particle fluence.69,70 In order to minimize the effects of the thermostat on the dynamics of the atoms after impact, the ballistic cascades are simulated in the NVE ensemble. Once the PKA comes to rest, a spherical region of 10 Å is defined around the PKA, wherein the dynamics is simulated in the NVE ensemble (while the rest of the system is kept at 300 K by a Berendsen thermostat). This is because, at this stage, most of the high-energy motion occurs at the vicinity of the PKA, while the rest of the system (far from the PKA) gradually absorbs the generated heat and ensures that the temperature gradually goes back to 300 K. An incident energy of 600 eV was chosen to simulate the 400 keV Ar+ ion incident energy while taking into consideration the need to rationalize computational cost (i.e., simulating collision cascades at higher incident energies requires larger system sizes and longer relaxation times). Thus, the incident neutron energy used in MD simulations is, therefore, lower than that used in the experiments. This is, however, an intrinsic limitation of MD simulations. Nonetheless, the incident energy was confirmed to not affect the final atomic structure—provided that (i) the incident energy is larger than the critical atomic threshold (displacement) energy, (ii) the system is large enough to avoid any spurious effects from the periodic boundary conditions, and (iii) the duration of the simulated dynamics of the system after each ballistic cascade is sufficiently long.45 During the ballistic cascade, a variable timestep is used—a constant timestep of 1 fs is used otherwise. The cascade dynamics is allowed to evolve for 15 ps, which is found to be long enough for the convergence of potential energy and stoppage of the PKA. The resulting structure is equilibrated in the NPT ensemble for 5 ps at 300 K under zero pressure after each cascade. This process is then iteratively repeated until both enthalpy and density plateaued.9,45,66,67,68 Herein, the input crystal structures for calcite and dolomite are based on those of Reeder and Mackgraf et al. (1985, 1986).20,71 These unit cells were replicated in all three directions to obtain a supercell having a sizes of (9 × 11 × 3) for calcite and (10 × 10 × 3) for dolomite, corresponding to 8910 and 9000 atoms, respectively. The replication sizes were selected to be at least twice as large as the maximum distance that the displaced atoms traveled upon a ballistic impact, as discussed in Hsiao et al.9,10 Because a large region is affected during each ballistic cascade, large system sizes are required to avoid spurious self-interactions arising from the periodic boundary conditions.
To offer realistic results, MD simulations rely on the use of accurate inter-atomic potentials. In the case of irradiation, the interatomic potential must be able to accurately describe both the pristine and disordered structures of the relevant system using a fixed set of parameters. Furthermore, the potential must be able to account for the high-energy interactions at short-range due to the ballistic collisions and high-velocity interactions of atoms occurring during the damage cascade. Therefore, the potentials of Raiteri et al. was used.72,73 This forcefield relies on a Buckingham formulation, which includes Coulombic interactions, an exponential repulsion term that captures the energy penalty associated with the overlap of the electronic clouds at short distance, and a longer-range van der Waals term that is written as: \(U = A\exp \left( { - \frac{r}{\rho }} \right) - \frac{C}{{r^6}}\), where, U is the interatomic potential energy, r the interatomic distance, and A, C, and ρ are parameters defined for each pair of atoms (see Table 3b). Note that the Buckingham-type potential used describes X–O interactions, wherein X = Ca, Mg, or O. In contrast, the carbonate groups are modeled as rigid molecules via harmonic potentials.72,73 The choice of this potential is motivated by the fact that this forcefield has successfully predicted the structure of both crystalline and amorphous carbonates.72,73
The effect of irradiation on the atomic topology of the carbonate minerals was analyzed within the framework of topological constraint theory (TCT).74,75,76 By reducing complex atomic networks into simple mechanical trusses, TCT captures their network topology while filtering out details that do not affect dissolution behavior.51 The network rigidity was evaluated by calculating the number of constraints per atom (nc), which includes the radial bond-stretching (BS) and angular bond-bending (BB) constraints that sustain the bond lengths and angles of the atom, respectively. Based on Maxwell’s stability criterion,77 this allows atomic networks to be described as either (i) flexible (nc < 3), i.e., showing some floppy internal modes of deformation,78 (ii) stressed-rigid (nc > 3), i.e., featuring some eigenstress due to mutually incompatible constraints,79,80 or (iii) isostatic (nc = 3), being rigid but free of any internal eigenstress.
Data availability
The authors declare that the main data supporting the findings of this study are available within the article. Extra data are available from the corresponding author upon request.
References
Morse, J. W. & Mackenzie, F. T. Geochemistry of Sedimentary Carbonates. (Elsevier, 1990).
Naik, T. R. Sustainability of concrete construction. Pract. Period. Struct. Des. Constr. 13, 98–103 (2008).
Solís-Carcaño, R. & Moreno, E. I. Evaluation of concrete made with crushed limestone aggregate based on ultrasonic pulse velocity. Constr. Build. Mater. 22, 1225–1231 (2008).
Aquino, C., Inoue, M., Miura, H., Mizuta, M. & Okamoto, T. The effects of limestone aggregate on concrete properties. Constr. Build. Mater. 24, 2363–2368 (2010).
Poitevin, P. Limestone aggregate concrete, usefulness and durability. Cem. Concr. Compos. 21, 89–97 (1999).
Field, K. G., Remec, I. & Pape, Y. L. Radiation effects in concrete for nuclear power plants – Part I: quantification of radiation exposure and radiation effects. Nucl. Eng. Des. 282, 126–143 (2015).
Pignatelli, I. et al. Direct experimental evidence for differing reactivity alterations of minerals following irradiation: the case of calcite and quartz. Sci. Rep. 6, 20155 (2016).
Maruyama, I. et al. Development of soundness assessment procedure for concrete members affected by neutron and gamma-ray irradiation. J. Adv. Concr. Technol. 15, 440–523 (2017).
Hsiao, Y.-H. et al. Effects of irradiation on albite’s chemical durability. J. Phys. Chem. A 121, 7835–7845 (2017).
Hsiao, Y.-H. et al. Role of electrochemical surface potential and irradiation on garnet-type almandine’s dissolution kinetics. J. Phys. Chem. C 122, 17268–17277 (2018).
Naus, D. J., Oland, C. B., Ellingwood, B. R., Hookham, C. J. & Graves, H. L. III Summary and conclusions of a program addressing aging of nuclear power plant concrete structures. Nucl. Eng. Des. 194, 73–96 (1999).
Ichikawa, T. & Koizumi, H. Possibility of radiation-induced degradation of concrete by alkali-silica reaction of aggregates. J. Nucl. Sci. Technol. 39, 880–884 (2002).
Ichikawa, T. & Kimura, T. Effect of nuclear radiation on alkali-silica reaction of concrete. J. Nucl. Sci. Technol. 44, 1281–1284 (2007).
Handin, J., Higgs, D. V., Lewis, D. R. & Weyl, P. K. Effects of gamma radiation on the experimental deformation of calcite and certain rocks. GSA Bull. 68, 1203–1224 (1957).
Nagabhushana, H., Prashantha, S. C., Nagabhushana, B. M., Lakshminarasappa, B. N. & Singh, F. Damage creation in swift heavy ion-irradiated calcite single crystals: Raman and Infrared study. Spectrochim. Acta A. Mol. Biomol. Spectrosc. 71, 1070–1073 (2008).
Wencka, M., Lijewski, S. & Hoffmann, S. K. Dynamics of CO2 − radiation defects in natural calcite studied by ESR, electron spin echo and electron spin relaxation. J. Phys. Condens. Matter 20, 255237 (2008).
Chou, L., Garrels, R. M. & Wollast, R. Comparative study of the kinetics and mechanisms of dissolution of carbonate minerals. Chem. Geol. 78, 269–282 (1989).
Pokrovsky, O. S., Golubev, S. V. & Schott, J. Dissolution kinetics of calcite, dolomite and magnesite at 25 °C and 0 to 50 atm pCO2. Chem. Geol. 217, 239–255 (2005).
Tribble, J. S., Arvidson, R. S., Lane, M. & Mackenzie, F. T. Crystal chemistry, and thermodynamic and kinetic properties of calcite, dolomite, apatite, and biogenic silica: applications to petrologic problems. Sediment. Geol. 95, 11–37 (1995).
MmxcRAFr, S. A. & Rrnnrn, R. J. High-temperature structure refinements of calcite and magnesite. Am. Mineral. 70, 590–600 (1985).
Krivokoneva, G., Ikhonina, Y., Solntseva, L. & Urmanova, A. Effects of Mg-Ca substitution on radiation resistance of calcite structures. Radiogr. Miner. Resour. 2, 82–87 (1977).
Shiraki, R., Rock, P. A. & Casey, W. H. Dissolution kinetics of calcite in 0.1 M NaCl solution at room temperature: an atomic force microscopic (AFM) study. Aquat. Geochem. 6, 87–108 (2000).
Dolgaleva, I. V., Gorichev, I. G., Izotov, A. D. & Stepanov, V. M. Modeling of the effect of pH on the calcite dissolution kinetics. Theor. Found. Chem. Eng. 39, 614–621 (2005).
Plummer, L. N., Wigley, T. M. L. & Parkhurst, D. L. The kinetics of calcite dissolution in CO2 -water systems at 5 degrees to 60 degrees C and 0.0 to 1.0 atm CO2. Am. J. Sci. 278, 179–216 (1978).
Busenberg, E. A comparative study of the dissolution and crystal growth kinetics of calcite and aragonite. U Geol. Bull. 1578, 139–168 (1986).
Pierre, A., Lamarche, J. M., Mercier, R., Foissy, A. & Persello, J. Calcium as potential determining ion in aqueous calcite suspensions. J. Dispers. Sci. Technol. 11, 611–635 (1990).
Sjöberg, E. L. & Rickard, D. T. Calcite dissolution kinetics: Surface speciation and the origin of the variable pH dependence. Chem. Geol. 42, 119–136 (1984).
Arvidson, R. S., Ertan, I. E., Amonette, J. E. & Luttge, A. Variation in calcite dissolution rates: a fundamental problem? Geochim. Cosmochim. Acta 67, 1623–1634 (2003).
Busenberg, E. & Plummer, N. The kinetics of dissolution of dolomite in CO2-H2O systems at 1.5 to 65 °C and 0 to 1 atm pCO2. Am. J. Sci. 282, 45–78 (1982).
Pokrovsky, O. S. & Schott, J. Kinetics and mechanism of dolomite dissolution in neutral to alkaline solutions revisited. Am. J. Sci. 301, 597–626 (2001).
Foreman, A. J. E. & Makin, M. J. Dislocation movement through random arrays of obstacles. Philos. Mag. J. Theor. Exp. Appl. Phys. 14, 911–924 (1966).
Raju, K. S. Radiation effects in calcite. Pramana 8, 266–275 (1977).
Meike, A. A micromechanical perspective on the role of dislocations in selective dissolution. Geochim. Cosmochim. Acta 54, 3347–3352 (1990).
Wong, C. F. Neutron radiation damage in some birefringent crystals. Phys. Lett. A 50, 346 (1974).
Ali, S. M. et al. A comparison of Raman, FTIR and ATR-FTIR micro spectroscopy for imaging human skin tissue sections. Anal. Methods 5, 2281–2291 (2013).
Yang, Y., Min, Y., Lococo, J. & Jun, Y.-S. Effects of Al/Si ordering on feldspar dissolution: Part I. Crystallographic control on the stoichiometry of dissolution reaction. Geochim. Cosmochim. Acta 126, 574–594 (2014).
Huang, C. K. & Kerr, P. F. Infrared study of the carbonate minerals. Am. Mineral. 45, 311–324 (1960).
Lane, M. D. & Christensen, P. R. Thermal infrared emission spectroscopy of anhydrous carbonates. J. Geophys. Res. 102, 25581–25592 (1997).
Edwards, H. G. M., Villar, S. E. J., Jehlicka, J. & Munshi, T. FT–Raman spectroscopic study of calcium-rich and magnesium-rich carbonate minerals. Spectrochim. Acta A. Mol. Biomol. Spectrosc. 61, 2273–2280 (2005).
Rutt, H. N. & Nicola, J. H. Raman spectra of carbonates of calcite structure. J. Phys. C. Solid State Phys. 7, 4522 (1974).
Bischoff, W. D., Sharma, S. K. & Mackenzie, F. T. Carbonate ion disorder in synthetic and biogenic magnesian calcites: Raman spectral study. Am. Mineral. 70, 581–589 (1985).
Krishnan, N. M. A., Le Pape, Y., Sant, G. & Bauchy, M. Effect of irradiation on silicate aggregates’ density and stiffness. J. Nucl. Mater. 512, 126–136 (2018).
Krishnan, N. M. A. et al. Density-stiffness scaling in minerals upon disordering: Irradiation vs. vitrification. Acta Mater. 166, 611–617 (2019).
Denisov, A. V., Dubrovskii, V. B. & Krivokoneva, G. K. Radiation changes in minerals of concrete aggregates and their analytical determination. Issues Nucl. Sci. Technol. 18, 31 (1979).
Krishnan, N. M. A. et al. Enthalpy landscape dictates the irradiation-induced disordering of quartz. Phys. Rev. X 7, 031019 (2017).
Kabacińska, Z. et al. Nanoscale effects of radiation (UV, X-ray, and γ) on calcite surfaces: Implications for its mechanical and physico-chemical properties. J. Phys. Chem. C 121, 13357–13369 (2017).
Smedskjaer, M. M., Bauchy, M., Mauro, J. C., Rzoska, S. J. & Bockowski, M. Unique effects of thermal and pressure histories on glass hardness: Structural and topological origin. J. Chem. Phys. 143, 164505 (2015).
Youssef, K. M., Zaddach, A. J., Niu, C., Irving, D. L. & Koch, C. C. A novel low-density, high-hardness, high-entropy alloy with close-packed single-phase nanocrystalline structures. Mater. Res. Lett. 3, 95–99 (2015).
Trachenko, K., Pruneda, J. M., Artacho, E. & Dove, M. T. How the nature of the chemical bond governs resistance to amorphization by radiation damage. Phys. Rev. B 71, 184104 (2005).
Trachenko, K. Understanding resistance to amorphization by radiation damage. J. Phys. Condens. Matter 16, R1491 (2004).
Pignatelli, I., Kumar, A., Bauchy, M. & Sant, G. Topological control on silicates’ dissolution kinetics. Langmuir 32, 4434–4439 (2016).
Mascaraque, N. et al. Dissolution kinetics of hot compressed oxide glasses. J. Phys. Chem. B 121, 9063–9072 (2017).
Mascaraque, N., Bauchy, M. & Smedskjaer, M. M. Correlating the network topology of oxide glasses with their chemical durability. J. Phys. Chem. B 121, 1139–1147 (2017).
Oey, T. et al. The role of the network-modifier’s field-strength in the chemical durability of aluminoborate glasses. J. Non-Cryst. Solids 505, 279–285 (2019).
Denisov, A., Dubrovskii, V. & Solovyov, V. Radiation resistance of mineral and polymer construction materials. ZAO MEI Publ. House (2012).
Douillard, L. & Duraud, J. P. Swift heavy ion amorphization of quartz — a comparative study of the particle amorphization mechanism of quartz. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. 107, 212–217 (1996).
Swanson, M. L., Parsons, J. R. & Hoelke, C. W. Damaged regions in neutron-irradiated and ion-bombarded Ge and Si. Radiat. Eff. 9, 249–256 (1971).
Cuomo, J. J., Rossnagel, S. M. (International B. M. C. & Kaufman, H. R. Handbook of Ion Beam Processing Technology (1989).
Averback, R. S., Benedek, R. & Merkle, K. L. Correlations between ion and neutron irradiations: Defect production and stage I recovery. J. Nucl. Mater. 75, 162–166 (1978).
Vandeginste, V. & John, C. M. Influence of climate and dolomite composition on dedolomitization: Insights from a multi-proxy study in the central Oman Mountains. J. Sediment. Res. 82, 177–195 (2012).
Wang, J. & Becker, U. Structure and carbonate orientation of vaterite (CaCO3). Am. Mineral. 94, 380–386 (2009).
Buhmann, D. & Dreybrodt, W. The kinetics of calcite dissolution and precipitation in geologically relevant situations of Karst areas 1. Open System. Chem. Geol. 48, 189–211 (1985).
Compton, R. G. & Brown, C. A. The inhibition of calcite dissolution/precipitation: Mg2+ cations. J. Colloid Interface Sci. 165, 445–449 (1994).
Ruiz-Agudo, E., Kowacz, M., Putnis, C. V. & Putnis, A. The role of background electrolytes on the kinetics and mechanism of calcite dissolution. Geochim. Cosmochim. Acta 74, 1256–1267 (2010).
Ruiz-Agudo, E., Putnis, C. V., Jiménez-López, C. & Rodriguez-Navarro, C. An atomic force microscopy study of calcite dissolution in saline solutions: The role of magnesium ions. Geochim. Cosmochim. Acta 73, 3201–3217 (2009).
Krishnan, N. M. A., Wang, B., Le Pape, Y., Sant, G. & Bauchy, M. Irradiation- vs. vitrification-induced disordering: The case of α-quartz and glassy silica. J. Chem. Phys. 146, 204502 (2017).
Krishnan, N. M. A., Wang, B., Le Pape, Y., Sant, G. & Bauchy, M. Irradiation-driven amorphous-to-glassy transition in quartz: The crucial role of the medium-range order in crystallization. Phys. Rev. Mater. 1, 053405 (2017).
Krishnan, N. M. A., Wang, B., Sant, G., Phillips, J. C. & Bauchy, M. Revealing the effect of irradiation on cement hydrates: evidence of a topological self-organization. ACS Appl. Mater. Interfaces 9, 32377–32385 (2017).
Onstott, T. C., Miller, M. L., Ewing, R. C., Arnold, G. W. & Walsh, D. S. Recoil refinements: Implications for the 40Ar/39Ar dating technique. Geochim. Cosmochim. Acta 59, 1821–1834 (1995).
Klaumünzer, S. et al. Severe radiation damage by heavy ions in glassy Pd80Si20. Acta Metall. 30, 1493–1502 (1982).
Reeder, R. J. & Markgraf, S. A. High-temperature crystal chemistry of dolomite. Am. Mineral. 71, 795–804 (1986).
Raiteri, P., Demichelis, R. & Gale, J. D. Thermodynamically consistent force field for molecular dynamics simulations of alkaline-earth carbonates and their aqueous speciation. J. Phys. Chem. C 119, 24447–24458 (2015).
Raiteri, P., Gale, J. D., Quigley, D. & Rodger, P. M. Derivation of an accurate force-field for simulating the growth of calcium carbonate from aqueous solution: a new model for the calcite−water interface. J. Phys. Chem. C. 114, 5997–6010 (2010).
Phillips, J. C. Topology of covalent non-crystalline solids I: Short-range order in chalcogenide alloys. J. Non-Cryst. Solids 34, 153–181 (1979).
Bauchy, M. Topological constraints and rigidity of network glasses from molecular dynamics simulations. ArXiv150606483 Cond-Mat (2015).
Bauchy, M. Deciphering the atomic genome of glasses by topological constraint theory and molecular dynamics: A review. Comput. Mater. Sci. 159, 95–102 (2019).
Maxwell, J. C.L. On the calculation of the equilibrium and stiffness of frames. Lond. Edinb. Dublin Philos. Mag. J. Sci. 27, 294–299 (1864).
Thorpe, M. F. Continuous deformations in random networks. J. Non-Cryst. Solids 57, 355–370 (1983).
Wang, F., Mamedov, S., Boolchand, P., Goodman, B. & Chandrasekhar, M. Pressure Raman effects and internal stress in network glasses. Phys. Rev. B 71, 174201 (2005).
Chubynsky, M. V., Brière, M.-A. & Mousseau, N. Self-organization with equilibration: A model for the intermediate phase in rigidity percolation. Phys. Rev. E 74, 016116 (2006).
Hsiao, Y.-H. Studies on irradiation and electric potential effects toward mineral atomic structure and chemical reactivity. Dissertation presented in partial fulfillment of the requirements for the degree of Doctor of Philosophy, Department of Civil Engineering University of California, Los Angeles (2019).
Momma, K. & Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Buckingham, R. A. The classical equation of state of gaseous helium, neon and argon. Proc. R. Soc. Lond. A: Math. Phys. Eng. Sci. 168, 264–283 (1938).
Acknowledgements
This work forms a part of Y.-H. Hsiao’s Ph.D. dissertation submitted to the University of California, Los Angeles (UCLA).81 As such, the authors acknowledge financial support for this research provisioned by the: Department of Energy’s Nuclear Energy University Program (DOE-NEUP: DE-NE0008398), National Science Foundation (CAREER Award: 1253269), and University of California, Los Angeles (UCLA). The contents of this paper reflect the views and opinions of the authors who are responsible for the accuracy of the data presented. This research was carried out in the Laboratory for the Chemistry of Construction Materials (LC2), Molecular Instrumentation Center, and Laboratory for the Physics of AmoRphous and Inorganic Solids (PARISlab) at UCLA. As such, the authors acknowledge the support that has made these laboratories and their operations possible.
Author information
Authors and Affiliations
Contributions
G.N.S. conceived the research. G.N.S., M.B., Y.H., B.W., E.C.L.P., I.P., N.M.A.K. designed the research. Y.H., I.P. and N.M.A.K. carried out the research. G.N.S., M.B., Y.H., B.W., E.C.L.P., I.P. and N.M.A.K. analyzed and interpreted the data. G.N.S., Y.H., B.W., E.C.L.P. and N.M.A.K. wrote the paper. All the authors contributed to the discussion and results, and approve the manuscript in its current form.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hsiao, YH., Wang, B., La Plante, E.C. et al. The effect of irradiation on the atomic structure and chemical durability of calcite and dolomite. npj Mater Degrad 3, 36 (2019). https://doi.org/10.1038/s41529-019-0098-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41529-019-0098-x
This article is cited by
-
Silicon ion radiation as a viable surrogate for emulating neutron radiation damage in silicates
npj Materials Degradation (2024)