Abstract
Nuclear waste glasses dissolve at the forward dissolution rate (rf) in very dilute aqueous solutions, which can isolate the impact of the glass composition from solution feedback and alteration product effects. While it has long been known that pH and temperature (T) strongly impact rf, the impacts of glass composition have remained uncertain. In this work, rf data from 19 nuclear waste glasses were used with the aim of identifying the effect of glass composition on rf. The rf values were modeled as: rf = k010–ηpHexp(−Ea/RT), with k0, η, Ea, and R, respectively, being the intrinsic rate constant, pH coefficient, apparent activation energy, and gas constant. However, no predictive correlation could be established between the individual model parameters (log[k0], η, and Ea) and glass composition for the glasses considered in this study, an outcome that was attributed to the strong positive correlation between the log[k0] and Ea parameters. Therefore, a model was fitted directly to the combined rf from all 19 glasses. This approach showed that 90% of the variation in rf data could be accounted for solely by T and pH effects. Therefore, any composition effects must be relatively small. After normalizing for differences in pH and T, the only notable differences in rf between the glasses were found to correlate with variations in the fraction of glass forming tetrahedra contributed by tetrahedral boron, f([4]B), with an abrupt threshold at a high value of f([4]B) (~0.22), where higher rf are predicted with no discernable composition effects below the threshold.
Similar content being viewed by others
Introduction
A common method to treat radioactive wastes is through vitrification, where the waste is converted to a glass matrix, commonly in the borosilicate family.1,2 In scenarios of long-term waste glass disposal, the most likely mechanism of release of radioactive and chemical hazards from the glass is through reactions with water. For this reason, the water–glass interaction has been an area of extensive research. In general, the long-term resistance of glass to aqueous corrosion, termed glass durability, is not an intrinsic property of the glass, but is rather the response of glass to a range of changing environmental factors.3 Significant among the factors influencing glass durability are temperature, near-field chemical conditions, including pH and concentrations of other solution species, and chemical composition of the glass itself.4 Of these variables, only the chemical composition of the glass can be controlled before the waste glass is disposed. Glass corrosion rates have been found to follow repeatable trends:3,5,6
-
A fast initial rate when glass corrodes in sufficiently dilute conditions to avoid solution feedback—termed forward dissolution rate, rf, and often called Stage I rate.
-
A slow rate when glass corrodes in solution concentrated in glass corrosion products such as H4SiO4—termed residual rate and often called Stage II rate.
-
A potential accelerated rate that is coincident with precipitation of glass components into influential crystalline phases—often called Stage III rate.
Previous studies in the literature have correlated borosilicate waste glass composition to either short-term test responses (e.g., Soxhlet,7,8 Product Consistency Test,9,10,11,12,13,14,15,16,17 Materials Characterization Center Test-1,7,9,13 Vapor Hydration Test,15,17,18,19 or similar) or on long-term rate in static conditions.4,18,20 But, of the characteristic rates listed above, only rf is independent of solution feedback from dissolved glass and near-field materials. This rate is therefore the focus of this work, which is aimed at isolating the intrinsic impact of waste glass composition on dissolution rates.
Because rf is known to be dependent on pH and temperature, the following equation, which is based on the work of Aagard and Helgeson,21 is commonly used to model forward dissolution rate of glass,22,23,24
where rf is the forward dissolution rate (g m−2 d−1), k0 is the intrinsic rate constant (g m−2 d−1), η is the pH power law coefficient, Ea is the apparent activation energy (J mol−1), R is the ideal gas constant (~8.314 J mol−1 K−1), and T is the absolute temperature (K). The sign in front of η is negative for acidic conditions and positive for alkaline conditions.
The most effective method to obtain the parameters in Eq. 1 is to measure the rate of glass dissolution in conditions sufficiently dilute as to preclude solution feedback effects while systematically (and independently) varying solution pH and T. The single-pass flow-through (SPFT) test was developed to achieve these conditions.25 See Supplementary Information Section 1 for brief comparison of methods. In several instances, SPFT data were used to investigate the effect of composition on rf of simple model glasses or natural glasses. In one such study, Pierce et al. measured rf (primarily at 40 °C) of a series of nepheline/malinkoite glasses with systematic substitution of B2O3 for Al2O3.26 These glasses showed no composition impact on rf until a composition threshold (B2O3/Al2O3 >1.5) was exceeded. Surpassing this composition threshold also corresponded with the observation of compositionally distinct microdomains in the glass. Hopf et al. studied the impact of varying the HfO2 concentration in a simple glass system by measuring rf at room temperature and pH 9.27 A significant impact of HfO2 was observed, where higher concentrations of HfO2 in the glass corresponded with a decrease in the glass dissolution rate. Other studies have also shown some compositional dependencies in rf of silicate glasses and minerals.28,29,30 All of these studies are for glass compositions well outside the range expected to be fabricated as a result of waste glass vitrification. Although they provided valuable information, these studies focused on varying the concentration of a single glass component.
Statistical analysis of a large data set covering a wide compositional range and including data at multiple pH and T values is needed to maximize the likelihood of reliably identifying correlations between rf and glass composition. For this reason, the present study focuses on the range of rf data available on borosilicate nuclear waste glasses. Within this range of glass compositions, we attempt to statistically determine the effect of the various glass components and glass structure on the dissolution rate of the glass.
In this study, the SPFT was applied to measure rf of a test glass (EWG-C) in alkaline solutions (pH(T) > 7) with systematic variation in pH and T. The measured rf data were then combined with similar data from 18 representative nuclear waste glasses found in literature. These 19 glasses represent all the waste glasses with rf data measured as functions of both pH and T known to these authors, and therefore represent the most likely data set available to quantify compositional effects. Measurements of rf by other methods for selected glasses are compared in the Supplementary Information section 1. Alkaline solutions were selected because the most data are available for these conditions as they represent the anticipated disposal environments. In addition, the response of log(rf) to changes in pH is linear in the alkaline range and thus avoids the non-linear responses that are observed when rf is measured in the neutral and acidic pH ranges.31 However, it is recommended that similar analyses be performed on the neutral to acidic pH ranges when sufficient data become available.
Results and discussion
Results from this study are divided into several subsections. First, the results of dissolution rate testing of the EWG-C glass are presented, followed by a combined database of glass compositions and rf. Rate model parameters (k0, η, and Ea) are fitted to individual glass rf data. The model coefficients from Eq. 1 are fit to glass composition in the next subsection. Finally, the combined rf data for all 19 glasses are fit simultaneously to pH, T, and composition.
EWG-C forward dissolution rate
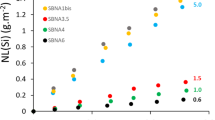
The EWG-C forward dissolution rate was determined at four temperatures (22, 40, 70, and 90 °C) and at six room temperature solution pH values (7 ≤ pH(22 °C) ≤ 12 with 1 pH unit intervals). To determine the experimental conditions where glass dissolves at the forward dissolution rate, the experiments were performed across a solution-flow-rate-to-glass-surface-area (q/S) range to determine conditions where the glass dissolution rate was nearly invariant with respect to changes in q/S. The associated forward dissolution rates are shown in Fig. 1. Rate model parameters were then determined from test results obtained from the range of test conditions (lines in Fig. 1).
Combined forward dissolution rate database
The compositions of glasses analyzed in this study are reported in Table 1. Combined, these data cover a substantial portion of the waste glass composition region including both high-level radioactive wastes and low-activity radioactive wastes from around the world. The range in composition is particularly wide for elements that generally comprise more than 5% of the glass composition. As examples, for Al2O3 (1.24–7.54 mol%), B2O3 (4.60–17.82 mol%), Na2O (6.55–27.35 mol%), and SiO2 (39.59–60.10 mol%). On the other hand, minor elements, which generally comprise less than 5% of the glass composition, have a more inconsistent coverage as compared to the major elements because they either only appear in selected compositions (e.g., SnO2 and TiO2) or the high concentrations of one component precludes the addition of another (e.g., high Na2O precludes the addition of amount of Li2O). The overall composition coverage is presented in Fig. 2, which shows a plot of the mole percents of glass components for the glasses used in this study.
Measured rf values based on normalized boron releases are listed in Table 2. See Supplementary Information Section 2 for a comparison of normalized boron and silicon release rates. The data span ranges of T, pH(T), and log[rf] of 20–91.1 °C, 5.5–12.98, and −4.31–1.08 log[g m−2 d−1], respectively. Eleven points with pH(T) < 7 were removed from the 338 data reported in Table 2.
Modeling of forward dissolution rate parameters for individual glasses
To fit k0, η, and Ea, the model parameters of Eq. 1, the equation was rearranged to a linear relationship as follows:
Linear regression was performed using JMP™ version 13.2.1 (SAS Institute, Cary, NC) on the rates in Table 2 to obtain the log[k0], η, and Ea values listed in Table 3. Outliers were identified in this fitting process with studentized residuals and the Bonferroni correction with a p value of 5%.32 The outliers are identified in Table 2 with square brackets (12 out of 327 data points or 3.7%). An example fit for ISG is shown graphically in Fig. 3. The root mean squared error (RMSE), an estimate of the differences between predicted and measured values, ranges from 0.081 to 0.245.
Composition effects on fit parameters
Each of the three fit parameters was fitted to linear functions of composition:
where ki, hi, and ei are fit parameters for the ith composition parameter; xi is the ith composition parameter; and n is the number of composition terms in the model. The stepwise regression routine in JMP was used to fit these three models. Composition-related parameters considered included:
-
each single-oxide concentration,
-
fraction of tetrahedral Al, B, and Si—f([4]Al), f([4]B), and f([4]Si), respectively,
-
ratio of estimated non-bridging oxygen per tetrahedra using two methods (NBO/T, and NBO/T′),
-
separate and combined alkali [Alk] and alkaline earth [AE] oxide mole fractions,
-
estimated N4, and
-
sum of four valent oxide (minus SiO2) mole fractions ([4 V]).
See Supplementary Information Section 3 for calculations of key composition-related parameters.
A number of different criteria were attempted for selecting the most appropriate model terms. The best results (judged by validation statistics) were obtained using a p value threshold of 0.20 (the p values were based on mean response). The best fit for the three model fit parameter shown in Eq. 3a, b, c as a function of glass composition parameters are shown in Table 4. Validation R2 values (\(R_{\rm{Val}}^2\)) were obtained using k-fold validation with five random splits of 20% of the data. A \(R_{\rm{Val}}^2\) significantly below the model fit R2 suggests a poorly predictive model as is seen in these models with \(R_{\rm{Fit}}^2\) values ranging from 0.443 to 0.889 and \(R_{\rm{Val}}^2\) ranging from 0.135 to 0.515 (0.263 to 0.711 below \(R_{\rm{Fit}}^2\)). The model for Ea clearly out performs the other models from a statistical standpoint. At present, there is no current theoretical basis or rationalization for the selected model terms. The coefficients are often in opposite directions than would be anticipated based on structural theories of glass. This general lack of fit may explain why previous attempts to model composition effects on rf have not been widely reported.
It is theorized that this lack of fit and broad range of estimated log[k0], η, and Ea are due to a strong correlation between Eq. 1 fit parameters, particularly log[k0] and Ea, as recently reported by Neeway et al.33 The fit parameter correlations are given in Table 3. The 80% positive correlation between log[k0] and Ea suggests that these parameters cannot be reliably estimated from these data. ISG is not unique in this respect. The parameter correlation coefficients for all 19 glasses are listed in Table 3, showing log[k0]−Ea correlations >0.782 for all fits. The positive sign on the correlation coefficient suggests that a model with nearly equal representation of the data can be generated with higher log[k0] so long as Ea is also increased, as explained in detail by Neeway et al.33 This strong correlation results in a nearly planar correlation between the three fit parameters, as shown in Fig. 4. The figure highlights the model parameters for all 19 glasses are confined to a nearly planar region.
Another approach to fitting Eq. 1 to data would be to use activation energies obtained with ab initio calculations and fit log[k0] and η to experimental data. This approach would effectively eliminate the fit of the parameter Ea and allow for an independent assessment of log[k0] without the correlation observed in the fits obtained here. However, results from systematic studies of alkali-boro-aluminosilicate glass reactions with water sufficient to perform this analysis are not yet available (see review by Du and Rimsza34).
Combined data fitting
Potential composition effects can be obtained by fitting the combined rf data set for all 19 glasses with composition terms associated with each of the three parameters. This approach can also be used to test if there are pH effects on Ea or T effects on η. The combined data set (19 glasses, 315 data points listed in Table 2 after removing 11 points tested at pH(T) < 7 and 12 points identified as outliers in individual glass fits) was fit to Eq. 2 with JMP. In total, six different fits were made to determine the effect of different glass compositions and structures. The reasoning and significance of each fit is described in subsequent paragraphs. Results of the fits, including mean parameter values and R2 values, are presented in Table 5.
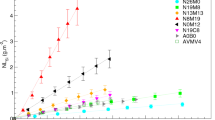
The first step was to fit log[k0], η, and Ea to all rf data without consideration for composition effects (fit 1). The results showed a reasonably good representation of the data with a few glasses being clear outliers—MT25 (green), MT30 (green), and IDF18-A161 (red) in Fig. 5. Overall, the fit is reasonably good, accounting for ~90% of the variation in data, suggesting that any composition effects are relatively small (representing <10% of the variation in measured rf). The RMSE is 0.323 (150–350% of the RMSEs from individual fits).
To determine the maximum extent for which composition could account for variation in rf data, and if that effect was associated with log[k0], η, and/or Ea, a model was fit with glass ID parameters that take on the value 1 for data for that particular glass and zero for all other data (e.g., all data for LD6-5412 would contain a 1 in the LD6-5412 parameter and zeros in the parameters for IDF18-A161, MT25, and MT30; etc.) (fit 2). This fit would adjust all three parameters for each of the 19 glasses if statistically significant differences were found (giving an R2 = 0.947 and RMSE = 0.231, roughly the lowest error that can be achieved with this data set fit to the model in Eq. 2). The results of this fit suggested that (1) composition effects are most significant for log[k0] and (2) the only significant effects (t value <0.0625) are seen for glass IDF18-A161, MT25, and MT30, all of which show significantly higher rates. Three possibilities can be considered to explain this result: (1) the rf data for these three glasses are experimental outliers, (2) these three glasses are in a different composition region that generally has higher rf, or (3) there is a smooth composition effect that result in these glasses having higher rates.
If the three outlying glasses are removed, no glass ID impacts are statistically significant and the resulting fit is quite good (fit 3), with R2 values comparable to the glass ID-related model with all glasses and in the range of individual glass fit values (see Table 3). To determine if the three outlying glasses are in a distinct composition region, we first consider their location in compositional space. The two MT glasses are the lowest in Al2O3 and highest in B2O3 of the available compositional space. IDF18-A161 is the lowest in SiO2 (39.6 mol%) and relatively high in B2O3. Current theory states that the rf should be controlled by the breaking of network former bonds.35,36 The glass composition was thus considered in terms of the fraction of the network tetrahedra that are from aluminum, boron, and silicon (f([4]Al), f([4]B), and f([4]Si), respectively). Figure 6 shows the glass compositions plotted to show location in f([4]Al), f([4]B), and f([4]Si) space. There is a clear distinction in the composition region for the three outlying glasses, in the high f([4]B) region (22–30% depending on f([4]Si)).
Ternary plot of glass composition in mole fraction tetrahedra. Red A = IDF18-A161, red M's = MT25 and MT30, and P’s = glasses from Pierce et al.38 (red P* being NeB4)
To determine if there is a smooth composition effect, a fourth model was fit considering a number of composition-related parameters, including (see Supplementary Information Section 3 for details):
-
each single-oxide concentration,
-
f([4]Al), f([4]B), and f([4]Si),
-
ratio of estimated non-bridging oxygen per tetrahedra using two methods (NBO/T and NBO/T′),
-
separate and combined alkali [Alk] and alkaline earth [AE] oxide mole fractions,
-
estimated N4, and
-
sum of four valent oxide (minus SiO2) mole fractions ([4V]).
Guided by stepwise regression and knowledge of structural effects, the compositional parameters with the highest impacts were selected. Of all the compositional effects, f([4]B) was found to be, by itself, the most significant compositional parameter. Fit 4, which accounts for the effect of f([4]B) on glass dissolution, is summarized in Table 5 and Fig. 7. This fit is close to as good as fits 2 and 3 with R2 values above 0.936 and RMSE = 0.253. The impact of f([4]B) is non-linear: a small effect at low concentrations and highly positive effect above roughly 0.23 (Fig. 7b). Insufficient data are available in this data set to determine if there is a smooth effect of f([4]B) on log[k0] or if the impact is abrupt. However, as seen in Fig. 7, the IDF18-A161 glass with lower f([4]B) than the MT glasses is under-predicted by the second-order model.
An additional fit (fit 5) of only the high f([4]B) glass data (IDF18-A161, MT25, and MT30) results in a reasonably good fit with Ea and η values similar to that of fit 3 and a constant log[k0] and no statistically significant composition effects. These results support the suggestion of an abrupt change in rf when crossing the f([4]B) threshold seen by colored points in Fig. 6. Fit 6 quantifies this approach where glasses on either side of the threshold are fitted to different log[k0] values with common Ea and η values. This latter fit has roughly the same fit statistics as that for the fit with glass IDs individually considered (fit 2) and distinctly better than the polynomial fit 4, suggesting the threshold separation of glasses accounts for nearly the full composition effect. See Supplementary Information Section 4 for additional approaches to fitting rf data to composition.
Experimental evidence from the literature supports the hypothesis that a compositional effect exists past a certain f([4]B) threshold value. Pierce et al.26 measured the rf of a series of nepheline/malinkoite glasses with systematic substitution of B2O3 for Al2O3 (NeB × glasses). The results showed that rf was invariant for the three lowest B2O3 (0–15 mol%; NeB0–NeB3) glasses (represented by black “P”s in Fig. 6). However, there was a significantly higher rate for the highest B2O3 glass (NeB4 at 20 mol%), shown as a red “P*” in Fig. 6, consistent with the results reported here. We note that Pierce et al.26 observed microdomains associated with NeB4. The microdomains were rich in Na and B and were distinct from microdomains rich in Si and Al. The authors posited that the relatively soluble Na-B domains were responsible for the increase in dissolution rates of this glass. Similar microdomains of unknown composition were reported by Neeway et al. in the X-ray amorphous regions of glass IDF18-A161 used for testing.37 In addition, roughly 8.7 wt% of sodalite crystals were identified in IDF18-A161, primarily at the surfaces of the sample. SPFT testing of IDF18-A161 was performed on regions of the sample that excluded the highly crystalline edges. However, this amount of sodium aluminosilicate crystal would significantly change the residual glass composition toward higher f([4]B), consistent with the MT and NeB4 glasses. No such microdomains were reported for MT25 and MT30, but the possibility that microdomains are present in these glasses and that these microdomains are contributing to the divergent dissolution behavior cannot be excluded.
Findings
The forward rate of dissolution (rf) is a measure of the glass corrosion rate in highly dilute systems. This rate is theorized to be the most directly sensitive to the composition and structure of the glass because solution feedback effects are minimized. The present study was performed to evaluate rf of waste glasses as functions of T, pH, and glass composition. The model accounts for the pH and T impacts on rf in alkaline solutions: rf = k010η∙pHexp(−Ea/RT). In this study, this model is shown to account for greater than 94% of the variation in measured log[rf] data for each of the 19 waste glasses tested with systematic variation in T and pH. The fit parameters of this equation—log[k0], η, and Ea—showed relatively broad variation between glasses, but could not be successfully correlated to glass composition as demonstrated by low R2 values. We hypothesize that the lack of fit with composition is caused by a high correlation between the parameters with >78% correlation between log[k0] and Ea parameters. Such strong correlations suggest that neither parameter can be uniquely defined given the scale of uncertainties in measured rf data. A method to isolate log[k0] and Ea while fitting rf data would be to use ab initio calculations of Ea, however, sufficient results are not yet available for waste glasses.
To better understand composition effects on rf, models were fit to the combined data from literature and the glass tested as part of this study, including the ISG. Roughly, 90% of variation in measured rf could be described by the model (Eq. 2) without any account of composition. The relatively small compositional effects were found to be primarily related to the log[k0] parameter with insignificant effects on Ea and η. The maximum potential impact of composition was determined by fitting glass ID as a composition parameter and was found to account for roughly 95% of the variation in measured rf data (R2 = 0.947 and RMSE = 0.231). When rf was fitted to glass composition, the fraction of glass forming tetrahedra from [4]B (f([4]B)) was found to best describe the data. The impact of f([4]B) was found to be non-linear with a step function best describing the data. This step function change was supported by results found in the literature.
Accounting for the step function change in dissolution rates, the ultimate model obtained is:
with equal fit statistics as the model fitted with glass IDs (R2 = 0.947, RMSE = 0.231), suggesting that the model accounts for composition effects within the uncertainty limits of these data and the functional form of pH and T dependence in Eq. 2. The glasses above the threshold include IDF18-A161, MT25, and MT30. Additional data would be necessary to refine the threshold that is now estimated to be at an f([4]B) value near 0.22. This threshold is consistent with the abrupt rate change seen by Pierce et al. in B2O3-doped nepheline/malinkoite glasses.38 The cause for this threshold could not be determined with data presented here but may be related to a percolation threshold, as discussed by Kerisit,39 or may be caused by the formation of compositionally distinct microdomains identified in IDF18-A161 and NeB4 glasses. Systematic studies to determine micro-structure and rf of glasses with variation in f([4]B) and f([4]Al) are needed to resolve the cause and exact location of the threshold. Additional modeling attempts should also aim at eliminating the correlation between log[k0] and Ea with estimates of Ea from first-principles calculations, once sufficient data are available.
Implications of broad glass composition regions with little variation in rf may suggest that the most impactful effect of waste glass composition on dissolution rate is linked to solution feedback effects. This assertion requires additional study to verify.
METHODS
The EWG-C glass was made by mixing measured amounts of dried reagent-grade carbonates or oxides. The mixture was melted at 1150 °C in a Pt(10%)Rh crucible for 1 h, after which the molten glass was poured onto a clean stainless steel plate. The quenched glass was then crushed in a tungsten carbide mill and remelted at 1150 °C for 1 h and again poured onto a clean stainless steel plate. The resulting glass was then subjected to the canister centerline cooling (CCC) heat schedule modeled for Hanford ILAW glasses expected to be made at WTP.40 The CCC schedule consisted of holding the molten glass at 1114 °C for ~20 min, cooling to 1000 °C in 16 min, cooling to 900 °C within 57 min, and cooling to 825 °C within 122 min. The glass was then allowed to cool to 600 °C in the furnace, at which point the glass was removed from the furnace and allowed to cool to room temperature.
The SPFT method25 is used to determine the kinetic rate law parameters, log[k0], Ea, and η presented in Eq. 1 for all the glasses studied here. The test allows for the measurement of reaction rates at fixed pH and test temperature. The system design enables a continuous flow of fresh solution into a reactor containing the material of interest. Effluent samples are collected periodically at room temperature, and analyzed for B, Na, Si, and Al using inductively coupled plasma-optical emission spectroscopy (ICP-OES). The configuration precludes recirculation of the effluent, and therefore makes a single pass through the reaction cell (an illustration of test setup is given in ref.24). The dissolution rate of the glass in the fixed test conditions is determined from three consecutive effluent sample concentrations, where the relative difference between the three samples differs by less than 15%, using the following equation:
where Ci,s is the steady-state concentration of element i (g m−3), \(\overline C _{i,b}\) is the average background concentration of element i (g m−3), q is the flow rate (m3 d−1), fi is the mass fraction of element i in the pristine glass (unitless), and S is the glass surface area available for reaction (m2). A series of experiments was first conducted at 40 and 90 °C and pH(22 °C) 9. The q/S for the tests at 40 °C was varied between 1.0 × 10−9 and 2.3 × 10−7 m s−1 (Fig. 8a) while the q/S for the tests at 90 °C was varied between 1.1 × 10−9 and 4.7 × 10−7 m s−1 (Fig. 8b). The experiments show that the glass dissolved slowest at low q/S values and the rate increased as q/S increased until a plateau was reached, where the dissolution rate was no longer dependent on q/S within experimental uncertainty (>2 × 10−7 m s−1 at 40 °C and >4 × 10−7 m s−1 at 90 °C). The information gathered from this experiment is then used to guide the selection of forward dissolution rate conditions for the remaining pH and temperature combinations (points in Fig. 1). In general, q/S values are increased with increases in experimental temperature and pH.24 Further test specifics are provided elsewhere.24,33
Data availability
The data that support the findings of this study are primarily reported in the paper or Supplementary Information, any data not reported is available from the corresponding author on reasonable request.
References
Vienna, J. D. Nuclear waste vitrification in the United States: recent developments and future options. Int. J. Appl. Glass Sci. 1, 309–321 (2010).
Donald, I. W., Metcalfe, B. L. & Taylor, R. N. J. Review: the immobilization of high level radioactive wastes using ceramics and glasses. J. Mater. Sci. 32, 5851–5887 (1997).
Vienna, J. D., Ryan, J. V., Gin, S. & Inagaki, Y. Current understanding and remaining challenges in modeling long-term degradation of borosilicate nuclear waste glasses. Int. J. Appl. Glass Sci. 4, 283–294 (2013).
Gin, S., Beaudoux, X., Angéli, F., Jégou, C. & Godon, N. Effect of composition on the short-term and long-term dissolution rates of ten borosilicate glasses of increasing complexity from 3 to 30 oxides. J. Noncryst. Solids 358, 2559–2570 (2012).
Gin, S. et al. An international initiative on long-term behavior of high-level nuclear waste glass. Mater. Today 16, 243–248 (2013).
Frankel, G. S. et al. Corrosion of glasses, ceramics, and metals; a comparative review. npj Mater. Degred. 2, 15 (2018).
Chick, L. A. et al. The Effects of Composition on Properties in an 11-Component Nuclear Waste Glass System. Report No. PNL-3188 (Pacific Northwest Laboratory, Richland, WA, 1981).
Frugier, P., Martin, C., Ribet, I., Advocat, T. & Gin, S. The effect of composition on the leaching of three nuclear waste glasses: R7T7, AVM and VRZ. J. Nucl. Mater. 346, 194–207 (2005).
Hrma, P. et al. in Ceramic Transactions (eds Jain, V. & Palmer, R.) Vol. 61, 497–504 (American Ceramic Society, Westerville, OH, 1995).
Jantzen, C. M., Pickett, J. B., Brown, K. G., Edwards, T. B. & Beam, D. C. Process/Product Models for the Defense Waste Processing Facility (DWPF): Part I. Predicting Glass Durability from Composition Using a THermodynamic Hydration Energy Reaction MOdel (THERMO). Report No. WSRC-TR-93-0672 (Westinghouse Savannah River Company, Aiken, SC, 1995).
Vienna, J. D., Hrma, P., Schweiger, M. J. & Langowski, M. H. in Ceramic Transactions Vol. 72, (eds Jain, V. & Peeler, D. K.) 307–316 (American Ceramic Society, Westerville, OH, 1996).
Pegg, I. L. et al. Scientific Basis for Nuclear Waste Management XII Vol. 127, 215–221 (Materials Research Society, Berlin, Germany, 1989).
Hrma, P. et al. Property/Composition Relationships for Hanford High-Level Waste Glasses Melting at 1150°C. Report No. PNL-10359 (Pacific Northwest Laboratory, Richland, WA, 1994).
Feng, X. & Pegg, I. L. A glass dissolution model for the effects of S/V on leachate pH. J. Noncryst. Solids 175, 281–293 (1994).
Piepel, G. F. et al. ILAW PCT, VHT, Viscosity, and Electrical Conductivity Model Development: VSL-07R1230-1. Report No. ORP-56502 (Vitreous State Laboratory, The Catholic University of America, Washington, DC, 2007).
Piepel, G. F. et al. IHLW PCT, Spinel T1%, Electrical Conductivity, and Viscosity Model Development: VSL-07R1240-4. Report No. ORP-56320 (Vitreous State Laboratory, The Catholic University of America, Washington, DC, 2008).
Vienna, J. D. et al. Glass Property Models and Constraints for Estimating the Glass to be Produced at Hanford by Implementing Current Advanced Glass Formulation Efforts. Report No. PNNL-22631, Rev. 1, ORP-58289 (Pacific Northwest National Laboratory, Richland, WA, 2013).
Vienna, J. D., Kim, D. S., Skorski, D. C. & Matyas, J. Hanford Immobilized LAW Product Acceptance Testing: Tanks Focus Area Results. Report No. PNNL-13744 (Pacific Northwest National Laboratory, Richland, WA, 2001).
Muller, I. S., Joseph, I., Perez-Cardenas, F. C. & Pegg, I. L. LAW Glass Testing and VHT Model Assessment. Report No. VSL-08R1410-1 (Vitreous State Laboratory at the Catholic University of America, Washington, DC, 2008).
Ribet, S., Muller, I. S., Pegg, I. L., Gin, S. & Frugier, P. Scientific Basis for Nuclear Waste Management XXVIII Vol. 824, 309–314 (Materials Research Society, San Francisco, CA, 2004).
Aagaard, P. & Helgeson, H. C. Thermodynamic and kinetic constraints on reaction rates among minerals and aqueous solutions I. Theoretical considerations. Am. J. Sci. 282, 237–285 (1982).
Grambow, B. A general rate equation for nuclear waste glass corrosion. Mater. Res. Soc. Symp. Proc. 44,15–27 (1985).
McGrail, B. P., Ebert, W. L., Bakel, A. J. & Peeler, D. K. Measurement of kinetic rate law parameters on a Na-Ca-Al borosilicate glass for low-activity waste. J. Nucl. Mater. 249, 175–189 (1997).
Pierce, E. M., Rodriguez, E. A., Calligan, L. J., Shaw, W. J. & McGrail, B. P. An experimental study of the dissolution rates of simulated aluminoborosilicate waste glasses as a function of pH and temperature under dilute conditions. Appl. Geochem. 23, 2559–2573 (2008).
ASTM. Standard Practice for Measurement of the Glass Dissolution Rate Using the Single-Pass Flow-Through Test Method. ASTM C1662-10 (ASTM International, West Conshohocken, PA, 2010).
Pierce, E. M., Reed, L. R., Shaw, W. J. & Icenhower, J. P. Effect of Al/B ratio on the dissolution of nepheline glass, Na3(Al, B)1-4Si4O16. Geochim. Cosmochim. Acta 69, A781–A781 (2005).
Hopf, J. et al. Glass–water interaction: effect of high-valence cations on glass structure and chemical durability. Geochim. Cosmochim. Acta 181, 54–71 (2016).
Hamilton, J. P., Brantley, S. L., Pantano, C. G., Criscenti, L. J. & Kubicki, J. D. Dissolution of nepheline, jadeite and albite glasses: toward better models for aluminosilicate dissolution. Geochim. Cosmochim. Acta 65, 3683–3702 (2001).
McGrail, B. P. et al. The structure of Na2O-Al2O3 -SiO2 glass: impact on sodium ion exchange in H2O and D2O. J. Noncryst. Solids 296, 10–26 (2001).
Blum, A. E. & Stillings, L. L. in Chemical Weathering Rates of Silicate Minerals Reviews In Mineralogy (eds. White, A. F. & Brantley, S. L.) 291–351 (Mineralogical Society of America, Chantilly, VA, 1995).
Strachan, D. M. Glass dissolution as a function of pH and its implications for understanding mechanisms and future experiments. Geochim. Cosmochim. Acta 219, 111–123 (2017).
Bonferroni, C. E. Teoria statistica delle classi e calcolo delle probabilità. Pubblicazioni del R Istituto Superiore di Scienze Economiche e Commerciali di Firenze (1936).
Neeway, J. J., Rieke, P. C., Parruzot, B. P., Ryan, J. V. & Asmussen, R. M. The dissolution behavior of borosilicate glasses in far-from equilibrium conditions. Geochim. Cosmochim. Acta 226, 132–148 (2018).
Du, J. & Rimsza, J. M. Atomistic computer simulations of water interactions and dissolution of inorganic glasses. Nat. Mater. Degrad. 2017, 1–16 (2017).
Grambow, B. Scientific Basis for Nuclear Waste Management VIII Vol. 44, 16–27 (Materials Research Society, Pittsburgh, Pennsylvania, 1985).
Grambow, B. Nuclear Waste Glass Dissolution: Mechanism, Model, and Application. Report No. JSS 87-02 (Hahn-Meitner-Institut: Berlin, Germany, 1987).
Neeway, J. J. et al. FY2016 ILAW Glass Corrosion Testing with the Single-Pass Flow-Through Method. Report No. PNNL-26169 (Pacific Northwest National Laboratory, Richland, WA, 2017).
Pierce, E. M. et al. Experimental determination of the effect of the ratio of B/Al on glass dissolution along the nepheline (NaAlSiO4)-malinkoite (NaBSiO4) join. Geochim. Cosmochim. Acta 74, 2634–2654 (2010).
Kerisit, S. N. & Pierce, E. M. Monte Carlo simulations of the dissolution of borosilicate and aluminoborosilicate glasses in dilute aqueous solutions. Geochim. Cosmochim. Acta 75(18), 5296–5309 (2011).
Petkus, L. L. Low Activity Container Centerline Cooling Data. Report No. CCN: 074181 (River Protection Project, Hanford Tank Waste Treatment and Immobilization Plant, Richland, WA, 2003).
Crum, J. V. et al. Baseline Glass Development for Combined Fission Products Waste Streams: Advanced Fuel Cycle Initiative. Report No. AFCI-WAST-WAST-MI-DV-2009-000075 (Pacific Northwest National Laboratory: Richland, WA, 2009).
Papathanassiu, A. et al. ILAW Glass Testing for Disposal at IDF: Phase 1 Testing. Report No. VSL-11R2270-1 (Vitreous State Laboratory, The Catholic University of America, Washington, DC, 2011).
Muller, I. S., Matlack, K. S. & Pegg, I. L. Enhanced LAW Glass Correlation - Phase 1. Report No. VSL-16R4000-1 (Vitreous State Laboratory, The Catholic University of America, Washington, DC, 2016).
Muller, I. S. & Pegg, I. L. FY 2015 ILAW Glass Testing for Disposal at IDF. Report No. VSL-15R3790-1 (Vitreous State Laboratory, The Catholic University of America, Washington, DC, 2015).
Pierce, E. M. et al. Waste Form Release Data Package for the 2005 Integrated Disposal Facility Performance Assessment. Report No. PNNL-14805 (Pacific Northwest National Laboratory, Richland, WA, 2004).
McGrail, B. P. et al. Waste Form Release Data Package for the 2001 Immobilized Low-Activity Waste Performance Assessment. Report No. PNNL-13043, Rev. 2 (Pacific Northwest National Laboratory, Richland, WA, 2001).
Feng, X. D. et al. Glass Optimization for Vitrification of Hanford Site Low-Level Tank Waste. Report No. PNNL-10918 (Pacific Northwest Laboratory, Richland, WA, 1996).
Cassingham, N. et al. The initial dissolution rates of simulated UK Magnox-ThORP blend nuclear waste glass as a function of pH, temperature and waste loading. Mineral. Mag. 79, 1529–1542 (2015).
Muller, I. S., Matlack, K. S. & Pegg, I. L. Enhanced LAW Glass Correlation - Phase 2. Report No. VSL-17R4140-1 (Vitreous State Laboratory, The Catholic University of America, Washington, DC, 2017).
Frugier, P. et al. SON68 nuclear glass dissolution kinetics: current state of knowledge and basis of the new GRAAL model. J. Nucl. Mater. 380, 8–21 (2008).
Jantzen, C. M. Glass Compositions and Frit Formulations Developed for DWPF. Report No. DPST-88-952 (Savannah River Laboratory, Aiken, SC, 1988).
Viragh, C., Abramowitz, H., Muller, I. S., Papathanassiu, A. E. & Pegg, I. L. FY2017 ILAW Glass SPFT Testing for Disposal at IDF: Glass IDF21-EC14. Report No. VSL-17R4320-1 (Vitreous State Laboratory, The Catholic University of America, Washington, DC, 2017).
Papathanassiu, A., Viragh, C., Muller, I. S., & Pegg, I. L. FY2016 ILAW Glass SPFT Testing for Disposal at IDF. Report No. VSL-17R3860-1 (Vitreous State Laboratory, The Catholic University of America, Washington, DC, 2017).
Neeway, J. J. et al. FY2017 ILAW Glass Corrosion Testing with the Single-Pass Flow-Through Method. Report No. PNNL-27098 (Pacific Northwest National Laboratory, Richland, WA, 2018).
Acknowledgements
This work was supported by the U.S. Department of Energy. The testing of EWG-C glass was supported by the Office of Environmental Management. The data compilation, analyses, and modeling and paper preparation were supported by the Office of Science, Basic Energy Sciences, as part of the Center for Performance and Design of Nuclear Waste Forms and Containers, an Energy Frontier Research Center (Award #DE-SC0016584). The Pacific Northwest National Laboratory is operated by Battelle for the DOE under contract DE-AC05-76RL01830. Conversations and advice from Jincheng Du (UNT), Peter Rieke (PNNL), Scott Cooley (PNNL), and Stephane Gin (CEA) helped to steer this research and are greatly appreciated. Matt Asmussen, Amanda Lawter, and Ian Leavy (PNNL) assisted in testing of the EWG-C glass and analyses of the associated solutions. Denis Strachan (PNNL) made helpful suggestions to the draft paper. Brian Riley (PNNL) helped to generate and format figures. The authors are grateful to very helpful review comments from Eric Pierce (ORNL), Maxime Fournier (CEA), and Hiro Inagaki (Kyushu University).
Author information
Authors and Affiliations
Contributions
All of the listed authors contributed to the writing of this paper. J.D.V. coordinated the effort, performed the modeling, and wrote the modeling sections. J.J.N. coordinated the EWG-C testing, compiled the test data from literature, and wrote the experimental methods and testing results sections. All authors contributed to the writing of the discussion.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vienna, J.D., Neeway, J.J., Ryan, J.V. et al. Impacts of glass composition, pH, and temperature on glass forward dissolution rate. npj Mater Degrad 2, 22 (2018). https://doi.org/10.1038/s41529-018-0042-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41529-018-0042-5
This article is cited by
-
Unveiling the effect of composition on nuclear waste immobilization glasses’ durability by nonparametric machine learning
npj Materials Degradation (2024)
-
Structure--property relationship and chemical durability of magnesium-containing borosilicate glasses with insight from topological constraints
npj Materials Degradation (2022)
-
Microbial interactions with silicate glasses
npj Materials Degradation (2021)
-
Forty years of durability assessment of nuclear waste glass by standard methods
npj Materials Degradation (2021)
-
Physical and optical properties of the International Simple Glass
npj Materials Degradation (2019)